Abstract
We introduce a model of proportional growth to explain the distribution Pg(g) of business-firm growth rates. The model predicts that Pg(g) is exponential in the central part and depicts an asymptotic power-law behavior in the tails with an exponent ζ = 3. Because of data limitations, previous studies in this field have been focusing exclusively on the Laplace shape of the body of the distribution. In this article, we test the model at different levels of aggregation in the economy, from products to firms to countries, and we find that the predictions of the model agree with empirical growth distributions and size-variance relationships.
Keywords: proportional growth, preferential attachment, Laplace distribution
Gibrat (1, 2), building on the work of the astronomers Kapteyn and Uven (3), assumed the expected value of the growth rate of a business firm's size to be proportional to the current size of the firm, which is called the law of proportionate effect (4, 5). Several models of proportional growth have been subsequently introduced in economics to explain the growth of business firms (6–8). Simon and co-workers (9–12) extended Gibrat's model by introducing an entry process according to which the number of firms rise over time. In the framework of Simon and co-workers, the market consists of a sequence of many independent “opportunities” that arise over time, each of size unity. Models in this tradition have been challenged by many researchers (13–17) who found that the firm-growth distribution is not Gaussian but displays a tent shape.
Here we introduce a general framework that provides a unifying explanation for the growth of business firms based on the number and size distribution of their elementary constituent components (18–25). Specifically, we present a model of proportional growth in both the number of units and their size, and we draw some general implications on the mechanisms that sustain business-firm growth (7, 11, 21, 26–28). According to the model, the probability density function (PDF) of growth rates is Laplace in the center (13) with power-law tails (29, 30) decaying as Pg(g) ∼ g–ζ, where ζ = 3.
Also, because of data limitations, previous studies in this field focus on the Laplace shape of the body of the distribution, which, however, is an unconditional object (31). Using a database on the size and growth of firms and products, we characterize the shape of the whole growth-rate distribution.
We test our model by analyzing different levels of aggregation of economic systems, from the “micro” level of products to the “macro” level of industrial sectors and national economies. We find that the model accurately predicts the shape of the PDF of growth rate at all levels of aggregation studied.
The Theoretical Framework
We model business firms as classes consisting of a random number of units. According to this view, a firm is represented as the aggregation of its constituent units such as divisions (22), businesses (20), or products (21). Accordingly, on a different level of coarse graining, a class can represent a national economy composed of economic units such as firms. In this article, we study the logarithm of the 1-year growth rate of classes g ≡ log[S(t + 1)/S(t)], where S(t) and S(t + 1) are the sizes of classes in the year t and t + 1 measured in monetary values [gross domestic product (GDP) for countries, sales for firms and products]. Our model is illustrated in Fig. 1. Two key sets of assumptions in the model are that the number of units in a class grows in proportion to the existing number of units (Assumptions 1–4) and the size of each unit fluctuates in proportion to its size (Assumptions 5 and 6).
Fig. 1.
Schematic representation of the model of proportional growth. At time t = 0, there are N(0) = 2 classes (□) and n(0) = 5 units (○) (Assumption 1). The area of each circle is proportional to the size ξ of the unit, and the size of each class is the sum of the areas of its constituent units (see Assumption 5). At the next time step, t = 1, a new unit is created (Assumption 2). With probability b the new unit is assigned to a new class (class 3 in this example) (Assumption 3). With probability 1 – b the new unit is assigned to an existing class with probability proportional to the number of units in the class (Assumption 4). In this example, a new unit is assigned to class 1 with probability 3/5 or to class 2 with probability 2/5. Finally, at each time step, every unit i grows or shrinks by a random factor ηi (Assumption 6).
Assumption 1. Each class α consists of Kα(t) number of units. At time t = 0 (time step measured by year, generally), there are N(0) classes consisting of n(0) total number of units. The initial average number of units in a class is thus n(0)/N(0).
Assumption 2. At each time step, a new unit is created. Thus, the number of units at time t is n(t) = n(0) + t.
Assumption 3. With birth probability b, this new unit is assigned to a new class so that the average number of classes at time t is N(t) = N(0) + bt.
Assumption 4. With probability 1 – b, a new unit is assigned to an existing class α with probability Pα = (1 – b) Kα(t)/n(t), so Kα(t + 1) = Kα(t) + 1.
For simplicity, we do not consider the decrease of the number of units in a class. In reality, elementary units enter and exit. Because we are considering the case of a growing economy, it is legitimate to assume that the entry rate is higher than the exit rate. On the average, the net entry rate of units can be simplified as a positive constant. In the model, the net entry rate of units is fixed at 1. Thus, at large t, it gives results equivalent to the ones that would have been obtained when considering a value for the exit rate of units.
Our goal is to find P(K), the probability distribution of the number of units in the classes at large t. This model in two limiting cases, (i) b = 0, Kα = 1 (α = 1, 2,... N(0)) and (ii) b ≠ 0, N(0) = 1, n(0) = 1, has exact analytical solutions P(K) = N(0)/t{t/[t + N(0)]}K [1 + O(1/t)] (32, 33) and limt→∞ P(K) = (1 + b′)Γ(K)Γ(2 + b′)/Γ (K + 2 + b′), where b′ = b/(1 – b) (34), respectively.
In the general case, the exact analytical solution is not known, and we obtain a numerical solution by computer simulations and compare it with the approximate mean-field solution (see, e.g., chapter 6 of ref. 35 and Appendix A).
Our results are consistent with the exactly solvable limiting cases as well as with the empirical data on the number of products in the pharmaceutical firms and can be summarized as follows. In the limit of large t, the distribution of K in the old classes that existed at t = 0 converges to an exponential distribution (36),
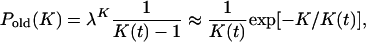 |
[1] |
where λ = 1 – 1/K(t) and K(t) is the average number of units in the old classes at time t, K(t) = {[n(0) + t]/n(0)}1–b·n(0)b/N(0). The distribution of units in the new classes created at t > 0 converges to a power law with an exponential cutoff,
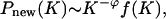 |
[2] |
where φ = 2 + b/(1 – b) and f(K) decays for K → ∞ faster than Pold(K). The distribution of units in all classes is given by
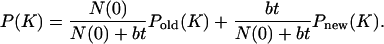 |
[3] |
The mean-field approximation for Pnew(K) is given by
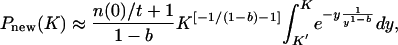 |
[4] |
where K′ = K{n(0)/[n(0) + t]}1–b.
Assumption 5. At time t, each class α has Kα(t) units of size ξi(t), i = 1,2,... Kα(t), where Kα and ξi > 0 are independent random variables taken from the distributions P(Kα) and Pξ(ξi), respectively. P(Kα) is defined by Eq. 3 and Pξ(ξi) is a given distribution with finite mean μξ and standard deviation σξ . We also assume that lnξi has finite mean mξ = 〈lnξi 〉 and variance 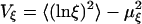 . The size of a class is defined as
. The size of a class is defined as  .
.
Assumption 6. At time t + 1, the size of each unit is decreased or increased by a random factor ηi(t) > 0 so that
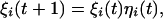 |
[5] |
where ηi(t) > 0, the growth rate of unit i, is an independent random variable taken from a distribution Pη(ηi), which has a finite mean μη and standard deviation ση . We also assume that lnηi has finite mean mη ≡ 〈ln ηi 〉, and variance 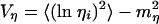 .
.
The growth rate of each class is defined as
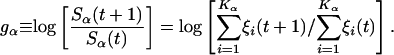 |
[6] |
Here we neglect the influx of the new units, so Kα = Kα(t + 1) = Kα(t). The resulting distribution of the growth rates of all classes is determined by
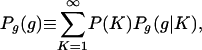 |
[7] |
where P(K) is the distribution of the number of units in the classes, computed in the previous stage of the model, and Pg(g|K) is the conditional distribution of growth rates of classes with a given number of units determined by the distribution Pξ(ξ) and Pη(η).
The analytical solution of this model can be obtained only for certain limiting cases, but a numerical solution can be computed easily for any set of assumptions. We investigate the model numerically and analytically (see Appendix B) and find:
- The conditional distribution of the logarithmic growth rates Pg(g|K) for the firms consisting of a fixed number of units converges to a Gaussian distribution for K → ∞,
where V is a function of parameters of the distribution Pξ(ξ) and Pη(η), and ḡ is the logarithm of mean growth rate of a unit, ḡ = ln μη. Thus, the width of this distribution decreases as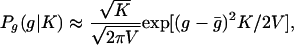
[8] 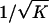 . This result is consistent with the observation that large firms with many production units fluctuate less than small firms (7, 18, 22, 37).
. This result is consistent with the observation that large firms with many production units fluctuate less than small firms (7, 18, 22, 37). - For g ≫ Vη, the distribution Pg(g) coincides with the distribution of the logarithms of the growth rates of the units:
In the case of power-law distribution P(K) ∼ K–φ, which dramatically increases for K → 1, the distribution Pg(g) is dominated by the growth rates of classes consisting of a single unit K = 1; thus, the distribution Pg(g) practically coincides with Pη(ln ηi) for all g. Indeed, our empirical observations confirm this result.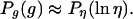
[9] If the distribution P(K) ∼ K–φ, φ > 2 for K → ∞, as happens in the presence of the influx of new units b ≠ 0, Pg(g) = C1 – C2|g|2φ–3, for g → 0, which in the limiting case b → 0, φ → 2 gives the cusp Pg(g) ∼ C1 – C2|g| (C1 and C2 are positive constants), similar to the behavior of the Laplace distribution PL(g) ∼ exp(–|g|C2) for g → 0.
- If the distribution P(K) weakly depends on K for K → 1, the distribution of Pg(g) can be approximated by a power law of g: Pg(g) ∼ |g|–3 in wide range
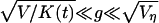 , where K(t) is the average number of units in a class. This case is realized for b = 0, t → ∞ when the distribution of P(K) is dominated by the exponential distribution and K(t) → ∞ as defined by Eq. 1. In this particular case, Pg(g) for
, where K(t) is the average number of units in a class. This case is realized for b = 0, t → ∞ when the distribution of P(K) is dominated by the exponential distribution and K(t) → ∞ as defined by Eq. 1. In this particular case, Pg(g) for  can be approximated by
can be approximated by 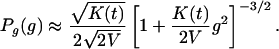
[10] - In the case in which the distribution P(K) is not dominated by one-unit classes but for K → ∞ behaves as a power law, which is the result of the mean-field solution for our model when t → ∞, the resulting distribution Pg(g) has three regimes: Pg(g) ∼ C1 – C2|g|2φ–3 for small g, Pg(g) ∼ |g|–3 for intermediate g, and Pg(g) ∼ P(ln η) for g → ∞. The approximate solution of Pg(g) is obtained by using Eq. 8 for Pg(g|K) for finite K, mean-field solution Eq. 4 in the limit t → ∞ for P(K), and replacing summation by integration in Eq. 7:
For b ≠ 0 the integral above cannot be expressed in elementary functions. In the b → 0 case, Eq. 11 yields the main result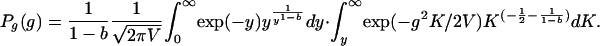
[11]
which combines the Laplace cusp for g → 0 and the power-law decay |g|–3 for g → ∞. Note that because of replacement of summation by integration in Eq. 7, the approximation Eq. 12 holds only for
[12] 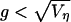 .
.
In Fig. 2a we compare the distributions given by Eq. 10, the mean-field approximation Eq. 11 for b = 0.1, and Eq. 12 for b 3 0. We find that all three distributions have very similar tentshape behavior in the central part. In Fig. 2b we also compare the distribution Eq. 12 with its asymptotic behaviors for g → 0 (Laplace cusp) and g → ∞ (power law) and find the crossover region between these two regimes.
Fig. 2.
The growth rate PDF, Pg(g). (a) Comparison of three different approximations given by Eq. 10, mean field approximation Eq. 11 for b = 0.1 and Eq. 12. Each Pg(g) shows similar tent shape behavior in the central part. We see there is little difference between the three cases, b = 0 (no entry), b = 0.1 (with entry), and Eq. 12. This means that entry of new classes (b > 0) does not perceptibly change the shape of Pg(g). Note that we use K(t)/V = 2.16 for Eq. 10 and V = 1 for Eq. 12. (b) The crossover of Pg(g) given by Eq. 12 between the Laplace distribution in the center and power law in the tails. For small g, Pg(g) follows a Laplace distribution Pg(g) ∼ exp(– |g|), and for large g, Pg(g) asymptotically follows an inverse cubic power law Pg(g) ∼ g–3.
The Empirical Evidence
To test our model, we analyze different levels of aggregation of economic systems, from the micro level of products to the macro level of industrial sectors and national economies.
First, we analyze a database, the pharmaceutical industry database (PHID), that records sales figures of the 189,303 products commercialized by 7,184 pharmaceutical firms in 21 countries from 1994 to 2004, covering the whole size distribution for products and firms and monitoring the flows of entry and exit at both levels (kindly provided by the epris program). Then, we study the growth rates of all U.S. publicly traded firms from 1973 to 2004 in all industries, based on Security Exchange Commission filings (Compustat). Finally, at the macro level, we study the growth rates of the GDP of 195 countries from 1960 to 2004 (World Bank).
Fig. 3 shows that the growth distributions of countries, firms, and products are well fitted by the distribution in Eq. 12 with different values of Vg. Indeed, growth distributions at any level of aggregation depict marked departures from a Gaussian shape. Moreover, even if the Pg(g) of GDP can be approximated by a Laplace distribution, the Pg(g) of firms and products are clearly more leptokurtic than Laplace. Based on our model, the growth distribution is Laplace in the body, with power-law tails. In fact, Fig. 4 shows that the central body part of the growth-rate distributions at any level of aggregation is well approximated by a double-exponential fit. Fig. 5 reveals that the asymptotic behaviors of g at any level of aggregation can be well fitted by power law with an exponent ζ = 3.
Fig. 3.
Empirical tests of Eq. 12 for the PDF Pg(g) of growth rates rescaled by  . Shown are country GDP (○), pharmaceutical firms (□), manufacturing firms (⋄), and pharmaceutical products (▵). The shapes of Pg(g) for all four levels of aggregation are well approximated by the PDF predicted by the model (dashed lines). Dashed lines are obtained based on Eq. 12 with Vg ≈ 4 × 10–4 for GDP, Vg ≈ 0.014 for pharmaceutical firms, Vg≈ 0.019 for manufacturing firms, and Vg ≈ 0.01 for products. After rescaling, the four PDFs can be fit by the same function. For clarity, the pharmaceutical firms are offset by a factor of 102, manufacturing firms by a factor of 104, and the pharmaceutical products by a factor of 106. Note that the data for pharmaceutical products extend from Pg(g) = 1 to Pg(g) ≈ 10–4, and the mismatch in the tail parts is because Pg(g) for large g is mainly determined by the logarithmic growth rates of units ln η.
. Shown are country GDP (○), pharmaceutical firms (□), manufacturing firms (⋄), and pharmaceutical products (▵). The shapes of Pg(g) for all four levels of aggregation are well approximated by the PDF predicted by the model (dashed lines). Dashed lines are obtained based on Eq. 12 with Vg ≈ 4 × 10–4 for GDP, Vg ≈ 0.014 for pharmaceutical firms, Vg≈ 0.019 for manufacturing firms, and Vg ≈ 0.01 for products. After rescaling, the four PDFs can be fit by the same function. For clarity, the pharmaceutical firms are offset by a factor of 102, manufacturing firms by a factor of 104, and the pharmaceutical products by a factor of 106. Note that the data for pharmaceutical products extend from Pg(g) = 1 to Pg(g) ≈ 10–4, and the mismatch in the tail parts is because Pg(g) for large g is mainly determined by the logarithmic growth rates of units ln η.
Fig. 4.
Empirical test of Eq. 12 for the central part in the PDF P(g) of growth rates rescaled by 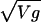 . Shown are four symbols: country GDP (○), pharmaceutical firms (□), manufacturing firms (⋄), and pharmaceutical products (▵). The shape of central parts for all four levels of aggregation can be well fit by a Laplace distribution (dashed lines). Note that Laplace distribution can fit Pg(g) only over a restricted range, from Pg(g) = 1 to Pg(g) ≈ 10–1.
. Shown are four symbols: country GDP (○), pharmaceutical firms (□), manufacturing firms (⋄), and pharmaceutical products (▵). The shape of central parts for all four levels of aggregation can be well fit by a Laplace distribution (dashed lines). Note that Laplace distribution can fit Pg(g) only over a restricted range, from Pg(g) = 1 to Pg(g) ≈ 10–1.
Fig. 5.
Empirical tests of Eq. 12 for the tail parts of the PDF of growth rates rescaled by 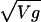 . The asymptotic behavior of g at any level of aggregation can be well approximated by power laws with exponents ζ ≈ 3 (dashed lines). The symbols are as follows: country GDP (left tail, ○; right tail, •), pharmaceutical firms (left tail, □; right tail, ▪), manufacturing firms (left tail, ⋄; right tail, ♦), and pharmaceutical products (left tail, ▵; right tail, ▴).
. The asymptotic behavior of g at any level of aggregation can be well approximated by power laws with exponents ζ ≈ 3 (dashed lines). The symbols are as follows: country GDP (left tail, ○; right tail, •), pharmaceutical firms (left tail, □; right tail, ▪), manufacturing firms (left tail, ⋄; right tail, ♦), and pharmaceutical products (left tail, ▵; right tail, ▴).
Our analysis in The Theoretical Framework predicts that the power-law regime of Pg(g) may vary depending on the behavior of P(K) for K → 1 and the distribution of the growth rates of units. In the case of the PHID, for which P(1) ≫ P(2) ≫ P(3)..., the growth-rate distribution of firms must be almost the same as the growth-rate distribution of products (as we stated in The Theoretical Framework). Hence, the power-law wings of Pg(g) for firms originate at the level of products. Because the PHID does not contain information on the subunits of products, we cannot test our prediction directly, but we can hypothesize that the distribution of the product subunits (number of customers or shipping ways) is less dominated by small K but has a sufficiently wide power-law regime because of the influx of new products. These rather plausible assumptions are sufficient to explain the shape of the distribution of the product growth rates, which is well described by Eq. 12.
The PHID allows us to test the empirical conditional distribution Pg(g|K) and the dependence of its variance σ2 on K, where K is the number of products. We find that σ ∼ K–0.28, which is significantly smaller than 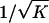 behavior. This result does not imply correlations among product growth rates on the firm level (21) but can be explained by the fact that for skewed distributions of product sizes Pξ(ξ) characterized by large Vξ, the convergence of Pg(g|K) to its Gaussian limit Eq. 8 is slow and the growth rates of the firms are determined by the growth of the few large products. Using the empirical values for the PHID μξ = 3.44, Vξ = 5.13, μη = 0.016, Vη = 0.36 and assuming log-normality of the distributions Pξ(ξ) and Pη(η), we find that the behavior of σ can be well approximated by a power law σ ∼ K–0.20 for K < 103. For this set of parameters, the convergence of Pg(g|K) to a Gaussian distribution takes place only for K > 105. This result is consistent with the observations of the power-law relationship between firm size and growth-rate variance reported earlier (13, 18, 19, 38).
behavior. This result does not imply correlations among product growth rates on the firm level (21) but can be explained by the fact that for skewed distributions of product sizes Pξ(ξ) characterized by large Vξ, the convergence of Pg(g|K) to its Gaussian limit Eq. 8 is slow and the growth rates of the firms are determined by the growth of the few large products. Using the empirical values for the PHID μξ = 3.44, Vξ = 5.13, μη = 0.016, Vη = 0.36 and assuming log-normality of the distributions Pξ(ξ) and Pη(η), we find that the behavior of σ can be well approximated by a power law σ ∼ K–0.20 for K < 103. For this set of parameters, the convergence of Pg(g|K) to a Gaussian distribution takes place only for K > 105. This result is consistent with the observations of the power-law relationship between firm size and growth-rate variance reported earlier (13, 18, 19, 38).
Discussion
Business firms grow in scale and scope. The scope of a firm is given by the number of its products. The scale of a firm is given by the size of its products. A firm such as Microsoft gets few big products, whereas Amazon sells a huge variety of goods, each of small size in terms of sales. In this article we argue that both mechanisms of growth are proportional. The number of products that a firm can launch successfully is proportional to the number of products that it has already commercialized. Once a product has been launched, its success depends on the number of customers who buy it and the price they are willing to pay. To a large extent, if products are different enough, the success of a product is independent from other products commercialized by the same company. Hence, the sales of products can be modeled as independent stochastic processes. Moreover, sometimes, new products are commercialized by new companies. As a result, small companies with few products can experience sudden jerks of growth resulting from the successful launch of a new product.
In this article, we find that the empirical distribution of firm growth rates exhibits a central part that is distributed according to a Laplace distribution and power-law wings Pg(g) ∼ g–ζ, where ζ = 3. If the distribution of number of units K is dominated by single-unit classes, the tails of firm growth distribution are primarily due to smaller firms composed of one or few products. The Laplace center of the distribution is shaped by big multiproduct firms. We find that the shape of the distribution of firm growth is almost the same in the presence of a small entry rate and with zero entry. We also find that the predictions of the model are accurate in the case of product growth rates, which implies that products can be considered as composed of elementary sale units, which evolve according to a random multiplicative process (6). Although there are several plausible explanations for the Laplace body of the distribution, which can be considered as an unconditional object (18, 31), the power-law decay of the tails has not been observed previously. We introduce a simple and general model that accounts for both the central part and the tails of the distribution. The shape of the business growth-rate distribution is due to the proportional growth of both the number and the size of the constituent units in the class. This result holds in the case of an open economy (with entry of new firms) as well as in the case of a closed economy (with no entry of new firms).
Acknowledgments
We thank S. Havlin, J. Nagler, and F. Wang for helpful discussions and suggestions. We thank the National Science Foundation and Merck Foundation (epris program) for financial support.
Appendix A: The Distribution of Units in Old and New Classes
Assume that at the beginning there are N(0) classes with n(0) units. Because at every time step one unit is added to the system and a new class is added with probability b, at moment t there are n(t) = n(0) + t units and N(t) = N(0) + bt classes, among which there are bt new classes with nnew units and N(0) old classes with nold units, such that nold + nnew = n(0) + t.
Because of the preferential attachment assumption, we have
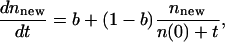 |
[A1] |
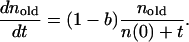 |
[A2] |
Solving the second differential equation and taking into account initial condition nold(0) = n(0), we obtain
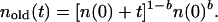 |
[A3] |
Analogously, the number of units at time t in the classes existing at time t0 is ne(t0, t) = [n(0)+t]1–b [n(0)+t0]b, where the subscript e means “existing.” The average number of units in old classes is
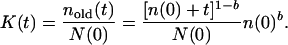 |
[A4] |
It is known (36) that for t → ∞ the preferential attachment model converges to the exponential distribution Eq. 1. Thus, we obtain Pold(K) in the form of Eq. 1 where K(t) is given by Eq. A4.
The number of units in the classes that appear at t0 is bdt, and the number of these classes is bdt. Because the probability that a class captures a new unit is proportional to the number of units it has already gotten at time t, the number of units at time t in the classes that appear at time t0 is nnew(t0, t) = ne(t0, t) · bdt/[n(0) + t0].
The average number of units in these classes is K(t0, t) = nnew(t0, t)/bdt = [n(0) + t]1–b/[n(0) + t0]1–b. Assuming that the distribution of units in these classes is given by a continuous approximation in Eq. 1, their contribution to the total distribution is
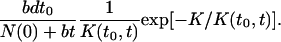 |
The contribution of all new classes to the distribution P(K) is
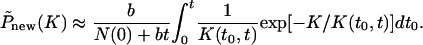 |
[A5] |
If we let y = K/K(t0, t), then P̃new(K) = bt/[N(0) + bt]Pnew(K), where
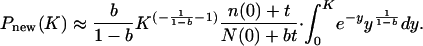 |
[A6] |
Note that Eq. A6 is not an exact solution but a continuous approximation that assumes K is a real number. Now we investigate the distribution in Eq. A6.
1. At fixed K when t → ∞, the low limit of integration in Eq. A6 goes to zero and we have
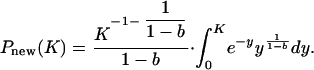 |
[A7] |
As K → ∞,
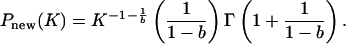 |
[A8] |
As K → 0, Pnew(K) = 1/(2 – b).
2. At fixed t when K → ∞, we use the partial integration to evaluate the incomplete Γ function: Γ(x, α+1) ≈ e–x xα. Therefore, from Eq. A6 we obtain
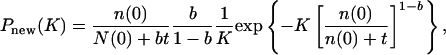 |
[A9] |
which always decays faster than Pold(K).
Appendix B: Calculation of the Growth Distribution of Classes P(g)
Let us assume that both the size and growth of units (ξi and ηi, respectively) are distributed log-normally
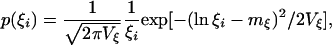 |
[A10] |
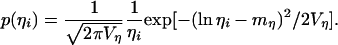 |
[A11] |
If units grow according to a multiplicative process, the size of units ξi′= ξiηi is distributed log-normally with Vξ′ = Vξ + Vη and mξ′ = mξ + mη.
The nth moment of the variable x distributed log-normally is given by
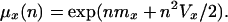 |
[A12] |
Thus, its mean is μx ≡ μx (n = 1) = exp(mx + Vx/2) and its variance is 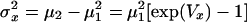 .
.
Let us now find the distribution of g growth rate of classes. It is defined as
 |
[A13] |
Here we neglect the influx of new units. According to the centrallimit theorem, the sum of K independent random variables with mean μ ≡ μξ(1) and finite variance 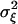 is
is
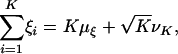 |
[A14] |
where νK is the random variable with the distribution converging to Gaussian
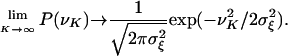 |
[A15] |
Because ln μη = mη + Vη/2 and ln μξ′ = ln μξ + ln μη, we have, after some algebra,
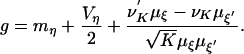 |
[A16] |
For large K the last term in Eq. A16 is the difference of two Gaussian variables, and that is a Gaussian variable itself. To find the distribution of g we must find its mean and variance. After some algebra,
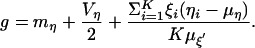 |
[A17] |
Because μξ′ = μξμη, the average of each term in the sum is μξ′ – μξμη = 0. The variance of each term in the sum is 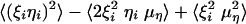 , where ξiηi,
, where ξiηi, 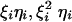 , and
, and 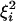 are all log-normal independent random variables. Particularly, (ξiηi)2 is log-normal with V = 4Vη + 4Vξ and m = 2mη + 2mξ;
are all log-normal independent random variables. Particularly, (ξiηi)2 is log-normal with V = 4Vη + 4Vξ and m = 2mη + 2mξ; 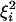 is log-normal with V = 4Vξ + Vη and m = 2m + mη;
is log-normal with V = 4Vξ + Vη and m = 2m + mη; 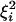 is log-normal with V = 4Vξ and m = 2mξ. Using Eqs. A12 and A17 and collecting all the terms, we find the variance of g:
is log-normal with V = 4Vξ and m = 2mξ. Using Eqs. A12 and A17 and collecting all the terms, we find the variance of g: 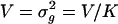 , where
, where
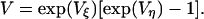 |
[A18] |
Therefore, for large K, g has a Gaussian distribution with mean ḡ = mη + Vη/2 and variance V/K.
The distribution of the growth rate of the old classes can be found by Eq. 7. To find a close form approximation, we replace the summation in Eq. 7 by integration and replace the distributions P(K) by Eq. 1 and P(g) by Eq. 8 as follows, assuming ḡ = 0.
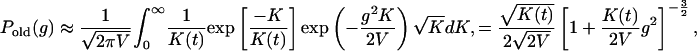 |
[A19] |
where K(t) is the average number of units in the old classes (see Eq. A4). This distribution decays as 1/g3 and thus does not have finite variance. In fact, we approximate the distribution of number of units in the old classes by a continuous function exp[–K/K(t)]/K(t), although in reality it is a discrete distribution, Pold(K) = λK(1/λ–1), where λ = exp[–1/K(t)]. The corrected distribution of growth rates is then given by the sum
 |
[A20] |
The slowest decaying term is  , which describes the behavior of the distribution when g → ∞. Thus, there is a crossover when
, which describes the behavior of the distribution when g → ∞. Thus, there is a crossover when 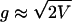 .
.
For the new classes, when t → ∞ the distribution of number of units is approximated by Eq. A7. Again replacing summation in Eq. 7 by integration and replacing P(g|K) by Eq. 8 and after switching the order of integration, we have Pnew(g) = Pg(g) defined in Eq. 11.As g → ∞, we can evaluate the second integral in Eq. 11 by partial integration:
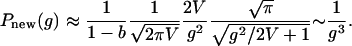 |
[A21] |
We compute the first derivative of the distribution defined in Eq. 11 by differentiating the integrand in the second integral with respect to g. The second integral converges as y → 0, and we find the behavior of the derivative for g → 0 by the substitution K* = Kg2/(2V). As g → 0, the derivative behaves as g·g2[–3/2+1/(1–b)] ∼ g2b/(1–b), which means that the function itself behaves as C2 – C1 |g|2b/(1–b)+1, where C2 and C1 are positive constants. For small b, this behavior is similar to the behavior of a Laplace distribution with variance 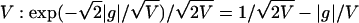 .
.
When b → 0, Eq. 11 can be simplified and, after some elementary calculus, we have Eq. 12, which behaves for 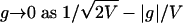 and for g → ∞ as V/(2g3). Thus, the distribution is well approximated by a Laplace distribution in the body with power-law tails. Because of the discrete nature of the distribution of the number of units, when
and for g → ∞ as V/(2g3). Thus, the distribution is well approximated by a Laplace distribution in the body with power-law tails. Because of the discrete nature of the distribution of the number of units, when 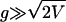 , the behavior for g → ∞ is dominated by const·exp(–g2/2V).
, the behavior for g → ∞ is dominated by const·exp(–g2/2V).
Author contributions: F.P., S.V.B., and H.E.S. designed research; D.F., F.P., S.V.B., M.R., K.M., K.Y., and H.E.S. performed research; S.V.B. contributed new reagents/analytic tools; D.F., S.V.B., M.R., K.M., and K.Y. analyzed data; and D.F., F.P., S.V.B., M.R., and K.M. wrote the paper.
Conflict of interest statement: No conflicts declared.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: PDF, probability density function; PHID, pharmaceutical industry database; GDP, gross domestic product.
References
- 1.Gibrat, R. (1930) Bull. Stat. Gén. 19, 469.10771136 [Google Scholar]
- 2.Gibrat, R. (1931) Les InégalitésÉconomiques (Librairie du Recueil Sirey, Paris).
- 3.Kapteyn, J. & Uven, M. J. (1916) Skew Frequency Curves in Biology and Statistics (Hoitsema Brothers, Groningen).
- 4.Zipf, G. (1949) Human Behavior and the Principle of Least Effort (Addison–Wesley, Cambridge, MA).
- 5.Gabaix, X. (1999) Q. J. Econ. 114, 739–767. [Google Scholar]
- 6.Steindl, J. (1965) Random Processes and the Growth of Firms: A Study of the Pareto Law (Griffin, London).
- 7.Sutton, J. (1997) J. Econ. Lit. 35, 40–59. [Google Scholar]
- 8.Kalecki, M. (1945) Econometrica 13, 161–170. [Google Scholar]
- 9.Simon, H. A. (1955) Biometrika 42, 425–440. [Google Scholar]
- 10.Simon, H. A. & Bonini, C. P. (1958) Am. Econ. Rev. 48, 607–617. [Google Scholar]
- 11.Ijiri, Y. & Simon, H. A. (1975) Proc. Natl. Acad. Sci. USA 72, 1654–1657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ijiri, Y. & Simon, H. A. (1977) Skew Distributions and the Sizes of Business Firms (North–Holland, Amsterdam).
- 13.Stanley, M. H. R., Amaral, L. A. N., Buldyrev, S. V., Havlin, S., Leschhorn, H., Maass, P., Salinger, M. A. & Stanley, H. E. (1996) Nature 379, 804–806. [Google Scholar]
- 14.Lee, Y., Amaral, L. A. N., Canning, D., Meyer, M. & Stanley, H. E. (1998) Phys. Rev. Lett. 81, 3275–3278. [Google Scholar]
- 15.Plerou, V., Amaral, L. A. N., Gopikrishnan, P., Meyer, M. & Stanley, H. E. (1999) Nature 433, 433–437. [Google Scholar]
- 16.Bottazzi, G., Dosi, G., Lippi, M., Pammolli, F. & Riccaboni, M. (2001) Int. J. Ind. Org. 19, 1161–1187. [Google Scholar]
- 17.Matia, K., Fu, D., Buldyrev, S. V., Pammolli, F., Riccaboni, M. & Stanley, H. E. (2004) Europhys. Lett. 67, 498–503. [Google Scholar]
- 18.Amaral, L. A. N., Buldyrev, S. V., Havlin, S., Leschhorn, H., Maass, P., Salinger, M. A., Stanley, H. E. & Stanley, M. H. R. (1997) J. Phys. I [French] 7, 621–633. [Google Scholar]
- 19.Buldyrev, S. V., Amaral, L. A. N., Havlin, S., Leschhorn, H., Maass, P., Salinger, M. A., Stanley, H. E. & Stanley, M. H. R. (1997) J. Phys. I [French] 7, 635–650. [Google Scholar]
- 20.Sutton, J. (2002) Physica A 312, 577–590. [Google Scholar]
- 21.Fabritiis, G. D., Pammolli, F. & Riccaboni, M. (2003) Physica A 324, 38–44. [Google Scholar]
- 22.Amaral, L. A. N., Buldyrev, S. V., Havlin, S., Salinger, M. A. & Stanley, H. E. (1998) Phys. Rev. Lett. 80, 1385–1388. [Google Scholar]
- 23.Takayasu, H. & Okuyama, K. (1998) Fractals 6, 67–79. [Google Scholar]
- 24.Canning, D., Amaral, L. A. N., Lee, Y., Meyer, M. & Stanley, H. E. (1998) Econ. Lett. 60, 335–341. [Google Scholar]
- 25.Buldyrev, S. V., Dokholyan, N. V., Erramilli, S., Hong, M., Kim, J. Y., Malescio, G. & Stanley, H. E. (2003) Physica A 330, 653–659. [Google Scholar]
- 26.Kalecki, M. R. (1945) Econometrica 13, 161–170. [Google Scholar]
- 27.Mansfield, D. E. (1962) Am. Econ. Rev. 52, 1024–1051. [Google Scholar]
- 28.Hall, B. H. (1987) J. Ind. Econ. 35, 583–606. [Google Scholar]
- 29.Reed, W. J. (2001) Econ. Lett. 74, 15–19. [Google Scholar]
- 30.Reed, W. J. & Hughes, B. D. (2002) Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 66, 067103. [DOI] [PubMed] [Google Scholar]
- 31.Kotz, S., Kozubowski, T. J. & Podgórski, K. (2001) The Laplace Distribution and Generalizations: A Revisit with Applications to Communications, Economics, Engineering, and Finance (Birkhauser, Boston).
- 32.Johnson, N. L. & Kotz, S. (1977) Urn Models and Their Applications (Wiley, New York).
- 33.Kotz, S., Mahmoud, H. & Robert, P. (2000) Stat. Probab. Lett. 49, 163–173. [Google Scholar]
- 34.Reed, W. J. & Hughes, B. D. (2004) Math. Biosci. 189(1), 97–102. [DOI] [PubMed] [Google Scholar]
- 35.Stanley, H. E. (1971) Introduction to Phase Transitions and Critical Phenomena (Oxford Univ. Press, Oxford).
- 36.Cox, D. R. & Miller, H. D. (1968) The Theory of Stochastic Processes (Chapman & Hall, London).
- 37.Hymer, S. & Pashigian, P. (1962) J. Polit. Econ. 70, 556–569. [Google Scholar]
- 38.Matia, K., Amaral, L. A. N., Luwel, M., Moed, H. F. & Stanley, H. E. (2005) J. Am. Soc. Inf. Sci. Technol. 56, 893–902. [Google Scholar]







