Skip to main content
NCBI home page
Journal of Athletic Training logoLink to Journal of Athletic Training
. 2005 Oct-Dec;40(4):298–304.

Single-Leg Jump-Landing Stabilization Times in Subjects With Functionally Unstable Ankles

Scott E Ross *, Kevin M Guskiewicz †, Bing Yu †
PMCID: PMC1323291  PMID: 16404451

Abstract

Context: Factors contributing to functional ankle instability may cause individuals with the condition to land from a jump differently than those with stable ankles.

Objective: To determine stabilization time differences during single-leg jump landings between stable and unstable ankle groups and to report the reliability and precision of time-to-stabilization measures.

Design: A mixed design with 1 between factor (ankle group) and 1 within factor (direction) was used to analyze the comparison between our 10 subjects with functional ankle instability and 10 subjects with stable ankles. Time to stabilization (seconds) was the dependent measure. Reliability for time-to-stabilization measures of our 12 additional subjects with stable ankles were assessed using intraclass correlation coefficients (ICC 2,7). Standard errors of measurements were also calculated for time-to-stabilization measures.

Setting: Sports medicine research laboratory.

Patients or Other Participant(s): Ten subjects with functional ankle instability who reported at least 2 sprains and ``giving way'' sensations at their ankles constituted the functional ankle instability group. Ten subjects without a history of ankle sprain injury served as healthy subjects. Twelve additional healthy subjects participated in the reliability study.

Intervention(s): Subjects performed a jump-landing test, which required them to jump 50% to 55% of their maximum vertical jump height and then land on a single leg on a force plate. After landing, they stabilized quickly and remained as motionless as possible in a single-leg stance for 20 s.

Main Outcome Measure(s): Anterior-posterior and medial/ lateral vibration magnitude curve fit time-to-stabilization.

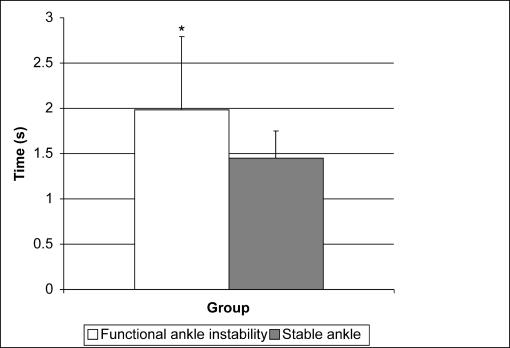
Results: Time to stabilization was longer for the functional ankle instability group (1.98 ± 0.81 s) than for the stable ankle group (1.45 ± 0.30 s) (P < .05). Reliability (standard error of the measurement) values for anterior/posterior and medial/lateral time-to-stabilization were 0.79 (0.15 s) and 0.65 (0.26 s), respectively.

Conclusions: Time to stabilization was longer for subjects with functional ankle instability than subjects with stable ankles. The ankle instability may have impaired the subjects' ability to stabilize after a single-leg jump landing. Reliabilities and standard errors of the measurements of time-to-stabilization measures were moderate and low, respectively.

Keywords: chronic ankle instability, dynamic balance, postural control

Functional ankle instability (FAI) is a condition that often develops as a result of ankle sprain injuries.1–3 This impairment is frequently characterized by recurrent ankle sprains and sensations of “giving way” at the ankle joint during physical activity. Although the exact mechanism remains unclear, FAI might result from one or a combination of the following factors: (1) ligamentous damage, (2) ankle muscle strength deficits, (3) delayed muscle reaction time, and (4) proprioception deficits at the ankle joint.2–10

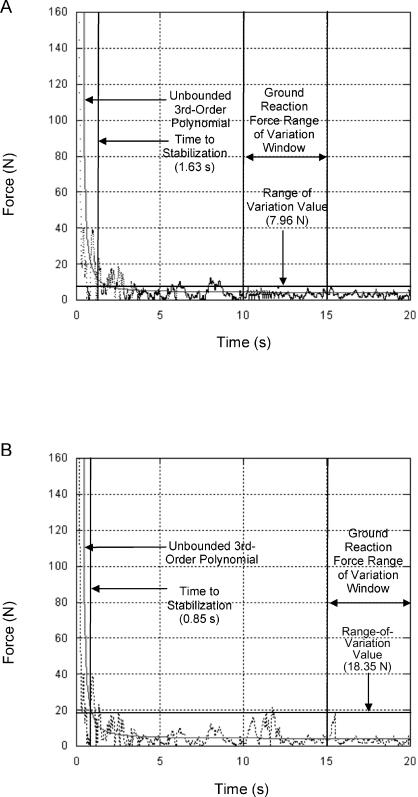
Researchers11–14 have speculated that these factors might cause individuals with FAI to land from a jump differently than individuals with stable ankles. Anterior-posterior (A/P) and medial-lateral (M/L) time to stabilization (TTS) have been used to evaluate the stability of subjects with FAI after a single-leg jump landing.13–16 Using a TTS calculation originally reported by Ross, Guskiewicz, et al13–15 longer TTS values have been noted for subjects with FAI than subjects with stable ankles (Figure 1). The first step in calculating TTS is to define the range of variation of a given ground reaction force component. Range-of-variation values of a given component of a ground reaction force are defined as the smallest absolute range value of a ground reaction force component during the last 10 seconds of the single-leg stance portion of a jump-landing task.15 A horizontal range-of-variation line that represents the smallest absolute range value of a component of the ground reaction force is superimposed over the data. An unbounded third-order polynomial is fit to the data, and TTS is the point at which this polynomial transects the range-of-variation line. In other words, TTS signifies when the ground reaction force range of variation at the beginning of a single-leg jump landing resembles the ground reaction force range of variation of a stabilized single-leg stance.

Figure 1. Time to stabilization calculation. A, The ground reaction force range-of-variation window (10–15 seconds) was used to calculate the range of variation. The solid horizontal black line represents the range of variation line of 7.96 N. The time to stabilization was the time (1.63 seconds) that the unbounded third-order polynomial transected the range-of-variation line. B, The ground reaction force range-of-variation window (15–20 seconds) was used to calculate the range of variation. The solid horizontal black line represents the range-of-variation line of 18.35 N. The time to stabilization was the time (0.85 seconds) that the unbounded third-order polynomial transected the range-of-variation line.

Figure 1

Open in a new tab

A shortcoming of this TTS calculation might be that the ground reaction force range-of-variation values used as reference variables to calculate A/P and M/L TTS are determined from single-leg stance stability. Subjects with FAI have been reported to have single-leg postural control deficits.2,3,5–9 Goldie et al3 reported that subjects with ankle instability had greater ground reaction force variations with quiet single-leg stance compared with those with uninjured ankles. We recently suggested that postural control deficits apparent with FAI might also cause greater range-of-variation values with single-leg stance.14 Subjects with stable ankles with lesser range of variation values (see Figure 1A) might take longer to reduce the range of variation of the beginning components of the ground reaction force than unstable ankle subjects with greater range-of-variation values (see Figure 1B) . To remedy this potential problem, we suggested that researchers use normalized range-of-variation reference variables that are not influenced by ankle instability for calculating TTS.14 Ankle group TTS comparisons would then become fair, because TTS for stable and unstable groups would be calculated from a normalized reference variable rather than a nonnormalized reference variable. The purpose of our study, therefore, was to examine potential TTS differences between subjects with FAI and subjects with stable ankles using A/P and M/L vibration magnitude curve-fit TTS calculations that normalize range-of-variation values between ankle groups. A secondary purpose was to report the reliability and precision of A/P and M/L vibration magnitude curve-fit TTS measures. Accurately measuring TTS with normalized range-of-variation values might help to ensure that individuals return to activity with adequate stability in both the frontal and sagittal planes of motion.

METHODS

Subjects

Ten subjects with stable ankles (5 males, 5 females) were matched to 10 subjects with FAI by height, mass, age, sex, and leg tested. Subjects with FAI had a mean height, mass, and age of 175.2 ± 8.5 cm, 73.4 ± 13.3 kg, and 22.0 ± 2.5 years, respectively. Subjects with stable ankles had a mean height, mass, and age of 175.8 ± 10.7 cm, 74.0 ± 16.9 kg, and 20.8 ± 1.3 years, respectively. An additional group of 12 subjects with stable ankles (6 males, 6 females) who were not matched to either the 10 subjects with stable ankles or 10 subjects with FAI participated in our reliability study. These 12 subjects had a mean height, mass, and age of 180.6 ± 12.2 cm, 77.4 ± 13.6 kg, and 20.8 ± 1.9 years, respectively. The 10 subjects with FAI and the 10 subjects with stable ankles did not participate in the reliability study. All subjects read and signed a consent form approved by The Committee for the Protection of the Rights of Human Subjects and received a test protocol orientation. Subjects wore gym clothing and athletic shoes during test sessions.

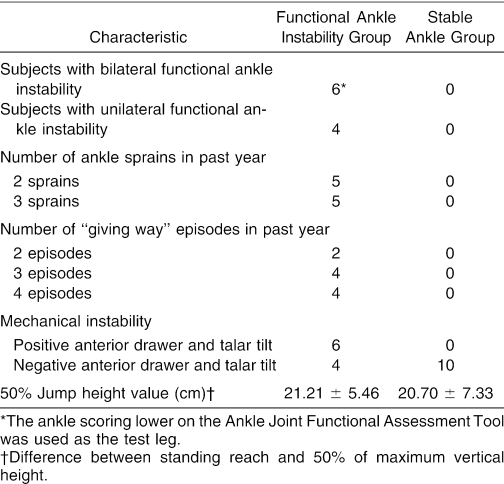
Subject characteristics are reported in Table 1. To qualify as candidates for FAI, subjects reported a history of a severe ankle sprain injury with at least 3 days of immobilization. In addition, they reported at least 2 additional ankle sprains and 2 “giving-way” sensations with weight-bearing activity within the year before their participation in this study. Subjects who sustained recurrent ankle sprains returned to activity within 2 days of injury and were not immobilized for any period with these subsequent ankle sprains. With each subsequent sprain, subjects reported signs and symptoms of an acute injury. These acute signs and symptoms of injury included pain, loss of function, mild point tenderness, swelling, and abnormal range of motion. At the time of the study, however, no subjects with FAI displayed acute signs and symptoms of injury. We assessed each subject's ankle stability with the Ankle Joint Functional Assessment Tool. This questionnaire has been used previously to assess FAI.9,14 Higher scores on this assessment represent greater ankle stability, and the maximum score is 48.9 Subjects with FAI had a mean score of 17 ± 4, and subjects with stable ankles had a mean score of 26 ± 4.

Table 1. Subject Characteristics.

graphic file with name i1062-6050-40-4-298-t01.jpg

Open in a new tab

Subjects with FAI did not report sustaining an ankle sprain injury within the 6 weeks before their participation. In addition, subjects were not receiving therapy for their instability at the time of this study, but 2 of 10 had previously participated in ankle rehabilitation. A history of lower extremity fracture, knee injury, or hip injury was an exclusion criterion for potential subjects. Subjects were also excluded if they reported visual impairments that affected their balance, vestibular deficits, or neurologic dysfunctions. Potential subjects with stable ankles could not participate if they reported a history of ankle sprain injury or sensations of giving way at the ankle with weight-bearing activity. All subjects participated in physical activity for at least 3 hours per week. Physical activity was defined as any bodily movement produced by skeletal muscle that results in energy expenditure.17 Our subjects participated in recreational sports, such as basketball, volleyball, soccer, and strength training.

Procedure

Subjects were assessed for maximum 2-footed vertical jump height as they jumped from 70 cm away from a Vertec (Sports Imports, Columbus, OH). Subjects were instructed to use a jumping technique that allowed them to jump as high as possible. They were allowed to swing their arms as they jumped but were then required to hold their reaching arm at 180° of shoulder flexion. Adjustable plastic rods on the Vertec allowed jump height assessment. After we recorded the maximum value of 3 jumps, plastic rods on the Vertec were set at 50% and 55% of a subject's maximal jump. While standing 70 cm away, subjects used a 2-footed jumping technique that allowed them to generate enough jumping force to reach the 50% mark with their fingertips. Subjects could swing their arms during this jump, but they were required to hold the reaching arm at 180° of shoulder flexion after take-off. The reaching arm was the arm ipsilateral to the functionally unstable ankle or the matched testing ankle of subjects with stable ankles. Subjects reached their minimal mark of 50%, but they were required to jump between 50% and 55% of their maximum jump height. Subjects were allowed to lower the reaching arm after touching this mark. Subjects were instructed to “stick” the landing on their test leg, stabilize as quickly as possible, and remain as motionless as possible in a single-leg stance for 20 seconds. We did not control for arm position, trunk flexion, or lower extremity flexion during foot contact or stance. Three practice trials and 7 testing trials were performed. Subjects were retested if they hopped or touched down with their non–weight-bearing leg during landing or failed to jump within the 50% to 55% jump mark.

Our additional 12 healthy subjects with stable ankles were tested during 2 sessions on the jump-landing protocol. Test sessions were separated by 24 hours, and our jump-landing protocol was repeated on the second day of testing. Each subject was randomly assigned a test leg, and this leg was used for both test sessions.

Data Collection

We used a strain gauge force plate (model 4060-08A; Bertec Corp, Columbus, OH) to measure ground reaction force signal data at a sampling rate of 180 Hz. Ground reaction force data collection began when the subject landed on the force plate and stopped after 20 seconds. Analog signals from the force plate were amplified by a factor of 2 with an amplifier (model AM-6701; Bertec Corp) and collected using the Peak Performance Motus analog-to-digital interface unit (Peak Performance Technologies Inc, Englewood, CO). The MotionSoft MSFPLT software (version 2.0; MotionSoft Inc, Chapel Hill, NC) converted digital data to ground reaction forces. Data were filtered using a second-order, recursive low-pass Butterworth digital filter with an estimated optimum cutoff frequency of 12.53 Hz.

Normalized Reference Variable

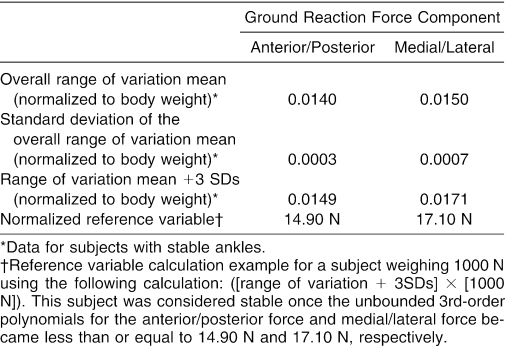
Before calculating the TTS, we analyzed the stable ankle group's components of the ground reaction force of the last 10 seconds of the stabilized single-leg stance portion of the single-leg jump landing.15 The smallest absolute ground reaction force ranges for the A/P and M/L components were accepted as optimal range-of-variation values.15 Each component for a subject was then divided by his or her body weight to normalize these variables. A mean range-of-variation value for each component of the ground reaction force was then formed from 7 trials collected for a single subject. This procedure was repeated for each subject, and then the range-of-variation means for each subject were used to calculate an overall mean range of variation for A/P and M/L components. We also calculated SDs for overall means of the A/P and M/L components. Three SDs of the overall mean were then added to each respective overall range-of-variation mean. We defined this variable as the range-of-variation mean + 3 SDs for the A/P and M/L components of the ground reaction force (Table 2).

Table 2. Reference Variable Calculations.

graphic file with name i1062-6050-40-4-298-t02.jpg

Open in a new tab

Vibration Magnitude Curve-Fit Time to Stabilization

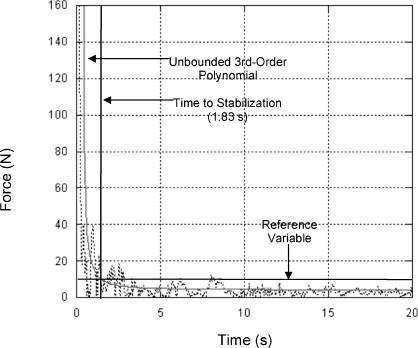
The vibration magnitude curve-fit TTS calculation is shown in Figure 2. This TTS measure was calculated using MotionSoft MSFPLT, and the word vibration indicates that the unbounded third-order polynomial fitting the data represents a decay curve. The A/P and M/L components of the ground reaction force data were analyzed separately for subjects in both groups. We multiplied range-of-variation means + 3 SDs for each component of the ground reaction force by a subject's body weight to obtain a reference variable for each subject that normalized the range-of-variation mean + 3 SDs to body weight (Table 2). A horizontal line was then inserted over the top of the data of a given ground reaction force component (Figure 2). The value of the horizontal line for the A/P ground reaction force data was equal to the A/P normalized reference variable, and the value of the horizontal line for the M/L ground reaction force data was equal to the M/L normalized reference variable. We then rectified the components of the ground reaction force data and fit an unbounded third-order polynomial to each component.15 The TTS for each component of the ground reaction force was the point at which the unbounded third-order polynomial transected the normalized reference variable. These calculations were repeated for each subject.

Figure 2. Vibration magnitude curve-fit time to stabilization calculation. The solid horizontal line represents the normalized reference variable (body weight × range-of-variation mean + 3 SDs). The solid vertical line represents the time to stabilization (1.83 seconds) or the point at which the unbounded third-order polynomial transected the horizontal reference variable line.

Figure 2

Open in a new tab

Statistical Analysis

We used SPSS statistical software (SPSS version 11.0; SPSS Inc, Chicago, IL) for statistical analyses. The α level was set a priori at .05 to indicate statistical significance. The average TTS value for each subject was calculated using the 7 test trials. We analyzed the comparison between our 10 subjects with FAI and 10 subjects with stable ankles via a mixed design with 1 between factor (ankle group) and 1 within factor (direction). The TTS (in seconds) was the dependent measure. Effect size (ES) and power for analysis of variance were calculated using the Cohen18 ES index and power of F test tables for the group-by-direction interaction, main effect for ankle group, and main effect for direction. The ES index used to calculate ES (F = σm/σ) represents the variability of group means divided by the common SD within our groups.18 Reliability of the TTS measures of our 12 additional subjects with stable ankles was assessed using intraclass correlation coefficients (ICCs) with the Shrout and Fleiss equation (2,k).19 The SEM values were also calculated for A/P TTS and M/L TTS.

RESULTS

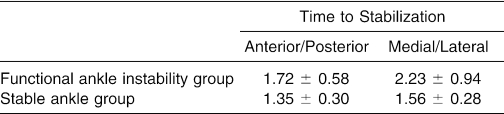
The main effect for ankle group displayed in Figure 3 indicates that the FAI group took longer to stabilize than the stable ankle group (F1,18 = 5.67, P = 0.03; ES = 0.40). A main effect for direction was found, and indicates that the M/L TTS of 1.90 ± 0.77s was longer than the A/P TTS of 1.54 ± 0.50s (F(1,18) = 6.37, P = 0.02; ES = 0.30). Table 3 displays the means ± SD associated with the non-significant ankle group by direction interaction (F1,18 = 1.07, P = .31; ES = 0.50, power = 0.57). The ICC(2,7) value for A/P TTS was 0.79, and the SEM value was 0.15 seconds. The M/L TTS ICC(2,7) value was 0.65, and the SEM was 0.26 seconds.

Figure 3. Time-to-stabilization mean and SDs are displayed. *Time to stabilization was longer for the functional ankle instability group than the stable ankle group.

Figure 3

Open in a new tab

Table 3. Time to Stabilization (s) (Mean ± SD).

graphic file with name i1062-6050-40-4-298-t03.jpg

Open in a new tab

DISCUSSION

Single-leg jump-landing tests might challenge the postural control system and allow clinicians to identify unstable landing patterns when proper dependent measures are used for analyses. Using the vibration magnitude curve-fit TTS calculation, we identified longer stabilization time for subjects with FAI than subjects with stable ankles after a single-leg jump landing. Identifying stabilization time deficits before returning to physical activity could have implications for decreasing recurrent ankle sprain injuries.

Previously reported methods for calculating stabilization times used a subject's range-of-variation value to determine TTS.13–16 Range-of-variation values are used as a measure of postural control, with greater values indicating postural instabilities.15 A potential limitation to this calculation is that the FAI and stable ankle groups actually might be different with regard to stabilization times, but differences might not be found because the FAI group subjects' own stability is being used as a reference variable. The FAI group might have greater range-of-variation values compared with the stable ankle group, yet the FAI group's polynomial curve might become asymptotic just as soon, or even sooner, than that of the stable ankle group if the FAI group subjects reach their range-of-variation status of greater instability in a shorter period. Any time subjects are normalized to a reference variable, in this case their own range-of-variation values, problems might occur if the phenomenon defining the group has influence over the reference variable.

This former method of TTS might not be a fair comparison between stable and unstable ankles because subjects' ankle instability might influence the reference variable once these subjects are stable in a single-leg stance. For a fair comparison, a normalized reference variable might be used that is not influenced by the condition these subjects potentially possess. The vibration magnitude curve-fit TTS measure, therefore, is designed to first calculate a normalized reference variable by multiplying the range-of-variation mean + 3 SDs of subjects with stable ankles by body weight. We chose 3 SDs because outliers typically fall beyond 3 SDs of the mean.20 We believe that subjects with FAI should perform within 3 SDs of the mean of subjects with stable ankles to attain stability. This normalized reference variable, therefore, allowed subjects in both groups to stabilize once they were functioning within 3 SDs of the mean range-of-variation value of subjects with stable ankles.

A potential limitation to this vibration magnitude curve-fit TTS calculation is that healthy subjects with stable ankles might not be “normal,” since some of these subjects might possess poor postural control during the stabilized single-leg stance portion of the jump landing. We tested 10 subjects with stable ankles to calculate our range-of-variation mean + 3 SDs, a number that might not be sufficient to calculate normalized data. If our control subjects did not have “normal” range-of-variation values, however, we believe that the differences between the 2 groups would not have been detected. Calculating range of variation + 3 SD values for a large number of control subjects should be the focus of future research. These data might then serve as normalized data for researchers to use when calculating stabilization times using the vibration magnitude curve-fit method. Calculating these data for a large sample of healthy subjects might eliminate the need to calculate range-of-variation mean + 3 SDs of healthy subjects every time researchers use TTS as a dependent measure.

Our current stabilization time means for subjects with unstable and stable ankles are shorter than those previously reported.13,14 Researchers have reported A/P TTS values ranging from 3.22 to 3.27 seconds for subjects with FAI and 2.30 to 2.33 seconds for subjects with stable ankles.13,14 Previously reported M/L TTS values have ranged from 2.48 to 2.70 seconds for subjects with FAI and 2.00 to 2.31 seconds for subjects with stable ankles.13,14 Wikstrom et al16 also used a similar TTS calculation, and they also reported greater A/P and M/L values than we do. Shorter TTS values in our study compared with other TTS values reported in the literature might be the result of a learning effect from our subjects performing a greater number of trials than those in other studies.13,14,16 Our subjects performed at least 10 successful trials (3 practice trials and 7 trials for data collection purposes). In addition, several subjects had to repeat unsuccessful trials because they touched down with their non–weight-bearing leg or they failed to “stick” the landing. Our current study design does not allow us to examine possible learning effects on our TTS values, but examining this issue should be the focus of future researchers.

Our significant main effect for group indicates that the TTS for the FAI group was longer than the TTS for the stable ankle group. We did not find differences between groups for each TTS direction analyzed. Longer A/P and M/L TTS values in subjects with FAI compared with subjects with stable ankles have been previously reported.13,14 We probably did not find group differences for each TTS direction because our power was low for our ankle group-by-direction interaction. Future investigators should examine the effects of increasing sample size on the ankle group-by-direction interaction.

Although the main effect for direction was not related to our research question, our significant finding indicates that the M/L TTS was longer than the A/P TTS. Nashner21 contended that postural instabilities might result from a narrow base of support, which decreases the limits of stability. Our subjects' narrow frontal-plane base of support might allow the center of gravity to approach the smaller frontal-plane limits of stability, which could destabilize posture and increase the time needed to stabilize after landing.

Evaluating the reliability and precision of the vibration magnitude TTS calculation was a secondary purpose of our study, and we believe that the ICC and SEM values are important for appreciating our results and comparing our values to those previously reported for the former TTS calculation. Interestingly, our current A/P TTS ICC value (0.79) is greater than our previous value reported for the former A/P TTS calculation (ICC = 0.61), but our current M/L TTS ICC value (0.65) is lower than our previous value reported for the former M/L TTS calculation (0.80).14 These ICC values for the vibration magnitude curve-fit and former TTS calculations are moderately consistent. The SEM values for our current A/P TTS (0.15 seconds) and M/L TTS (0.26 seconds) are lower than those previously reported for the former A/P TTS (0.30 seconds) and M/L TTS (0.32 seconds).14 Denegar and Ball22 have suggested that imperfect reliability might be acceptable if SEM values are low. A low SEM value indicates more precision of the measurement.22 We believe, therefore, that our vibration magnitude curve-fit TTS is a more precise measure than the former method of TTS that did not use normalized range-of-variation values.

Causal factors of FAI that have been suggested to impair single-leg postural control are ligament integrity deficits, ankle muscle strength deficits, peroneal nerve dysfunction, and proprioception deficits.2–10 Goldie et al3 suggested that the causal factors of FAI might be responsible for greater accelerations of the center of gravity with quiet single-leg stance compared with uninjured ankles. They also reported that these accelerations require muscle forces to stabilize the center of gravity within the limits of stability, and large stabilizing muscle forces are reflected by large ground reaction forces.23 Thus, ground reaction force values become lower once the center of gravity stops moving rapidly, and stable posture is achieved by rotating the center of gravity slowly through the limits of stability.23 Based on these reports by Goldie et al,3,23 we speculate that the TTS reflects the point in time when movements of the center of gravity after landing from a jump become similar to movements of the center of gravity that resemble single-leg stability. Causal factors of FAI that might be responsible for impairing single-leg postural control, therefore, might also be responsible for hampering the ability of subjects with FAI to decelerate their center of gravity when transitioning from landing to stabilized single-leg stance.

Researchers11–16 have speculated that individuals with FAI possess poor landing strategies, which predispose them to injury. Our current results indicate that subjects with FAI land on a single leg differently than do subjects with stable ankles. Other researchers who have compared single-leg landings between stable and unstable ankles have reported that subjects with FAI land with (1) greater knee flexion and dorsiflexion,11 (2) shorter time to reach peak lateral and anterior ground reaction forces,12 (3) different magnitudes of time-averaged forces through phases of the post–ground contact period,12 (4) lower soleus muscle activity at ground contact,13 and (5) longer stabilization times.13,14 Single-leg jump-landing tests are designed to allow a certain degree of functionality, which permits subjects to choose their landing strategies. Allowing subjects to use various landing techniques, however, is a potential limitation to these single-leg jump-landing findings. Single-leg landing TTS differences, for example, might simply be a result of groups using different strategies to land and stabilize when performing a jump landing. Landing strategies might be different for subjects with FAI outside a laboratory setting. Whether these landing patterns examined in a laboratory setting are detrimental to subjects with FAI is unknown, and future researchers should determine the relationship among TTS, episodes of recurrent ankle sprains, and episodes of giving way.

Clinical Significance

Proper landing techniques are imperative for stabilizing the ankle during a jump landing. Awkward landings could permit the foot to invert excessively and, consequently, cause ankle ligament sprains. Using TTS calculations to analyze landing patterns could provide clinicians with information on an individual's ability to stabilize after a single-leg jump landing. When comparing the TTS of a single-leg jump landing between a group of individuals with FAI and a healthy group, however, a measure that provides equal comparisons between groups is needed. Although other methods used to calculate TTS have detected differences between stable and unstable ankles, this former method might potentially allow individuals with large range-of-variation values to reach stability more quickly. Using the vibration magnitude curve-fit TTS allows for equal group comparisons between FAI and stable ankle groups, because the reference variable used to calculate TTS is normalized between groups. We suggest that researchers and clinicians use the vibration magnitude curve-fit TTS to evaluate landing patterns of individuals with FAI after a single-leg jump-landing. The vibration magnitude curve-fit TTS could identify abnormal stabilization times, and clinicians could correct these deficiencies before returning an individual to physical activity.

Footnotes

Scott E. Ross, PhD, ATC, and Kevin M. Guskiewicz, PhD, ATC, contributed to conception and design; acquisition and analysis and interpretation of the data; and drafting, critical revision, and final approval of the article. Bing Yu, PhD, contributed to conception and design; analysis and interpretation of the data; and drafting, critical revision, and final approval of the article.

Address correspondence to Scott E. Ross, PhD, ATC, Virginia Commonwealth University, PO Box 842020, 1015 West Main Street, Richmond, VA 23284. Address e-mail to seross@vcu.edu.

REFERENCES

  1. Bahr R, Karlsen R, Lian O, Ovrebo R. Incidence and mechanisms of acute ankle inversion injuries in volleyball: a retrospective cohort study. Am J Sports Med. 1994;22:595–600. doi: 10.1177/036354659402200505. [DOI] [PubMed] [Google Scholar]
  2. Freeman MA, Dean MR, Hanham IW. The etiology and prevention of functional instability of the foot. J Bone Joint Surg Br. 1965;47:678–685. [PubMed] [Google Scholar]
  3. Goldie PA, Evans OM, Bach TM. Postural control following inversion injuries of the ankle. Arch Phys Med Rehabil. 1994;75:969–975. [PubMed] [Google Scholar]
  4. Bernier JN, Perrin DH. Effect of coordination training on proprioception of the functionally unstable ankle. J Orthop Sports Phys Ther. 1998;27:264–275. doi: 10.2519/jospt.1998.27.4.264. [DOI] [PubMed] [Google Scholar]
  5. Ryan L. Mechanical stability, muscle strength and proprioception in the functionally unstable ankle. Aust Physiother. 1994;40:41–47. doi: 10.1016/S0004-9514(14)60453-0. [DOI] [PubMed] [Google Scholar]
  6. Tropp H. Pronator muscle weakness in functional instability of the ankle joint. Int J Sports Med. 1986;7:291–294. doi: 10.1055/s-2008-1025777. [DOI] [PubMed] [Google Scholar]
  7. Konradsen L, Ravn JB. Prolonged peroneal reaction time in ankle instability. Int J Sports Med. 1991;12:290–292. doi: 10.1055/s-2007-1024683. [DOI] [PubMed] [Google Scholar]
  8. Matsusaka N, Yokoyama S, Tsurusaki T, Inokuchi S, Okita M. Effect of ankle disk training combined with tactile stimulation to the leg and foot on functional instability of the ankle. Am J Sports Med. 2001;29:25–30. doi: 10.1177/03635465010290010901. [DOI] [PubMed] [Google Scholar]
  9. Rozzi SL, Lephart SM, Sterner R, Kuligowski L. Balance training for persons with functionally unstable ankles. J Orthop Sports Phys Ther. 1999;29:478–486. doi: 10.2519/jospt.1999.29.8.478. [DOI] [PubMed] [Google Scholar]
  10. Lephart SM, Pincivero DM, Giraldo JL, Fu FH. The role of proprioception in the management and rehabilitation of athletic injuries. Am J Sports Med. 1997;25:130–137. doi: 10.1177/036354659702500126. [DOI] [PubMed] [Google Scholar]
  11. Caulfield BM, Garrett M. Functional instability of the ankle: differences in patterns of ankle and knee movement prior to and post landing in a single leg jump. Int J Sports Med. 2002;23:64–68. doi: 10.1055/s-2002-19272. [DOI] [PubMed] [Google Scholar]
  12. Caulfield C, Garrett M. Changes in ground reaction force during jump landing in subjects with functional instability of the ankle joint. Clin Biomech (Bristol, Avon) 2004;19:617–621. doi: 10.1016/j.clinbiomech.2004.03.001. [DOI] [PubMed] [Google Scholar]
  13. Brown CN, Ross SE, Mynark R, Guskiewicz KM. Assessing functional ankle instability with joint position sense, time to stabilization, and electromyography. J Sport Rehabil. 2004;13:122–134. [Google Scholar]
  14. Ross SE, Guskiewicz KM. Examination of static and dynamic postural stability in individuals with functionally stable and unstable ankles. Clin J Sport Med. 2004;14:332–338. doi: 10.1097/00042752-200411000-00002. [DOI] [PubMed] [Google Scholar]
  15. Ross SE, Guskiewicz KM. Time to stabilization: a method for analyzing dynamic postural stability. Athl Ther Today. 2003;8(3):37–39. [Google Scholar]
  16. Wikstrom EA, Tillman MD, Borsa PA. Detection of dynamic stability deficits in subjects with functional ankle instability. Med Sci Sports Exerc. 2005;37:169–175. doi: 10.1249/01.mss.0000149887.84238.6c. [DOI] [PubMed] [Google Scholar]
  17. Caspersen CJ, Powell KE, Christenson GM. Physical activity, exercise, and physical fitness: definitions and distinctions for health-related research. Public Health Rep. 1985;100:126–131. [PMC free article] [PubMed] [Google Scholar]
  18. Cohen J. Statistical Power Analysis for the Behavioral Sciences. 2nd ed. Hillsdale, NJ: Lawrence Erlbaum Assoc; 1988:36,311.
  19. Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull. 1979;86:420–428. doi: 10.1037//0033-2909.86.2.420. [DOI] [PubMed] [Google Scholar]
  20. Jacobsen B. Univariate descriptive statistics. In: Munro B, ed. Statistical Methods for Health Care Research. 3rd ed. Philadelphia, PA: Lippincott; 1993:30–52.
  21. Nashner L. Practical biomechanics and physiology of balance. In: Jacobson G, Newman C, Kartush J, eds. Handbook of Balance Function Testing. Chicago, IL: Singular; 1993:261–269.
  22. Denegar CR, Ball DW. Assessing reliability and precision of measurement: an introduction to intraclass correlation and standard error of measurement. J Sport Rehabil. 1993;2:35–42. [Google Scholar]
  23. Goldie PA, Bach TM, Evans OM. Force platform measures for evaluating postural control: reliability and validity. Arch Phys Med Rehabil. 1989;70:510–517. [PubMed] [Google Scholar]

Articles from Journal of Athletic Training are provided here courtesy of National Athletic Trainers Association

RESOURCES