Hydration Energies and Structures of Alkaline Earth Metal Ions, M²⁺ (H₂O)_n, n = 5–7, M = Mg, Ca, Sr, and Ba

Abstract

The evaporation of water from hydrated alkaline earth metal ions, produced by electrospray ionization, was studied in a Fourier transform mass spectrometer. Zero-pressure-limit dissociation rate constants for loss of a single water molecule from the hydrated divalent metal ions, M²⁺(H₂O)_n (M = Mg, Ca, and Sr for n = 5–7, and M = Ba for n = 4–7), are measured as a function of temperature using blackbody infrared radiative dissociation. From these values, zero-pressure-limit Arrhenius parameters are obtained. By modeling the dissociation kinetics using a master equation formalism, threshold dissociation energies (E_o) are determined. These reactions should have a negligible reverse activation barrier; therefore, E_o values should be approximately equal to the binding energy or hydration enthalpy at 0 K. For the hepta- and hexahydrated ions at low temperature, binding energies follow the trend expected on the basis of ionic radii: Mg > Ca > Sr > Ba. For the hexahydrated ions at high temperature, binding energies follow the order Ca > Mg > Sr > Ba. The same order is observed for the pentahydrated ions. Collisional dissociation experiments on the tetrahydrated species result in relative dissociation rates that directly correlate with the size of the metals. These results indicate the presence of two isomers for hexahydrated magnesium ions: a low-temperature isomer in which the six water molecules are located in the first solvation shell, and a high-temperature isomer with the most likely structure corresponding to four water molecules in the inner shell and two water molecules in the second shell. These results also indicate that the pentahydrated magnesium ions have a structure with four water molecules in the first solvation shell and one in the outer shell. The dissociation kinetics for the hexa- and pentahydrated clusters of Ca²⁺, Sr²⁺, and Ba²⁺ are consistent with structures in which all the water molecules are located in the first solvation shell.

Introduction

Investigations of the structure and reactivity of clusters can provide information relating the chemistry of an individual ion or molecule to that of its bulk form. For studies of hydrated ions and molecules, the ultimate goal is to relate the intrinsic physical properties of a bare ion or molecule to those in aqueous solution. From such measurements, the role of solvent on ion structure and reactivity can be deduced. The structure and reactivity of hydrated molecules and singly charged ions have been extensively investigated by both experiment¹ and theory.² Pioneering studies, such as those of Castleman and co-workers on water clathrates,^1a have provided experimental evidence indicating the importance of hydrogen-bonding networks in the structure and stability of solvent clusters. In contrast to the extensive literature available on singly charged ions, reports on the structure and energetics of multivalent ions are limited.

The development of ionization methods that combine liquid introduction with mass spectrometry has greatly increased the types of solvated ions that can be investigated experimentally. In 1989, Röllgen and co-workers demonstrated that hydrated, doubly charged metal ions such as Sr²⁺ and Ba²⁺ can be produced by thermospray.³ Shortly thereafter, Kebarle and co-workers used electrospray ionization to generate distributions of hydrated, doubly charged ions for several metals.⁴ In combination with high-pressure mass spectrometry, free energies of hydration for individual water molecules in the second solvation shell were measured. More recently, free energies⁵ and enthalpies^5,6 of hydration for both inner- and outer-shell water molecules have been reported. Posey and co-workers⁷ have combined electrospray ionization and photofragmentation mass spectrometry to study divalent transition metal–ligand complexes with methanol and dimethyl sulfoxide (DMSO) molecules located in the second solvation shell. Information about gas-phase structure is deduced from solvent evaporation resulting from electronic excitation of the metal-to-ligand charge-transfer band of these clusters. These experiments also demonstrate that some of the solution properties of these complexes as well as the oxidation states of the metal center are preserved with limited solvation. Stace and co-workers⁸ generated hydrated Cu²⁺ ions by electron impact ionization of neutral metal–solvent clusters formed by combining a molecular beam of water and argon with metal vapor generated from a Knudsen effusion cell. Several groups have also produced extensively hydrated, singly and multiply charged biomolecule ions using electrospray⁹ and are investigating the structure and energetics of these ions using a variety of experimental methods.

Information about the structure and energetics of hydrated divalent metal ions has also been obtained from theory. Successive binding energies and gas-phase structures for hydrated alkaline earth metal ions have been determined by several groups,² and the effects of different coordination geometries and cation size on the calculated thermochemical properties have been investigated. These calculations, however, have only been done on metal ions surrounded by a relatively small number of water molecules. For inner-shell water molecules bound to divalent metal ions, there is very little experimental data available for direct comparison with calculations.

The first measurements of the binding energy for inner-shell water molecules attached to a divalent metal were recently reported by Rodriguez-Cruz et al. for Ni²⁺(H₂O)_6–8 and Ca²⁺(H₂O)_5–7 ions.^6a The measured values for calcium are in good agreement with the B3LYP-calculated values of Pavlov et al.^2c and also with subsequent enthalpy values measured by Kebarle and co-workers.⁵ Recently, we reported binding energies obtained from blackbody infrared radiative dissociation experiments on hexahydrated alkaline earth metal ions.^6b At low temperatures, the binding energies increase with decreasing metal size (Ba < Sr < Ca < Mg). This trend is consistent with the expected reactivity based on ionic radii. At high temperature, binding energies follow the order Ba < Sr < Mg < Ca. The Arrhenius data for hexahydrated Mg²⁺ are not linear, indicating the presence of two isomeric structures for this ion.

In our initial report, the exact nature of these two isomers was not clear. Here, we show evidence that the two structures of this ion correspond to a conformation in which all six water molecules are located in the inner shell at low temperature and a high-temperature structure in which the waters are distributed between two solvation shells, with four water molecules in the inner shell and two in the outer shell the most likely configuration. Binding energies for the pentahydrated alkaline earth divalent ions are also reported. For Mg²⁺(H₂O)₅, the preferred structure appears to be one in which four water molecules are in the inner shell and one is in the outer shell. For Mg²⁺(H₂O)₄, collisional dissociation results indicate that all four water molecules are located in the first solvation shell. The structures for penta- and hexahydrated Mg²⁺ at high temperature are not the lowest energy structures predicted by theory.

Experimental Section

Chemicals.

Chloride salts of Be, Sr, and Ba were obtained from Aldrich (Milwaukee, WI); chloride salts of Mg and Ca were obtained from Fisher Scientific (Fair Lawn, NJ). These samples were used as received. Solutions of the metal ions were prepared by dissolving the corresponding chloride salt in deionized water to a metal ion concentration of ~10⁻⁴ M. Solutions for hydrogen/deuterium exchange experiments were prepared by dissolving the metal salts in deuterated water obtained from Cambridge Isotope Laboratories (Andover, MA).

Blackbody Infrared Radiative Dissociation (BIRD).

All experiments were performed using an external electrospray ionization source Fourier transform mass spectrometer that has been described previously.¹⁰ Hydrated metal ions are generated using nanoelectrospray ionization at flow rates of 10–100 nL/min. Nanoelectrospray tips are prepared from aluminosilicate tubing (1.0 mm o.d., 0.68 mm i.d.) using a micropipet puller (Sutter Instruments model P-87, Novato, CA). The hydrated ions are guided through five stages of differential pumping toward a rectangular cell located in the center of a 2.7-T superconducting magnet. Ions are loaded into the cell for 5 s. A pulse of N₂ gas (10⁻⁶ Torr), introduced during the ion accumulation time, is used to increase the trapping efficiency and thermalization of the ions. This trapping gas is also introduced for 2 s after the ion load event. The base pressure in the cell returns to (4–8) × 10⁻⁹ Torr after a 2-s delay. Next, the ion of interest is mass selected using a combination of single-frequency and stored waveform inverse Fourier transform (SWIFT) excitation waveforms. The isolated ions are then allowed to undergo unimolecular dissociation for times ranging from 10 to 300 s at pressures below 10⁻⁸ Torr. At these low pressures, ions are activated by absorption of blackbody photons generated by the heated vacuum chamber walls.^10–12 All ions are detected using a broad-band chirp excitation with a sweep rate of 3200 Hz/μs. Data are acquired using an Odyssey data system (Finnigan, Madison, WI). From the abundances of parent and daughter ions as a function of reaction time, unimolecular dissociation rate constants are obtained. Kinetic data from the BIRD experiments were obtained as a function of temperature, from which Arrhenius parameters for loss of one water molecule from each of the hydrated ions are obtained. Kinetics for hydrated metal ions that dissociate within a temperature range of 22–210 °C (the maximum temperature range accessible with the current instrumentation) are reported.

Collisionally Activated Dissociation.

Sustained off-resonance irradiation collisionally activated dissociation (SORI–CAD) experiments were performed in the same instrument. After isolation of the cluster of interest, a single-frequency, low-amplitude excitation waveform is applied 5000 Hz above the ion cyclotron frequency (about 1–2 m/z unit lower than the ion of interest) for times ranging from 0 to 30 s. Nitrogen was used as a collision gas and was introduced at pressures between 1.7 and 2.5 × 10⁻⁶ Torr for 1 s prior to, during, and 1 s after the SORI waveform. A delay of 3 s was used before ion detection in order to allow the base pressure in the cell to return to ~5 × 10⁻⁹ Torr. Kinetic data from the SORI–CAD experiments were obtained by monitoring the abundance of the parent and daughter ions as a function of the duration of the single-frequency excitation waveform. For a specific cluster type, the kinetics of dissociation were investigated under similar center-of-mass collision energy (E_com) and average collision frequency. These parameters were adjusted by varying the SORI waveform amplitude and the collision gas pressure. The effect of adjusting these parameters on the internal energy of the ions has been investigated previously.¹³

Structure Calculations.

Molecular dynamics simulations for Mg²⁺ and Ca²⁺ clusters were performed using the AMBER force field included with the Insight/Discover suite of programs (Biosym Technologies, San Diego, CA). Structures from dynamics were used as starting geometries for ab initio calculations at the RHF/STO-3G level. Molecular dynamics simulations were not performed for the Sr²⁺ and Br²⁺ clusters. Instead, starting geometries for Sr²⁺ were obtained by substituting the metal ion in the ab initio Ca²⁺ structures. These Sr²⁺ structures were subsequently optimized at the RHF/STO-3G level. Starting geometries for Ba²⁺ were obtained by substituting the metal in the Sr²⁺ clusters and then optimized at the B3LYP/LANL2DZP level. Ab initio and hybrid method calculations were performed using GAUSSIAN 92 (Gaussian, Inc., Pittsburgh, PA). The STO-3G basis set is not defined for Ba. The LANL2DZP is a basis set that contains an effective core potential and two valence shells for Ba and uses the DZP basis set of Dunning for oxygen and hydrogen atoms.¹⁴ Frequency calculations on these minimized structures provided reactant frequency sets and transition dipole moments for use in the master equation modeling.

Master Equation Modeling.

A detailed description of our implementation of the master equation formalism is given elsewhere.¹² The master equation is a set of coupled differential equations describing the time evolution of a system, in this case the internal energy of a population of ions. Ions in the BIRD experiment can gain energy through absorption of infrared photons, can lose energy through photon emission, and are removed from the reacting (precursor) population through unimolecular dissociation. The master equation simulates this process numerically by dividing the population into energy bins of 100 cm⁻¹ and following the population through a series of defined time steps. The population in a given energy bin can increase by photon absorption from a lower energy state or emission of a photon from a higher energy state. Similarly, an energy bin can be depopulated through absorption or emission of a photon or by dissociation. Einstein A and B coefficients combined with the Planck distribution at a given temperature are used to calculate photon absorption and emission rates at that temperature. Microcanonical dissociation rates are calculated using RRKM theory. A 10-cm⁻¹ grain size is used for density of state calculations. The initial population is chosen to have a Boltzmann distribution of internal energies at the lowest temperature of the BIRD experiment; the modeling is insensitive to the choice of the initial population distribution. The criteria for a fit in the modeling are that the calculated zero-pressure Arrhenius parameters match the measured values within experimental error and that the unimolecular dissociation rates calculated are within a factor of 2 of the measured values.

Vibrational frequencies for both the reactant and transition state as well as transition dipole moments are necessary to calculate the radiative and microcanonical dissociation rates used in the master equation. The calculated vibrational frequencies for the reactant (scaled by 0.91 for RHF calculations) and a range of transition dipole moments were used for the modeling. The transition state was not modeled explicitly. Transition state frequency sets were constructed by modifying six frequencies in the reactant frequency sets. For single-shell structures, a frequency corresponding to a metal–oxygen stretch mode was removed as the reaction coordinate. For two-shell structures, the frequency removed was that corresponding to a hydrogen bond stretch. Five other frequencies were varied systematically to produce rapid energy exchange limit Arrhenius A factors between 10¹⁴ and 10^17.5 s⁻¹ so as to model a range of “loose” transition states. The calculated transition dipole moments were multiplied by factors of 0.5, 1.0, and 1.5, to vary the integrated transition dipoles over a 9-fold range. This takes into account a wide range of uncertainties in the calculated radiative rates. The data for Mg²⁺(H₂O)₆ at low temperature could not be fit using these radiative rates. The transition dipole moments for this cluster were multiplied by 2.0, 3.0, and 4.0 (radiative rates 4–16 times higher than the RHF-calculated values).

Energy Calculations.

Structures used in the master equation modeling were also used as starting structures for higher level geometry optimizations and energy calculations. Hybrid method B3LYP calculations were performed using Jaguar v 3.0 and 3.5 (Schrodinger, Inc., Portland, OR). Geometry optimizations were done using the LACVP** basis set provided with the Jaguar package. This basis set uses effective core potentials of Hay and Wadt¹⁵ for the large metals calcium, strontium, and barium. Other atoms are described using the 6-31G** basis. Zero-point energies were computed from frequencies calculated at the RHF/LACVP** level (frequencies were scaled by 0.91).

Results and Discussion

Electrospray Ionization Mass Spectra.

Electrospray ionization from aqueous solutions of MCl₂ results in an abundant distribution of hydrated, doubly charged metal ions for all the metals except Be. For Be, a distribution of BeOH⁺(H₂O)_n is obtained. Electrospray ionization mass spectra showing the distribution of hydrated ions at room temperature (no reaction delay) for the other metals are given in Figure 1. The relative abundances of these clusters can be varied somewhat by changing electrospray source conditions. For example, Mg²⁺-(H₂O)₆ or Mg²⁺(H₂O)₄ could be made the base peak in the spectrum, but the abundances of both these ions were consistently larger than that of Mg²⁺(H₂O)₅.

Figure 1.

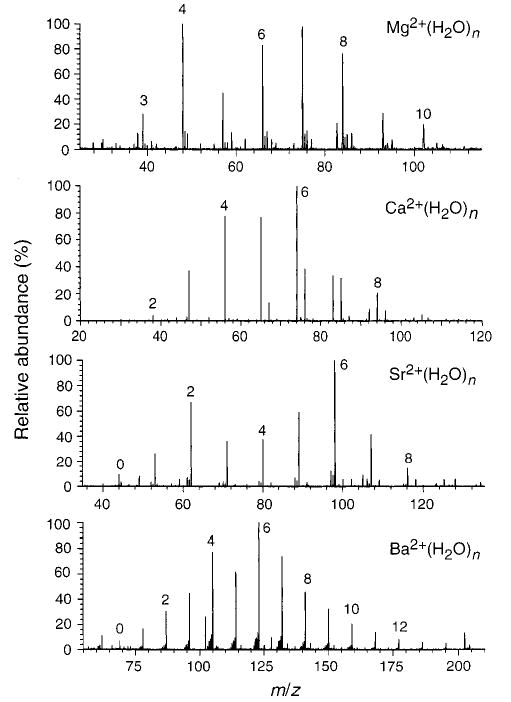
Nanoelectrospray ionization mass spectra obtained from aqueous solutions of (a) Mg²⁺, (b) Ca²⁺, (c) Sr²⁺, and (d) Ba²⁺.

The inability to observe smaller hydrated clusters of Be²⁺ has also been reported by Kebarle and co-workers.⁵ Under similar experimental conditions, abundant Cu²⁺(H₂O)_n ions can be formed when electrospraying from aqueous solutions. Be and Cu have similar second ionization energies, 18.2 and 20.3 eV, respectively.¹⁶ However, their ionic radii differ significantly. For a coordination number of 6, the ionic radius of Be²⁺ is 45 pm, whereas that of Cu²⁺ is 73 pm.¹⁶ Due to its smaller radius, Be²⁺(H₂O)_n has a higher propensity to undergo a proton-transfer reaction at lower extents of hydration, producing BeOH⁺(H₂O)_n−2 and H₃O⁺ ions. The potential energy surface for this proton-transfer reaction versus simple water loss has been calculated at the DFT level for dihydrated alkaline earth metal dications.¹⁷ The energetics of the process to form MOH⁺ and H₃O⁺ is strongly correlated with the radius of the metal. The correlation between reactivity and the second ionization potential of the metal is only indirect. Larger clusters of Be²⁺(H₂O)_n have been observed, and the loss of individual water molecules from these has been investigated.⁵ However, these larger clusters are not sufficiently stable to be observed under the conditions of our experiment.

Blackbody Infrared Radiative Dissociation Kinetics.

At 25 °C, the hydrated metal ions of Mg²⁺, Ca²⁺, Sr²⁺, and Ba²⁺ undergo successive evaporation of water with time down to clusters with six water molecules attached. To dissociate these ions, as well as ions with fewer water molecules attached, higher cell temperatures are required. Figure 2a shows the blackbody infrared radiative dissociation (BIRD) kinetic data for M²⁺(H₂O)₇ at 40 °C. In this figure, the natural log of the normalized abundance of the precursor ion, ln([M²⁺(H₂O)_n]/{[M²⁺(H₂O)_n] + [M²⁺(H₂O)_n−1]}), is plotted as a function of time (first-order kinetics). These heptahydrated metal ions dissociate readily at low temperatures. The rates follow the expected trend in ionic radii: Ba²⁺ > Sr²⁺ > Ca²⁺ > Mg²⁺. The clusters with larger metal ions clearly dissociate at a faster rate that those containing the smaller metals.

Figure 2.

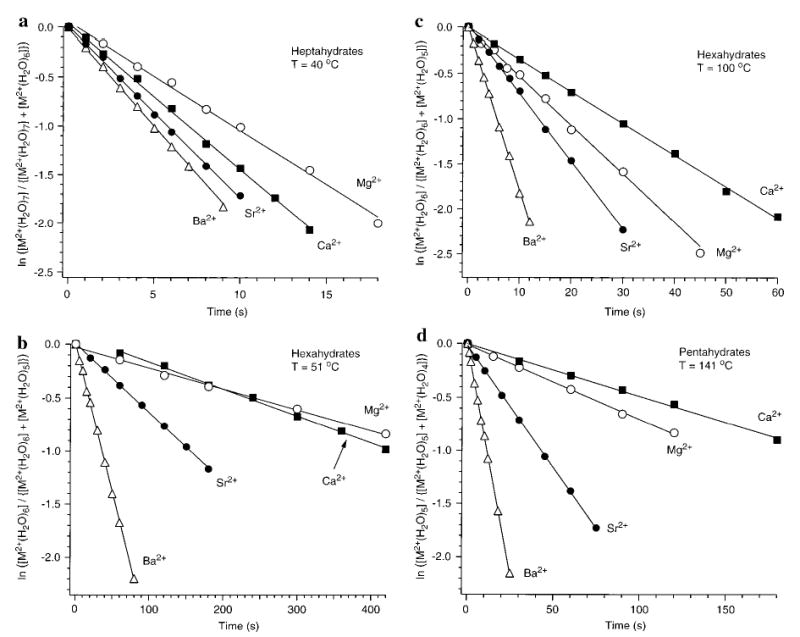
Blackbody infrared radiative dissociation data for (a) M²⁺(H₂O)₇ at 40 °C, (b) M²⁺(H₂O)₆ at 51 °C, (c) M²⁺(H₂O)₆ at 100 °C, and (d) M²⁺(H₂O)₅ at 141 °C. M = magnesium (○), calcium (▪), strontium (•), and barium (▵).

At higher cell temperatures, loss of water from the hexahydrated species is observed. Figure 2b and c shows the dissociation kinetic data for the hexahydrated metals at 51 and 100 °C, respectively. The ordering of the dissociation rates at low temperature is still consistent with the metals’ ionic radii. Surprisingly, the ordering at high temperature is not. Mg²⁺-(H₂O)₆ dissociates faster than Ca²⁺(H₂O)₆ at temperatures above 60 °C. For Ca²⁺(H₂O)₆ at low temperature, an induction period prior to dissociation is apparent. This could be due to the ion population not reaching a steady state of internal energy prior to dissociation, or it could be due to the ion population isomerizing to a less stable structure. The 2 s of N₂ gas introduced prior to isolation for all ions reduced but did not eliminate the induction period for Ca²⁺(H₂O)₆. The rate constant measured for this ion after the induction period does not depend on the duration of the N₂ gas pulse, indicating that the ions reach a steady state. Dissociation rate constants are obtained from the kinetic data after the induction period. At even higher temperatures, where the pentahydrated species dissociate, the same unexpected ordering in dissociation rates is observed (Figure 2d). The fifth water molecule is more readily dissociated from Mg²⁺ than from Ca²⁺ at temperatures between 130 and 210 °C. For the M²⁺(H₂O)₄ ions, only Ba could be dissociated at the maximum temperatures possible with our current instrumentation (210 °C).

For all the clusters investigated, the ion corresponding to the loss of a single water molecule is the only dissociation product observed. The abundances of both precursor M²⁺(H₂O)_n and fragment M²⁺(H₂O)_n−1 ions are measured as a function of reaction time. Unimolecular dissociation rate constants are determined at each temperature from the slope of plots of the natural log of the normalized abundance of the precursor ion, ln([M²⁺(H₂O)_n]/{[M²⁺(H₂O)_n] + [M²⁺(H₂O)_n−1]}), as a function of time. As an illustration, Figure 3 shows the kinetic plots for the unimolecular dissociation of Mg²⁺(H₂O)₆ ions at all the temperatures investigated. All the data have zero y-intercepts and show excellent linear behavior (R > 0.997), indicating that the ion population has reached a steady state prior to dissociation. Furthermore, no second-order behavior is observed at any temperature. This indicates that dissociation occurs from only one structure or from multiple structures that rapidly interconvert.

Figure 3.

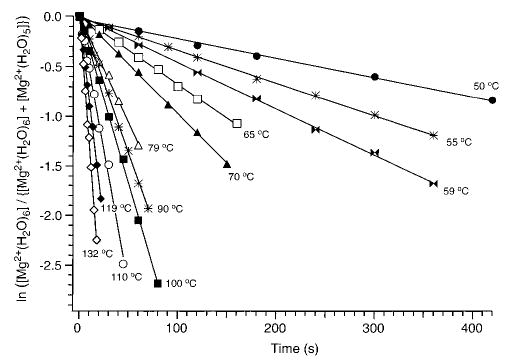
Blackbody infrared radiative dissociation data for Mg²⁺(H₂O)₆ ions between 50 and 132 °C.

Arrhenius Activation Parameters in the Zero-Pressure Limit.

Dissociation rate constants were measured for all hydrated ions that dissociated with rate constants between 0.0015 and 0.30 s⁻¹ over a temperature range of 22–210 °C. This is the full kinetic range measurable with our current experimental apparatus. These data are summarized in the Arrhenius plot shown in Figure 4. As expected, the thermal stability of the ions increases as n decreases. From these data, the zero-pressure-limit activation energy and preexponential factor are obtained from the slope and y-intercept, respectively. These values for each of the ions are given in Table 1.

Figure 4.

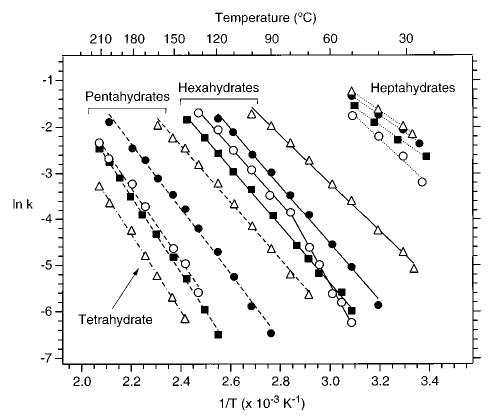
Arrhenius plot for the dissociation of the heptahydrated (dotted lines), hexahydrated (solid lines), and pentahydrated (dashed lines) alkaline earth metal ions. The Arrhenius data for the tetrahydrated barium ions are also shown (dashed–dotted line). Magnesium, calcium, strontium, and barium ions are represented by ○, ▪, •, and ▵, respectively.

Table 1.

Measured Zero-Pressure-Limit Arrhenius Parameters, Threshold Dissociation Energies, Estimated Hydration Enthaply, and Previously Reported Binding Energies and Hydration Enthalpy Values for Loss of One Water Molecule from M²⁺(H₂O)_n Clusters^a

						calculations
M2+	n	log A	Ea	Eo	estimated ΔH298 b	Bock et al.c	Glendening et al.d	Pavlov et al.e	HPMSl
Mg	5	6.1 ± 0.3	15.7 ± 0.5	25.5 ± 1.3	26.3	36.7	29.4	28.0,f 24.4g
	6	10.3 ± 0.4	19.3 ± 0.6	23.5 ± 1.6	24.2	34.0	29.2	24.5,h 19.6,i 23.7j	24.6
		5.7 ± 0.2	12.3 ± 0.4	21.1 ± 1.3	23.4
	7	5.9 ± 0.7	9.9 ± 0.9	17.5 ± 1.2	18.7			19.0k	20.3
Ca	5	6.4 ± 0.1	16.5 ± 0.2	26.3 ± 1.4	26.7	34.2	30.1	27.7,f 22.1g
	6	5.8 ± 0.1	12.4 ± 0.1	21.6 ± 0.8	22.0	31.8	27.2	24.7,h 18.8,i 21.6j	25.3
	7	4.3 ± 0.3	7.4 ± 0.4	16.4 ± 1.2	16.8 (7,0)	21.4		17.6k	16.9
					17.7 (6,1)
Sr	5	5.7 ± 0.2	14.0 ± 0.3	23.8 ± 0.9	23.9		27.8
	6	6.1 ± 0.2	12.4 ± 0.3	20.6 ± 1.0	20.9		25.3		22.7
	7	4.3 ± 0.2	7.3 ± 0.3	16.8 ± 0.9	17.1				17.0
Ba	4	6.1 ± 0.2	16.5 ± 0.3	25.6 ± 0.9	26.4		29.1
	5	5.4 ± 0.1	12.3 ± 0.3	21.1 ± 0.6	21.7		24.6		23.9
	6	5.4 ± 0.2	10.3 ± 0.3	17.9 ± 0.6	18.6		22.5		19.8
	7	4.4 ± 0.1	7.3 ± 0.2	15.2 ± 0.7	16.0				16.9

^aEnergy values reported in kcal/mol.

^bΔH²⁹⁸ estimated from E_o assuming no reverse activation barrier and using calculated frequencies.

^cSuccessive hydration enthalpies, ΔH²⁹⁸, obtained from MP2 calculations (see ref 2a).

^dSuccessive hydration enthalpies, ΔH²⁹⁸, obtained from MP2 calculations (see ref 2b).

^eSuccessive binding energies obtained from density functional theory calculations using

^fM²⁺(H₂O)₅,

^gM²⁺(H₂O)₄(H₂O),

^hM²⁺(H₂O)₆,

ⁱM²⁺(H₂O)₅(H₂O),

^jM²⁺(H₂O)₄(H₂O)₂, and

^kM²⁺(H₂O)₆(H₂O) structures (see ref 2c).

^lHydration enthalpy, ΔH²⁹⁸, values obtained from high-pressure mass spectrometry equilibrium experiments (see ref 5).

A striking feature in the Figure 4 data is that the Arrhenius data for Mg²⁺(H₂O)₆ are not linear; the slope changes at ~80 °C. This unusual Arrhenius behavior indicates that two isomers of this ion are present in this temperature range. The zero-pressure-limit activation energies for both isomers are given in Table 1.

Master Equation Modeling.

Under the experimental conditions used, the ion population does not have a Boltzmann distribution of internal energies. The measured zero-pressure-limit Arrhenius parameters are lower than those that would be measured if the ion population had a Boltzmann distribution of energies (the rapid energy exchange, or REX, limit).^11a The threshold dissociation energy (E_o), the thermochemical value of interest, is derived from the measured Arrhenius parameters in the zero-pressure limit by using master equation modeling. The use of master equation modeling to obtain threshold dissociation energies has been described in detail elsewhere.¹² The master equation modeling process simulates the experiment by calculating radiative rates of absorption and emission and rates of dissociation. The vibrational frequencies and transition dipole moments necessary for the master equation modeling are calculated for each of the ions using ab initio (Mg, Ca, and Sr clusters) or hybrid density functional theory (Ba clusters) methods. These values are somewhat dependent on the structure used for each ion.

For some of the clusters investigated here, multiple structures were considered for the modeling. The heptahydrated clusters of the larger metals strontium and barium were modeled with all seven water molecules located in the first solvation shell around the metal (a (7,0) structure). For the heptahydrated calcium ion, both a (7,0) and a (6,1) structure were modeled. In the latter structure, six water molecules are located in the first shell, and the seventh water molecule is located in the second shell and is hydrogen bonded to two water molecules of the first shell. For the smaller heptahydrated magnesium ion, only the (6,1) structure was modeled. For the hexahydrated metals, threshold energy values were obtained using a (6,0) structure (Figure 5a). For Mg²⁺(H₂O)₆, two additional structures were modeled in which the waters are distributed between the first and second solvation shells around the metal. These (5,1) and (4,2) structures have one and two water molecules located in the outer solvation shell, respectively (Figure 5b and c). A (5,0) structure was used to model the pentahydrated ions; for magnesium, a (4,1) structure was also modeled. The choice of structure has only a small effect on the value of E_o obtained from the master equation modeling. For example, for hexahydrated Mg²⁺ at high temperatures, the ranges of E_o which fit the experimental data were 19.8–21.4, 19.8–21.7, and 20.1–22.4 kcal/mol for the (4,2), (5,1), and (6,0) structures, respectively. Thus, for this species, we report an E_o value of 21.1 ± 1.3 kcal/mol, a range which includes the values of E_o obtained from all the structures modeled.

Figure 5.

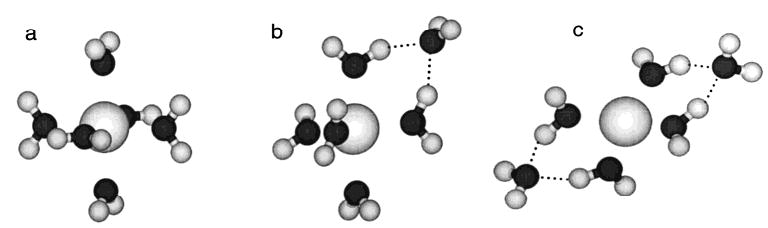
Representative geometries for the (a) Mg²⁺(H₂O)₆, (b) Mg²⁺(H₂O)₅(H₂O), and (c) Mg²⁺(H₂O)₄(H₂O)₂ structures. Hydrogen bonds are indicated with dashed lines.

Threshold dissociation energy values obtained using the modeled parameters and the experimental data are given in Table 1. The range of E_o values reported includes the range of parameters modeled for each one of the structures, the 9-fold variation in the calculated radiative rate constants, and the 10^3.5-s⁻¹ variation in preexponential REX limit A factors, as well as uncertainties in the experimental measurements. For comparison, successive binding energies obtained from recently reported MP2 and DFT calculations² as well as hydration enthalpies from HPMS experiments⁵ are also included in Table 1.

It should be noted that, using the normal range in radiative rates and REX limit A factors, no value of E_o was found to give fits to the experimentally measured zero-pressure E_a, log A, and unimolecular dissociation rate constants for Mg²⁺(H₂O)₆ at low temperature (below 80 °C). Even using a log A of 19.7, which corresponds to the ΔS measured by Kebarle and co-workers⁵ in equilibrium experiments, calculated unimolecular dissociation rate constants were too low by a factor of 4. The data could be fit by multiplying the transition dipole moments by a factor of 3 (integrated rates by a factor of 9) and using high A factors. It appears that radiative rates for Mg²⁺(H₂O)₆ at low temperatures are underestimated in our calculations. The underlying physical reason for the underestimation of the transition dipole moments is not known. Higher than normal values were also required to fit experimental data for proton-bound dimers of N-acetyl-alanine methyl ester.^12b Despite this, excellent agreement with the previously published ΔH value was obtained. The range of E_o’s reported in Table 1 for Mg²⁺(H₂O)₆ at low temperatures is derived by using a transition dipole multiplication factor of 4.0 and includes fits obtained using all three structures [(6,0), (5,1), and (4,2)]. If the rate data in a narrower temperature range (50–70 °C) are used to fit the low-temperature structure, then the experimental data can be fit using a transition dipole multiplication factor of 2.0. The E_o calculated using this narrow temperature range is 23.1 ± 1.2 kcal/mol. This range is within the range of E_o’s calculated using data over a temperature range of 50–80 °C and a higher transition dipole multiplication factor (Table 1).

Binding Energies.

For reactions in which the reverse activation barrier is negligible, the value of E_o corresponds to the binding energy of the ligand. For the reactions measured here, the reverse activation barrier is expected to be very small. Thus, the threshold dissociation energies obtained from these experiments should be approximately the same as the hydration energies at 0 K. We estimate the ΔH²⁹⁸ of hydration from the E_o values by assuming that there is no activation barrier and using RHF/STO-3G frequencies for all metals except Ba, for which B3LYP/LANL2DZP is used. Only one structure for each of these ions was used in these calculations, except for heptahydrated Ca²⁺, for which ΔH²⁹⁸ was estimated for two different structures. For the heptahydrated ions, the values of E_o are similar for all the metals studied but increase slightly with decreasing cation size. A wider range of E_o values is obtained for the hexahydrated ions at low temperature, but the values for Mg and Ca are similar at higher temperature, with the Mg cluster having a slightly lower binding energy. Kebarle and co-workers⁵ have also reported ΔH values for Mg²⁺(H₂O)₆ that are slightly lower than those obtained for Ca²⁺(H₂O)₆ over the temperature range ~150–230 °C. For the pentahydrates, the E_o increases from barium to calcium, but the value for Mg²⁺(H₂O)₅ is slightly below that of Ca²⁺(H₂O)₅! This is consistent with the trend in dissociation rate constants measured for these ions. The only binding energy for M²⁺(H₂O)₄ ions obtainable from these experiments is that of barium. The other tetrahydrated metal ions did not dissociate to a significant extent, even after 180 s at 210 °C, the highest temperature attainable with the current instrumentation.

The values of E_o and ΔH²⁹⁸ (estimated) reported here are in very good agreement with those calculated by Pavlov et al.^2c and also with ΔH²⁹⁸ values recently measured by Kebarle⁵ using high-pressure mass spectrometry for all ions for which the data overlap. The good agreement suggests that the binding energies reported for the other ions should be accurate to within a few kilocalories per mole.

Collisionally Activated Dissociation Kinetics.

The dissociation kinetics for Mg²⁺(H₂O)₆ at high temperature and for Mg²⁺(H₂O)₅ over the entire measurable temperature range do not follow the expected trend in cation size. To determine if this anomalous behavior also occurs for Mg²⁺(H₂O)₄, dissociation kinetics of the tetrahydrated ions were measured using sustained off-resonance irradiation collisionally activated dissociation (SORI–CAD). In this method, the kinetic energy of an ion is increased by applying a low-amplitude waveform with a frequency that is slightly off the ion cyclotron resonance frequency.¹⁸ Ions are excited and subsequently de-excited with a frequency corresponding to the frequency difference between the SORI waveform and the ion cyclotron frequency (the beat frequency). This excitation/de-excitation cycle is repeated many times, during which the ion can undergo many low-energy collisions. This process results in a relatively “slow heating” of the ion. Using this technique, Schnier et al.¹³ demonstrated that it is possible to measure accurate dissociation rate constants from which information about the internal energy of an ion can be obtained. While the information obtained from this method is currently more qualitative than that provided by the BIRD measurements, it does allow higher energy dissociation channels to be accessed. This is necessary in order to dissociate all the tetrahydrated ions except for barium.

To compare the data for different ions, both the center-of-mass collision energy (E_com) and the collision frequency for a given M²⁺(H₂O)_n cluster were kept constant. This was done by varying the amplitude of the off-resonance waveform to fix E_com and by varying the collision gas pressure to keep the average collision frequency constant. The values of E_com and average collision frequency used for each type of cluster are given in Table 2.

Table 2.

Average Center-of-Mass Collision Energies and Average Collision Frequencies for Dissociation of M²⁺(H₂O)_n Ions Using SORI–CAD

n	average Ecom (kcal/mol)	average collision frequency (Hz)a
4	5.3	59
5	1.8	40
6	0.96	29
7	0.59	25

^aCalculated using hard-sphere collision cross sections.

Figure 6 shows the kinetic data obtained from SORI–CAD experiments of the doubly charged metal ions. For the tetrahydrated clusters, data obtained using E_com = 5.3 kcal/mol and a collision frequency of 59 s⁻¹ are shown in Figure 6a. The dissociation rates follow the order Ba > Sr > Ca > Mg. This order directly correlates with the ionic radii of the metals. For the pentahydrated clusters, data obtained using E_com = 1.8 kcal/mol and a collision frequency of 40 s⁻¹ are shown in Figure 6b. The dissociation rates follow the order Ba > Sr > Mg > Ca. This is the same order as that observed by BIRD! The dissociation rate constants obtained from these data are consistent with the SORI–CAD process slowly heating the ions to effective temperatures or energies corresponding to about 170 °C. Similar results are observed for the hexahydrated ions (Figure 6c, E_com = 0.96 kcal/mol, collision frequency = 29 s⁻¹). Under these conditions, the dissociation rate constants follow the order Ba > Sr > Mg > Ca. This is the ordering observed by BIRD at high temperatures.

Figure 6.

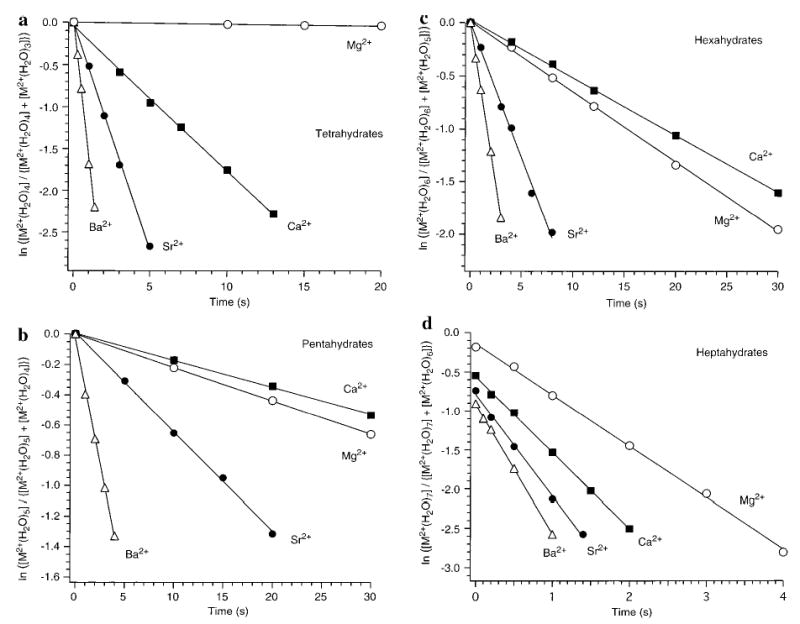
Collisional activated dissociation data for (a) M²⁺(H₂O)₄, (b) M²⁺(H₂O)₅, (c) M²⁺(H₂O)₆, and (d) M²⁺(H₂O)₇ clusters. M = magnesium (○), calcium (▪), strontium (•), and barium (▵). Average center-of-mass energies and average collision frequencies are given in Table 2.

For the heptahydrated clusters (Figure 6d), significant dissociation is observed even without application of the off-resonance waveform. This is due to the fact that these ions dissociate readily at room temperature due to absorption of blackbody photons. This effect is reflected in the nonzero y-intercepts of these kinetic data. The extent of dissociation prior to the application of the SORI waveform is the largest for Ba²⁺(H₂O)₇ and decreases with decreasing metal ionic radius. To measure the SORI–CAD kinetics, an average center-of-mass collision energy of 0.59 kcal/mol and an average collision frequency of 25 s⁻¹ were used. Under these conditions, the relative dissociation rates follow the order Ba > Sr > Ca > Mg. This order in reactivity is the same as that observed by BIRD.

The trends observed by SORI–CAD for n = 5–7 are the same as those observed by BIRD. This suggests that the SORI–CAD trend for n = 4 would also be observed by BIRD at higher temperatures than currently accessible. It should be noted, however, that the SORI–CAD method provides only qualitative information. The collision frequency values were calculated by modeling the (6,0), (5,0), and (4,0) clusters as hard spheres with a radius equal to the metal–hydrogen distance from the modeled structures. Clearly, the collisional cross section depends on the structure, but this dependence is minor. For example, the collision cross section of the (6,0) structure for hexahydrated Mg²⁺ is 8% smaller than that of the (4,2) structure.¹⁹ The internal energy transferred into these clusters by collisions may also depend on the metal ion identity and structure. The infrared radiative emission from these clusters also depends slightly on the metal ion and structure so that these ions are not “heated” identically with this method. Nevertheless, the kinetics for Mg²⁺ and Ca²⁺ are sufficiently different for all these clusters that these factors are not likely to affect the conclusions drawn from these data.

H/D Exchange.

To further investigate the structural differences observed in these clusters, gas-phase hydrogen/deuterium (H/D) exchange experiments were performed. Nanoelectrospray from D₂O solutions of metal ion chloride salts results in only partially deuterated cluster distributions due to back exchange that occurs during the ion injection process. Adding D₂O vapor in the cell ((1–2) × 10⁻⁸ Torr) results in further exchange until completely deuterated clusters are produced. The rates as well as the extent of exchange for magnesium and calcium hexahydrated clusters at both high and low temperature were similar and did not provide information about possible differences in ion structure.

Ion Structures.

Our experimental results are consistent with Ca, Sr, and Ba hexahydrated clusters in which all six water molecules are located in the first hydration shell, or (6,0) structures. For Mg²⁺(H₂O)₆, the two isomers most likely correspond to a (6,0) structure at low temperature and either a (5,1) or a (4,2) structure at high temperature. Our calculations^6b as well as those of Pavlov et al.^2c indicate that the (6,0) structure is the most stable one. At the B3LYP level, the 0 K energy (including a zero-point correction) of the (6,0) structure is lower than those of the (5,1) and (4,2) structures by 2.3 and 4.8 kcal/mol, respectively.^6b This same ordering in stability is reported by Pavlov et al.^2c In their calculations, the (6,0) structure was also found to be more stable than the (5,1) and (4,2) structures by 3.7 and 4.4 kcal/mol, respectively. In Pavlov’s lowest energy (5,1) structure, the outer-shell water molecule has one hydrogen bond to an inner-shell water molecule. In our lowest energy (5,1) structure, the outer-shell water molecule hydrogen bonds to two inner-shell waters (Figure 5b). Previously, we reported^6b that the relative entropies of the possible structures of the hexahydrates might explain the change in structure of the Mg cluster with temperature. However, these calculations did not include symmetry considerations.

The higher temperature structure of Mg²⁺(H₂O)₆ most likely corresponds to a (4,2) conformation. If the (5,1) structure were more stable, dissociation of this ion would most likely produce a (5,0) structure. It seems less likely that a (5,1) structure would dissociate to a (4,1) structure, although we cannot rule out this possibility. If the high-temperature structure were a (5,1) structure which dissociated to a (5,0) structure, then the dissociation kinetics of M²⁺(H₂O)₅ would be expected to follow the trend in cation size. However, the kinetics for M²⁺(H₂O)₅ follow the same order observed for the hexahydrated ions at high temperature and not the trend in cation size. In addition, the E_o for Mg²⁺(H₂O)₅ is slightly less than that for Ca²⁺(H₂O)₅. These results are consistent with Mg²⁺(H₂O)₅ being a (4,1) structure, whereas all the other pentahydrated metals have (5,0) structures. For the tetrahydrated ions, the trend in collisional dissociation rates correlate with the cation size, consistent with all these ions having (4,0) structures.

For the heptahydrated ions, the dissociation data obtained do not allow us to draw any conclusions about their structures. While a (6,1) structure would probably be preferred for the smaller ion magnesium, both (6,1) and (7,0) structures could be present for the bigger metals.

These results are consistent with some computational data on M²⁺(H₂O)_n clusters but are inconsistent with others. Our theoretical and experimental results indicate that the (6,0) structure is the most stable one for all the metals at low temperatures. This is consistent with computational data of others.^2c However, our calculations, as well as those of Pavlov et al., indicate that for magnesium, the (5,1) structure is slightly more stable than the (4,2) structure. But, the experimental data is more consistent with a (4,2) structure. Although our conclusions about these structures are derived from dissociation data, these data are extremely sensitive to ion structure. It is more difficult to rationalize these results with a (5,1) structure for hexahydrated Mg²⁺ at high temperature, although we cannot rule out this possibility.

Similarly, computational results of Pavlov et al.^2c indicate that the (5,0) structure of magnesium is 3.6 kcal/mol more stable than the (4,1) structure. However, our experimental results indicate that the (4,1) structure is more stable for Mg²⁺ within the temperature range investigated.

Conclusions

The kinetics of sequential evaporation of water molecules from hydrated alkaline earth metal ions were measured using blackbody infrared radiative dissociation and collisionally activated dissociation experiments. Binding energies for individual water molecules were determined from Arrhenius activation parameters in the zero-pressure-limit and master equation modeling of the kinetic data. The binding energies for the hepta-and hexahydrated metals at low temperature follow the trend Ba < Sr < Ca < Mg, consistent with the ionic radii of the metals. In contrast, the binding energies for the high-temperature hexahydrates and the pentahydrated ions follow the order Ba < Sr < Mg < Ca. The change in slope observed in the Arrhenius plot for Mg²⁺(H₂O)₆ indicates the presence of two isomeric structures for this ion. Kinetic data from collisionally activated dissociation experiments at constant average center-of-mass collision energy and collision frequency follow the same trend observed by BIRD for the hepta-, hexa-, and pentahydrated ions. For the tetrahydrates, the relative dissociation rates show a direct correlation with the size of the metal ions. These data, in combination with the BIRD results, indicate that the unexpected reactivity observed for the penta- and hexahydrated Mg²⁺ ions at high temperature is due to structures in which the dissociating waters are located in the second solvation shell around the metal and are consistent with a (4,1) and (4,2) structure for these ions. The structures are not predicted to be the most stable structures by theory.