Binding Energies of Hexahydrated Alkaline Earth Metal Ions, M²⁺(H₂O)₆, M = Mg, Ca, Sr, Ba: Evidence of Isomeric Structures for Magnesium

One strategy that has commonly been used to gain a more detailed understanding of ion chemistry in bulk solution is to investigate the structure and energetics of solvated ions in the gas phase. While solvation of singly charged metal ions has been studied extensively during the last two decades,¹ significantly less information about doubly and triply charged metal ions is known. Solvated divalent metal ions can now be readily produced using electrospray ionization (ESI).^2–5 This has led to a significant interest in obtaining thermochemical information about these ions with both experiment^3–5 and theory.^6–8 Kebarle and co-workers measured the Gibbs free energies of hydration for water molecules located in the second solvation shell of a variety of divalent metal ions using equilibrium experiments.³ More recently, Posey and co-workers combined ESI with laser photofragmentation mass spectrometry to study divalent transition metal–ligand complexes with methanol in the second solvation shell.⁴ Binding energies of inner solvent shell water molecules around Ni²⁺ and Ca²⁺ ions have been determined from blackbody infrared radiative dissociation (BIRD) experiments.⁵ Here, BIRD kinetics of the hexahydrated alkaline earth metal ions, Mg²⁺, Ca²⁺, Sr²⁺, and Ba²⁺, are presented. At low temperatures, binding energies obtained from these kinetic data are directly correlated with the radii of the metal ions (Mg²⁺ > Ca²⁺ > Sr²⁺ > Ba²⁺). In contrast, the binding energies at higher temperatures follow the trend Ca²⁺ > Mg²⁺ > Sr²⁺ > Ba²⁺. This is the first direct evidence for two distinct gas-phase structures for a hydrated divalent metal ion.

Experiments were performed using an external electrospray ionization source Fourier transform mass spectrometer that has been described previously.⁹ Hydrated alkaline earth M²⁺(H₂O)_n ions were generated from ~10⁻⁴ M aqueous solutions of the metal chloride salts using nanoelectrospray. Ions are loaded into the cell for 5 s during which time N₂ gas (10⁻⁶ Torr) is introduced. Dissociation kinetics of the mass-selected ion are investigated at pressures <10⁻⁸ Torr. At these pressures, ion activation occurs by absorption of blackbody photons emitted by the heated vacuum chamber walls.^9–11 Unimolecular dissociation rate constants in the zero-pressure limit are measured as a function of temperature (22–140 °C) from which Arrhenius activation parameters are obtained. Under these conditions, the ion population does not have a Boltzmann distribution of internal energies.¹⁰ Measured Arrhenius preexponentials and activation energies are smaller than those measured in the rapid energy exchange (REX) limit. To determine the threshold dissociation energies, master equation modeling of the kinetic data is necessary.¹² The application of the master equation model to obtain threshold dissociation energies has been described in detail previously.¹¹ The reverse activation barriers for these dissociation reactions should be negligible. Thus, the threshold dissociation energy should be equal to the binding energy.

For all metal ion hydrates, dissociation occurs exclusively by loss of one water molecule. The kinetics are first order at all temperatures. Figure 1 shows the Arrhenius plots for dissociation of M²⁺(H₂O)₆ and M²⁺(H₂O)₇. For the heptahydrated clusters, the dissociation rate constants follow the trend Ba²⁺ > Sr²⁺ > Ca²⁺ > Mg²⁺. This trend is consistent with the expected reactivity based on the ionic radii of the metals (water molecules attached to larger metal ions are expected to be less strongly bound). For the hexahydrated ions, this same ordering of rate constants is observed at low temperatures. In striking contrast, the order is Ba²⁺ > Sr²⁺ > Mg²⁺ > Ca²⁺ at higher temperatures; the slope of the Arrhenius plot for Mg²⁺(H₂O)₆ changes around 80°C! BIRD rate constants for the pentahydrated species have the same trend as that observed for the hexahydrated species at high temperature (Ba²⁺ > Sr²⁺ > Mg²⁺ > Ca²⁺).¹³ Thus, these dissociation kinetics do not follow the trend expected based on ionic radii. The change in the slope of the Arrhenius plot for Mg²⁺-(H₂O)₆ shows the presence of two distinct gas-phase structuresfor this ion. The first-order behavior (>80% precursor ion depletion) at all temperatures indicates the presence of one structure or several structures that interconvert.

Figure 1.

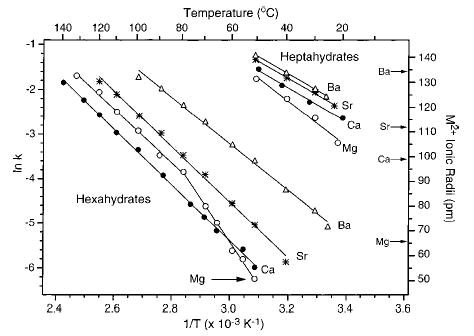
Arrhenius plots obtained from blackbody infrared radiative dissociation data of the hexa- and heptahydrated alkaline earth metal ions; Mg²⁺ (○), Ca²⁺ (•), Sr²⁺ (*), and Ba²⁺ (▵).

The measured zero-pressure limit Arrhenius parameters and the binding energies (E_o) obtained from master equation modeling of the kinetic data are given in Table 1. The low-temperature E_o’s consistently increase with decreasing cation size. At high temperatures, the binding energy of the sixth water molecule to Mg²⁺ (21.1 kcal/mol) is less than that at low temperatures (23.5 kcal/mol). It is also slightly less than that for the larger calcium cation (21.6 kcal/mol). For Mg²⁺(H₂O)_6, anomalously large radiative rate constants were used in the modeling in order to fit the kinetic data at low temperature. The reason for this is not clear, but this suggests that the error in E_o at low temperature may be larger than reported. The unexpected ordering of binding energies at high temperature is consistent with ΔH values recently reported by Kebarle and co-workers from equilibrium experiments at 170–225°C.^3a Recent density functional theory (DFT) calculations by Pavlov et al.⁸ have been used to evaluate structures for hydrated divalent magnesium and calcium ions, M²⁺(H₂O)_m-(H₂O)_n, where m and n correspond to the number of water molecules in the first and second shell, respectively. The successive water binding energies (ΔE_binding) reported for these structures are also included in Table 1.

Table 1.

Measured Zero-Pressure Limit Arrhenius Parameters and E_O Values Obtained from Master Equation Modeling for Loss of Water from M²⁺(H₂O)₆ Ions^a

M	Ea (kcal/mol)b	log Ab	Eo (kcal/mol)c	ΔEbinding (kcal/mol)d
Mg	19.3 ± 0.6	10.3 ± 0.4	23.5 ± 1.6	24.5,e 20.8,f
	12.3 ± 0.4	5.7 ± 0.2	21.1 ± 0.8	19.6,g 23.7h
Ca	12.4 ± 0.1	5.8 ± 0.1	21.6 ± 0.8	24.7,e 18.5,f 18.8,g 21.6h
Sr	12.4 ± 0.3	6.1 ± 0.2	20.6 ± 1.0
Ba	10.3 ± 0.3	5.4 ± 0.2	17.9 ± 0.6

^aPreviously reported B3LYP calculations of successive binding energies are also given.

^bReported errors are obtained from linear least squares analysis of the Arrhenius data.

^cReported errors indicate both experimental error as well as the range of parameters used in the modeling.

^dReference 8.

^eM²⁺(H₂O)₆.

^fM²⁺(H₂O)₅(H₂O) where the water in the second shell is H-bonded to one water in the inner shell.

^gM²⁺(H₂O)₅(H₂O) where the water in the second shell is H-bonded to two different waters in the first shell.

^hM²⁺(H₂O)₄(H₂O)₂.

To further investigate this unexpected reactivity of Mg²⁺(H₂O)₆, we also performed DFT calculations on all four hexahydrated divalent metals.¹⁴ Three different types of structures were studied in which the six water molecules are either all in the first shell or distributed between the first and second solvation shells around the metals. By the use of the nomenclature of Pavlov et al., the structures investigated were M²⁺(H₂O)₆, M²⁺(H₂O)₅(H₂O),¹⁵ and M²⁺(H₂O)₄(H₂O)₂. Calculations indicate that the order of stability is M²⁺(H₂O)₆ > M²⁺(H₂O)₅(H₂O) > M²⁺(H₂O)₄(H₂O)₂ for all of the metals. The energy differences between each of the higher energy structures and the M²⁺(H₂O)₆ conformation are reported in Table 2. Also included in the table are the values of Pavlov et al.⁸ for magnesium and calcium. At this level of theory, all three hexahydrated Mg²⁺ structures have energies within 5 kcal/mol. Several similar energy structures for hexahydrated barium ions were also found. However, no evidence of multiple gas-phase hexahydrated barium structures was observed over the temperature range of these experiments

Table 2.

B3LYP Energy Differences between M²⁺(H₂O)₅(H₂O) and M²⁺(H₂O)₄(H₂O)₂ and the Most Stable M²⁺(H₂O)₆ Structure^a

structure	ΔE(elec. + ZPE)b (kcal/mol)	ΔEtotalc (kcal/mol)
Mg2+(H2O)5(H2O)d	2.3	4.9
Mg2+(H2O)4(H2O)2	4.8	4.4
Ca2+(H2O)5(H2O)d	4.2	5.9
Ca2+(H2O)4(H2O)2	9.6	8.7
Sr2+(H2O)5(H2O)d	3.2
Sr2+(H2O)4(H2O)2	7.5
Ba2+(H2O)5(H2O)d	1.6
Ba2+(H2O)4(H2O)2	3.9

^aPreviously reported values for Mg²⁺ and Ca²⁺ are also shown.

^bThis work;

^cValues from Pavlov and co-workers (ref ⁸).

^dValues reported for structures in which the second shell water molecule is hydrogen-bonded to two inner-shell water molecules.

Although the experimental evidence for two distinct structures for Mg²⁺(H₂O)₆ is clear, the exact nature of these isomers is not. One possibility is that the isomers have different number of water molecules in the first and second shell. The results of DFT calculations show that all three hexahydrated Mg²⁺ structures investigated have 0 K energies within 5 kcal/mol (Table 2). The entropies of Mg²⁺(H₂O)₅(H₂O) and Mg ²⁺(H₂O)₄(H₂O)₂ under standard conditions are higher than that of Mg²⁺(H₂O)₆. The opposite is true for the Ca²⁺, Sr²⁺, and Ba²⁺ hexahydrates. The anomalous entropy for Mg²⁺(H₂O)₆ is presumably due to the crowding of the six water molecules around the much smaller metal ion. This would suggest that the higher temperature structure corresponds to a two-shell structure. Another possible explanation is that one of the isomers is a salt-bridge structure (Scheme 1). Such a salt-bridge structure was found to be stable at the semiempirical PM3 level of theory, but not with the density functional levels of theory applied. The proton-transfer process necessary for the formation of a salt-bridge is expected to occur more readily for hydrated Mg than for the larger metal hydrates.^3b

Scheme 1.

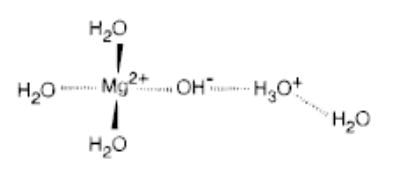
In conclusion, evidence for two distinct isomeric structures of Mg²⁺(H₂O)₆ is presented. This is the first experimental evidence for two isomeric structures of hydrated metal dications. Binding energies of water to Mg²⁺(H₂O)₇ and Mg²⁺(H₂O)₆ (low temperature) follow the expected trend in cation size. These values for Mg²⁺(H₂O)₆ (high temperature) do not. Calculations suggest that the most stable structure for M²⁺(H₂O)₆ is one in which all of the water molecules are in the inner shell. However, further experiments and higher level calculations are necessary to definitively elucidate these structures.