Transcriptional response of steady-state yeast cultures to transient perturbations in carbon source

Abstract

To understand the dynamics of transcriptional response to changing environments, well defined, easily controlled, and short-term perturbation experiments were undertaken. We subjected steady-state cultures of Saccharomyces cerevisiae in chemostats growing on limiting galactose to two different size pulses of glucose, well known to be a preferred carbon source. Although these pulses were not large enough to change growth rates or cell size, ≈25% of the genes changed their expression at least 2-fold. Using DNA microarrays to estimate mRNA abundance, we found a number of distinguishable patterns of transcriptional response among the many genes whose expression changed. Many of these genes were already known to be regulated by particular transcription factors; we estimated five potentially relevant transcription factor activities from the observed changes in gene expression (i.e., Mig1p, Gal4p, Cat8p, Rgt1p, Adr1p, and Rcs1p). With these estimates, for two regulatory circuits involving interaction among multiple regulators we could generate dynamical models that quantitatively account for the observed transcriptional responses to the transient perturbations.

Yeast has evolved to respond rapidly and effectively to fluctuations in temperature, nutrients, and other environmental changes. When environmental conditions change abruptly, cells must rapidly adjust their genomic expression program to adapt to the new conditions. Most environmental perturbations studied to date are complex and appear to provoke multiple regulatory systems simultaneously; Gasch et al. (1) found thousands of genes affected, directly or indirectly, by a great variety of stresses, including such things as starvation, oxidative stress, and heat shock. Furthermore, long-term perturbations, such as introduction of mutations or shifts of medium (2, 3), are inevitably complicated by long-term adaptations as well as short-term responses.

We developed an experimental design intended to focus on the immediate response to environmental change, by making very small and specific perturbations to an otherwise rigorously controlled environment. Cultures growing at steady state in galactose-limited chemostats were subjected to pulses of added glucose, well known to be a preferred source of carbon and energy (4, 5). A single bolus of glucose was added to the growth vessel, and the concentration was allowed to fall naturally by the combination of the constant dilution characteristic of the chemostat and metabolism by the cells. Two sizes of pulse (0.2 or 2.0 g/liter) were administered, so that we could observe a kind of “dose-response” to the same perturbation. The perturbations were small enough to prevent noticeable growth rate alteration and other major physiological changes; however, they proved sufficient to provoke substantial changes in transcript levels. By pulsing with glucose, a metabolite expected to be preferentially consumed by the cells, we expected to capture, over time, two opposite events: response to the addition of the preferred metabolite and then to its disappearance over time.

The cellular response, in terms of transcriptional control, can be represented by the transcription factor activity (TFA) (6, 7). Transcription factors (TFs) become active through series of signal transduction events triggered by extracellular or intercellular metabolites. Activation by translocation, phosphorylation, ligand binding, or other biochemical modifications renders the TF capable of DNA binding and results in gene expression. Direct measurement of TFA profiles is not usually possible; therefore, we treated them as intrinsic (hidden) state variables. Global methods for TFA estimation (8-10) require assumptions of steady-state mRNA production and constant mRNA degradation rate, which do not hold in our case. Therefore, we estimated each TFA locally using mRNA levels of sets of downstream genes thought to be directly regulated by the factor(s). In our analysis we also were able to combine TFA profiles to capture combinatorial regulation of the transcripts.

Results

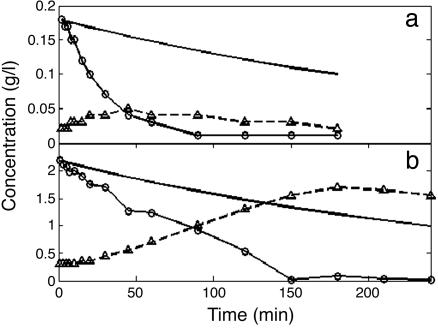
Response to Glucose Pulses. When glucose was added to the cultures growing at steady state in limiting galactose, its concentration immediately began to fall at a rate substantially higher than the rate of dilution (Fig. 1), as expected if the cells immediately began to metabolize it. The observed t_1/2 was three times shorter than that predicted for dilution alone for the high-glucose pulse and approximately nine times shorter for the low-glucose pulse. During each pulse, ethanol concentration increased until the glucose supply was exhausted, ≈45 min for the low pulse and 150 min for the high pulse. No significant change was found in cell number and size (<10%), confirming the expectation that these perturbations were small enough to prevent major changes in cell physiology.

Fig. 1.

Glucose (○) and ethanol (▵) concentrations observed after the 0.2 g/liter (a) and 2.0 g/liter (b) pulses of glucose. The glucose concentrations predicted solely from dilution in the chemostat are shown by the solid line.

General Transcriptional Response to the Pulses. Analysis of the genome-wide pattern of transcription on DNA microarrays (for the complete microarray data see Materials and Methods; see also Supporting Methods, Table 1, and Fig. 7, which are published as supporting information on the PNAS web site) showed that 25% of the yeast genes showed at least a 2-fold change in mRNA levels during the 3 h after the pulse of glucose (i.e., approximately one generation's time). We used go term finder (11) to assign the biological processes associated with the responding genes. The main groups of responders are involved in hexose transport, galactose metabolism, ribosome biosynthesis and assembly, hexose metabolism, tricarboxylic acid cycle, energy reserve metabolism, glucose metabolism, gluconeogenesis, and siderophore transport. Most responding genes were previously observed to be induced during the diauxic shift in batch cultures growing in glucose (12). This shift, which occurs as glucose is exhausted, triggered a change of at least 2-fold in ≈27% of the genes, surprisingly similar to the result found here for just short pulses of glucose.

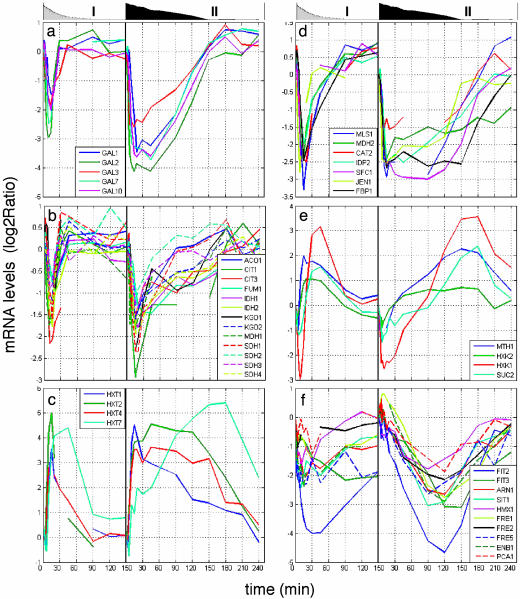
Fig. 2 shows representative mRNA profiles of particular relevance, including the GAL genes themselves (Fig. 2a), in both the low- and high-glucose pulses. The observed fall in the glucose concentration is plotted for comparison. Surveying the kinetics of responses of all these genes to the addition of glucose, we could classify several types of transcriptional response in both the high- and low-glucose pulses.

Fig. 2.

Gene expression patterns of GAL genes (a), tricarboxylic acid cycle genes (b), glucose transporters (c), gluconeogenesis (d), genes with bidirectional response (e), and iron homeostasis genes (f). The left side of each plot shows the low-glucose pulse, and the right side shows the high-glucose pulse. The graphs above the panels are area plots of glucose concentration: low-glucose (0.2 g/liter) pulses (I) and high-glucose (2.0 g/liter) pulses (II).

Burst-Like Response. mRNA levels changed immediately in response to the pulse and then rebounded very quickly. Burst-like response genes include most of the responding genes, including the tricarboxylic acid cycle genes and the ribosomal genes (Fig. 2b). The GAL genes appear to fall into this class (Fig. 2a). One remarkable feature of all of the profiles is that the amplitude of the immediate responses differed only minimally between the high- and low-glucose pulses, although there were substantial differences in duration in some of the profiles.

Lasting Response. Immediate changes in mRNA levels lasted until well after the glucose was exhausted. Lasting response genes included low-affinity glucose transporters (HXT2 and HXT4) (Fig. 2c), glycolysis genes (ENO1, ENO2, and CDC19), and many gluconeogenesis genes (Fig. 2d).

Bidirectional Response. mRNA levels for this class first dipped below the starting level and then rose to a higher peak. Among these genes were MTH1, HXK1, HXK2, and SUC2 (Fig. 2e). The transcripts' amplitudes were not significantly different between the two glucose pulses, but the duration was higher with the higher pulse. There are several other genes involved in carbon metabolism that share the same expression pattern as SUC2: UGP1, GSY1, TPS1, and HXT17.

Slow Repression. mRNA levels slowly decreased until glucose was exhausted. This profile included many iron ion homeostasis genes (Fig. 2f). Their minimum level was achieved at t ≈ 120 min for the high-glucose pulse, as compared with all other repressed transcripts, which reached minima after less than t = 20 min. The pattern is much less clear (and may not really have been achieved) in the low-glucose pulse, with the exception of the FIT2 gene, which is involved in siderophore retention on the cell surface and thus probably belongs to the iron homeostasis group.

Diverse Profiles for Glucose Transporters. The genes encoding glucose transporters Hxt1p, Hxt2p, and Hxt4p were promptly expressed after glucose addition (Fig. 2c), but the mRNA level for HXT1 began to fall after a short time. The HXT7 mRNA level was the last to rise, with time to half max of 60 min in the high-glucose pulse, compared with ≈7 min for the others. The amplitudes are again not significantly different between the two pulses. The activation concentration of the various glucose transporters is correlated well with their previously published affinities for glucose (13, 14). These results are entirely consistent with what has been published about the regulation of these glucose transporter genes. The HXT1, HXT2, and HXT4 genes are regulated by Rgt1p (15-17), which accounts for their fast and lasting response to glucose. Rgt1p is a repressor, which also acts as an activator of HXT1 at high glucose levels; this explains the earlier decrease in HXT1 mRNA, when Rgt1p no longer activates it. The basis of HXT7 regulation is unknown.

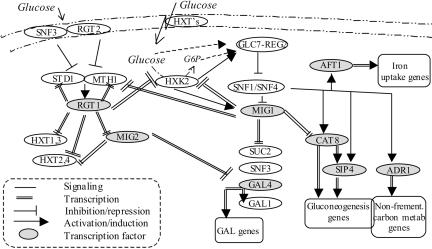
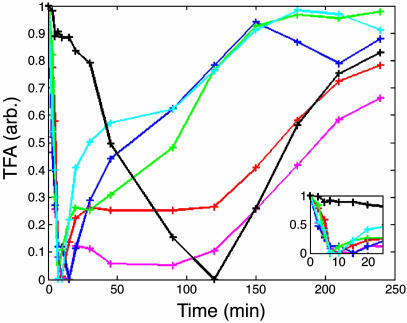
TFAs. To model the regulatory mechanism that generates the observed responses, we plotted a map of the known glucose regulatory events based on the literature (Fig. 3) and estimated the TFAs in arbitrary units as a function of time (Fig. 4) for the TFs involved (see Materials and Methods). The rate of initial change in activity was observed to be the same for all TFs except Rcs1p/Aft1p. Regardless of the regulatory role, activators (Gal4p, Cat8p, and Adr1p) or repressors (Mig1p and Rgt1p), and the direction of the change in activity [increasing for Mig1p or decreasing (the others)], the t_1/2 of the response is ≈8 min for both high pulses (Fig. 4 Inset) and low pulses (data not shown). Mig1p, Adr1p, and Gal4p have similar profiles of a short-term change in activity, whereas Cat8p and Rgt1p activities are prolonged. Rcs1p has a slower initial response, but it has a derepression rate similar to those of Rgt1p and Cat8p. With these TFA values in hand, we were able to model some of the responses to the glucose pulses.

Fig. 3.

Mechanism of glucose repression and induction. Glucose is transported into the cell by Hxt transporters with diverse affinities. Intracellular glucose is converted to glucose-6-phosphate primarily by Hxk2p and then fermented to ethanol and CO₂ (5). Snf1p protein kinase is one of the main players in glucose repression and the induction pathway; it regulates the activities of TFs of glucose repression genes (Mig1p) and gluconeogenesis (Cat8p-Sip4p and Adr1p). In the presence of glucose, Snf1 is deactivated by the phosphatase, Glc7p-Reg1p, in a Hxk2p-dependent manner (15). Once inhibition by Snf1p is released, Mig1p is phosphorylated, enters the nucleus, and represses the expression of alternative carbon source utilization genes (e.g., GAL4, SUC2, SNF3, and gluconeogenesis TF genes CAT8 and SIP5) (5). Iron uptake and transport genes are induced throughout Snf1p/Snf4p and the TF Rcs1p, independent of iron starvation (22). A separate sensing pathway mediates glucose induction of mainly glucose transporter genes. Extracellular glucose binds to glucose receptors Snf3p or Rgt2p (with high and low affinities, respectively) to generate a signal that inactivates the transcriptional receptor Rgt1p. This signal induces the HXT genes, MIG2, and its own activators, STD1 and MTH1 (29, 16). The glucose signal inhibits Rgt1p-mediated expression by stimulating the degradation of Mth1p and Std1p (28). The two pathways, Snf1-Mig1 and Rgt1, are interconnected in both protein signaling and transcriptional levels mainly throughout Mth1p and Hxk2p, which are regulated by both Mig1p and Rgt1p (18, 30) and have a signaling role in the pathways. In addition, Mig1p regulates one of the sensors of the Rgt1 pathway, Snf3p, where Rgt1p regulates the transporters that bring the Snf1 pathway into action. Another glucose sensing and signaling mechanism, not shown here, is responsible for activation of ribosomal and glycolysis genes and repression of glycogen, trehalose, and stress genes through Gpr1p, cAMP, and PKA (4).

Fig. 4.

The estimated TFAs with the 2 g/liter glucose pulse, 1-Mig1 (blue), Gal4 (green), Cat8 (red), Rgt1 (pink), Adr1 (cyan), and Rcs1 (black). (Inset) A zoom-in to the initial time points.

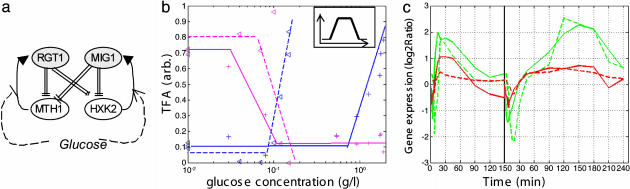
Bidirectional Response Model for Genes Controlled by Rgt1p and Mig1p. In our data, HXK2 and MTH1 (Fig. 2e) displayed similar transcript patterns: for the high pulse, a sharp decrease until t = 10 min, followed by a gradual increase to higher than initial levels, reaching their peak when glucose was depleted and then dropping down. For the low pulse the same pattern appeared, with a compressed time scale. Two repressors, Mig1p and Rgt1p, which are oppositely responsive to glucose (Fig. 5a), have been reported to regulate both genes (15, 18). When glucose levels increase, Rgt1p repression is relieved and repression by Mig1p is enhanced.

Fig. 5.

Bidirectional response model. (a) Mig1-Rgt1 circuits. (b) The estimated TFA during derepression. Blue, Mig1p; pink, Rgt1p; solid line, high pulse; dashed line, low pulse. (Inset) The combined factors pattern of gene activation. (c) The expression of MTH1 (green) and HXK2 (red) genes, measured (solid line) and model-predicted (dashed line)

The TFA plot (Fig. 5b) reveals the different thresholds of the repressors, with Rgt1p at ≈0.03 g/liter and Mig1p at ≈0.7 g/liter, so that, when the glucose pulse begins, there is Mig1p-dependent repression, which is relieved when glucose concentration drops below 0.7; then, when it drops below 0.03 g/liter, Rgt1p is activated to reestablish repression. As described in Materials and Methods, a quantitative model of regulation of the mRNA level for the HXK2 and MTH1 genes by combined TFs was generated. As shown in Fig. 5c, the model succeeded in producing the observed bidirectional mRNA profile, including amplitude and duration, for both the low-glucose and high-glucose pulses.

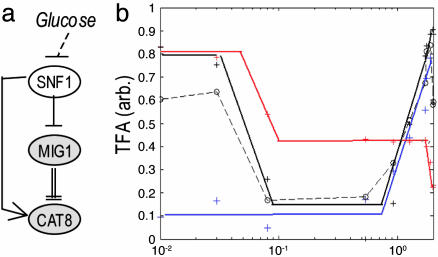
Lasting Response Model for Genes Regulated by Cat8p, Mig1p, and the Snf1p Kinase. The lasting response genes that are regulated under the transcriptional activator Cat8p were used to calculate its active profile; the CAT8 gene itself is under Mig1p regulation (19) and was used to calculate active Mig1p's profile. Both Mig1p and Cat8p receive signal from glucose throughout Snf1p (19) in a feed-forward manner. High glucose initiates the repression of CAT8 by Mig1p (decreasing the number of activator molecules) and also directly decreases the activity of Cat8p itself (Fig. 6a).

Fig. 6.

Lasting response. (a) Mig1-Cat8 circuit. (b) The estimated active TFs during derepression after a high-glucose pulse. Blue, Mig1p; red, Cat8p; black solid line, Rcs1p; black dashed line, predicted Snf1p activity.

The TFA curves (Fig. 6b) show that Mig1p and Cat8p have different glucose (or Snf1p) thresholds; Cat8p's final threshold is at an ≈10-fold lower concentration than that of Mig1p (from the high pulse data), indicating the short-term Mig1p activity. Therefore, the lasting response of Cat8p might be attributed to Snf1p and not to Mig1p. Although Mig1p's activity is also regulated by Snf1p (20, 21), it has different kinetics. This finding could be explained either by different thresholds or by different Snf1p complexes involved in each interaction. The pattern of Snf1p signaling activity is estimated by substituting Mig1p activity from that of Cat8p; it correlates well with the pattern of Rcs1p transcriptional activity, downstream of Snf1p (22).

Comparing the TFAs for the Two Pulses. Rgt1p's activities have similar dependency on the concentration of glucose for the two pulses (Fig. 5b); Cat8p displays similar behavior (data not shown). However, Mig1p's activity does not depend linearly on the glucose level; its thresholds are different for the different pulses (≈0.8 g/liter for the high pulse and ≈0.08 g/liter for the low pulse) (Fig. 5b). In the glucose ranges that we tested (both commonly regarded as “low-glucose”) it seems to act as a digital pulse, with the same amplitude and width, regardless of glucose level. Direct measurements of Mig1p localization at different glycolytic rates (23) support this interpretation.

Discussion

We designed our experiment in the hope that the stimulus and response could be observed cleanly in a procedure that minimizes the introduction of confounding physiological changes. To this end, we arranged for the cells to be in a steady state, so that gene expression pattern and metabolic fluxes could be safely assumed to be constant and any changes could be attributable to the perturbation. The addition of a small amount of glucose, although a major factor for the cell's metabolism, as indicated by the immediate responses of so many genes, nevertheless did not alter the cell growth rate and size.

Thus, we are reasonably confident that all responses that we observe are, directly or indirectly, consequences of just the brief glucose pulse and not any other component in the system. Moreover, the small stimulation allowed us to capture interesting patterns of regulation that could be masked with high/saturated doses, and, by following the kinetics, new correlations in gene expression could be revealed. Cells grown in chemostat are “poor but not starving” (24, 25), and, indeed, no explicitly starvation-related and stress-response genes were activated (except for “stress” genes that were previously known to be induced by glucose-related pathways).

Most responding genes have a burst-like expression pattern, relatively uncorrelated with the measured glucose and ethanol concentrations and consumption rates. Even a low added-glucose level triggered the subsequent transcriptional responses, although the duration sometimes was truncated relative to a longer pulse. One of the TFs involved, Mig1p, also reflects this behavior, because it seems to act as a digital pulse. The initial response to very low levels of glucose added to the culture imply the high importance of fast adaptation to it. We suggest that there is more than one discrete wave of transcriptional response to glucose appearance, where each wave “reevaluates” the level of glucose, and maybe also its derivatives, and responds appropriately. Similar discrete regulation was found with responses to stress with the SOS DNA repair system in Escherichia coli (26) and the human p53-mdm2 (27). To test this suggestion, analysis of single-cell response with high temporal resolution is required.

Bidirectional response is generated by repression of two TFs with different activity thresholds (Mig1p and Rgt1p). Their downstream genes, HXK2 and MTH1 (28-30), participate in the regulation of two of the glucose pathways (HXK2 may also have a role in the cAMP-related pathway). They are regulated in opposing directions by glucose, with low expression at high and at very low glucose levels and high expression at an intermediate level, which implies adaptivity. For Mth1p, which is a sensor for glucose, protein production is the mean to achieve adaptivity, because the protein is degraded in the presence of glucose. The high gene expression at intermediate glucose levels increases its sensitivity to glucose at that range.

The expression pattern of Mth1 and Hxk2 was captured by using a simple model. We suggest that contradicting signals also regulate SUC2, HXK1, and the additional genes with similar expression patterns.

Iron ion homeostasis genes respond to glucose signals through Snf1p regardless of iron deprivation signals. We suggest that this signaling pathway is an evolutionary adaptation to successive cellular events; i.e., if a consequence of glucose addition is the impending depletion of Fe ions, a cell that would start expressing the iron homeostasis genes once glucose is added will have an advantage over a cell that will do that only when iron is depleted. This kind of anticipatory coordinated expression could explain the large number of mRNAs changing in response to glucose throughout glucose signaling pathways.

The sharp drop in mRNA levels of the repressed genes is due to a high degradation rate. The mRNA's half-lives representing degradation under glucose exponential growth (31) are ≈3-fold higher than those detected in our experiments. It was recently reported that feeding glucose to cells growing on other carbon sources increases the mRNA degradation rate for a few genes (JEN1 and FBP1) (32). It is possible that the same phenomenon occurs with the larger set of genes we see in our experiments.

To conclude, we believe that experiments designed around short perturbations of cells growing in steady state may be of general use in understanding metabolic regulatory networks. Estimated active TF response curves generated as described above provide a complex picture of the cells' dynamical regulation, but one that can readily be used to produce models that can be compared with experimental observations. In turn, successes in such modeling can provide experimental support for proposed regulatory modules. Extending the scope of the analysis by additional estimated TFAs would provide a broader view of the cellular response and enable additional modules to be supported by experimental evidence.

Materials and Methods

Strain and Growth. DBY10085 is a haploid prototrophic derivative of CEN.PK122 (Mata;UR A;LEU;HIS;TRP;M AL2-8^C;SUC2). Minimal defined medium contains, in addition to carbon source, CaCl₂·H₂O (0.1 g/liter), NaCl (0.1 g/liter), Mg₂(SO₄)₂·7H₂O (0.5 g/liter), K₂HPO₄ (1 g/liter), (NH₄)₂SO₄ (5 g/liter), boric acid (0.5 mg/liter), CuSO₄·5H₂O (0.04 mg/liter), KI (0.1 mg/liter), FeCl₃·5H₂O (0.2 mg/liter), MnSO₄·H₂O (0.4 mg/liter), Na₂MoO₄·2H₂O (0.2 mg/liter), ZnSO₄·5H₂O (0.4 mg/liter), biotin (2 μg/liter), calcium pantothenate (400 μg/liter), folic acid (2 μg/liter), inositol (2 mg/liter), niacin (400 μg/liter), p-aminobenzoic acid (200 μg/liter), pyridoxine HCl (400 μg/liter), riboflavin (200 μg/liter), and thiamine HCl (400 μg/liter).

Chemostat. A 300-ml fermenter vessel was adapted as a chemostat by using minimal defined medium with 2 g/liter galactose, 5 standard liters/min air flow, and stirring at 400 rpm at 30°C. The dilution rate was ≈0.2 vol/h. Once the chemostat culture achieved a constant cell number for at least 3 vol changes, a glucose pulse (enough to bring the transient concentration in the vessel to 0.2 or 2.0 g/liter) was injected into the vessel. In experiment set A, samples were collected at t = 0, 5, 10, 20, 30, 45, 60, and 90 min. In experiment set B, samples were collected at t = 0, 1, 3, 5, 7, 10, 15, 20, 30, 45, 60, 90, 120, 150, 180, 210, and 240 min for the high-level pulse, and at t = 0, 2, 4, 6, 8, 10, 15, 20, 30, 45, 60, 90, 120, 150, and 180 min for the low-level pulse. The same samples were used to measure glucose and ethanol concentrations, cell number and size, and mRNA levels. The results presented here are from set B; the reference for the DNA microarrays was the t = 0 sample. All of the features we describe for set B appeared also in set A.

Physiological Measurements. At each time point a sample was withdrawn and divided for the following analyses.

Cell density, number, and size. A 1-ml sample was sonicated (a 10-s 50% duty cycle). The density was measured by light scattering at 600 nm, and cell number and size were measured in a Coulter counter (model Z2, Beckman Coulter).

Glucose and ethanol. A 1-ml sample was centrifuged at high speed to remove cells; the supernatant was stored at -20°C. The residual glucose and ethanol concentration in the growth medium were assayed by enzyme-coupled NADH oxidation reactions (assay kits from R-Biopharm, Darmstadt, Germany).

RNA Isolation, Labeling, Microarray Hybridization, and Analysis. Five-milliliter samples were vacuum-filtered onto a nylon filter, which was quickly placed into a tube and stored in liquid nitrogen at -80°C. RNA was extracted from culture filtrate by the acid-phenol method followed by ethanol precipitation (33), amplified (MessageAmp aRNA Kit, Ambion), and labeled with Cy3 (time points) or Cy5 (reference). Cy5- and Cy3-labeled probes were hybridized together to microarrays printed with PCR-amplified fragments containing all known and predicted Saccharomyces cerevisiae ORFs (12). Microarrays were washed and then scanned with a GenePix 4000B laser scanner (Axon Instruments, Foster City, CA), and the images were analyzed by using genepix pro software. Resulting microarray data were submitted to the Stanford MicroArray Database (34) (http://genome-www5.stanford.edu).

Results for each gene and time point are expressed as log₂ of the ratio of sample signal divided by the reference signal. Spots were filtered by correlation (0.6), level over background (at least 80% of pixels > background + 1 SD), and by manual gridding of the image.

Models. The mRNA signal is modeled as

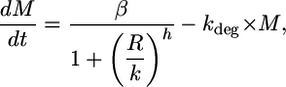[1]

for a TF that functions as a repressor, where M is the mRNA level, R is the effective repressor concentration, β is the maximal production rate, k is the affinity of the TF (concentration at half maximal repression), h is Hill coefficient (indicating the level of cooperativity), and k_deg is a rate constant for mRNA degradation. The model assumes that cell growth rate remains constant.

Rewriting Eq. 1, we get the mRNA production term X:

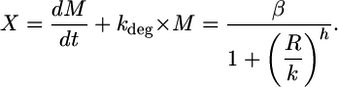[2]

For TF that functions as an activator we get

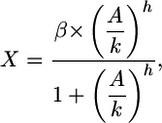[3]

where A is the activating TF concentration.

For a combined activator-repressor model we get

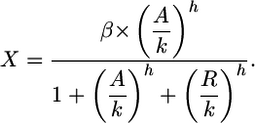[4]

More complex combined models were tested, but the resulting predictions were not significantly altered.

TFA Estimation. The relative transcription activity of Mig1, Cat8-Sip4, Rgt1, Gal4, Adr1, and Rcs1 were calculated. mRNA log₂ (ratio) values of the genes were used with missing values estimated by knnimpute (35). The left side of Eq. 2 was calculated as k_deg = log₂/minimal t_1/2; it is assumed that k_deg values are constant over the experiment's time, except at t = 0, where values from ref. 31 were used. We transformed the ratio model to a bilinear form and determined the parameter R (or A) using singular-value decomposition (for details see ref. 7). Their levels were set in the range [0, 1]. Nonlinear least squares was used to calculate the parameters k and h (lsqnonlin matlab 7, Mathworks, Natick, MA). Cat8p activity is combined with that of Sip4, because they are inseparable, and, similarly, Mig2p is combined with Mig1p. Rcs1p activity was calculated for the high pulse only, because the data for the low pulse was too noisy. Estimation of other TFs (Sfp1/Fhl1/Ifh, ribosomal biogenesis TFs) was not attempted here.