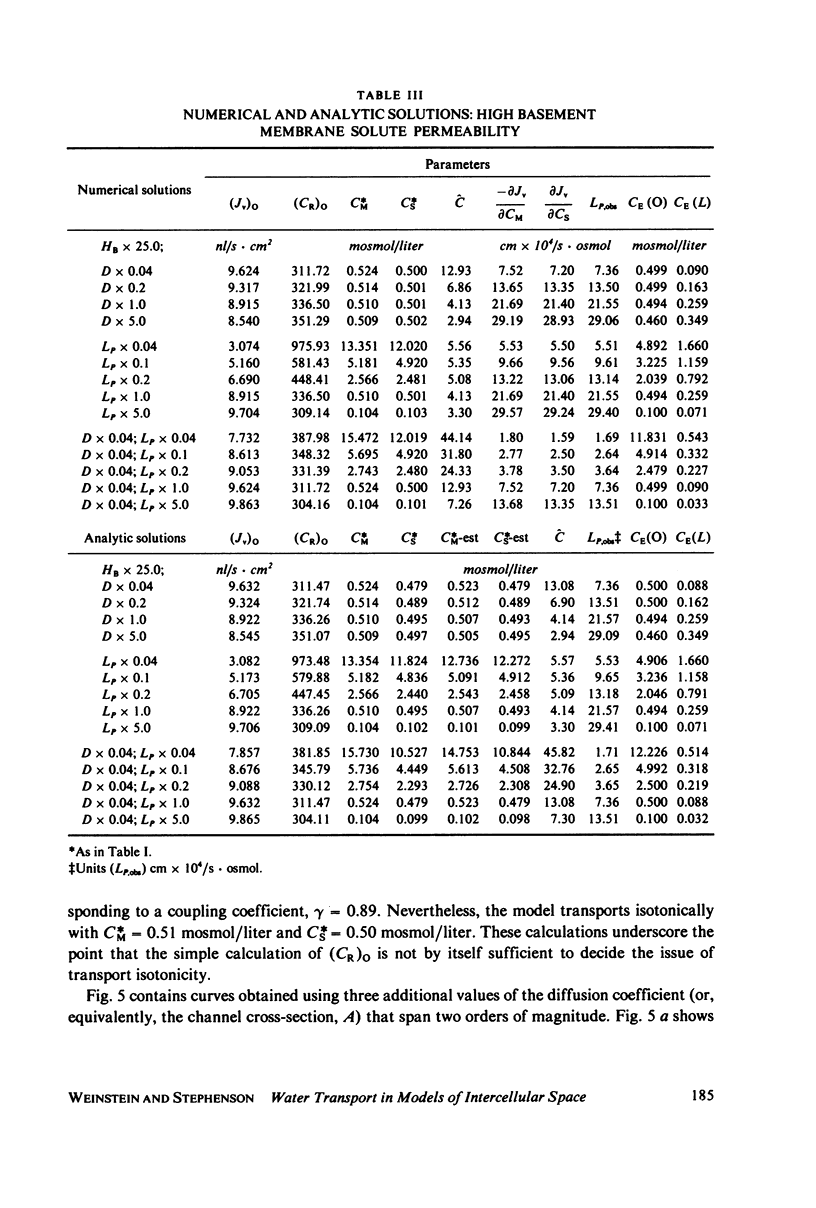
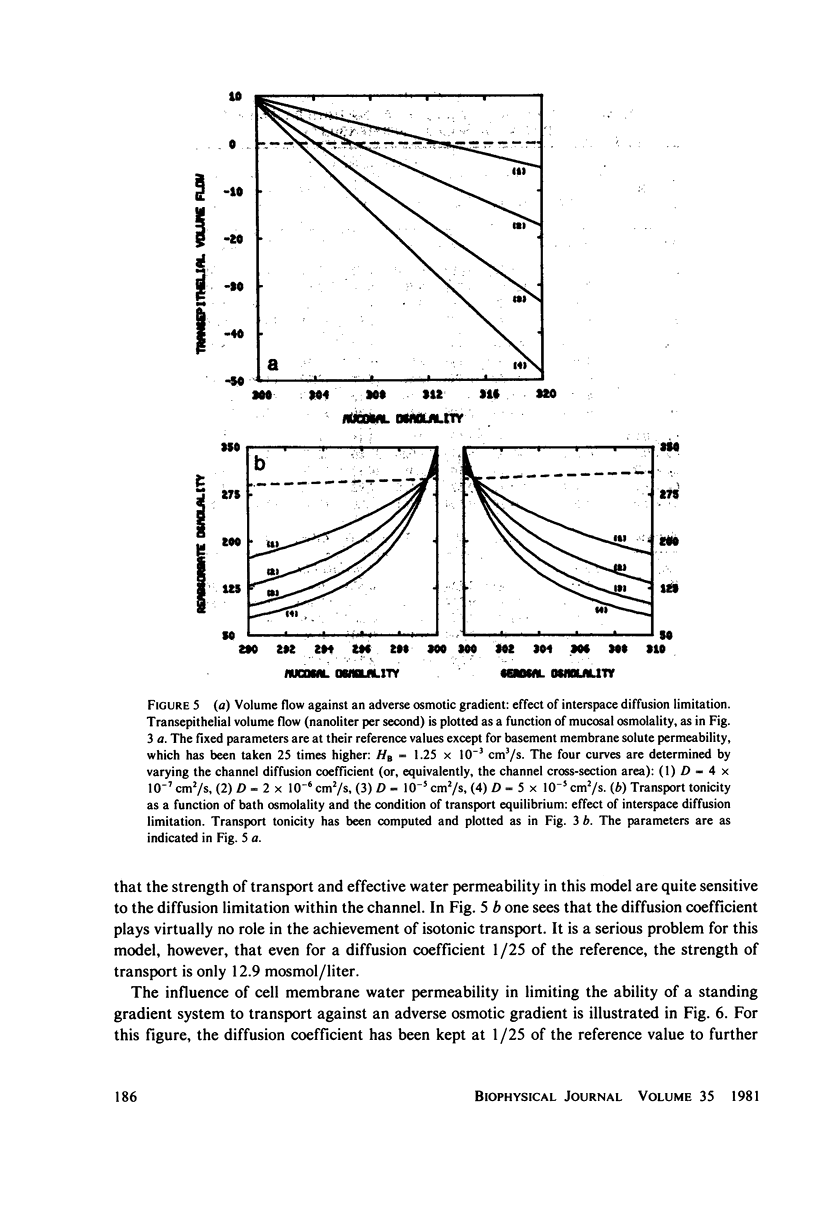
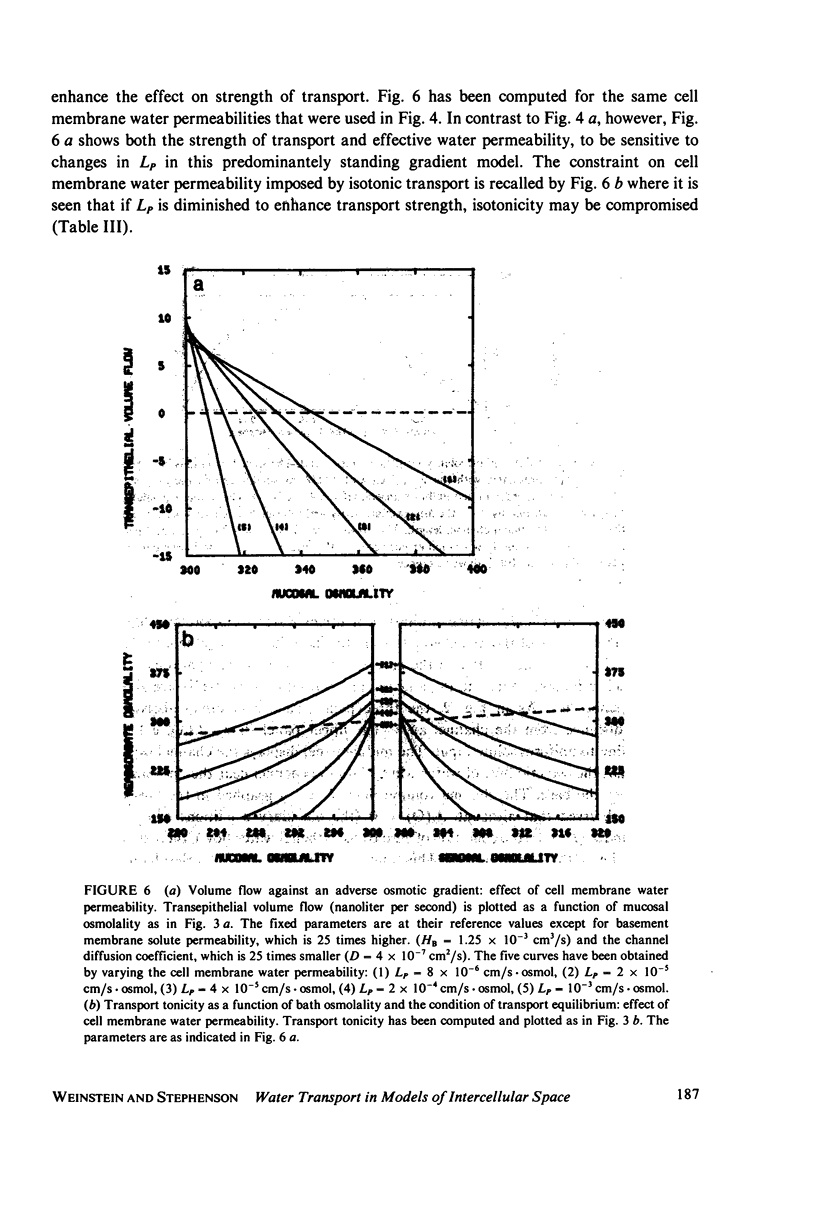
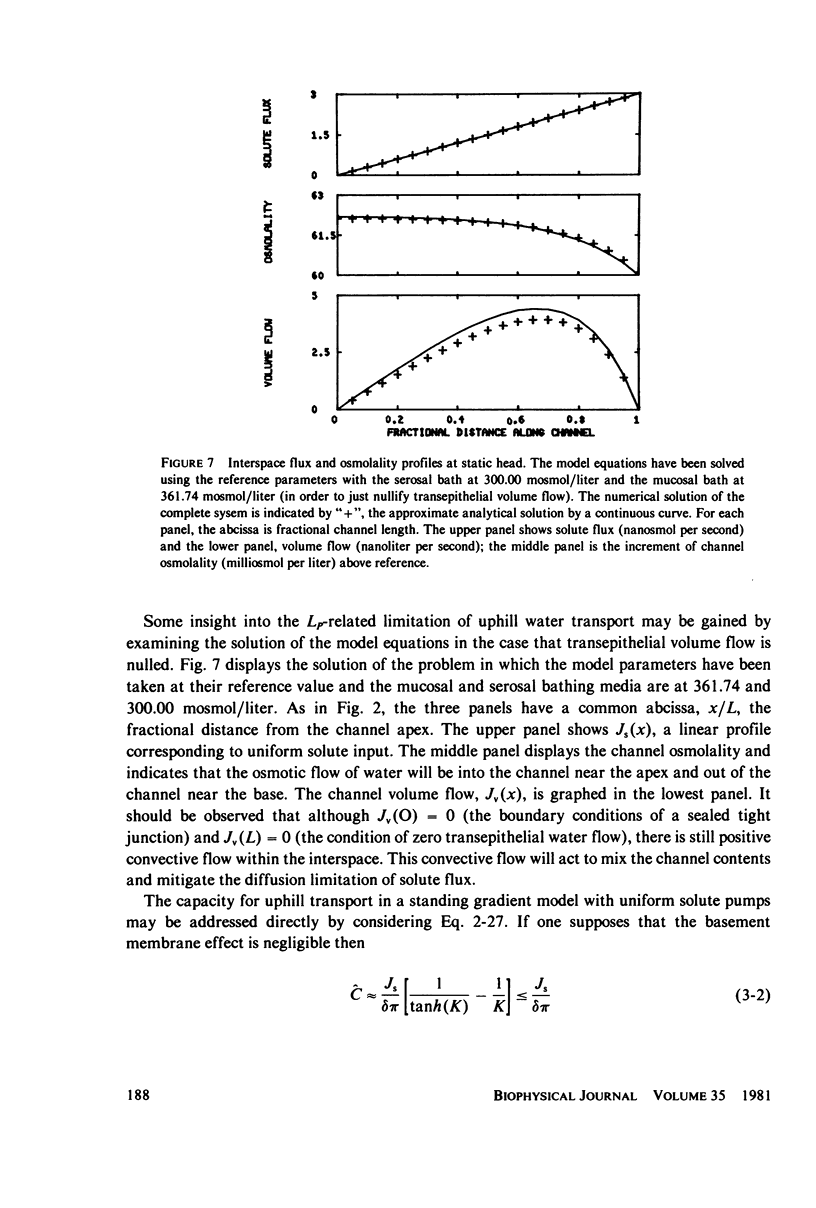
Abstract
A standing gradient model of the lateral intercellular space is presented which includes a basement membrane of finite solute permeability. The solution to the model equations is estimated analytically using the "isotonic convection approximation" of Segel. In the case of solute pumps uniformly distributed along the length of the channel, the achievement of isotonic transport depends only on the water permeability of the cell membranes. The ability of the model to transport water against an adverse osmotic gradient is the sum of two terms: The first term is simply that for a well-stirred compartment model and reflects basement membrane solute permeability. The second term measures the added strength due to diffusion limitation within the interspace. It is observed, however, that the ability for uphill water transport due to diffusion limitation is diminished by high cell membrane water permeability. For physiologically relevant parameters, it appears that the high water permeability required for isotonic transport renders the contribution of the standing gradient relatively ineffective in transport against an osmotic gradient. Finally, when the model transports both isotonically and against a gradient, it is shown that substantial intraepithelial solute polarization effects are unavoidable. Thus, the measured epithelial water permeability will grossly underestimate the water permeability of the cell membranes. The accuracy of the analytic approximation is demonstrated by numerical solution of the complete model equations.
Full text
PDF
















Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Blom H., Helander H. F. Quantitative electron microscopical studies on in vitro incubated rabbit gallbladder epithelium. J Membr Biol. 1977 Oct 3;37(1):45–61. doi: 10.1007/BF01940923. [DOI] [PubMed] [Google Scholar]
- CURRAN P. F., MACINTOSH J. R. A model system for biological water transport. Nature. 1962 Jan 27;193:347–348. doi: 10.1038/193347a0. [DOI] [PubMed] [Google Scholar]
- CURRAN P. F. Na, Cl, and water transport by rat ileum in vitro. J Gen Physiol. 1960 Jul;43:1137–1148. doi: 10.1085/jgp.43.6.1137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CURRAN P. F., SOLOMON A. K. Ion and water fluxes in the ileum of rats. J Gen Physiol. 1957 Sep 20;41(1):143–168. doi: 10.1085/jgp.41.1.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DIAMOND J. M. THE MECHANISM OF ISOTONIC WATER TRANSPORT. J Gen Physiol. 1964 Sep;48:15–42. doi: 10.1085/jgp.48.1.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DIAMOND J. M. TRANSPORT OF SALT AND WATER IN RABBIT AND GUINEA PIG GALL BLADDER. J Gen Physiol. 1964 Sep;48:1–14. doi: 10.1085/jgp.48.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiBona D. R., Mills J. W. Distribution of Na+-pump sites in transporting epithelia. Fed Proc. 1979 Feb;38(2):134–143. [PubMed] [Google Scholar]
- Diamond J. M., Bossert W. H. Standing-gradient osmotic flow. A mechanism for coupling of water and solute transport in epithelia. J Gen Physiol. 1967 Sep;50(8):2061–2083. doi: 10.1085/jgp.50.8.2061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diamond J. M. Non-linear osmosis. J Physiol. 1966 Mar;183(1):58–82. doi: 10.1113/jphysiol.1966.sp007851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diamond J. M. Osmotic water flow in leaky epithelia. J Membr Biol. 1979 Dec 31;51(3-4):195–216. doi: 10.1007/BF01869084. [DOI] [PubMed] [Google Scholar]
- Hill A. E. Solute-solvent coupling in epithelia: a critical examination of the standing-gradient osmotic flow theory. Proc R Soc Lond B Biol Sci. 1975 Jun 20;190(1098):99–114. doi: 10.1098/rspb.1975.0081. [DOI] [PubMed] [Google Scholar]
- Hill B. S., Hill A. E. Fluid transfer by Necturus gall bladder epithelium as a function of osmolarity. Proc R Soc Lond B Biol Sci. 1978 Feb 23;200(1139):151–162. doi: 10.1098/rspb.1978.0012. [DOI] [PubMed] [Google Scholar]
- Huss R. E., Marsh D. J. A model of NaCl and water flow through paracellular pathways of renal proximal tubules. J Membr Biol. 1975;23(3-4):305–347. doi: 10.1007/BF01870256. [DOI] [PubMed] [Google Scholar]
- Hénin S., Cremaschi D., Schettino T., Meyer G., Donin C. L., Cotelli F. Electrical parameters in gallbladders of different species. Their contribution to the origin of the transmural potential difference. J Membr Biol. 1977 Jun 3;34(1):73–91. doi: 10.1007/BF01870294. [DOI] [PubMed] [Google Scholar]
- Kyte J. Immunoferritin determination of the distribution of (Na+ + K+) ATPase over the plasma membranes of renal convoluted tubules. II. Proximal segment. J Cell Biol. 1976 Feb;68(2):304–318. doi: 10.1083/jcb.68.2.304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- OGILVIE J. T., McINTOSH J. R., CURRAN P. F. Volume flow in a series-membrane system. Biochim Biophys Acta. 1963 May 21;66:441–444. [PubMed] [Google Scholar]
- Sackin H., Boulpaep E. L. Models for coupling of salt and water transport; Proximal tubular reabsorption in Necturus kidney. J Gen Physiol. 1975 Dec;66(6):671–733. doi: 10.1085/jgp.66.6.671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segel L. A. Standing-gradient flows driven by active solute transport. J Theor Biol. 1970 Nov;29(2):233–250. doi: 10.1016/0022-5193(70)90020-2. [DOI] [PubMed] [Google Scholar]
- Sha'afi R. I., Rich G. T., Sidel V. W., Bossert W., Solomon A. K. The effect of the unstirred layer on human red cell water permeability. J Gen Physiol. 1967 May;50(5):1377–1399. doi: 10.1085/jgp.50.5.1377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stirling C. E. Radioautographic localization of sodium pump sites in rabbit intestine. J Cell Biol. 1972 Jun;53(3):704–714. doi: 10.1083/jcb.53.3.704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHITLOCK R. T., WHEELER H. O. COUPLED TRANSPORT OF SOLUTE AND WATER ACROSS RABBIT GALLBLADDER EPITHELIUM. J Clin Invest. 1964 Dec;43:2249–2265. doi: 10.1172/JCI105099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinstein A. M., Stephenson J. L. Electrolyte transport across a simple epithelium. Steady-state and transient analysis. Biophys J. 1979 Aug;27(2):165–186. doi: 10.1016/S0006-3495(79)85209-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright E. M., Diamond J. M. Effects of pH and polyvalent cations on the selective permeability of gall-bladder epithelium to monovalent ions. Biochim Biophys Acta. 1968 Aug;163(1):57–74. doi: 10.1016/0005-2736(68)90033-3. [DOI] [PubMed] [Google Scholar]
- van Os C. H., Wiedner G., Wright E. M. Volume flows across gallbladder epithelium induced by small hydrostatic and osmotic gradients. J Membr Biol. 1979 Aug;49(1):1–20. doi: 10.1007/BF01871037. [DOI] [PubMed] [Google Scholar]


