Morphological homeostasis in cortical dendrites

Abstract

Neurons have significant potential for the homeostatic regulation of a broad range of functional features, from gene expression to synaptic excitability. In this article, we show that dendritic morphology may also be under intrinsic homeostatic control. We present the results from a statistical analysis of a large collection of digitally reconstructed neurons, demonstrating that fluctuations in dendritic size in one given portion of a neuron are systematically counterbalanced by the remaining dendrites in the same cell. As a result, the total dendritic measure (e.g., number of branches, length, and surface area) of each neuron in a given morphological class is, on average, significantly less random than would be expected if trees (and their parts) were regulated independently during development. This observation is general across scales that range from gross basal/apical subdivisions to individual branches and bifurcations, and its statistical significance is robust among various brain regions, cell types, and experimental conditions. Given the pivotal dendritic role in signal integration, synaptic plasticity, and network connectivity, these findings add a dimension to the functional characterization of neuronal homeostasis.

Central nervous system neurons have significant homeostatic control of essential functions, such as synaptic excitability (1), metabolic regulation (2), gene expression (3), and response to injury or pathology (4, 5). Moreover, molecular homeostasis in the cytoskeleton contributes to the architecture and survival of dendrites and axons (6).

Dendrites play a crucial role in signal integration, synaptic plasticity, and network connectivity (7). In the mammalian cortex, dendritic size is a primary determinant of the neuron's electrotonic properties (8, 9) and number of input synapses (10, 11). Dendritic size is variable among both neuronal classes and individual cells of each class. Several factors, both extrinsic and intrinsic to the neuron, could be involved in the regulation of dendritic size (12). These factors include genetic control, chemical or electrical signals from incoming fibers, other local humoral influences, physical constraints in the tissue, and competition for limited resources.

If various components of a neuron (e.g., individual dendritic trees) were each independently regulated, fluctuations in the size of one component would have, on average, no effect on other components. If the trees of a cell were mainly coregulated by common factors (e.g., local external cues or genetic instructions), however, a larger-than-average size of one component would predict larger-than-average sizes of other components in the same cell (e.g., people with big hands also tend to have big feet). In contrast, if the various parts of a cell were mutually regulated by internal competition, fluctuations in size of one component would tend to be compensated by opposite deviations in the rest of the neuron, leading to a form of morphological homeostasis.

The routine 3D digital reconstruction of neuronal morphology has recently provided the neuroscience community with high-quality single-cell anatomical data suitable for quantitative analysis (13). Using a large collection of such data, we made a series of consistent observations on dendritic size (number of branches, total length, and surface area) in the rat hippocampus and monkey neocortex, under a variety of experimental conditions. In particular, we analyzed three levels of structural organization: (i) the balance between entire basal and apical arborizations in single pyramidal cells, (ii) the decomposition of an arborization in individual trees originating from the soma, and (iii) the partition of branching subtrees into two daughters and four granddaughters.

We show that, at each of these levels, dendritic size appears to be under intrinsic homeostatic control, exhibiting significantly higher global stability than could be expected if the regulation of local components were not coordinated during development. Fluctuations in dendritic size in a given portion of a neuron are systematically counterbalanced by the remaining dendrites in the same cell. As a result, the total dendritic extension of each cell is stabilized for a given morphological class and anatomical location.

Results

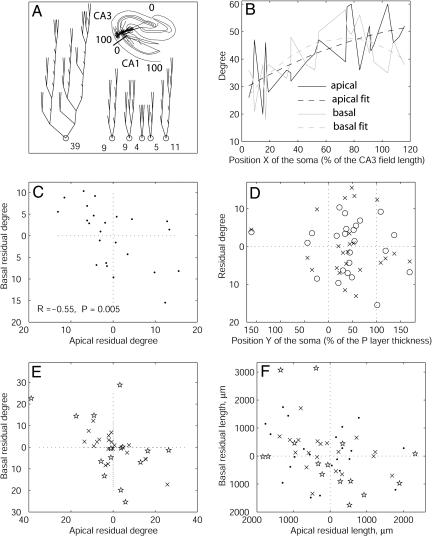
The first level of structural organization we investigated is the partitioning of individual pyramidal cells of the rat hippocampus into basal and apical arborizations. The dendritic size of pyramidal cells depends on their position in the CA3 and CA1 fields (14). For example, CA3 pyramidal cells have smaller dendritic fields near the hilus and larger trees close to CA1 (Fig. 1A). An analysis of the Amaral CA3 data set (see Materials and Methods) showed that both apical and basal dendrites follow the same trend, with the total number of their terminations (their degree) increasing as a function of the somatic position (X) in the field (Fig. 1B). This dependence was fitted with quadratic functions (polynomials of power between 2 and 5 yielded similar results).

Fig. 1.

Morphological homeostasis between apical and basal dendrites in hippocampal pyramidal cells. (A) Schematic representation of the one apical (Left) and five basal trees of a pyramidal cell. The numbers at the bottom are the count of terminal tips (degree). (Inset) Transversal position of the pyramidal cell in the hippocampus. The thick bar perpendicular to the cytoarchitectonic layers indicates the CA3/CA1 boundary. The position within CA3 and CA1 can be quantified as a percentage. (B) Apical and basal degree of Amaral CA3 pyramidal cells vs. their anatomical position (X > 100 correspond to field CA2). Each point of the full lines corresponds to one of the 23 cells. The dashed lines are quadratic fits. (C) Scatter plot of the difference between measured and fitted data (residual degrees). Fluctuations in basal and apical size are significantly anticorrelated. (D) Residual degree of basal (×) and apical (○) arborizations as a function of the somatic depth in the pyramidal layer (no correlation observed). (E) Scatter plot of residual degrees for Amaral CA1 cells (×) and Turner CA3 cells (⋆) analyzed as in panels A-C. A negative correlation is observed in both cases (see text for R and P values). (F) Scatter plot of residual lengths for Amaral CA3 cells (•), Amaral CA1 cells (×), and Turner CA3 cells (⋆) (values were divided by 10). A negative correlation is observed in all three cases (see text for R and P values).

The fluctuation of size in each arborization can be defined as the difference between the measured value for the given cell and the expected value for the corresponding anatomical position, i.e., the deviation of the experimental point from the fitted line. When such residual degree was analyzed separately for basal and apical trees (Fig. 1C), a strong and significant negative correlation was observed between the two measures (R = -0.55; P = 0.005). If neuronal size primarily resulted from tight genetic control or from the competition with surrounding cells for external resources, a positive correlation would be expected between fluctuations of basal and apical arborizations. In principle, the observed negative correlation might be explained by anatomical constraints, such as the somatic depth within the pyramidal layer. For example, neurons in which the soma is closer to the stratum oriens might have more space to grow toward the stratum radiatum, resulting in larger apical and smaller basal arborizations (and vice versa for somas located on the opposite extreme of the pyramidal layer). We tested this possibility directly (Fig. 1D) and found no correlation between apical and basal fluctuations and the somatic depth (position Y)in the pyramidal layer (|R| < 0.1; P > 0.1). Thus, the observed negative correlation between the size fluctuation of basal and apical arborizations in CA3 pyramidal cells appears to be due to an internal homeostatic mechanism.

To test the generality of this finding, we analyzed the other archives of pyramidal neurons for which the anatomical position of the soma is precisely known: another data set from the same experimental preparation but a different hippocampal region (Amaral CA1) and a set of neurons from the same hippocampal region (CA3) but reconstructed with different experimental techniques (Turner CA3). In both cases (Fig. 1E), we observed a significantly negative correlation between the residual degrees of basal and apical arborizations (R =-0.68 and P = 0.001 for Amaral CA1; R = -0.80 and P = 0.0005 for Turner CA3). We further characterized fluctuations in the size of basal and apical arborization by measuring dendritic length instead of the number of terminals (Fig. 1F). Negative trends in the correlation between basal and apical residual length were observed in all three data sets (R = -0.42 and P = 0.043 for Amaral CA3; R = -0.60 and P = 0.005 for Amaral CA1; R =-0.36 and P = 0.183 for Turner CA3). Similar observations held for other measures of dendritic size, such as surface area (not shown in Fig. 1), albeit with lower and less consistent statistical significance (R = -0.16 and P = 0.446 for Amaral CA3; R =-0.54 and P = 0.015 for Amaral CA1; R =-0.38 and P = 0.161 for Turner CA3).

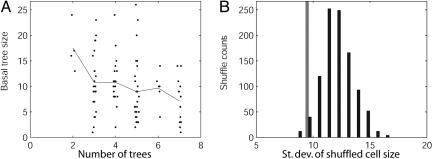
We continued this analysis at a lower level of structural organization, namely the composition of an individual arborization (e.g., the basal dendrites of a pyramidal cell) as a set of single trees stemming from the soma. We first observed that in CA3 pyramidal cells with a larger number of basal trees, the individual trees tend to be smaller (Fig. 2A), which is consistent with the general notion of morphological homeostasis.

Fig. 2.

Morphological homeostasis among individual basal trees in hippocampal pyramidal cells. (A) Analysis of basal tree degree as a function of the number of trees in the neuron for Amaral CA3 cells. Each point corresponds to an individual tree (small horizontal scattering has been added to improve visualization); the line represents the averages across a vertical set. The negative correlation is statistically significant (R =-0.25; P = 0.001). (B) Histogram of changes in the standard deviation of total basal degree in Amaral CA3 cells on random shuffling of basal trees among neurons with the same number of trees. The average of 1,000 runs is significantly greater than the original value of standard deviation (gray bar). The corresponding percent increase is labeled ΔSTD% in Table 1.

What further can be inferred about any mutual dependence of the size of individual trees in cells with the same number of trees? Consider the total size of the arborization of each cell (i.e., the sum of the sizes of all trees in that cell's arborization). If the size of individual trees within a cell were positively correlated, cells with a larger tree would tend to have other larger trees, and cells with smaller trees would tend to have other smaller trees. In this scenario, if trees were shuffled among cells, larger and smaller trees would be mixed, causing on average a reduction in the variance of the total arborization size in the population. Alternatively, if the size of trees were independent of each other, tree shuffling among cells would not change the variance of the total arborization size in the population. Finally, if the size of trees were negatively correlated (i.e., cells with a greater-than-average tree would probably also have a smaller-than-average tree), tree shuffling would cause an increase in the variance of the total arborization size in the population.

To discriminate among these alternative possibilities, we performed multiple runs of random shuffling of basal trees, among neurons with the same number of basal trees, within the Amaral CA3 pyramidal cells. The results, quantified in terms of degree (Fig. 2B), clearly demonstrated a consistent and highly significant increase in the standard deviation of total arborization size (original standard deviation, 9.1; average standard deviation of 1,000 shuffle runs, 11.9; percent increase, +30.77%; P < 0.001). The sizes of individual basal trees within a given pyramidal cell are thus negatively correlated with each other, again consistently with an internal homeostatic control of dendritic morphology.

The analyses of the negative correlation between tree size and the number of trees per cell and of the percent increase in the standard deviation of total cell size on shuffling of trees among cells with the same number of trees (ΔSTD%) were repeated on all available data sets. In particular, we considered two additional groups of CA3 pyramidal cells (including the group used in Fig. 1 E and F), five groups of CA1 pyramidal cells (including the group used in Fig. 1 E and F), two groups of dentate granule cells, and four groups of pyramidal cells in the monkey prefrontal cortex. Moreover, we repeated both tree-level analyses by using the total length and surface area instead of degree as measures of size (Table 1).

Table 1. Morphological homeostasis among individual dendritic trees in 14 classes of neurons.

	No. of cells	No. of trees	Size per no. of tree correlation (P value)			ΔSTD% (P value)
Database			Degree	Length	Area	Degree	Length	Area
1. Amaral CA3	24	167	−0.25 (0.00112)	−0.21 (0.00689)	−0.22 (0.00366)	11.88 (<10E-5)	11.02 (<10E-5)	9.28 (<10E-5)
2. Amaral CA1	20	116	−0.21 (0.02068)	−0.26 (0.00491)	−0.26 (0.00435)	20.03 (<10E-5)	21.70 (<10E-5)	19.60 (<10E-5)
3. Barrionuevo CA3	8	53	−0.12 (0.40913)	−0.11 (0.41578)	−0.24 (0.08552)	30.60 (<10E-5)	56.43 (<10E-5)	7.50 (<10E-5)
4. Gulyas CA1	18	108	−0.18 (0.06170)	−0.19 (0.05098)	−0.20 (0.03429)	43.92 (<10E-5)	48.49 (<10E-5)	56.63 (<10E-5)
5. Wearne Local Young	20	130	−0.16 (0.07359)	−0.16 (0.06147)	−0.16 (0.06258)	6.01 (<10E-5)	22.14 (<10E-5)	24.65 (<10E-5)
6. Wearne Local Old	17	106	−0.24 (0.01414)	−0.25 (0.01029)	−0.24 (0.01453)	−24.31 (<10E-5)	−19.81 (<10E-5)	−20.59 (<10E-5)
7. Wearne Long Young	24	188	−0.20 (0.00511)	−0.17 (0.01857)	−0.18 (0.01409)	17.12 (<10E-5)	23.62 (<10E-5)	7.75 (<10E-5)
8. Wearne Long Old	19	134	−0.04 (0.64189)	−0.06 (0.50890)	−0.05 (0.56972)	−1.39 (0.03542)	−8.47 (<10E-5)	−7.41 (<10E-5)
9. Claiborne DG	36	144	−0.36 (0.00001)	−0.47 (0.00000)	−0.43 (0.00000)	14.01 (<10E-5)	5.06 (<10E-5)	5.05 (<10E-5)
10. Turner CA1 Vivo	24	73	−0.42 (0.00023)	−0.46 (0.00004)	−0.29 (0.01421)	−4.50 (<10E-5)	−4.50 (<10E-5)	−22.83 (<10E-5)
11. Turner CA1 Aged	15	39	−0.50 (0.00113)	−0.51 (0.00093)	−0.49 (0.00151)	−0.33 (0.56265)	23.99 (<10E-5)	18.07 (<10E-5)
12. Turner CA1 Vitro	10	31	−0.17 (0.35267)	−0.20 (0.28530)	−0.15 (0.42870)	172.97 (<10E-5)	57.93 (<10E-5)	−0.87 (0.76409)
13. Turner CA3	15	69	−0.23 (0.05352)	−0.22 (0.07268)	−0.26 (0.03165)	0.42 (0.40112)	−0.51 (0.25299)	−2.56 (<10E-5)
14. Turner DG	19	42	−0.56 (0.00010)	−0.58 (0.00006)	−0.37 (0.01490)	17.77 (<10E-5)	28.14 (<10E-5)	−6.31 (<10E-5)

The size per no. of tree correlation values in the degree column correspond to the analysis in Fig. 2A. The ΔSTD% values constitute the percent increase of the standard deviation of cell size on random shuffling (corresponding to the analysis of Fig. 2B).

In all 14 cell classes and for each morphometric measure, the correlation between tree size and the number of trees per cell was negative, and in the majority of these cases, this measure was statistically significant. Interestingly, the average correlation factor over the 14 groups of cells was very close for the three measures of size (-0.26 for degree, -0.27 for length, and -0.25 for area). Tree shuffling among cells with the same number of trees also resulted in a statistically significant percent increase in the standard deviations of cell size in the majority of neuronal classes and for each measure of size. This phenomenon was more prominent for degree and length (an average ΔSTD% of 23 and 19, respectively) than for area (an average ΔSTD% of 6).

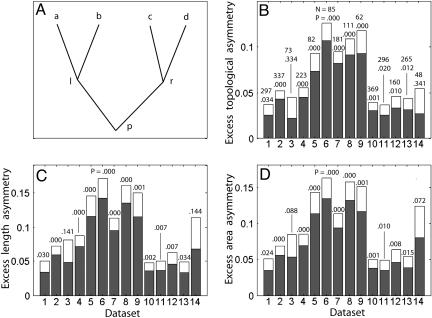
Finally, we moved our analysis to the level of subtrees (see Materials and Methods). We call a subtree the portion of an arborization that stems from a given branch (as opposed to a whole tree, which stems from the soma). A process similar to the tree shuffling described above can be applied to any bifurcation p in which two daughter branches, l and r, each have at least two additional daughters (a and b and c and d, respectively) (see Fig. 3A). The idea of morphological homeostasis implies that fluctuations in the size of the daughters of one branch (e.g., a and b) would tend to compensate fluctuations of the opposite sign in the daughters of the other branch (c and d). In this case, randomly swapping either a or b with c or d would lead to a more symmetric distribution of dendritic size between the two daughters of p.

Fig. 3.

Morphological homeostasis in individual subtrees. (A) Schematization of the partition of the degree p of a bifurcating branch into the two daughters l and r and the four granddaughters a, b, c, and d. (B) Excess partition asymmetry for all data sets (1, Amaral CA3; 2, Amaral CA1; 3, Barrionuevo CA3; 4, Gulyás CA1; 5, Wearne Local Young; 6, Wearne Local Old; 7, Wearne Long Young; 8, Wearne Long Old; 9, Claiborne DG; 10, Turner CA1 Vivo; 11, Turner CA1 Aged; 12, Turner CA1 Vitro; 13, Turner CA3; 14, Turner DG). Averages (gray bars) and standard errors (white tops) were calculated over all bifurcations with two nonterminal daughters in all cells within each class. The numbers of such bifurcations and the P value assessing positivity of the mean are indicated over each bar. (C and D) A representation of the same analysis performed using length asymmetry and area asymmetry instead of partition asymmetry, respectively.

This phenomenon can be described by using the topological measure of partition asymmetry, A_p (15), again using the degree as a measure of dendritic size. In particular, a quantity we called excess partition asymmetry, E_p, represents the difference between the partition asymmetry actually measured in a branch and the average of the partition asymmetry computed for the same branch after all possible shuffling of the granddaughter branches (Eqs. 1-3 in Materials and Methods). If the subtrees of the daughters of a given branch were mutually independent, E_p would be, on average, zero. In contrast, if a and b were negatively correlated with c and d (revealing morphological homeostasis), E_p would tend to be positive.

For all cell classes analyzed in this study, the average of the excess partition asymmetry over all dendritic subtrees was systematically positive, in most cases with very high statistical significance (Fig. 3B). When length and surface area were used instead of the degree as a measure of dendritic size, the average excess length and area asymmetries also revealed systematically positive and largely significant values over all 14 available cell groups (Fig. 3 C and D). The excess partition was also measured from subtrees grouped by their order (i.e., number of bifurcations from the soma) and degree (size of the subtree). The excess partition was positive in almost all subtree groups and, interestingly, failed to reveal any statistically significant variation with respect to either the degree or the order of the subtrees (|R| < 0.1; P > 0.5). This finding suggests that the phenomenon of morphological homeostasis is generally robust for all subtree sizes and at any distance from the soma.

The results of this analysis are by no means arithmetically trivial consequences of the definition of asymmetry or of the general structure of binary trees. To illustrate this, we artificially generated a set of stochastic neurons in which trees and subtrees were all built independent of each other (see Materials and Methods). The average excess partition asymmetry, 〈E_p 〉, computed over all 4,128 branches with two bifurcating daughters in this data set, was 0.00, with the standard deviation 0.20 (the assessment of positivity was nonsignificant; P = 0.18). The mean partition asymmetry (±SD) in this data set was 0.79 ± 0.32. Additionally, selecting the branching probability as a function of branch order (16) allowed the manipulation of the mean partition asymmetry within a broad interval (including 0 and the whole range of biologically plausible values) while leaving 〈E_p 〉 = 0.

Discussion

Neuronal dendrites are instrumental in the formation and maintenance of network connectivity, the integration of electric inputs, and the regulation of synaptic plasticity. It should not be surprising, therefore, that sophisticated molecular cascades are involved in the control of dendritic growth (6, 17). In this study, we provided evidence that the size of dendrites may be under internal homeostatic control. In particular, fluctuations in dendritic number, length, or membrane area in one part of a neuron tend to be counterbalanced in other parts of the same neuron. These observations are consistent across scales, from overall basal/apical arborizations to individual (sub)trees of any size. The results are also considerably robust on the basis of a large data set of >250 neurons from two species, two brain regions and four subregions, five cell types, several ages, six independent laboratories, and several different preparation methods. Preliminary analysis of a small number of cerebellar Purkinje cells indicated positive excess partition asymmetry (data not shown), but whether the evidence for morphological homeostasis extends beyond cortical regions and/or to inhibitory neurons remains to be verified.

These results must be considered in the broader context of homeostatic control of neuronal functions. For example, reversible regression of hippocampal principal dendrites induced by chronic stress produces only small alterations of somatic firing (18) compared with what would be expected given such morphological effects (19). Thus, cells have a means to sustain damage, as physiological homeostasis compensates for morphological changes. More generally, average neuronal activity levels are maintained by homeostatic plasticity mechanisms that dynamically adjust synaptic strengths in the correct direction to promote stability (1). Our findings, complementary to the above, characterize compensatory phenomena at the morphological level that may be vital for the functional sustainability of cortical neurons.

These mechanisms may be in effect during early development as well as in adult neurons, which in the cortex are known to exhibit morphological plasticity (7, 20, 21). For example, whereas hippocampal neurogenesis may be essential in learning (22), the proper control of the new neuron shape and size could be critical for their functional integration in the preexisting network. Our analysis demonstrates that the total dendritic size of each cell in a given morphological class exhibits significantly higher stability than if trees and their parts were regulated individually and independently. Such morphological homeostatic control might be necessary and sufficient for a neuron to be both adaptive and functionally sustainable.

An important question relates to the biochemical and biophysical mechanisms underlying these observations. We have excluded several possible explanations that are based on extrinsic factors. For example, the anatomical position of the soma in the cytoarchitectural layer, which is related to the volume available for growth, has no correlation with the morphological homeostasis in the basal/apical partition of pyramidal cells (Fig. 1D). Another potential candidate is the response of a cell to incoming fibers and their activity. Although this or other extrinsic factors could conceivably account for one of the observed phenomena in selected cell classes (e.g., at the level of the basal/apical partition), it is unclear how they could explain all the results reported here. In particular, local extrinsic factors would instead lead to an opposite-sign effect, as nearby components of the dendritic arborization (e.g., subtrees) would be under similar influences.

A more likely mechanism is based on intrinsic intracellular factors. A centralized (e.g., genetic) control of growth would result in correlated, rather than anticorrelated, fluctuations within individual cells. The observed results are instead compatible with the concept of limited intracellular resources that are nonuniformly distributed along the dendritic tree. Morphological homeostasis could result from a direct competition among the various components of an individual neuron at multiple scales. Although the metabolic cost of morphological growth may be incurred locally (e.g., at the growth cone level), the balance would be experienced globally (at the subtree, tree, and whole neuron level), limiting the abilities of other parts of the same cell to develop further.

Other studies implicate competition as an important factor in neuronal development (23). The computational model developed by van Pelt and colleagues (15, 16) describes dendritic growth as a stochastic process of segment branching. In this model, the branching probability is modulated by the number of terminals in the growing tree, consistent with the idea of competition for limited resources. Such a lower-level mechanism can be made explicit by introducing a quantitative dependence of branching on the concentration of chemicals produced in the soma and transported to the terminals either actively or by diffusion (16, 23).

It is tempting to speculate on the nature of the limiting factor that eventually determines dendritic size and its distribution in the cell on the basis of the comparison of different morphometric measures of the observed homeostasis. In the analysis of both the overall basal/apical arborizations (Fig. 1) and shuffling of individual trees (Table 1), a stronger effect was observed with respect to the number of branches than to surface area. This finding could indicate that the developmental cost associated with branching is a more stringent or direct determinant of shape than that of membrane expansion. However, the lower precision and reliability in the measurement of dendritic diameter compared with the count of terminal tips (13) could also explain the different statistical significance.

The direct experimental investigation of the mechanisms of early dendritic growth and branching remains challenging. Thus, mechanistic inferences, based on the analysis of adult morphologies such as those formulated here, must be taken seriously. In particular, the hypothesis that the dendritic-size balance among the various component of a neuron is due to intrinsic rather than extrinsic constraints can be experimentally disproved by carrying out the same quantitative analysis in acutely dissociated cultures of the same cellular classes. If these homeostatic phenomena are a secondary consequence of somatic packing, laminated incoming fibers, or parallel arrangement of dendrites, they should all disappear in a dish. A more direct experimental test could involve the use of wide-field, time-lapse visualization of microtubule growth (24). We hypothesize that fluctuations in the growth rate of one branch with respect to the population average would tend to be compensated within the same neuron. Interestingly, axonal outgrowth in tissue culture clearly shows anticorrelated behavior in the individual growth cone velocity and acceleration (25), suggesting that morphological homeostasis may not be limited to dendritic arborizations.

Materials and Methods

All 3D morphologies analyzed in this study were complete digital reconstructions of intracellularly characterized, injected, and stained neurons. In these files, dendrites are represented as (branching) chains of segments. Each segment is connected to one other segment in the path to the soma and may be connected on the other extremity to 2, 1, or 0 other segments (bifurcation, continuation point, or terminal tip, respectively). All segments are described in the file by their ending point coordinates, diameters, and connectivity to other segments (13). The 14 experimental data sets and 1 simulated data set used in this research are described below.

Amaral CA3 and CA1. Twenty-four CA3 and 23 CA1 pyramidal cells from the rat hippocampus were used (14). These neurons were injected and reconstructed from whole slices and kindly provided by D. G. Amaral (University of California, Davis) for public distribution. The X somatic positions along the transversal pyramidal layer (Fig. 1A Inset) are explicitly reported in the original reference for each neuron (14). We extracted the Y somatic positions in the transversal direction perpendicular to the pyramidal layer from the digital line drawing of the hippocampal boundaries in each reconstruction file. In particular, we calculated the distance of the center of the soma from the external boundary of the pyramidal layer, normalized by the local thickness of the pyramidal layer. These measures range from -2 to 2, with most somata centered within the layer (-1 to 1).

Claiborne DG. Thirty-six granule cells from the rat dentate gyrus used in our previous studies (26, 27) were from the internet archive of B. J. Claiborne (University of Texas, San Antonio, TX). These neurons were injected and reconstructed from whole slices (9, 20).

Barrionuevo CA3. Eight CA3 pyramidal cells from the rat hippocampus injected and reconstructed from whole slices (28) were kindly provided by G. Barrionuevo (University of Pittsburgh, Pittsburgh).

Gulyás CA1. Eighteen CA1 pyramidal cells from the rat hippocampus injected in vivo and reconstructed from serial sections were used (29).

Turner CA3. Fifteen of 18 CA3 pyramidal cells from the rat hippocampus injected in vivo and reconstructed from serial sections were studied (30). Three cells (60a, 56b, and 48b) were excluded a priori from analysis because their anatomical locations (posterior/ventral) were inconsistent with the rest of the set. Reconstructions were obtained from www.compneuro.org. We measured the X somatic positions along the transversal pyramidal layer from the figures from ref. 30. Apriori with respect to any data analysis (and in analogy with the Amaral data sets), we assigned the position values of 0%, 50%, and 100% in correspondence to the CA3/hilus boundary, the sharp angle in field CA3b, and the CA3/CA2 boundary, respectively.

Turner CA1 Vivo, CA1 Aged, and CA1 Vitro. Twenty-four CA1 pyramidal cells from young rats injected in vivo and reconstructed from serial sections (Turner CA1 Vivo), 15 CA1 pyramidal cells from aged rats injected and reconstructed from whole slices (CA1 Aged), and 10 CA1 pyramidal cells from young rats injected and reconstructed from whole slices (CA1 Vitro) (31) were studied. Files were obtained from the same archive as the Turner CA3 cells and partially edited for morphological integrity (32).

Turner DG. Nineteen granule cells from the rat dentate gyrus (33) were obtained from the same archive as the Turner CA3 cells.

Wearne Long Young, Long Old, Local Young, and Local Old. Twenty-four Wearne Long Young, 19 Wearne Long Old, 20 Wearne Local Young, and 17 Wearne Local Old pyramidal cells from macaque monkey prefrontal cortex, reconstructed from whole slices, were used (21).

Finally, one simulated data set was created by randomly generating 1,000 tree topologies with the following algorithm. A tree starts as a single open node. At each step, a random open node is selected. With an equal probability of 50%, the selected node can either bifurcate, producing two daughter open nodes, or terminate, becoming a closed node. The process terminates when there are no more open nodes or the limiting size is exceeded. The resulting tree is added to the data set if its degree is within the range of 10-100 and is discarded otherwise.

All statistical analysis was carried out in the matlab environment (MathWorks, Natick, MA) on a Pentium III (667 MHz, 128 Mb RAM). The code is available on request.

Analysis of Subtrees. Consider a bifurcation, p, leading to two subtrees, l and r, with at least one additional bifurcation each (Fig. 3A). Before the degrees of the four granddaughter branches (a, b, c, and d) are known, each granddaughter can be assumed to have the same expected degree m (also unknown). Fluctuations in the size of the granddaughters can be defined as the deviations of a, b, c, and d from m.

If the subtrees of a given branch were independent of each other, fluctuations in a, b, c, and d would be uncorrelated. If, in contrast, fluctuations in the daughters of one branch (a and b) tended to compensate for fluctuations of the opposite sign in the daughters of the other branch (c and d), a random swap of either a or b with c or d would lead to a more symmetric distribution of degrees between the two daughters (l and r) of p. This measure can be expressed by using the following topological definition of partition asymmetry A_p (15):

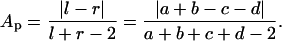[1]

All possible permutations of the set {a, b, c, d} result in three potentially distinct values of the partition asymmetry. Therefore, in addition to Eq. 1:

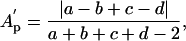[2]

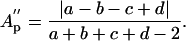Now, we can define the excess partition asymmetry, E_p, of a branch as the difference between the actual partition asymmetry A_p and the average of the partition asymmetry computed for the same branch over all permutations of the numbers a, b, c, and d (or, equivalently, of their fluctuations with respect to m):

[3]

If the fluctuations in a, b, c, and d are uncorrelated, E_p is, on average, zero. In contrast, if a and b are negatively correlated with c and d (revealing morphological homeostasis), E_p tends to be positive.

The definition of partition asymmetry (and correspondingly that of excess partition asymmetry) can be extended to other measures of dendritic size, including total length, L (length asymmetry, A^l), and membrane surface area S (area asymmetry, A^s):

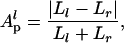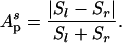[4]