Abstract
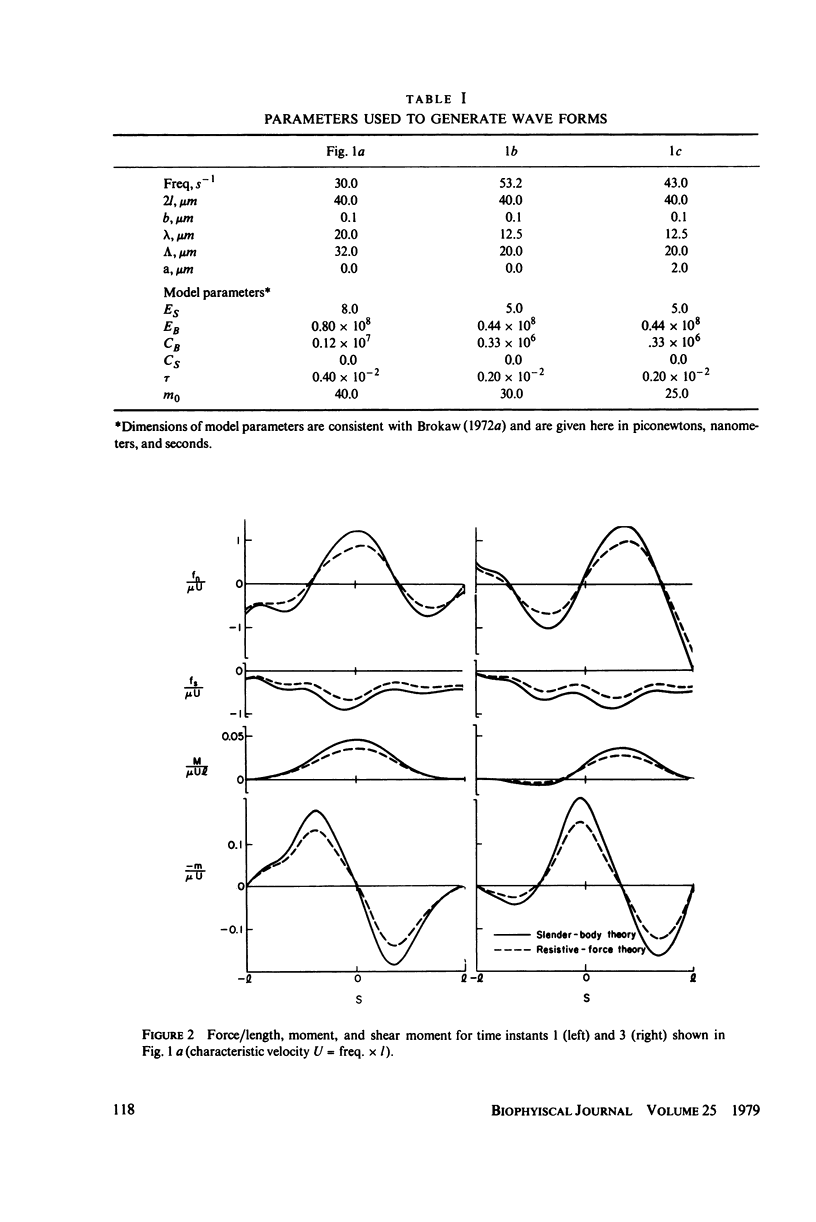
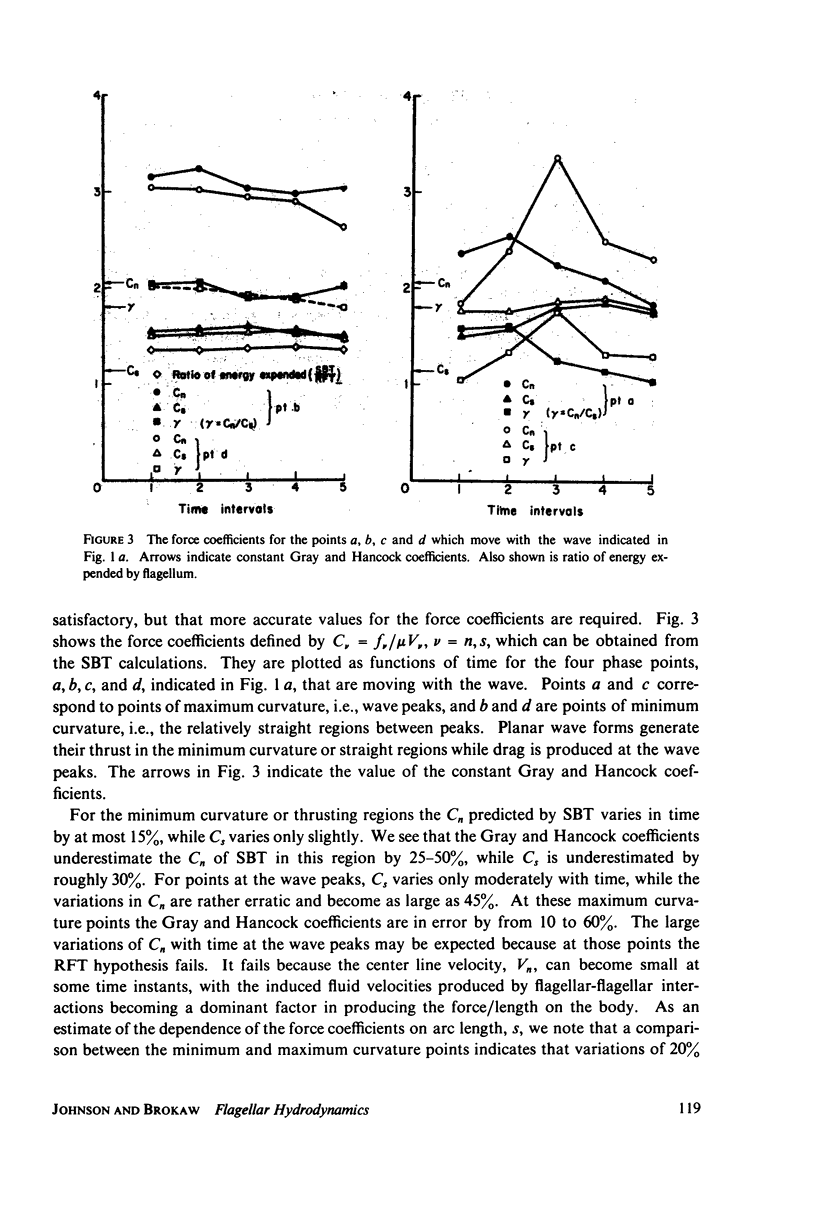
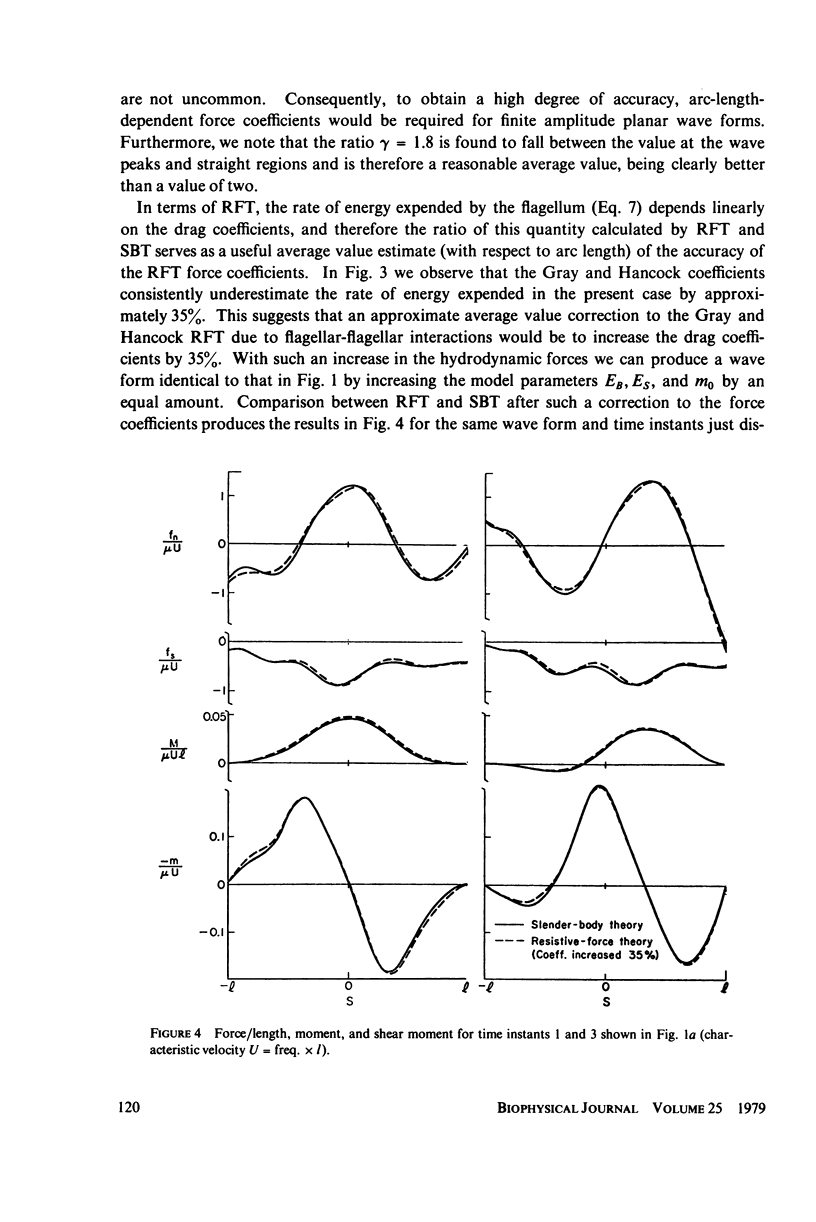
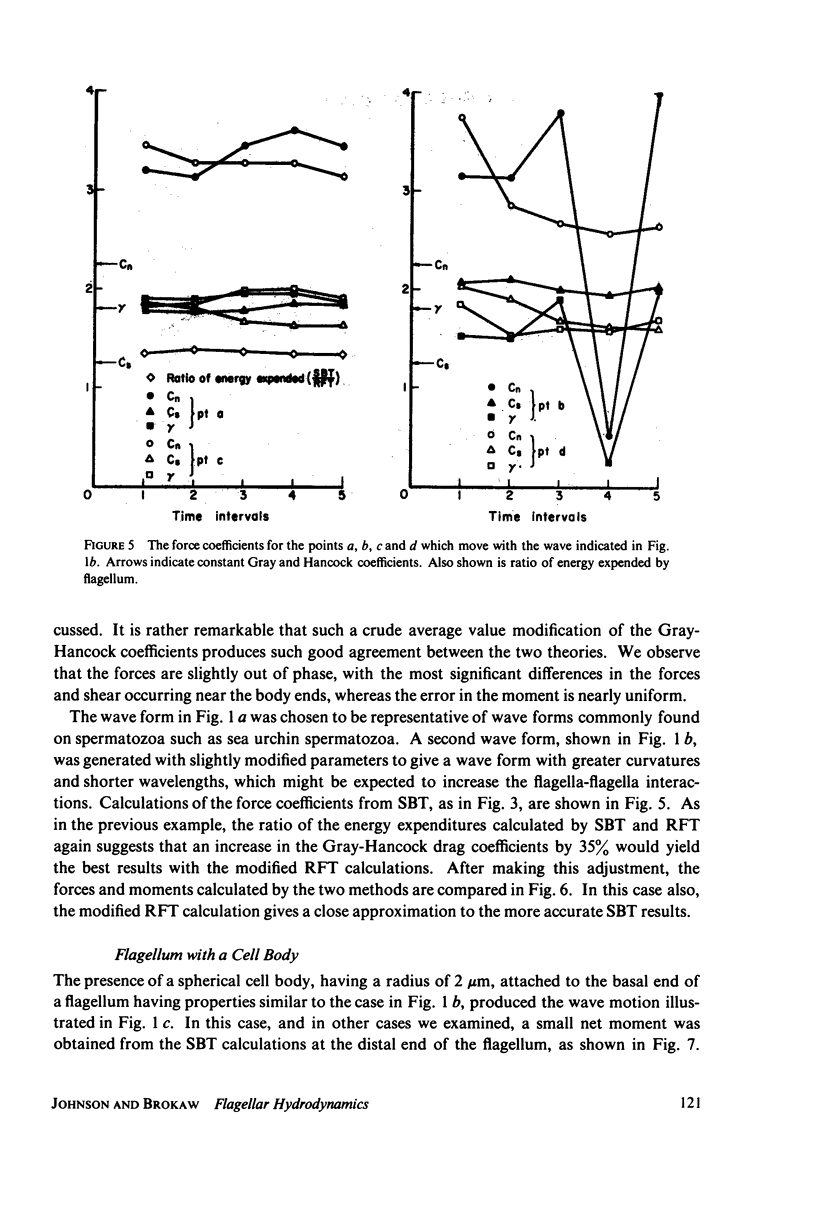
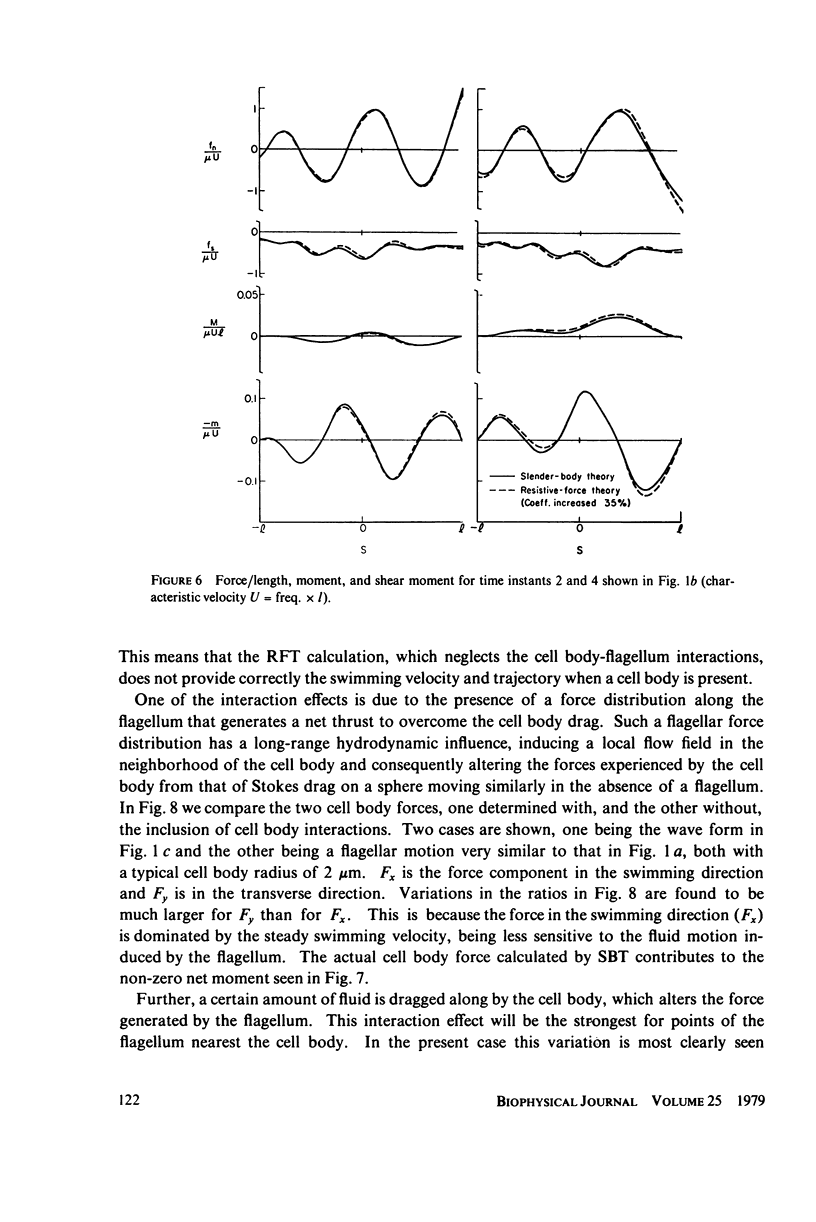
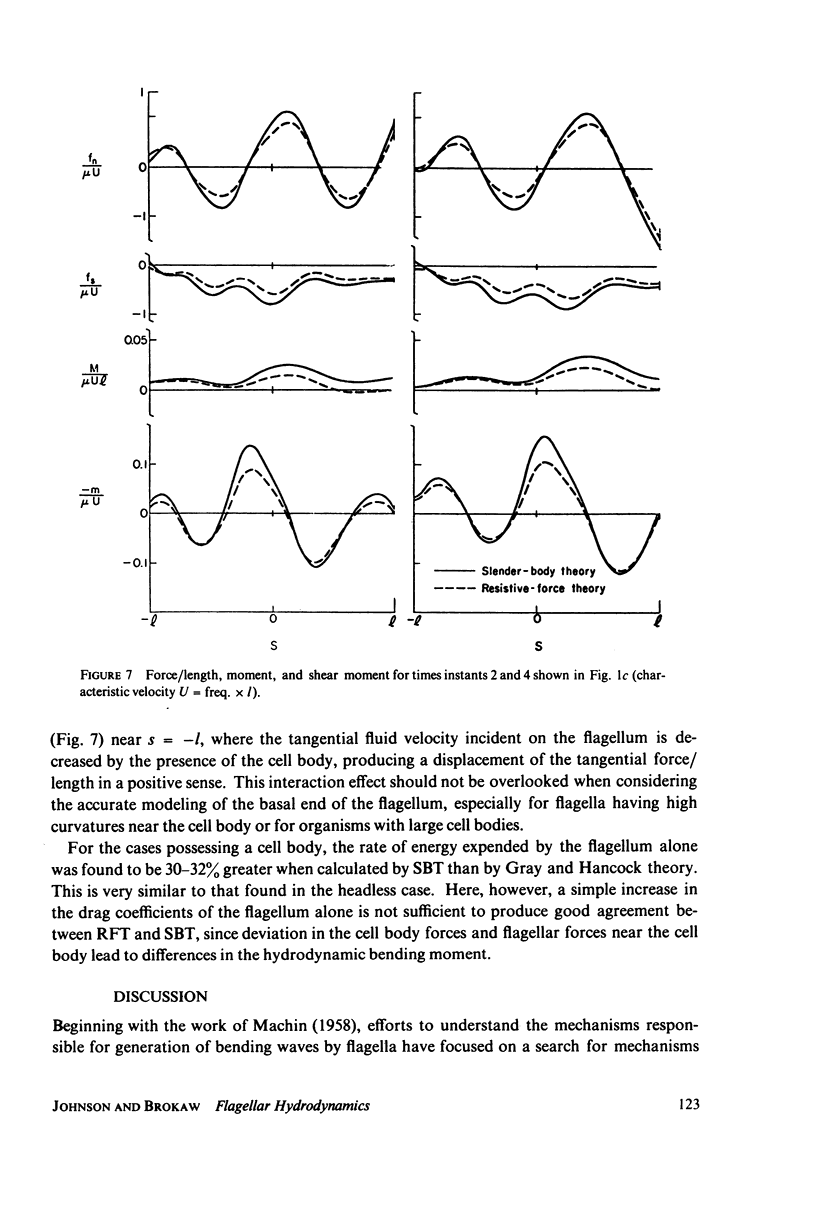
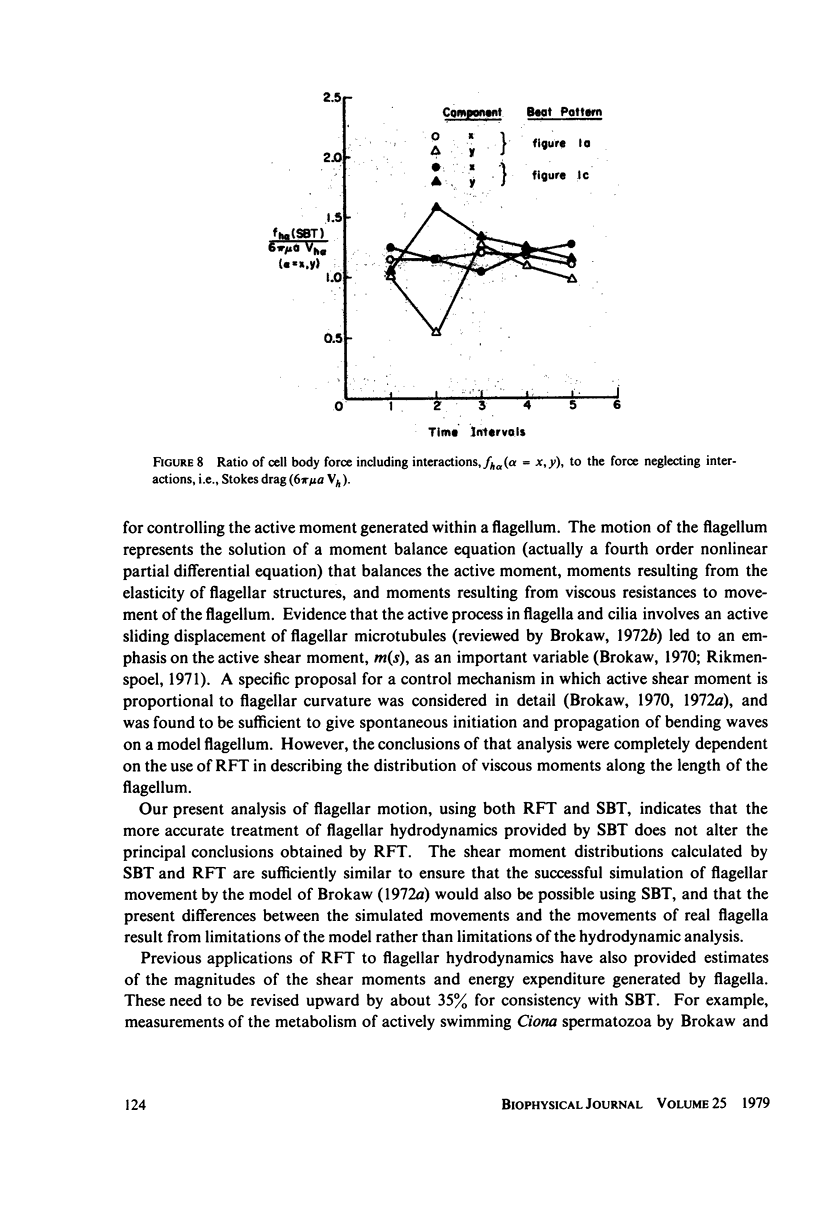
This paper investigates the accuracy of the resistive-force theory (Gray and Hancock method) which is commonly used for hydrodynamic analysis of swimming flagella. We made a comparison between the forces, bending moments, and shear moments calculated by resistive-force theory and by the more accurate slender-body theory for large-amplitude, planar wave forms computed for a flagellar model. By making an upward empirical adjustment, by about 35%, of the classical drag coefficient values used in the resistive-force theory calculations, we obtained good agreement between the distributions of the forces and moments along the length of the flagellum predicted by the two methods when the flagellum has no cell body attached. After this adjustment, we found the rate of energy expenditure calculated by the two methods for the few typical test cases to be almost identical. The resistive-force theory is thus completely satisfactory for use in analysis of mechanisms for the control of flagellar bending, at the current level of sophistication of this analysis. We also examined the effects of the presence of a cell body attached to one end of the flagellum, which modifies the flow field experienced by the flagellum. This interaction, which is not considered in resistive-force theory, is probably insignificant for small cell bodies, such as the heads of simple spermatozoa, but for larger cell bodies, or cell bodies that have large-amplitude motions transverse to the swimming direction, use of slender-body theory is required for accurate analysis.
Full text
PDF







Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Blum J. J., Lubliner J. Biophysics of flagellar motility. Annu Rev Biophys Bioeng. 1973;2:181–219. doi: 10.1146/annurev.bb.02.060173.001145. [DOI] [PubMed] [Google Scholar]
- Brokaw C. J. Bending moments in free-swimming flagella. J Exp Biol. 1970 Oct;53(2):445–464. doi: 10.1242/jeb.53.2.445. [DOI] [PubMed] [Google Scholar]
- Brokaw C. J., Benedict B. Mechanochemical coupling in flagella. II. Effects of viscosity and thiourea on metabolism and motility of Ciona spermatozoa. J Gen Physiol. 1968 Aug;52(2):283–299. doi: 10.1085/jgp.52.2.283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brokaw C. J. Computer simulation of flagellar movement. I. Demonstration of stable bend propagation and bend initiation by the sliding filament model. Biophys J. 1972 May;12(5):564–586. doi: 10.1016/S0006-3495(72)86104-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brokaw C. J. Flagellar movement: a sliding filament model. Science. 1972 Nov 3;178(4060):455–462. doi: 10.1126/science.178.4060.455. [DOI] [PubMed] [Google Scholar]
- Brokaw C. J. Non-sinusoidal bending waves of sperm flagella. J Exp Biol. 1965 Aug;43(1):155–169. doi: 10.1242/jeb.43.1.155. [DOI] [PubMed] [Google Scholar]
- Rikmenspoel R. Contractile mechanisms in flagella. Biophys J. 1971 May;11(5):446–463. doi: 10.1016/S0006-3495(71)86227-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen J. S., Tam P. Y., Shack W. J., Lardner T. J. Large amplitude motion of self-propelling slender filaments at low Reynolds numbers. J Biomech. 1975 Jul;8(3-4):229–236. doi: 10.1016/0021-9290(75)90029-9. [DOI] [PubMed] [Google Scholar]


