Abstract
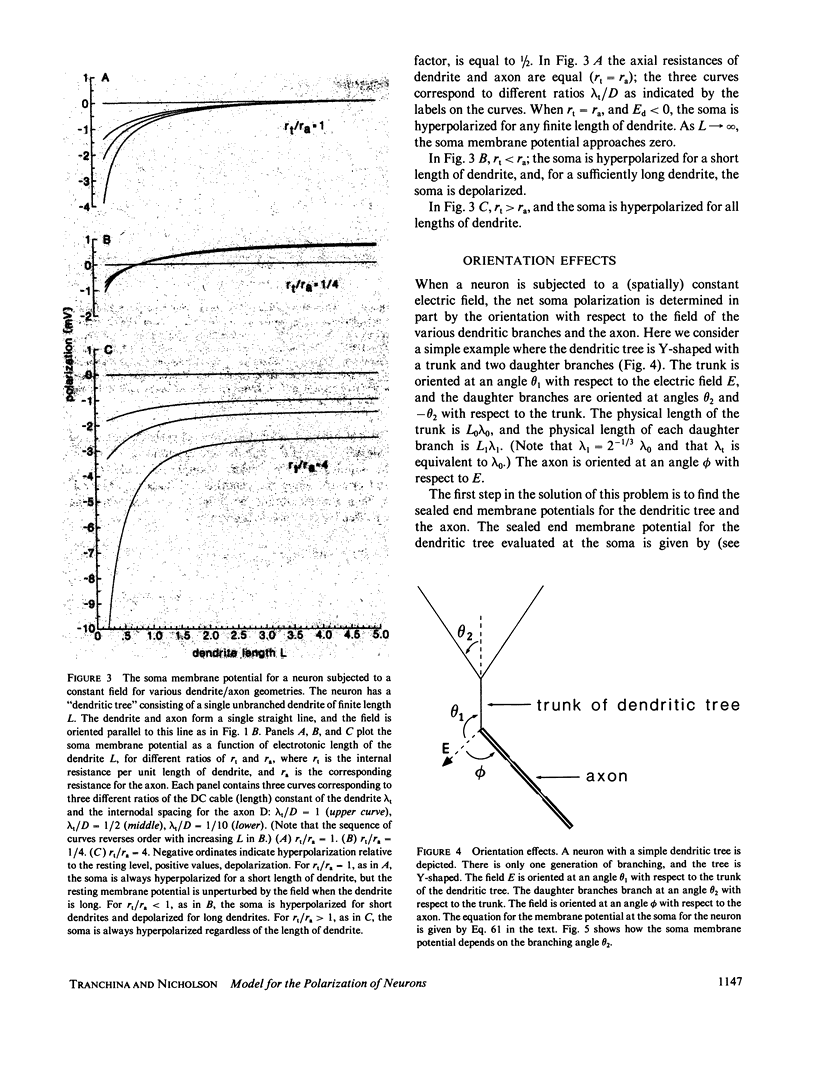
A model is presented for the subthreshold polarization of a neuron by an applied electric field. It gives insight into how morphological features of a neuron affect its polarizability. The neuronal model consists of one or more extensively branched dendritic trees, a lumped somatic impedance, and a myelinated axon with nodes of Ranvier. The dendritic trees branch according to the 3/2-power rule of Rall, so that each tree has an equivalent cylinder representation. Equations for the membrane potential at the soma and at the nodes of Ranvier, given an arbitrary specified external potential, are derived. The solutions determine the contributions made by the dendritic tree and the axon to the net polarization at the soma. In the case of a spatially constant electric field, both the magnitude and sign of the polarization depend on simple combinations of parameters describing the neuron. One important combination is given by the ratio of internal resistances for longitudinal current spread along the dendritic tree trunk and along the axon. A second is given by the ratio between the DC space constant for the dendritic tree trunk and the distance between nodes of Ranvier in the axon. A third is given by the product of the electric field and the space constant for the trunk of the dendritic tree. When a neuron with a straight axon is subjected to a constant field, the membrane potential decays exponentially with distance from the soma. Thus, the soma seems to be a likely site for action potential initiation when the field is strong enough to elicit suprathreshold polarization. In a simple example, the way in which orientation of the various parts of the neuron affects its polarization is examined. When an axon with a bend is subjected to a spatially constant field, polarization is focused at the bend, and this is another likely site for action potential initiation.
Full text
PDF
















Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Andrietti F., Bernardini G. Segmented and "equivalent" representation of the cable equation. Biophys J. 1984 Nov;46(5):615–623. doi: 10.1016/S0006-3495(84)84060-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett E. F., Barrett J. N. Intracellular recording from vertebrate myelinated axons: mechanism of the depolarizing afterpotential. J Physiol. 1982 Feb;323:117–144. doi: 10.1113/jphysiol.1982.sp014064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bawin S. M., Sheppard A. R., Mahoney M. D., Abu-Assal M., Adey W. R. Comparison between the effects of extracellular direct and sinusoidal currents on excitability in hippocampal slices. Brain Res. 1986 Jan 8;362(2):350–354. doi: 10.1016/0006-8993(86)90461-0. [DOI] [PubMed] [Google Scholar]
- BeMent S. L., Ranck J. B., Jr A model for electrical stimulation of central myelinated fibers with monopolar electrodes. Exp Neurol. 1969 Jun;24(2):171–186. doi: 10.1016/0014-4886(69)90013-2. [DOI] [PubMed] [Google Scholar]
- Blight A. R. Computer simulation of action potentials and afterpotentials in mammalian myelinated axons: the case for a lower resistance myelin sheath. Neuroscience. 1985 May;15(1):13–31. doi: 10.1016/0306-4522(85)90119-8. [DOI] [PubMed] [Google Scholar]
- Chan C. Y., Nicholson C. Modulation by applied electric fields of Purkinje and stellate cell activity in the isolated turtle cerebellum. J Physiol. 1986 Feb;371:89–114. doi: 10.1113/jphysiol.1986.sp015963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Funch P. G., Faber D. S. Measurement of myelin sheath resistances: implications for axonal conduction and pathophysiology. Science. 1984 Aug 3;225(4661):538–540. doi: 10.1126/science.6204382. [DOI] [PubMed] [Google Scholar]
- Hentall I. D. The membrane potential along an ideal axon in a radial electric field. Brain Res. 1985 Jun 17;336(2):387–389. doi: 10.1016/0006-8993(85)90675-4. [DOI] [PubMed] [Google Scholar]
- RALL W. Theory of physiological properties of dendrites. Ann N Y Acad Sci. 1962 Mar 2;96:1071–1092. doi: 10.1111/j.1749-6632.1962.tb54120.x. [DOI] [PubMed] [Google Scholar]
- RANCK J. B., Jr Analysis of specific impedance of rabbit cerebral cortex. Exp Neurol. 1963 Feb;7:153–174. doi: 10.1016/s0014-4886(63)80006-0. [DOI] [PubMed] [Google Scholar]
- Rall W., Rinzel J. Branch input resistance and steady attenuation for input to one branch of a dendritic neuron model. Biophys J. 1973 Jul;13(7):648–687. doi: 10.1016/S0006-3495(73)86014-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranck J. B., Jr Which elements are excited in electrical stimulation of mammalian central nervous system: a review. Brain Res. 1975 Nov 21;98(3):417–440. doi: 10.1016/0006-8993(75)90364-9. [DOI] [PubMed] [Google Scholar]
- STEN-KNUDSEN O. Is muscle contraction initiated by internal current flow? J Physiol. 1960 May;151:363–384. doi: 10.1113/jphysiol.1960.sp006444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snow R. W., Dudek F. E. Electrical fields directly contribute to action potential synchronization during convulsant-induced epileptiform bursts. Brain Res. 1984 Dec 3;323(1):114–118. doi: 10.1016/0006-8993(84)90271-3. [DOI] [PubMed] [Google Scholar]
- Taylor C. P., Krnjević K., Ropert N. Facilitation of hippocampal CA3 pyramidal cell firing by electrical fields generated antidromically. Neuroscience. 1984 Jan;11(1):101–109. doi: 10.1016/0306-4522(84)90216-1. [DOI] [PubMed] [Google Scholar]
- Traub R. D., Dudek F. E., Snow R. W., Knowles W. D. Computer simulations indicate that electrical field effects contribute to the shape of the epileptiform field potential. Neuroscience. 1985 Aug;15(4):947–958. doi: 10.1016/0306-4522(85)90245-3. [DOI] [PubMed] [Google Scholar]


