Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 1988 Sep;54(3):495–508. doi: 10.1016/S0006-3495(88)82982-5

On the measurement of shear elastic moduli and viscosities of erythrocyte plasma membranes by transient deformation in high frequency electric fields.

H Engelhardt 1, E Sackmann 1
PMCID: PMC1330348  PMID: 3207837

Abstract

We present a new method to measure the shear elastic moduli and viscosities of erythrocyte membranes which is based on the fixation and transient deformation of cells in a high-frequency electric field. A frequency domain of constant force (arising by Maxwell Wagner polarization) is selected to minimize dissipative effects. The electric force is thus calculated by electrostatic principles by considering the cell as a conducting body in a dielectric fluid and neglecting membrane polarization effects. The elongation A of the cells perpendicular to their rotational axis exhibits a linear regime (A proportional to Maxwell tension or to square of the electric field E2) at small, and a nonlinear regime (A proportional to square root of Maxwell tension or to the electric field E) at large extensions with a cross-over at A approximately 0.5 micron. The nonlinearity leads to amplitude-dependent response times and to differences of the viscoelastic response and relaxation functions. The cells exhibit pronounced yet completely reversible tip formations at large extensions. Absolute values of the shear elastic modulus, mu, and membrane viscosity, eta, are determined by assuming that field-induced stretching of the biconcave cell may be approximately described in terms of a sphere to ellipsoid deformation. The (nonlinear) elongation-vs.-force relationship calculated by the elastic theory of shells agress well with the experimentally observed curves and the values of mu = 6.1 x 10(-6) N/m and eta = 3.4 x 10(-7) Ns/m are in good agreement with the micropipette results of Evans and co-workers. The effect of physical, biochemical, and disease-induced structural changes on the viscoelastic parameters is studied. The variability of mu and eta of a cell population of a healthy donor is +/- 45%, which is mainly due to differences in the cell age. The average mu value of cells of different healthy donors scatters by +/- 18%. Osmotic deflation of the cells leads to a fivefold increase of mu and 10-fold increase of eta at 500 mosm. The shear modulus mu increases with temperature showing that the cytoskeleton does not behave as a network of entropy elastic springs. Elliptic cells of patients suffering from elliptocytosis of the Leach phenotype exhibit a threefold larger value of mu than normal discocytes of control donors. Cross-linking of the spectrin by the divalent S-H agents diamide (1 mM, 15 min incubation) leads to an eightfold increase of mu whereas eta is essentially constant. The effect of diamide is reversed after treatment with S-S bond splitting agents.

Full text

PDF
495

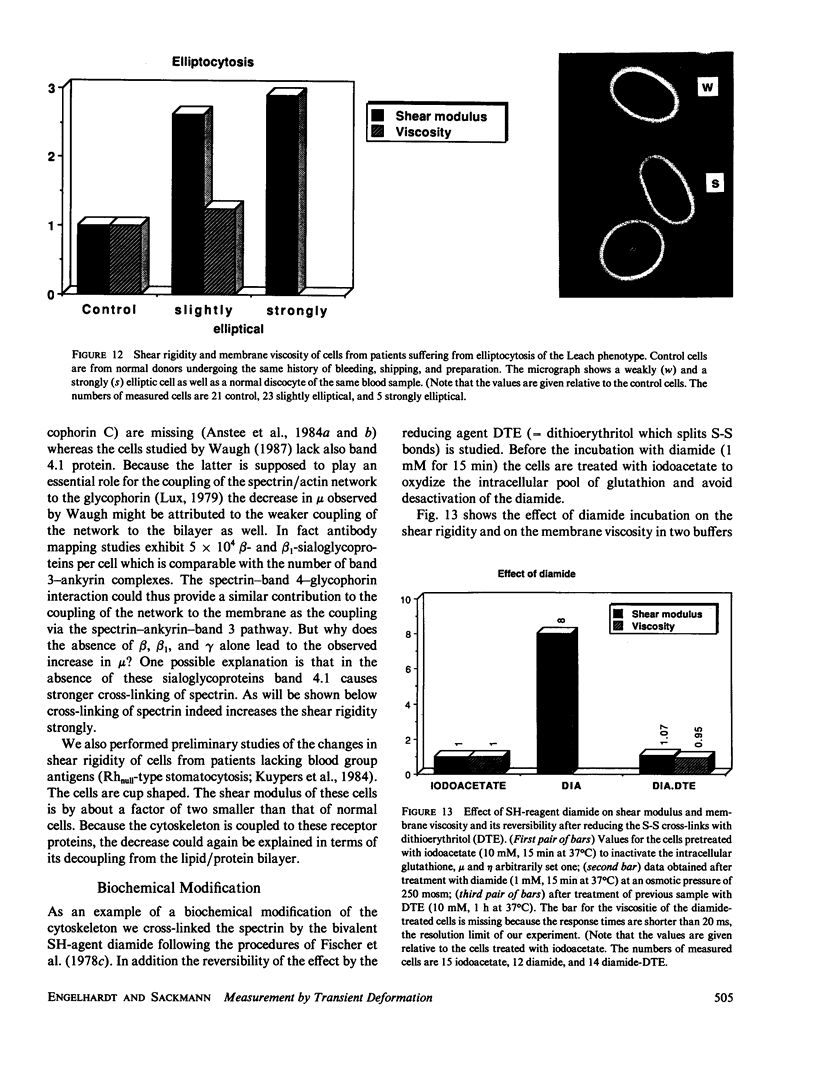
Images in this article

496FIGURE 1
on p.496
497FIGURE 2
on p.497
499FIGURE 5
on p.499
505FIGURE 12
on p.505

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Anstee D. J., Parsons S. F., Ridgwell K., Tanner M. J., Merry A. H., Thomson E. E., Judson P. A., Johnson P., Bates S., Fraser I. D. Two individuals with elliptocytic red cells apparently lack three minor erythrocyte membrane sialoglycoproteins. Biochem J. 1984 Mar 1;218(2):615–619. doi: 10.1042/bj2180615. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Anstee D. J., Ridgwell K., Tanner M. J., Daniels G. L., Parsons S. F. Individuals lacking the Gerbich blood-group antigen have alterations in the human erythrocyte membrane sialoglycoproteins beta and gamma. Biochem J. 1984 Jul 1;221(1):97–104. doi: 10.1042/bj2210097. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bryant G., Wolfe J. Electromechanical stresses produced in the plasma membranes of suspended cells by applied electric fields. J Membr Biol. 1987;96(2):129–139. doi: 10.1007/BF01869239. [DOI] [PubMed] [Google Scholar]
  4. Bull B. S., Weinstein R. S., Korpman R. A. On the thickness of the red cell membrane skeleton: quantitative electron microscopy of maximally narrowed isthmus regions of intact cells. Blood Cells. 1986;12(1):25–42. [PubMed] [Google Scholar]
  5. Clark M. R., Shohet S. B. Red cell senescence. Clin Haematol. 1985 Feb;14(1):223–257. [PubMed] [Google Scholar]
  6. Engelhardt H., Gaub H., Sackmann E. Viscoelastic properties of erythrocyte membranes in high-frequency electric fields. 1984 Jan 26-Feb 1Nature. 307(5949):378–380. doi: 10.1038/307378a0. [DOI] [PubMed] [Google Scholar]
  7. Evans E. A. Bending elastic modulus of red blood cell membrane derived from buckling instability in micropipet aspiration tests. Biophys J. 1983 Jul;43(1):27–30. doi: 10.1016/S0006-3495(83)84319-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Fischer T. M., Haest C. W., Stöhr-Liesen M., Schmid-Schönbein H., Skalak R. The stress-free shape of the red blood cell membrane. Biophys J. 1981 Jun;34(3):409–422. doi: 10.1016/S0006-3495(81)84859-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Fischer T. M., Haest C. W., Stöhr M., Kamp D., Deuticke B. Selective alteration of erythrocyte deformabiliby by SH-reagents: evidence for an involvement of spectrin in membrane shear elasticity. Biochim Biophys Acta. 1978 Jul 4;510(2):270–282. doi: 10.1016/0005-2736(78)90027-5. [DOI] [PubMed] [Google Scholar]
  10. Fischer T. M., Stöhr-Lissen M., Schmid-Schönbein H. The red cell as a fluid droplet: tank tread-like motion of the human erythrocyte membrane in shear flow. Science. 1978 Nov 24;202(4370):894–896. doi: 10.1126/science.715448. [DOI] [PubMed] [Google Scholar]
  11. Fricke K., Sackmann E. Variation of frequency spectrum of the erythrocyte flickering caused by aging, osmolarity, temperature and pathological changes. Biochim Biophys Acta. 1984 Mar 23;803(3):145–152. doi: 10.1016/0167-4889(84)90004-1. [DOI] [PubMed] [Google Scholar]
  12. Fricke K., Wirthensohn K., Laxhuber R., Sackmann E. Flicker spectroscopy of erythrocytes. A sensitive method to study subtle changes of membrane bending stiffness. Eur Biophys J. 1986;14(2):67–81. doi: 10.1007/BF00263063. [DOI] [PubMed] [Google Scholar]
  13. Glaser R., Herrmann A. The sedimentation velocity of individual human erythrocytes as a function of temperature. Biorheology. 1980;17(3):289–291. [PubMed] [Google Scholar]
  14. Haest C. W., Kamp D., Plasa G., Deuticke B. Intra- and intermolecular cross-linking of membrane proteins in intact erythrocytes and ghosts by SH-oxidizing agents. Biochim Biophys Acta. 1977 Sep 5;469(2):226–230. doi: 10.1016/0005-2736(77)90186-9. [DOI] [PubMed] [Google Scholar]
  15. Hochmuth R. M., Buxbaum K. L., Evans E. A. Temperature dependence of the viscoelastic recovery of red cell membrane. Biophys J. 1980 Jan;29(1):177–182. doi: 10.1016/S0006-3495(80)85124-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Hochmuth R. M., Worthy P. R., Evans E. A. Red cell extensional recovery and the determination of membrane viscosity. Biophys J. 1979 Apr;26(1):101–114. doi: 10.1016/S0006-3495(79)85238-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kapitza H. G., Sackmann E. Local measurement of lateral motion in erythrocyte membranes by photobleaching technique. Biochim Biophys Acta. 1980;595(1):56–64. doi: 10.1016/0005-2736(80)90247-3. [DOI] [PubMed] [Google Scholar]
  18. Kurantsin-Mills J., Lessin L. S. Aggregation of intramembrane particles in erythrocyte membranes treated with diamide. Biochim Biophys Acta. 1981 Feb 20;641(1):129–137. doi: 10.1016/0005-2736(81)90576-9. [DOI] [PubMed] [Google Scholar]
  19. Kuypers F., van Linde-Sibenius-Trip M., Roelofsen B., Tanner M. J., Anstee D. J., Op den Kamp J. A. Rhnull human erythrocytes have an abnormal membrane phospholipid organization. Biochem J. 1984 Aug 1;221(3):931–934. doi: 10.1042/bj2210931. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lux S. E. Spectrin-actin membrane skeleton of normal and abnormal red blood cells. Semin Hematol. 1979 Jan;16(1):21–51. [PubMed] [Google Scholar]
  21. Petersen N. O., McConnaughey W. B., Elson E. L. Dependence of locally measured cellular deformability on position on the cell, temperature, and cytochalasin B. Proc Natl Acad Sci U S A. 1982 Sep;79(17):5327–5331. doi: 10.1073/pnas.79.17.5327. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Pfafferott C., Nash G. B., Meiselman H. J. Red blood cell deformation in shear flow. Effects of internal and external phase viscosity and of in vivo aging. Biophys J. 1985 May;47(5):695–704. doi: 10.1016/S0006-3495(85)83966-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Stokke B. T., Mikkelsen A., Elgsaeter A. Spectrin, human erythrocyte shapes, and mechanochemical properties. Biophys J. 1986 Jan;49(1):319–327. doi: 10.1016/S0006-3495(86)83644-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Waugh R. E. Effects of inherited membrane abnormalities on the viscoelastic properties of erythrocyte membrane. Biophys J. 1987 Mar;51(3):363–369. doi: 10.1016/S0006-3495(87)83358-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Zarda P. R., Chien S., Skalak R. Elastic deformations of red blood cells. J Biomech. 1977;10(4):211–221. doi: 10.1016/0021-9290(77)90044-6. [DOI] [PubMed] [Google Scholar]
  26. Zimmermann U., Vienken J., Pilwat G. Rotation of cells in an alternating electric field: the occurrence of a resonance frequency. Z Naturforsch C. 1981 Jan-Feb;36(1-2):173–177. doi: 10.1515/znc-1981-1-229. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES