Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1989 Mar;55(3):489–498. doi: 10.1016/S0006-3495(89)82842-5

Continuum model of voltage-dependent gating. Macroscopic conductance, gating current, and single-channel behavior.

D G Levitt 1
PMCID: PMC1330502  PMID: 2467698

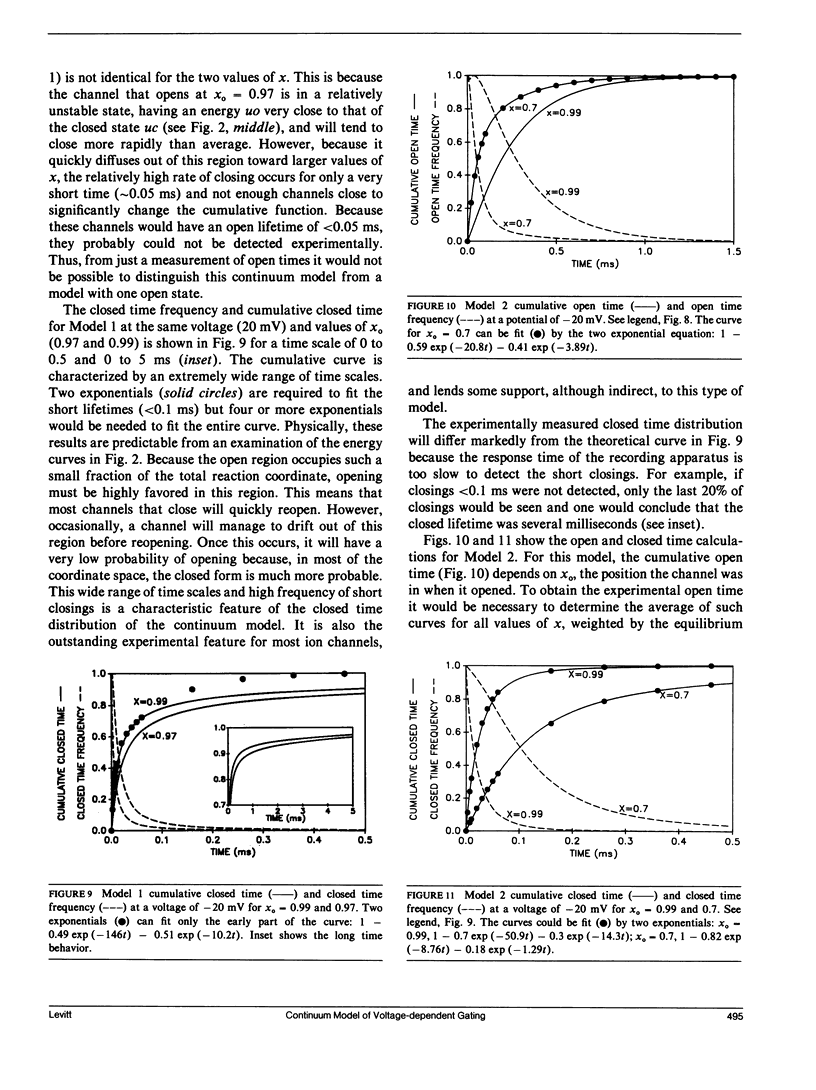
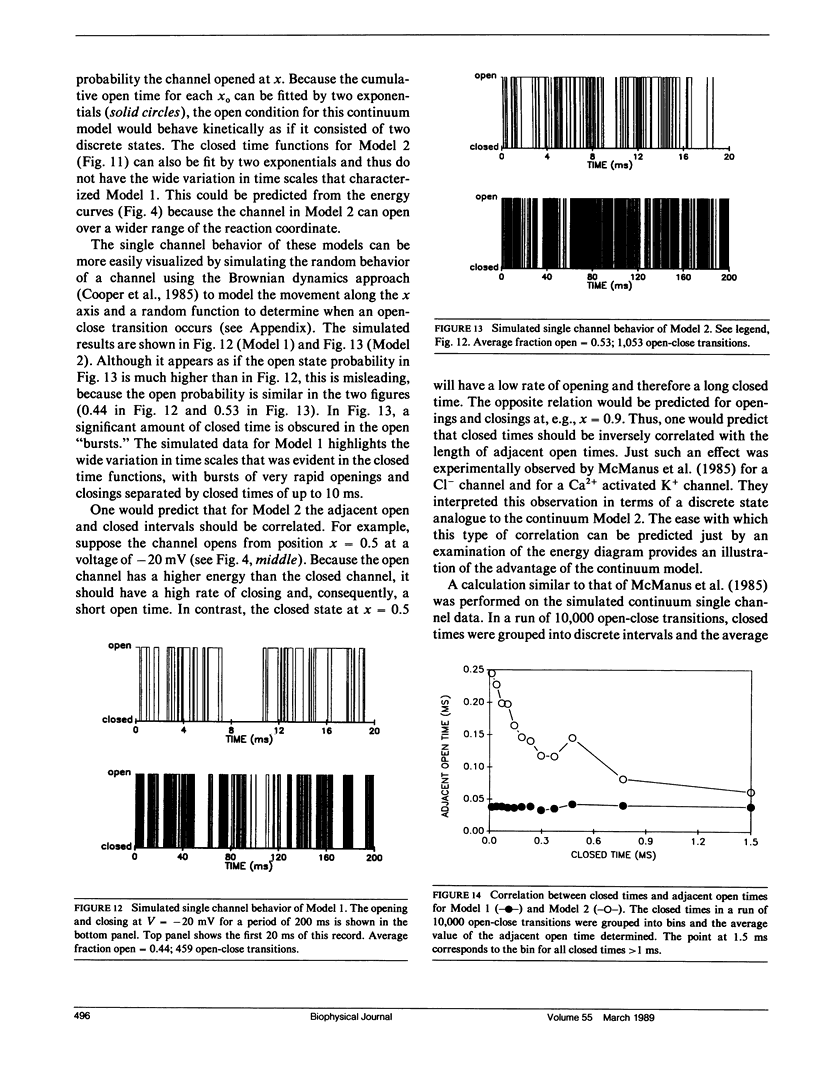
Abstract

It is assumed that the conformational change of the voltage-gated channel is continuous, characterized by movement along a generalized one-dimensional reaction coordinate, x, varying from 0 to 1. This large conformational change is coupled to the movement of most of the gating charge. Superimposed on this large movement is a smaller, very fast conformational change that opens or closes the channel. The large conformational change perturbs the channel so that opening is favored near x = 1 and closing is favored near x = 0. The movement along the x axis is described by a generalized Nernst-Planck equation, whereas the open-close transition is modeled as a discrete reaction-rate process. The macroscopic conductance, gating current, and single-channel behavior of a simple, linearized version of the model is described. Although the model has only seven adjustable constants (about the same as would be required for a conventional three-state model), it can mimic the behavior of the delayed rectified K+ channel with 12 or more closed states. The single-channel behavior of the model can have bursts of rapid openings and closings, separated by long closed times. If the conformational change is assumed to correspond to the rotation and translation of charged helices, then this model can be used to estimate the effective rotational diffusion coefficient of the helix. Such calculations for the delayed rectifier K+ channel indicate that the motion must be very restricted.

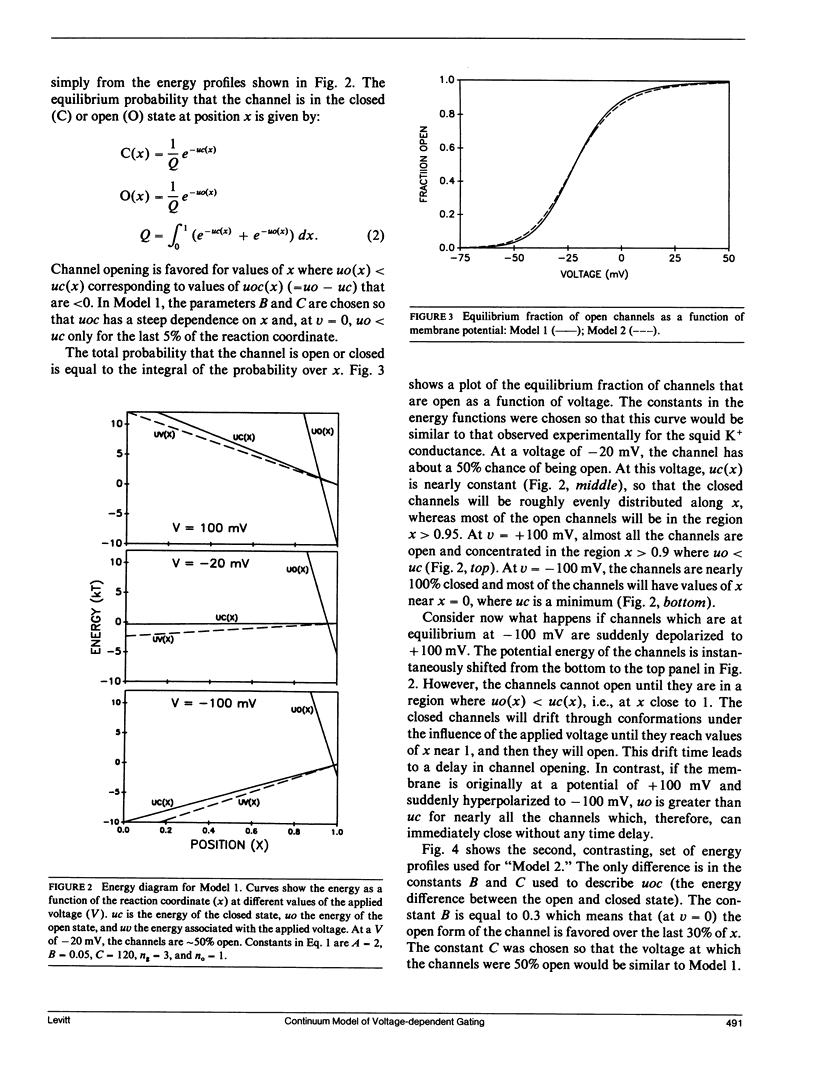
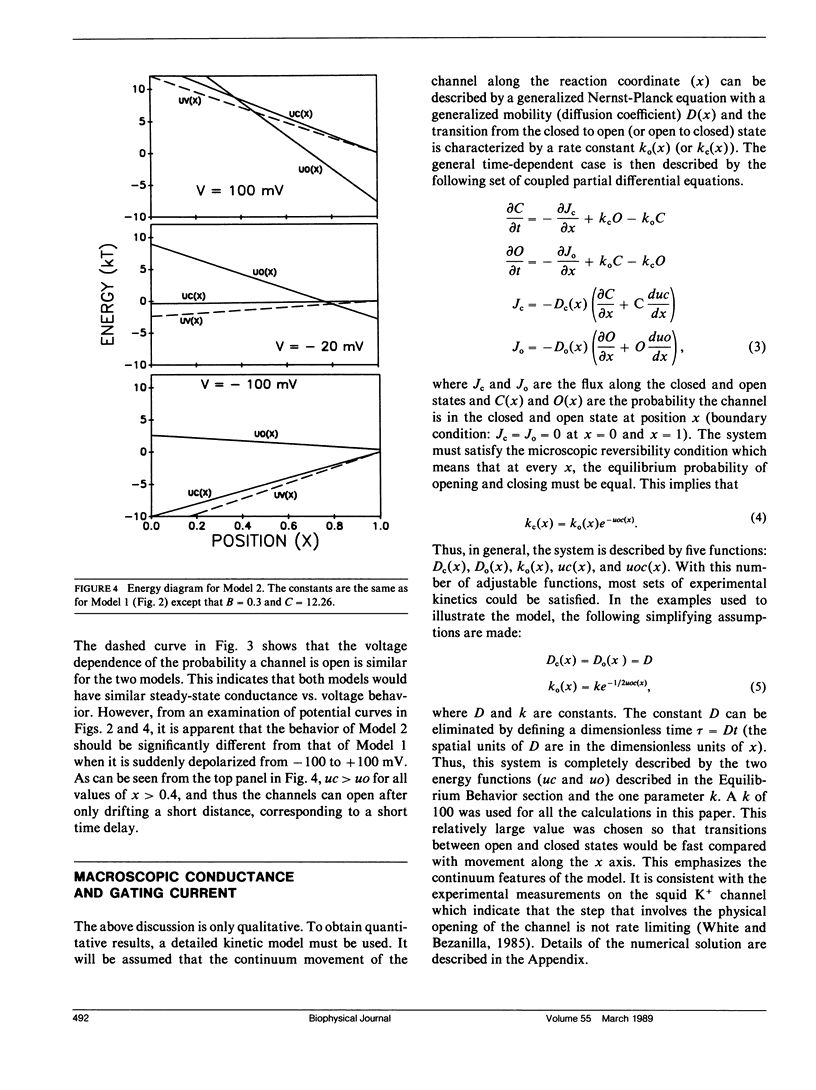
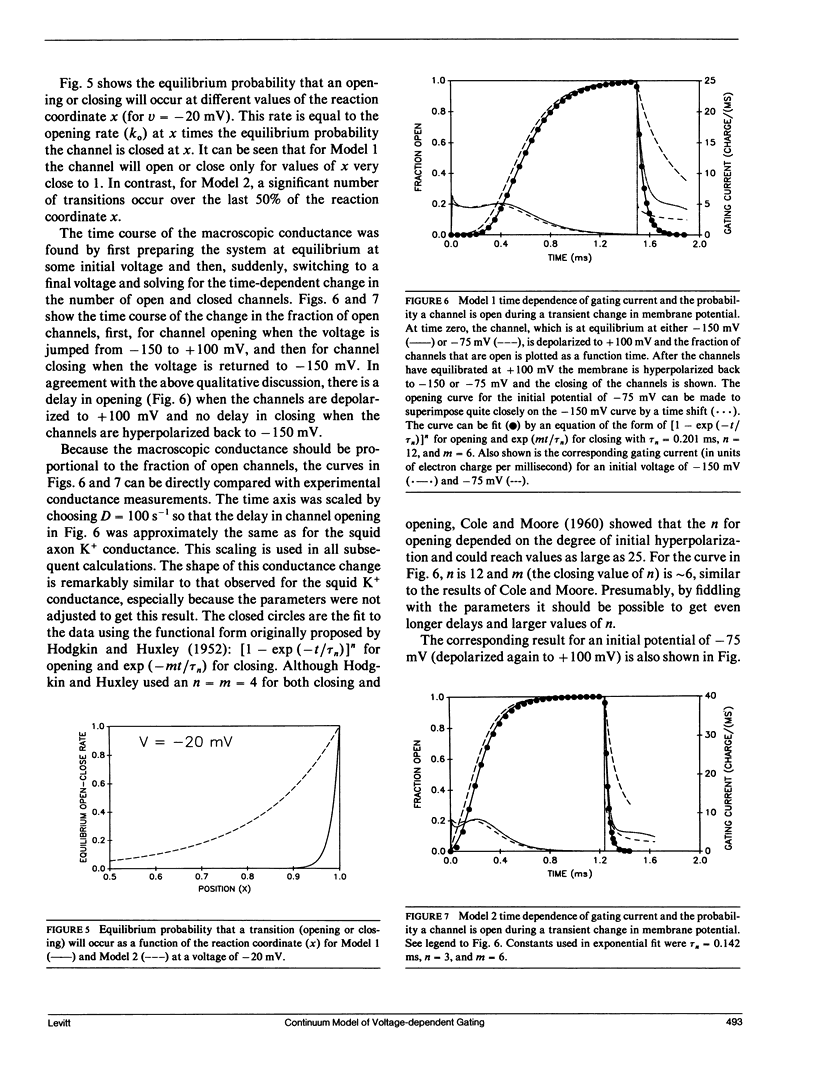
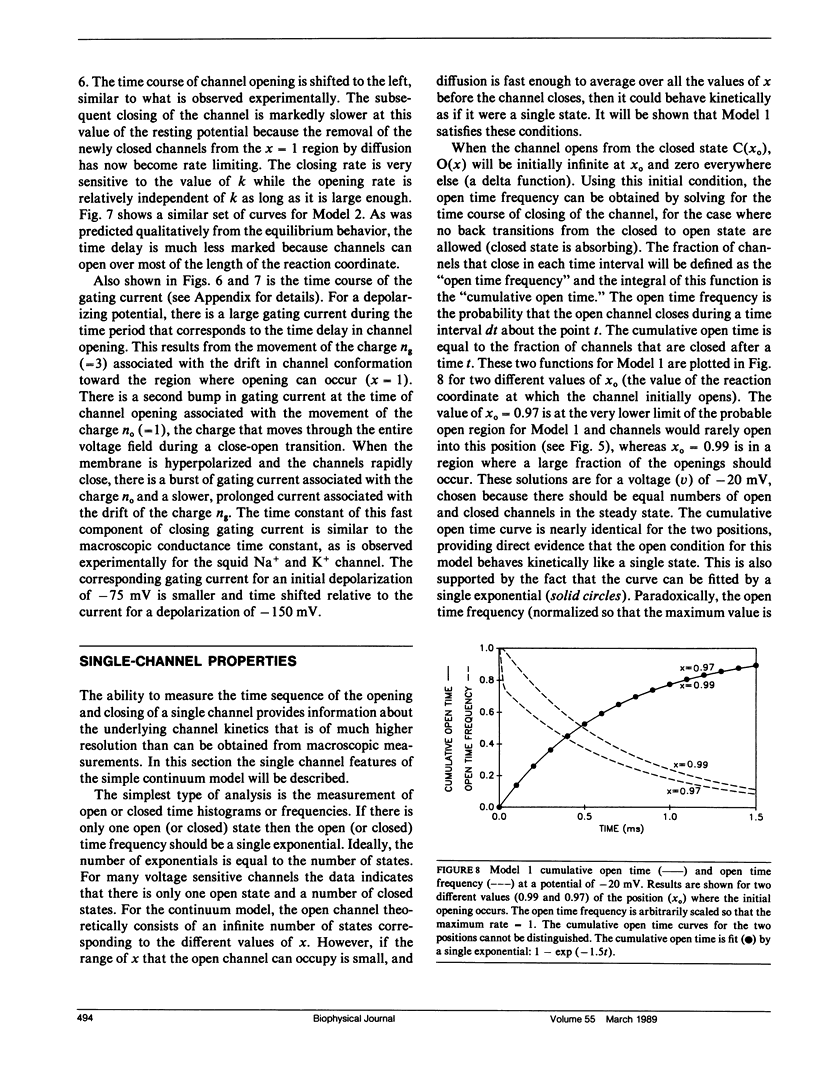
Full text

PDF
489

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Blatz A. L., Magleby K. L. Correcting single channel data for missed events. Biophys J. 1986 May;49(5):967–980. doi: 10.1016/S0006-3495(86)83725-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. COLE K. S., MOORE J. W. Potassium ion current in the squid giant axon: dynamic characteristic. Biophys J. 1960 Sep;1:1–14. doi: 10.1016/s0006-3495(60)86871-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Colquhoun D., Sakmann B. Fluctuations in the microsecond time range of the current through single acetylcholine receptor ion channels. Nature. 1981 Dec 3;294(5840):464–466. doi: 10.1038/294464a0. [DOI] [PubMed] [Google Scholar]
  4. Cooper K., Jakobsson E., Wolynes P. The theory of ion transport through membrane channels. Prog Biophys Mol Biol. 1985;46(1):51–96. doi: 10.1016/0079-6107(85)90012-4. [DOI] [PubMed] [Google Scholar]
  5. HODGKIN A. L., HUXLEY A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952 Aug;117(4):500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Horn R., Lange K. Estimating kinetic constants from single channel data. Biophys J. 1983 Aug;43(2):207–223. doi: 10.1016/S0006-3495(83)84341-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Liebovitch L. S., Sullivan J. M. Fractal analysis of a voltage-dependent potassium channel from cultured mouse hippocampal neurons. Biophys J. 1987 Dec;52(6):979–988. doi: 10.1016/S0006-3495(87)83290-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Läuger P. Internal motions in proteins and gating kinetics of ionic channels. Biophys J. 1988 Jun;53(6):877–884. doi: 10.1016/S0006-3495(88)83168-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. McManus O. B., Blatz A. L., Magleby K. L. Inverse relationship of the durations of adjacent open and shut intervals for C1 and K channels. Nature. 1985 Oct 17;317(6038):625–627. doi: 10.1038/317625a0. [DOI] [PubMed] [Google Scholar]
  10. Millhauser G. L., Salpeter E. E., Oswald R. E. Diffusion models of ion-channel gating and the origin of power-law distributions from single-channel recording. Proc Natl Acad Sci U S A. 1988 Mar;85(5):1503–1507. doi: 10.1073/pnas.85.5.1503. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Peters R., Cherry R. J. Lateral and rotational diffusion of bacteriorhodopsin in lipid bilayers: experimental test of the Saffman-Delbrück equations. Proc Natl Acad Sci U S A. 1982 Jul;79(14):4317–4321. doi: 10.1073/pnas.79.14.4317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Roux B., Sauvé R. A general solution to the time interval omission problem applied to single channel analysis. Biophys J. 1985 Jul;48(1):149–158. doi: 10.1016/S0006-3495(85)83768-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Taylor R. E., Bezanilla F. Sodium and gating current time shifts resulting from changes in initial conditions. J Gen Physiol. 1983 Jun;81(6):773–784. doi: 10.1085/jgp.81.6.773. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. White M. M., Bezanilla F. Activation of squid axon K+ channels. Ionic and gating current studies. J Gen Physiol. 1985 Apr;85(4):539–554. doi: 10.1085/jgp.85.4.539. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES