Experiment and theory for heterogeneous nucleation of protein crystals in a porous medium

Abstract

The determination of high-resolution structures of proteins requires crystals of suitable quality. Because of the new impetus given to structural biology by structural genomics/proteomics, the problem of crystallizing proteins is becoming increasingly acute. There is therefore an urgent requirement for the development of new efficient methods to aid crystal growth. Nucleation is the crucial step that determines the entire crystallization process. Hence, the holy grail is to design a “universal nucleant,” a substrate that induces the nucleation of crystals of any protein. We report a theory for nucleation on disordered porous media and its experimental testing and validation using a mesoporous bioactive gel-glass. This material induced the crystallization of the largest number of proteins ever crystallized using a single nucleant. The combination of the model and the experimental results opens up the scope for the rational design of nucleants, leading to alternative means of controlling crystallization.

The study of the nucleation and growth of protein crystals is one of the most important and underdeveloped areas of structural biology. Crystallization has always been, and still remains, a very difficult task, often referred to as the “bottleneck” of structure determination. The ability to control the nucleation phase is pivotal in the quest to overcome the bottleneck of protein crystallization (1).

Protein crystals are grown from supersaturated aqueous solutions. Homogeneous nucleation takes place in the bulk of the solution, when the supersaturation is high enough for the free-energy barrier to nucleus formation to be overcome. Heterogeneous nucleation is caused by the presence in the solution of solid material, which can be an already formed crystal of the molecule to be crystallized (a “seed” crystal) or a different type of solid substance that has nucleation-inducing properties (a “nucleant”). It can occur even when the supersaturation is not sufficient for homogeneous nucleation, in what is called the metastable zone of conditions (2).

Because growth in the metastable zone affords kinetic advantages that often lead to larger and better-ordered crystals than those grown at higher supersaturations, an aim of protein crystallizers is to be able to induce heterogeneous nucleation (2). Thus, a search for a “universal nucleant” has been ongoing for 2 decades (e.g., refs. 2–4). Such a nucleant could enhance the chances of any single trial producing crystalline material.

In 1988, McPherson and Shlichta (3) introduced the idea of controlling nucleation using mineral substrates as epitaxial nucleants for protein crystallization. This initiative has been pursued over the past 17 years by employing a variety of substrates (e.g., refs. 2 and 4–7), but none have proved to be generally applicable as nucleants.

More recently, Chayen et al. (8) proposed the idea of using a porous substrate containing pore sizes that are comparable with the size of the protein molecules. Such pores may confine and concentrate the protein molecules and thereby encourage them to form crystalline nuclei. Successful use of porous silicon in crystallizing several proteins indicated that it is feasible to apply porous material to crystallization (8). Porous silicon with pore sizes ranging from 5 to 10 nm (the estimated standard deviation is 3 nm) has been shown experimentally to be an effective nucleation-inducing material for protein crystals: five of six tested proteins crystallized from metastable solutions in its presence (8). The proteins tested varied in molecular mass from 14.5 to 320 kDa. Other porous materials, such as Sephadex beads of various sizes, carbon powder, alumino-silicates [VPI-5 (9)], mesoporous molecular sieves [MCM-41 (10)], and zeolites of various mesh sizes were generally unsuccessful (7, 8). In contrast to porous silicon, these materials exhibit minimal variation of pore size and shape.

Cacciuto et al. (11) recently studied, by numerical simulation, the nucleation of the hard-sphere model of colloids. They observed that the model colloid crystallized on curved surfaces, including concave surfaces that may be considered as models for part of a pore. The concave surface acted as a nucleant, and its ability to do so depended on its curvature.

Inspired by the experiments on porous silicon (8) and the computer simulation results (11), we have developed a theoretical model that relates the variability in the pore sizes of a porous medium to the ability of the porous medium to facilitate the heterogeneous nucleation of a protein crystal. It predicts the features required by a porous material to be a candidate for a widely applicable nucleant. We report here this theory and its experimental testing and validation employing a totally different porous material, namely mesoporous bioactive gel-glass.

Statistical Theory and Discussion

Consider a porous medium immersed in a solution of protein. The surface of the porous medium has n_pore pores in contact with the solution. The surface of the material of which the porous medium is made is assumed to attract the protein molecules in the solution. A porous medium with n_pore pores on its surface contributes an amount R to the rate of heterogeneous nucleation, where R is given by

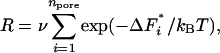[1]

where ΔF*_i is the free-energy barrier to heterogeneous nucleation in pore i, and ν is the attempt frequency for nucleation (12). We assume that in each pore heterogeneous nucleation is simply the crossing of a free-energy barrier of some height ΔF*_i that varies from pore to pore, and that the attempt frequency ν is the same in all pores. k_B and T are the Boltzmann constant and the absolute temperature, respectively. ν has dimensions of inverse time. It is of the order of the rate at which protein molecules diffuse from the solution and onto the growing nucleus (12).

A disordered porous medium, as opposed to, say, a zeolite, will have a distribution of pore sizes. There will be some mean pore diameter m_d and some standard deviation σ_d of the pore sizes around this mean. Also, an individual pore is characterized not only by its diameter but also by its shape: there may be two pores, one long and thin and the other one more spherical but both with the same average diameter. Thus, each pore is specified not only by its diameter d but also by some set of shape parameters. In principle, if we knew the distribution of pore sizes and shapes and could calculate the barrier as a function of them, we could calculate the rate of Eq. 1. However, apart from some data on the diameter distribution we have none of these parameters. Therefore, we have developed a simple phenomenological model for the diameter and shape variation of the free energy of the critical nucleus that simply expresses the diameter variation as a Taylor series around the optimum pore size and the shape variation as simply a random variable. We also treat the diameter as a random variable. The use of a single shape parameter is just for simplicity. We will denote the diameter and shape parameter of pore i by d_i and s_i, respectively. The shape parameter s is defined so the shape of pore i contributes an amount s_i to the free energy of the nucleus. In addition, we define s so that its mean 〈s 〉 = 0.

There will be some optimum diameter, d_o, the diameter at which the free-energy barrier is lowest. We denote this lowest value of the barrier by 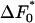. Expanding around this minimum value we have that the free-energy barrier in pore i is

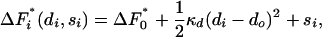[2]

where we have kept only the leading, quadratic term. The stiffness constant that gives the increase in free-energy barrier as the pore gets too big or too small is κ_d.

Taking the d_i and s_i from probability distribution functions p_d and p_s, respectively, the mean or expectation value of the rate of heterogeneous nucleation is given by

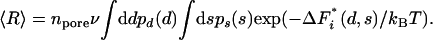[3]

We assume that both the diameters d and shapes s have Gaussian probability distribution functions, with widths of σ_d and σ_s, respectively. The mean diameter is m_d, and by definition the mean of s is zero. Then, Eq. 3 can easily be evaluated, and the average of the rate R is given by

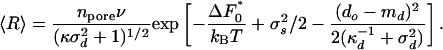[4]

The right-hand side of the equation is the number of pores times the average rate in pores of the optimum size, 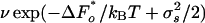, and times the overlap of two Gaussians: one being the distribution of pore diameters and the other is the rate variation, the exponential of Eq. 2.

The equation for the rate 〈R 〉, Eq. 4, contains the exponential of 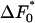: the free-energy barrier in a pore of optimum size and most probable value (s = 0) of the shape parameter. We do not know what the value of 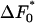is, and so we cannot make any predictions about the absolute nucleation rate, only on how it varies. Thus, when we plot the rate, we use arbitrary units for the 〈R 〉 axis and simply study its variation with parameters such as the sizes of both the pores and the proteins. We will assume that the surface of the solid of which the porous medium is composed at least weakly attracts the protein molecules; of course, if there was a repulsion between the two, the protein molecules would be excluded from the pores and the porous medium would be unable to act as a nucleant.

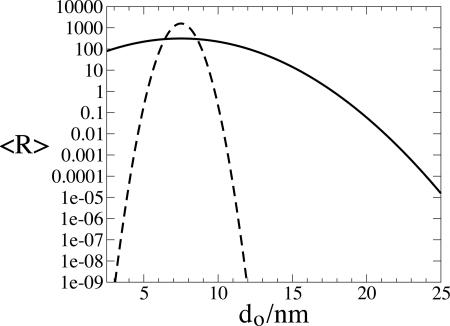
Because the proteins studied in the experiments had different radii and so presumably different optimum pore sizes, we plot in Fig. 1 the nucleation rate as a function of the optimum pore size, d_o. The other parameters are kept fixed. We expect d_o to increase with the size of the protein. Thus, the x axis of Fig. 1 approximately corresponds to the size of the critical nucleus, which is a few times the diameter of the protein. The solid curve is for a porous medium with a wide distribution of pore sizes, σ_d = 3 nm, and the dashed curve is for a narrow distribution, σ_d = 0.5 nm. For the wide distribution, the nucleation rate varies by little more than an order of magnitude for nuclei with d_o across the whole range from 2.5 to 15 nm. Thus, we predict that a porous medium with a wide distribution of pore sizes causes rapid nucleation of proteins with a wide range of sizes. In contrast, the porous medium with the narrow range of pore sizes will only be an effective nucleant for nuclei of a very specific size.

Fig. 1.

The average rate of heterogeneous nucleation per site, 〈R 〉 (in arbitrary units), as a function of the optimum pore size for nucleation of a protein, d_o. The pores have a mean pore diameter m_d = 7.5 nm, and we have plotted results for pore-size standard deviations σ_d = 3 nm, the solid curve, and 0.5 nm, the dashed curve. The stiffness coefficient for the variation of the barrier with pore size κ_d was set to be κ_d = 10k_BT nm^–2.

In protein crystallization and many other areas, it is crucial to not only induce nucleation but to control it: too many nuclei forming can be as severe a problem as no nuclei forming. So, we will now consider how many nuclei form on a given piece of a porous medium. Typically, most of the pores will be the wrong shape and size and so have large free energy barriers associated with them; the nuclei form only in the small fraction of pores that are just right for nucleation. Now, we are interested in conditions when nucleation is occurring; thus, we require at least one pore to have a low barrier to nucleation. We denote the minimum of the set of all n_pore free-energy barriers F*_i by F*_min. Then, we require that F*_min be relatively small, say, ≈10kT. The question then is how many pores have barriers F*_i that are only a little larger than F*_min. Pores with barriers F*_i ≫ F*_min will be irrelevant. The obvious way to define an effective number of pores that contribute to the nucleation rate is to define this effective number N_eff to be the ratio of the total nucleation rate to the rate in the pore with the lowest barrier, hence

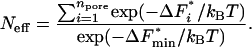[5]

It is easy to see that N_eff is a good indicator of how many nuclei will form: if all pores have almost the same barrier, N_eff ≃ n_pore, whereas in the other limit if the barrier in the pore with the lowest barrier is much lower than that in all other pores, N_eff ≃ 1.

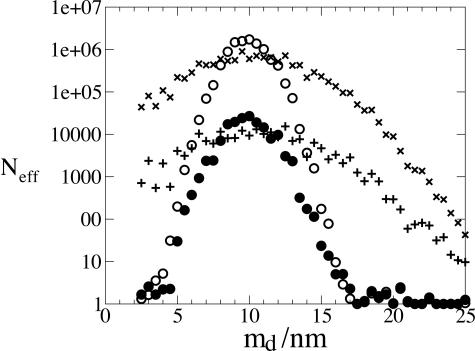
It is straightforward to calculate N_eff numerically from Eq. 5, provided n_pore is not to large. We have done so for sets of n_pore = 10⁹ pores nucleating proteins whose optimum pore diameter d_o = 10 nm. We consider sets of porous media with mean diameters m_d from 2.5 to 25 nm, in steps of 0.5 nm, and plot the results in Fig. 2. The crosses and pluses represent porous media with a wide range of pore sizes, σ_d = 3 nm, and the circles represent media with a narrow range of pore sizes, σ_d = 1 nm. The open circles and crosses represent pores with a narrow distribution of shapes, σ_s = 1kT, whereas the other points indicate a wider distribution, σ_s = 2kT. Each cross, plus, or circle is the result of generating 10⁹ pores with random free-energy barriers, and so it corresponds to an independent sample of a porous medium.

Fig. 2.

The effective number of pores N_eff contributing to the nucleation rate, as a function of the mean pore size m_d. The total number of pores n_pore = 10⁹. The optimum size of pore for the protein d_o = 10 nm. The open and filled circles are for a narrow distribution of pore sizes, σ_d = 1 nm, and the crosses and pluses are for a wider distribution, σ_d = 3 nm. The open circles and crosses are for narrow distributions of the shape parameter, σ_s = 1kT, and the filled circles and pluses are for wider distributions, σ_s = 2kT. The stiffness coefficient κ_d = 10k_BT nm^–2.

There are a number of interesting features in Fig. 2: (i) N_eff is always much less than n_pore; (ii) even for a sample of 10⁹ pores there is significant statistical noise; (iii) when the mean pore size and the optimum pore size are far apart, particularly if σ_d is low, only a handful or perhaps only one pore contributes a significant amount to the nucleation rate; and (iv) for porous media with a wide distribution of pore sizes, over quite a large range of differences between the mean pore diameters and the optimum pore size, tens or hundreds of pores have low barriers. The last observation is particularly useful because the formation of a few nuclei is ideal, neither too many nor too few. If a nucleant can induce only a few nuclei without carefully fine tuning its mean pore diameter to a precise value in relation to the (unknown) optimum pore diameter, then it will tend to be an effective nucleant for many proteins.

Features (ii) and (iii) are related. Of course, the pores with diameters near d₀ dominate the rate, and when the difference |d_o – m_d| is large in comparison with the width of the distribution of pore sizes, σ_d, then these pores come from the tail of the distribution of pore sizes. So, then only a handful of pores contribute significantly to the rate, as can be seen in Fig. 2. Thus, the rate, Eq. 1, is a sum of only a handful of terms, each of which is the exponential of a random variable, and hence there is significant variation from one sample of the pores to another. By contrast, when many pores contribute to the rate, N_eff ≫ 1, the central limit theorem of statistics tells us that sample to sample variation will be small. Here, we see that the curve of the points is smooth only when N_eff is large. The smooth curve implies that if the calculation were repeated with a different set of random variables for the free-energy barriers in the pores, then an almost identical set of results would be obtained, whereas when the data points trace a ragged curve, then repeating the calculation would give a significantly different N_eff and nucleation rate. In this case, there will be significant variation between nominally identical samples of the porous medium. The statistics of this variability is dealt with in more detail elsewhere (13).

Experimental Methods and Results

Our statistical model has suggested that, generically, mesoporous materials with wide pore-size distributions are good candidates for widely applicable nucleants, not just porous silicon (8). The suggestion is that if the material has a wide distribution of pore shapes and sizes, a few will be just right for nucleation. This prediction was tested by experiments on a porous material chemically very different from porous silicon: mesoporous bioactive CaO–P₂O₅–SiO₂ gel-glass particles of 2- to 10-nm pore size (14, 15). Note that although the gel-glass is chemically very different from porous silicon, like the silicon it has a wide distribution of pore sizes and shapes, and the pores are also approximately as large as the nucleus of a protein crystal.

Proteins can crystallize spontaneously only at conditions of supersaturation sufficient for the free-energy barrier to crystallization to be overcome, but, when stable nuclei are already present, crystallization may proceed at lower supersaturations (in theory, to the saturation level). This situation is usually presented as a “crystallization phase diagram,” showing part of the parameter space around some crystallization condition. A crystallization phase diagram is thus a useful summary of crystallization trials, where each trial is a “point” in the search space, as well as a guide to finding the metastable zone. Because there are many parameters involved in a crystallization trial (pH, temperature, etc.) phase diagrams are usually 2D “slices” of the search space. One of the parameters shown is the protein concentration, and the other can be any other controllable parameter, usually the concentration of the main precipitating agent. The main features of such a crystallization phase diagram are a solubility curve, which indicates the concentration of protein at saturation, against one or more controllable parameters, and a supersolubility curve, which indicates the supersaturation above which spontaneous nucleation can take place at the corresponding values of the other parameters. The supersolubility curve is thus the upper limit of the metastable zone.

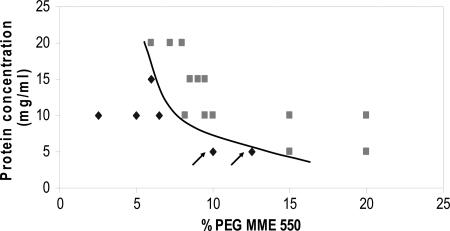
Supersolubility curves of the crystallization phase diagrams of thaumatin, trypsin, lobster α-crustacyanin, lysozyme, c-phycocyanin, myosin-binding protein-C, and α-actinin actin-binding protein were determined by setting up crystallization trials for each of these proteins and recording their progress at regular intervals for several weeks. By using either the microbatch or vapor-diffusion hanging-drop methods, the concentrations both of the protein and precipitating agents were varied until the supersolubility curve could be determined. These experiments gave 2D phase diagrams. All trials were performed at 20°C. In the case of the microbatch method, 1 μl of protein solution was mixed with 1 μl of precipitating agents using the IMPAX robot (16) and incubated under paraffin oil in Terazaki-type plates (Nunc). For the vapor-diffusion method, Linbro plates were used. The crystallization drops were dispensed on silanized glass coverslips that were inverted above 1 ml of reservoirs and sealed with Apiezon C oil (M & I Materials Ltd., Manchester, U.K.). The drops consisted of 1 μl of protein stock mixed with 1 μl of reservoir solution. A phase diagram for α-crustacyanin is shown in Fig. 3. It was obtained by the automated microbatch method and, in addition to the poly(ethylene glycol) monomethylether 550, whose concentration gradient is shown, all of the crystallization drops also contained 100 mM Mes buffer (pH 6.3).

Fig. 3.

The supersolubility curve of the phase diagram of α-crustacyanin obtained with poly(ethylene glycol) monomethylether (PEG MME) as a precipitant. The supersolubility curve is defined as the line separating conditions where spontaneous nucleation (or phase separation, precipitation) occurs from those where the crystallization solution remains clear if left undisturbed. The squares represent conditions at which nucleation occurs without use of a nucleant. The diamonds represent conditions at which the solution remains clear in the absence of nucleant. The arrows indicate conditions at which the mesoporous bioactive gel-glass particles induced nucleation.

Hen egg-white lysozyme (L-6876), thaumatin from Thaumatococcus daniellii (T-7638), and porcine pancreas trypsin (T-0134) were purchased from Sigma. The c-phycocyanin was prepared and purified in-house (17); α-actinin actin-binding protein was provided by M. Pusey and L. Karr (both of the National Aeronautics and Space Administration); myosin-binding protein-C was provided by C. Redwood (Oxford University, Oxford); and lobster α-crustacyanin was provided by P. Zagalsky (Royal Holloway College, London). Poly(ethylene glycol) products and the salts used were purchased from Sigma. To control nucleation, it is necessary to work in very clean conditions. Hence, α-actinin actin binding protein, lysozyme, trypsin, thaumatin, and myosin-binding protein-C stock solutions were filtered with a 300,000-molecular-weight cut-off filter, and the c-phycocyanin and α-crustacyanin were filtered with a 0.22-mm mesh size filter (Ultrafree-MC, Millipore) before setting up the experiments. The gel-glass nucleant was applied to the above seven proteins. Three of those are standard proteins that crystallize with ease and were used as benchmarks (lysozyme, thaumatin, and trypsin). The other proteins are not standard ones, and they are more difficult to crystallize.

One gel-glass grain (diameter ≈100 μm) was placed using thin tweezers or a whisker in each trial, set at conditions below the supersolubility curve of the respective protein. These conditions, referred to as metastable, do not allow crystal nucleation, but they are ideal for the growth of well-ordered crystals from an existing nucleus (2). The bio-glass was easier to use than the porous silicon because it was made in grains that could easily be placed into the crystallization trials, whereas the porous silicon consisted of wafers that had to be broken into small pieces before use. Also, before x-ray diffraction is attempted, to prevent the bio-glass particle from interfering with the proper alignment of the crystal in the beam, or with the actual diffraction, the crystal is usually easily detached from the particle by using a whisker or the cryoloop itself.

In the presence of the gel-glass nucleant, crystals of seven of the seven proteins tested were obtained at metastable conditions. No crystals were formed in control trials containing the same conditions without the nucleant. To be sure that the nucleation described is definitely due to the presence of the gel-glass nucleant, numerous controls were performed. Aliquots of the same solutions were used to set up a series of crystallization experiments. At the same time as the gel-glass particles were added to at least triplicate drops, three types of perturbation controls were performed as follows: (i) some of the neighboring drops were poked with a whisker or an acupuncture needle to mimic the nucleant addition; (ii) other drops had a variety of different materials inserted into them, e.g., porous material with pores of uniform size, hair, crushed glass, nail filings, dust, fullerenes; and (iii) a few drops were just kept in air for a time equal to the time it takes to add the nucleant. None of the above controls produced any crystals. In the case of α-crustacyanin, the conditions at which gel-glass particles were added to the solution is shown in Fig. 3, and crystals growing on the particle are presented in Fig. 4.

Fig. 4.

Photograph under a light microscope of crystals of α-crustacyanin from lobster shell, growing on a bioactive gel-glass particle immersed in the crystallization solution. (Scale bar: 200 μm.)

The nucleant was effective for a range of pH values, corresponding to crystallization conditions at pH values lower (lysozyme, thaumatin), higher (c-phycocyanin, α-crustacyanin), or approximately equal (trypsin, myosin-binding protein-C) to the protein isoelectric points. This observation, combined with the fact that the same material did not induce nucleation when its pores were of unsuitable sizes (very small compared with protein diameters), indicates that the nucleation-inducing properties are not (primarily) due to electrostatic interactions between surface charges on the protein molecules and on the nucleant particles.

Conclusion

The approach presented here to nucleating protein crystals on mesoporous materials has opened up a very promising avenue for protein crystallization. Two materials that are chemically very different, but have in common a wide pore-size distribution, have both been shown to be effective nucleants, whereas materials with minimal pore-size variation have failed. Our theory and these experimental results suggest that it is desirable to have a disordered porous medium, one where the pores are highly nonuniform, because use of such a porous medium makes it likely that one or more pores will have very low barriers to nucleation. The theory also suggests ways to rationally select and design nucleants to optimize the difficult task of crystallizing proteins and other important materials.