Nitric oxide inhibition of respiration involves both competitive (heme) and noncompetitive (copper) binding to cytochrome c oxidase

Abstract

NO reversibly inhibits mitochondrial respiration via binding to cytochrome c oxidase (CCO). This inhibition has been proposed to be a physiological control mechanism and/or to contribute to pathophysiology. Oxygen reacts with CCO at a heme iron:copper binuclear center (a₃/Cu_B). Reports have variously suggested that during inhibition NO can interact with the binuclear center containing zero (fully oxidized), one (singly reduced), and two (fully reduced) additional electrons. It has also been suggested that two NO molecules can interact with the enzyme simultaneously. We used steady-state and kinetic modeling techniques to reevaluate NO inhibition of CCO. At high flux and low oxygen tensions NO interacts predominantly with the fully reduced (ferrous/cuprous) center in competition with oxygen. However, as the oxygen tension is raised (or the consumption rate is decreased) the reaction with the oxidized enzyme becomes increasingly important. There is no requirement for NO to bind to the singly reduced binuclear center. NO interacts with either ferrous heme iron or oxidized copper, but not both simultaneously. The affinity (K_D) of NO for the oxygen-binding ferrous heme site is 0.2 nM. The noncompetitive interaction with oxidized copper results in oxidation of NO to nitrite and behaves kinetically as if it had an apparent affinity of 28 nM; at low levels of NO, significant binding to copper can occur without appreciable enzyme inhibition. The combination of competitive (heme) and noncompetitive (copper) modes of binding enables NO to interact with mitochondria across the full in vivo dynamic range of oxygen tension and consumption rates.

NO is a physiological signaling molecule produced in vivo by enzymes of the NO synthase family. The NO signaling pathway is classically mediated by activation of soluble guanylate cyclase (1–3). However, in 1994 it was additionally shown that mitochondrial oxygen consumption by cytochrome c oxidase (CCO) is reversibly inhibited by NO in a manner apparently competitive with the oxygen tension (4–6). Inhibition of mitochondrial respiration by NO at CCO has since been implicated in a wide range of physiological processes (7–12), and several of these require a competitive (with respect to oxygen) element to the interaction, e.g., activating hypoxia-inducible factor (13); maintaining flow-metabolism coupling in the brain (14); and allowing cells distant from capillaries to maintain adequate oxygenation (15). Under pathological conditions such as sepsis, the elevated NO concentration, generated by inducible NO synthase, is associated with mitochondrial dysfunction and is implicated in mortality in the critically ill (16).

However, the detailed molecular mechanism of CCO inhibition by NO has not yet been unequivocally established. The oxygen-binding center of CCO is bimetallic, and dioxygen reacts at this site only when both the heme a₃ iron and the adjacent copper (Cu_B) are reduced (17). Functional studies initially suggested that NO inhibits by binding reversibly and competitively with oxygen (4–6, 18, 19); however, NO not only reacts rapidly with reduced heme a₃ (20) but also has the capability to react with cupric Cu_B (21–24) as well as possibly with the latter in its cuprous state (23). We (25, 26) and others (27, 28) demonstrated that NO not only binds rapidly to cupric Cu_B but also reduces it to the cuprous state, producing nitrite, which is subsequently released from the binuclear center (29). NO similarly interacts rapidly with cupric copper centers in other oxidases (e.g., laccase; refs. 30 and 31). This promiscuity has led to a number of hypotheses proposing that these alternative interactions are physiologically relevant (12, 32).

Only one NO molecule per binuclear center should be needed to inhibit competitively with oxygen (6), and both the (oxidized or reduced) mammalian enzyme (33) and reduced bacterial enzyme (34) bind NO with a 1:1 stoichiometry. But flash photolysis and molecular dynamics energy minimization studies have suggested that two NO molecules can be accommodated at the fully reduced binuclear center of Paracoccus denitrificans CCO (35, 36); two NO molecules were also reported to bind simultaneously to the homologous heme:copper active site of the Escherichia coli quinol bo₃ oxidase (ref. 37, but see ref. 38 for an alternative explanation). It has correspondingly been claimed that, in steady-state experiments with both mammalian cells (39) and mitochondria (40), two NO molecules can bind simultaneously during inhibition of enzyme activity.

The rapid inhibition of the oxidase by NO also suggested that it may bind an intermediate in the catalytic cycle unavailable to oxygen, making it a more effective inhibitor than predicted thermodynamically by allowing it to “outcompete” oxygen kinetically (41). Nevertheless, we suggested that the steady-state inhibition constants observed in vivo are broadly consistent with simple equilibrium NO binding to the same enzyme intermediate as oxygen binds, namely, the fully reduced binuclear center (7, 42). A recent paper has attempted to explain all of the extant data within the framework of this simple, one-site, competitive model (43). However, we report here experimental and modeling studies to demonstrate that, contrary to this recent report, a simple competitive model (43) is inadequate to describe NO interactions with the enzyme. It is also not necessary to postulate that two NO molecules bind per binuclear center (39, 40). Instead, the enzyme can bind NO either at reduced heme iron (competitive with oxygen) or at oxidized copper (noncompetitive with oxygen). We show that the latter reaction is vital for enabling NO to control mitochondrial function throughout the wide range of physiological oxygen tensions and oxygen consumption rates.

Results

Calculation of CCO K_i (NO) at High Enzyme Turnover. To directly test the theory that NO can outcompete oxygen by binding to both the fully reduced and single-electron-reduced binuclear center we compared NO inhibition with that of a “classical,” purely competitive inhibitor of CCO, carbon monoxide (CO). Like oxygen, CO can bind to reduced heme iron only when the adjacent copper site is also reduced (17). The test was to measure the apparent K_m (O₂) at different inhibitor concentrations, for both CO and NO, under identical conditions; the true K_i was then calculated from these data (see Supporting Methods, which is published as supporting information on the PNAS web site). The calculated K_i was 0.18 nM in the pure enzyme and 0.22 nM in submitochondrial particles (see Fig. 6, which is published as supporting information on the PNAS web site). Comparison of the K_i values for NO and CO (0.2 nM and 0.3 μM, respectively) shows that inhibition by NO at high enzyme turnover is 1,000- to 2,000-fold more effective than that by CO. For a classical competitive inhibitor the true K_i can be obtained from k_off/k_on. Here the experimental K_i (NO) value obtained (0.2 nM) is not inconsistent with the previously measured (20) on rate (1 × 10⁸ M^–1 s^–1) and off rate (0.01 s^–1) (28) for NO binding to the fully reduced binuclear center; therefore, it is not necessary to postulate that NO accesses an alternative enzyme species to oxygen at high turnover. Note that these experiments were done at 35°C, close to the temperature (37°C) of the reported off rate of 0.01 s^–1. The literature value for the NO on rate is available only at 20°C, but in general the temperature dependency of ligand association to heme proteins (44) is insignificant compared with the temperature dependency of ligand dissociation.

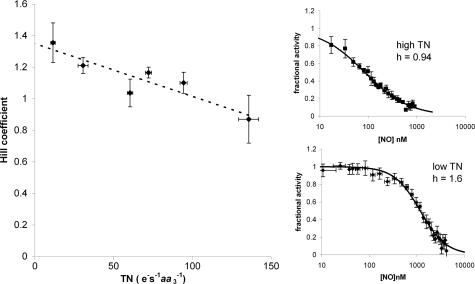
Reassessment of Hill Coefficients for NO Binding. Advocates of a two-site model for NO inhibition have analyzed the NO concentration dependence of the fractional inhibition. Plots of log [NO] versus fractional inhibition have given apparent Hill coefficients >1 (as much as 2 in some cases). The authors (39, 40) have suggested that this is evidence for cooperative NO binding to the enzyme (in analogy to oxygen's binding to hemoglobin, for example). However, in a complex multisubstrate enzyme such as CCO, such interpretations of the kinetic data are fraught with difficulty. We therefore reassessed the significance of these Hill coefficients by measuring them over a range of enzyme turnover conditions and at different oxygen concentrations. We found that the measured Hill coefficient was not a constant, but correlated with enzyme turnover, as shown in Fig. 1. Fig. 1 Left shows that, at low turnover, the Hill coefficient (h) is >1, but, as enzyme turnover increases, h approaches unity. This finding can be seen clearly in the individual Hill plots, shown in Fig. 1 Right. Also evident from these plots is that the concentration of NO required for 50% inhibition increases as turnover decreases. In Fig. 1 Upper Right, where enzyme turnover is high, the apparent IC_50(NO) is 84 nM, whereas in the low turnover plot the apparent IC_50(NO) is 1,170 nM. There was no statistically significant correlation between [O₂] and the value of h (data not shown).

Fig. 1.

Hill coefficients for NO inhibition as a function of enzyme turnover. (Left) Hill coefficients (h) obtained from fitting (see Methods) experimental results obtained at 150 μM O₂. Points represent data averaged over intervals of 25 turnover numbers (TNs). Error bars represent SEM; n = 4–12. TN had a significant negative correlation with h (P < 0.05), indicated by the dashed line (although the relationship is unlikely to be strictly linear). (Right) Hill plots of fractional activity as a function of NO at high (Upper) and low (Lower) turnover. The solid line shows the best fit to the experimental data (points) by using nonlinear regression (h = 0.94 and IC₅₀ = 84 nM NO in Upper; h = 1.6 and IC₅₀ = 1,170 nM NO in Lower). For illustrative purposes the data (collected at 1-s resolution) were averaged (±SEM) over 5s.

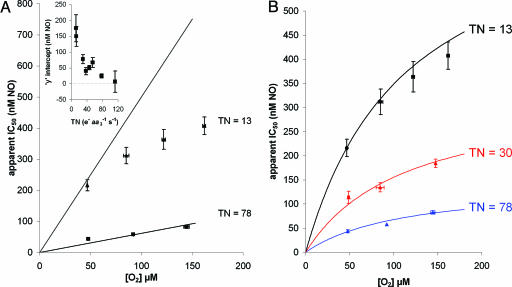
Mode of Inhibition: Simple Competitive Inhibition or More Complex? To test whether or not NO binds purely in competition with oxygen, we performed a detailed kinetic analysis of the oxygen competition of NO inhibition. Although all previous in vitro and in vivo data have demonstrated that decreasing the oxygen tension enhances NO inhibition, this is not the same as proving that NO binds only in a purely competitive mode. In Fig. 2A the experimental data (apparent IC_50(NO) as a function of [O₂]) for high and low enzyme turnovers are shown with fit lines corresponding to the simple competitive model described recently by Antunes et al. (43). For a purely competitive inhibitor the intercept on the y axis should be the true K_i (0.2 nM in both the Antunes model and from our results; see Fig. 6). At high enzyme turnovers the data approximated the pure competitive model. However, for the low turnover data the numbers were inconsistent with the model (forcing the y intercept through 0.2 nM is clearly not appropriate). This apparent deviation from the true K_i as turnover decreases can be seen more clearly in Fig. 2 A Inset, which compares the intercept (apparent IC_50(NO) at zero oxygen) across a range of turnovers. It is clear from the data that, at low enzyme turnover, the inhibition by NO, although still sensitive to the oxygen tension, is not purely competitive. To fit the data in Fig. 2 A, this observation was taken into account, and the model of Antunes et al. (43) was expanded to include an additional interaction at a noncompetitive site, consistent with previous observations that NO can react with the oxidized copper of the binuclear center, resulting in oxidation of NO to nitrite (25, 26).

Fig. 2.

Apparent IC₅₀ for NO as a function of [O₂] at different enzyme TN. (A) Data points represent experimental data: ▴, TN = 13; ▪, TN = 78 (e^– s^–1 aa₃^–1). Error bars represent SEM. Solid lines represent best fit obtained according to the theoretical model proposed by Antunes et al. (43). The optimal rate constants for the fit were obtained by linear regression at the higher TN value. The values of the rate constants obtained were then used to attempt to predict the data at the lower turnover. (Inset) The apparent IC₅₀ for NO as a function of TN at zero oxygen (i.e., y-axis from linear regression with no theoretical constraints). Error bars represent SEM. (B) Here the data are fitted to an expanded model (Fig. 3) in which NO can interact both competitively and noncompetitively with oxygen when the binuclear center is in either the reduced (ferrous a₃) or oxidized (cupric Cu_B) state.

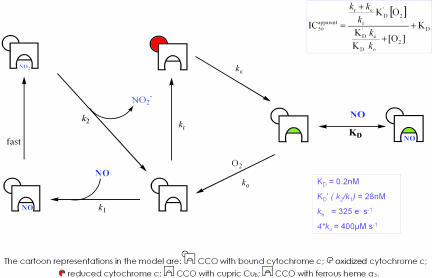
Fig. 2B shows that, by incorporating the interaction of NO with the noncompetitive site (oxidized Cu_B) into the model, the data can be fitted at high, medium, and low turnovers. The calculated apparent “affinity” (K_i = k₂/k₁) for the noncompetitive interaction with oxidized Cu_B is surprisingly low (28 nM). The essential elements of this equilibrium model, as shown in Fig. 3, are therefore (i) the competitive (with oxygen) reversible binding of NO to the fully reduced binuclear center with a K_i of 0.2 nM and (ii) a noncompetitive reaction with oxidized Cu_B with a K_i(app) of 28 nM.

Fig. 3.

A theoretical model that can explain NO inhibition under all conditions of enzyme turnover and oxygen tension. In this model NO can interact both competitively with oxygen and noncompetitively, reacting with the binuclear center in either the reduced (ferrous a₃) or oxidized (cupric Cu_B) state. The equation for IC₅₀ is a rectangular hyperbola, in which the upper value of IC^apparent₅₀ is related to turnover (k_r) (see boxed equation), and K_D′ = k₂/k₁. The fitted values of K_D and K_D′ were 0.2 nM and 28 nM, respectively. The rate of reaction with oxygen (k_o) is 4 * 100 μM^–1, where the factor 4 appears because four electrons are moved to oxygen per reaction step. The internal electron transfer rate k_e is set at 325 s^–1. Values of k_r (initial reduction rate of the binuclear center) are set to accord with the measured turnovers (Fig. 2). Note that, although a number of iron:oxygen intermediates (e.g., ferryl) are also likely to be present during turnover, the interactions of NO with these oxidized species (26, 27) are formally included in the reaction step governed by k₁, and so this added complexity does not affect the conclusions drawn from this model. Additionally, the reaction step governed by k₂ is more complex than indicated because the nitrite dissociation rate depends on the redox state of the binuclear center (29). Thus, K_D′ represents an apparent, not true, affinity constant. (Note that cytochrome c is illustrated bound to CCO to denote the source of electrons, but this does not imply cytochrome c remains bound throughout multiple catalytic cycles.)

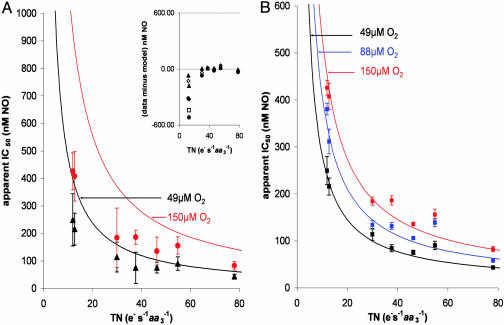
One important consequence of the purely competitive model is that NO inhibition depends strongly on the enzyme turnover (43). In Fig. 4 we provide experimental evidence supporting this idea; the increase in apparent IC_50(NO) that occurred with a decrease in enzyme turnover, illustrated in the Hill plots of Fig. 1, is extended across a wide range of enzyme turnovers. The experimental data plotted in Fig. 4A are shown with fit lines that correspond to the purely competitive model, whereas in Fig. 4B the fit lines correspond to the expanded model that includes both competitive and noncompetitive interactions, described above. Both models clearly approximate the data at high enzyme turnover. However, as shown in Fig. 4A Inset, when enzyme turnover decreases the purely competitive model begins to deviate from the experimental results, and only the two-site model fits the full range of experimental data. In the purely competitive model (Fig. 4A) nanomolar inhibition constants increase to micromolar levels as enzyme turnover is lowered. This finding would mean that at low turnovers no conceivable physiological level of NO could control mitochondrial respiration. Although our data agree with the principle that NO is a weaker inhibitor at lower rates of oxygen consumption, the inclusion of the second noncompetitive site attenuates this effect; the rise in the apparent inhibition constant at low turnover is less dramatic in the model that includes the noncompetitive interaction, with NO being more than twice as effective an inhibitor than predicted from the purely competitive model.

Fig. 4.

Apparent IC₅₀ for NO as a function of enzyme turnover at different [O₂]. (A) Points represent experimental data, error bars represent 95% confidence limit, and solid lines are theoretical fits obtained by using the model and associated equation proposed by Antunes et al. (43): IC₅₀ = K_i (1 + k_O2app/k_iv [O₂]), where K_i = 0.2 nM, k_iv is the turnover number in units of e^– s^–1aa₃^–1, and k_O2app was calculated according to Verkhovsky et al. (53). (Inset) the residual obtained after subtracting the theoretical fits from the actual data (•, 150 μM O₂; □, 122 μM O₂; ⋄, 88 μM O₂; ▴, 49 μM O₂). (B) The same data points with solid fit lines corresponding to our model; equation and values are shown in Fig. 3 and its legend (error bars represent SEM). A model in which NO interacts with the binuclear center in both oxidized and reduced states clearly fits the data more closely than does the simple competitive model.

Discussion

We found that, under conditions of maximal enzyme turnover, the dominant NO-inhibited species of CCO is the NO–ferrous heme a₃ complex with the adjacent Cu_B also reduced (cuprous). The experimental K_D (0.2 nM) is identical to the ratio of NO off and on rates with fully reduced enzyme, and spectral evidence for this species under catalytic conditions has been published by Sarti et al. (28). However, other secondary effects become apparent at lower turnovers.

Torres et al. (45) proposed a second low-affinity inhibitory site because the rates of NO inhibition onset and formation of the ferrous NO species were greater than the corresponding on and off rates for ferrous a₃–NO complex formation. They obtained an approximate K_D value of 100 nM for the oxygen-independent inhibitory component and suggested a reversible binding of NO to give a cuprous–NO species. After addition of another electron to give the fully reduced binuclear center the Cu-bound NO could then move to the iron.

A similar model in which NO binds to a single electron-reduced binuclear center was proposed by Giuffre et al. (41), who suggested that NO could bind to ferrous heme a₃ with an adjacent cupric copper. Although we cannot rule out such an interaction, it does not appear necessary to explain the steady-state kinetics of inhibition.

The essential difference between our present model and these two earlier versions is that we propose that NO does not merely bind reversibly to one of the partially or fully reduced forms of the oxidase but binds specifically to Cu_B when the binuclear center is fully oxidized (26). The bound NO then performs redox chemistry to reduce the enzyme and concurrently form nitrite; inhibition by the resulting binuclear center nitrite complex is relieved by nitrite dissociation upon further reduction (25, 29). Spectral evidence for this nitrite-inhibited complex has also been reported by Sarti et al. (28) under conditions of low enzyme turnover.

We also investigated the question of the number of NO molecules required to inhibit the enzyme and find that the value of the Hill coefficient (h) increases as enzyme turnover decreases. This observation is expected for a process where inhibiting the enzyme turnover perturbs the substrate concentration in the steady state; as NO inhibits CCO the cytochrome c becomes more reduced, “buffering” the inhibition. This effect, known as the branching chain phenomenon, has been previously described for CO inhibition of CCO, where it is well characterized that there is only a single binding site (46). By analogy we conclude that only one NO molecule is required to inhibit CCO, although the site of interaction can depend on the redox state of the enzyme. The report that two NO molecules per enzyme are required for inhibition (39) involved experiments with whole cells that were respiring much more slowly than the maximal rate obtained here with pure CCO. Such a low turnover could explain the high reported value of h. We have shown (7, 42) that another claim for an apparent requirement for two NO molecules to inhibit the enzyme (40) can be reinterpreted in alternative ways that do not require the double interaction. The evidence for the simultaneous binding of two NO to the P. denitrificans enzyme is more convincing, but the conditions used indicate that the binding of the second NO would be very slow (35, 36). This finding is not in agreement with the previous observations under catalytic conditions, where the onset of NO inhibition is rapid (45, 47). The second NO molecule, if bound, is therefore not responsible for any part of the inhibition.

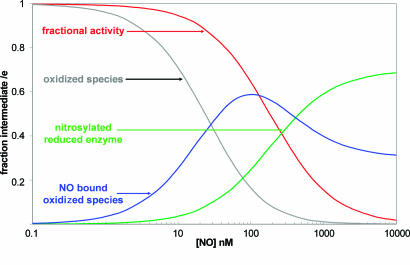
We thus conclude that the simplified model of Fig. 3 is both necessary and sufficient to interpret the present data and other similar reported data. However, in addition to explaining the observed inhibition kinetics, predictions that our model makes about enzyme intermediate levels have important consequences for the suggested signaling role of the NO interaction with CCO (11). Fig. 5 shows the populations of the major oxidase intermediates during simulated steady-state fluxes, as predicted by the model in Fig. 3. At a rate of electron transfer simulating a substrate or ADP-limited respiratory chain (15 e^– s^–1), the sequestering of part of the oxidized enzyme as a ferric/cupric NO or nitrite complex occurs at lower concentrations of NO than that required for observable inhibition. Maximal occupancy of the latter species occurs at intermediate NO levels. At the highest NO concentrations the classical NO–ferrous/cuprous species begins to accumulate and, at low levels of oxygen, to approach completion. But at higher oxygen levels the oxidase, when fully inhibited at micromolar NO levels, is held in a mixed population of the ferric/cupric and ferrous/cuprous forms (see Fig. 7). Further experiments with spectrophotometrically measurable levels of the inhibited steady-state oxidase are under way to examine this prediction. Because both the NO–heme (28) and NO–copper bonds are photolabile (24), but with different wavelength sensitivities, a detailed study of the photoaction spectra for relief of inhibition could also be used to refine this model (48).

Fig. 5.

Predicted populations of oxidase intermediates and computed turnover as a function of [NO]. The model shown in Fig. 3 was used to generate the predicted populations of oxidized enzyme, NO complexes of oxidized enzyme, and the final NO–ferrous complex. The values shown were obtained for an observed turnover of 15 sec^–1, at 49 μMO₂, using the parameters: k_o = 400 μM; k_r = 15.7 sec^–1; k_e = 325 sec^–1; K_D = 0.2 nM; and K′_D = 28 nM. Population of these species at 49, 88, and 150 μM O₂ can be seen in Fig. 7, which is published as supporting information on the PNAS web site.

We show here that the enzyme can “sense” NO levels at its Cu_B site, with limited effect on oxygen consumption (and importantly energy transduction). The finding that NO interacts with oxidized CCO at lower concentrations than that required for inhibition may have important physiological consequences. NO has been suggested to play a key role in mitochondrial signaling by means of its effect on CCO. Criticisms of this theory are based on the (higher) levels of NO required to control mitochondrial oxygen consumption compared with that required to activate other signaling pathways, notably guanylate cyclase (39, 49). However, it is apparent that NO can reduce mitochondrial cytochromes at NO/O₂ ratios that do not inhibit oxygen consumption (50). In the case of cytochrome c, the increased steady-state reduction can signal via modulating the production of superoxide (11). Our work provides an underpinning biophysical mechanism for this effect.

To summarize, we have demonstrated that NO inhibition at mitochondrial CCO has a competitive high-affinity inhibition site (ferrous heme a₃) and a noncompetitive, lower-affinity site (cupric Cu_B). Mitochondrial oxygen consumption has a very large dynamic range (e.g., 20-fold after muscle activation) and operates within a wide range of cellular pO₂. The combination of these two sites is therefore required for NO to be able to interact with mitochondria across this dynamic range.

Methods

Enzyme Preparation. Beef heart CCO was purified by the method of Yonetani (51), except that the solubilization buffer contained 0.1% lauryl maltoside (n-dodecyl b-d-maltoside, from Sigma) instead of 1% Emasol. Enzyme concentrations were calculated by using e_605–630 = 38,000 M^–1cm^–1 for the dithionite-reduced enzyme (52).

Preparation of Keilin and Hartree Type Submitochondrial Particles. See Supporting Methods.

Inhibition of CCO by CO and Measurement of Dissolved CO. See Supporting Methods.

Reduction of Oxygen by CCO and Variation of Enzyme Turnover. Oxygen was reduced by either purified CCO or submitochondrial particles in the presence of ascorbate, N,N,N′,N′,tetramethyl-p-phenylenediamine (TMPD), and cytochrome c (all from Sigma), in 0.1 M KPi (pH 7.4) at 35°C, and in the presence of 0.1% lauryl maltoside for the pure enzyme only. Maximal enzyme turnover (rate of O₂ reduction/[CCO]) was obtained in the presence of 300 μM TMPD, 30 μM cytochrome c, and 10 mM ascorbate. Lower rates of enzyme turnover were obtained by omitting TMPD and using lower concentrations of cytochrome c and ascorbate.

Calculation of K_i (NO) from the Effect of NO on K_m(O₂)^apparent at High Turnover. See Supporting Methods.

Inhibition of CCO by NO and Calculation of IC₅₀ and Hill Coefficient. Experiments were performed in a chamber protected from ambient light because of the light sensitivity of NO and CO inhibition. Reversible inhibition of oxygen reduction by CCO was effected by addition of an aliquot of the fast-releasing NO donor (t_1/2 = 1.8 s) Proli-NONOate (Alexis Biochemicals). As the NO in solution decayed, the rate of oxygen consumption by CCO recovered. The apparent IC₅₀ and Hill coefficient were obtained from plots of rate against [NO] (see Fig. 8, which is published as supporting information on the PNAS web site) fitted to an adaptation of the Hill equation, v = Vi^h/K_0.5^h + i^h, where v is velocity, V is limiting velocity, i is inhibitor concentration, K_0.5 is concentration of i giving 50% V, and h is the Hill coefficient. The actual equation used was V = –(Vi^h/K_0.5^h + i^h) + a, which corrects for the nonenzymatic autooxidation rate (caused by ascorbate/cytochrome c) when the enzyme is fully inhibited. Here V is fixed to the observed experimental maximal rate minus the observed experimental autooxidation rate, and a is fixed to the observed experimental maximal rate, which includes the autooxidation rate.

Measurements of Dissolved Oxygen and NO. Simultaneous NO and oxygen measurements were made in a glass oxygen electrode chamber with a Digital Model 10 controller (Rank Brothers, Cambridge, U.K.). The chamber was fitted with a specially adapted flow-through plunger to accommodate an ISO-NO NO electrode connected to an ISO-NO MK2 NO meter (World Precision Instruments, Stevenage, U.K.). The NO electrode was calibrated with KNO₃/acid iodide according to the manufacturer's instructions. Oxygen and NO meters were connected to a MacLab 8E data acquisition system and analyzed with chart v4.2 software (ADInstruments, Castle Hill, Australia).