High-speed microfluidic differential manometer for cellular-scale hydrodynamics

Abstract

We propose a broadly applicable high-speed microfluidic approach for measuring dynamical pressure-drop variations along a micrometer-sized channel and illustrate the potential of the technique by presenting measurements of the additional pressure drop produced at the scale of individual flowing cells. The influence of drug-modified mechanical properties of the cell membrane is shown. Finally, single hemolysis events during flow are recorded simultaneously with the critical pressure drop for the rupture of the membrane. This scale-independent measurement approach can be applied to any dynamical process or event that changes the hydrodynamic resistance of micro- or nanochannels.

Fluid motions at the micrometer scale are at the heart of many recent developments in microfabrication (1), separation processes (2), cellular-scale identifications (3), DNA sequencing (4), protein crystallization (5) and many basic transport pathways in plants (6), in the microcirculation (7), and specific to industrial processes. The main characteristics of these advances lie in the manipulation and understanding of the dynamics of “soft” objects such as polymers (8) (e.g., DNA), drops (9, 10), microemulsions (11), microfoams (12), cells (13), vesicles and microcapsules (14). In fact, the interaction of the flow with these deformable entities is a tool to further investigate the details of their mechanical properties and their structural features (e.g., the entropic elasticity of a polymer, the viscoelastic properties of a capsule, or the rheology of the liquid film between microbubbles in a foam). For the case of strong confinement offered by microchannels, the flow and shape of any close-fitting soft object is controlled by a competition among the properties of the objects, the fluid pressure, and the viscous stresses acting on the boundaries that resist the motion. The hydrodynamic resistance resulting from this fluid–structure interaction is reflected in a dynamical variation of the pressure drop along the channel during the flow and hence represents a crucial parameter to be measured.

Nevertheless, rapid variations of pressure are very difficult to measure at the micrometer scale and below. Indeed, the difficulties do not originate from the lack of precision sensors commercially available or those described in the research literature (15). The problem is a subtle mix of pragmatism and technological limits. In addition to issues of dead volumes in standard pressure-measurement techniques (16–18) and those associated with interfacing microelectromechanical system devices to standard pressure gauges (19), existing techniques are simply difficult to implement [lasers, quadrant diodes, deformable membranes, multistep process of production (16–18)] and are unable to measure at millisecond rates the pressure changes in micrometer-scale flows. For instance, when a single red blood cell (RBC) enters a channel of 5 × 5 μm, the volume variation produced by a flow at physiological speeds of a few millimeters per second is ≈100 fL in a few milliseconds, which represents a typical pressure-drop variation of tens to hundreds of pascals. Such rapid pressure measurements at the cellular scale, crucial to future device and microcirculatory advances, are not available at this time. Here we report a technique that overcomes these limitations and demonstrate the ability to measure rapid variations of pressure drop between two points in a microfluidic device. The technique needs no external elements and is easy to implement with soft lithography. The basic principle should naturally allow similar measurements of pressure variations in nanochannels.

We chose to illustrate the flexibility of our approach by focusing on blood cells, which allows us to provide insights into outstanding problems in hemodynamics. Indeed, there is a long history of the study of cells at the micrometer scale for assessing mechanical properties (20) and cell shape (21) and for applying these ideas for understanding microcirculatory diseases (22, 23). In fact, the main approach for characterizing the influence of possible diseases on a suspension of cells is the filtration technique (23–25). Briefly, the cells flow through a multipore polycarbonate membrane, and the measured pressure-drop versus flow-rate relation (or the mean passage time of the cells) serves as an index of the deformability state in a population of healthy or sick cells (23, 26). Even if the potential of this technique is for the analysis of large samples, the resultant data reflect only the average properties: the technique is not able to resolve information at the scale of a particular pore or a single cell. Recent advances in microsystems technology allow direct observation of the flow of cells in microchannel arrays similar to the filtration geometry (27, 28); for example, area and volume measurements for cell populations have been reported. However, the fact remains that the most basic mechanical measurements that are characteristic of the physical state of individual cells in physiological flow conditions have not been accomplished.

We propose several illustrations of our differential micromanometer that address these issues and indicate further avenues for studies of dynamics and hemorheology. We measure (i) the pressure-drop variation associated with the motion of single and multiple RBCs and white blood cells (WBCs) in a microchannel, (ii) the additional pressure drop associated with the flow of drug-treated cells, and (iii) single hemolysis events.

Measurement Principle

To measure simultaneously the dynamical deformation of the cells and the variation of the pressure drop produced by their motion in the channel, we developed a device with twin channels: a test channel (Fig. 1A Upper) and an identical control, or “comparator,” channel (Fig. 1A Lower), both of which produce downstream two parallel and adjacent streams of fluid. To maintain a stable interface, the two fluids are miscible, and the liquid flowing through the control channel is dyed to visualize the interface downstream. Hence, the principle of the measurement lies in the use of the second control channel to detect any variation of pressure in the test channel when a cell, or another object, is flowing through it. In effect, for a given applied pressure difference across the device, the placement of an object in the channel decreases the flow rate and consequently increases the pressure drop that occurs in the narrow test section. A change in the pressure drop along the channel alters the position of the interface downstream. The measurement of this deflection allows the pressure to be determined after a basic calibration procedure (see next paragraph), and consequently we are able to monitor the time-dependent dynamical changes in the pressure drop in the test channel. In the particular case of steady channel flow, Groisman et al. (29) used a similar approach of comparator channels for static measurements of pressure drop in a microfluidic “diode” (i.e., a device in which the pressure varies nonlinearly with flow rate and the direction of flow). We note that for the experiment reported here by directly imaging the two-channel system, it is possible to obtain simultaneously the sequence of deformation of suspended particles and the dynamical variations of the pressure drop. Finally, we emphasize that our measurement technique is general and can be applied to any dynamical process by changing the hydrodynamic resistance of the test channel relative to the control channel (chemical reactions, changing viscosity, etc).

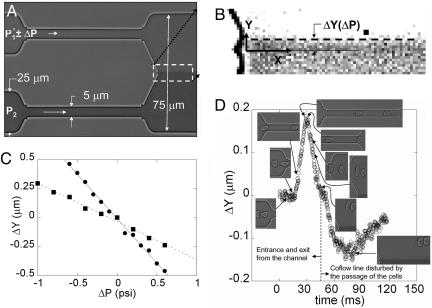
Fig. 1.

The height of the channels measured by a profilometer is the same in all of the devices and is equal to 4.7 μm. (A) Calibration of the excess pressure drop in the upper channel. The pressures P₁ and P₂ are fixed when no RBCs are flowing so that the fluid–fluid interface is centered in the exit channel. (B) Image analysis determines the variation ΔY of the position of the co-flowing line that marks the interface. (C) Variation of ΔY as a function of the change in pressure, ΔP, in the upper channel for two different upstream pressures P₁ at 5 psi (•) and 10 psi (▪). The slope ΔY/ΔP at 5 psi is twice the slope at 10 psi in absolute value. (D) Variation of the relative position ΔY of the interface as a function of time when cells enter the channel (Inset). The dashed vertical line separates the plot into two regions. (Left) Valid points for the pressure-drop measurement. (Right) Points caused by the exiting cells passing close to, and thus disturbing, the co-flowing line that marks the interface.

Device, Calibration, and Cells

The microfluidic device was manufactured by using principles of soft lithography (30, †). The typical dimensions of the device are shown in Fig. 1 A. The dimensions are fixed by the size of the object chosen for study. In the case of blood cells, we produced the test and comparator channels at ≈5 × 5 μm in cross section so as to deform the cells significantly. We mount our microfluidic device onto an inverted Leica (Deerfield, IL) DM IRB microscope coupled with a Leica ×100 objective (NPlan) for bright-field imaging (numerical aperture, 1.25) to observe the motion of the cells. A high-speed camera (Phantom V5, Vision Research, Inc., Wayne, NJ) is used to follow the motion and the deformation of the cells through the capillaries; typically, we use an imaging rate of a few thousands frame per second. The field of view of the camera (1024 × 1024) allows simultaneous observation of the cells and the deflection of the interface.

It first is necessary to calibrate the deflection of the interface as a function of the pressure drop. The flow is produced by pressurizing the fluids in the syringes connected to the two inlets of the microfluidic device. With no RBCs in the solution, the pressure P₁ applied in the test channel and the pressure P₂ in the control channel are fixed so that the fluid–fluid interface downstream is centered in the main exit channel (Fig. 1 A). We change the pressure P₁ in small increments ΔP without changing the pressure P₂ in the control channel and follow the displacement of the interface in the Y direction by performing image analysis with matlab software (Fig. 1B). The variation ΔY is linear in ΔP for the two initial working pressures applied: P₁ = 5 psi, and P₁ = 10 psi (Fig. 1C). Also, the slope of ΔY(ΔP) at P₁ = 5 psi is twice as large as the slope at P₁ = 10 psi (in absolute value); both responses are expected for small variations of this viscously driven flow.

The RBCs used during the experiment are extracted from a droplet of blood obtained by pricking a finger of a healthy donor. The blood sample is diluted and washed twice with a solution of PBS at an osmolarity of 300 mOs (physiological value). All of the solutions are made with dextran of molecular weight 2 × 10⁶ at a concentration of 9% (wt/wt). The viscosity of the solutions is 47 centipoise. All of the solutions are at a pH of 7.4. The viscosity of the ink solution has been measured to be 1.07 centipoise, i.e., approximately the viscosity of water.

To obtain rigidified RBCs, which allows characterization of the changes in pressure drop caused by mechanical changes in the cell membrane, an extra step is added in the process of dilution. The RBCs are maintained in PBS solution containing a given concentration of glutaraldehyde [0.001–0.01% (vol/vol)] at 25°C for 4 min. The rigidified cells then are dispersed in the PBS solution with the same osmolarity, pH, and viscosity as described previously. In the process of blood separation, a few WBCs are separated with the RBCs, which allows the study of their motion in the microchannels as well.

Results

Pressure-Drop Change due to Blood Cells. After calibration of the interface deflection as a function of the change in pressure drop, the dilute suspension of RBCs is introduced in the device. Each time a cell enters the test channel (Fig. 1D Inset), we record a movie of the whole field of view, which allows us to follow the position of the interface (Fig. 1B) and the deformation of the cell. Each event is analyzed with matlab software to measure the dynamical variations of the interface position (i.e., the pressure drop) as a function of time and the deformation of the cell. An example of the measured pressure-drop variations after the entry of a cell into a channel and continuing until after the cell has exited the channel is shown in Fig. 1D. The second bump in Fig. 1D corresponds to the exit of the cell near the co-flow line, which directly disturbs the position of the interface, but does not have any physical significance in terms of the global pressure-drop variations.

Two comments about details of the measurement approach are in order. First, PDMS channels are known to be deformable under pressure-driven flow. Thus, it is necessary to estimate the maximum deformation produced by the passage of a cell, which causes a pressure drop ΔP. The additional strain in the walls of the PDMS channel is estimated by the ratio of ΔP (of the order 700 Pa) to the Young modulus of PDMS (≈5 × 10⁵Pa), which is <10^–3. Hence, any such deformation is negligible. Second, the time response of our system is related to the pressure-driven flow characteristics. There are three different time scales relevant to describe the time resolution of the device: (i) the time scale related to the propagation of sound waves (speed c) along the channel (length L and height H), which controls the axial development of the velocity profile and is estimated to be ≈L/c ≈ 10^–6 to 10^-7 s; (ii) the time scale associated with the diffusion of vorticity across the channel, which controls the evolution of the nearly parabolic velocity profile and is estimated to be ≈H²/ν ≈ 10^–6, where ν is the kinematic viscosity of the fluid); and (iii) the time scale associated with the fluid rearrangement because of the pressure changes, which is the longest time scale in the problem. This last time scale is of the order of 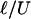, where 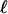is the length on which the velocity of the fluid is disturbed (typically the cell size). With the estimates 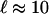μm and the mean velocity of the fluid passing in the channels U ≈ 1 cm/s, this time scale is of the order of a few milliseconds. This time can be even shorter for higher mean speeds U, which suggests a way to reduce and tune the time response of the device by working at higher injection pressures (i.e., higher flow mean speeds). Finally, we note that experimentally we visually observe on the high-speed movie the link between the motion (and instantaneous position) of the cell and the deformation of the interface.

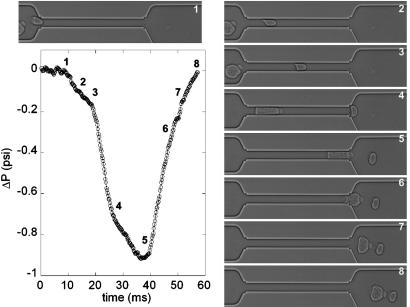
The next illustration of our technique consists in the measurement of the complete sequence of the deformation and the time evolution of the excess pressure drop when the cells flow in the channel as shown in Fig. 2. An RBC enters the channel, followed shortly thereafter by a larger (and stiffer) WBC. The time trace of the pressure-drop variations can be compared with the images of the sequence of deformations represented in the figure. The time evolution of the pressure drop while the same cell is in the channel, and away from either the entrance or exit, is a consequence of the deformation of the cell. This example illustrates the ability to monitor dynamically pressure drop and mechanical processes comparable to in vivo conditions that occur in the microcirculation.

Fig. 2.

Sequence showing the deformation first of an RBC and then a WBC, which pass successively through the upper channel. A plot of the variation of the pressure drop is shown as a function of time (in milliseconds). The corresponding position and shape of the cells are represented on the plot by the numbering of the sequence.

Recent advances in computational mechanics have treated cell entry and translation in cylindrical geometries with models for the mechanical response of the cell. In one study (14), the RBC is treated as a viscous droplet surrounded by a thin elastic membrane of two-dimensional modulus E_S. The dynamical response of these systems depends on the capillary number, which is a dimensionless parameter ε = μV₀/E_S, where μ is the viscosity of the outer fluid and V₀ is the mean velocity of the fluid in the channel. For example, the maximum additional pressure drop ΔP_add during the flow is calculated to be ΔP_add = O(10–100)μV₀/R_t for 10^–3 < ε < 0.05, where R_t is the radius of the circular capillary (see figure 14 in ref. 14). Using the measurements shown in Fig. 3, our results give ΔP_add = 16 μV₀/R_t, which is in good agreement with the order of magnitude from the computational model. Finally, we note that the computational models provide ΔP_add as a function of the position along the channel, and our results are in qualitative agreement. A detailed comparison of simulation and experiment would require the same geometry and should, in principle, allow extraction of the mechanical properties.

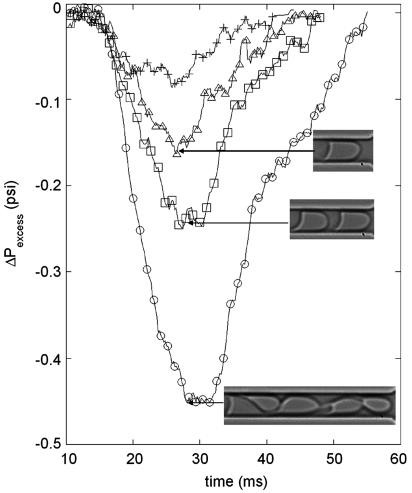
Fig. 3.

Pressure drop versus time for different conditions characterizing the state of the RBCs; the driving pressure is 5 psi. +, healthy RBC; open symbols, RBCs treated with 0.001% glutaraldehyde; ▵, one RBC; □, a train of two RBCs; ○, a train of five RBCs.

The interactions of cells, and their number density, in the microcirculation impact the overall pressure drop in a tissue and is still not well understood (31). Next, we report in Fig. 3 results that suggest a way to study these hydrodynamic interactions of cells through the measurement of the pressure drop for the flow of one, two, and five cells translating through a microchannel (cells are closely spaced, similar to a rouleaux). The pressure drop systematically increases as the number of cells increases, but the results are not simply proportional to the number of cells. This qualitative response is typical of confined geometries with suspended particles spaced closer than the microchannel width.

Pressure-Drop Change due to Membrane-Modified Cells. Next, we consider the change in the hydrodynamic resistance that occurs when the mechanical properties of the cells are modified. In Fig. 3, we compare a single healthy cell with a glutaraldehyde-treated cell, which is known to be stiffer (25): the pressure drop is enhanced after treatment with glutaraldehyde, and the stationary shape of the cell is obtained at later times. Thus, we conclude that our approach allows differentiation of cells with different mechanical properties or geometrical features, which may provide a simple biomedical tool for clinical hemorheology and pharmaceutical testing.

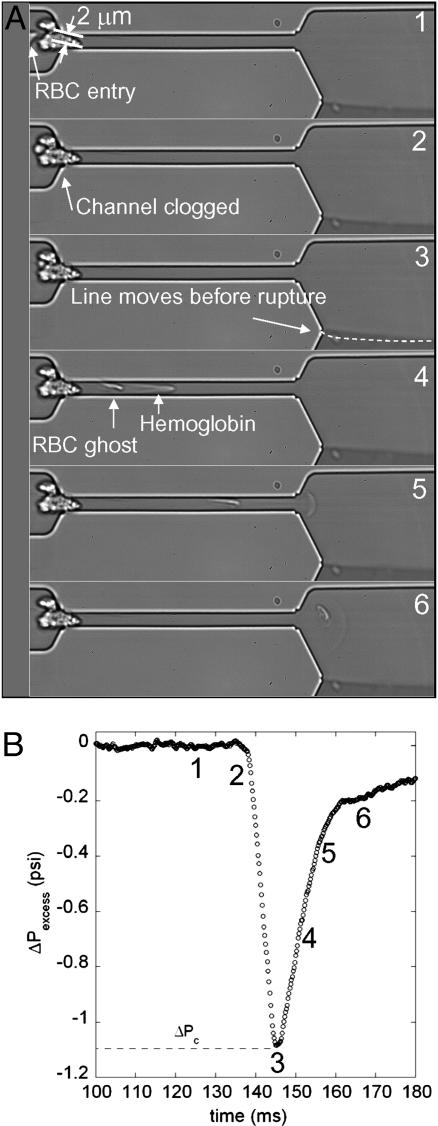
Hemolysis. As a final example that illustrates the insights that can be obtained with our microfluidic differential manometer in Fig. 4, we visualize a cell blocking the entrance to a channel (Fig. 4A2) and the subsequent hemolysis event (the cell membrane ruptures) (Fig. 4 A4–A6). When the blockage event begins, the pressure drop increases linearly over <10 ms and reaches a maximum value of ≈1.1 psi when hemolysis happens. We then see the ghost of the RBC (Fig. 4 A4–A6) as well as the hemoglobin solution, which follows the parabolic velocity distribution. This critical value of stress that is necessary for hemolysis is in good agreement with the approximate value of 4,000 Pa ≈ 0.6 psi found with static micropipette experiment on preswollen RBCs (32). It is interesting to note also that malaria-infected RBCs have increased rigidity, which is associated with organ failure. Microfluidic approaches have been used recently to examine qualitatively the flow-induced hemolysis (or “pitting”) of malaria-infected cells (7), and our methodology provides a quantitative approach for more in-depth studies of these systems.

Fig. 4.

Hemolysis of an RBC passing through a narrow constriction formed by some particulate matter that clogs the entry of the upper channel. The equivalent size of the entry pore is 2 μm.

In summary, we have provided an approach for time-dependent pressure-drop measurements at the micrometer scale with millisecond resolution. We have shown how insights into mechanical processes can be obtained at the scale of individual cells. These ideas naturally apply to other soft objects and to nanoscale flows.