Two types of cytotoxic lymphocyte regulation explain kinetics of immune response to human immunodeficiency virus

Abstract

The organization of the cytotoxic T lymphocyte (CTL) response at organismal level is poorly understood. We propose a mathematical model describing the interaction between HIV and its host that explains 20 quantitative observations made in HIV-infected individuals and simian immunodeficiency virus-infected monkeys, including acute infection and response to various antiretroviral therapy regimens. The model is built on two modes of CTL activation: direct activation by infected cells and indirect activation by CD4 helper cells activated by small amounts of virus. Effective infection of helper cells by virus leads to a stable chronic infection at high virus load. We assume that CTLs control virus by killing infected cells. We explain the lack of correlation between the CTL number and the virus decay rate in therapy and predict that individuals with a high virus load can be switched to a low-viremia state that will maintain stability after therapy, but the switch requires fine adjustment of therapy regimen based on the model and individual parameters.

A wealth of information on molecular mechanisms of cytotoxic T lymphocyte (CTL) response controlling virus replication has been accumulated. Yet, the organization of the host–virus system at the level of the organism remains unknown. Open issues include the relevant cell phenotypes, the order of their differentiation, and control of their proliferation and death. It is also unknown why some notorious viruses (e.g., HIV, hepatitis B and C viruses) are not cleared but persist at high levels. Further progress in the area requires implementation of a system approach that views the host–virus system as a network of interacting elements and reverseengineers it from the increasing flow of experimental data. Frequent quantitation of CTLs, helper cells, and virus by modern, accurate assays provides input information.

There has been substantial amount of mathematical work addressing important features of the CTL response (1–4). In the present work, we expand our previous model of CTL response during acute infection with simian immunodeficiency virus (SIV) and four strains of lymphocytic choriomeningitis virus (5) to explain properties of a chronic HIV infection. We present a series of 20 experimental facts that we analyze in three groups to reconstruct model blocks for dynamics of infected and infectible cells, CD4 helper cells, and CTLs. Then, we connect the three parts together and test the resulting model by fitting it to several kinetic experiments. We show that various observations can be understood from two key facts: that helper cells are infected with virus and that effector CTLs are activated either directly by antigen or by helper cells activated by antigen. In particular, the model explains the existence of two steady states in an HIV/SIV infection with strongly different virus loads and predicts that they are controlled by two distinct effector CTL subsets. Mathematical equations and additional simulations are given in Supporting Text, which is published as supporting information on the PNAS web site.

Results and Discussion

Constructing a Model from Separate Observations. In the present subsection, we infer parts of a model from groups of experimental observations (Facts).

Cells permissive for virus replication.

Fact 1. HIV is able to infect both resting and activated CD4 T cells, with resting cells being infected at a lower efficiency.

Fact 2. The turnover rate of CD4 T cells in HIV-infected individuals is increased severalfold as compared with uninfected controls (6, 7).

Fact 3. The virus load does not experience significant oscillations during its rebound after transient or transiently efficacious antiretroviral therapy (ART) (8, 9).

Fact 4. After transient ART, the virus load does not significantly overshoot its pretreatment level, although, before the virus rebound, the number of CD4 cells exceeds the predrug level (8, 9).

Fact 5. In monkeys acutely infected with a variant of SIV-mac251, the first peak of the virus load is followed by a second, smaller peak (10).

Fact 6. (a) In SIV-infected monkeys who received soluble BrdUrd, a compound that inserts into dividing chromosomes, the fraction of BrdUrd-labeled CD4 cells increases during labeling and decreases afterward at similar exponential rates (6, 7). (b) Experiments on labeling with deuterated glucose, which measure the total amount of label in cells, produced similar results (11).

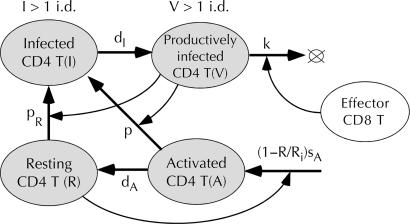
To explain these observations, we will take into account two types of CD4 T cells permissive for virus replication (Facts 1 and 2). Resting CD4 T cells, R (Fig. 1), support virus replication in the beginning of infection (12, 13), whereas their activated dividing precursor cells, A, dominate at later times (12, 13). Because activated cells become resting cells in a short time, the number of activated cells A is small and responds rapidly to temporal changes in the virus load, damping its oscillations around a steady state (Fact 3). The assumption that activated cells come from a source other than division of preexisting resting cells, R, explains the lack of virus overshoot, the second virus peak in acute infection, and the rapid loss of label in the BrdUrd experiment (Facts 4–6). Expansion of CD4 T cells during transient drug therapy will not result in virus overshooting of the steady-state level, if we assume that dominant permissive cells, A, are supplied from a source independent on CD4 count at low CD4 counts (Fact 4). A constant source explains why virus is able to replicate and form a second peak in the face of strong CD4 T cell depletion in acute infection (Fact 5).

Fig. 1.

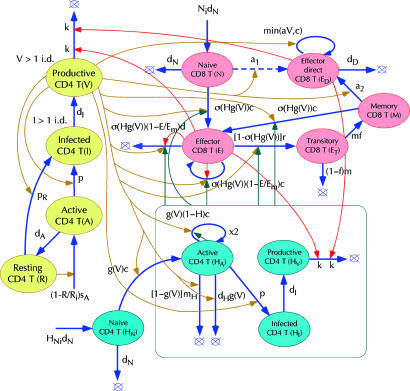
Partial model describing dynamics of cells infected with HIV/SIV and permissive for its replication. Ovals, cell compartments; uppercase letters, cell numbers in compartments (dynamic variables); thick arrows, flow of cells from one compartment to another because of change of phenotype or death; thin arrows, control (linear by default) of cell flow between two compartments by a third compartment; lowercase letters and R_i, constant proportionality coefficients (model parameters). Compartment V represents infected cells producing virus. Short-lived virus is cleared, if V and I are below 1 i.d. = 1 productively infected cell per animal = 10^–2 copies of RNA per ml (monkey) = 3.4 × 10^–10 p27 ng/ml.

To explain Fact 6a, Mohri et al. (6) introduced a source and assumed that, for some reason, it supplies labeled cells in the presence of and unlabeled cells in the absence of soluble BrdUrd. The biological origin of “source” is unclear; probably, it represents the mechanism of memory cell homeostasis. Grossman et al. (14) proposed that source originates from very long-lived precursors of memory cells that undergo rapid proliferation bursts, during which cells become labeled (only) in the presence of soluble label. For the source to stay constant, the long-lived precursors should be weakly infectable with HIV.

Infected cells and their control by CTLs.

Fact 7. (a) Depletion of CD8 T cells in rhesus macaques chronically infected with SIV results in an increase of the virus load by one to several orders of magnitude (15). (b) A strong inverse correlation between viremia and CTL response is observed in humans (16).

Fact 8. The infected cell lifetime inferred from the initial viremia decay rate under ART is ≈1 day (8, 17) and does not correlate with the CTL number (16, 18).

Fact 9. In vitro, most cells infected with HIV die within a few days.

Fact 10. The amount of HIV RNA per infected (either activated or resting) CD4 cell at any one time does not change significantly during ART (<50%).

Fact 11. An infected cell starts to produce HIV proteins within ≈24 h after virus entry.

Fact 12. In an average chronic infection, the net turnover rate of productively infected cells inferred from the 1-day lifetime, 10⁷ to 10⁸ cells per day (19), is slower than the turnover rate of all CD4 T cells, ≈10⁹ cells per day (6, 7).

Fact 7 shows that CTLs control HIV replication in vivo. Facts 8 and 9 induced Ogg et al. (16) to conclude that virus itself rather than CTLs kill cells and that CTLs control infection by either inhibiting virus production inside of cells or by blocking virus transmission between cells. Fact 10 excludes the first, but not the second, scenario. The idea that the usual CTL function (killing infected cells) is not important for HIV and that, instead, CTLs exert control over HIV by using a mechanism specific for this virus, is intriguing. Yet, our task is to seek the simplest explanation of facts. We can interpret Facts 8, 9, and 12 based on the well known delay of virus replication and assuming the usual, lytic mechanism of CTLs (Fact 11). We split the infection cycle of a cell into a nonproductive interval that is known to be ≈1 day (denoted I in Fig. 1) and a productive interval (V) and neglect the effect of CTLs on virus production or transmission, i.e., on parameter p (Fig. 1). Suppose, at their steady-state concentration, CTLs kill a productively infected cell within a time much shorter than 1 day (Fig. 2a). Then, the average infected cell lifetime is determined mostly by the nonproductive interval and depends only weakly on the CTL number (Fact 8). That a productively infected cell would die several days later because of viral pathogenicity (Fact 9) is irrelevant, unless CTLs are strongly depleted. The same idea shows that the turnover of productively infected cells is much more rapid than inferred previously (Fact 12), because it is determined by a short productive interval, rather than the infected cell lifetime. The specific time dependence of virus production after the delay is subsumed by parameters p and k used below as fitting parameters. Neglecting the delay in virus replication either requires invoking transmission-blocking and indirect killing of CD4 T cells by virus or predicts strong variation of virus decay rate during the first week of ART and across patients, in contrast to experiments.

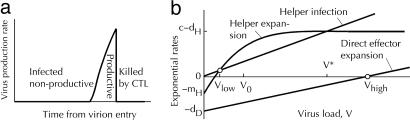
Fig. 2.

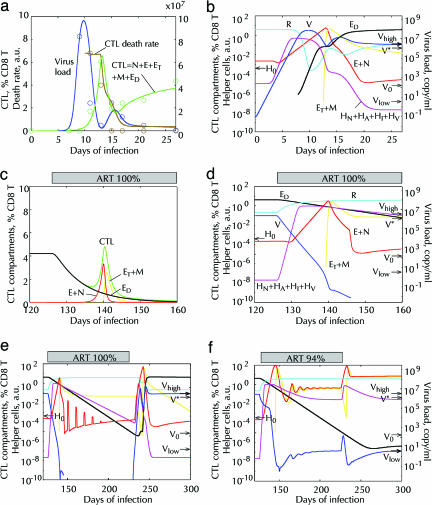
Virus production and two steady states (sketch). (a) Time dependence of virus production by an infected cell (sketch). (b) Net expansion and infection rates of activated helper cells, H_A, and the net expansion rate of direct effector cells, E_D, as functions of the virus load. Small circles, two stable steady states. Values at x-axis: V_high = d_D/a, V_low ≈ V_om_H/(c – d_H), V* = (c – d_H)/p. The helper cell number in the low-virus steady state: H₂ = H₀[(c – d_H)/m_H]ln[(c – d + r)/(c – d)].

We do not consider free virus particles as a separate compartment, because their lifetime is short (20, 21) and, probably, constant and not affected by antibodies because of their weak neutralization efficiency (22). Therefore, with few exceptions, the free virus load, at any time, should be proportional to the number of productively infected cells, V. A small fraction of infected cells that have unusually long nonproductive interval are termed latently infected cells. We do not consider them as a separate compartment but account for their effects, important at low virus loads, by injecting small amounts of virus (see below).

HIV-specific CTL response. Facts relevant for CTL regulation are as follows.

Fact 13. The chronic stage of a HIV/SIV infection is a stable quasi-steady state: the numbers of relevant cell compartments stay almost constant, because their replenishment compensates for their death.

Fact 14. There are two types of steady state characterized by drastically different virus loads (23–26). Approximately 75% and 25% of monkeys infected with SIVmac251 develop moderately high (10⁵ to 10⁶ copies per ml) and very low virus loads (<10³ copies per ml), respectively (27). The second group is smaller in humans infected with HIV-1. The CTL response levels (in humans) are 0.1–0.2% and 0.2–2% CD8 T cell count, respectively (16).

Fact 15. (a) Potent ART administered to high-viremia individuals depletes virus to very low (often undetectable) levels and brings the CTL number below the low-viremia state (16, 23, 26). (b) Interruption of ART after many months has two possible outcomes: virus either rebounds to the predrug level or stays low (27, 28). In either case, CTLs rebound to a level similar to the predrug level (28).

Fact 16. The helper-cell response to HIV measured with a lymphocyte proliferation assay correlates negatively with the virus load (29, 30).

Fact 17. CTLs isolated from infected individuals can be induced to divide either by antigen-presenting cells or by helper cells activated with soluble antigen (or by cytokines secreted by helper cells).

Fact 18. CTL kinetics in the beginning of ART in infected humans consists of three phases (25): the CTL number decreases severalfold or more, increases, and decreases to a constant level represented by memory cells (23).

Fact 19. Multiphase CTL kinetics also is observed in monkeys acutely infected with a passaged isolate of SIVmac251 (10). The initial CTL expansion, soon after a viremia peak, is followed by a drop in the CTL number concurrent with a decrease in the CTL death rate. Another increase of viremia is followed by a slower expansion of CTLs with a small death rate. Finally, viremia falls again and reaches a steady-state level.

Fact 20. The second viremia peak is not pronounced in acute infection with SIVsmE660 (9), HIV (31), SHIV (32), and some other isolates of SIVmac251.

Long-term chronic infection represents a stable equilibrium between death and proliferation of all relevant cell types. A broad class of dynamic models predicts such behavior (Fact 13). Other observations, including a second steady state and various kinetic features, are more specific and more difficult to explain. The two modes of CTL activation (Fact 17) provide the clue. We postulate that two distinct subtypes of effector CTLs, those activated directly by antigen (termed “direct effector”; E_D in Fig. 3) and those regulated by helper cells (E in Fig. 3), are responsible for two different steady states (Fact 14). In the high-virus steady state, helper cells are infected and depleted to very low levels (Fact 16), and direct effector CTLs control the virus. In the low-virus-load state, the virus load is controlled by CTLs that depend on CD4 helper cells that are activated by small amounts of virus. The virus load is too low to maintain proliferation of direct CTLs. As we demonstrate below, interplay between the two modes of CTL activation naturally explains the nonmonotonous dynamics of CTLs and virus observed after infection and under ART (Facts 18–20). Intermittent or moderately efficacious ART can switch the system from the high-viremia to the low-viremia state that, once established, maintains stability on its own (Fact 15).

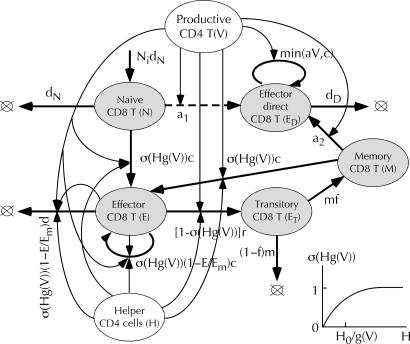
Fig. 3.

Partial model of CTL dynamics. Loops with arrows, cell division. Dashed line, a variant model where direct effector cells are produced from naïve cells, not memory cells. The rest of the notation is as in Fig. 1. (Inset) σ(Hg(V)) = 1 – exp[–Hg(V)/H₀], nonlinear control of CTL by helper cells and virus.

The model of CTL regulation is shown in Fig. 3. The part that describes helper-dependent CTLs is similar to a model we developed earlier (5) for acute infections with SIVmac251 (10) and lymphocytic choriomeningitis virus (33). Naïve cells are activated by helper cells to become effector cells, which keep dividing as long as they receive signals from helper cells detecting virus. Once signals become low, CTLs progress to a short-term memory (“transitory”) phenotype and then either die or become long-term memory cells. In the presence of virus and helper cells, memory cells are reactivated into secondary helper-dependent effector cells. An important addition is the direct effector cells that represent progenitors of memory cells activated by the virus independently of helper cells. To explain the dynamics of some SIV strains, we also considered a variant of the model where direct effector cells are progenitors of naïve cells. We do not consider anergic cells here, although anergy is important for lymphocytic choriomeningitis virus infection (3, 33). We also do not include the death and homeostatic replenishment of virus-specific memory cells, because these processes are too slow to affect any of experiments we discuss. To prevent effector cells from disappearing altogether when the helper cell count or the virus load are low, we include in the model a weak constant source of naïve cells (Fig. 3). Introduction of transitory CTLs is necessary to fit kinetics during acute infection and ART (see below).

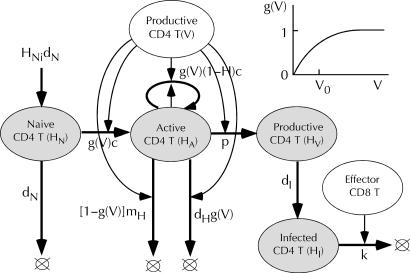
Virus-specific helper cells. Correlation between the level of HIV-specific CD4 helper cell response and viremia (Fact 16), the fact that virus infects CD4 cells much more effectively than other cell types, and anomalies of the CTL response in an HIV/SIV infection (Fact 19) demonstrate a key role for CD4 helper cells in anti-HIV response. Unlike professional antigen-presenting cells featured as regulatory cells in our previous model (5), CD4 T cells can rapidly divide and are antigen-specific. Few data are available on kinetics of virus-specific CD4 cells. Homann et al. (34) used the tetramer assay to measure kinetic response to one epitope of the Armstrong strain of lymphocytic choriomeningitis virus. They observed rapid expansion and, after virus clearance, rapid decay of CD4 cells, followed by slower decay and, then, by a low-level long-term memory phase. Because we are not aware of any detailed data on HIV that could support a more complex model, we consider a single compartment of uninfected activated CD4 T cells, H_A (Fig. 4). The fraction of helper cells recognizing virus [g(V)], dividing, and dying because of activation-induced death is assumed to be proportional to the virus load, V, at very low loads, V << V₀, and reach 1 at higher loads, V >> V₀. A low activation threshold V₀, which implies collective signaling between activated helper cells, explains the existence of the low-virus steady state under an active helper cell response. After the virus is cleared or strongly depleted, helper cells die out very slowly, which accounts for the slow phase of decay (34). Memory helper cells are not included in this part of the model. A constant weak source of naïve cells prevents helper cells from disappearing. Similar to nonspecific CD4 cells, virus-specific CD4 cells can become infected, H_I, then productively infected, H_V, and then killed by CTLs (compare Figs. 1 and 4).

Fig. 4.

Partial model of dynamics of virus-specific CD4 T helper cells. (Inset) Nonlinear control of helper cells by virus, g(V) = 1 – exp(–V/V₀). The remaining notation is as in Figs. 1 and 3.

Full model. To obtain a full model of a HIV infection, we have to specify connections between the three parts described above. CTLs affect the numbers of nonspecific and virus-specific CD4 T cells by killing them when they are at the productive stage of infection (V and H_V). When CTLs and infected cells are dilute in the tissue, the killing rate is expected to be linearly proportional to the CTL number (linear control; Fig. 5). Because direct effector cells divide when they encounter individual infected cells, the overall division incidence is expected to be linearly proportional to the virus load. Regulation of helper-dependent CTLs is somewhat more complex. We postulate that the division, death, and differentiation rates of these cells are all proportional to the nonlinear function σ(Hg(V)), where H = H_A + H_I + H_V is the total number of activated virus-specific helper cells, and g(V) is defined above. As illustrated in Fig. 3 Inset, control function σ is linear in its argument, when Hg(V) << H₀, and reaches saturation at Hg(V) >> H₀, which corresponds to the maximum speed of cell division. Thus, CTLs switch from rapid expansion to differentiation into memory cells at a characteristic number of helper cells, H ∼ H₀ (provided that the virus load exceeds activation threshold for helper cells, V₀). The proposed mechanism ensures rapid collective activation of the CTL response at low virus loads and, generally, is much more efficient than direct activation by antigen. (What makes it inefficient in the case of HIV is that the virus infects helper cells.) The presence of factor g(V) in the argument of control function σ is necessary to provide quick negative feedback from virus to CTLs that ensures stability of the low-virus steady state observed in experiment. The lack of g(V) in the argument, as we checked, results in delayed feedback and diverging oscillations.

Fig. 5.

Full model of HIV/SIV infection. Ovals in yellow, red, and cyan represent parts of the model from Figs. 1 (nonspecific CD4 T cells), 3 (virus-specific CD8 T cells), and 4 (virus-specific helper CD4 T cells), respectively. Colored thin arrows, respective control. Nonlinear control function: σ(Hg(V)) = 1 – exp[–Hg(V)/H₀], where H = H_A + H_I + H_V. The rest of the notation is as in Figs. 1, 3, and 4.

Two Steady States. The model shown in Fig. 5 and described by equations in Supporting Text predicts two steady states (Fig. 2b and legend). In the first, the virus load, V_high = d_D/a, is determined from the condition that the death and the proliferation of direct effector cells cancel each other. Because the virus load is higher than the level V* at which infection and expansion of helper cells cancel each other, helper, helper-dependent effector, and memory cells are depleted to low levels maintained by weak flow from respective naïve cells. In the second steady state, the virus load stays at a low level V_low, such that expansion of helper cells is compensated by their infection. The steady-state number of helper cells, H_A = H_low, ensures that the net expansion rate of helper-dependent effector cells is zero. Direct effector cells almost do not proliferate because of the lack of virus and are depleted. Which of the two steady states takes place depends on the individual model parameters and initial conditions set in each experiment.

Note that, in the interval of virus loads, V_low << V << V*, helper cells are predicted to expand (Fig. 2b). Therefore, the high-virus state, although stable on a short time scale, will be unstable in the long term, if the virus load falls within the interval, V_high < V*, or p < a(c – d_H)/d_D. In this case, a switch to the low-virus state will eventually occur, as actually observed in some SIV-infected animals (27). Thus, HIV/SIV can persist at high levels only because of efficient infection of helper cells. In contrast, the low-virus state will be stable regardless of infection of helper cells, although this state may be difficult to establish.

Simulated Experiments. To verify our qualitative considerations on the quantitative level, we carried out numeric simulation of some cited experiments (Supporting Text). These simulations relate units of virus load used in different experiments with SIVmac251 comparing the average peak and steady-state virus loads between experiments (19, 26, 27), which yields, for 7 kg macaques, 1 infectious dose (i.d.) = 1 productively infected cell = 10^–2 copies of RNA per ml = 3.4 × 10^–10 ng of p27 per ml. We express the numbers of infected (V and I) and permissive (R and A) cells in the same units. When both V and I are below 1 i.d., they are set at zero. The virus-specific helper cell number (not measured in experiments on HIV/SIV) is defined relative to its maximum possible value.

None of the cited experiments, considered alone, contain sufficient information to determine all model parameters. Different experiments are performed in genetically different individuals and are subject to considerable parameter variation. To partly resolve this difficulty, we adjusted parameter values to fit the most informative experiment [CTL response to acute SIVmac251 infection (10)] accurately and match other kinetic experiments for representative individuals on the semiquantitative level. The aim of this exercise was to determine whether the model could explain the entire set of experiments. The parameter value set (Fig. 6 legend) should be considered a representative example.

Fig. 6.

Fitting of three experiments consecutive in time, acute infection (10), onset of ART (25), long-term and interrupted ART (28), based on the model (Fig. 5, without the dashed arrow). (a and b) Acute infection with 20 infectious doses (0.2 RNA copy per ml) of virus. (a) Circle, data for animal p88 infected with SIVmac251 (10). Solid lines, best-fit predicted dependencies. (b) Predicted cell numbers in six important cell compartments (on the curves). The values of V and R are shown in virus units on the right y-axis. Arrows show the values of V_low, V_high, and V* (Fig. 2 and legend) and H₀.(c and d) First weeks of 100% efficacious ART (p = p_R = 0) simulating experiment in ref. 25. Predicted cell compartments are shown in linear (c) and logarithmic (d) scale. (e and f) Simulated kinetics of interrupted ART similar to experiment in ref. 28. Drug efficacy: 100% (e) and 94% (f): p(126 < t < 236) = 0.06p(t < 126). One-day pulses of 5 i.d. of virus (V) each 10th day simulate bursts from latent reservoirs. (a–f) Fitting parameters (Fig. 5): p = 100 per day per virus unit (vu); R_i = 3.8vu; d_A = 0.94/day; d_I = 1.26/day; H_Ni = 10^–5; N_i = 2.2 × 10^–3 % CD8 cells; f = 0.14; c = 3.41/day; d = 2.42/day; k = 1.06/day per cell; r = 6.5/day; V₀ = 4.3 × 10^–6vu; H₀ = 4 × 10^–4; a = 1.4/day per vu; d_D = 0.13/day; m = 1.18/day; d_H = 0.085/day; p_R = 1.98/day per vu; s_A = 0.44vu/day. Here, vu = 1 p27 ng/ml = 3 × 10⁷ RNA copies per ml. Fixed parameters: d_N = 10^–3 per day; m_H = 0.1/day; E_m = 100%.

Acute infection. Here, we fit CTL and virus kinetics to data from an acute SIVmac251 infection (10) (Fig. 6a) by using the parameter set derived above. The chain of events leading to a high-virus steady state is evident from kinetics of separate compartments. Six important compartments are shown in Fig. 6b. The entire set of compartments is shown in Fig. 7, which is published as supporting information on the PNAS web site. Initially, the virus load, V, increases exponentially in time. When it exceeds V_low (Fig. 2b), activated helper cells, H_A, expand. When their number exceeds characteristic value H₀ defined above [at this moment, g(V) = 1], rapid expansion of helper-dependent CTLs starts. After the virus depletes CD4 T cells, its growth becomes limited by the intensity of the source of activated cells, s_A, and slows down to linear. When virus load grows higher and exceeds level V* (Fig. 2b), activated helper cells stop their expansion, because they become infected faster than divide. Then, effector CTLs deplete the virus (first virus peak) and infected helper cells, which stops their own expansion and transfers them to the transitory and then the memory compartment (E_T, then M). The change in CTL phenotype is observed as a drop in CTL death rate (Fig. 6a). Depletion of effector cells allows virus to grow again. Then, memory cells are activated by virus and become direct effector cells, E_D, that bring virus load down to a steady-state level (shown as zero in Fig. 6a because of the low sensitivity of the virus assay). The predicted switch of the dominant permissive compartment from resting, R, to activated cells, A, and a deep depletion of resting cells near the time of the (first) virus peak (Fig. 7) agree with recent studies (12, 13).

The second virus peak observed for SIVmac251 isolate used in ref. 10 is not pronounced for other SIV strains (Fact 20). Our simulation of SIVsmE660 kinetics (see Fig. 8, which is published as supporting information on the PNAS web site) shows a better fit for the model variant in which direct effector cells are descendants of naïve rather than memory cells (dashed arrow in Figs. 3 and 5). Further, even for secondary direct effectors, small changes in parameter values can destroy the second peak (results not shown). The SIV isolate used in ref. 10 is useful, because it reveals both types of CTLs, important for interpreting other experiments on our list. Highly potent ART: First weeks. The next simulation shows changes in cell compartments after the onset of highly potent ART started when in the high-virus steady state (Fig. 6 c and d). We continue our simulation from the previous experiment using the same parameter set. We introduce ART by setting infectivity parameters p and p_R to zero. The results are similar to the three-phase CTL kinetics observed in human patients (compare Fig. 6c with figure 1 A–D in ref. 25). In the steady state, most CTLs are direct effector cells, E_D, that are depleted under ART because of rapid decay of the virus load. When the virus load, V, falls below level V* (Fig. 2b), helper cells start to expand, causing, when their level exceeds H₀, subsequent proliferation of helper-dependent CTLs, E. When the virus load decreases below the level ≈V₀H₀/H, helper-dependent effector cells, E, cease proliferation and become transitory cells that either die or become long-lived memory cells, M. Finally, once the virus load is below the low-steady-state point V_low (Fig. 2b), the helper cell number starts to decline.

Thus, for a sufficiently slow virus decay, a transitory CTL expansion is predicted, as has actually been observed in several patients (25). The prediction that the right slope of the CTL peak is dominated by cells with memory phenotype, E_T, also agrees with the experiment (24).

Interrupted and long-term ART. Now we consider kinetics during ART on longer time scales (Fig. 6e). After short-lived infected cells are cleared and, among CTLs, only memory cells remain at high levels, latent virus reservoirs produce infrequent bursts of virus replication that are cleared by ART and short peaks of reactivated helper-dependent CTLs. When therapy is interrupted, one such virus burst initiates virus rebound to the pretreatment level.

Partly efficacious long-term ART. In the previous simulation, virus is depleted so rapidly that the low-virus state is missed. If the drug efficacy is <100% [p is replaced with p*(1 – efficacy/100)], the virus decays slower because of rapid expansion of activated cells (A) (Fig. 6f). For intermediate drug efficacies, the model predicts a transition to the low-virus steady state that remains stable even after ART interruption. Such a transition is observed in some cases of intermittent or low-concentration ART (27, 28). Note that if the drug is too inefficient (for our parameter set, <90%), the high-virus steady state will be preserved. The existence of a drug efficacy window depends on model parameters.

Simulations of short-term ART (9) and artificial depletion of CTLs (15, 35) are given in Figs. 8 and 9, which are published as supporting information on the PNAS web site, respectively.

Connection to Experiment and Therapy. Simulation results shown in Figs. 6 and 7 offer many opportunities for testing predictions of the model, for example

1. Depending on the drug efficacy and timing of therapy interruption, there may be three possible outcomes of long-term ART, as described above.

2. After a switch from a high-virus to a low-virus state (Fig. 6f), the steady-state number of virus-specific CD4 T cells (34) will increase by several orders of magnitude.

3. An average CTL isolated in the high-virus-state SIV-infected monkeys will have a stronger proliferative response to antigen and a weaker response to helper cells than in the low-virus state.

At the moment, achieving full clearance of virus seems to be problematic because of hidden virus reservoirs. To delay the onset of AIDS in a person and decrease the chance of interperson transmission, it would be useful to develop a strategy of stabilization of low viremia controlled by an active immune response. Our simulation (Fig. 6 e and f) predicts that transition to the low steady state is, indeed, possible, under specific therapy regimens. The results also explain the failure of empiric attempts at “structured therapy interruption” and demonstrate the need for fine adjustment of therapy regimen based on a specific model of CTL response.

Because physiology and model parameters will vary from animal to animal, it is difficult to combine information from multiple experiments in separate animals. To take full advantage of the model, it is imperative to conduct multiple experiments sequentially, starting from acute infection, in each animal of a small group. All sequential experiments should be modeled in a single simulation (Fig. 6). The aim of such work is to reconstitute the structure of the system, rather than collect statistics for one experiment across a large group of animals.

An early model of helper-dependent CTL response (36, 37) predicted two steady states in the presence of helper cell infection and a switch from the high-virus to the low-virus state under certain drug regiments. Because the model was developed before the cited experiments and is very simple, it is not surprising that it disagrees with most of them (e.g., it predicts zero CTL number in the high-virus state). Our model develops these important ideas further and is sufficiently detailed to help with therapy design.

A number of factors of HIV dynamics have been left out in the present work. In particular, we neglected spatial distribution of cells and virus within (38) and between (39) different organs, considered a single-epitope response, and did not include some other immune cell types, e.g., macrophages and dendritic cells that are important for initiating the immune response. We also neglected antibody effects and did not consider (short-lived) free virus, under the approximation that antibodies are not efficient. The robustness of insights generated by our analysis requires further model elaborations that address these issues. This task is a large one, and the future experimental tests will determine the need for specific modifications of the model.