Abstract
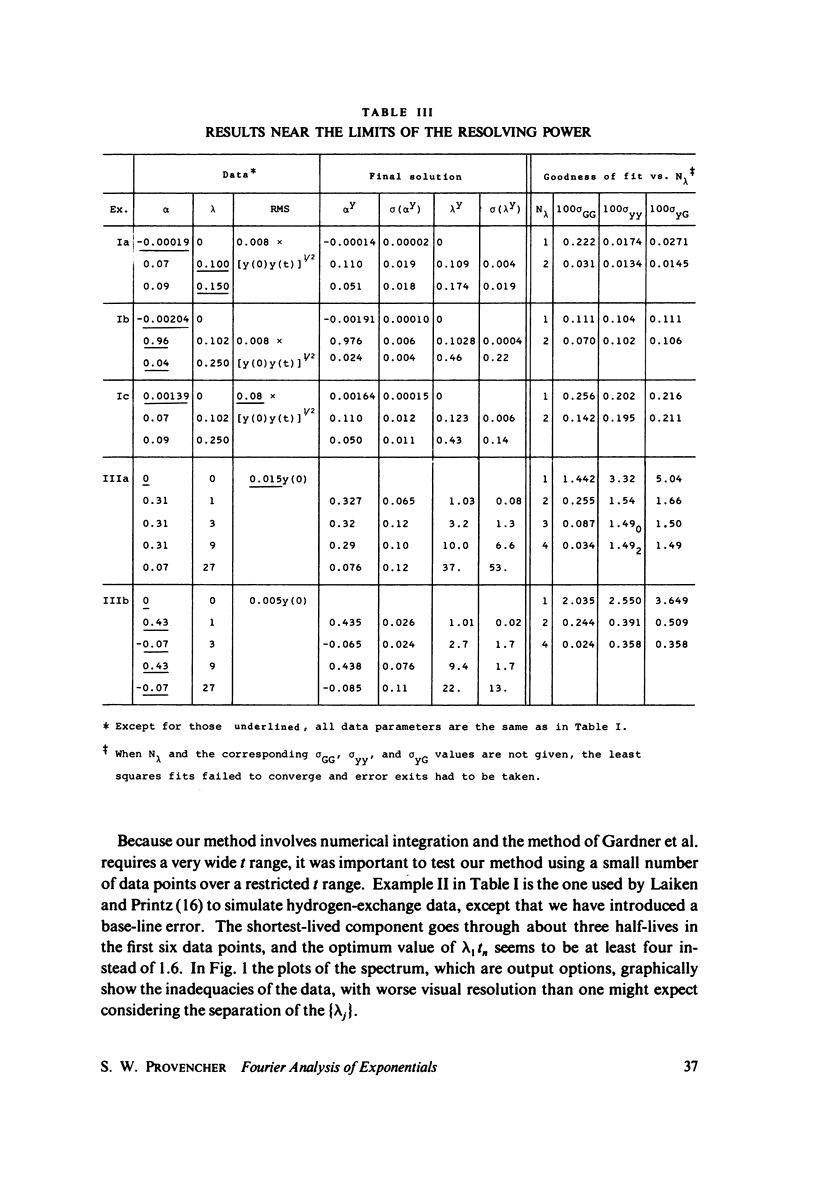
A method based on the Fourier convolution theorem is developed for the analysis of data composed of random noise, plus an unknown constant "base line," plus a sum of (or an integral over a continuous spectrum of) exponential decay functions. The Fourier method's usual serious practical limitation of needing high accuracy data over a very wide range is eliminated by the introduction of convergence parameters and a Gaussian taper window. A computer program is described for the analysis of discrete spectra, where the data involves only a sum of exponentials. The program is completely automatic in that the only necessary inputs are the raw data (not necessarily in equal intervals of time); no potentially biased initial guesses concerning either the number or the values of the components are needed. The outputs include the number of components, the amplitudes and time constants together with their estimated errors, and a spectral plot of the solution. The limiting resolving power of the method is studied by analyzing a wide range of simulated two-, three-, and four-component data. The results seem to indicate that the method is applicable over a considerably wider range of conditions than nonlinear least squares or the method of moments.
Full text
PDF













Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Atkins G. L. A versatile digital computer program for non-linear regression analysis. Biochim Biophys Acta. 1971 Dec 21;252(3):405–420. doi: 10.1016/0304-4165(71)90142-5. [DOI] [PubMed] [Google Scholar]
- Dyson R. D., Isenberg I. Analysis of exponential curves by a method of moments, with special attention to sedimentation equilibrium and fluorescence decay. Biochemistry. 1971 Aug 17;10(17):3233–3241. doi: 10.1021/bi00793a012. [DOI] [PubMed] [Google Scholar]
- GARDNER D. G. Resolution of multi-component exponential decay curves using Fourier transforms. Ann N Y Acad Sci. 1963 May 10;108:195–203. doi: 10.1111/j.1749-6632.1963.tb13374.x. [DOI] [PubMed] [Google Scholar]
- Isenberg I., Dyson R. D., Hanson R. Studies on the analysis of fluorescence decay data by the method of moments. Biophys J. 1973 Oct;13(10):1090–1115. doi: 10.1016/S0006-3495(73)86047-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson M. L., Schuster T. M. Analysis of relaxation kinetics data by a nonlinear least squares method. Biophys Chem. 1974 Jun;2(1):32–41. doi: 10.1016/0301-4622(74)80021-9. [DOI] [PubMed] [Google Scholar]
- Laiken S. L., Printz M. P. Kinetic class analysis of hydrogen-exchange data. Biochemistry. 1970 Mar 31;9(7):1547–1553. doi: 10.1021/bi00809a011. [DOI] [PubMed] [Google Scholar]
- Provencher S. W. Numerical solution of linear integral equations of the first kind. Calculation of molecular weight distributions from sedimentation equilibrium data. J Chem Phys. 1967 Apr 15;46(8):3229–3236. doi: 10.1063/1.1841194. [DOI] [PubMed] [Google Scholar]
- Schwarz G. Chemical relaxation of co-operative conformational transitions of linear biopolymers. J Theor Biol. 1972 Sep;36(3):569–580. doi: 10.1016/0022-5193(72)90009-4. [DOI] [PubMed] [Google Scholar]


