Abstract
Alternative models have been presented to provide explanations for the sequence-dependent variation of the DNA minor groove width. In a structural model groove narrowing in A-tracts results from direct, short-range interactions among DNA bases. In an electrostatic model, the narrow minor groove of A-tracts is proposed to respond to sequence-dependent localization of water and cations. Molecular dynamics simulations on partially methylphosphonate substituted helical chains of d(TATAGGCCTATA) and d(CGCGAATTCGCG) duplexes have been carried out to help evaluate the effects of neutralizing DNA phosphate groups on the minor groove width. The results show that the time-average minor groove width of the GGCC duplex becomes significantly more narrow on neutralizing the phosphate backbone with methylphosphonates. The minor groove of the AATT sequence is normally narrow and the methylphosphonate substitutions have a smaller but measurable affect on this sequence. These results and models provide a system that can be tested by experiment and they support the hypothesis that the electrostatic environment around the minor groove affects the groove width in a sequence-dependent dynamic and time-average manner.
INTRODUCTION
The X-ray crystal structure of [d(CGCGAATTCGCG)]2 determined by Dickerson and co-workers (1) provided the first detailed view of a complete turn of the double helix and demonstrated that some sequences cause the conformation of DNA to deviate from the canonical B-form. For example, the DNA minor groove is typically narrower in A-tracts than in G-tracts in crystal structures (2–5). That X-ray structure also demonstrated that a ‘spine of hydration’, composed of localized, geometrically arranged water molecules in the minor groove, appears to be an integral structural component of A-tract DNA (2). More recent high resolution X-ray data from [d(CGCGAATTCGCG)]2 crystals showed that additional localized water molecules can assemble atop the spine of hydration to form a ‘fused hexagon’ hydration motif (6,7). X-ray analysis indicates that water molecules in G-tract minor grooves generally assume a motif that has been termed a ‘double ribbon’ (8). Also, it has been observed that when the minor groove of a G-tract is narrow, localized cross-strand water molecules can be found at the GC step, for example in the minor groove of the DNA duplex d(CCAGGCCTGG) (9,10). The concept of sequence-specific variations in conformation and hydration is supported by the results of NMR (11–17), chemical footprinting (4) and computation (18–20).
The observation of DNA sequence-specific effects raises important questions about their molecular origin, particularly about the influence of solvent components on structure, that cannot be answered by static structures alone. The influence of electrostatic interactions and of base–base interactions on DNA structure are topics of broad importance that are being debated from different viewpoints. In one view ion–DNA interactions have significant effects on the structure of the double helix (21,22); the electrostatic model. The possible effects of base–base interactions and of DNA sequence on DNA structure have also been described (23–25); the base–base interaction or intrinsic structure model. Because ion interactions in the electrostatic model and base interactions in the structure model should have a particularly pronounced effect on the width of the minor groove, this width has evolved into a useful and very clear parameter for evaluation of the influence of different factors on DNA structure (26,27). Other helical parameters may not be as directly or strongly correlated with DNA–ion interactions (26,27). In the base–base interaction or intrinsic structure model, direct, short-range interactions among DNA bases are primarily responsible for variations in minor groove width. In the electrostatic model variations in minor groove width originate primarily from sequence-specific interactions of water molecules and cations with DNA.
The intrinsic structure and electrostatic models make opposing predictions as to the effects of changes in environment and chemical modification on DNA conformation. The intrinsic structure model predicts that the width of the minor groove is essentially independent of electrostatic environment and intramolecular electrostatic interactions. That model predicts that groove width would be invariant to changes in cation distribution, cation type and chemical modifications that alter intramolecular phosphate repulsion. In contrast, the electrostatic model predicts that minor groove width would respond according to Coulomb’s Law to changes in electrostatic shielding of phosphate groups by cations and to chemical modification of phosphate groups. An increase in the shielding of cross-groove phosphate groups by cations or a decrease in their electrostatic repulsion upon chemical modification would be expected to decrease the width of the minor groove. Williams and co-workers have presented X-ray evidence in support of this model (21), which was later challenged by Chui and Dickerson (28). Obviously, additional methods to investigate the influence of ions on minor groove width are needed.
In previous molecular dynamics (MD) studies (26,27), we showed that the time-average minor groove width and its fluctuations are modulated by phosphate–phosphate repulsion across the groove. When cations localize at base sites near the floor or at phosphates near the lip of the minor groove and shield cross-strand phosphate oxygens from each other, the groove is narrow. When cations are absent from the minor groove and expose charged phosphate oxygens to each other, the groove is wide. Thus, the electrostatic environment within the minor groove affects the groove width in both dynamic and time-average analyses. The observation that the average minor groove width of A-tracts is narrower than the minor groove of G-tracts (3–5) is explained by our previous results (27) that cations spend more time in the A-tract than in the G-tract region. Differences in minor groove electrostatic potential (29,30), base functional groups along the floor of the groove (21,22) and hydration (27) contribute to the differences in distributions of cations in A-tracts relative to G-tracts.
Although the MD results described above clearly define a correlation between cation position and DNA structure, particularly minor groove width, they are difficult to directly test by experiment. In an effort to define an experimental system that can test the importance of electrostatic effects on DNA structure, our attention was drawn to the work of Maher and co-workers on methylphosphonate modified DNA (31,32). The authors showed that patches of cross-strand methylphosphonate groups can neutralize one face of the DNA and, when in phase in a DNA double helix, strongly influence the curvature of the DNA. The electrostatic model predicts that such neutral cross-strand groups would also result in a narrow minor groove, independent of the local sequence, while the structure model predicts that such modifications will have only minor effects on groove width.
As a first step to test this prediction we have carried out MD simulations on [d(TATAGGCCTATA)]2 modified in the central GGCC region with methylphosphonate groups. The GC minor groove is normally wide, but the electrostatic model predicts that it will become narrow when neutralized. As a control study, similar MD simulations were conducted on [d(CGCGAATTCGCG)]2 neutralized by methylphosphonate groups in the central region. It should be noted that the results of our predictions could be tested by structural biology methods such as X-ray crystallography and NMR spectroscopy with DNA duplexes chemically modified with methylphosphonate groups, as in the experiments of Maher and co-workers (31,32).
MATERIALS AND METHODS
In all MD calculations the starting structure of our simulation was the canonical B-DNA (33) generated using the SYBYL software package. The DNA duplex, ∼40 Å long, was solvated with approximately 4000 TIP3P water molecules (34) such that solvent was placed 11 Å around the duplex to fill a periodic box size of ∼45 × 45 × 60 Å. Twenty Na+ and 10 Cl– ions were placed around the DNA using the LEAP module in AMBER 5.0 in order to obtain electrostatic neutrality and a NaCl concentration of ∼0.15 M. All simulations were carried out using the sander module of the AMBER 5.0 (35) package with the all-atom force field of Cornell et al. (36).
Equilibration was carried out on the system by using the following protocol. At the start of the equilibration, 500 kcal/mol restraints were placed on the DNA molecule. The water and ions were minimized for 1000 steps, followed by molecular dynamics for 25 ps, which allowed the solvent to relax. After these initial simulations, the particle mesh Ewald method (37–41) within AMBER 5.0 was used. The equilibration was continued with a 25 ps MD run at 300 K with a 300 kcal/mol restraint placed on the DNA molecule. This was followed by five rounds of 600 step minimization on the entire system, starting with a 25 kcal/mol restraint on the solute and reducing it by 5 kcal/mol during each subsequent round. Finally, with no restraints, the entire system was heated from 100 to 300 K over 10 ps. All MD simulations were carried out in the NPT ensemble with periodic boundary conditions at a constant temperature of 300 K with the Berendsen temperature algorithm (42) and at a pressure of 1 bar. The SHAKE (43) algorithm was applied to all bonds involving hydrogen atoms and an integration time step of 2.0 fs was used. Lennard-Jones interactions were subjected to a 9 Å cut-off and the non-bonded pair lists were updated at every step. The center of mass energy was removed every 100 ps.
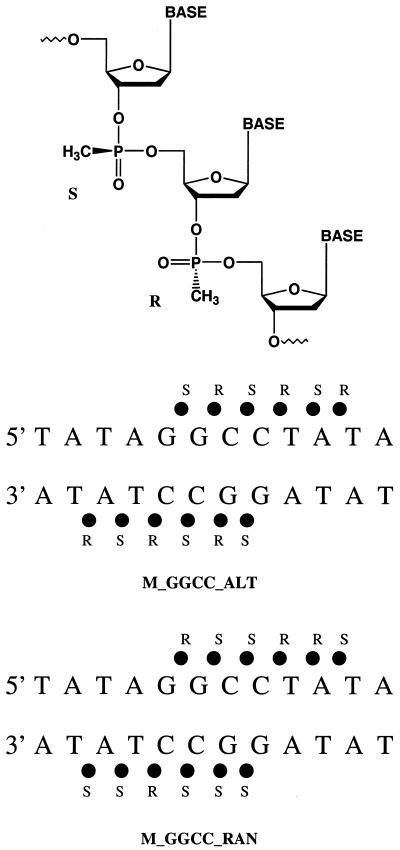
The force field parameters of the methylphosphonate backbone were developed in analogy to existing parameters in the force field of Cornell et al. and based on the ab initio calculations of small molecules using Gaussian98 (44). The atomic charges of methylphosphonate were determined using the restrained electrostatic potential fitting procedure (RESP) (45–47) at the HF/6-31G* level of theory. The charges for the methylphosphonate backbone and the additional force field parameters used are presented in Figures 1 and S1.
Figure 1.
Chemical structure of the methylphosphonate modified DNA backbone (top). The partial charges on the phosphorous, 3′ ester oxygen, 5′ ester oxygen, sp2 phosphoryl oxygen, methyl carbon and methyl hydrogens are 1.09, –0.397, –0.378, –0.664, –0.458 and 0.136, respectively. Schematic representations of the methylphosphonate modified DNA backbone showing the 12 phosphate groups that are modified to methylphosphonates in the MD simulations described here (bottom).
The results were analyzed with the carnal and rdparm modules of AMBER 5.0, Curves 5.1 (48–50) and some in-house programs written to help correlate DNA structure and ion positions (26,27). Instead of just measuring the shortest phosphate–phosphate distances between the backbones of the DNA when measuring the minor groove width, Curves 5.1 was used because it provides a continuous measurement of groove geometry by defining a smooth space curve passing through all the phosphorous atoms of each backbone. The detailed algorithm of the Curves 5.1 program can found in Stofer and Lavery (50). In order to ensure that the initial structure of DNA had a minimal effect on the results, we did not use the first 500 ps of the trajectories in the MD simulations in the final analysis. All the molecular graphics images were produced using the SYBYL program from Tripos Inc.
RESULTS
Selection of methylphosphonate DNA analogs
Realizing that it is not possible to conduct simulations on all variations of methylphosphonate isomers at the positions shown in Figure 1 with a DNA of 12 bp, we carried out MD simulations on [d(TATAGGCCTATA)]2 and [d(CGCGAATTCGCG)]2 substituted at selected positions with methylphosphonate groups. The results are compared with previous simulations on the same, but unmodified, DNA sequences (26,27). Six central anionic phosphates of each DNA dodecamer were changed to methylphosphonates (Fig. 1). The total formal charge of each DNA dodecamer duplex was reduced from 22 to 10 by these modifications and cross-strand charged group repulsion in the center of each duplex was eliminated. To mimic solution studies of methylphosphonates, which are synthesized with random stereochemistry, patterns of alternating methylphosphonate diastereomers, R and S, were first used along each backbone (Fig. 1). It should be noted, however, that the methylphosphonates are neutral in either the R or S configuration. In an additional simulation with a modified d(TATAGGCCTATA) duplex, the methylphosphonates were placed with randomly selected diastereomers (Fig. 1) along the backbone. For the sequences and substitution patterns used in these experiments no major differences in the final structures of the DNAs with different patterns of methylphosphonate isomers were observed (see below).
Five 10 ns MD simulations were carried out and analyzed in this study. The simulation on the methylphosphonate duplex 5′-d(TpApTpApGmSGmRCmSCmRTmSAmRTpA)-3′ is referred to as M_GGCC_ALT. A similar simulation, M_AATT_ALT, was carried out on the duplex 5′-CpGpCpGpAmSAmRTmSTmRCmSGmRCpG-3′. In another simulation, M_GGCC_RAN, of the modified GGCC duplex, (5′-TpApTpApGmRGmSCmSCmRTmRAmSTpA-3′)·(5′-TpApTpApGmSGmSCmSCmRTmSAmSTpA-3′), random methylphosphonate diastereomers were placed along the backbone of the DNA based on a random number generator. Finally, two control MD simulations of the GGCC and AATT duplexes with unmodified phosphate groups from previous work (26,27) were compared with the methylphosphonate analogs.
Comparison of the methylphosphonate modified GGCC duplex to its unmodified parent
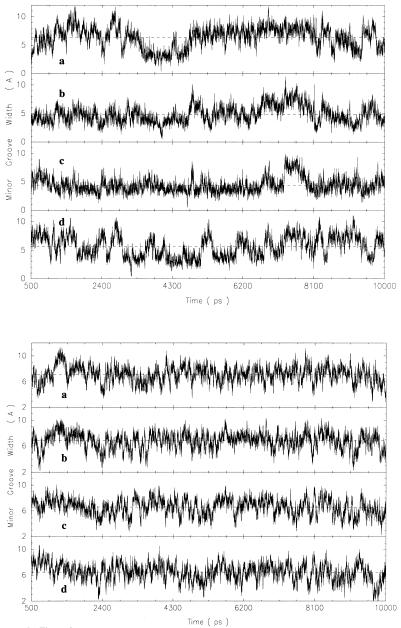
Based on the root mean square deviation of the simulations from the initial conformations, the DNA relaxed rapidly and remained stable over the time period of all simulations. It has been noted that full solvent equilibration can take up to 3 ns (51) and all simulations were run for 10 ns. The first 500 ps of the trajectories were excluded from each time-average conformation determination to ensure stability of the DNA. The minor groove width of the modified GGCC DNA, M_GGCC_ALT, ranges from ∼2.0 to 10.0 Å across the minor groove at P6–P20, P7–P19, P8–P18 and P9–P17 during the course of the MD simulation, as can be seen from the time-dependent plot in Figure 2 (top). This variation in amplitude is similar to the range of minor groove widths of the unmodified GGCC sequence (Fig. 2, bottom). The minor groove of the unmodified GGCC sequence remains wide most of the time but transiently becomes narrow relative to the minor groove width of the canonical B-form DNA of 5.9 Å. In contrast, the minor groove of M_GGCC_ALT remains narrow most of the time and occasionally becomes wide. The average minor groove width of the unmodified GGCC sequence is ∼6.0 Å near the central phosphate–phosphate pairs and is 4.0 Å for that of M_GGCC_ALT at the same location (versus 5.9 Å for the canonical B DNA).
Figure 2.
Time-dependent fluctuations of the minor groove width, calculated using CURVES 5.1, of the central G-tract of methylphosphonate modified duplex, M_GGCC_ALT (top), and the unmodified duplex (bottom) at the (a) P6–P20, (b) P7–P19, (c) P8–P18 and (d) P9–P17 cross-strand groups over the entire simulation.
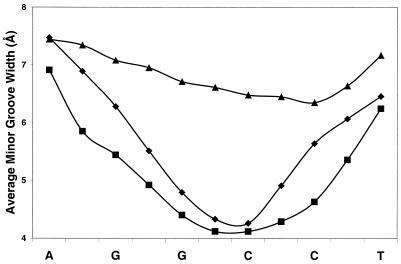
Figure 3 shows that the minor groove widths at the central G-tracts of M_GGCC_ALT and M_GGCC_RAN, averaged over the final 9.5 ns of the simulations, are narrow compared with that in B-form DNA and the unmodified dodecamer of the same sequence (Fig. 3). The minor groove widths at the central G-tracts of the methylphosphonate DNA analogs are ∼4.0 Å and widen to ∼7.0 Å at the duplex termini. The minor groove widths of the central, neutralized region of M_GGCC_ALT and M_GGCC_RAN are ∼3 Å less than that of the unmodified dodecamer of the same sequence. The minor groove width of the unmodified dodecamer is more uniform along the helix with a width of ∼6.5 Å (Fig. 3).
Figure 3.
Effect of phosphate neutralization on the time-average minor groove width profile of the central G-tract of the GGCC duplexes. The triangles show the unmodified GGCC duplex, the diamonds show the alternating methylphosphonate modified duplex (M_GGCC_ALT) and the squares show the random methylphosphonate modified duplex (M_GGCC_RAN).
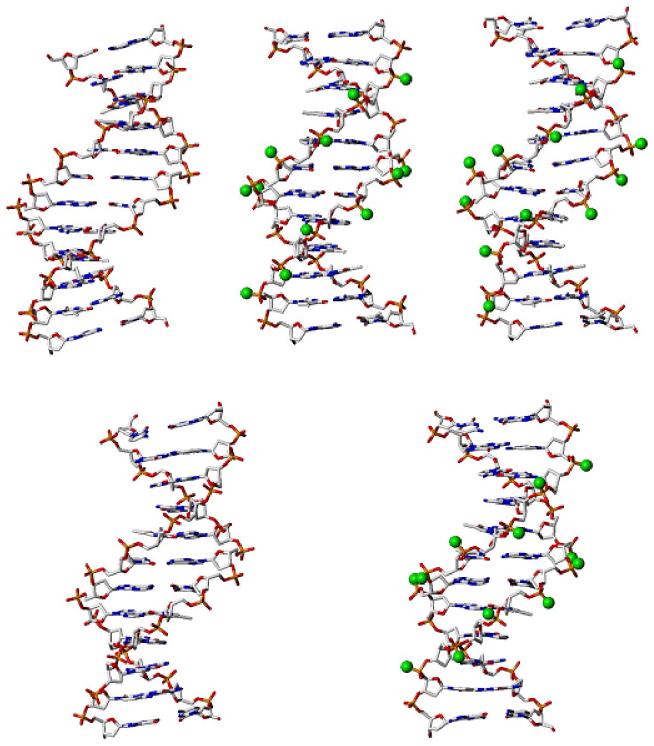
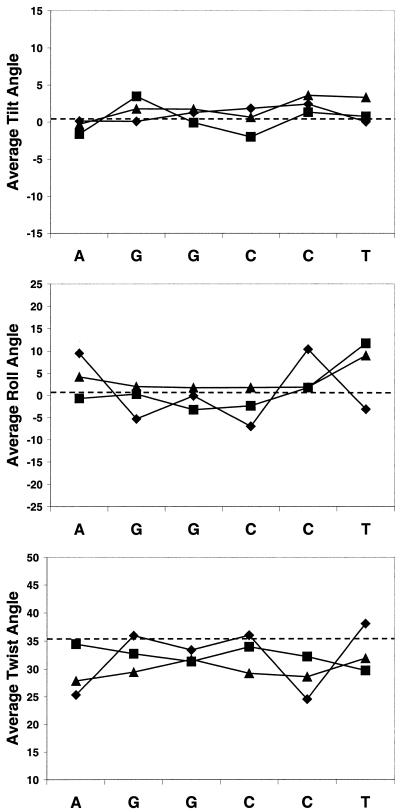
The models in Figure 4 (top) illustrate that the minor groove widths of the G-tracts of M_GGCC_ALT and M_GGCC_RAN are narrower than that of the unmodified GGCC duplex. The spherical balls in M_GGCC_ALT and M_GGCC_RAN represent the methyl groups of the methylphosphonate analogs. The tilt and roll angles of the unmodified GGCC, M_GGCC_ALT and M_GGCC_RAN DNA are similar to each other and average around the values of the canonical B-form DNA, as shown in Figure 5. Also, the twist angles of the three simulations are similar, but are slightly lower than that of the B-form DNA (Fig. 5). The lower twist is expected from simulations of DNA with the force field of Cornell et al. (52).
Figure 4.
Stick representation of time-average GGCC (top) and AATT (bottom) duplexes with and without methylphosphonates in the central G-tract and A-tract, respectively. (Top left) Unmodified GGCC, with a wide minor groove; (top center) M_GGCC_ALT, with a narrow minor groove; (top right) M_GGCC_RAN, with a narrow minor groove. (Bottom left) Unmodified AATT duplex; (bottom right) M_AATT_ALT duplex. Carbon atoms of the methyl groups of the methylphosphonate analogs are represented as green spheres.
Figure 5.
Plots of tilt, twist and roll angles of the central G-tract of the GGCC duplexes. Triangle, unmodified GGCC duplex; diamond, M_GGCC_ALT; square, M_GGCC_RAN.
Comparison of the methylphosphonate modified AATT duplex with its unmodified parent
The time-average minor groove width of the central A-tract of the unmodified AATT duplex is narrow and the groove width of the modified AATT duplex, M_AATT_ALT, is even narrower than that of the unmodified dodecamer (Fig. S2). The chemical conversion of the central phosphates to methylphosphonates and complete neutralization of this region of DNA causes the minor groove to narrow by an additional ∼1.0 Å. Figure 4 (bottom) depicts the time-average structure of models of the unmodified AATT and modified AATT, M_AATT_ALT, sequences with the carbon atoms of the methyl groups of the methylphosphonate analogs represented as green balls. The helical backbone structures of the unmodified AATT and M_AATT_ALT are similar to each other and to B-form DNA, as can be seen from the plot of the tilt, twist and roll angles in Figure S3.
Sodium ion distribution and structured water molecules in the minor groove
The MD simulations reported here also show that conversion to neutral phosphate linkages alters the distribution of cations surrounding DNA. The unmodified AATT duplex has 45 sodium ions per 100 ps interacting with the cross-strand phosphate–phosphate groups at the central region of the duplex at the lip of the minor groove, as previously described (26). The unmodified GGCC duplex has 19 cation interactions per 100 ps at a comparable NaCl concentration (27). In contrast, there is only approximately one ion interaction per 100 ps for both the methylphosphonate modified GGCC and AATT duplexes.
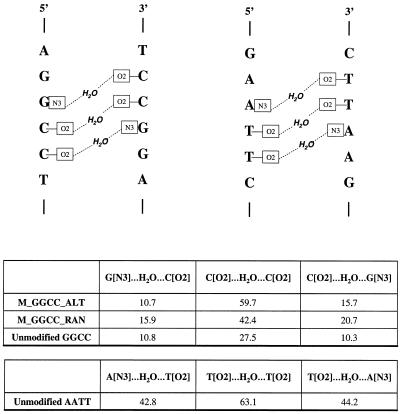
A water molecule was assumed to form a cross-strand interaction between two atoms on opposite strands, for example between O2 of T on one strand and O2 of T on the other strand, if the oxygen of the water molecule was within 3.0 Å of both T O2 groups. Over the entire simulation of the unmodified AATT, cross-strand water molecules between O2 of T on one strand and O2 of T on the other strand at the central region (AT step) are observed ∼63% of the time, as shown in Figure 6. Cross-strand structured water molecules at the adjacent site, N3 of A on one strand and O2 of T on the other strand and vice versa, are found to be present ∼43 and 44% of the time, respectively. Water molecules are also observed in the minor groove of the modified and unmodified GGCC sequences, as also shown in Figure 6. The cross-strand water molecules between the O2 of C on one strand and O2 of C on the other strand at the central region (GC step) of M_GGCC_ALT, M_GGCC_RAN and unmodified GGCC are found to be present for ∼60, 42 and 28% of the simulation periods, respectively. The water molecules at adjacent sites at the 5′- and 3′-ends of the central site of M_GGCC_ALT, M_GGCC_RAN and unmodified GGCC are present ∼11 and 16%, 16 and 21% and 11 and 10% of the entire simulations, respectively.
Figure 6.
Schematic representation of cross-strand water molecules in the minor groove of the A-tract and G-tract (top). Over the entire simulation of the unmodified AATT and GGCC and methylphosphonate modified GGCC the percentages of cross-strand water molecules are presented (bottom).
DISCUSSION
The influence of electrostatic forces on the local conformation of DNA has broad application to questions of nucleic acid bending, folding and global structure. The questions addressed here relate to the electrostatic environment of the DNA double helix in solution and specifically to the influence of this environment on minor groove width. We previously conducted simulations on the duplex form of d(CGCGAATTCGCG), termed the AATT duplex (26), initially crystallized and studied in detail by Dickerson and co-workers (1). To compare an A-tract with a G-tract, we have also carried out simulations on the duplex form of d(TATAGGCCTATA), termed the GGCC duplex (27). Analysis of those MD trajectories revealed that fluctuations in monovalent cation positions are influenced by sequence and the cation positions are coupled to fluctuations in minor groove width (26,27). When cations transiently enter the lip or localize near the floor of the minor groove, cross-groove phosphate–phosphate repulsions are attenuated and the minor groove width decreases. When the cations dissociate, the groove in that region quickly widens. A-tracts contain relatively high time-average concentrations of cations near the floor and within the lip of the minor groove in comparison with G-tracts.
As described in the Introduction, an electrostatic model in which sequence-specific variations in groove width depend on variations in cross-strand phosphate repulsion (21,22,31) predicts that chemical modifications that eliminate repulsion should cause groove narrowing. Here we examine limiting relationships between minor groove width and cross-groove electrostatic repulsion, by using methylphosphonate modifications that abolish anionic charge. Experimentally, methylphosphonate-substituted DNA molecules have been studied to investigate such diverse topics as antisense therapeutics and electrostatic effects on DNA bending (31,32,53–65). Strauss and Maher used methylphosphonate substitution to test the hypothesis that proteins with cationic surfaces can induce substantial DNA bending by neutralizing phosphate groups on one DNA face. By conducting a series of electrophoretic experiments, they showed that B-DNA bends when phosphates on one duplex face are substituted with methylphosphonate analogs. These results clearly show the importance of the electrostatic environment on the global structure of DNA. Here we are specifically interested in the effect of neutralizing the phosphate groups on the width of the DNA minor groove. We are working with relatively short DNA fragments, therefore the effect of neutralizing the phosphate groups on curvature is not studied. Longer sequences and simulation times would be needed to accurately examine the curvature of DNA duplexes. Moreover, McConnell and Beveridge, using long DNA duplexes of 25 and 30 bp, have studied curvature in detail and shown that there is a correlation between DNA bending and ion distributions (66).
The results of the simulations performed here are consistent with the electrostatic model of DNA deformation. During the simulations, the time-average minor groove is narrow when the electrostatic repulsion across the minor groove is eliminated by chemical modification. With the sequences and modified positions used in this research narrowing of the minor groove does not appear to depend on the specific stereochemistry of the modified phosphate, as indicated by similarities in DNA duplexes with alternating and random stereochemistries of the methylphosphonate. Both the G-tract and the A-tract (Figs 3, 4 and S2) minor grooves narrow when the cross-strand phosphate repulsion is eliminated. However, the proportional effect on the G-tract is much greater than the effect on the A-tract because the unmodified G-tract has a larger average minor groove width than the unmodified A-tract.
In order to conclude that the change in electrostatic environment of the modified DNA is responsible for the narrowing of the minor groove width, it is important to compare the global conformations of the methylphosphonate modified DNA duplexes with the unmodified parent DNA. Using two-dimensional nuclear Overhauser effect (2D-NOE) data, Bower et al. (67) were able to make 1H NMR chemical shift assignments for Rp-Rp and Sp-Sp methylphosphonate modified duplexes of [d(GGAATTCC)]2. The chemical shifts were shown to be similar to those reported (68) for the unmodified B-type duplex. Also, Hausheer et al. (69), using MD techniques, showed that fully substituted methylphosphonate double-stranded DNAs of sequence d(AT)5·d(AT)5 and d(GC)5·d(GC)5 had similar global conformational properties to B-form DNA. Our calculations support these results. It can be seen from Figures 5 and S3 that the general B-form conformation of the modified DNA duplexes is conserved but that methylphosphonate substitution strongly affects minor groove width in GC sequences.
In previous studies of cation interactions (26,27) it was shown that the electrostatic repulsion of phosphate groups across the minor groove causes the groove to widen. This effect of electrostatic repulsion is felt across the minor groove more than that across the major groove because the major groove width of the B-form DNA is around twice that of the minor groove. Therefore, neutralizing the phosphate groups will reduce the repulsion across the minor groove much more than it will across the major groove, thus causing the minor groove to become narrower. It is now clear from these and previous studies that the minor groove of DNA duplexes can assume different widths, from more narrow to wider than the B-conformation, depending on the solution environment and/or backbone modifications.
As also mentioned in the Introduction, X-ray analysis indicates that localized water molecules in the minor groove appear to be an integral part of DNA structure. One of the consequences of the minor groove width fluctuation is the linkage it has with minor groove hydration, as previously observed by Chui and Dickerson (28). As the minor groove narrows a highly ordered spine of hydration is formed, which is lost when the minor groove widens. Our results show that in MD simulations the minor groove of AATT has more cross-strand water molecules at the central AT step than those of M_GGCC_ALT and M_GGCC_RAN at the central GC step (Fig. 6). There is a clear correlation between the width of the minor groove and the percentage of structured water molecules in the minor groove. The narrower the minor groove the greater the number of cross-strand water interactions. It is interesting to note that the narrower methylphosphonate modified GGCC minor grooves have more than twice the amount of cross-strand water molecules than that of the unmodified GGCC parent. Consistent with these results, it is observed from the X-ray crystal structures of three GGCC duplexes of d(CCAGGCCTGG) (NDB id bdjb27, bdjb49 and bdjb50) with narrow minor groove widths, narrower than that of the canonical B-form DNA, that they have a localized cross-strand water molecule at the central GC step. The distances of the oxygen atom of the water molecules from the O2 groups of the two C residues on opposite strands are 2.82 and 3.03, 2.88 and 3.51, and 2.8 and 3.49 Å for bdjb27, bdjb49 and bdjb50, respectively.
It is important to ask what angles or helical parameters are directly associated with the width of the minor groove? The phase, amplitude, χ, γ, δ, ε, ζ, α and β angles for both strands and the minor groove width at several base pairs were extracted over the entire simulation. The aim was to see if there is any relationship or correlation between these torsion angles and the minor groove width. A very weak correlation was observed, approximately 0.48. Also, using a machine learning predictive model, decision tree (70–72), an attempt was made to deduce rules governing relationships between torsion angles and minor groove width. A rule would specify what the different torsion angles have to be in order for the minor groove width to fall within a certain range, for example the phase angle should be less than a certain value (p) and the χ torsion angle should be greater than a certain value (c) and the γ torsion angle should be less than a certain value (g), etc. for the minor groove width to fall within a certain range (mg1 and mg2). A correlation coefficient of about 0.87 was obtained. However, about 2200 rules relating groove width and torsion angles were deduced. This result indicates that there is not one angle or small group of angle parameters that control the width of the minor groove in the DNA molecule. The groove width at a particular base pair is controlled not only by the torsion angles at that base pair (locally), but also by the helical parameters at adjacent base pairs (globally). Furthermore, no correlation was found between the base–base parameters, shear, stretch, stagger, buckle and propeller twist and the minor groove width. These results clearly show that the narrow minor groove width observed for DNA when ions interact with phosphate groups or when phosphates are chemically neutralized can be achieved by numerous combinations of torsional angles. All of these combinations result in a narrow groove when phosphate repulsions across the minor groove are neutralized.
SUPPLEMENTARY MATERIAL
Supplementary Material is available at NAR Online.
Acknowledgments
ACKNOWLEDGEMENTS
The authors thank Dr L. J. Maher for helpful discussions and suggestions. This work was supported by NIH and Bill and Melinda Gates Foundation grants to W.D.W. and an NSF Grant to L.D.W. Computers were purchased with support from the Georgia Research Alliance.
REFERENCES
- 1.Wing R., Drew,H., Takano,T., Broka,C., Tanaka,S., Itakura,K. and Dickerson,R.E. (1980) Crystal structure analysis of a complete turn of B-DNA. Nature, 287, 755–758. [DOI] [PubMed] [Google Scholar]
- 2.Drew H.R. and Dickerson,R.E. (1981) Structure of a B-DNA dodecamer. III. Geometry of hydration. J. Mol. Biol., 151, 535–556. [DOI] [PubMed] [Google Scholar]
- 3.Dickerson R.E. and Drew,H.R. (1981) Structure of a B-DNA dodecamer. II. Influence of base sequence on helix structure. J. Mol. Biol., 149, 761–786. [DOI] [PubMed] [Google Scholar]
- 4.Burkhoff A.M. and Tullius,T.D. (1987) The unusual conformation adopted by the adenine tracts in kinetoplast DNA. Cell, 48, 935–943. [DOI] [PubMed] [Google Scholar]
- 5.Alexeev D.G., Lipanov,A.A. and Skuratovskii,I.Y. (1987) Poly(dA)-poly(dT) is a B-type double helix with a distinctively narrow minor groove. Nature, 325, 821–823. [DOI] [PubMed] [Google Scholar]
- 6.Shui X., McFail-Isom,L., Hu,G.G. and Williams,L.D. (1998) The B-DNA dodecamer at high resolution reveals a spine of water on sodium. Biochemistry, 37, 8341–8355. [DOI] [PubMed] [Google Scholar]
- 7.Chiu T.K., Kaczor-Grzeskowiak,M. and Dickerson,R.E. (1999) Absence of minor groove monovalent cations in the crosslinked dodecamer C-G-C-G-A-A-T-T-C-G-C-G. J. Mol. Biol., 292, 589–608. [DOI] [PubMed] [Google Scholar]
- 8.Grzeskowiak K., Yanagi,K., Prive,G.G. and Dickerson,R.E. (1991) The structure of B-helical C-G-A-T-C-G-A-T-C-G and comparison with C-C-A-A-C-G-T-T-G-G. The effect of base pair reversals. J. Mol. Biol., 266, 8861–8883. [DOI] [PubMed] [Google Scholar]
- 9.Heinemann U. and Hahn,M. (1992) C-C-A-G-G-C-m5C-T-G-G. Helical fine structure, hydration and comparison with C-C-A-G-G-C-C-T-G-G. J. Biol. Chem., 267, 7332–7341. [PubMed] [Google Scholar]
- 10.Hahn M. and Heinemann,U. (1993) DNA helix structure and refinement algorithm: comparison of models for d(CCAGGCm5CTGG) derived from NUCLSQ, TNT and X-PLOR. Acta Crystallogr., D49, 468–477. [DOI] [PubMed] [Google Scholar]
- 11.Fedoroff O., Reid,B.R. and Chuprina,V.P. (1994) Sequence dependence of DNA structure in solution. J. Mol. Biol., 235, 325–330. [DOI] [PubMed] [Google Scholar]
- 12.Liepinsh E., Otting,G. and Wuthrich,K. (1992) NMR observation of individual molecules of hydration water bound to DNA duplexes: direct evidence for a spine of hydration water present in aqueous solution. Nucleic Acids Res., 20, 6549–6553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jacobson A., Leupin,W., Liepinsh,E. and Otting,F. (1996) Minor groove hydration of DNA in aqueous solution: sequence-dependent next neighbor effect of the hydration lifetimes in d(TTAA)2 segments measured by NMR spectroscopy. Nucleic Acids Res., 24, 2911–2918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Halle B. and Denisov,V.P. (1998) Water and monovalent ions in the minor groove of B-DNA oligonucleotides as seen by NMR. Biopolymers, 48, 210–233. [DOI] [PubMed] [Google Scholar]
- 15.Denisov V.P. and Halle,B. (2000) Sequence-specific binding of counterions to B-DNA. Proc. Natl Acad. Sci. USA, 97, 629–633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hud N.V. and Feigon,J. (1997) Localization of divalent metal ions in the minor groove of DNA A-tracts. J. Am. Chem. Soc., 119, 5756–5757. [Google Scholar]
- 17.Hud N.V., Sklenar,V. and Feigon,J. (1999) Localization of ammonium ions in the minor groove of DNA duplexes in solution and the origin of DNA A-tract bending. J. Mol. Biol., 286, 651–660. [DOI] [PubMed] [Google Scholar]
- 18.Young M.A., Ravishanker,G. and Beveridge,D.L. (1997) A 5-nanosecond molecular dynamics trajectory for B-DNA: analysis of structure, motions and solvation. Biophys. J., 73, 2313–2336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Beveridge D.L. and McConnell,K.J. (2000) Nucleic acids: theory and computer simulation, Y2K. Curr. Opin. Struct. Biol., 10, 182–196. [DOI] [PubMed] [Google Scholar]
- 20.Young M.A., Jayaram,B. and Beveridge,D.L. (1997) Intrusion of counterions into the spine of hydration in the minor groove of B-DNA: fractional occupancy of electronegative pockets. J. Am. Chem. Soc., 119, 59–69. [Google Scholar]
- 21.McFail-Isom L., Sines,C.C. and Williams,L.D. (1999) DNA structure: cations in charge? Curr. Opin. Struct. Biol., 9, 298–304. [DOI] [PubMed] [Google Scholar]
- 22.Williams L.D. and Maher,L.J.,III (2000) Electrostatic mechanisms of DNA deformation. Annu. Rev. Biophys. Biomol. Struct., 29, 497–521. [DOI] [PubMed] [Google Scholar]
- 23.Calladine C.R. and Drew,H.R. (1997) Understanding DNA: The Molecule and How It Works. Academic Press, San Diego, CA.
- 24.Hassan M.A.E. and Calladine,C.R. (1996) Propeller-twisting of base-pairs and the conformational mobility of dinucleotide steps in DNA. J. Mol. Biol., 259, 95–103. [DOI] [PubMed] [Google Scholar]
- 25.Dickerson R.E. (1983) Base sequence and helix structure variation in B and A DNA. J. Mol. Biol., 166, 419–441. [DOI] [PubMed] [Google Scholar]
- 26.Hamelberg D., McFail-Isom,L., Williams,L.D. and Wilson,W.D. (2000) Flexible structure of DNA: ion dependence of minor-groove structure and dynamics. J. Am. Chem. Soc., 122, 10513–10520. [Google Scholar]
- 27.Hamelberg D., Williams,L.D. and Wilson,W.D. (2001) Influence of the dynamic positions of cations on the structure of the DNA minor groove: sequence-dependent effects. J. Am. Chem. Soc., 123, 7745–7755. [DOI] [PubMed] [Google Scholar]
- 28.Chiu T.K. and Dickerson,R.E. (2000) 1 Å crystal structures of B-DNA reveal sequence-specific binding and groove-specific bending of DNA by magnesium and calcium. J. Mol. Biol., 301, 915–945. [DOI] [PubMed] [Google Scholar]
- 29.Lavery R. and Pullman,B. (1981) The molecular electrostatic potential, steric accessibility and hydration of Dickerson’s B-DNA dodecamer d(CpGpCpGpApApTpTpCpGpCpG). Nucleic Acids Res., 9, 3765–3777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lavery R. and Pullman,B. (1985) The dependence of the surface electrostatic potential of B-DNA on environmental factors. J. Biomol. Struct. Dyn., 2, 1021–1032. [DOI] [PubMed] [Google Scholar]
- 31.Strauss J.K. and Maher,L.J.,III (1994) DNA bending by asymmetric phosphate neutralization. Science, 266, 1829–1834. [DOI] [PubMed] [Google Scholar]
- 32.Strauss-Soukup J.K., Vaghefi,M.M., Hogrefe,R.I. and Maher,L.J.,III (1997) Effects of neutralization pattern and stereochemistry on DNA bending by methylphosphonate substitutions. Biochemistry, 36, 8692–8698. [DOI] [PubMed] [Google Scholar]
- 33.Arnott S. and Hukins,D.W. (1972) Optimised parameters for A-DNA and B-DNA. Biochem. Biophys. Res. Commun., 47, 1504–1509. [DOI] [PubMed] [Google Scholar]
- 34.Jorgensen W.L., Chandrasekhar,J., Madura,J.D., Impey,R.W. and Klein,M.L. (1983) Comparison of simple potential functions for simulating liquid water. J. Chem. Phys., 79, 926–935. [Google Scholar]
- 35.Case D.A., Pearlman,D.A., Caldwell,J.W., Cheatham,T.E.,III, Ross,W.S., Simmerling,C.L., Darden,T.A., Merz,K.M., Stanton,R.V., Cheng,A.L., Vincent,J.J., Crowley,M., Ferguson,D.M., Radmer,R.J., Seibel,G.L., Singh,U.C., Weiner,P.K. and Kollman,P.A. (1997) Amber v.5. University of California, San Francisco, CA.
- 36.Cornell W.D., Cieplak,P., Bayly,C.I., Gould,I.R.,Jr, Merz,K.M., Ferguson,D.M., Spellmeyer,D.C., Fox,T., Caldwell,J.W. and Kollman,P.A. (1995) A second generation force field for the simulation of proteins, nucleic acids and organic molecules. J. Am. Chem. Soc., 117, 5179–5197. [Google Scholar]
- 37.York D.M., Darden,T.A. and Pedersen,L.G. (1993) The effect of long-range electrostatic interactions in simulations of macromolecular crystals—a comparison of the Ewald and truncated list methods. J. Chem. Phys., 99, 8345–8348. [Google Scholar]
- 38.York D.M., Yang,W., Lee,H., Darden,T.A. and Pedersen,L.G. (1995) Toward the accurate modeling of DNA: the importance of long-range electrostatics. J. Am. Chem. Soc., 117, 5001–5002. [Google Scholar]
- 39.Essmann U., Perera,L., Berkowitz,M.L., Darden,T.A., Lee,H. and Pedersen,L.G. (1995) A smooth particle mesh ewald method. J. Chem. Phys., 103, 8577–8593. [Google Scholar]
- 40.Darden T.A., York,D.M. and Pedersen,L.G. (1993) Particle mesh Ewald: an N log(N) method for Ewald sums in large systems. J. Chem. Phys., 98, 10089–10092. [Google Scholar]
- 41.Lee H., Darden,T.A. and Pedersen,L.G. (1995) Accurate crystal molecular dynamics simulations using particle mesh Ewald–RNA dinucleotides- ApU and GpC. Chem. Phys. Lett., 243, 229–235. [Google Scholar]
- 42.Berendsen H.J.C., van Gunsteren,W.F., Postma,J.P.M. and DiNola,A. (1984) Molecular dynamics with coupling to an external bath. J. Chem. Phys., 81, 3684–3690. [Google Scholar]
- 43.Ryckaert J.P., Ciccotti,G. and Berendsen,H.J.C. (1977) Numerical integration of the Cartesian equations of motion of a system with comstraints: molecular dynamics of n-alkanes. J. Comput. Phys., 23, 327–341. [Google Scholar]
- 44.Frisch M.J., Trucks,G.W., Schlegel,H.B., Scuseria,G.E., Robb,M.A., Cheeseman,J.R., Zakrzewski,V.G., Montgomery,J.A., Stratmann,R.E., Burant,J.C., Dapprich,S., Millam,J.M., Daniels,A.D., Kudin,K.N., Strain,M.C., Farkas,O., Tomasi,J., Barone,V., Cossi,M., Cammi,R., Mennucci,B., Pomelli,C., Adamo,C., Clifford,S., Ochterski,J., Petersson,G.A., Ayala,P.Y., Cui,Q., Morokuma,K., Malick,D.K., Rabuck,A.D., Raghavachari,K., Foresman,J.B., Cioslowski,J., Ortiz,J.V., Baboul,A.G., Stefanov,B.B., Liu,G., Piskorz,P., Komaromi,I., Gomperts,R., Martin,R.L., Fox,D.J., Keith,T., Al-Laham,M.A., Peng,C.Y., Nanayakkara,A., Gonzalez,C., Challacombe,M., Gill,P.M.W., Johnson,B., Chen,W., Wong,M.W., Andres,J.L., Gonzalez,C., Head-Gordon,M., Replogle,E.S. and Pople,J.A. (1998) Gaussian98. Gaussian Inc., Pittsburgh, PA.
- 45.Bayly C.I., Cieplak,P., Cornell,W.D. and Kollman,P.A. (1993) A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model. J. Phys. Chem., 97, 10269–10280. [Google Scholar]
- 46.Cornell W.D., Cieplak,P., Balyl,C.I. and Kollman,P.A. (1993) Application of RESP charges to calculate conformational energies, hydrogen bond energies and free energies of solvation. J. Am. Chem. Soc., 115, 9620–9631. [Google Scholar]
- 47.Cieplak P., Cornell,W.D., Balyl,C.I. and Kollman,P.A. (1995) Application of the multimolecule and multiconformation RESP methodology to biopolymers: derivation for DNA, RNA and proteins. J. Comput. Chem., 16, 1357–1377. [Google Scholar]
- 48.Lavery R. and Sklenar,H. (1988) The definition of generalized helicoidal parameters and of axis curvature for irregular nucleic acids. J. Biomol. Struct. Dyn., 6, 63–91. [DOI] [PubMed] [Google Scholar]
- 49.Lavery R. and Sklenar,H. (1989) Defining the structure of irregular nucleic acids: conventions and principles. J. Biomol. Struct. Dyn., 6, 655–667. [DOI] [PubMed] [Google Scholar]
- 50.Stofer E. and Lavery,R. (1994) Measuring the geometry of DNA grooves. Biopolymers, 34, 337–346. [DOI] [PubMed] [Google Scholar]
- 51.Feig M. and Pettitt,B.M. (1998) Structural equilibrium of DNA represented with different force fields. Biophys. J., 75, 134–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Cheatham T.E. III, Cieplak,P. and Kollman,P.A. (1999) A modified version of the Cornell et al. force field with improved sugar pucker phases and helical repeat. J. Biomol. Struct. Dyn., 16, 845–862. [DOI] [PubMed] [Google Scholar]
- 53.Miller P.S. and Ts’o,P.O. (1987) A new approach to chemotherapy based on molecular biology and nucleic acid chemistry: Matagen (masking tape for gene expression). Anticancer Drug Des., 2, 117–128. [PubMed] [Google Scholar]
- 54.Maher L.J. and Dolnick,B.J. (1988) Comparative hybrid arrest by tandem antisense oligodeoxyribonucleotides or oligodeoxyribonucleoside methylphosphonates in a cell-free system. Nucleic Acids Res., 16, 3341–3358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Miller P.S., Agris,C.H., Aurelian,L., Blake,K.R., Murakami,A., Reddy,M.P., Spitz,S.A. and Ts’o,P.O. (1985) Control of ribonucleic acid function by oligonucleoside methylphosphonates. Biochimie, 67, 769–776. [DOI] [PubMed] [Google Scholar]
- 56.Blake K.R., Murakami,A. and Miller,P.S. (1985) Inhibition of rabbit globin mRNA translation by sequence-specific oligodeoxyribonucleotides. Biochemistry, 24, 6132–6138. [DOI] [PubMed] [Google Scholar]
- 57.Blake K.R., Murakami,A., Spitz,S.A., Glave,S.A., Reddy,M.P., Ts’o,P.O. and Miller,P.S. (1985) Hybridization arrest of globin synthesis in rabbit reticulocyte lysates and cells by oligodeoxyribonucleoside methylphosphonates. Biochemistry, 24, 6139–6145. [DOI] [PubMed] [Google Scholar]
- 58.Murakami A., Blake,K.R. and Miller,P.S. (1985) Characterization of sequence-specific oligodeoxyribonucleoside methylphosphonates and their interaction with rabbit globin mRNA. Biochemistry, 24, 4041–4046. [DOI] [PubMed] [Google Scholar]
- 59.Smith C.C., Aurelian,L., Reddy,M.P., Miller,P.S. and Ts’o,P.O. (1986) Antiviral effect of an oligo(nucleoside methylphosphonate) complementary to the splice junction of herpes simplex virus type 1 immediate early pre-mRNAs 4 and 5. Proc. Natl Acad. Sci. USA, 83, 2787–2791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Agris C.H., Blake,K.R., Miller,P.S., Reddy,M.P. and Ts’o,P.O. (1986) Inhibition of vesicular stomatitis virus protein synthesis and infection by sequence-specific oligodeoxyribonucleoside methylphosphonates. Biochemistry, 25, 6268–6275. [DOI] [PubMed] [Google Scholar]
- 61.Chang E.H., Miller,P.S., Cushman,C., Devadas,K., Pirollo,K.F., Ts’o,P.O. and Yu,Z.P. (1991) Antisense inhibition of ras p21 expression that is sensitive to a point mutation. Biochemistry, 30, 8283–8286. [DOI] [PubMed] [Google Scholar]
- 62.Jayaraman K., McParland,K., Miller,P. and Ts’o,P.O. (1981) Selective inhibition of Escherichia coli protein synthesis and growth by nonionic oligonucleotides complementary to the 3′ end of 16S rRNA. Proc. Natl Acad. Sci. USA, 78, 1537–1541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Miller P.S., Yano,J., Yano,E., Carroll,C., Jayaraman,K. and Ts’o,P.O. (1979) Nonionic nucleic acid analogues. Synthesis and characterization of dideoxyribonucleoside methylphosphonates. Biochemistry, 18, 5134–5143. [DOI] [PubMed] [Google Scholar]
- 64.Miller P.S., McParland,K.B., Jayaraman,K. and Ts’o,P.O. (1981) Biochemical and biological effects of nonionic nucleic acid methylphosphonates. Biochemistry, 20, 1874–1880. [DOI] [PubMed] [Google Scholar]
- 65.Spiller D.G., Giles,R.V., Broughton,C.M., Grzybowski,J., Ruddell,C.J., Tidd,D.M. and Clark,R.E. (1998) The influence of target protein half-life on the effectiveness of antisense oligonucleotide analog-mediated biologic responses. Antisense Nucleic Acid Drug Dev., 8, 281–293. [DOI] [PubMed] [Google Scholar]
- 66.McConnell K.J. and Beveridge,D.L. (2000) DNA structure: what’s in charge? J. Mol. Biol., 304, 803–820. [DOI] [PubMed] [Google Scholar]
- 67.Bower M., Summers,M.F., Powell,C., Shinozuka,K., Regan,J.B., Zon,G. and Wilson,W.D. (1987) Oligodeoxyribonucleoside methylphosphonates. NMR and UV spectroscopic studies of Rp-Rp and Sp-Sp methylphosphonate (Me) modified duplexes of (d[GGAATTCC])2. Nucleic Acids Res., 15, 4915–4930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Broido M.S., James,T.L., Zon,G. and Keepers,J.W. (1985) Investigation of the solution structure of a DNA octamer [d(GGAATTCC)]2 using two-dimensional nuclear Overhauser enhancement spectroscopy. Eur. J. Biochem., 150, 117–128. [DOI] [PubMed] [Google Scholar]
- 69.Hausheer F.H., Singh,U.C., Palmer,T.C. and Saxe,J.D. (1990) Dynamic properties and electrostatic potential surface of neutral DNA heteropolymers. J. Am. Chem. Soc., 112, 9468–9474. [Google Scholar]
- 70.Quinlan J.R. (1986) Induction of decision trees. Machine Learn., 1, 81–106. [Google Scholar]
- 71.Quinlan J.R. (1993) C4.5: Programs for Machine Learning, the Morgan Kaufmann Series on Machine Learning. Morgan Kaufmann, San Mateo, CA.
- 72.Breiman L. (1984) Classification and Regression Trees, the Wadsworth Statistics/Probability Series. Wadsworth International Group, Belmont, CA.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.