Subspace algorithms for noise reduction in cochlear implants

Abstract

A single-channel algorithm is proposed for noise reduction in cochlear implants. The proposed algorithm is based on subspace principles and projects the noisy speech vector onto "signal" and “noise” subspaces. An estimate of the clean signal is made by retaining only the components in the signal subspace. The performance of the subspace reduction algorithm is evaluated using 14 subjects wearing the Clarion device. Results indicated that the subspace algorithm produced significant improvements in sentence recognition scores compared to the subjects' daily strategy, at least in stationary noise. Further work is needed to extend the subspace algorithm to non-stationary noise environments.

I. INTRODUCTION

Several noise-reduction algorithms have been proposed for cochlear implant (CI) users (van Hoesel and Clark, 1995; Hamacher et al., 1997; Wouters and Vanden Berghe, 2001). Most of these algorithms, however, were based on the assumption that two or more microphones were available. Van Hoesel and Clark (1995) tested an adaptive beamforming technique with four Nucleus-22 implantees using signals from two microphones – one behind each ear- to reduce noise coming from 90^o of the patients. Results indicated that adaptive beamforming with two microphones can bring substantial benefits to CI users in conditions for which reverberation is moderate and only one source is predominantly interfering with speech. Adding, however, a second microphone contralateral to the implant is ergonomically difficult without requiring the CI users to wear headphones or a neckloop [bilateral implants might provide the means, but their benefit is still being investigated]. Alternatively, monaural multi-microphone techniques can be used and such techniques are now becoming commercially available (e.g., BEAM in Nucleus devices).

In general, single-microphone noise reduction algorithms are more desirable and cosmetically more appealing than the algorithms based on multiple-microphone inputs. A few single-microphone noise-reduction strategies (Weiss, 1993; Hochberg et al., 1992; Yang and Fu, 2005) have been proposed for cochlear implants, some of which were implemented on old cochlear implant processors based on feature extraction strategies (F0/F1/F2 and MPEAK strategies) and some of which were implemented on the latest processors. Weiss (1993) demonstrated that preprocessing the signal with a standard noise reduction algorithm could reduce the errors in formant extraction. The latest speech processors, however, are not based on feature extraction strategies but are based on vocoder-type strategies. Recently, Yang and Fu (2005) evaluated a spectral-subtractive algorithm using the latest implant processors. Significant benefits in sentence recognition were observed for all subjects with the spectral-subtractive algorithm, particularly for speech embedded in speech-shaped noise.

In brief, only a few studies (e.g., Yang and Fu, 2005) were conducted to investigate the benefits of pre-processing the noisy speech signal by a noise reduction algorithm and feeding the enhanced signal to implant listeners. The present study evaluates the performance of a subspace noise reduction algorithm which is used as a pre-processor for signal enhancement.

II. EXPERIMENT 1: EVALUATION OF SUBSPACE ALGORITHM

In this experiment, we investigate the potential benefits of first preprocessing the noisy signal with a noise reduction algorithm and then feeding the “enhanced” signal to the CI processor. For noise reduction, we use a custom subspace-based algorithm (Hu and Loizou, 2002).

A. Subjects

A total of 14 Clarion implant users participated in this experiment consisting of nine Clarion CII patients and 5 Clarion S-Series patients. The majority of the CII patients were fitted with the CIS strategy, and the S-Series patients were fitted with the SAS strategy. All subjects had at least 1 yr of experience with their implant device (see Table I).

TABLE I.

Subject information.

Subject	Age	Implant	CI use (yr)	HINT score (Quiet)
S1	41	Clarion CII	2	57
S2	26	Clarion CII	2	55
S3	39	Clarion CII	1	90
S4	41	Clarion CII	2	52
S5	70	Clarion CII	2	60
S6	55	Clarion CII	1	86
S7	58	Clarion CII	2	88
S8	66	Clarion CII	3	95
S9	38	Clarion CII	4	35
SS1	56	Clarion S-Series	1	60
SS2	45	Clarion S-Series	1	94
SS3	40	Clarion S-Series	1	55
SS4	52	Clarion S-Series	1	79
SS5	43	Clarion S-Series	1	80

B. Subspace algorithm

The signal subspace algorithm was originally developed by Ephraim and Van Trees (1995) for white input noise and was later extended to handle colored noise (e.g., speech-shaped noise) by Hu and Loizou (2002). The underlying principle of the subspace algorithm is based on the projection of the noisy speech vector (consisting of, say, a segment of speech) onto two subspaces: the "signal" subspace and the "noise" subspace. The noise subspace contains only signal components due to the noise, and the signal subspace contains primarily the clean signal. Therefore, an estimate of the clean signal can be made by removing the components of the signal in the noise subspace and retaining only the components of the signal in the signal subspace.

Let y be the noisy vector, and let $\widehat{x}=Hy$ be an estimate of the clean signal vector, where H is a transformation matrix. The noise reduction problem can be formulated as that of finding a transformation matrix H, which when applied to the noisy vector would yield the clean signal. After applying such a transformation to the noisy signal, we can express the error between the estimated signal $\widehat{x}$ and the true clean signal x as: $\varepsilon =\widehat{x}-x=(H-I)x+H\mathrm{\hspace{0.17em} }n$ where n is the noise vector. Since the transformation matrix will not be perfect, it will introduce some speech distortion, which is quantified by first term of the error term, i.e. by (H-I)x. The second term (H n) quantifies the amount of noise distortion introduced by the transformation matrix. As the speech and noise distortion (as defined above) are decoupled, one can find the optimal transformation matrix H that would minimize the speech distortion subject to the noise distortion falling below a preset threshold. The solution to this constrained minimization problem for colored noise is given by (Hu and Loizou, 2002):

$$H_{opt}=V^{-T}\mathrm{\Lambda }{(\mathrm{\Lambda }+\mu I)}^{-1}{V}^{-T}$$ (1)

where μis a parameter (typical values for μ = 1–20), V is an eigenvector matrix and Λ is a diagonal eigenvalue matrix obtained from the noisy speech vector (more details can be found in Hu and Loizou, 2002, 2003). In our implementation, we used a variable μwhich took values in the range of 1 to 20 depending on the estimated short-term signal-to-noise ratio (see Hu and Loizou, 2003).

The above equation has the following interesting interpretation. The matrix VT acts like a data-dependent transform and projects the noisy speech vector into the noise and signal subspaces. The diagonal matrix Λ(Λ + μI)⁻1 multiplies the components of the signal in the signal subspace by a gain while zeroing out the components of the signal in the noise subspace. Finally, the matrix V⁻T transforms back the projected signal, i.e., it acts like an inverse transform.

The implementation of the above signal subspace algorithm can be summarized into two steps. Step 1. For each frame of noisy speech (y), use the above transformation given in Eq. 1 to obtain an estimate of the clean signal vector $\widehat{x}$, i.e., $\widehat{x}=H_{opt}\mathrm{\hspace{0.17em} }y$. Step 2: Use the estimated signal $\widehat{x}$ as input to the CI processor.

The above estimator was applied to 4-ms duration frames of the noisy signal, which overlapped each other by 50%. The enhanced speech vectors were Hamming windowed and combined using the overlap and add approach. No voice activity detection algorithm was used in our approach to update the noise covariance matrix needed to compute the matrix V. The noise covariance matrix was estimated using speech vectors from the initial silent frames of the sentences. Although this procedure for estimating the noise covariance matrix is adequate for stationary noise (such as the one used in this study), it is not adequate for non-stationary environments in which the background spectra (and consequently the noise covariance matrices) constantly change. In non-stationary environments (e.g., restaurant noise), the noise covariance matrix could be estimated and updated whenever a speech-absent segment is detected based on a voice activity detector or a noise-estimation algorithm.

C. Procedure

HINT sentences (Nilsson et al., 1994) corrupted in +5 dB S/N speech-shaped noise (taken from the HINT database) were used for evaluation. Six lists (60 sentences) were processed off-line in MATLAB by the subspace noise reduction algorithm. The processed sentences were presented directly to the subjects via the auxiliary input jack of their CI processor at a comfortable listening level. Subjects were fitted with their daily strategy. For comparative purposes, subjects were also presented with six different lists (60 sentences) of HINT sentences corrupted in +5 dB speech-shaped noise, i.e., unprocessed sentences. The presentation order of pre-processed and un-processed sentences was randomized between subjects.

D. Results and Discussion

The sentences were scored in terms of percent of words identified correctly (all words were scored). Figure 1 shows the percent correct scores for all subjects. The mean score obtained with sentences preprocessed by the subspace algorithm was 44% correct, and the mean score obtained with unprocessed sentences was 19% correct. ANOVA (repeated measures) tests indicated that the sentence scores obtained with the subspace algorithm were significantly higher [F(1,13)=33.1, p<0.0005] than the scores obtained with the un-processed sentences. As can be seen from Fig. 1, most subjects benefited from the noise reduction algorithm. Subject’s SS4 score, for instance, improved from 0% correct to 40% correct. Similarly, subjects’ SS1 and SS2 scores improved from roughly 0% to 50% correct.

Figure 1.

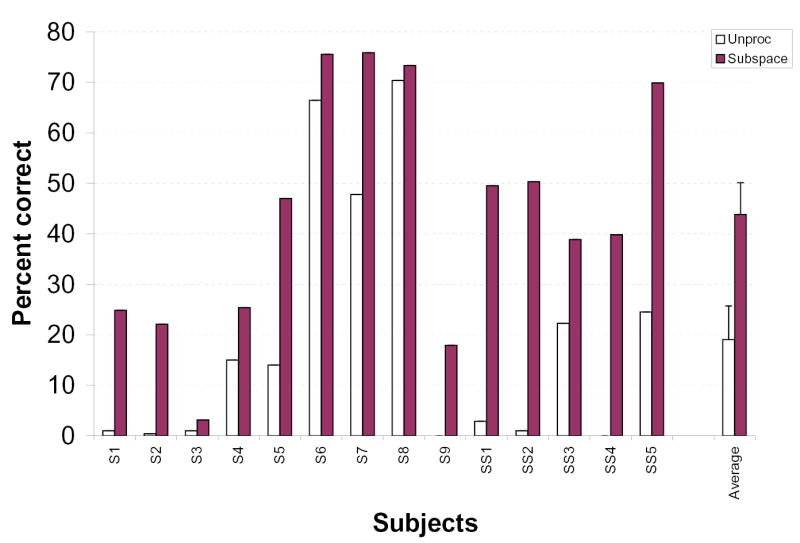
Subjects' performance on identification of words in sentences embedded in +5 dB S/N speech-shaped noise and preprocessed (dark bars) by the subspace algorithm or left un-processed (white bars). Subjects S1–S9 were Clarion CII patients and subjects SS1–SS5 were Clarion S-Series patients. Error bars indicate standard errors of the mean.

The above results indicate that the subspace algorithm can provide significant benefits to CI users in regards to recognition of sentences corrupted by stationary noise. It should be noted that the above signal subspace algorithm was only tested in stationary noise and it is not clear whether such intelligibility benefit would be maintained if the algorithm was tested in non-stationary environments (e.g., restaurant, multi-talker babble). Further work is needed to extend the subspace algorithm to non-stationary noise environments, particularly with regards to updating the noise covariance matrix based on perhaps a voice activity detector or a noise-estimation algorithm.