Metabolic Flux Responses to Pyruvate Kinase Knockout in Escherichia coli

Abstract

The intracellular carbon flux distribution in wild-type and pyruvate kinase-deficient Escherichia coli was estimated using biosynthetically directed fractional ¹³C labeling experiments with [U-¹³C₆]glucose in glucose- or ammonia-limited chemostats, two-dimensional nuclear magnetic resonance (NMR) spectroscopy of cellular amino acids, and a comprehensive isotopomer model. The general response to disruption of both pyruvate kinase isoenzymes in E. coli was a local flux rerouting via the combined reactions of phosphoenolpyruvate (PEP) carboxylase and malic enzyme. Responses in the pentose phosphate pathway and the tricarboxylic acid cycle were strongly dependent on the environmental conditions. In addition, high futile cycling activity via the gluconeogenic PEP carboxykinase was identified at a low dilution rate in glucose-limited chemostat culture of pyruvate kinase-deficient E. coli, with a turnover that is comparable to the specific glucose uptake rate. Furthermore, flux analysis in mutant cultures indicates that glucose uptake in E. coli is not catalyzed exclusively by the phosphotransferase system in glucose-limited cultures at a low dilution rate. Reliability of the flux estimates thus obtained was verified by statistical error analysis and by comparison to intracellular carbon flux ratios that were independently calculated from the same NMR data by metabolic flux ratio analysis.

The central carbon pathways fulfill anabolic and catabolic functions by providing cofactors and building blocks for macromolecular synthesis as well as energy. While some single-gene knockout mutations in central metabolism preclude growth on glucose, a majority of such variations can potentially be compensated for either by isoenzymes (39) or by a rerouting of carbon fluxes through alternative pathways (7, 15, 20, 42). Usually, the phenotypes of knockout mutants is characterized by quantitative physiological analysis, and conclusions on intracellular metabolism are then based on qualitative interpretation of these results. To reveal cause and effect relationships, however, it is important to gain deeper insight into the complex metabolic responses at the level of intracellular metabolite concentrations and fluxes. These intracellular carbon fluxes, or in vivo reaction rates, are per se nonmeasurable quantities that cannot usually be inferred directly from in vitro enzyme activities because not all in vivo effector concentrations are known. Hence, the intracellular reaction rates are commonly estimated by methods of metabolic flux analysis, which provide a holistic perspective on metabolism (52, 54).

The most common approach is based on flux balancing analysis within a stoichiometric model of cellular metabolism (26, 41, 50, 52). In this approach, uptake and secretion rates and biosynthetic requirements are balanced in a stoichiometric model, assuming quasi-steady-state material balances on the intermediates. In many cases, however, limited extracellular data and stoichiometric constraints lead to underdetermined systems, so that additional information is derived from various assumptions on biological functions (54). Consequently, the flux estimates often depend on the validity of rather arbitrary assumptions, e.g., on cofactor balances, energy stoichiometry, or in vivo enzyme activities.

Additional information to unambiguously define the otherwise underdetermined systems has been obtained from ¹³C-labeling experiments (47). In this approach, products of metabolism are analyzed by methods that can distinguish between different isotope labeling patterns, in particular nuclear magnetic resonance (NMR) and mass spectrometry. These data are then used, often in combination with material balances, to obtain a more faithful picture of the intracellular carbon flux distribution during the course of such a labeling experiment or to identify the topology of a metabolic network (10, 43, 46, 47, 54).

One particular type of experiment is based on biosynthetically directed fractional ¹³C labeling by cofeeding of unlabeled and uniformly ¹³C-labeled [U-¹³C₆]glucose (49). Using two-dimensional NMR spectroscopy, the relative abundance of multiplets due to ¹³C-¹³C scalar coupling between adjacent carbon positions in the amino acids is analyzed in protein hydrolysates from cells that are grown on such glucose mixtures. Using probabilistic equations, metabolic flux ratio (METAFoR) analysis then enables a direct and analytical interpretation of the observed ¹³C-labeling pattern in the two-dimensional NMR spectra and yields information on the origin of a given metabolite.

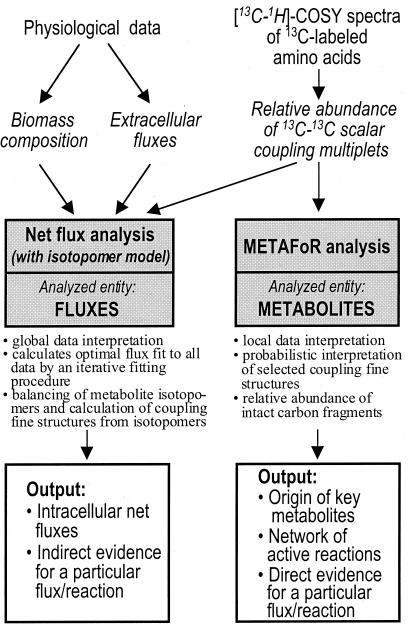
Exchange fluxes are quantitatively considered to correct for their potential influence on the ¹³C-labeling pattern. These results allow conclusions on active reactions and pathways in a bioreaction network and in some cases direct estimation of ratios of intracellular carbon fluxes (48, 49) (Fig. 1). In addition to analyses of various bacterial systems (24, 40, 48), METAFoR analysis was recently also applied to compartmentalized microorganisms (28).

FIG. 1.

Flow chart for metabolic flux ratio (METAFoR) and metabolic net flux analysis. Input information for the calculations is italicized.

As an alternative to analytical interpretation of certain isotope isomer (isotopomer) data by METAFoR analysis, the two-dimensional NMR data may also be used for balancing all isotopomers within a comprehensive model of metabolism, which can provide significantly improved resolution (12, 44, 54, 57). Akin to the above material balancing within a stoichiometric model, the labeling state of all metabolic intermediates is then balanced in such an isotopomer model (Fig. 1). This enables integrated and quantitative interpretation of all extracellular flux, biomass composition, and NMR data. The intracellular net flux distribution is then estimated by the identification of a best fit to the available data in an iterative fitting procedure. Such rigorous accounting of the isotopomer distribution in all metabolites within a comprehensive metabolic model using appropriate software retrieves the maximum information from experimentally determined labeling data and has been used successfully to estimate net fluxes in complex reaction networks (12, 34, 45, 54). The downsides of this maximum information retrieval are (i) a rather complex model that renders intuitive interpretation of the results difficult and (ii) indirect evidence for a particular flux or reaction because it was obtained from a fit to all data. Consequently, rigorous statistical analysis is mandatory to critically evaluate the confidence regions for the estimated fluxes (12, 54, 56).

Here we use the complementary methods of METAFoR analysis (48) and net flux analysis (12) to quantitatively investigate how Escherichia coli metabolism responds to knockout of both pyruvate kinase isoenzymes in glucose- and ammonia-limited chemostat culture. This enzyme is of particular importance in cellular metabolism because it catalyzes a physiologically irreversible reaction and is subject to different levels of allosteric control (20). These allosteric properties are a critical component in carbon flux regulation because their manipulation was shown to enhance or redirect glycolytic fluxes in resting E. coli (16, 17).

MATERIALS AND METHODS

Bacterial strains, media, and growth conditions.

Throughout this study, E. coli JM101 [F⁻ traD36 lacI^q Δ(lacZ)M15 proA⁺B⁺ supE thi Δ(lac-proAB)] and its pyruvate kinase-deficient but otherwise isogenic derivative PB25 (pykA::kan pykF::cat) were used (35). Inocula were grown overnight from a picked colony in baffled shake flasks at 37°C in M9 minimal medium containing 5 g of glucose per liter, 42 mM Na₂HPO₄, 22 mM KH₂PO₄, 19 mM NH₄Cl, and 9 mM NaCl. The following components were sterilized separately and then added (per liter of final medium): 1 ml of 1 M MgSO₄, 1 ml of 0.1 M CaCl₂, and 1 ml of 1-mg thiamine HCl (filter sterilized).

Continuous cultivation was performed at 37°C in aerobic chemostats with a working volume of 1 liter in a 2-liter bioreactor (LH-Inceltech), equipped with pH, dissolved oxygen, and temperature probes. The pH was maintained at a value of 7.00 ± 0.03 by addition of 4 M NaOH, and the fermentation volume was kept constant by a weight-controlled pump. Agitation speed at 600 rpm and a constant airflow of 0.5 liter per min, achieved by a mass flow controller, ensured dissolved oxygen concentrations well above 50%.

For glucose-limited chemostats, a modified M9 medium was used that contained (per liter of deionized water): 3.6 g of glucose, 1.0 g of NH₄Cl, 0.5 g of NaCl, 5.3 g of NaH₂PO₄ · 2H₂O, 3.0 g of KH₂PO₄, 11 mg of CaCl₂, 0.2 g of MgSO₄, 0.1 g of thiamine HCl, 1 ml of polypropylene glycol 2000 as an antifoam agent, and 10 ml of trace element solution containing (per liter) 16.67 g of FeCl₃ · 6H₂O, 0.18 g of ZnSO₄ · 7H₂O, 0.12 g of CuCl₂ · 2H₂O, 0.12 g of MnSO₄ · H₂O, 0.18 g of CoCl₂ · 6H₂O, and 22.25 g of Na₂EDTA · 2H₂O.

For ammonia-limited chemostats, the glucose concentration in the modified M9 medium was increased to 5.5 and 8.5 g/liter for JM101 and PB25, respectively, and the concentration of the sole nitrogen source, NH₄Cl, was reduced to 0.35 g/liter for both strains. All other components were kept at the same concentration as in the glucose-limited experiments. Chemostat media were sterilized by passing through a filter with a pore size of 0.2 μm. PB25 cultures were supplemented with kanamycin and chloramphenicol at final concentrations of 10 mg/liter.

Labeling experiments were initiated after the chemostat cultures appeared to be in steady state, which was defined as stable optical density readings at 600 nm (OD₆₀₀) and stable oxygen and carbon dioxide concentrations in the bioreactor effluent gas for at least two volume changes. Physiological steady states in glucose-limited chemostats were usually achieved within five to six volume changes after initiation of dilution, whereas ammonia-limited cultures required 10 to 14 volume changes to attain a stable steady state. The feed medium with unlabeled glucose was then replaced by an identical medium that contained the same glucose concentration as a mixture of 90% (wt/wt) natural glucose and 10% (wt/wt) [U-¹³C₆]glucose (¹³C, >98%; Isotech). Biomass aliquots for NMR analysis were withdrawn after about one volume change, so that between 55 and 65% of the biomass was fractionally ¹³C labeled.

Analytical procedures.

Cellular dry weight was determined from cell pellets of 10-ml culture aliquots that were centrifuged at 3,000 × g in preweighed glass tubes, washed once with deionized water, and dried at 85°C for 24 h. Prior to weighing, the pellets were cooled under vacuum to room temperature in a desiccator to prevent water adsorption. Organic acids in culture supernatants were first detected by high-pressure liquid chromatography (HPLC) analysis (Perkin Elmer) at a wavelength of 210 nm, using a Supelcogel C8 column (4.6 by 250 mm) and 0.2 N phosphoric acid as the mobile phase at a flow rate of 0.3 ml/min and at room temperature.

Quantitative determination of glucose, ethanol, acetate, formate, succinate, fumarate, pyruvate, and 2-oxoglutarate concentrations was done enzymatically (Synchron CX5CE; Beckman) with reagent kits supplied by the manufacturer or by following standard protocols (4). Concentrations of carbon dioxide and oxygen in the bioreactor feed and effluent gas were determined with a mass spectrometer (Prima 600; Fisons Instruments). To verify the carbon balance of a cultivation, total organic carbon in the supernatants was determined using a commercial kit (Lange). The relative contribution of protein, RNA, and glycogen to the macromolecular biomass composition was determined as described previously (13).

In vitro pyruvate kinase activity was determined in crude cell extracts from 10-ml culture aliquots that were centrifuged at 3,000 × g and 4°C for 15 min. After decanting the supernatant, pellets were stored at −20°C until further analysis. Crude cell extracts were prepared from the resuspended pellets in 5 ml of 0.9% (wt/vol) NaCl in 10 mM MgSO₄ by disruption with a French press (SLM Aminco; SLM Instruments) at 20,000 lb/in². Pyruvate kinase activity was then determined based on the subsequent conversions of phosphoenolpyruvate (PEP) to pyruvate and pyruvate to lactate by an NADH-linked lactate dehydrogenase. The rate of decrease in NADH concentration was followed spectrophotometrically at 340 nm (3).

Determination of physiological parameters.

Dilution rate (D) and thus μ are constant in chemostats; hence, the consumption and production rates were determined from the concentration difference of the various compounds in the feed medium (or air) and the culture (or gas) effluent. The specific consumption rates for glucose (q_glc) and O₂ (q_O2) and production rates for the metabolic by-products and CO₂ (q_CO2) were normalized to the steady-state biomass concentration. The biomass yield on glucose (Y_X/S) was determined as the coefficient of the steady-state biomass versus glucose concentration in the culture broth.

For systematic error analysis, three to six independent samples were analyzed to derive mean values and mean errors. Additionally, an average systematic measurement error of 3% of the mean value was assumed for all analytical methods (23). The Gaussian law of error propagation was used to calculate the 90% confidence intervals for the reported physiological parameters.

NMR spectroscopy and data analysis.

For NMR sample preparation, 300 to 400 ml of culture was harvested and centrifuged at 1,200 × g for 20 min at 4°C. The pellets were washed twice with 20 mM Tris-HCl (pH 7.6) and centrifuged again. Subsequently, the pellets were resuspended in 6 ml of 6 M HCl, sealed into Pyrex glass tubes, and hydrolyzed for 24 h at 105°C. The hydrolysate was filtered through a 0.2-μm-pore-size filter, lyophilized, and redissolved in 700 μl of 20 mM ²HCl in ²H₂O. During this procedure, cysteine and tryptophan were oxidized and asparagine and glutamate were deaminated, which, however, does not reduce the information that can be obtained from biosynthetically directed fractional labeling experiments (48).

Two-dimensional proton-detected heteronuclear single-quantum ¹³C-¹H correlation NMR spectroscopy ([¹³C,¹H]-COSY) was performed as described previously (42, 48). The spectra were recorded at a ¹H resonance frequency of 500 MHz with a Bruker DRX500 spectrophotometer; the sample temperature was 40°C. For each sample, one spectrum was recorded for the aliphatic ¹³C-¹H moieties and one for 2the aromatic ¹³C-¹H groups, with measurement times of 4.5 to 6 h and 2.5 h per spectrum, respectively. The relative abundances of ¹³C-¹³C scalar coupling multiplets in the [¹³C,¹H]-COSY cross peaks were evaluated with the program FCAL (21, 49). One-dimensional ¹H NMR spectra were recorded to determine the overall degree of ¹³C labeling in the amino acids from the ¹³C-¹H satellites of well-resolved signals, which corresponds to P₁ in the probabilistic equations of Szyperski (48).

METAFoR analysis.

Using the program FCAL (21, 49), the relative abundances of intact carbon fragments originating from a single source molecule of glucose (ƒ values) were calculated with probabilistic equations (48) from the relative intensities, I, of the superimposed multiplet fine structures in the individual [¹³C,¹H]-COSY cross peaks. Specifically, these data for the following carbon atom positions in the amino acids were used to derive information on the metabolic origin of their precursors: α-His, β-His, and δ²-His for pentose phosphates; δ^x-Tyr and ε^x-Tyr for erythrose-4-phosphate; α-Ser, β-Ser, and α-Gly for 3-phosphoglycerate; α-Tyr, β-Tyr, α-Phe, and β-Phe for phosphoenolpyruvate; α-Ala, β-Ala, α-Val, γ¹-Val, γ²-Val, β-Leu, δ¹-Leu, δ²-Leu, and γ²-Ile for pyruvate; α-Leu for acetyl-coenzyme A; α-Glu, β-Glu, γ-Glu, α-Pro, β-Pro, γ-Pro, δ-Pro, β-Arg, γ-Arg, and δ-Arg, for oxoglutarate; β-Lys, γ-Lys, δ-Lys, and ε-Lys for oxalacetate/pyruvate (used only for net flux analysis); and α-Asp, β-Asp, α-Met, α-Thr, β-Thr, γ-Thr, α-Ile, δ-Ile, and γ¹-Ile for oxalacetate (48).

Employing the Gaussian law of error propagation, the experimental error was estimated from the analysis of the intensities of redundant ¹³C-scalar coupling multiplets and the signal-to-noise ratio of the [¹³C,¹H]-COSY spectra.

Bioreaction network.

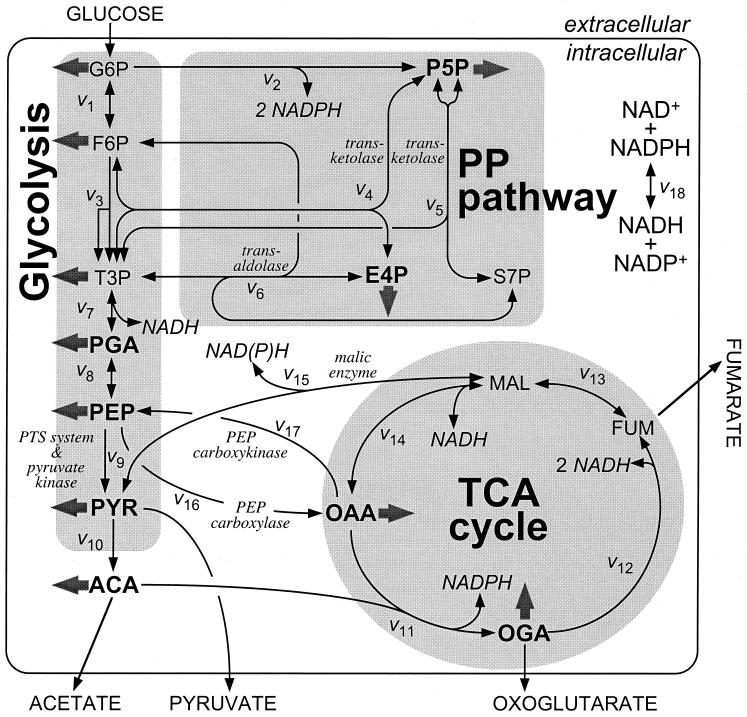
The bioreaction network (Fig. 2) was compiled from textbooks (22, 32) and the EcoCyc database (27). The reactions catalyzed by phosphofructokinase (v₃), pyruvate kinase and phosphotransferase (PTS) system for glucose uptake (v₉), pyruvate dehydrogenase (v₁₀), citrate synthase (v₁₁), 2-oxoglutarate dehydrogenase (v₁₂), PEP carboxylase (v₁₆), and PEP carboxykinase (v₁₇) and the reactions of the oxidative pentose phosphate pathway (v₂) were considered physiologically irreversible on the basis of their thermodynamic properties (32). Based on previous observations with the presently studied system (42), glycine cleavage was assumed to be reversible.

FIG. 2.

Bioreaction network of E. coli central carbon metabolism. Arrows indicate the assumed reaction reversibility or irreversibility. Fluxes to biomass building blocks are indicated by solid arrows. The isotopomer distribution in bold metabolites is directly accessible by [¹³C,¹H]-COSY NMR of amino acids. Abbreviations: G6P, glucose-6-phosphate; F6P, fructose-6-phosphate; P5P, pentose phosphates; PP pathway, pentose phosphate pathway; E4P, erythrose-4-phosphate; S7P, seduheptulose-7-phosphate; T3P, triose-3-phosphate; PGA, 3-phosphoglycerate; ACA, acetyl-coenzyme A; ACE, acetate; OGA, 2-oxoglutarate; PYR. pyruvate; FUM, fumarate; MAL, malate; OAA, oxaloacetate; and PTS system, PEP:carbohydrate phosphotransferase system for glucose uptake.

The conversion of pyruvate to extracellular acetate is usually assumed to occur via pyruvate dehydrogenase (v₁₀), phosphotransacetylase, and acetate kinase (23) but may also be catalyzed in a one-step reaction by pyruvate oxidase (1). This latter reaction may be active in acetate-producing cultures, such as the ammonia-limited chemostats investigated here. Both reaction sequence, however, create the same ¹³C-labeling pattern, so that our present analysis cannot differentiate between the two routes, but the flux results are not affected by the potential presence of pyruvate oxidase.

The malic isoenzymes (v₁₅) in E. coli were reported to be primarily NAD⁺ or NADP⁺ dependent (30). Consistently, in vitro malic enzyme activities in crude cell extracts of our chemostat cultures revealed similar activities with either cofactor (data not shown). Initially, all fluxes were calculated for bioreaction networks containing the NAD⁺-dependent malic enzyme. The influence of potential NADP⁺-dependent malic enzyme operation on the estimated fluxes was elucidated in a separate calculation. The reversible transfer of reducing equivalents from NADPH to NAD⁺ was assumed to occur in an energy-independent fashion via a transhydrogenase (v₁₈). This reaction is probably catalyzed by UdhA (5), since overexpression of UdhA improves the growth rate of E. coli phosphoglucose isomerase mutants that overproduce NADPH from glucose catabolism via the pentose phosphate pathway (7).

In addition to glucose uptake via the PTS system that couples PEP to pyruvate conversion to uptake, an ATP-dependent ABC transport system with high affinity for glucose was reported to be active in E. coli under glucose limitation (18). Unfortunately, it is not possible to distinguish between the carbon fluxes through these two uptake systems by the methodology employed here. To avoid a priori assumptions on their relative contributions that would bias the flux calculations, glucose uptake was modeled as glucose + ATP → glucose-6-phosphate + ADP (1). For all solutions in which the estimated relative PEP to pyruvate flux (v₉) exceeds 100%, this equation is equivalent to the explicit formulation of the PTS reaction. This equation, however, allows solutions with a PEP to pyruvate flux below 100%, which would then indicate that glucose uptake does not occur exclusively via PTS.

Calculation of metabolic net fluxes.

The optimal carbon flux distribution in the bioreaction network was calculated as a best fit to all available physiological data, the macromolecular biomass composition, and the relative abundances of the ¹³C-¹³C scalar coupling multiplets of the aforementioned 45 amino acid carbon positions in the [¹³C,¹H]-COSY spectra. This was done with a previously described comprehensive isotopomer model of bacterial central carbon and amino acid metabolism (12).

Initially, isotopomer balances of all metabolites that are represented in the model are calculated from a randomly chosen flux distribution (Fig. 1). Relative NMR multiplet intensities are then simulated from this isotopomer distribution and compared to the experimentally determined signals. The quality of the fit is judged by the χ² (error) value. Through an iterative process of flux estimation and signal fitting, a flux solution is sought that corresponds to the minimal χ² criterion. This optimal solution represents the maximum-likelihood flux distribution in the investigated metabolic system for a given set of physiological and NMR data. To identify the global error minimum by this iterative procedure, a range-restricted evolutionary algorithm was used (2). The final solution was obtained by restarting a modified direction-set search algorithm according to Powell’s quadratic convergent method at the optimal flux solution identified by the global search evolutionary algorithm (38).

All experimental errors were quantitatively considered in the calculation by allowing extracellular fluxes of the optimal solution to vary within the experimentally determined confidence region. For NMR error treatment, we used a previously described model that assumes a proportional and a constant component, which reflect signal separation quality and integration accuracy as well as background noise, respectively (12). Finally, statistical quality of flux estimates was evaluated using a linear approximation of the model around the optimum flux solution (12, 56).

For a comprehensive description of ¹³C-labeling experiments for metabolic research we refer to recent reviews (47, 54). Briefly, ¹³C-labeling-based studies of metabolic fluxes depend on the following key assumptions (51, 55): (i) the various ¹³C isotope isomers of the metabolic intermediates are in an isotopomeric steady state; (ii) ¹³C isotope effects on biochemical reaction rates are insignificant, i.e., enzymes do not discriminate between ¹³C-labeled and unlabeled metabolites; (iii) metabolite channeling or compartmentation is not relevant unless it is specifically included in the model; (iv) complete biochemical knowledge of the fate of each carbon atom in the model is known or can be inferred from the obtained ¹³C-labeling data; and (v) the stoichiometry of all biochemical reactions is known.

Previous ¹³C-labeling experiments in our laboratories and by others have amply demonstrated that the assumptions i, ii, and iii are valid for prokaryotic cells. Specifically, there is presently no evidence for a biased distribution of ¹³C label into amino acids, which would result if assumptions i or ii were not valid. With the exception of an unusually large intracellular glutamate pool in Corynebacterium glutamicum (54), typical metabolite pool sizes are 0.2 to 10 mM in bacteria (6, 19), so that isotopomeric steady states are usually achieved within minutes (12, 53) while labeling experiments last hours. Assumptions iv and v are reasonable for E. coli, and our ¹³C-labeling data from METAFoR analysis confirm the textbook knowledge on the biochemical reaction network.

Independently, the isotopomer model employed can be used to statistically verify or reject an assumed metabolic network (12). Moreover, the calculated χ² values allow us to evaluate the quality of a flux fit to the data and the correctness of the assumed network (this is similar to R² values in linear regression analysis). In other words, high χ² values indicate inconsistent data, missing reactions, or an unsuitable error model.

A potential mathematical-computational complication is the fact that flux solutions obtained by a fitting algorithm cannot be proven to be unique. In this work, we increased the confidence in the uniqueness of the presented solutions by repeating the iterative flux estimation procedure from different random starting points. Moreover, METAFoR analysis is completely unbiased by this problem and thus serves as an independent verification of the estimated net fluxes. The most important and sometimes underestimated problem of metabolic flux analysis is whether or not a particular flux is actually determined by the available data (29, 54). This identifiability problem is a strong function of the particular labeling experiment performed, e.g., [1-¹³C]- versus [U-¹³C₆]glucose, but also of the metabolic system investigated, the actual distribution of fluxes within this system, and the available data (12, 29). To this end, we have critically evaluated all flux estimates presented and identified those fluxes that are not accurately determined by the presently available data.

RESULTS

Physiology of E. coli JM101 and PB25 in chemostat culture.

To investigate quantitative physiological effects of pyruvate kinase knockout, we grew E. coli JM101 and its pyruvate kinase-deficient derivative PB25 (35) in aerobic chemostats under glucose or ammonia limitation (Table 1), which represent bioenergetically very different regimens with profound effects on cellular physiology (31, 42).

TABLE 1.

Aerobic growth parameters of glucose (C)- and ammonia (N)-limited chemostat cultures of E. coli JM101 and PB25^a

E. coli strain and chemostat conditions (D, h−1)	YX/S (g g−1)	qglucose (mmol g−1 h−1)	qO2 (mmol g−1 h−1)	qCO2 (mmol g−1 h−1)	qacetate (mmol g−1 h−1)	q2-oxoglutarate (mmol g−1 h −1)	qpyruvate (mmol g−1 h−1)	qfumarate (mmol g−1 h−1)	C balance (%)
JM101
C-limited (0.09)	0.37 ± 0.03	1.4 ± 0.2	4.6 ± 0.7	4.9 ± 0.5	0	0	0	0	99 ± 9
C-limited (0.40)	0.46 ± 0.03	4.8 ± 0.4	11.8 ± 1.4	12.4 ± 1.1	0	0	0	0	94 ± 7
N-limitedb (0.09)	0.22 ± 0.02	2.2 ± 0.3	5.1 ± 0.9	5.2 ± 0.4	1.3 ± 0.1	0	0.1 ± 0	0	93 ± 7
PB25
C-limited (0.08)	0.33 ± 0.02	1.4 ± 0.1	5.5 ± 0.9	5.6 ± 0.5	0	0	0	0	104 ± 8
C-limited (0.40)	0.44 ± 0.03	5.0 ± 0.4	12.8 ± 1.6	13.7 ± 1.3	0	0	0	0	95 ± 7
N-limitedc (0.08)	0.17 ± 0.01	2.7 ± 0.3	7.0 ± 1.5	6.3 ± 0.7	1.2 ± 0.1	0.2 ± 0	0	0.1 ± 0	96 ± 8

^aFormate, succinate, and ethanol concentrations were below detection level in all experiments.

^bResidual glucose concentration of 4.07 g/liter.

^cResidual glucose concentration of 1.60 g/liter.

Under glucose-limited conditions, both strains converted glucose quantitatively to biomass and CO₂, without any by-product formation. While both strains exhibited very similar growth characteristics, the biomass yield on glucose appeared to be slightly lower in PB25. Comparing ammonia- and glucose-limited cultures, a significant increase in the specific glucose uptake rate and a drastically reduced biomass yield were found for both strains at comparable dilution rates. Under ammonia-limited conditions, PB25 exhibited higher glucose uptake and CO₂ production rates than its parent JM101. These changes amount to a significantly reduced biomass yield of PB25 on glucose compared to JM101. While the major metabolic by-product in both strains was acetate, PB25 also produced the somewhat unusual by-products 2-oxoglutarate and fumarate.

To obtain accurate information on the specific precursor requirements for subsequent flux analysis, it was important to know the macromolecular biomass composition, which is known to change with environmental conditions and growth rate. For this purpose, we 2determined the relative fraction of the major biomass components of E. coli: protein, RNA, and glycogen (Table 2). As expected, the content of RNA increased with the growth rate and the content of the reserve carbohydrate glycogen was significantly increased under ammonia limitation. The remaining fraction of biomass was assigned to undetermined, minor macromolecules such as DNA, lipids, or peptidoglycan, based on the stoichiometric principles outlined elsewhere (13, 41).

TABLE 2.

Protein, RNA, and glycogen content of glucose (C)- and ammonia (N)-limited chemostat cultures of E. coli JM101 and PB25

E. coli strain and chemostat conditions (D, h−1)	% of total
	Protein	RNA	Glycogen
JM101
C-limited (0.09)	69.8 ± 6.8	7.2 ± 0.5	1.2 ± 0.1
C-limited (0.40)	61.7 ± 7.0	15.4 ± 1.0	2.9 ± 0.3
N-limited (0.09)	60.2 ± 5.9	11.3 ± 0.8	10.2 ± 0.9
PB25
C-limited (0.08)	56.8 ± 4.8	9.6 ± 0.8	2.5 ± 0.3
C-limited (0.40)	53.8 ± 5.1	13.5 ± 1.3	1.1 ± 0.1
N-limited (0.08)	52.2 ± 4.4	10.5 ± 0.9	4.2 ± 0.5

Network analysis by METAFoR analysis.

The relative abundances of ¹³C-¹³C scalar coupling multiplets in the [¹³C,¹H]-COSY spectra of hydrolyzed biomass aliquots from the labeling experiments (Fig. 3) were first interpreted using METAFoR analysis (Table 3) (48). This method provides relative information on the origin of key metabolites in central metabolism from different precursor molecules (Fig. 1). These results allow us to infer the network of active reactions and in some cases they allow us to conclude directly on actual ratios of carbon fluxes (48), as will be shown later. In most cases, however, the METAFoR results are not be directly comparable to net fluxes or ratios of net fluxes.

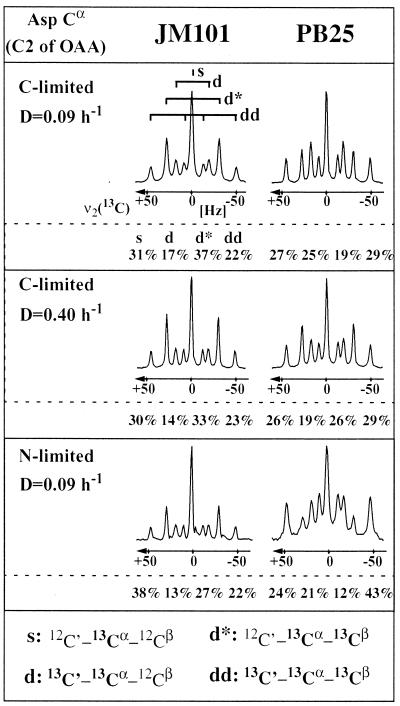
FIG. 3.

¹³C-¹³C scalar coupling multiplets in the cross-sections of C^α in aspartate from [¹³C,¹H]-COSY NMR of amino acids isolated from glucose (C)- or ammonia (N)-limited chemostat cultures of E. coli JM101 and PB25 after biosynthetically directed fractional ¹³C labeling. As indicated in the top left cross-section, the multiplets consist of a singlet (s) representing the ¹²C′–¹³C^α–¹²C^β isotopomer, a doublet (d) originating from ¹²C′–¹³C^α–¹³C^β, a second doublet (d*) for ¹³C′–¹³C^α–¹²C^β, and a doublet of doublets (dd) arising from ¹³C′–¹³C^α–¹³C^β. In each panel, the relative abundances of the different isotopomers are indicated. The relative abundances of the different components reflect the metabolic state of the organism. They are the directly observed parameters used for calculating with probabilistic equations (48) the relative abundances of intact carbon fragments originating from a single source molecule of glucose. Aspartate corresponds directly to its metabolic precursor oxaloacetate (OAA).

TABLE 3.

Origin of metabolic intermediates in glucose (C)- and ammonia (N)-limited chemostat cultures as determined by METAFoR analysis^a

Metabolite	% of total pool in strain and chemostat conditions (D, h−1):
	E. coli JM101			E. coli PB25
	C-limited (0.09)	C-limited (0.40)	N-limited (0.09)	C-limited (0.08)	C-limited (0.40)	N-limited (0.08)
P5P from G6P (lb)	9 ± 2	12 ± 2	0 ± 2	1 ± 2	14 ± 2	1 ± 2
P5P from T3P + C2	91 ± 2	88 ± 2	100 ± 2	99 ± 2	86 ± 2	99 ± 2
P5P from E4P	35 ± 2	21 ± 2	32 ± 2	26 ± 2	22 ± 2	23 ± 2
E4P from F6P (lb)	10 ± 4	26 ± 4	17 ± 4	39 ± 4	23 ± 4	n.d.b
PEP via transketolase (ub)	66 ± 11	31 ± 7	1 ± 7	41 ± 19	37 ± 8	26 ± 20
OAA from PEP	36 ± 2	38 ± 1	38 ± 7	71 ± 2	54 ± 2	85 ± 3
PEP from OAA	16 ± 4	7 ± 4	15 ± 5	38 ± 7	15 ± 2	4 ± 13
PYR from MAL (lb)	5 ± 2	4 ± 2	10 ± 2	25 ± 2	13 ± 2	9 ± 3
PYR from MAL (ub)	7 ± 3	6 ± 3	16 ± 3	85 ± 9	29 ± 4	59 ± 20
ACA from PYR	>98	>98	>95	>95	>98	88 ± 2
OGA from OAA	>95	>94	>93	>96	>95	>99
ICT from SUC + GOX	0 ± 7	0 ± 6	2 ± 7	0 ± 4	0 ± 4	6 ± 4
OAA exchanged to FUM	50 ± 22	69 ± 12	51 ± 12	68 ± 13	73 ± 10	50 ± 7
SER from GLY + C1	42 ± 2	21 ± 2	31 ± 3	41 ± 3	23 ± 2	39 ± 3
GLY from CO2 + C1	1 ± 3	1 ± 3	5 ± 3	0 ± 3	0 ± 3	5 ± 4

^aFor abbreviations, see Fig. 2 legend. lb, lower bound; ub, upper bound; ICT, isocitrate; SUC, succinate; GOX, glyoxylate; SER, serine; GLY, glycine.

^bn.d., not determined.

For example, the METAFoR value of pentose phosphates from glucose-6-phosphate quantifies the lower bound for pentose phosphate molecules that were directly derived from glucose-6-phosphate versus those pentose phosphate molecules that do not contain the intact carbon backbone from a source molecule of glucose and hence were converted at least once by transketolase or transaldolase (Fig. 2). In all cases investigated, this fraction of pentose phosphates from glucose-6-phosphate is well below 20% (Table 3), demonstrating that the majority of pentose phosphate molecules were cut by enzymes of the nonoxidative pentose phosphate pathway. This, however, does not imply that the net flux to pentose phosphates is primarily via the nonoxidative pentose phosphate pathway, because rapid equilibration of the pentose pools in combination with rapid exchange via transketolase and/or transaldolase may lead to the same labeling pattern in pentose phosphate. In fact, we will show in the following that there is a catabolic net flux through the oxidative pentose phosphate pathway in most cases investigated here.

In agreement with previous results (42), this METAFoR analysis provides evidence for the activity of two enzymes that are generally considered to be inactive in E. coli grown on glucose, PEP carboxykinase and malic enzyme (Table 3). These enzymes catalyze the gluconeogenic conversion of oxaloacetate to PEP and the conversion of malate to pyruvate, respectively (Fig. 2). The glyoxylate shunt consisting of isocitrate lyase and malate synthase was found to be inactive, since only a negligibly small fraction of isocitrate molecules (observed in 2-oxoglutarate) carried the characteristic labeling pattern of the reversible cleavage from succinate and glyoxylate, catalyzed by isocitrate lyase (Table 3). For the follow-up studies, the glyoxylate shunt was therefore not included in the bioreaction network. Glycine cleavage was negligible under all conditions, but significant reversibility was seen for the cleavage of serine to glycine and a C1 unit (Table 3).

Comparing both strains under identical conditions, consistently higher fractions of oxaloacetate and pyruvate were found to originate from PEP and malate, respectively, in PB25 (Table 3). This information was obtained from the [¹³C,¹H]-COSY spectra using the probabilistic equations of METAFoR analysis (48). The higher fraction of oxaloacetate originating from PEP can, however, also be qualitatively assessed from direct inspection of the scalar coupling multiplets in [¹³C,¹H]-COSY spectra of α-Asp (Fig. 3), which gives access to a subset of all aspartate isotopomers. Specifically, the abundances of the d and dd components in the multiplets of α-Asp relate to the oxaloacetate molecules (the direct precursor of Asp) that have been generated by carboxylation of PEP and not by a complete turn of the tricarboxylic acid (TCA) cycle (48). The abundance of the d and dd components is always higher in the PB25 cultures than in the JM101 cultures, which illustrates a higher fraction of oxaloacetate isotopomers with ¹³C label in both the α and the β positions, so that a higher fraction of oxaloacetate must originate from carboxylation of PEP via the anaplerotic reaction in PB25. These results indicate that the fluxes from PEP to oxaloacetate and malate to 2pyruvate via PEP carboxylase and malic enzyme compensate to some extent for the pyruvate kinase knockout, as was described earlier (42).

Ammonia limitation induced the following, expected metabolic response in wild-type E. coli (42): (i) increase in pyruvate molecules originating from malate, indicating increased in vivo activity of the malic enzyme; (ii) reduction of PEP molecules derived from transketolase and almost exclusive origin of the pentose phosphate pool from triose-3-phosphate and a C2 unit, suggesting low oxidative pentose phosphate pathway activity (Table 3). Both the physiological and the METAFoR data were highly reproducible, as was evidenced by the fact that values for duplicates of the glucose-limited chemostat experiments at the lower dilution rate were identical within the reported confidence intervals (data not shown).

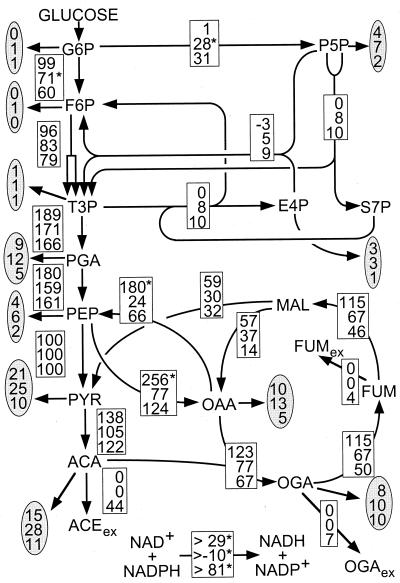
Estimation of metabolic net fluxes in E. coli JM101.

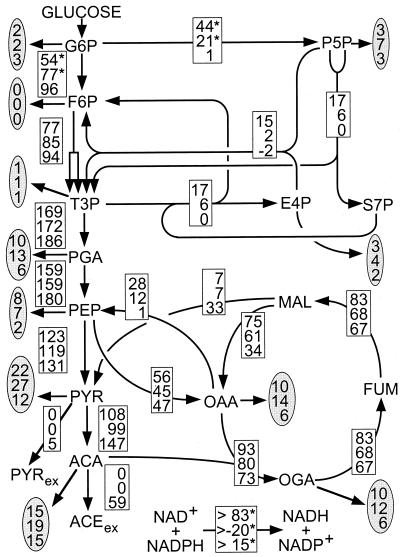
To obtain higher resolution on the intracellular fluxes, the relative abundances of ¹³C-¹³C scalar coupling multiplets (data not shown) and the physiological data (Table 1) were combined in a comprehensive isotopomer model of E. coli central metabolism for net flux analysis (Fig. 1). Different growth rates had little influence on the overall flux distribution under glucose limitation (top two values in Fig. 4). The only differences were reduced fluxes through the TCA cycle (v_11–14) and the gluconeogenic PEP carboxykinase from oxaloacetate to PEP at the higher growth rate.

FIG. 4.

Metabolic flux distribution in chemostat cultures of E. coli JM101. The chemostats were operated under glucose limitation at a D of 0.09 (top entry in the boxes) and 0.40 h⁻¹ (middle) or under ammonia limitation at a D of 0.09 h⁻¹ (bottom). Flux values are relative to the specific glucose uptake rate and represent the mean of five to eight independent flux calculations that were initiated from random starting points. The maximum deviation among these independent calculations was 6, 8, and 3% of the specific glucose uptake rate for the top, middle, and bottom flux estimates given in the boxes, respectively. The only exceptions are fluxes marked by an asterisk, where the maximum deviation was 20% for the fluxes that branch off glucose-6-phosphate in the glucose-limited cases and less than 40% in the transhydrogenase fluxes. The χ² values (representing the quality of the fit) of the top, middle, and bottom flux estimates were 67, 46, and 160, respectively. Arrows indicate the direction of the estimated fluxes. Extracellular metabolites are denoted by the subscript ex, and fluxes into biomass are given in the shaded ovals. For abbreviations, see the legend to Fig. 2.

Changing the limiting nutrient from glucose to ammonia, however, dramatically altered the flux distribution. Most strikingly, glucose is catabolized entirely via glycolysis (v₁) under ammonia limitation, while the oxidative pentose phosphate pathway (v₂) was reduced to an extremely low level (bottom values in the boxes of Fig. 4), as has also been described for Bacillus subtilis (14). In fact, the biosynthetic requirement for erythrose-4-phosphate was met by fluxes through the nonoxidative branch of the pentose phosphate pathway, as indicated by the negative value in v₄ under this condition. This result is consistent with the METAFoR analysis, which showed that pentose phosphate originates exclusively from the nonoxidative pentose phosphate pathway and that very little, if any, PEP is derived through transketolase. Moreover, the flux from malate to pyruvate via malic enzyme was significantly increased, so that a major portion of the secreted acetate actually originates from the TCA cycle. In contrast, the flux from oxaloacetate to PEP via the PEP carboxykinase was reduced.

The flux estimates in Fig. 4 are mean values from five to eight independent flux calculations with each data set, which were initiated from different starting points. Generally, the independently calculated flux solutions were very similar, deviating between 2 and maximally 8%. This indicates that global error minima were indeed identified in the fitting procedure with χ² values (see legend to Fig. 4) in the range of those typically found in bacterial systems (12, 14). These low χ² values prove that the estimated fluxes fit well to the experimentally determined data. As a consequence of the particular labeling experiments performed here, the fluxes that branch off glucose-6-phosphate and the transhydrogenase are less well determined, as was previously described for experiments with uniformly labeled glucose (12, 29).

An important aspect of the interpretation of flux estimates is the extent to which the available data actually determine a given intracellular flux. To further investigate this question, we calculated the confidence regions of our flux estimates with a linearized model (12, 56). Applying such a statistical error model to each of the five to eight aforementioned individual flux solutions, we obtained 68% confidence intervals that were very similar to the maximum deviations within the individual flux solutions, i.e., about 5% (data not shown). One exception were the fluxes that interconnect PEP, pyruvate, malate, and oxaloacetate, for which the 68% confidence region was about ±10%.

Consistent with deviations in the individual solutions, this statistical analysis revealed that fluxes through the oxidative pentose phosphate pathway and the transhydrogenase are the least well determined. For the two glucose-limited chemostat cultures, the 68% confidence region of the oxidative pentose phosphate pathway flux is 20 to 65% and 0 to 50% of the glucose uptake rate for low and high D, respectively. For the ammonia-limited chemostat culture, the confidence interval of the oxidative pentose phosphate pathway is significantly lower (data not shown), so that in this particular case the pentose phosphate pathway flux is well determined.

Bidirectional reaction steps and their impact on the labeling state of the system are included in the flux model, but the estimated exchange fluxes provide only qualitative information in most cases (Table 4). For example, the exchange fluxes between fumarate and malate (v₁₃) and malate and oxaloacetate (v₁₄) were always larger than the glucose uptake flux, while the exchange flux between pentose phosphate + erythrose-4-phosphate and fructose-6-phosphate + triose-3-phosphate (v₄) was always much smaller than that. In many cases, however, particular exchange fluxes must be considered not determined because they were found to vary significantly in independently derived flux solutions, although the net flux estimates in these solutions were very similar.

TABLE 4.

Exchange flux estimates from net flux analysis with glucose (C)- and ammonia (N)-limited chemostat cultures of E. coli JM101 and PB25^a

Reaction	Relative exchange fluxb in strain and chemostat conditions (D, h−1):
	E. coli JM101			E. coli PB25
	C-limited (0.09)	C-limited (0.40)	N-limited (0.09)	C-limited (0.08)	C-limited (0.40)	N-limited (0.08)
G6P to F6P (v1)	n.d.	High	n.d.	n.d.	n.d.	High
P5P + E4P to F6P + T3P (v4)	0	Low	0	Low	Low	0
2 P5P to S7P + T3P (v5)	High	n.d.	n.d.	n.d.	n.d.	n.d.
S7P + T3P to E4P + F6P (v6)	Low	n.d.	n.d.	High	n.d.	n.d.
T3P to PGA (v7)	n.d.	n.d.	n.d.	n.d.	n.d.	Low
PGA to PEP (v8)	n.d.	n.d.	Low	n.d.	n.d.	Low
FUM to MAL (v13)	High	High	High	High	High	High
MAL to OAA (v14)	High	High	High	High	High	High
PGA to SER	Low	Low	0	0	Low	0
SER to GLY + C1 unit	Low	Low	Low	Low	Low	Low

^aFor abbreviations, see Fig. 2 legend and Table 3, footnote ^a.

^bFluxes in the reverse direction that are higher or lower than the glucose uptake rate. n.d., the exchange flux is not determined with the current data set.

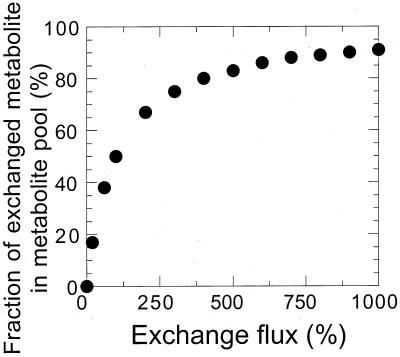
It should be noted that a low exchange flux in Table 4 may very well be compatible with a significant fraction of the corresponding metabolite’s originating from this exchange flux, as obtained by METAFoR analysis (Table 3), e.g., serine from glycine and C1 unit. This is because of the different perspective that the two methods offer —metabolites versus fluxes — and the nonlinear correlation between these values (Fig. 5). Thus, even a very high exchange flux of 1,000% (10-fold the glucose uptake rate) may lead to only 90% metabolites in the substrate pool that originate from the reverse reaction, while even a low exchange flux will lead to a significant number of molecules that originate from the reverse reaction.

FIG. 5.

Simulation of the correlation between exchange flux and metabolite pool composition. For simplicity, a single reversible reaction was simulated in steady state. The metabolite obtained from the exchange reaction exhibits a different ¹³C-labeling pattern than metabolites that were not (yet) converted by this reaction, such as, for example, in carboxylation reactions where unlabeled C from carbon dioxide is introduced.

The flux solutions presented here were obtained with a model that assumed NAD⁺ dependence of the malic enzyme. However, E. coli is expected to operate an NADP⁺-dependent malic enzyme as well (30). While the present methodology cannot distinguish between fluxes through these two isoenzymes, we investigated the impact on the flux estimations. Altering cofactor dependence of the malic enzyme does not influence the overall flux distribution because the carbon fluxes are largely determined by the isotopomer distribution. The only influence is on the flux of reducing equivalents via transhydrogenase, which would, for an entirely NADP⁺-dependent malic enzyme, increase by the estimated malic enzyme flux. Hence, the transhydrogenase flux (v₁₈) that is estimated with our NAD⁺-dependent malic enzyme network represents a lower bound. While the reactions connecting PEP and oxaloacetate were considered irreversible in the presently used model, we cannot exclude that some of the estimated fluxes from PEP to oxaloacetate and vice versa are in fact catalyzed by the reverse reaction of the other enzyme.

Estimation of metabolic net fluxes in pyruvate-deficient E. coli.

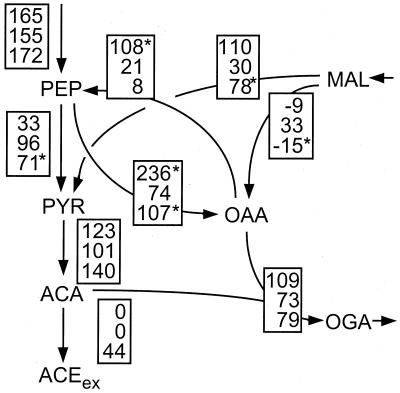
METAFoR analysis provided already qualitative evidence that pyruvate kinase deficiency in E. coli PB25 is counteracted by local flux rerouting via PEP carboxylase and malic enzyme (Table 3) (42). To quantitatively investigate metabolic responses to the knockout, we performed net flux analysis within our isotopomer model by assuming that conversion of PEP to pyruvate occurs exclusively via the PTS system in the mutant.

As expected, fluxes through PEP carboxylase were significantly higher in PB25 than in JM101 under all conditions investigated (Fig. 6). Although higher in glucose-limited PB25, fluxes through malic enzyme were not increased in ammonia-limited PB25, possibly because this flux was already unusually high in the corresponding JM101 culture. At the higher D, fluxes through the pentose phosphate pathway and TCA cycle were remarkably similar in both strains. At the lower D, however, glucose-limited PB25 exhibited lower pentose phosphate pathway and higher TCA cycle fluxes than JM101. Under ammonia limitation, this pattern was reversed.

FIG. 6.

Metabolic flux distribution in chemostat cultures of pyruvate kinase-deficient E. coli PB25, assuming stoichiometric conversion of PEP to pyruvate with glucose uptake via the PTS system. The chemostats were operated under glucose limitation at D values of 0.08 (top entry in the boxes) and 0.40 h⁻¹ (middle) or under ammonia limitation at D = 0.08 h⁻¹ (bottom). Flux values are relative to the specific glucose uptake rate and represent the mean of five to eight independent flux calculations that were initiated from random starting points. The maximum deviation of these independent calculations was 2, 4, and 5% of the specific glucose uptake rate for the top, middle, and bottom flux estimates given in the boxes, respectively. Fluxes marked by asterisks deviated by at most 20%. The χ² values of the top, middle, and bottom flux estimates were 200, 47, and 509, respectively. The arrows indicate the direction of the estimated fluxes. Extracellular metabolites are denoted by the subscript ex, and fluxes into biomass are given in the shaded ovals. For abbreviations, see the legend to Fig. 2.

The flux solution obtained for the ammonia-limited PB25 culture has by far the highest χ² value (509) of all presented solutions. Since we could not identify any inconsistent data (set), this high value indicates either that one or more reactions were not considered in the network or that the error model is not suitable for this particular experiment. Consequently, the corresponding flux estimates are less reliable than the other solutions presented here.

In contrast to the results obtained with JM101, the flux distribution of PB25 changed significantly with the growth rate under glucose limitation (Fig. 6). This is most evident for the reactions connecting PEP, oxaloacetate, and malate, which are much higher for D = 0.08 h⁻¹ than for D = 0.40 h⁻¹. In particular, very high fluxes through PEP carboxykinase were seen (Fig. 6), which constitutes an ATP-dissipating futile cycle in combination with PEP carboxylase.

The relatively high flux estimates for the reactions catalyzed by PEP carboxylase and PEP carboxykinase in glucose-limited PB25 at the low D (top entry in the boxes in Fig. 6) warrant a note of caution. In this particular case, the two reactions are not independent of each other. Thus, these two fluxes could potentially be higher or lower without affecting the net flux from PEP to oxaloacetate of 76%. Direct evidence from METAFoR analysis, however, shows that the anaplerotic PEP carboxylase flux from PEP to oxaloacetate must be very high relative to the malate dehydrogenase flux to oxaloacetate; i.e., 71% oxaloacetate originates from PEP (Table 3). This can also be assessed qualitatively from the relative abundance of ¹³C-¹³C scalar coupling multiplets in [¹³C,¹H]-COSY spectra of α-Asp (Fig. 3).

Consistently, all independent flux calculations resulted in rather similar flux estimates for these two reactions, which indicates that the labeling data contain information that allows differentiating between these two fluxes. Moreover, statistical analysis with the linearized model revealed that the PEP carboxykinase flux is, with 68% confidence, at least 80% in glucose-limited PB25 at the low D (data not shown). More direct evidence for such a high gluconeogenic flux via PEP carboxykinase was again obtained from METAFoR analysis, which revealed an unusually high fraction of 38% of PEP molecules originating from oxaloacetate (Table 3; compare also Fig. 5). This result is independent of the net flux estimates because it was obtained directly from the relative abundance of ¹³C-¹³C scalar coupling multiplets.

The above flux estimates for PB25 were computed with a model that assumed both the absence of pyruvate kinase activity and glucose uptake exclusively via the PTS system. An important question, however, is whether such comprehensive flux analysis can actually identify the absence of an enzyme without explicitly including the knockout in the model. To address this issue, we repeated the flux calculations with the same experimental data on PB25 but without any constraint on the flux between PEP and pyruvate. Thus, in principle, this flux could be higher or lower than the glucose uptake rate, which would indicate residual pyruvate kinase activity or glucose uptake via a non-PTS system, respectively.

The result of this calculation shows that for all experimental conditions, the PEP to pyruvate flux was significantly lower in PB25 (Fig. 7) than in the wild-type strain (Fig. 4). Thus, our method can indeed capture the influence of pyruvate kinase knockout without a priori knowledge. The estimated flux distribution in the glucose-limited culture at D = 0.40 h⁻¹ was remarkably independent of the assumed model (middle entries in the boxes in Fig. 4 and 5), and hence the correct flux distribution was identified without explicitly including the knockout. This was also evidenced by the almost identical χ² value obtained with either model for this particular solution.

FIG. 7.

Metabolic flux distribution at the glycolysis-TCA cycle interface in chemostat cultures of pyruvate kinase-deficient E. coli PB25 calculated without any a priori assumptions on the activities of pyruvate kinase and the PTS system. This analysis was done with the experimental data used in Fig. 6 to elucidate whether our method identifies a reduced flux from PEP to pyruvate without explicitly including the pyruvate kinase knockout in the model. Flux values are relative to the specific glucose uptake rate and represent the mean of five to eight independent flux calculations that were initiated from random starting points. The maximum deviation of these independent calculations was 6, 6, and 2 to 8% of the specific glucose uptake rate for the top, middle, and bottom flux estimates given in the boxes, respectively. Fluxes marked by asterisks deviated by maximally 20%. The χ² values of the top, middle, and bottom flux estimates were 105, 46, and 450, respectively. The arrows indicate the direction of the estimated fluxes. Extracellular metabolites are denoted by the subscript ex. For abbreviations, see the legend to Fig. 2.

In the other two solutions that were obtained with this “less-constrained” model (Fig. 7), however, certain fluxes differed significantly from those that were obtained when pyruvate kinase was omitted from the network (Fig. 6). Many of these differences were not well determined in the less-constrained model (indicated by asterisks in Fig. 7), which was also reflected in the confidence regions computed with the linearized model (data not shown). Hence, the solutions presented in Fig. 6 are more reliable, which is not surprising because the bioreaction network of PB25 was more accurately represented in the computer model used to obtain these solutions. Nevertheless, the local flux rerouting and the high futile PEP carboxykinase flux were consistently identified with the less-constrained model in glucose-limited PB25 at the low D.

In glucose-limited PB25 at D = 0.08 h⁻¹, however, the PEP to pyruvate flux was estimated to be much lower (33%) than the glucose uptake rate when using this less-constrained model (Fig. 7). Since this estimate is relatively well determined, it appears that glucose uptake is not catalyzed exclusively by the PTS system.

DISCUSSION

The primary objective of this work was the quantitative elucidation of metabolic flux responses to pyruvate kinase knockout in E. coli, which does not appear to have any appreciable impact on the growth physiology on glucose. For this purpose, metabolic flux analysis was performed by rigorous accounting of quantitative physiological data and the relative abundance of ¹³C-¹³C coupling fine structure multiples from a [U-¹³C₆]glucose labeling experiment within a comprehensive isotopomer model of E. coli metabolism. The results showed clearly that disruption of both pyruvate kinase isoenzymes is, under all conditions, primarily counteracted by local flux rerouting via the combined reactions of PEP carboxylase and malic enzyme (Fig. 3 to 5). This local flux rerouting acts in concert with the PTS system (38) to provide sufficient pyruvate during growth on glucose. This result is consistent with a METAFoR analysis of the same experiments (Table 3) and those previously published for PB25 during exponential growth in batch culture (43).

We found no evidence for the activation of other potential bypass reactions that are supposedly inactive during growth on glucose, i.e., either the methylglyoxal shunt (from dihydroxyacetone phosphate to pyruvate) (22), the Entner-Doudoroff pathway (33), or the reverse reaction of the PEP synthase (22), although we cannot exclude minor contributions from the methylglyoxal shunt or the Entner-Doudoroff pathway. Such potential minor contributions, could, however, not explain the observed differences in the isotopomer compositions of pyruvate and oxaloacetate and thus would not affect the present conclusions on the local flux rerouting.

At the high D in glucose-limited culture, local flux rerouting was the only metabolic response to pyruvate kinase knockout. At the low D, in contrast, additional, previously unrecognized net flux responses were identified. First, the flux through the oxidative pentose phosphate pathway is relatively high in glucose-limited and low in ammonia-limited wild-type E. coli (Fig. 4), whereas the opposite relations are seen in PB25 (Fig. 6). Thus, it seems that stimulation of glucose catabolism via the pentose phosphate pathway in PB25 occurs only under some conditions, such as ammonia limitation (Fig. 6), or in nongrowing cells (36). Second, the TCA cycle flux response is inversely correlated with pentose phosphate pathway fluxes, i.e., ammonia-limited PB25 exhibits significantly reduced TCA cycle activity and also reduced acetate formation compared to JM101. Contrary to what may be expected, the relative TCA cycle activity in PB25 is even increased at the low D under glucose limitation. This is surprising because PB25 exhibits reduced flux from PEP to pyruvate and hence cannot use the normal route to supply more carbon to the TCA cycle. Instead, additional carbon flux into the TCA cycle is achieved by high fluxes through PEP carboxylase and malic enzyme, which exceed even the wild-type activity of pyruvate kinase under these conditions (Fig. 6). Third, PB25 exhibits extraordinary high fluxes through PEP carboxykinase at the low D. This may lead to ATP dissipation because this enzyme constitutes, in combination with PEP carboxylase, a futile cycle during growth on glucose.

Although futile cycling could be induced by simultaneous overexpression of PEP carboxykinase and PEP carboxylase in E. coli (9), it is generally maintained at a low level (8, 9, 11). In E. coli and B. subtilis, relative PEP carboxykinase fluxes are usually well below 30% of glucose uptake (12, 14, 40, 42). The sole exception is C. glutamicum, for which a PEP carboxykinase flux of about 70% of the specific glucose uptake rate was recently reported in carbon-limited chemostat culture at D = 0.1 h⁻¹ (34). In the glucose-limited PB25 culture at D = 0.08 h⁻¹, this futile cycle activity was in the range of the glucose uptake rate, independent of the assumed network model.

Although the present data do not allow a more accurate determination, the futile PEP carboxykinase flux was statistically verified to be at least 80% of the glucose uptake rate. A significant increase in this futile cycle activity was independently verified by METAFoR analysis, which revealed a high fraction of PEP molecules originating from oxaloacetate (Table 3; Fig. 8). Thus, under severe glucose limitation at the low D, metabolic perturbations resulting from pyruvate kinase knockout led to strongly increased futile cycling via PEP carboxykinase, which may contribute to the somewhat reduced biomass yield under this condition (Table 1).

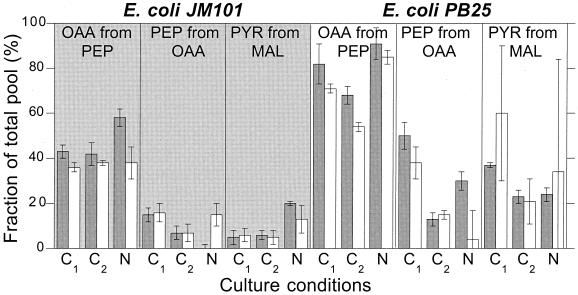
FIG. 8.

Comparison of metabolic flux ratios obtained from METAFoR analysis (white bars) (Table 3) or calculated from the estimated net flux distribution (gray bars) (Fig. 3 and 4) of E. coli JM101 (shaded background) and PB25 (white background). The chemostat culture conditions were glucose limitation at D = 0.09 (C₁) and D = 0.40 h⁻¹ (C₂) and ammonia limitation at D = 0.09 h⁻¹ (N). For abbreviations, see the legend to Fig. 2.

Isotopomer balancing-based net flux analysis does not necessarily depend on a priori knowledge on the genetic modification. In the presently studied pyruvate kinase knockout strain of E. coli, metabolic net flux analysis correctly identified strongly reduced fluxes from PEP to pyruvate in PB25 (Fig. 7) compared to the control experiment (Fig. 4). It remains to be seen, however, whether such comprehensive analysis can in practice support the identification of the most probable active bioreaction network, as was predicted on theoretical grounds (12).

The calculations depicted in Fig. 7 also gave indication of a possible novel regulation mechanism for the flux from PEP to pyruvate. In wild-type E. coli, both pyruvate kinase and the PTS system catalyze this flux, and the data available in the present study do not allow differentiation between these two possible contributions. In the pyruvate kinase-deficient mutant, in contrast, only the PTS system is left, so that the PEP to pyruvate flux estimate is a direct reflection of the upper bound on its contribution to glucose uptake. Thus, in the glucose-limited culture at D = 0.09 h⁻¹, up to 67% of glucose uptake was found to be mediated by another system. This agrees with the observation that a high-affinity glucose transport system, the ATP-dependent Mgl system, is derepressed in E. coli under severe glucose limitation in chemostat culture (18).

Generally the residual glucose concentration increases with D in glucose-limited chemostats (25), so that the glucose concentration was probably sufficient to repress Mgl expression in glucose-limited culture at the high dilution rate as well as in ammonia-limited culture with a residual glucose concentration of 1.6 g/liter. The operation of a second, non-PTS system for glucose uptake under certain conditions is also supported by the recent finding that a PTS knockout mutant does grow, albeit slowly, on glucose as the sole carbon source in batch culture (18a).

Three different approaches were used to verify the reliability of our flux estimates. First, multiple flux estimation runs were initiated from randomly chosen starting points to verify that unique solutions were identified. Second, statistical error analysis was done with a linearized model to calculate confidence regions around the estimates (12, 29, 56). The good agreement between these computational analyses provides strong evidence for the reliability of the flux estimates. In the third approach, we compared, for the first time, the net flux estimates to the independently calculated flux ratios from METAFoR analysis. For three of the METAFoR values, it was possible to calculate the corresponding values directly from the net flux estimates (Fig. 8). These results are generally in very good agreement despite the very different nature of the methods employed. In particular, all metabolic responses to the knockout are consistent, which provides further evidence for the validity of both methods.