Abstract
In this work, we investigate the slow dynamics of 1-butyl-3-methylimidazolium hexafluorophosphate, a very popular room-temperature ionic solvent. Our study predicts the existence of heterogeneity in the liquid and shows that this heterogeneity is the underlying microscopic cause for the recently reported “red-edge effect” (REE) observed in the study of fluorescence of the organic probe 2-amino-7-nitrofluorene. This theoretical work explains in microscopic terms the relation between REE and dynamic heterogeneity in a room-temperature ionic liquid (IL). The REE is typical of micellar or colloidal systems, which are characterized by microscopic environments that are structurally very different. In contrast, in the case of this room-temperature IL, the REE occurs because of the long period during which molecules are trapped in quasistatic local solvent cages. This trapping time, which is longer than the lifetime of the excited-state probe, together with the inability of the surroundings to adiabatically relax, induces a set of site-specific spectroscopic responses. Subensembles of fluorescent molecules associated with particular local environments absorb and emit at different frequencies. We describe in detail the absorption wavelength-dependent emission spectra of 2-amino-7-nitrofluorene and show that this dependence on λex is characteristic of the IL and, as is to be expected, is absent in the case of a normal solvent such as methanol.
Keywords: dynamic heterogeneity, excitation wavelength-dependent fluorescence
Ionic liquids are important to chemists for three reasons. (i) They can dissolve a wide range of polar and nonpolar organic and inorganic molecules. (ii) Although they are liquids at room temperature, their vapor pressures are negligible. (iii) New chemical reactions and industrial processes are being discovered that can only be carried out in these solvents. As opposed to most other organic solvents, these liquids have the potential of being greener reaction media because they are nonvolatile.
The number of different ionic liquids that can be made by choosing particular organic cations and noncoordinating anions is enormous (1). Most of these compounds have yet to be synthesized, and their solvation and selectivity properties for photochemical reactions remain terra incognita.
In this work, we focus our attention on the system 1-butyl-3-methylimidazolium cation ([BMIM+]) hexafluorophosphate anion ([PF–6]) and the fluorescent probe 2-amino-7-nitrofluorene (ANF) (Fig. 1). In what follows, systems displaying non-Gaussian rotational or translational diffusion are termed “dynamically heterogeneous.” Systems in which properties such as solvation energies computed using different initial phase space points but identical thermodynamic conditions (average temperature, volume, and number of particles) do not get solvent averaged on some relevant time scale such as the fluorescence lifetime of the probe or some typical time scale for chemical reactivity are said to have “locally heterogeneous environments.” In other words, the existence of locally heterogeneous environments is a consequence of the loss of ergodicity on some relevant time scale of interest.
Fig. 1.
[BMIM+], [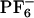 ], and fluorescent probe ANF.
], and fluorescent probe ANF.
Experimental evidence both for non-Gaussian dynamics (2–22) and the existence of locally heterogeneous environments (23, 24) in ionic liquids has recently emerged in the literature. From the limited x-ray crystal structure available, we know that different imidazolium-based solvents tend to crystallize into disordered solids (25), and depending on the cooling rate, one observes crystal polymorphism (26). Experiments show that several of these systems have a tendency toward glassy behavior, and, depending on the length of the alkyl substituents to the imidazolium cation, their properties range from those of normal liquids to glassy or even liquid crystals (27–29). From a time-resolved perspective, Maroncelli and coworkers (10) show that rotational correlation functions, obtained from anisotropy decay data of different organic dyes, fit stretched exponentials. This nonexponential behavior is typical of supercooled liquids and is not normal for conventional solvents. Further evidence of the glassy dynamics of room-temperature ionic liquids arises from the optical heterodyne-detected optical Kerr effect experiments of Fayer and coworkers (30). In their work, they show that the intermediate power law of mode coupling theory spans a duration from 1 ps to several hundred picoseconds or even longer in the case of 1-ethyl-3-methylimidazolium nitrate. In a recent time-resolved study using coumarin 153, Petrich and coworkers (20) found that at least 50% of the solvation response happens within 100 ps, and the rest occurs on a much longer time scale.
We recently predicted that imidazolium-based ionic liquids are not only dynamically heterogeneous but also display locally heterogeneous environments.‡,§ The most compelling experimental evidence supporting this prediction is given by a striking finding by Samanta and coworkers (23, 24). In their study of time-dependent fluorescence of dipolar molecules in imidazolium-based liquids, they observed that ANF exhibits an excitation-wavelength-dependent fluorescence spectrum. This phenomenon, which is called the “red-edge effect” (REE), is characteristic of low-temperature glasses, polymers, and organized assemblies like micelles. As Samanta and coworkers (23) explain in their paper, this phenomenon is commonly due to heterogeneity in space (i.e., multiple solvation environments). It is surprising that little theoretical or computational work has considered the REE, although this phenomenon was first reported 30 years ago in several different systems (31–33).
Computational studies by several groups (34–67) provide molecular-level understanding of the dynamics in ionic liquids (ILs). Berne and coworkers (34) showed that room-temperature dynamics of [BMIM+][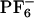 ] is slow and similar to that of supercooled liquids. Kim and coworkers (63, 64) were the first to study the time dependent Stokes shift in [BMIM+][
] is slow and similar to that of supercooled liquids. Kim and coworkers (63, 64) were the first to study the time dependent Stokes shift in [BMIM+][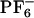 ] as probed by electronically photoexciting a rigid model diatomic solute probe. In their thought-provoking paper (63), they argue that the short time subpicosecond relaxation dynamics after photoexcitation of the solute probe is responsible for ≈50% of the relaxation, and that the remaining relaxation is nonexponential. Voth and coworkers (66, 67) have carried out seminal work on the glassy dynamics and effects of polarizability in 1-ethyl-3-methylimidazolium nitrate. In their simulations at 400 K, they predict that the maximum deviation from Gaussian diffusion for this system occurs at ≈100 ps, but considerable deviation can still be found at 500 ps. We will show that in the case of [BMIM+][
] as probed by electronically photoexciting a rigid model diatomic solute probe. In their thought-provoking paper (63), they argue that the short time subpicosecond relaxation dynamics after photoexcitation of the solute probe is responsible for ≈50% of the relaxation, and that the remaining relaxation is nonexponential. Voth and coworkers (66, 67) have carried out seminal work on the glassy dynamics and effects of polarizability in 1-ethyl-3-methylimidazolium nitrate. In their simulations at 400 K, they predict that the maximum deviation from Gaussian diffusion for this system occurs at ≈100 ps, but considerable deviation can still be found at 500 ps. We will show that in the case of [BMIM+][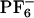 ], the vast majority of particles move slower than expected from normal Gaussian or Fickian diffusion but that there are subsets of particles that move much faster. Our results indicate that these subgroups (slow and fast) appear to be correlated in space. We will demonstrate that relaxation in this solvent is very slow, in contrast to the case of normal liquids where solvent averaging after photoexcitation of a probe molecule is fast. One of the consequences of this lack of relaxation of the solvent upon perturbation is poor energy transfer between solute and solvent, which results in a site-specific response of each particular probe molecule in the liquid and is the microscopic origin for the experimentally observed REE. We also will show that both experiments and our calculations appear to predict the existence of an isoemissive point or region in the absorption wavelength-dependent emission spectra of ANF in similar ILs.
], the vast majority of particles move slower than expected from normal Gaussian or Fickian diffusion but that there are subsets of particles that move much faster. Our results indicate that these subgroups (slow and fast) appear to be correlated in space. We will demonstrate that relaxation in this solvent is very slow, in contrast to the case of normal liquids where solvent averaging after photoexcitation of a probe molecule is fast. One of the consequences of this lack of relaxation of the solvent upon perturbation is poor energy transfer between solute and solvent, which results in a site-specific response of each particular probe molecule in the liquid and is the microscopic origin for the experimentally observed REE. We also will show that both experiments and our calculations appear to predict the existence of an isoemissive point or region in the absorption wavelength-dependent emission spectra of ANF in similar ILs.
Methods
We performed molecular dynamics (MD) simulation for the system [BMIM+][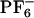 ]. Simulations were carried out by using the software gromacs (68, 69). Potential energy parameters are those previously published by Berne and coworkers (34). Periodic boundary conditions were employed using the particle mesh ewald method to treat long-range electrostatic interactions (34, 45). All systems were initially equilibrated for several hundred picoseconds in the NPT (constant number of particles, pressure, and temperature) ensemble by using the Berendsen method until trending in the volume was no longer observed (69). This equilibration time was sufficient because initial liquid configurations were obtained from previously equilibrated long trajectories from ref. 45. Neat liquid simulations were performed at 300, 400, and 500 K. Production runs in the case of the neat liquid were carried out in the NVE ensemble (constant number of particles, volume, and energy) by using 256 pairs of ions. These NVE runs were 3 ns in duration for the runs at 400 and 500 K and 9 ns in the case of the run at 300 K. To compute the absorption and emission spectra of ANF in the IL, we used an ensemble of 12 MD trajectories. Each of these trajectories consisted of an ANF molecule and 125 pairs of [BMIM+][
]. Simulations were carried out by using the software gromacs (68, 69). Potential energy parameters are those previously published by Berne and coworkers (34). Periodic boundary conditions were employed using the particle mesh ewald method to treat long-range electrostatic interactions (34, 45). All systems were initially equilibrated for several hundred picoseconds in the NPT (constant number of particles, pressure, and temperature) ensemble by using the Berendsen method until trending in the volume was no longer observed (69). This equilibration time was sufficient because initial liquid configurations were obtained from previously equilibrated long trajectories from ref. 45. Neat liquid simulations were performed at 300, 400, and 500 K. Production runs in the case of the neat liquid were carried out in the NVE ensemble (constant number of particles, volume, and energy) by using 256 pairs of ions. These NVE runs were 3 ns in duration for the runs at 400 and 500 K and 9 ns in the case of the run at 300 K. To compute the absorption and emission spectra of ANF in the IL, we used an ensemble of 12 MD trajectories. Each of these trajectories consisted of an ANF molecule and 125 pairs of [BMIM+][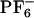 ] solvent ions. To compare the absorption wavelength-dependent emission of ANF in the IL with that in a typical organic solvent, we also studied a system consisting of an ANF solute solvated by 179 methanol solvent molecules. All trajectories involving ANF in its ground or excited electronic state were ≈1.5 ns in duration.
] solvent ions. To compare the absorption wavelength-dependent emission of ANF in the IL with that in a typical organic solvent, we also studied a system consisting of an ANF solute solvated by 179 methanol solvent molecules. All trajectories involving ANF in its ground or excited electronic state were ≈1.5 ns in duration.
The ground-state charge distribution for ANF was obtained from an ab initio calculation at the (HF/6-31G*) theory level using the gaussian program (70). The excited-state charge distribution was estimated by computing the ground (S0) and first singlet excited-state (S1) charge difference using the ZINDO Hamiltonian with configuration interaction (71). These calculations were performed with the software hyperchem 7 (Hypercube, Gainesville, FL). The charge distribution in the excited state used for our MD calculations was obtained by adding the charge difference obtained from the ZINDO calculation to the ground-state charges obtained by the Hartree–Fock method. The calculated ground- and excited-state dipole moments were 7.73 and 18.73 debye, respectively. This methodology has already been successfully applied by Maroncelli and coworkers (72) to study solvatochromism of betaine-30. Lennard–Jones, stretching, bending, and torsional parameters for ANF were taken to be the same in the ground and excited electronic state. This approximation is reasonable given that ANF is a fairly rigid planar molecule. These parameters and those for methanol were adopted from the OPLS-AA force field (73). The S0 to S1 state energy gap ΔE can be expressed as
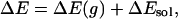 |
[1] |
where ΔE(g) denotes gas-phase or intramolecular energy difference that is independent of the solvent, and ΔEsol is the solvent–solute interaction energy difference arising from the different charge distributions in the ground and excited electronic state. In our MD calculations, ΔE(g) is taken as an arbitrary fixed constant that simply shifts all points in the spectrum by the same amount. The value of this constant is chosen so that the energy scale of our calculations coincides with experimental values. Considering that different trajectories have different contribution to the whole emission spectrum, we have the following formula to calculate the spectra:
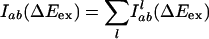 |
[2] |
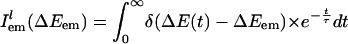 |
[3] |
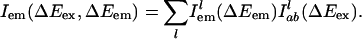 |
[4] |
Here, 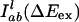 is the probability distribution of absorption energy gaps ΔEex in trajectory l. Iab(ΔEex) denotes the total probability distribution at vertical transition excitation energy ΔEex.
is the probability distribution of absorption energy gaps ΔEex in trajectory l. Iab(ΔEex) denotes the total probability distribution at vertical transition excitation energy ΔEex. 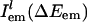 is the probability distribution of emission energy gaps ΔEem weighted by an exponential decay corresponding to the lifetime of the probe [assumed to be 100 ps as in [BMIM+][BF4–] (23)]. Iem(ΔEex, ΔEem) denotes the intensity or joint probability distribution of emission energy ΔEem when excitation energy is ΔEex. No attempt has been made in these classical simulations to take into account Frank–Condon factors or other quantum selection rules. Emission spectra in this work are always reported as area normalized.
is the probability distribution of emission energy gaps ΔEem weighted by an exponential decay corresponding to the lifetime of the probe [assumed to be 100 ps as in [BMIM+][BF4–] (23)]. Iem(ΔEex, ΔEem) denotes the intensity or joint probability distribution of emission energy ΔEem when excitation energy is ΔEex. No attempt has been made in these classical simulations to take into account Frank–Condon factors or other quantum selection rules. Emission spectra in this work are always reported as area normalized.
Results
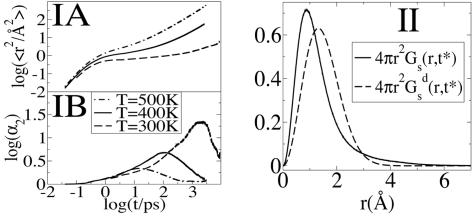
Dynamic Heterogeneity. We have studied the mean square displacement (MSD) of cations and anions as a function of time for three different temperatures. Fig. 2IA shows a logarithmic plot of MSD as a function of time in the case of the center of mass of the cationic ring. Very similar functions are obtained in the case of the anions, indicating that cationic and anionic diffusive rates are highly correlated. At all temperatures investigated, the MSD displays three typical regions: an initial subpicosecond ballistic region, an intermediate cage region, and a long time diffusive region. The subpicosecond ballistic region (slope = 2) is separated from the diffusive region (slope = 1) by a plateau with slope close to zero in which ions are trapped in local cages. The duration of this cage regime varies with temperature. At 500 K this plateau is nearly absent as in a normal liquid, but close to room temperature the plateau region is of the order of nanoseconds as can be appreciated in Fig. 2IA. The fact that the intermediate cage regime is so long compared with most other liquids at room temperature has significant consequences in terms of spectroscopy. This point will be discussed in detail below.
Fig. 2.
MSD, non-Gaussian parameter and the self part of the van Hove correlation function. (IA) MSD vs. time for the center of mass of the cationic ring at 300, 400 and 500 K. (IB) Comparison of the non-Gaussian parameter α2 vs. time for the cations at 300, 400, and 500 K. At 400 K the maximum is at t* = 109 ps, whereas at 300 K it shifts to 2.48 ns. (II) The self part of the van Hove correlation function for the cations and its standard Gaussian form at the time t = t* for the system at 300 K. Because this system is isotropic, we only consider the radial part: 4π r2Gs(r, t*).
To better understand the translational behavior of the IL, we computed the self part of the time-dependent van Hove correlation function (74)
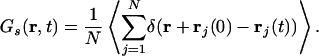 |
[5] |
Here, 4π r2Gs(r, t)dr is the probability of finding at time t an ion in the vicinity dr of points at the distance r given that initially the particle was located at the origin. For typical liquids Gs(r, t) has a Gaussian form given by
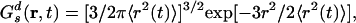 |
[6] |
where 〈r2(t) 〉 is the MSD of the particles. Deviations from Gaussian behavior can be characterized by the non-Gaussian parameter defined as α2(t) = 3 〈r4(t) 〉/5 〈r2(t) 〉2 – 1 (75–79).
Fig. 2IB shows α2 as a function of time in the case of the cations at 300 and 400 K. At 300 K, the non-Gaussian parameter reaches its maximum at time t* = 2.48 ns where the self van Hove correlation function has its maximum deviation from Gaussian behavior. Consistent with the findings of Del Popolo and Voth (67) in a similar IL, we observe that at 400 K the maximum deviation from Gaussian behavior occurs at 109 ps. By using the data at 300 K, we computed the self van Hove correlation function Gs(r, t*) and the standard Gaussian function 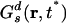 . Fig. 2II clearly shows that Gs(r, t*) and
. Fig. 2II clearly shows that Gs(r, t*) and 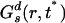 , intersect at a distance of ≈2.9 Å. As we can appreciate, most ions appear to diffuse slower than expected from Gaussian diffusion, but a group of ions exists that diffuse much faster. This point can be seen from the fact that Gs(r, t*) has a much longer tail than the corresponding Gaussian function
, intersect at a distance of ≈2.9 Å. As we can appreciate, most ions appear to diffuse slower than expected from Gaussian diffusion, but a group of ions exists that diffuse much faster. This point can be seen from the fact that Gs(r, t*) has a much longer tail than the corresponding Gaussian function 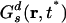 .
.
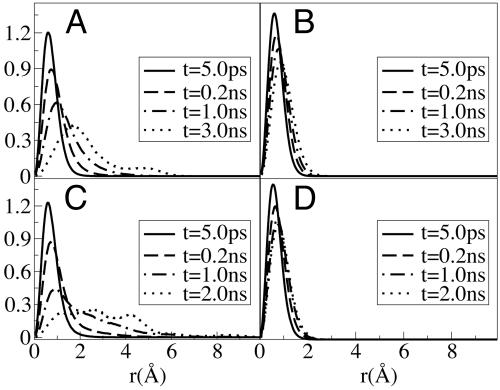
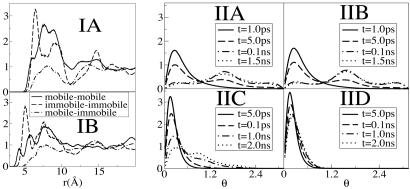
We use the approach previously introduced by Kob and coworkers (78) to define two cationic and anionic subensembles. We computed the displacement of all ions during time windows [t0, t0 + t*] and defined in each case the set of anions and cations with top 10% maximum mobility as cationic and anionic mobile subensembles. Cations and anions in the bottom 10% mobility range are defined as those belonging to the immobile subensembles. By analyzing Gs(r, t) plotted in Fig. 3, we find that anions in the mobile subensemble have in average moved further in 200 ps than those in the immobile subensemble did in 3,000 ps. The same phenomenon can be appreciated in the case of the cations where for the mobile subensemble the van Hove correlation function shows longer tails at 200 ps than in the case of the immobile subensemble at 2,000 ps. Particularly interesting is the appearance of multiple peaks in the van Hove distribution at longer times. These multiple peaks are indicative of hopping processes (80). These hopping processes imply that within the mobile subensemble, some particles move much faster than others. Interestingly these subensembles of “slow” and “fast” diffusing ions appear to be correlated in space. Proof that mobile ions are clustered in space and are far removed from the subset of immobile ions is given by corresponding radial distribution functions displayed in Fig. 4IA and B. We can see from these plots that the diagonal terms gmobile–mobile and gimmobile–immobile have large first peaks, whereas the cross terms gmobile–immobile show a depletion of density at short distances. These results imply that the correlation between either the mobile or immobile particles is much higher than the mobile–immobile cross correlation. Similar correlation was recently observed in the MD simulations of supercooled water and supercooled Lennard–Jones liquids (78–81).
Fig. 3.
The self part of the van Hove correlation function Gs(r, t) for anions (A and B) and cations (C and D) in the mobile ensemble (A and C) and the immobile ensemble (B and D) at four different times. Mobile and immobile subensembles are defined in the text.
Fig. 4.
Radial distribution functions and rotational analog of the self van Hove correlation function. (I) Diagonal (mobile–mobile) (immobile–immobile) and off-diagonal (mobile–immobile) radial distribution functions in the case of the anions (A) and the cations (B). First peaks in the case of the diagonal terms are large, indicating strong spatial correlation and clustering. Off-diagonal terms show density depletion at short distances, consistent with the idea that groups of mobile and immobile particles are separated in space. (II) G(θ, t) in the case of the anions (A and B) and the cations (C and D) in the mobile subensemble (A and C) and in the immobile subensemble (B and D) at different times. The units of θ are in radians.
Rotational diffusion of solute and solvent is important in ILs because in a slow viscous solvent it provides a local mechanism for energy transfer and fast relaxation once a probe molecule has been photoexcited and its charge distribution distorted. To investigate solvent reorientational dynamics, we used an approach previously introduced by Ribeiro (80) in the study of a high temperature molten salt. We define an orientation analog of the self van Hove correlation function, G(θ, t): G(θ, t) = 〈δ[θ – θi(t)] 〉, where θi(t) = cos–1[ui(t)·ui(0)]. To gauge whether translational mobility is decoupled from rotational mobility, we display in Fig. 4II G(θ, t) for those anions and cations belonging to the translationally mobile and translationally immobile subensembles. Fig. 4 IIA and IIB clearly prove that translational mobility is totally decoupled from rotational mobility in the case of the [PF–] anions. In both cases, at 5.0 ps, G(θ, t) has a primary and a secondary peak. The secondary peak corresponding to an angle of ≈90°. This peak becomes more prominent at larger times. This behavior is characteristic of rotational hopping processes that, because of the high degree of symmetry of the anion, leave the ion in an orientational configuration indistinguishable from the original one. As opposed to the anionic case, in the case of the cations we see that rotational and translational mobility are strongly coupled. G(θ, t) at 100 ps in the case of the translationally mobile subensemble of cations is similar to G(θ, t) at 2,000 ps in the case of the corresponding translationally immobile subensemble. For those cations in the mobile subensemble, we find multiple peaks at large distance indicating the existence of reorientational hopping processes consistent with those observed for the same subgroup in our study of translational mobility.
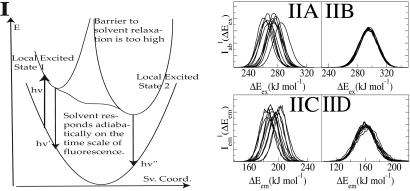
Local Environments and the Absorption Wavelength-Dependent Emission Spectra of ANF. Absorption wavelength-dependent emission of a probe molecule occurs when solvent relaxation is slower than its fluorescence lifetime (33). This type of phenomenon is very atypical for a normal liquid and is commonly found in colloidal gels or micelles. Fig. 5I describes two possible scenarios. In both cases one photoexcites a molecule into local excited state 1. If solvent relaxation is slow compared with fluorescence, then emission occurs from this local environment. If, on the other hand, the solvent behaves adiabatically, meaning that it adjusts to the change in dipole moment of the excited-state probe on a time scale much faster than the fluorescence lifetime, then the emission is from the solvent relaxed local state 2. It is clear that in a solvent that is locally heterogeneous on the time scale of emission one can selectively photoexcite either local excited state 1 or 2 and therefore guide the outcome of a photochemical reaction given that these two do not interchange.
Fig. 5.
Ground and excited-state energy diagram as a function of the solvent reorganization coordinate and absorption/emission spectra of ANF in IL and methanol. (I) Energy diagram showing two possible scenarios. In one case, the response of the solvent is adiabatic, and no REE is observed. In the other case, solvent relaxation is slow, and excited-state local environments do not interconvert. In this case one can observe REE. Sv. coord., solvent coordinate. (II) Overlayed are different curves that correspond to the spectrum of ANF in [BMIM+][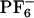 ] computed from each of our 12 MD trajectories; [absorption (IIA) and emission (IIC)] as well as in methanol [absorption (IIB) and emission (IID)]. In the case of the IL we observe site-specific spectra, whereas in methanol all spectra are superimposable. Each of these individual spectra contributes to the total signal (see Eqs. 2 and 3).
] computed from each of our 12 MD trajectories; [absorption (IIA) and emission (IIC)] as well as in methanol [absorption (IIB) and emission (IID)]. In the case of the IL we observe site-specific spectra, whereas in methanol all spectra are superimposable. Each of these individual spectra contributes to the total signal (see Eqs. 2 and 3).
To study this phenomenon from a molecular perspective, we performed MD simulations of ANF in methanol and in [BMIM+][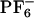 ](see Methods). Each trajectory was first equilibrated in the ground electronic state, and subsequently its corresponding absorption spectrum was computed by making a histogram of the ground- to excited-state energy gaps along simulation. After 800 ps the charge distribution for ANF was changed to that in the first singlet excited electronic state. To compute the emission spectrum arising from each individual trajectory, we performed the same kind of computation, only in this case the dynamics was driven by the excited state potential. Fig. 5II shows absorption and emission spectra of ANF computed in the IL and in methanol. It is clear from these plots that in methanol both in the case of emission and absorption the spectra generated from different trajectories are nearly superimposable. Conversely, in the IL, the different spectra corresponding to different trajectories are widely different. The behavior of each of these trajectories gives rise to a site-specific response and is the cause for the observed REE. In each of these trajectories, ANF is in a different solvent environment that does not adiabatically relax after photoexcitation. By applying Eq. 2, we computed corresponding ensemble-averaged absorption spectra. Fig. 6IA shows the λex-dependent emission spectra of ANF in [BMIM+][
](see Methods). Each trajectory was first equilibrated in the ground electronic state, and subsequently its corresponding absorption spectrum was computed by making a histogram of the ground- to excited-state energy gaps along simulation. After 800 ps the charge distribution for ANF was changed to that in the first singlet excited electronic state. To compute the emission spectrum arising from each individual trajectory, we performed the same kind of computation, only in this case the dynamics was driven by the excited state potential. Fig. 5II shows absorption and emission spectra of ANF computed in the IL and in methanol. It is clear from these plots that in methanol both in the case of emission and absorption the spectra generated from different trajectories are nearly superimposable. Conversely, in the IL, the different spectra corresponding to different trajectories are widely different. The behavior of each of these trajectories gives rise to a site-specific response and is the cause for the observed REE. In each of these trajectories, ANF is in a different solvent environment that does not adiabatically relax after photoexcitation. By applying Eq. 2, we computed corresponding ensemble-averaged absorption spectra. Fig. 6IA shows the λex-dependent emission spectra of ANF in [BMIM+][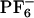 ]. In Fig. 6IB we compare our results with Samanta's experimental data (23) for the maximum in the different emission spectra as a function of excitation wavelength. The slope of
]. In Fig. 6IB we compare our results with Samanta's experimental data (23) for the maximum in the different emission spectra as a function of excitation wavelength. The slope of 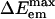 as a function of excitation energy is larger than the one experimentally reported. Nonetheless, these results are in very good agreement with experiments, particularly taking into account that we only included 12 independent trajectories in our ensemble averages. It is clear that solvent dynamics is not adiabatic in the case of the IL. In the experiment, subensembles of ANF molecules characterized by their slowly relaxing local surrounding are responsible for the different emission spectra obtained by changing λex. We also show for comparison results of our simulations of ANF in methanol in which, as expected, no REE is found because solvent relaxation (i.e., averaging) is fast and no locally heterogeneous environments are present. The absence of REE can be appreciated by noticing that the emission frequency is independent from the absorption frequency.
as a function of excitation energy is larger than the one experimentally reported. Nonetheless, these results are in very good agreement with experiments, particularly taking into account that we only included 12 independent trajectories in our ensemble averages. It is clear that solvent dynamics is not adiabatic in the case of the IL. In the experiment, subensembles of ANF molecules characterized by their slowly relaxing local surrounding are responsible for the different emission spectra obtained by changing λex. We also show for comparison results of our simulations of ANF in methanol in which, as expected, no REE is found because solvent relaxation (i.e., averaging) is fast and no locally heterogeneous environments are present. The absence of REE can be appreciated by noticing that the emission frequency is independent from the absorption frequency.
Fig. 6.
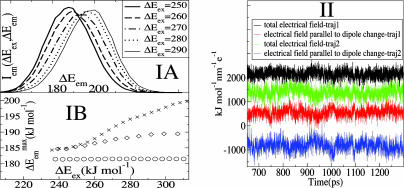
Fluorescence spectra of ANF and analysis of the electric field behavior along different trajectories. (IA) Fluorescence spectra of ANF as a function of excitation energy at room temperature in [BMIM+][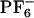 ] (see Eq. 4). (IB)
] (see Eq. 4). (IB) 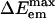 vs. ΔEex both for ANF in [BMIM+][
vs. ΔEex both for ANF in [BMIM+][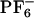 ](×), in methanol (○) and experimental data in [BMIM+][
](×), in methanol (○) and experimental data in [BMIM+][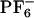 ] ⋄). As explained in the text, to display all maxima on the same energy scale as in the experiment, the same constant corresponding to ΔEgas has been added to all points computed in the IL. An arbitrary constant has also been added to all maxima in methanol. We clearly see from this graph that whereas there is a λex dependence in the fluorescence spectra of ANF in the IL, as is to be expected, this effect is absent in methanol. (II) Absolute value of the electric field due to the solvent at the location of one of the carbon atoms close to the center of mass of ANF and the projection of this electric field onto the direction of the ground to excited state dipole moment change
] ⋄). As explained in the text, to display all maxima on the same energy scale as in the experiment, the same constant corresponding to ΔEgas has been added to all points computed in the IL. An arbitrary constant has also been added to all maxima in methanol. We clearly see from this graph that whereas there is a λex dependence in the fluorescence spectra of ANF in the IL, as is to be expected, this effect is absent in methanol. (II) Absolute value of the electric field due to the solvent at the location of one of the carbon atoms close to the center of mass of ANF and the projection of this electric field onto the direction of the ground to excited state dipole moment change 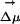 as a function of time for two different trajectories. As can be appreciated the projection of the electric field onto
as a function of time for two different trajectories. As can be appreciated the projection of the electric field onto 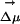 is different in each trajectory but nearly constant with respect to time. This phenomenon of constancy with respect to time and variation with respect to space is the cause for the experimentally observed REE.
is different in each trajectory but nearly constant with respect to time. This phenomenon of constancy with respect to time and variation with respect to space is the cause for the experimentally observed REE.
An interesting feature in Fig. 6IA that can also be observed in Samanta's data are the apparent presence of an isoemissive point or region in the absorption wavelength-dependent emission spectra of ANF in a similar IL. In our calculations, all area normalized spectra cross at an approximate ΔEem = 193 kJ/mol. One isoemissive point can be characteristic of the presence of two species in solution. In our case these species could potentially correspond to ANF in two characteristic solvent environments with different polarity. Is the experimentally observed REE due to local environments with different polarity? Is there a connection between the local heterogeneity that induce REE and the fact that this IL is dynamically heterogeneous?
Discussion: Relation Between REE and Dynamic Heterogeneity
In previous sections, we have demonstrated that ([BMIM+][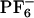 ]) shows non-Gaussian diffusion patterns with subensembles of ions that can be distinguished by their mobility. We also have demonstrated that the experimentally observed REE in the case of ANF can be accounted for by analyzing an ensemble of independent MD trajectories. A very important issue yet remains unanswered. What characterizes these local environments that do not relax on the time scale of emission? Are we in the presence of a liquid with polar and apolar local domains?
]) shows non-Gaussian diffusion patterns with subensembles of ions that can be distinguished by their mobility. We also have demonstrated that the experimentally observed REE in the case of ANF can be accounted for by analyzing an ensemble of independent MD trajectories. A very important issue yet remains unanswered. What characterizes these local environments that do not relax on the time scale of emission? Are we in the presence of a liquid with polar and apolar local domains?
Fig. 6II sheds light on this question. For the sake of clarity, we may assume that our molecular probe ANF is characterized by a dipole moment 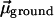 in the ground electronic state and
in the ground electronic state and 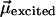 in the excited electronic state. The dipole moment change in going from ground to excited state is
in the excited electronic state. The dipole moment change in going from ground to excited state is  . Fig. 6II shows the magnitude and projection of the electric field only due to the solvent onto
. Fig. 6II shows the magnitude and projection of the electric field only due to the solvent onto 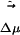 . This projection is taken at the location of one of the carbon atoms, which is approximately at the center of mass of ANF. It is clear from Fig. 6II that neither the absolute value of the electric field nor its projection along
. This projection is taken at the location of one of the carbon atoms, which is approximately at the center of mass of ANF. It is clear from Fig. 6II that neither the absolute value of the electric field nor its projection along 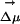 significantly varies throughout each of the two simulations. In fact, this behavior is very characteristic of all our MD runs. If we compare different trajectories, the absolute value of the electric field significantly varies from one to the other, but it remains fairly constant as a function of time in each particular run. The same thing can be said about its projection onto
significantly varies throughout each of the two simulations. In fact, this behavior is very characteristic of all our MD runs. If we compare different trajectories, the absolute value of the electric field significantly varies from one to the other, but it remains fairly constant as a function of time in each particular run. The same thing can be said about its projection onto 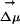 . In our simulations the gap between ground and excited state is solely determined by electrostatics. We find the value of the solute–solvent electrostatic energy to be trajectory-dependent but nearly time-independent, at least on a nanosecond time scale, for each particular run. A similar situation occurs for trajectories driven by the excited-state ANF potential. After an initial transient behavior neither the electric field due to the solvent nor
. In our simulations the gap between ground and excited state is solely determined by electrostatics. We find the value of the solute–solvent electrostatic energy to be trajectory-dependent but nearly time-independent, at least on a nanosecond time scale, for each particular run. A similar situation occurs for trajectories driven by the excited-state ANF potential. After an initial transient behavior neither the electric field due to the solvent nor 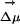 appreciably change. This phenomenon is clearly a property of the slow dynamics of the solvent and is related to the fact that at room temperature the intermediate cage regime spans a duration on the order of nanoseconds as can be appreciated in Fig. 2. We conclude that the existence of locally heterogeneous environments responsible for the REE is mainly due to the fact that the typical lifetime for fluorescence in ANF is shorter than the time on which this probe is trapped inside quasistatic solvent cages. Electric field and
appreciably change. This phenomenon is clearly a property of the slow dynamics of the solvent and is related to the fact that at room temperature the intermediate cage regime spans a duration on the order of nanoseconds as can be appreciated in Fig. 2. We conclude that the existence of locally heterogeneous environments responsible for the REE is mainly due to the fact that the typical lifetime for fluorescence in ANF is shorter than the time on which this probe is trapped inside quasistatic solvent cages. Electric field and 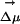 occur at particular relative orientations that are site-specific and that remain relatively constant on this time scale.
occur at particular relative orientations that are site-specific and that remain relatively constant on this time scale.
Conclusions
We have demonstrated that the dynamics of [BMIM+][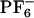 ] is in many ways analogous to that of other glassy or supercooled liquids. This solvent shows non-Gaussian rotational and translational diffusion, and the temporal extent of this nonideality is on the order of nanoseconds at room temperature. There is a strong temperature dependence for this phenomenon. At 500 K, the system behaves nearly like a normal Gaussian fluid, whereas at 300 K, there is a large deviation from Fickian behavior. Subsets of mobile and immobile particles are clustered in space. Mobile and immobile subgroups appear to be far apart. Within the mobile subensemble of cations, van Hove correlation functions show secondary peaks indicating that subgroup of ions exist that display hopping events. Rotationally and translationally mobile subensembles are highly correlated in the case of the cations but totally decoupled in the case of the anions. This behavior is due to the higher symmetry of [
] is in many ways analogous to that of other glassy or supercooled liquids. This solvent shows non-Gaussian rotational and translational diffusion, and the temporal extent of this nonideality is on the order of nanoseconds at room temperature. There is a strong temperature dependence for this phenomenon. At 500 K, the system behaves nearly like a normal Gaussian fluid, whereas at 300 K, there is a large deviation from Fickian behavior. Subsets of mobile and immobile particles are clustered in space. Mobile and immobile subgroups appear to be far apart. Within the mobile subensemble of cations, van Hove correlation functions show secondary peaks indicating that subgroup of ions exist that display hopping events. Rotationally and translationally mobile subensembles are highly correlated in the case of the cations but totally decoupled in the case of the anions. This behavior is due to the higher symmetry of [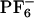 ]. Rotational hopping processes are present both in the case of the cations and the anions.
]. Rotational hopping processes are present both in the case of the cations and the anions.
When ANF is photoexcited in this solvent, the emission spectrum is absorption wavelength-dependent, signifying that excitation of different solute molecules gives rise to site-specific emission responses. The origin of the REE is the existence of persistent excited-state environments that do not get solvent averaged on a time scale relevant to fluorescence. We find that this phenomenon is due to the slow translational and reorientational cage dynamics of the solvent. In our ensemble calculations that accurately reproduce the experimental observations, we find that, on a nanosecond time scale, both the electric field because of the solvent at a particular solute site and the orientation of 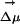 , the difference between dipole moments of the probe in the ground and excited states does not significantly change in time. Conversely, by analyzing different trajectories, we find that the magnitude and direction of the solvent electric field at a given point in the molecule as well as the electrostatic energy of interaction between solute and solvent significantly change. This phenomenon of constancy with respect to time but variation with respect to space is the origin of the experimentally observed REE. In contrast, in the case of micelles and other heterogeneous systems, the phenomenon is due to local domains that are structurally different. In the case of micelles, these domains have typical length scales that can be detected by means of neutron scattering or other techniques, whereas in this particular IL the structural heterogeneity does not appear to have the same origin. In this case the phenomenon is due to the long time scale on which the fluid relaxes upon external perturbation.
, the difference between dipole moments of the probe in the ground and excited states does not significantly change in time. Conversely, by analyzing different trajectories, we find that the magnitude and direction of the solvent electric field at a given point in the molecule as well as the electrostatic energy of interaction between solute and solvent significantly change. This phenomenon of constancy with respect to time but variation with respect to space is the origin of the experimentally observed REE. In contrast, in the case of micelles and other heterogeneous systems, the phenomenon is due to local domains that are structurally different. In the case of micelles, these domains have typical length scales that can be detected by means of neutron scattering or other techniques, whereas in this particular IL the structural heterogeneity does not appear to have the same origin. In this case the phenomenon is due to the long time scale on which the fluid relaxes upon external perturbation.
Acknowledgments
We thank Profs. Cheatum and Geng for instructive discussions. We also thank Prof. Samanta for providing original experimental data plotted in Fig. 6. Finally, we thank the reviewers of our original manuscript for comments and suggestions that made for a much better article. This work was supported by American Chemical Society Grant PRF-G #41450-G6 and University of Iowa Grant MSFP #85022915.
Conflict of interest statement: No conflicts declared.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: [BMIM+], 1-butyl-3-methylimidazolium cation; [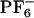 ], hexafluorophosphate anion; ANF, 2-amino-7-nitrofluorene; MD, molecular dynamics; MSD, mean square displacement; REE, red-edge effect; IL, ionic liquid.
], hexafluorophosphate anion; ANF, 2-amino-7-nitrofluorene; MD, molecular dynamics; MSD, mean square displacement; REE, red-edge effect; IL, ionic liquid.
Footnotes
Margulis, C. J. (2005) Abstracts of Papers, 229th ACS National Meeting, San Diego, CA, March 13–17, 2005 (Am. Chem. Soc., Washington, DC), p. PHYS-051 (abstr.).
Margulis, C. J. (2004) Abstracts of Papers, 228th ACS National Meeting, Philadelphia, PA, August 22–26, 2004 (Am. Chem. Soc., Washington, DC), p. PHYS-125 (abstr.).
References
- 1.Forsyth, S. A., Pringle, J. M. & MacFarlane, D. R. (2004) Aust. J. Chem. 57, 113–119. [Google Scholar]
- 2.Arzhantsev, S. & Maroncelli, M. (2005) Appl. Spectrosc. 59, 206–220. [DOI] [PubMed] [Google Scholar]
- 3.Ito, N., Arzhantsev, S., Heitz, M. & Maroncelli, M. (2004) J. Phys. Chem. B 108, 5771–5777. [Google Scholar]
- 4.Ingram, J. A., Moog, R. S., Ito, N., Biswas, R. & Maroncelli, M. (2003) J. Phys. Chem. B 107, 5926–5932. [Google Scholar]
- 5.Antony, J. H., Mertens, D., Dolle, A., Wasserscheid, P. & Carper, W. R. (2003) Chemphyschem 4, 588–594. [DOI] [PubMed] [Google Scholar]
- 6.Ozawa, R., Hayashi, S., Saha, S., Kobayashi, A. & Hamaguchi, H. (2003) Chem. Lett. 32, 948–949. [Google Scholar]
- 7.Chakrabarty, D., Seth, D., Chakraborty, A. & Sarkar, N. (2005) J. Phys. Chem. B 109, 5753–5758. [DOI] [PubMed] [Google Scholar]
- 8.Every, H. A., Bishop, A. G., MacFarlane, D. R., Oradd, G. & Forsyth, M. (2004) Phys. Chem. Chem. Phys. 6, 1758–1765. [Google Scholar]
- 9.Umecky, T., Kanakubo, M. & Ikushima, Y. (2005) Fluid Phase Equilib. 228, 329–333. [Google Scholar]
- 10.Ito, N., Arzhantsev, S. & Maroncelli, M. (2004) Chem. Phys. Lett. 396, 83–91. [Google Scholar]
- 11.Karmakar, R. & Samanta, A. (2002) J. Phys. Chem. A 106, 4447–4452. [Google Scholar]
- 12.Karmakar, R. & Samanta, A. (2002) J. Phys. Chem. A 106, 6670–6675. [Google Scholar]
- 13.Karmakar, R. & Samanta, A. (2003) Chem. Phys. Lett. 376, 638–645. [Google Scholar]
- 14.Saha, S., Mandal, P. K. & Samanta, A. (2004) Phys. Chem. Chem. Phys. 6, 3106–3110. [Google Scholar]
- 15.Carmichael, A. J. & Seddon, K. R. (2000) J. Phys. Org. Chem. 13, 591–595. [Google Scholar]
- 16.Aki, S. N. V. K., Brennecke, J. F. & Samanta, A. (2001) Chem. Comm., 413–414.
- 17.Muldoon, M. J., Gordon, C. M. & Dunkin, I. R. (2001) J. Chem. Soc. Perkin Trans. 2, 433–435. [Google Scholar]
- 18.Wasserscheid, P., Gordon, C. M., Hilgers, C., Muldoon, M. J. & Dunkin, I. R. (2001) Chem. Comm., 1700–1700.
- 19.McLean, A. J., Muldoon, M. J., Gordon, C. M. & Dunkin, I. R. (2002) Chem. Comm., 1880–1881. [DOI] [PubMed]
- 20.Chowdhury, P. K., Halder, M., Sanders, L., Calhoun, T., Anderson, J. L., Armstrong, D. W., Song, X. & Petrich, J. W. (2004) J. Phys. Chem. B 108, 10245–10255. [Google Scholar]
- 21.Gordon, C. M., McLean, A. J., Muldoon, M. J. & Dunkin, I. R. (2002) Am. Chem. Soc. Symp. Ser. 818, 428–443. [Google Scholar]
- 22.Giraud, G., Gordon, C. M., Dunkin, I. R. & Wynne, K. (2003) J. Chem. Phys. 119, 464–477. [Google Scholar]
- 23.Mandal, P., Sarkar, M & Samanta, A. (2004) J. Phys. Chem. A 108, 9048–9053. [Google Scholar]
- 24.Paul, A., Mandal, P. K. & Samanta, A. (2005) J. Phys. Chem. B 109, 9148–9153. [DOI] [PubMed] [Google Scholar]
- 25.Larsen, A. S., Holbrey, J. D., Tham, F. S. & Reed, C. A. (2000) J. Am. Chem. Soc. 122, 7264–7272. [Google Scholar]
- 26.Holbrey, J. D., Reichert, W. M., Nieuwenhuyzen, M., Johnston, S., Seddon, K. R. & Rogers, R. D. (2003) Chem. Comm., 1636–1637.
- 27.Ramos, J. J. M., Afonso, C. A. M. & Branco, L. C. (2003) J. Therm. Anal. Calorim. 71, 659–666. [Google Scholar]
- 28.Wilkes, J. S. (2004) J. Mol. Catal. A Chem. 214, 11–17. [Google Scholar]
- 29.Holbrey, J. D. & Seddon, K. R. (1999) Clean Technol. Environ. Policy 1, 223–236. [Google Scholar]
- 30.Cang, H., Li, J. & Fayer, M. D. (2003) J. Chem. Phys. 119, 13017–13023. [Google Scholar]
- 31.Galley, W. & Purkey, R. (1970) Proc. Natl. Acad. Sci. USA 67, 1116–1121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Weber, G. & Shinitzky, M. (1970) Proc. Natl. Acad. Sci. USA 65, 823–830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Demchenko, A. (2002) Luminescence 17, 19–42. [DOI] [PubMed] [Google Scholar]
- 34.Margulis, C. J., Stern, H. A. & Berne, B. J. (2002) J. Phys. Chem. B 106, 12017–12021. [Google Scholar]
- 35.Hanke, C. G., Price, S. L. & Lynden-Bell, R. M. (2001) Mol. Phys. 99, 801–809. [Google Scholar]
- 36.Rasaiah, J. C. & Lynden-Bell, R. M. (2001) Philos. Trans. R. Soc. London Ser. A 359, 1545–1574. [Google Scholar]
- 37.Hanke, C. G., Atamas, N. A. & Lynden-Bell, R. M. (2002) Green Chem. 4, 107–111. [Google Scholar]
- 38.Hanke, C. G. & Lynden-Bell, R. M. (2003) J. Phys. Chem. B 107, 10873–10878. [Google Scholar]
- 39.Lynden-Bell, R. M. (2003) Mol. Phys. 101, 2625–2633. [Google Scholar]
- 40.Del Popolo, M. G., Lynden-Bell, R. M. & Kohanoff, J. (2005) J. Phys. Chem. B 109, 5895–5902. [DOI] [PubMed] [Google Scholar]
- 41.Lynden-Bell, R. M., Kohanoff, J. & Del Popolo, M. G. (2005) Faraday Discuss. 129, 57–67. [DOI] [PubMed] [Google Scholar]
- 42.Harper, J. B. & Lynden-Bell, R. M. (2004) Mol. Phys. 102, 85–94. [Google Scholar]
- 43.Lynden-Bell, R. M., Atamas, N. A., Vasilyuk, A. & Hanke, C. G. (2002) Mol. Phys. 100, 3225–3229. [Google Scholar]
- 44.Hanke, C. G., Johansson, A., Harper, J. B. & Lynden-Bell, R. M. (2003) Chem. Phys. Lett. 374, 85–90. [Google Scholar]
- 45.Margulis, C. J. (2004) Mol. Phys. 102, 829–838. [Google Scholar]
- 46.Crosthwaite, J. M., Ropel, L. J., Anthony, J. L., Aki, S. N. V. K., Maginn, E. J. & Brennecke, J. F. (2005) Am. Chem. Soc. Symp. Ser. 901, 292–300. [Google Scholar]
- 47.Crosthwaite, J. M., Aki, S. N. V. K., Maginn, E. J. & Brennecke, J. F. (2005) Fluid Phase Equilib. 228, 303–309. [Google Scholar]
- 48.Shah, J. K. & Maginn, E. J. (2005) J. Phys. Chem. B 109, 10395–10405. [DOI] [PubMed] [Google Scholar]
- 49.Anthony, J. L., Anderson, J. L., Maginn, E. J. & Brennecke, J. F. (2005) J. Phys. Chem. B 109, 6366–6374. [DOI] [PubMed] [Google Scholar]
- 50.Shah, J. K. & Maginn, E. J. (2004) Fluid Phase Equilib. 222, 195–203. [Google Scholar]
- 51.Cadena, C., Anthony, J. L., Shah, J. K., Morrow, T. I., Brennecke, J. F. & Maginn, E. J. (2004) J. Am. Chem. Soc. 126, 5300–5308. [DOI] [PubMed] [Google Scholar]
- 52.Crosthwaite, J. M., Aki, S. N. V. K., Maginn, E. J. & Brennecke, J. F. (2004) J. Phys. Chem. B 108, 5113–5119. [DOI] [PubMed] [Google Scholar]
- 53.Eike, D. M., Brennecke, J. F. & Maginn, E. J. (2004) Ind. Eng. Chem. Res. 43, 1039–1048. [Google Scholar]
- 54.Anthony, J. L., Crosthwaite, J. M., Hert, D. G., Aki, S. N. V. K., Maginn, E. J. & Brennecke, J. F. (2003) Am. Chem. Soc. Symp. Ser. 856, 110–120. [Google Scholar]
- 55.Morrow, T. I. & Maginn, E. J. (2003) Am. Chem. Soc. Symp. Ser. 856, 162–173. [Google Scholar]
- 56.Morrow, T. I. & Maginn, E. J. (2003) J. Phys. Chem. B 106, 12807–12813, and correction (2003) 107, 9160. [Google Scholar]
- 57.Anthony, J. L., Maginn, E. J. & Brennecke, J. F. (2002) Ionic Liquids 818, 260–269. [Google Scholar]
- 58.Morrow, T. I. & Maginn, E. J. (2002) J. Phys. Chem. B 106, 12807–12813. [Google Scholar]
- 59.Anthony, J. L., Maginn, E. J. & Brennecke, J. F. (2002) J. Phys. Chem. B 106, 7315–7320. [Google Scholar]
- 60.Shah, J. K., Brennecke, J. F. & Maginn, E. J. (2002) Green Chem. 4, 112–118. [Google Scholar]
- 61.Anthony, J. L., Maginn, E. J. & Brennecke, J. F. (2001) J. Phys. Chem. B 105, 10942–10949. [Google Scholar]
- 62.Brennecke, J. F. & Maginn, E. J. (2001) AlChE J. 47, 2384–2389. [Google Scholar]
- 63.Shim, Y., Duan, J. S., Choi, M. Y. & Kim, H. J. (2003) J. Chem. Phys. 119, 6411–6414. [Google Scholar]
- 64.Shim, Y., Choi, M. Y. & Kim, H. J. (2005) J. Chem. Phys. 122, 044511. [DOI] [PubMed] [Google Scholar]
- 65.Kobrak, M. N. & Znamenskiy, V. (2004) Chem. Phys. Lett. 395, 127–132. [Google Scholar]
- 66.Yan, T. Y., Burnham, C. J., Del Popolo, M. G. & Voth, G. A. (2004) J. Phys. Chem. B 108, 11877–11881. [Google Scholar]
- 67.Del Popolo, M. G. & Voth, G. A. (2004) J. Phys. Chem. B 108, 1744–1752. [Google Scholar]
- 68.Lindahl, E., Hess, B. & van derSpoel, D. (2001) J. Mol. Mod. 7, 306–317. [Google Scholar]
- 69.Berendsen, H. J. C., van derSpoel, D. & vanDrunen, R. (1995) Comp. Phys. Comm. 91, 43–56. [Google Scholar]
- 70.gaussian03 (2003) (Gaussian, Inc., Pittsburgh), Revision A.1.
- 71.Ridley, J. & Zerner, M. (1973) Theor. Chim. Acta 32, 111–134. [Google Scholar]
- 72.Mente, S. R. & Maroncelli, M. (1999) J. Phys. Chem. B 103, 7704–7719. [Google Scholar]
- 73.Jorgensen, W., Maxwell, D. & Tirado-Rives, J. (1996) J. Am. Chem. Soc. 118, 11225–11236. [Google Scholar]
- 74.Hove, V. (1954) Phys. Rev. 95, 249–262. [Google Scholar]
- 75.Rahman, A. (1964) Phys. Rev. 136, A405–A411. [Google Scholar]
- 76.Kob, W. & Andersen, H. (1994) Phys. Rev. Lett. 73, 1376–1379. [DOI] [PubMed] [Google Scholar]
- 77.Kob, W. & Andersen, H. (1995) Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 51, 4626–4641. [DOI] [PubMed] [Google Scholar]
- 78.Kob, W., Donati, C., Plimpton, S., Poole, P. & Glotzer, S. (1997) Phys. Rev. Lett. 79, 2827–2830. [Google Scholar]
- 79.Giovambattista, N., Mazza, M., Buldyrev, S., Starr, F. & Stanley, H. (2004) J. Phys. Chem. B 108, 6655–6661. [Google Scholar]
- 80.Ribeiro, M. (2004) Phys. Chem. Chem. Phys. 6, 771–774. [Google Scholar]
- 81.Donati, C., Douglas, J., Kob, W., Plimpton, S., Poole, P. & Glotzer, S. (1998) Phys. Rev. Lett. 80, 2338–2341. [Google Scholar]