Skip to main content
NCBI home page
The Journal of Physiology logoLink to The Journal of Physiology
. 1974 Jan;236(2):341–361. doi: 10.1113/jphysiol.1974.sp010438

The stochastic properties of spontaneous quantal release of transmitter at the frog neuromuscular junction

Ira Cohen, Hiroshi Kita, William Van Der Kloot
PMCID: PMC1350805  PMID: 16992438

Abstract

1. Earlier results showed that it is unlikely that spontaneous quantal release of transmitter at the frog neuromuscular junction is produced by a Poisson process.

2. Data sets were tested, by using the u statistic, to see whether if they are assumed to be generated by a Poisson process, the mean interval is changing monotonically with time. By this critieria, some of the data sets are stationary, others are not.

3. A variety of mathematical transforms are employed on empirical data sets to characterize the properties of the spontaneous quantal release.

(a) The intensity function, which calculates the frequency distribution of all possible combinations of intervals, shows an excess of short intervals, without any sign of periodicity.

(b) The variance—time curve, which estimates the accumulated variance of the series as a function of time into the series, lies significantly above the Poisson prediction.

(c) The power spectrum, whether calculated on the intervals or on the number of intervals in time bins, deviates significantly from the Poisson prediction at the low frequencies.

(d) The ln-survivor curve has two phases: a concave section for the short intervals, and a roughly linear section for the intervals of greater length.

These transforms indicate that the min.e.p.p.s are clustered.

4. A series of models for spontaneous quantal release were considered.

(a) A Poisson model. Rejected because of consistent failure to fit the data.

(b) A periodic model. Rejected because the intervals should be ordered rather than clustered.

(c) A time-dependent model, in which quantal release is governed by a Poisson process with a mean interval that is oscillating in time. This model will generate clustering; by the transforms the model can be shown to closely fit the data. However, an autocorrelation of min.e.p.p. amplitudes shows that there is a relationship between the amplitudes and their position in the series. This is not predicted by the time-dependent oscillating model.

(d) A branching Poisson model, in which a primary release, generated by a Poisson process, is likely to be followed by one or more subsidiary releases from the same site. The parameters of the branching model can be determined from ln-survivor curves. Theoretical curves, created with these parameters, give power spectra, variance—time curves, and ln-survivor curves that strongly resemble those calculated from the data. The model also predicts a significant autocorrelation of amplitudes.

5. Min.e.p.p.s recorded with an extracellular electrode also fit well to a branching Poisson model.

6. The effects of raised [Ca2+]o on the intervals between min.e.p.p.s were studied. In our experiments the change in extracellular solution did not produce any notable change in release statistics.

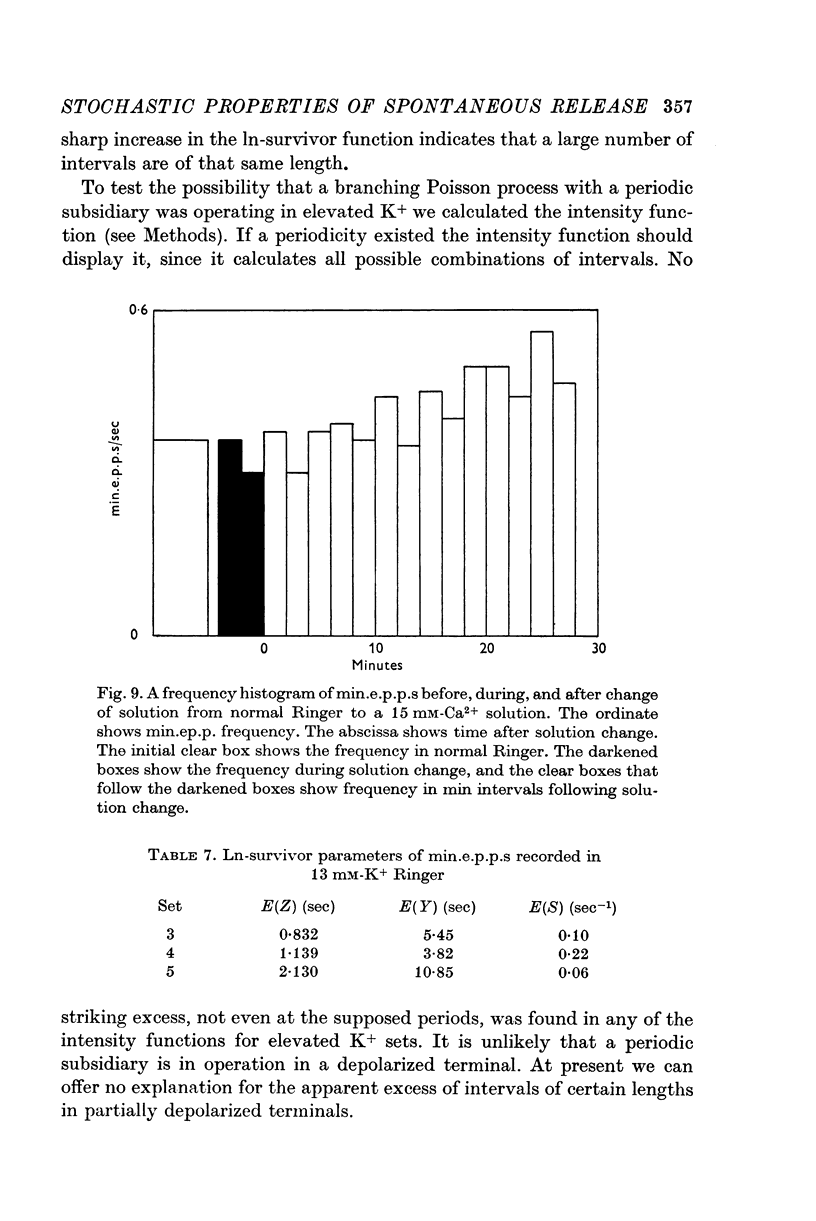
7. The effects of elevated [K+]o on the intervals between spontaneous releases were studied. Depolarization of the nerve terminal increases the frequency of primary releases and decreases the chance of having subsidiary releases.

8. Possible physical mechanisms by which quantal release of transmitter from a nerve terminal would fit a branching Poisson model are described.

Full text

PDF
341

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. BROOKS V. B. An intracellular study of the action of repetitive nerve volleys and of botulinum toxin on miniature end-plate potentials. J Physiol. 1956 Nov 28;134(2):264–277. doi: 10.1113/jphysiol.1956.sp005642. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Birks R. I., Burstyn P. G., Firth D. R. The form of sodium-calcium competition at the frog myoneural junction. J Gen Physiol. 1968 Dec;52(6):887–907. doi: 10.1085/jgp.52.6.887. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Cohen I., Kita H., Van Der Kloot W. The intervals between miniature end-plate potentials in the frog are unlikely to be independently or exponentially distributed. J Physiol. 1974 Jan;236(2):327–339. doi: 10.1113/jphysiol.1974.sp010437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Cohen I., Kita H., Van der Kloot W. Miniature end-plate potentials: evidence that the intervals are not fit by a Poisson distribution. Brain Res. 1973 May 17;54:318–323. doi: 10.1016/0006-8993(73)90054-1. [DOI] [PubMed] [Google Scholar]
  5. DEL CASTILLO J., KATZ B. Statistical factors involved in neuromuscular facilitation and depression. J Physiol. 1954 Jun 28;124(3):574–585. doi: 10.1113/jphysiol.1954.sp005130. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. FATT P., KATZ B. Spontaneous subthreshold activity at motor nerve endings. J Physiol. 1952 May;117(1):109–128. [PMC free article] [PubMed] [Google Scholar]
  7. HUBBARD J. I. REPETITIVE STIMULATION AT THE MAMMALIAN NEUROMUSCULAR JUNCTION, AND THE MOBILIZATION OF TRANSMITTER. J Physiol. 1963 Dec;169:641–662. doi: 10.1113/jphysiol.1963.sp007286. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Hubbard J. I., Jones S. F., Landau E. M. On the mechanism by which calcium and magnesium affect the spontaneous release of transmitter from mammalian motor nerve terminals. J Physiol. 1968 Feb;194(2):355–380. doi: 10.1113/jphysiol.1968.sp008413. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Hubbard J. I., Jones S. F. Spontaneous quantal transmitter release: a statistical analysis and some implications. J Physiol. 1973 Jul;232(1):1–21. doi: 10.1113/jphysiol.1973.sp010254. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Hubbard J. I. Mechanism of transmitter release. Prog Biophys Mol Biol. 1970;21:33–124. [PubMed] [Google Scholar]
  11. Mallart A., Martin A. R. An analysis of facilitation of transmitter release at the neuromuscular junction of the frog. J Physiol. 1967 Dec;193(3):679–694. doi: 10.1113/jphysiol.1967.sp008388. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Rahamimoff R., Yaari Y. Delayed release of transmitter at the frog neuromuscular junction. J Physiol. 1973 Jan;228(1):241–257. doi: 10.1113/jphysiol.1973.sp010084. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Rotshenker S., Rahamimoff R. Neuromuscular synapse: stochastic properties of spontaneous release of transmitter. Science. 1970 Nov 6;170(3958):648–649. doi: 10.1126/science.170.3958.648. [DOI] [PubMed] [Google Scholar]

Articles from The Journal of Physiology are provided here courtesy of The Physiological Society

RESOURCES