Abstract
Mortality patterns and trajectories in closely related populations are likely to be similar in some respects, and differences are unlikely to increase in the long run. It should therefore be possible to improve the mortality forecasts for individual countries by taking into account the patterns in a larger group. Using the Human Mortality Database, we apply the Lee-Carter model to a group of populations, allowing each its own age pattern and level of mortality but imposing shared rates of change by age. Our forecasts also allow divergent patterns to continue for a while before tapering off. We forecast greater longevity gains for the US and lesser ones for Japan relative to separate forecasts.
Background
The populations of the world are becoming more closely linked by communication, transportation, trade, technology, and disease. Wilson (2001) documented a global convergence in mortality levels. Increasingly it seems improper to prepare mortality forecasts for individual national populations in isolation from one another and still more so for the regions within a country. Individual forecasts, even when based on similar extrapolative procedures, are likely to imply increasing divergence in life expectancy in the long run, counter to this expected and observed trend toward convergence. In this article we consider how a particular extrapolative method, originally developed by Lee and Carter (1992), can be modified to forecast mortality for countries by taking into account their membership in a group, rather than individually. We approach the problem in two steps: first, we identify the central tendencies within the group, using what we call a common factor approach; second, we give the historical particularities of each country their due weight in projecting individual-country trends in the short or medium term, while letting them taper off in the long term over which divergence no longer occurs. Thus, in the short term, inter-country mortality differences in trends may be preserved, but ultimately age-specific death rates within the group of countries are constrained to maintain a constant ratio to one another.
In 1992, Lee and Carter developed a method (henceforth the LC method) to forecast mortality. The LC method reduces the role of subjective judgment by extrapolating historical trends and forecasts probability distributions of age-specific death rates (ASDR) using standard time-series procedures, as we briefly indicate next.
Let the death rate of age x at time t be m(x,t), for t =0, 1, 2, …, T and x=0, 1, …, w, and let the average over time of log(m(x,t)) be a(x). The LC method first applies the singular value decomposition (SVD) on {log[m(x,t)]−a(x)} to obtain
| (1) |
The purpose of using SVD is to transform the task of forecasting an age-specific vector log[m(x,t)] into that of forecasting a scalar k(t), with minimized modeling error . The second stage of the LC method is to adjust k(t) to fit the reported life expectancy at time t, ignoring the resulting small increase in fitting errors. This second stage makes the model fit historical life expectancy exactly (see also Booth, Tickle and Smith 2004). (The original LC method fits the observed total number of deaths in the second stage, but fitting life expectancy is simpler and works just as well. Some analysts prefer to skip the second stage and forecast the original k(t) directly.) The adjusted k(t) is then modeled using standard time-series methods. In most applications to date, a random walk with drift (RWD) fits well, although it is not always the best model overall. Unless some other time-series model is found to be substantially better, it is advisable to use RWD because of its simplicity and straightforward interpretation. The RWD is expressed as follows:
| (2) |
where d is the drift term and σ is the standard deviation of random changes in k(t). After d and σ are estimated in (2), k(t) at t>T is forecast stochastically and then used to forecast ASDRs through (1). Tests were performed for the US in which forecasts that were based on data before certain dates were compared to corresponding observations after those dates (Lee and Miller 2001). The resulting forecasts underestimated out-of-sample mortality decline, but by substantially less than had official projections. The probability intervals were reasonably accurate. The 95% probability intervals covered 97% of the subsequently observed life expectancies.
The ordinary LC method works well for a single population, which could be either one sex or two sexes combined. How to use the LC method to forecast mortality for the two sexes of a population, however, has been a problem. Dealing with two sexes separately, the b(x) for males in (1) and d in (2) would be different from those of females, and thus forecasts of male mortality would differ increasingly from forecasts for female mortality over time, diverging in a way that has not been observed in history. Carter and Lee (1992) suggested using the same k(t) for both sexes, but the sex-specific b(x)s still lead to divergent forecasting. For instance, the male death rate was forecast to be ten times higher than the female at age 25 in year 2015 and even higher subsequently (Girosi and King [2004] discussed similar problems with the LC method).
In a study of provincial mortality forecasts for Canada, Lee and Nault (1993) noted the divergence problem and suggested using the same b(x) and k(t) for each province, but they also remarked that such a solution would work only if the historical b(x)s do not vary significantly by province. Similarly, a study (Tuljapurkar, Li and Boe 2000) that applied the LC method separately to the G7 countries found that over a 50 year forecast horizon, the largest gap in life expectancy among these countries increased from about 4 to 8 years. Is such an increased gap plausible? It may be. But it would be difficult to rationalize a continuing divergence of this sort in the more-distant future. In the second half of the 20th century, there was, in general, a faster increase in life expectancy in countries with higher mortality (United Nations 1998). This trend has been documented for developed countries as well (White 2002). These results indicate that international life expectancy has been converging. If such differential rates of mortality decline were to hold in the future, life expectancy would begin to diverge after a formerly high-mortality country overtook the old leaders and became the leading one itself (Lee and Rofman [1994] encountered this problem in preparing forecasts for Chile). Such a change of leading country occurred many times in the 20th century (Oeppen and Vaupel, 2002), but the divergence in life expectancy did not. Instead, mortality decline in the new leading country decelerated, perhaps because it no longer had models to emulate once it became the leader (Wilmoth, 1998). Therefore, it seems that a long-term divergence in life expectancy is unlikely. To avoid divergent forecasting for members of a group of countries, the LC method should not be used for the individual populations separately. Aside from the problem of divergent forecasts, it seems likely that forecasts for individual countries could be improved by exploiting the additional information contained in the experience of similar countries.
In general, the problem can be put as follows. Consider a group of populations that have similar socioeconomic conditions and close connections. These populations could be males and females in the same country, different provinces or races in a country, different countries in a region, and so on. The definition of a group is intentionally left vague and would depend on the forecaster’s judgment. Obviously, mortality differences between these populations should not increase over time indefinitely if the similar socioeconomic conditions and close connections were to continue. The question we address is how to use the LC method to forecast mortality for these populations. Lee (in press) proposed a general framework to solve this problem in which a common trend of life expectancy or k(t) is first described in various models, and individual countries are then projected to converge to this trend. This framework avoids the divergent problem in the long run and allows diversity among countries in the short term. In this article, we build on the LC method to develop an approach within this general framework.
Extending the LC method
To avoid long-run divergence in mean mortality forecasts for a group using the LC method, it is a necessary and sufficient condition that all populations in the group have the same b(x) and the same drift term for k(t). If all populations have the same b(x) and drift term, then the ratios of the mean ASDRs among populations would be constant over time at each age in the forecasts, so the condition is sufficient. If a population’s b(x) or drift term differs from that of others, its forecast of some ASDR would differ from others’ increasingly over time, as shown in Appendix Table A1. Thus, the condition that the b(x) and the drift term of k(t) be the same for members of the group is also necessary. Because it is unlikely that two or more different k(t)s would have identical drift terms, in practice this necessary and sufficient condition requires that all populations have the same b(x) and k(t).
Table A1.
Nine situations of drift terms and b(x,i) and b(x,j)
| d(i)=d(j) | d(i)>d(j) | d(i)<d(j) | ||
|---|---|---|---|---|
| b(x,i)=b(x,j) | ||||
| b(x,i)>b(x,j) | If not diverge at x when b(x,i)d(i) = b(x,j)d(j) then must diverge at another age y, since it is impossible to have b(y,i)d(i) = b(y,j)d(j) for all y≠x, according to (1a). | |||
| b(x,i)<b(x,j) | If not diverge at x when b(x,i)d (i) = b(x,j)d (j) then must diverge at another age y, since it is impossible to have b(y,i)d (i) = b(y,j)d(j) for all y≠x, according to (1a). | |||
It can be seen from above table that for any x, m(x,t,i) diverges from m(x,t,j) if d(i) ≠d(j) or b(x,i)≠b(x,j). Therefore, d(i)=d(j) and b(x,i)=b(x,j) is the necessary condition that m(x,t,i) does not diverge from m(x,t,j).
Given that all populations in the group must have the same b(x) and k(t), which we denote B(x) and K(t), respectively, what values should they take? Consider a group of populations for which mortality is to be forecast. It is obvious that B(x) and K(t) should be chosen to best describe the mortality change of this whole group. Therefore, the B(x) and K(t) should be obtained from applying the ordinary LC method to the whole group, with the K(t) adjusted to fit the group’s average life expectancy i and then modeled as a RWD to forecast the common trend in future mortality change.
The a(x) are estimated separately for each individual population in this group (a(x,i) for country i), since they do not cause long-term divergence and hence need not be the same for each population. Let the ASDR at age x and time t of the ith population be m(x,t,i). The a(x,i) should minimize the total error in modeling log(m(x,t,i)) and therefore can be obtained from the following ordinary least-squares (OLS) regression:
| (3) |
Because K(t) sums to zero, a(x,i) is solved from (3) as
| (4) |
which is the average over time of log(m(x,t,i)), just as when LC is applied to the ith population separately.
We call [a(x,i)+B(x)K(t)] the common factor model of the ith population. In this model, the change over time in mortality is described by B(x)K(t), which is the common factor for each population in the group. We could forecast mortality for the members of the group using this model, which would maintain the same ratios of ASDRs across countries that were observed on average over the sample period. The forecast would imply neither divergence nor convergence. In the remainder of the article we will discuss a way in which this baseline common factor projection may be improved. However, this common factor model may be of interest in its own right, as well.
We can construct an explanation ratio, denoted RC (i), to measure how well the common factor model works for the ith population,
| (5) |
Without adjusting K(t), the RC (i) cannot be bigger than the explanation ratio of applying the LC method separately to the ith population (which we denote as RS (i) ) because B(x)K(t) does not minimize modeling errors for the ith population. If in the analyst’s judgment RC (i) is too small, then a specific factor can be introduced to improve the performance of the common factor model, as explained next. We do not suggest any formal test of goodness of fit.
The specific factor of the ith population describes the residual matrix of the common factor model, [log(m(x,t,i)) − a(x, i) − B(x)K (t)], which is an age vector changing over time. Following the strategy of the ordinary LC method, we apply the SVD to convert the task of modeling this time-varying vector into modeling a scalar k(t,i) and use a constant vector b(x,i) to describe the age pattern. In other words, the specific factor of the ith population, which we denote as b(x,i)k(t,i), is obtained using the first-order vectors b(x,i) and k(t,i) derived from applying the SVD to the residual matrix of the common factor model. Consequently, we obtain the augmented common factor model as
| (6) |
The last term in (6) represents modeling error, and b(x,i)k(t,i) allows for a short- or medium-term difference between the rate of change in country i’s death rates and that rate of change implied by the common factor. But if these differences persist over the long run, then the forecasts would be divergent. So this approach will be successful only if the k(t,i) factors each tend toward some constant level over time. In this way, the fitted model will accommodate some continuation of historical convergent or divergent trends for each country before it locks into a constant relative position in the hierarchy of long term forecasts of group mortality.
We can assess how well this model works for the ith population by constructing a new explanation ratio, which we denote as RAC (i),
| (7) |
The RAC (i) is larger than RC (i) because b(x,i)k(t,i) minimizes the modeling error of (6).
The vector b(x,i) describes the differences between the patterns of change by age in mortality for the ith population and for the group as a whole. Thus, the values of b(x,i) may not be positive at all ages. Raising k(t,i) will increase the ASDR at ages where the values of b(x,i) are positive but reduce the ASDR at ages when the b(x,i) are negative, with offsetting effects on life expectancy. For this reason, it may not be possible to choose a value of k(t,i) that exactly fits a given level of life expectancy, or if such a level exists, it may correspond to a significant reduction in RAC (i). For these reasons, we do not adjust k(t,i) to fit the life expectancy of the ith population.
Because the k(t,i) in (6) must tend toward a constant value for this approach to work, the approach fails if k(t,i) has a trending long-term mean, as does the random walk with a non-zero drift term that is typically used in the ordinary LC method. Applications may succeed, however, if k(t,i) is a random walk without drift (RW) or a first-order autoregressive model (AR(1)) with a coefficient that yields a bounded short-term trend in k(t,i):
| (8) |
where c0 (i) and c1 (i) are coefficients and σi is the standard deviation of the AR(1) model. The literature (e.g., Kendall and Ord, 1990:105) shows that parameters of AR models with a constant, of which (8) is the simplest, can be estimated by OLS using lagged values in the series as independent variables, that such OLS estimates are asymptotically unbiased and efficient, and that the goodness of fit can be naturally measured by the explanation ratio. If the RAC (i) and the explanation ratio for the RW or AR(1) model of k(t,i) are large enough and the estimated c1 (i) is smaller than 1, then the ith population can be included in the group. Otherwise, it should be excluded from the group, or higher-order AR models should be used if the analysis of k(t,i) suggests so.
In summary, for the ith population, if RC (i) is large enough or if RAC (i) is large enough and the k(t,i) can be well modeled, it can be included in the group; otherwise, it should be excluded. However, these criteria, which are intentionally somewhat vague, should be tempered by judgment. If RC (i) is relatively small, but the reasons for the poor fit can be understood as being due to historical forces that are deemed transitory, then the forecaster may decide to include that country in the group for forecasting purposes in any case. If a population is excluded from the group, the common factor and the other populations’ specific factor should be re-estimated, and whether another population should be included in the group should also be reexamined by repeating the procedure described earlier.
We now turn to forecasting. The standard errors of the drift term, , of the AR(1) coefficients, and , are well known as
| (9) |
where is the estimated value of σ in (2), in which k(t) should be replaced by K(t), and is the estimated value of σi in (8). In forecasting, estimating errors should be taken into account, so the stochastic trajectories of K(t) and k(t,i) are
| (10) |
where ε and ηi are standard normal variables and independent of each other. When k(t,i) is modeled as RW, its forecast takes the form of K(t) with a zero drift term.
The pure random terms in the models of K(t) and k(t,i), namely, e(t) and ei (t), can be assumed to be independent because one describes the random effect that is common for the group, and another is specific for the ith population. Furthermore, pure random terms in the models of k(t,i) and k(t,j) can also be assumed to be independent because they describe special random changes in different populations. Finally, subtracting (6) at T from that at t, the ASDR of the ith population in this group is forecast as
| (11) |
In (11), the B(x)K(t) specifies the long-term trend and random fluctuations that are common for the whole group, while b(x,i)k(t,i) describes the short-term changes that are special only for the ith population.
We call this procedure the augmented common factor LC method, of which the ordinary LC method is a special case that uses only a specific factor. The strategy suggested by Lee and Nault (1993) is another special case, which includes only the common factor. The two-factor method was proposed in general form by Lee (in press), of which the augmented common factor LC method is, perhaps, the simplest realization based on the ordinary LC method.ii
Remarks
In a typical population, age-specific death rates have a strong tendency to move up and down together over time. The LC method uses this tendency by modeling the changes over time in ASDR as driven by a scalar k(t). Although such a strategy implies that the modeled death rates are correlated perfectly across ages, we believe that this strategy is preferable to modeling these interage correlations in detail. However, some analysts, such as Denton, Feaver and Spencer (2001), and the U.S. Congressional Budget Office (2001), have done so.
In a properly defined group, all populations’ age-specific death rates should tend to move up and down together over time, a tendency captured by the common factor. For each individual population, however, we expect that its mortality change will differ from that described by the common factor. If this difference is systematic and significant, a specific factor for this individual population is required. When this specific factor is used, the modeled changes in ASDR are neither perfectly correlated across age within one population (because it has two components) nor entirely independent between populations (because they have a common component).
We should also mention that coherent forecasts of ASDR guarantee non-divergent forecasts of life expectancy in the long run. But in the short term, the change in a population’s ASDR or life expectancy may differ from the others, diverging or converging. There are other ways to avoid divergent forecasts. For example, Vaupel and Schnabel (2004) suggested that the common trend be the ‘best-practice’ mortality decline (see Oeppen and Vaupel, 2002) and that the life expectancy of individual populations converge to this common trend through various AR models.
Applications
Two-sex forecast
We first apply the common factor LC method to forecast two-sex mortalityiii, which is usually necessary in population forecasting, taking Sweden as our example. Following the suggestion of Lee and Miller (2001), we use data starting from 1950 to avoid non-linear k(t) through the last available year 2002, from the Human Mortality Database. The explanation ratios are shown in Table 1.
Table 1.
Explanation ratios of male and female populations of Sweden
| Separate-LC explanation ratio RS (i) | Common Factor explanation ratio RC (i) | Augmented Common Factor explanation ratio RAC (i) | RW explanation ratio RRW (i) | AR(1) explanation ratio RAR(1) (i) | |
|---|---|---|---|---|---|
| Male | .857 | .883 | .932 | −5.462 | .880 |
| Female | .932 | .895 | .927 | −6.805 | .876 |
In Table 1, we judge the RC (i) to be quite high for each sex, so we conclude that the two populations’ mortality can be forecast coherently, at least by the common factor model.iv Because the higher RAC (i) indicates that a specific factor improves the fit considerably, we move forward to model the k(t,i). The negative explanation ratios for the RW model indicate that it is worse than treating k(t,i) as a pure random variablev, which is, however, not feasible because in forecasting, errors should be correlated and accumulated over time. We therefore turn to the next feasible and simplest model, namely, AR(1). Because the explanation ratios of the AR(1) model are smaller than RC (i), to introduce a specific factor is, in fact, to “improve” a better model by using a worse one. And even if the explanation ratio of AR(1) were marginally higher than RC (i), it might not be worth introducing a specific factor that would bring additional complexity. Thus, we conclude that coherent forecasts should be made by using the common factor model.
The medianvi values of life expectancy, from coherent and separate LC forecasts, are compared in Figure 1. The difference between male and female life expectancies was 4.4 years in 2002 and is forecast to be 3.0 and 7.6 years in 2100 by the coherent and separate LC forecasts, respectively. Although the divergent trend in life expectancy, from 4.4 in 2002 to 7.6 years in 2100, may be acceptable to some readers, the problem of separate forecasts emerges more sharply in the ratio of male-to-female median ASDR. In 2002, this ratio was 1.16 at age 0. In separate forecasts, however, it becomes 0.74 in 2100, implying that the death rate at age 0 for males would be lower than that of females, which cannot be justified by empirical evidence. On the other hand, in the common factor model, this ratio remains at the 2002 level at any time and for every age, which is the simplest approximation to the historical coherent trend. The convergent trend between the life expectancies of males and females, from 4.4 in 2002 to 3.0 years in 2100, is a consequence of the general decline in ASDR, not a result of convergence between the ASDR of males and females.
Figure 1.
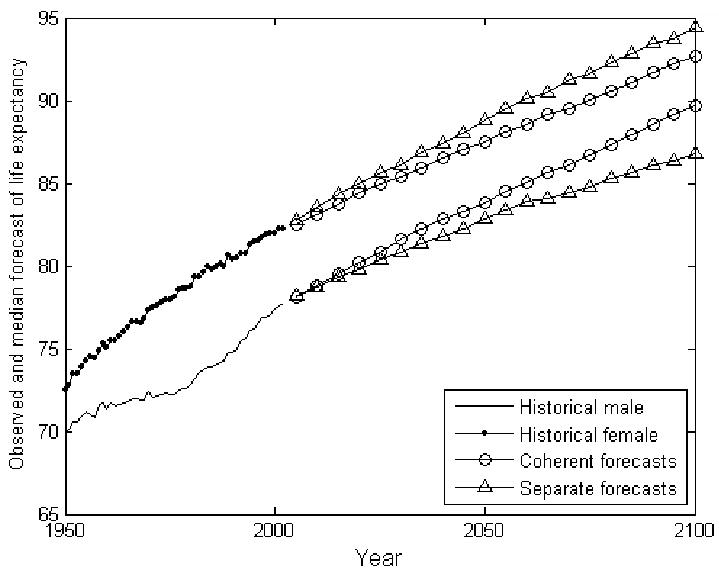
Coherent and separate forecasts of life expectancy, Sweden
Group forecast
The second application is to forecast mortality coherently for the 15 low-mortality countries in the Human Mortality Database, as listed in Table 2. Supplemented by data from the World Health Organization used by Tuljapurkar et al. (2000), these 15 countries’ ASDR and age-specific populations are available for a common period from 1952 through 1996. Using these data, we calculate average ASDR across the 15 countries, weighting by their population sizes. The B(x) and K(t) are then obtained using the ordinary LC method, yielding patterns that are typical for low-mortality countries as is shown in Figure 2. The explanation ratios are listed in Table 2.
Table 2.
Explanation ratios of 15 low-mortality populations
| Separate-LC explanation ratio RS (i) | Common Factor explanation ratio RC (i) | Augmented Common Factor explanation ratio RAC (i) | RW explanation ratio RRW (i) | AR(1) explanation ratio RAR(1) (i) | |
|---|---|---|---|---|---|
| Austria | .94 | .91 | .95 | −5.04 | .87 |
| Canada | .96 | .94 | .98 | −4.72 | .87 |
| Denmark | .83 | .39 | .84 | .01 | .98 |
| England | .95 | .84 | .96 | −1.21 | .96 |
| Finland | .94 | .92 | .94 | −15.72 | .68 |
| France | .94 | .88 | .95 | −1.98 | .94 |
| Germany(W) | .97 | .92 | .96 | −3.66 | .90 |
| Italy | .93 | .91 | .96 | −1.64 | .95 |
| Japan | .97 | .77 | .98 | .33 | .99 |
| The Netherlands | .93 | .82 | .93 | −2.16 | .94 |
| Norway | .88 | .70 | .90 | −.44 | .97 |
| Spain | .90 | .86 | .94 | −2.80 | .94 |
| Sweden | .93 | .88 | .93 | −3.43 | .91 |
| Switzerland | .93 | .88 | .94 | −3.75 | .90 |
| USA | .96 | .78 | .96 | −.98 | .96 |
Figure 2.
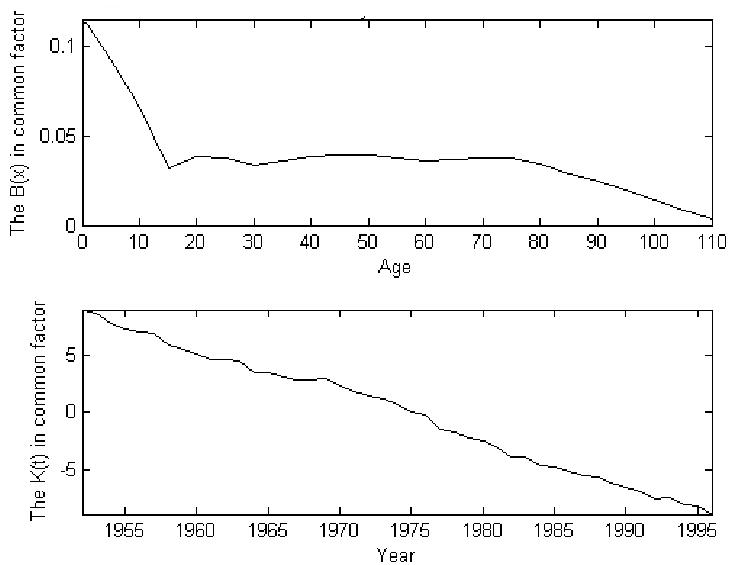
The common factor values of B(x) and K(t) for 15 low-mortality countries
Except for Denmark, Japan, Norway, and the US, the values of RC (i) are higher than 0.82, suggesting that there indeed exists a common trend, and that the common factor model captures this trend quite well. The mortality of the 11 countries with high RC (i) can be coherently forecast by the common factor model. There remain four other countries whose RC (i) are low enough to be troubling, ranging from 0.39 for Denmark to 0.78 for the US, and we now investigate whether they can be included in the low-mortality group through the use of specific factors b(x,i)k(t,i). Because adding a specific factor must always improve model performance, we introduce b(x,i)k(t,i) for all the 15 countries. For many countries, we find negative values of b(x,i) over a substantial range of ages, as is shown in Figure 3. In these cases, a second stage fitting life expectancy would require large changes in k(t,i) and result in significant reductions of RAC (i) as we discussed earlier.
Figure 3.
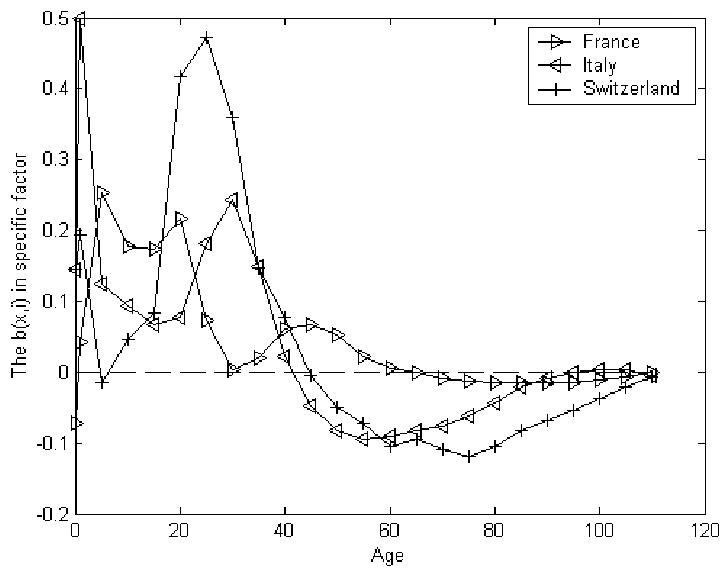
Typical b(x, i) with significant negative values
The values of RAC (i) are higher than 0.84 for all countries, as can be seen in Table 2, suggesting that we should move to the next step of modeling the time series of k(t,i). The explanation ratios show that the RW model does not work well for any country, but the RAR(1) (i) is higher than RC (i) for the eleven countries that are listed in Table 3. Examples of two typical k(t,i) that can be successfully modeled as AR(1) are plotted in Figure 4.
Table 3.
Results of fitting the model of AR(1) with constant
| Pr{(c1 (i) ≥ 1} | |||||||
|---|---|---|---|---|---|---|---|
| Denmark | .14 | .05 | .99 | .02 | .35 | 17.88 | .33 |
| England | .07 | .04 | .93 | .03 | .02 | 1.06 | .24 |
| France | .02 | .03 | .95 | .04 | .12 | .44 | .18 |
| Italy | −.02 | .02 | .92 | .04 | .01 | −0.27 | .12 |
| Japan | −.27 | .05 | .95 | .01 | <.01 | −5.61 | .34 |
| The Netherlands | .10 | .05 | .94 | .04 | .04 | 1.61 | .33 |
| Norway | .10 | .05 | .95 | .03 | .03 | 2.03 | .33 |
| Spain | −.05 | .04 | .86 | .04 | <.01 | −.35 | .25 |
| Sweden | .03 | .04 | .93 | .05 | .06 | .47 | .28 |
| Switzerland | .01 | .02 | .95 | .05 | .18 | .23 | .12 |
| USA | .10 | .04 | .98 | .03 | .24 | 4.39 | .28 |
Figure 4.
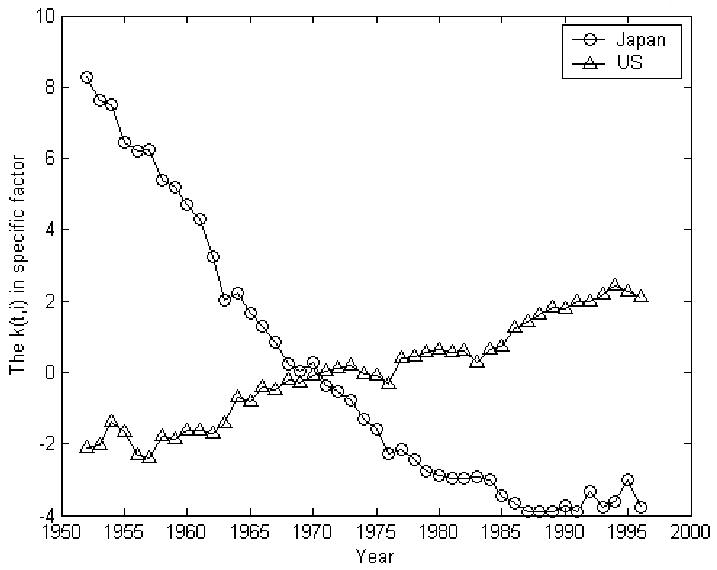
Typical k(t, i) that fits convergent AR(1) model
For countries in Table 3, introducing an AR(1)-specific factor improves the model, which is feasible because the values of ĉ1(i) are smaller than 1. Although the ĉ1(i) for Denmark is very close to 1, which makes the k(∞,i) significantly higher than the others, the probability that the true value of ĉ1(i) is larger than 1 is only 0.35 because the error in estimating ĉ1(i) is small. Fortunately, Denmark, Japan, Norway, and the US are among the countries for which the AR(1) model fits adequately, with the lowest explanation ratio 0.84. We suggest that all 15 countries should be included in the low-mortality group, although whether 0.84 is a high-enough threshold for inclusion could be questioned.
We now turn to forecasting. For the K(t) shown in Figure 2, the drift term and its standard error are estimated as −0.401 and 0.046, respectively. The K(t) and k(t,i) are then forecast using (10) and m(x,t,i) using (11). Figure 5 illustrates (for selected countries and age groups) how the augmented common factor LC method guarantees that long-term forecasts are non-divergent while allowing for short-term diversity. In Figure 5, the values of log[m(x,t)/m(x,T)] for the age group 20–24 are shown both within the sample (t≤T=1996) and for forecasts (t>T). For this age group, the death rate in Japan declined faster historically than in the fitted common factor model, which, in turn, dropped faster than that of the United States, as is depicted by the three curves for t<T. For t=T, of course, each curve passes through zero by construction. How does projected mortality change in the future? If we were using just the common factor approach, the curves for both the US and Japan would follow the central common factor line. However, with the augmented common factor method, the trends relative to the common factor are projected to continue for a while in the future, although eventually their position relative to the common factor will stabilize.
Figure 5.

Log of 20–24 death rate relative to value in 1996 for Japan and US, illustrating short-term specific factor and long term common factor in forecasts
The coherent forecasts of life expectancy for Japan, the US, and Denmark are listed in Table 4 and shown in Figure 6. Forecasts of life expectancy using the ordinary LC method separately for each country are displayed in Figure 6 and Table 4 for comparison. We see that the forecast for Japan is for smaller increases than under the separate LC method, while it is for larger increases for the US and Denmark, two countries that lagged during the historical period. The standard deviation of life expectancy between these 15 countries was 1.2 years in 1996. Applying the ordinary LC method separately, this standard deviation is 2.5 years in 2050 for the median forecasts, more than double of that in 1996. Using the augmented common factor LC method, this standard deviation is 1.3 years in 2050, which is almost the same as in 1996, illustrating the non-divergence of the forecasts. On the other hand, the uncertainty of the life expectancy forecasts can be described using a large collection of stochastic trajectories given by (10). To obtain a smooth median forecast and 95% confidence intervals, we found that 500 trajectories are enough and hence used them in this article for K(t) and each k(t,i). Averaging across countries, the 95% probability interval is reduced from 6.1 years in the ordinary LC method to 4.9 years in the augmented common factor LC method. A possible explanation is that the common factor used in the augmented common factor LC method tends to reduce random changes that are not perfectly correlated among countries.
Table 4.
Life expectancies at time t, e(t), of low-mortality countries
| e1996 | Median of e2050 from coherent forecast | Median of e2050 from separate forecast | The 95% confidence interval of e2050, from coherent forecast | The 95% confidence interval of e2050, from separate forecast | |
|---|---|---|---|---|---|
| Austria | 77.4 | 84.8 | 84.9 | 3.8 | 4.8 |
| Canada | 78.4 | 86.3 | 85.4 | 4.2 | 3.5 |
| Denmark | 75.8 | 82.2 | 80.1 | 10.6 | 9.1 |
| England | 77.1 | 84.9 | 83.7 | 4.8 | 5.9 |
| Finland | 76.9 | 84.7 | 85.8 | 4.1 | 7.9 |
| France | 78.0 | 85.8 | 86.7 | 4.2 | 6.5 |
| Germany(W) | 77.1 | 84.8 | 84.6 | 3.8 | 4.8 |
| Italy | 78.5 | 86.1 | 87.1 | 4.1 | 6.7 |
| Japan | 80.5 | 88.1 | 90.9 | 4.3 | 4.7 |
| The Netherlands | 77.6 | 85.4 | 83.0 | 4.5 | 6.5 |
| Norway | 78.2 | 85.2 | 83.0 | 6.1 | 6.5 |
| Spain | 78.2 | 85.9 | 86.2 | 4.0 | 6.8 |
| Sweden | 79.0 | 86.1 | 85.6 | 4.5 | 6.0 |
| Switzerland | 79.1 | 86.5 | 87.5 | 4.5 | 6.1 |
| USA | 76.3 | 84.9 | 84.0 | 5.4 | 5.7 |
| 15 countries | SD=1.2 | SD=1.3 | SD=2.5 | Mean=4.9 | Mean=6.1 |
Figure 6.
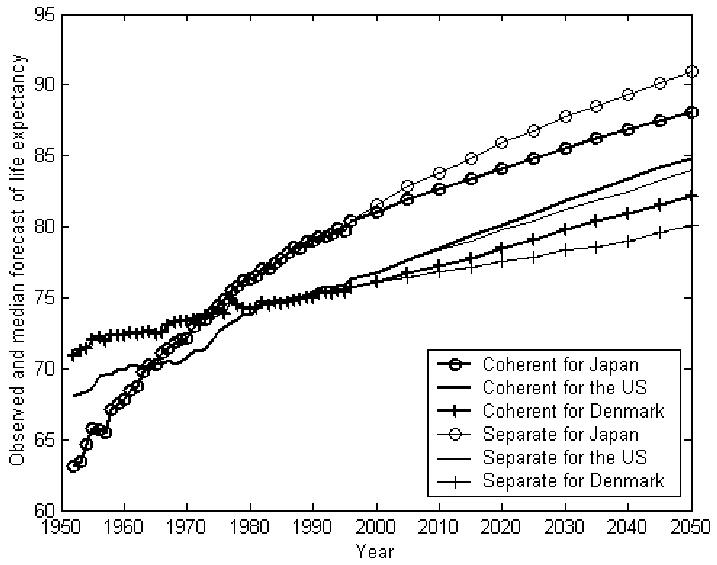
Coherent and separate forecasts of life expectancy
Forecasts for out-of-group populations
Sometimes a population may not have been regarded as belonging to a certain group in the past, but its mortality may be expected to follow the group’s in the future. This may be the case for minorities in a nation or for those who live in a remote area of a country. The remaining six countries in the Human Mortality Database—Bulgaria, the Czech Republic, the former East Germany, Hungary, Lithuania and Russia—may also be viewed this way, relative to the group of 15 low-mortality countries. Although these countries were not in the low-mortality group in 1952 to 1996, they may catch up to and join the low-mortality group in the future. Arguably, the experience of the low-mortality group is a better guide to their future than their own histories would be. We can formally apply the augmented common factor LC method to these countries, just as we did for countries in the low-mortality group. The only difference is that these out-of-group countries do not contribute to formulating the common factor B(x)K(t) because we believe that their history was governed by a different process. Imposing the common factor on the six populations, we find the explanation ratios shown in Table 5.
Table 5.
Explanation ratios of 6 East-European populations
| Separate-LC explanation ratio RS (i) | Common Factor explanation ratio RC (i) | Augmented Common Factor explanation ratio RAC (i) | The RW explanation ratio RRW (i) | The AR(1) explanation ratio RAR(1) (i) | |
|---|---|---|---|---|---|
| Bulgaria | .79 | .09 | .71 | −3.96 | .89 |
| The Czech Republic | .89 | .35 | .91 | −.47 | .97 |
| Germany (E) | .91 | .61 | .88 | −2.27 | .93 |
| Hungary | .83 | .09 | .91 | −.01 | .98 |
| Lithuania | .85 | .39 | .84 | −.50 | .96 |
| Russia | .73 | −3.48 | .46 |
For Russia, the RC (i) is negative, indicating that the common factor makes fitting worse than using only a(x,i), which suggests that the common trend of mortality change in low-mortality countries did not exist in Russia for the period of interest. Similar situations are identified by the small values of RC (i) for all these East European countries. Moreover, the augmented common factor model does not work for Russia either because its RAC (i) is only 0.46. It is clear that a coherent forecast for Russia cannot be made using the augmented common factor LC method, regardless of how its k(t,i) is modeled.
The values of RAC (i) for the other five populations encourage us to proceed to model k(t,i), although it is debatable whether the 0.71 for Bulgaria is high enough. Again, the RW model does not work, and the results for the AR(1) are listed in Table 6.
Table 6.
Results of fitting AR(1) for the 5 East-European populations
| Pr{(c1 (i) ≥ 1} | |||||||
|---|---|---|---|---|---|---|---|
| Bulgaria | .19 | .21 | 1.00 | .05 | .62 | ||
| The Czech Republic | .12 | .07 | .98 | .03 | .23 | 5.84 | .47 |
| Germany(E) | .10 | .08 | .93 | .04 | .05 | 1.42 | .54 |
| Hungary | .18 | .08 | 1.01 | .02 | .68 | ||
| Lithuania | .28 | .16 | .98 | .03 | .39 | 16.54 | .93 |
For Bulgaria and Hungary, the estimated AR(1) coefficient is larger than 1. Although higher-order AR models may be introduced, the k(t,i) for these countries, shown in Figure 7, do not seem to be promising. We therefore abandon using the augmented common factor LC method to forecast mortality for Bulgaria, Hungary, and Russia.
Figure 7.
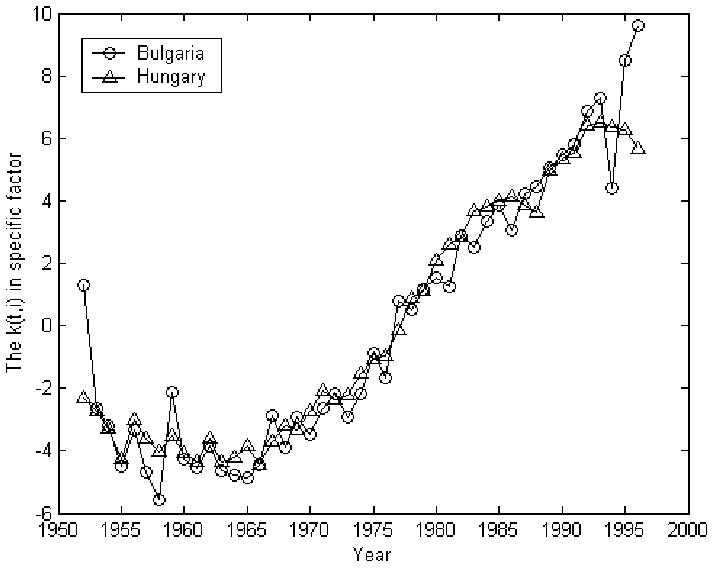
Typical k(t,i) that fits neither RW not AR(1) model
The life expectancies of the Czech Republic, the former East Germany, and Lithuania, forecast by the coherent and ordinary LC methods, are compared in Table 7. Coherent forecasts yield higher life expectancy in 2050 than the separate forecasts. Life expectancy in Lithuania is forecast to reach 77.5 in 2050 in the coherent forecast, which seems much more plausible than the 66.6 projected by LC used separately. Contrary to the case of the low-mortality group, the forecasting uncertainty is greater for the coherent forecasts. The smaller uncertainty estimated for the separate forecast, however, does not have a solid basis. Consider Lithuania as an example, for which the data start in 1960. In a separate forecast, the k(t) increases over time and b(x) has negative values only at young ages, as shown in the first and second panels of Figure 8. This forecast indicates that in the historical period of interest, the death rate declined at young ages but increased elsewhere. Forecasting such a trend to continue would yield highly implausible results, as is reflected in the third panel of Figure 8, which shows the median and 95% probability intervals of forecast life expectancy. The median forecast of life expectancy declines over time. In the coherent forecast, the normal B(x) and K(t) in Figure 1 produce a decline in mortality at all ages, at least in the long term, and forecast life expectancy rises over time, as is shown in the fourth panel in Figure 8.
Table 7.
Life expectancies at time t (e(t)) of selected East European countries
| e1996 | Median of e2050 from coherent forecast | Median of e2050 from separate forecast | The 95% confidence interval of e2050, from coherent forecast | The 95% confidence interval of e2050, from separate forecast | |
|---|---|---|---|---|---|
| The Czech Republic | 73.8 | 80.8 | 78.6 | 14.7 | 7.4 |
| Germany(E) | 75.5 | 83.2 | 81.1 | 7.2 | 7.9 |
| Lithuania | 71.5 | 77.5 | 66.6 | 26.1 | 13.9 |
| 3 countries | SD=2.0 | SD=2.9 | SD=7.8 | Mean=16.0 | Mean=9.7 |
Figure 8.
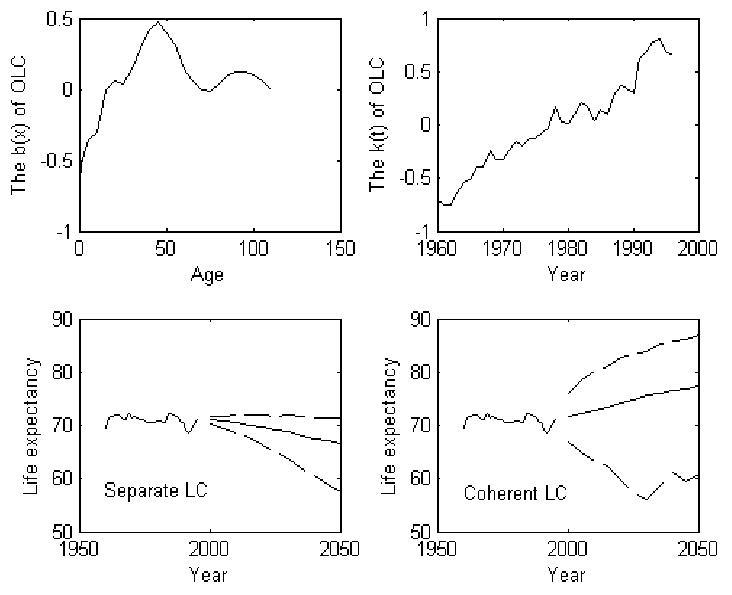
Coherent and separate forecasts of Lithuania
Discussion
The augmented common factor LC method that we derived in this article aims to model and forecast mortality for a group of populations in a coherent way, taking advantage of commonalities in their historical experience and age patterns, while acknowledging their individual differences in levels, age patterns, and trends. Populations that are sufficiently similar to be grouped together may nonetheless have somewhat different mortality histories. Our approach here is based on the idea that such past differences should not lead us to expect continuing long-run divergence in the future, but neither should we expect the future to obliterate all past differences.
Populations may be treated as a group when they have similar socioeconomic conditions and close connections and when these conditions are expected to continue in the future. Obviously these criteria are vague and require subjective judgment to apply. Geographic proximity may sometimes be deemed relevant and sometimes not. Certainly, though, these conditions should usually be met by the male and female populations in any region. Application to sex-specific mortality in Russia, with its large differences, would be a useful experiment. Application to sex differences in mortality trends resulting from historical differences in smoking behavior in many industrial nations would also be a valuable experiment.
The 15 low-mortality countries in the Human Mortality Database also seemed to satisfy these criteria for group inclusion, though their socioeconomic conditions still differ, and some are more closely connected than others. The trend toward regional integration and globalization should only strengthen the case. We do not expect the mortality of these populations to diverge over the long run.
The method we propose first identifies the common trend of mortality change in these populations by fitting an ordinary LC model to their aggregate. This common model describes a common rate of change for mortality at each age. However, these common rates of change are applied to different initial levels and age patterns of mortality in each population, resulting in the common factor model. Forecasts then preserve in perpetuity the ratios of the populations’ ASDR. Some populations’ mortality change can be adequately described and forecast by the common factor model, as reflected by the minor difference between the RC (i) and RS (i) in Table 2, which implies a similarity in historical mortality change among populations. We were encouraged to find that 11 out of 15 of the populations could be modeled quite well by the common factor, confirming the existence of a common pattern of mortality change for the low-mortality countries. For these 11 countries, life expectancy forecasts to 2050 differed little whether we used the augmented common factor model or applied the ordinary LC method separately, as was shown in Table 4.
Mortality in Denmark, Japan, Norway, and the US did not fit well using the common factor model. However, adding a population-specific component to the model substantially improved the fit. This component describes the particularities of individual countries experience in the sample period and projects these particular trends to continue to a limited extent, as is shown in Figure 5. If there were no trend in k(t,i) or if any trend was extended linearly, then this augmented common factor model would reduce to the ordinary LC method provided that the b(x,i) were similar to B(x). This line of thought suggests that the augmented common factor model would forecast mortality decline faster than would the ordinary LC when k(∞,i) is positive, and vice versa. In fact, this is what happened. The forecasts of life expectancy for Denmark, Norway, and the US, based on the augmented common factor LC method, were higher than those based on the ordinary LC method, and their k(∞,i) s were positive. These forecasts were lower for Japan, however, whose k(∞,i) was negative. For these four countries, the differences between the results of the augmented common factor method and the ordinary LC method were somewhat larger than for the other low-mortality countries, for which the basic common factor model worked well, as can be seen in Table 4.
We conclude that the augmented common factor LC method worked well for the 15 low-mortality countries as a group. It also appears to have worked well for a two-sex mortality forecast. The basis of this success is a real coherent trend in mortality for the two sexes and within the low-mortality group. The method would not work, or, at least, not work so well without such a basis.
In some cases, populations that had different mortality histories than some reference group may nonetheless be expected to behave like that group in the future. The augmented common factor method can be used to assess, on statistical grounds, whether one or more populations could be viewed as following the mortality change of another group. However, statistics aside, one may have other reasons for choosing to assume such a pattern in the future. Here, we consider only the statistical reasons. We take East European countries in the Human Mortality Database as an example. Applying the augmented common factor LC method to these countries, we found that the Czech Republic, the former East Germany, and Lithuania could be treated as following the low-mortality group, but Bulgaria, Hungary, and Russia could not.
Even if one were interested only in a forecast for a particular country, such as the US, we believe it would improve the forecast to place it in an international context, drawing on the experience of similar countries. The methods developed in this article are a step in this direction.
Appendix
Let there be two populations i and j and so two drift terms d(i) and d(j). Let us focus on age group x, so there are two values of b(x,i) and b(x,j). In general, d(i) and b(x,i) are non-zero and:
| (1a) |
There are nine asymptotic situations, as in Appendix Table A1.
Footnotes
An early version of this article was presented at the meeting on Demographic and Economic Dynamics, 26—29 May 2003, Palo Alto, California. Research for this article was funded by grants from NIA: R37-AG11761 and R03-AG024314-01.
If our goal was to fit the experience of each country as well as possible, then we could do so by averaging the mortality rates across unweighted members of the group.
Girosi and King (2004) point out that anomalies in trends in the age-specific death rate trends for a specific country can lead projected future trends to diverge in implausible ways when the Lee-Carter method is used. The methods developed in this article, although intended for a different purpose, will also reduce this problem to the extent that it is due to transient features of a population’s mortality history.
For a number of years, researchers at the University of California at Berkeley, Mountain View Research, and Stanford University have been forecasting sex-specific mortality using a procedure that is similar to the common factor model, with a common k(t) and b(x) but different a(x). However, this procedure has not been described in any publication.
In Table 1, the outcome that RC (i) > RS (i) for males is the possible but deviant result of adjusting k(t) in the ordinary, and K(t) in the augmented common factor, LC method. This outcome would not be possible for first-stage estimates.
The explanation ratio for the RW or AR(1) in (8) is . For AR(1), the minimum value of R would be 0 if minimizing σi resulted in c0=c1=0. Because fitting RW does not minimize σi btu merely sets it as by forcing c0=0 and c1=1, the R of RW can be negative, which implies that the modeling error of RW is larger than that of treating k(t,i) as a pure random variable.
LC forecasts have a central value equal to the median, not the mean, mortality level. They do so because fitting and forecasting are initially done on the log-transformed ASDR, and then these forecasts are non-linearly transformed (exponentiated) to get the ASDR.
References
- Booth, H., L. Tickle and L. Smith. 2004. “Evaluation of the Variants of the Lee-Carter Method of Forecasting Mortality: A Multi-Country Comparison.” Paper presented at the 2004 annual meeting of Population Association of America, Boston.
- Carter L, Lee RD. “Modeling and Forecasting US sex differentials in mortality”. International Journal of Forecasting. 1992;8:393–411. doi: 10.1016/0169-2070(92)90055-e. [DOI] [PubMed] [Google Scholar]
- Congressional Budget Office. 2001. “Uncertainty in Social Security’s Long Term Finances: A Stochastic Analysis.” http://www.cbo.gov/showdoc.cfm?index=3235&sequence=0
- Denton, F., C. Feaver and B. Spencer. 2001. “Time Series Properties and Stochastic Forecasts: Some Econometrics of Mortality from The Canadian Laboratory.” QSEP Research Reports No. 360
- Girosi, F. and G. King. 2004. “Demographic Forecasting.” Draft book manuscript (http://gking.harvard.edu/files/smooth.pdf).
- Human Mortality Database. (University of California, Berkeley, USA, and Max Planck Institute for Demographic Research, Germany. Available at www.mortality.org or www.humanmortality.de, data downloaded on June 2004.)
- Kendall, M. and J. K. Ord, 1990. “Time Series.” Edward Arnold, Suffolk, Great Britain.
- Lee, R. D. in press. “Mortality forecasts and Linear Life Expectancy Trends.” Working paper presented at a workshop on mortality held in Lund, Sweden.
- Lee RD, Carter L. “Modeling and Forecasting the Time Series of U.S. Mortality”. Journal of the American Statistical Association. 1992;87:659–71. [Google Scholar]
- Lee, R. D. and F. Nault. 1993. “Modeling and Forecasting Provincial Mortality in Canada.” Paper presented at World Congress of the IUSSP, Montreal, Canada.
- Lee RD, Miller T. “Evaluating the Performance of the Lee-Carter method for Forecasting Mortality”. Demography. 2001;38:537–49. doi: 10.1353/dem.2001.0036. [DOI] [PubMed] [Google Scholar]
- Lee RD, Rofman R. “Modelación y Proyeeción de la Mortalidad en Chile.” (Modeling and Forecasting Mortality in Chile) NOTAS. 1994;22:182–213. [PubMed] [Google Scholar]
- Oeppen J, Vaupel JW. “Broken limits to life expectancy”. Science. 2002;296:1029–31. doi: 10.1126/science.1069675. [DOI] [PubMed] [Google Scholar]
- Tuljapurkar S, Li N, Boe C. ”A Universal Pattern of Mortality change in the G7 Countries. Nature. 2000;405:789–92. doi: 10.1038/35015561. [DOI] [PubMed] [Google Scholar]
- United Nations. 1998. “World Population Prospects: The 1996 Revision.” Population Division, United Nations.
- Vaupel, J. M. and S. Schnabel. 2004. “Forecasting Best-Practice Life Expectancy to Forecast national Life Expectancy.” Paper presented at the 2004 annual meeting of Population Association of America, Boston.
- White KM. “Longevity advances in high-income countries, 1955—96”. Population and Development Review. 2002;28(1):59–76. [Google Scholar]
- Wilmoth JR. “Is the pace of Japanese mortality decline converging toward international trends?”. Population and Development Review. 1998;24(3):593–600. [Google Scholar]
- Wilson C. “On the Scale of Global Demographic Convergence 1950–2000”. Population and Development Review. 2001;27(1):155–172. doi: 10.1111/j.1728-4457.2001.00155.x. [DOI] [PubMed] [Google Scholar]


