A comprehensive continuous-time model for the appearance of CGH signal due to chromosomal missegregations during mitosis

Abstract

Aneuploidy, the gain or loss of large regions of the genome, is a common feature in cancer cells. Irregularities in chromosomal copy number caused by missegregations of chromosomes during mitosis can be visualized by cytogenetic techniques including fluorescence in situ hybridization (FISH), spectral karyotyping (SKY) and comparative genomic hybridization (CGH). In the current work, we consider the propagation of irregular copy numbers throughout a cell population as the individual cells progress through ordinary mitotic cell cycles. We use an algebraic model to track the different copy numbers as states in a stochastic process, based on the model of chromosome instability of Gusev, Kagansky, and Dooley, and consider the average copy number of a particular chromosome within a cell population as a function of the cell division rate. We review a number of mathematical models for determining the length of the cell cycle, including the Smith-Martin transition probability model and the “sloppy size” model of Wheals, Tyson and Diekmann. The program MITOSIM simulates the growth of a population of cells using the aforementioned models of the cell cycle. MITOSIM allows the cell population to grow, with occasional resampling, until the average copy number of a given chromosome in the population reaches a preset threshold signifying a positive copy number alteration in this region. MITOSIM calculates the relationship between the missegregation rate and the growth rate of the cell population. This allows the user to test hypotheses regarding the effect chromosomal aberrations have upon the cell cycle, cell growth rates, and time to population dominance.

1 Introduction

The vast majority of solid tumors of epithelial origin (carcinomas) often have genomic imbalances that range from defined chromosomal bands to entire chromosome arms and, in the most extreme cases, entire chromosomes [1]. This aneuploidy is specific for different tumor types, specific for certain tumor stages, and late tumor passages (such as in metastases or in established cell lines) still very faithfully maintain the cancer specific distribution of genomic imbalances seen in earlier stages [1]. These facts suggest that continuous selection pressure for the maintenance of these aberrations exists. Cytogenetic analyses have also shown that early chromosomal imbalances occur in clusters in a low percentage of cells, and that, at later stages of tumorigenesis, cells that maintain such aberrations constitute the majority of tumor cells [2]. Because chromosomal aneuploidy can result from errors during the segregation phase of mitosis, we present, in the current work, a comprehensive mathematical theory for the propagation of copy number abnormalities, combining missegregation models with a number of models for modeling intermitosis time. For the missegregation models, we start from a synchronized model of Gusev et al. [3, 4] and show it can be modified to be made asynchronous, while enhancing the ability to analyze the model algebraically. We also present simulation software modeling the accumulation of copy number abnormalities to aid in interpretation of laboratory data on population dynamics in cancer cell lines.

Studies in population genetics have well established the idea that biological variants occur in all populations and at different ratios. Under certain conditions, particular alleles or genes can confer a selective advantage. Some examples of this are antibiotic resistance in bacteria [5, 6], malaria resistance in people heterozygous for the sickle cell allele of hemoglobin [7–9] and the evolution of drug resistance in tumors [10–12]. Cells with the ability to repair DNA after ionizing radiation have much greater survival rates compared to cells lacking any number of these repair enzymes [13–16]. A faster growth rate or the capacity to overcome death or senescence will, all other things being equal, confer upon a variant cell the ability to eventually overtake and dominate a population. In fact, this is one of the fundamental principles of tumorigenesis.

Another well-established tenet of cancer research is that there is an increase in the number of genomic aberrations during the progression from a benign cell mass to a metastatic tumor [17]. These alterations of the cellular blueprint can take many forms. Small point mutagenic events, as in the case of mismatch repair deficient colorectal tumors [18–20], can accumulate in the genome and affect the function of individual proteins either by rendering them incapable of performing their biological function or by conferring upon them new functions. Amplifications or deletions modify the copy number of a given gene(s) thereby affecting protein expression levels. The affected genes are typically oncogenes or tumor suppressor genes, respectively, which ultimately alter cell division rates and/or the ability to arrest the cell cycle to allow repair of damaged DNA. A study by Visakorpi et al. [21] shows that amplification of the androgen receptor gene is selected for in tumors resistant to androgen deprivation therapy. Also, thousands of genes can be gained or lost simultaneously through the unequal partitioning of chromosomes during mitosis or non-reciprocal chromosome rearrangements. These gross chromosomal aneuploidies affect the expression of most of the genes on the involved chromosome [22–26].

Cytogenetic observations have provided ample evidence that the gain of chromosome 7 in colorectal polyps is often the earliest detectable genetic aberration [27–31]. It has been speculated that this specific chromosomal gain confers a growth advantage through an increase in the copy number of the epidermal growth factor receptor gene located at 7p13 [32–34]. Some of the mathematical explanation and all of the simulations below are based on the example of colorectal polyps and chromosome 7. Likewise, the loss of 17p in these same tumors may enable the cells to bypass the cell cycle arrest checkpoint as a result of the decreased copy number of the TP53 gene. Acquisition of extra copies of chromosome 3q in cervical carcinomas may allow the cells to escape senescence via an increase in the number of hTERC genes, since the encoded RNA is part of the machinery involved in the maintenance of telomere length [2]. These strictly conserved recurrent aberrations and genomic imbalances within or across tumor types are presumed by many to be instrumental for tumorigenesis, and are therefore assumed to confer a selective advantage. However, they shed little light on how large the selective advantage is and how the advantage is achieved from one generation to the next.

One hypothesis for the advantage conferred upon cancer cells by means of chromosomal aneuploidy is that they can increase the rate of cell division. Thus, once a copy number change occurs in a few cells, these cells and their descendants could dominate the population. Suppose our protocol is to count a “gain” in a chromosome (i) once its observed average copy number is at least 2 + δ, for some value of δ > 0. Given a hypothesized rate p for chromosome missegregation and a function T_d that estimates the population doubling time as a function of the copy number i, one quantity of interest is the amount of time required to change the average copy number in our population of cells from 2 to 2 + δ. Several researchers have proposed that, in cancers of epithelial origin and derived cancer cell lines, chromosome missegregation and the resulting aneuploidy are dominant genetic aberrations [17, 35–37].

Two laboratory techniques now in wide use to measure aberrations in cancer cells are spectral karyotyping (SKY)/multiplex FISH (M-FISH) [38, 39] and comparative genomic hybridization (CGH) [40]. SKY shows chromosomal rearrangements qualitatively in color in metaphases from individual cells in a sample preparation. CGH, on the other hand, measures deviations from the normal chromosome copy number (2 for autosomes) quantitatively averaged over the entire sample. Since CGH/SKY/M-FISH studies can allow us to measure the average copy number, an estimate of the time required for a shift in the copy number of a given chromosomal region to appear in the population would enable us to decide if the assumed values of p and T_d(i) are biologically plausible.

To study the influence of chromosomal imbalances on cell division rates, we analyzed a mathematical model for cell growth, using parameters such as chromosome missegregation rates and population doubling times. Our goal for this model is to allow us to theoretically determine whether it would be feasible, and how long it would take, to shift the chromosome profile of a continuously growing cell population. This model could ultimately be used to refine the various parameters after in situ experimentation.

In Section 2, we present our exponential model for cell division with missegregation errors. First, we consider a synchronized model for mitosis, with fixed intermitotic times, based on the work of Gusev et al. We then consider a continuous time model using an exponential distribution for intermitotic times. We show that the exponential model is amenable to methods from Markov analysis and linear algebra. Using a computer algebra system, and given a value of δ > 0, it is possible to obtain an analytic estimate for the time T_δ needed to change the average copy number from 2 to 2 + δ. In Section 3.1, we summarize a well-established mitosis model of Smith and Martin [41], the “transition probability model,” that includes a constant lag time before mitosis may occur in any daughter cell. The Smith-Martin model is, in principle, more complex than our exponential model because of an extra parameter (the lag). However, we point out that this parameter can be eliminated in the asymptotic, steady state by a change of variables. Thus, the derivations in Section 2 remain applicable with the addition of a constant lag. In Section 3.2, we summarize a different model of mitosis proposed by Wheals [42] and Tyson and Diekmann [43] called the “sloppy size” model. In Section 4, we present a computer program MITOSIM that simulates mitosis using either the exponential, lagged exponential or sloppy size models, and tracks the propagation of copy number aberrations as they randomly appear in the population. We show results of representative MITOSIM runs and demonstrate that they are in good agreement with analytical results for the exponential and lagged exponential models.

2 Mathematical models for mitosis

2.1 A discrete time model for tumor growth

To clarify the issues involved in modeling mitosis, we first consider an idealized scenario where all the cells in the population have been synchronized to undergo mitosis simultaneously, and we make a further assumption that intermitotic times are constant. This simple model is very similar to the model considered in [3] to study the propagation of chromosomal segregation errors over the long term. The general Gusev model [3, 4] allows for modeling segregation errors over all chromosomal pairs simultaneously, but we prefer to focus on only one chromosomal pair at a time, as the explosion in the number of possible combinations of copy numbers makes computations unwieldy and seriously weakens the statistical power of any measurements.

Suppose we fix our attention on a specific chromosome, for example, chromosome 7 in a colorectal cancer cell line, whose copy number is allowed to range from 1 to k. Suppose also there is a constant missegregation probability p: If a cell with copy number i missegregates during mitosis, it produces two daughter cells, one with copy number i−1 and one with copy number i+1. We enforce boundary conditions on the allowed copy numbers: if i=1, the cell with the smaller copy number dies, and if i=k, the cell with the larger copy number dies. If no chromosomal missegregation occurs, each of the two daughter cells has copy number i.

This process can be described by a transition matrix M(p) = (m_ij), where m_ij is the expected number of cells in state i after mitosis, for each cell in state j before mitosis. Thus

• m_ii = 2(1− p) for all i

• m_ij = p if |i − j|=1, with 1 ≤ i, j ≤ k, and

• m_ij = 0 for i − j > 1.

Let v(t) be the vector describing the distribution of cells in each state as a function of time, t, such that v(0) is the initial state, and let M^t be the t-fold matrix product of M=M(p) with itself. The expected distribution of cells at time t is v(t,p)= M^tv(0). While the exact number of cells in each state would be of interest, CGH technology only measures the average copy number in the cell population. To calculate this quantity, we use the vectors z_k = (1, 2,…, k) and 1_k = (1,1,…,1) (a vector with k entries). The average copy number in the distribution v(t) can be calculated as

$$r(t,p)=\frac{v(t,p){{}^{‵}z}_k}{v(t,p){{}^{‵}1}_k}.$$

To help determine the long-term behavior of r(t,p), let $u(t,p)=\frac{v(t,p)}{v(t,p){{}^{‵}1}_k}$, the vector in the direction of v(t) scaled so the sum of its entries equals 1.

Let us consider the case where k=5. Let r(t,p) denote the average copy number of chromosome 7 after t generations. We use the software package Mathematica [44] (calculations omitted) to calculate r (t, p) for k=5:

$$r(t,p)=\frac{3\left({\lambda }_1^t-3{\lambda }_3^t+\left(3-2\sqrt{3}\right){\lambda }_4^t+\left(3+2\sqrt{3}\right){\lambda }_5^t\right)}{\left(\left(3+2\sqrt{3}\right){\lambda }_5^t+\left(3-2\sqrt{3}\right){\lambda }_4^t\right)},$$ (2.1)

where λ_i is the i^th eigenvalue of the matrix M(p). Given any value for p, and any threshold r_min, we can use Equation (2.1) to find the smallest integral value for t for which r (t, p) > r_min. For example, if p=0.01 and r_min = 2.4, we note that r(2858, 0.01) = 2.39931, while r(2859, 0.01) = 2.40008.

2.2 Comparison with Gusev models

Gusev et al. [3] have presented two models for chromosomal missegregations. In [3], they use the following framework: During the segregation phase of mitosis, any chromosome can witness a segregation error (with probability p) that sends both copies of that particular chromosome to one of the two resulting daughter cells. Thus, for example, a diploid cell will witness missegregations events of both copies of a given chromosome with probability p², and half the time both missegregations will result in a tetrasomic daughter cell (as well as a non-viable nullisomic daughter cell). Our model ignores this possibility as highly improbable and is nearly identical to the Gusev model for small values of p, as the matrix entries in the Gusev model corresponding to higher powers of p are dominated by the linear terms.

In [4], Gusev et al. consider the longer-term, but not asymptotic behavior of this system. Their simulations are constrained by memory limits, since they keep all cells that are used. They present simulations that have evolved for 200 generations, and claim to have studied simulations with more generations, though still with fewer than 1000 generations. Curiously, they find that the modal copy number in the cell population is 1, i.e. the cell population is dominated by monosomic cells, even when the system is seeded with one diploid cell. This phenomenon is a result of their decision to structure the underlying Markov chain such that monosomic cells are less likely (albeit only slightly less likely) to witness missegregations than cells with higher copy number. Thus, the stationary distribution of this system has highest weight on the monosomic state. In contrast, if the Markov chain were structured with identical missegregation rates for all cells, then the stationary distribution would necessarily be symmetrical about the mean of the copy numbers allowed (k/2 in our nomenclature).

In practice, though chromosomal losses are commonly observed in tumor cells, it is far from desirable to have a mathematical framework that necessarily implies that monosomic cells must represent the dominant clone line. Similarly, it would be undesirable to require an expected average copy number as high as k/2. In the following work, we allow for a variety of possible stationary distributions by allowing variation of the mitosis rates as a function of the copy number of the chromosome in question. It would also be desirable to allow for variation of the segregation rates by copy number and, when possible, by chromosome type. The current work does not concern itself with the problem of tracking missegregations across different chromosomes, as this more difficult problem leads to computational unwieldiness. By restricting our attention to one chromosome we only need consider a k-state Markov chain, where k is the maximum allowed copy number. If we were to consider all of C chromosomes simultaneously, this would require a Markov chain with k^C states. Gusev et al. (4) use such a Markov chain, but to achieve computational feasibility are forced to use a biologically unrealistic fixed intermitotic time to study the long-term behavior of the system. Also, the Gusev Markov chain implicitly makes the biologically unrealistic assumption that all copy number aberrations should be equally likely, ignoring the selective advantage or disadvantage given by individual aberrations. Studies have shown (e.g., [17]) that copy number aberrations are not uniformly distributed, and, in fact, certain aberrations tend to be much more likely than others.

2.3 Continuous time modeling

While the discrete time model in Section 2.1 is useful for examining the long-term behavior of a synchronized population of cells with a constant mitosis rate, the assumptions used are biologically unrealistic. Consider, for example, the role of the APC gene, a tumor suppressor that controls cell birth and death processes. It is believed that the inactivation or loss of both copies of APC leads to an increased cell birth to death ratio [45]. Thus, clone lines including this mutation would grow rapidly in the cell population. To address the problem of continuously varying mitosis rates in an asynchronous population, we need to shift from a discrete time model to a continuous time model for mitosis. The simulations of Gusev et al. [3] use two distributions for intermitotic time: a truncated normal distribution and a uniform distribution. Neither possibility has a biological justification, and both contradict studies modeling intermitotic times with real data [41–43, 46–49]. We prefer an exponential distribution, for reasons that will become clear in Section 3.

Suppose that the time T for a cell c with copy number i to undergo mitosis can be described as an exponentially distributed random variable with parameter λ_i, and let X_i(t) denote the number of cells with copy number i, for i = 1, 2, …, k. We can describe the overall behavior of this system using a system of differential equations:

$$X_i{}^{\prime }(t)=(1-{\lambda }_i)X_i(t)+2{\lambda }_i(1-p)X_i(t)+r_{i-1}p{X}_{i-1}(t)+{\lambda }_{i+1}p{X}_{i+1}(t).$$

The expected behavior of the system is described by M(t) = exp(Qt), where

$$Q=\left(\begin{array}{lllllll}1+\lambda -2{\lambda }_{1}p\hfill & {\lambda }_{2}p\hfill & 0\hfill & \cdots \hfill & \cdots \hfill & \cdots \hfill & 0\hfill \\ {\lambda }_{1}p\hfill & \ddots \hfill & \hfill & \hfill & \hfill & \hfill & ⋮\hfill \\ ⋮\hfill & \hfill & \ddots \hfill & {\lambda }_{i}p\hfill & 0\hfill & \hfill & ⋮\hfill \\ ⋮\hfill & \hfill & {\lambda }_{i-1}p\hfill & 1+{\lambda }_i-2{\lambda }_{i}p\hfill & {\lambda }_{i+1}p\hfill & \hfill & ⋮\hfill \\ ⋮\hfill & \hfill & 0\hfill & {\lambda }_{i}p\hfill & \ddots \hfill & \hfill & 0\hfill \\ ⋮\hfill & \hfill & \hfill & \hfill & \hfill & \ddots \hfill & {\lambda }_{k}p\hfill \\ 0\hfill & \cdots \hfill & \cdots \hfill & \cdots \hfill & 0\hfill & {\lambda }_{k-1}p\hfill & 1+{\lambda }_k-2{\lambda }_{k}p\hfill \end{array}\right),$$

i.e. q_ii = 1 + λ_i − 2λ_ip, q_i−1i = q_i+1i = λ_ip, and q_ij = 0 for |i − j|> 1. Given known values for the mitosis rates (λ_i), we can express the entries of M(t) in closed form as a function of p (although the exact formulae can be quite complicated). Given the decomposition of Q

as Q=HDH⁻¹, where $D=\left(\begin{array}{ccc}{d}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & d_k\end{array}\right)$is s a diagonal matrix, note

that $\text{exp}(Dt)=\left(\begin{array}{ccc}\text{exp}(d_{1}t)& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & \text{exp}(d_{k}t)\end{array}\right).$ We can then express M(t) as

M(t)= Hexp(Dt)H⁻¹

Consider a cell population growing at an exponential rate. The relationship between the doubling time T_d of the population and the exponential parameter λ is given by $\lambda =\frac{\text{log}2}{T_d}$. As an example, consider the case where the doubling time of a population of unaltered cells is 18 hours, k = 5, and cells with three or more copies of chromosome log 7 have an increased rate of growth with a doubling time of 17 hours; i.e., ${\lambda }_1={\lambda }_2=\frac{\text{log}2}{18}$, and ${\lambda }_3={\lambda }_4={\lambda }_5=\frac{\text{log}2}{17}$. Let us consider a missegregation rate of p = .01 (suggested by Lengauer et al. [35]) and examine the behavior of M(t). In this case,

$$Q=\left(\begin{array}{lllll}1.03774\hfill & 0.000385\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0.000385\hfill & 1.03774\hfill & 0.0004077\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0.000385\hfill & 1.03996\hfill & 0.0004077\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0.0004077\hfill & 1.03996\hfill & 0.0004077\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0.0004077\hfill & 1.03996\hfill \end{array}\right).$$

Let us assume we start with one cell with copy number 2. At time t, the expected state of the system can be described as

$$v(t)=M(t)v(0)=exp(Qt)\left(\begin{array}{l}0\hfill \\ 1\hfill \\ 0\hfill \\ 0\hfill \\ 0\hfill \end{array}\right)=\left(\begin{array}{l}{v}_1(t)\hfill \\ v_2(t)\hfill \\ v_3(t)\hfill \\ v_4(t)\hfill \\ v_5(t)\hfill \end{array}\right).$$

In this formulation, each function v_i(t) is a linear combination of the non-zero entries of exp(Dt), i.e. a linear sum of five exponential functions. We are interested in the value of t for which the average copy number of a cell in the population will be at least 2.4, as this is the threshold for detection of a copy number aberration using the CGH methodology as explained below. (See du Manoir et al [50] for an extended discussion of threshold choices in CGH studies.) The average copy number in a sample can be found by considering the ratio

$$r(t)=\frac{z_5{}^{‵}u(t)}{1_5{}^{‵}u(t)},$$

where, as in Section 2.1, z₅ = (1, 2,3, 4,5) and 1₅ = (1,1,1,1,1). The numerator of this ratio counts the total number of chromosomes of interest (e.g., chromosome 7 in a colorectal polyp), while the denominator counts the total number of cells. With the parameters chosen, r(809.374) =2.4000005. Thus with the parameters chosen, one would expect a CGH signal that would be interpreted as a gain sometime between 809 and 810 hours, i.e. after 33 days and 17–18 hours. This is considerably faster than the estimate from Section 2.1, a result attributable to the increased mitosis rate hypothesized for cells with larger copy numbers.

In the CGH literature, a gain is considered to be present when the fluorescence ratio comparing a tumor cell to a healthy cell is 1.2 or greater. In principle, the fluorescence ratio of 1.2 corresponds to an average copy number in the tumor cells of at least 2*1.2=2.4. In experimental practice, when the fluorescence ratio is 1.2, the average copy number may be slightly higher or lower than 2.4 due to imprecision.

3 Modeling mitosis: a historical perspective

3.1 Transition probability model

In Section 2, we considered some simple models for mitosis, to facilitate a simultaneous consideration of mitosis and mutation. In this section, we consider several historical models for mitosis.

Smith and Martin provided one of the first coherent mathematical models of the cell cycle [41]. The cell cycle can be broken into four phases: the G₁ phase before DNA synthesis, the S phase during which DNA is synthesized, the G₂ phase after DNA synthesis and before the M phase, when mitosis occurs. Whereas the G₂, S, and M phases are typically of fixed duration in most cell types, the length of the G₁ phase can vary greatly, even within a single tissue sample. Smith and Martin proposed modeling the process as consisting of a state of indeterminate length (state A), contained in the G₁ phase, and a state of fixed length encompassing the other three phases (state B).

This process is modeled as follows: let T be a random variable describing the intermitotic time of a cell c. Then T = T_A + T_B, where T_A is a random variable describing the time spent in state A and T_B is a constant describing the time spent in state B. Consideration of observed interphase data led Smith and Martin to conclude that T is exponentially distributed.

The assumption that T is exponentially distributed has been widely used in practical flow cytometry (see e.g., Sahar et al [51]and Bertuzzi et al [52]), with or without the additional assumptions of the transition probability model. The assumption of an exponential distribution was used implicitly by Gray [53] to generate simulated data that was later used by Dean [54] to design and test the popular software SFIT for estimating DNA distributions in flow cytometry. Smith and Martin showed that the transition probability model together with the conclusion that T is exponentially distributed imply that T_A is exponentially distributed (see Appendix). Let λ_A be the parameter of this distribution, such that, for values of t greater than T_B and small values of Δt, P[T ∈(t,t + Δt) | T > t] ≈ λ_AΔt.

Suppose a population of cells is growing according to the Smith-Martin model. Let A(t) denote the set of cells in state A at time t, B(t) denote the set of cells in phase B at time t and let N (t) = |A(t) ∪ B(t)|. Cell lines usually have a doubling time that is experimentally repeatable if there is enough space to grow and culture conditions (such as the amount and type of nutrients in the media) are approximately the same. This observation implies that, if one ignores cell loss, then the behavior of the system as a whole can be modeled as exponential growth, such that N(t) = N(0) exp(λt) for some constant λ.

We consider the growth rate as follows: let c be a cell chosen uniformly from X(t) = A(t) ∪ B(t), and let T be the amount of time that passes before c undergoes mitosis. An exponential distribution P is based on the proposition that there is a constant $\lambda =\underset{\Delta t\to 0}{lim}P[T<\tau +\Delta t|T>\tau ]$ that is independent of τ. Smith and Martin provided a formula relating λ, λ_A and T_B. We present the formula and its derivation in the Appendix.

3.2 Sloppy size models

The Smith-Martin model for mitosis described in Section 3.1 provides a good fit for observed statistics of the cell cycle [55], and has been widely used and highly cited. The essential hypothesis that time to mitosis is exponentially distributed was used in developing the SFIT software, as noted above. However, its simplicity has been criticized for example, by Murphy et al [46] for failing to explain the correlations in generation times of sister cells, by Tyson [56] for failing to match some experimental data comparing the size and age of cells at mitosis, and by Koch [57] for lacking a biological basis. The exponential distribution, which Smith and Martin use to describe the lag time the cell experiences in the A state, is used often in the physical sciences but rarely in biological sciences. Whereas the exponential distribution requires a “memoryless” system, biological systems tend to be too complex to be accurately described as memoryless. Thus, the Smith-Martin model does not allow for any correlation between cell mass and the probability of mitosis, nor does it allow for any correlation between the intermitotic times of sister cells.

In contrast to the transition probability model, which expresses the probability of mitosis as a (fixed) function of time, the sloppy size model first proposed by Wheals [42] and then formalized by Tyson and Diekmann [43], expresses the probability of mitosis as a function of cell size (where ‘size’ can mean mass, volume, length, or some other measure of the cell). In later papers [47, 58], which benefited from increased understanding of the molecular mechanisms of mitosis, size was modeled as the number of molecules of one or more proteins in the mitosis-associated CDC protein family.

In sloppy size modeling, it is typical to scale cell sizes to lie in the interval (0,1). The sloppy size model also presumes that there is a constant a, with 0.5 < a <1, such that cell mitosis only occurs in those cells whose size is at least a, but must occur in any cell before it reaches a size of 1 (on this scale). The lower bound serves the mathematical purpose of preventing the possibility of a new daughter cell from a mitosis immediately redividing a second time. Some biological justification for the lower bound on a can be found in the experimental data of Wheals [42], although that study concerns itself solely with asymmetric cell division in yeast.

Each daughter cell resulting from a mitosis inherits approximately half of the size s of the parent cell (and thus has size in the interval (a/2,1/2)). To allow some deviation in the sizes of the daughter cells, we divide the cell mass into two parts of size rx and (1−r)x, where r is normally distributed about μ=0.5 with a standard deviation of σ=0.016. These values of μ and σ have been estimated by Sveiczer et al [48]. Letting x(t) represent the size of a cell at time t, we model cell growth using a growth function V(x) according to the differential equation

$$\frac{dx}{dt}=V(x).$$

Tyson and Diekmann [43] suggest a number of candidates for V(x), two of which we discuss below.

In the sloppy size model, mitoses occur according to a probability distribution b(x) on the size variable x; i.e., if Δt is the length of a small interval, the probability of witnessing a mitosis of a cell of size x is b(x)Δt.

Consider an individual cell c. Let x(0) be the size of c at the time of its separation from a parent cell. Then c will grow to at least the size a before mitosis is possible. Letting T₀ denote the amount of time required for this initial stage of growth, we observe that

$$T_0={\int }_{x(0)}^a{[V(x)]}^{-1}dx.$$

For x > a, let P(x) be the probability that c will grow to at least size x before dividing. Then

$$P(x)=\text{exp}\left(-\underset{a}{\overset{x}{\int }}\frac{b(\xi )}{V(\xi )}d\xi \right).$$

With the constraint that no cell grows greater than 1, the choices of b and V must result in the equality P(1) = 0, i.e.

$$\underset{x\to 1^{-}}{lim}\underset{a}{\overset{x}{\int }}\frac{b(\xi )}{V(\xi )}d\xi =\infty .$$

To model exponential growth, we let V(x) = kx for some constant k. With this choice of V, the distribution b must have a singularity near x=1 and must approach zero as x approaches a from above, since b(x) = 0 for x ≤ a. To ensure continuity on the interval (0,1), Tyson and Diekmann suggested the following choice for b:

$$b(x)=\{\begin{array}{cc}0,& 0<x<a,\\ \frac{\widehat{b}{(x-a)}^2}{(1-x)},& a<x<1,\end{array}$$

where $\widehat{b}$ is a constant such that $\underset{0}{\overset{1}{\int }}b(\xi )d\xi =1$.. Alternatively, rather than forcing the mitosis probability distribution to have a singularity as x approaches 1, we could use a growth function that leads to decelerating growth as x approaches 1. The logistic growth function V(x) = kx(1 − x) allows the usage of any bounded distribution b with the constraint that b = 0 outside the interval (a,1). Following [43], we have used

$$b(x)=\{\begin{array}{cc}0,& 0<x<a,\\ \widehat{b}{(x-a)}^2,& a<x<1,\end{array}$$

again with $\widehat{b}$ chosen such that $\underset{0}{\overset{1}{\int }}b(\xi )d\xi =1$.

4 Simulation software

4.1 Software description

We have developed the software package MITOSIM, implementing the model of chromosomal missegregation described in Section 2 and the models of mitosis described in Section 3. MITOSIM maintains a queue of cells, ordered by the time to mitosis. The basic function is sampleTime: this function selects the cell at the front of the queue, creates two daughter cells, randomly determines whether the chromosomes divide equally to the two daughter cells, and calculates the subsequent division times for each daughter cell. Division time can be calculated according to any of the following distributions: normal, exponential, exponential with user-provided lag, discrete, constant, and sloppy size (with either exponential or logistic cell growth).

MITOSIM tests for chromosomal missegregation with each simulated mitosis. If no missegregation occurs, a cell with copy number i for the chromosome under consideration yields two daughter cells with copy number i, but a missegregation produces one daughter cell with copy number i−1 and one with copy number i+1 for the chromosome in question. Only cells with copy numbers in the range [1,k] are considered viable: if i−1 = 0, the cell has lost all copies of the genes residing on that chromosome (i.e. is nullisomic), is not considered to be viable and is removed from the simulation. Similarly, if i = k, the cell with copy number i+1 is considered not to be viable and is removed from the simulation.

After each mitosis, the program adjusts the total chromosome count: $\sum _c\#c$ where c ranges over the cells in the queue, and #c is the copy number of the selected chromosome in cell c. The total copy number is then divided by the number of cells to calculate the average copy number. If the average copy number exceeds a user-provided threshold, the program notes the time elapsed and terminates, returning statistics including total time elapsed, total number of mitoses, total number of missegregations, total number of cells eliminated due to a zero or an excessively high copy number, and the average doubling time witnessed as the population grew.

In the laboratory setting, the cell lines may be resampled after a predetermined period of time, to maintain a limit to the size of the cell population. This resampling is modeled by MITOSIM by including each cell uniformly with a constant probability when a certain amount of time has passed. In theory, the resampling process should have a negligible effect on the average copy number, presuming the minimum sample size is sufficiently large (the default setting uses n=1000). Also, using similar logic, this modeling ignores the possibility of regular cell death, as random cell deaths should have a negligible effect on the average copy number of the population.

4.2 Parameter settings

To test MITOSIM, we modeled the growth of intestinal cells, with a specific eye toward the presence or absence of chromosome 7. We tested the rate of signal appearance based on two possibilities: a null hypothesis that missegregation of chromosome 7 has no effect on mitosis rates, and the hypothesis that cells with extra copies of chromosome 7 divide at an accelerated rate. The increased rate of cell division was calculated based on the following information.

On average, the lining of the colon is replaced (through a combination of shedding and apoptosis) every 3–5 days in mammals [59]. Thus, a proliferating crypt cell must divide around once every 96 hours in order to keep pace with the rate of cell loss. A colon polyp of 1 cm³ containing 1×10⁹ cells takes about 7 years to develop, and would require 30 population doublings (i.e. 2³⁰). The healthy colon tissue growing at a standard exponential rate would go through approximately 640 generations over a seven year period. Thus, the appearance of a tumor reflecting an additional 30 population doublings could be accomplished by an increase in the growth rate of approximately 5%. We have modeled this increase in the growth rate by assuming that cells with at least one extra copy of chromosome 7 witness an increase in their mitosis rates of approximately 5% per extra copy. These calculations assume that an increase in cell proliferation, and not a marked reduction in apoptosis, is the dominant result of a genetic growth advantage. This is supported by the fact that Ki67 protein levels, a marker of cell proliferation, are increased [60].

Most CGH studies declare that a gain of a chromosomal region has occurred when the fluorescence ratio exceeds 1.2, which corresponds to 2.4 chromosomes per test cell against 2 chromosomes per reference cell. Thus, we have enforced a stopping point when the average copy number for cells in the population of the chromosome under consideration exceeded 2.4. (The value of 2.4 is provided as input by the user; analogous experiments could be done using any threshold.) CGH is the typical research tool used to assess gains and losses of chromosome material in tumor samples since it can be performed without needing the tumor to grow in culture, and also can be used (retrospectively) on formalin-fixed archived material. Nullisomic cells (i.e. cells missing all copies of a given chromosome) were eliminated from the simulation population because such cells are usually not observed in vivo.

4.3 Comparison of various distributions

In this section, we consider the time required for the stop threshold to be reached under various conditions. We tested each of the following distributions: exponential, exponential + 4 hour lag, exponential + 8 hour lag, normal, sloppy size with an exponential growth rate, and sloppy size with a logistic growth rate. To test the null hypothesis, we calibrated the parameters of each distribution to have a doubling time of 18 hours. The 18 hour estimate was based on the behavior of colorectal cancer cell lines HCT116 (American Type Culture Collection cat # CCL-247), p53HCT116 [60], and DLD-1 (American Type Culture Collection cat # CCL-221) in our laboratory. The calibration was done analytically for the various exponential distributions, and by simulation for the sloppy size distributions. (The normal distribution was simply set to have a mean mitosis time of 18 hours, as the expected intermitotic time equals the expected doubling time in this case.) In contrast to the 5-state model used in prior sections, these simulations were performed using a 7-state model. Results of these simulations are shown in Figure 1.

Figure 1.

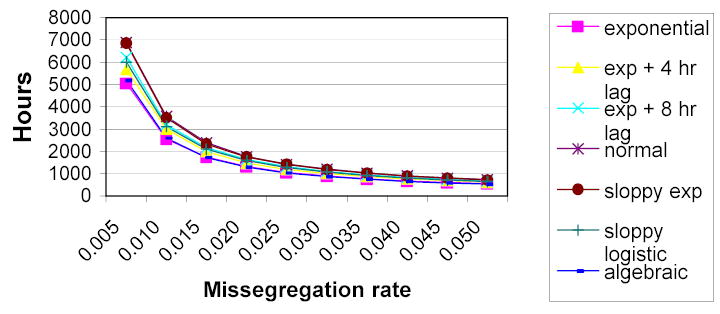
Signal times for constant rate mitosis models

Figure 1 also includes a curve labeled “algebraic” that shows the values expected according to Mathematica calculations performed as described in Section 2.2 (but using 7 states instead of 5). As we see, the plot of signal time vs. missegregation rate is nearly identical regardless of which distribution is used to model the cell cycle when the missegregations rate is high.

To test the effect of an increased division rate, we then performed the same test, but scaled the rate of the cell cycle as a function of the number of chromosomes in a cell. Using the rough approximation of a 5% increase in the cell division rate for tumor cells, we scaled the mitosis rate parameters such that doubling times were decreased by 1 hour for each extra copy of chromosome 7 (and increased the doubling time of cells with copy number 1 by one hour). This hypothesis led to considerably faster growth of aberrant subpopulations, and to considerably faster achievement of the stop threshold. Results are shown in Figure 2.

Figure 2.

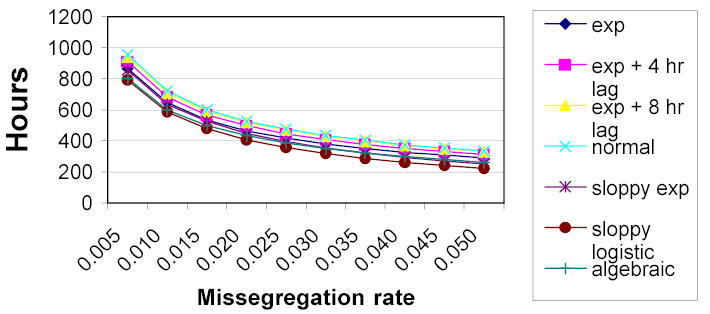
Signal times for varying rate mitosis models

Again, we see that the shape of the curve does not depend on the choice of the distribution used to simulate the cell cycle. The exponential curve suggests that, regardless of the distribution used for intermitotic times at the cellular level, an asynchronous population will observe mitoses at an exponential rate.

4.4 Calculating p-values

Ultimately, the intended uses of MITOSIM are to test hypotheses about the missegregation ratio, the growth advantage for cells with extra chromosomes, and other parameters of the model. To compare two parameter settings P₁ and P₂ in a hypothesis testing framework, it is desirable to know to what extent the output distributions for time to CGH signal (and other outputs) under P₁ and P₂ overlap, if at all. Suppose that parameter setting P₁ results in generally shorter times to reach the CGH ratio of 1.2. Then one could say that the time distribution for P₁ differs from that of P₂ at P-value (confidence level) a, if the lower (1 − α) fraction of the times for P₁ do not overlap with the times for P₂ or if the upper (1−α) fraction of the times for P₂ do not overlap with the times for P₁; which rule is applicable depends on which of P₁ or P₂ corresponds to the “null hypothesis”. The standard value of α is 0.05. To facilitate such tests, MITOSIM prints out the 0.05 and 0.95 level for time to CGH signal and other quantities of interest.

Consider two examples based on the simulations summarized in Figures 1 and 2. First compare P₁ = 5% mitotic advantage for an extra copy to P₂ = no advantage, with other settings fixed at exp + 8hr lag for the time to mitosis and 0.01 as the missegregation rate [35]. In this case, we consider P₂ as the null hypothesis. The 0.95 level for time to CGH signal under P₁ is 818.73 hours, while the minimum time under P₂ is 1440.02 hours, so these parameter settings lead to statistically distinguishable outcomes. Second, compare P₁ = 0.05 missegregation ration, P₂ = 0.01 missegregation ratio, and P₃ = 0.005 missegregation ratio with all other settings fixed at 5% mitotic advantage and exp+8hr lag time for mitosis time. Again we consider P₂ as the null hypothesis, since 0.01 was the missegregation ratio measured in [35] for a colorectal cancer cell line. Under the P₁ hypothesis, 95% of the simulations required less that 363.01 hours, while none of the 1000 simulations under the P₂ hypothesis took less than 506.3 hours, which indicates that P₁ and P₂ can be statistically distinguished. In contrast, under the P₃ hypothesis, 95% of the simulations required at least 774.97 hours, a threshold also achieved by 166 of the P₂ simulations, indicating that the P₂ and P₃ distributions have a non-trivial overlap.

5 Discussion

We have presented a matrix algebra model, and accompanying simulation software MITOSIM, to consider the effects of chromosome copy number changes in cancer cell lines on mitosis times. Our simulations with MITOSIM agree with estimates of the matrix algebra model calculated using the software package Mathematica [44]. This modeling can be useful in testing hypotheses about why aberrant cells eventually dominate the population in a tumor. The presence of chromosome copy number changes can be measured by CGH. A much simpler modeling and simulation method has been used by Roschke et al. [61] to test predictions about chromosome rearrangements in cancer cell lines as measured by SKY.

The work of Gusev et al. [3, 4] introduced the possibility of an algebraic model for chromosomal missegregations. Nowak et al. [62] and Komarova et al. [63] have also used mathematical modeling to investigate the onset of cancer and the role played by chromosomal instability during this process. The Nowak/Komarova models, though mathematically sophisticated, are more concerned with isolated genes than aneuploidy, and are not suitable for modeling the appearance of CGH signal in a population of cells.

There are numerous ways in which our models are more useful and relevant to real cell line data than the models of Gusev et al. First, the previous models did not allow for variability in the growth rates of cells with different copy numbers, which is the hypothesis we wish to test. Second, the Gusev model, by treating missegregations of each chromosome as an independent event with equal likelihood (as opposed to considering missegregations by chromosome type), creates a situation where monosomic cells are necessarily found in the most stable cell lines. While some chromosomal losses are believed to lead to a selective advantage for the respective clone line, it is undesirable for a mathematical model to have this as a necessary relationship. Third, our non-synchronized model using the exponential time distribution, with or without lag, can be solved algebraically to find the time to CGH signal for any amount of time; in contrast, the Gusev et al. method requires repeated multiplication of a non-sparse matrix. Fourth, the predictions of our models are expressed in terms of average copy number, which can be directly estimated in the laboratory by CGH. The Gusev et al. model does not lead to predictions easily testable by CGH or SKY. Fifth, we introduced in MITOSIM the technique of sampling, which overcomes the limitation on simulation time that Gusev et al. encountered. Sampling in the simulation is realistic because cell lines are sampled every few population doublings when they are grown in the laboratory.

The software MITOSIM offers two classes of cell cycle models, the transition probability of Smith and Martin [41] and the sloppy size control model as formulated by Tyson and Diekmann [43]. When viewed in the aggregate, a population of cells growing according to the complex process known as the cell cycle lends itself to analysis using the tools of linear algebra. The key to the current analysis is the usefulness of the exponential distribution that arises in the Smith-Martin model. The idea that the Smith-Martin model is a good starting point to make analytic estimates is also emphasized by Cain and Chau [64] and Baker et al [65], for example.

Aside from the transition probability model and the sloppy size model, there have been a number of previous models for the distributions of intermitotic times or the growth of cell populations. Some studies have focused on the statistical properties of intermitotic times, as did Smith and Martin. In [46, 66], the Eyring-Stover survival theory was shown to better explain the observed positive correlation between sister cells than the Smith-Martin model (which implies no such correlation). Cain and Chau [64] extended the Smith-Martin model to consider variables such as cell death, a post-mitotic state of constant length, and also introduced substrate-dependent unbalanced growth using variable cell maturity velocity and/or an extra quiescent state during the B phase that growing cells can randomly enter or depart [67].

Tomasovic et al [68] used matrix algebra to estimate and compare parameters of the cell cycle under different conditions. This work attempted to estimate delays in the cell cycle caused by either x-rays or a drug, using a state space corresponding to time periods in the cell cycle. In theory, this type of approach can be used for any further refinement of time, though it would only be useful when distinct observations are available for each of the time periods in question. A set of coupled differential equations structurally similar to those we used for continuous time modeling was proposed by Gray [53]. Like Tomasovic et al., Gray used the states to mean subintervals of the cell cycle. He used the differential equations to drive a computer simulation and parameter fitting for the cell cycle, but did not use matrix algebra to obtain closed-form solutions.

Other models of the cell cycle have focused less on the intermitotic times than on either the cell sizes or the accumulation of mitosis initiator enzymes, just as the sloppy size model does. Kimmel et al [49] modeled mitosis probabilities purely as a function of the accumulation of the unequal division of nucleic acids. The 4-parameter continuum model of Cooper [69] is another model for cell mitosis where occurrence of mitosis happens as a function of cell size or of the amount of mitosis initiator in each cell. The continuum model suggests that variable lengths of the G₁-phase are a consequence, rather than a cause, of varying intermitotic times. Since the lengths of the M, G₂, and S phases are essentially constant, the variation in intermitotic times, regardless of its cause, leads to a variation in the length of the G₁ phase. This model can explain the lack of the G₁ phase in prokaryotic cells, a lack generally ignored by most models.

There are several other models of the cell cycle, which might be considered as alternatives. For most of the models mentioned here, it is unclear how to represent the simple hypothesis that an extra copy of a chromosome leads to faster mitosis within the numerous model parameters. One model, the “tandem model” proposed by Tyson and Hanngsen [70], is intermediate between the two models we have considered. The tandem model uses two states like the Smith-Martin model but uses rigid size control instead of sloppy size control.

Koch has considered the historical evolution of the transition probability model, and has criticized it for being primarily phenomenological, with insufficient biological motivation [57]. But for our purposes, namely considering the large-scale growth behavior of a cell population while trying to reduce the number of variables considered, the transition probability model appears to be adequate. All of the models we considered, including the more complex sloppy size models, yielded nearly identical exponential decay curves (Figures 1, 2) describing the appearance of CGH signal as a function of missegregation rate. One can see some differences in the estimated time for low missegregation rates in Figure 1 when the expected mitosis time is the same for all copy numbers, but the ability to discriminate between small advantage for extra copies (Figure 2) and no advantage (Figure 1) is virtually identical. Thus, though the sloppy size model (and presumably other models) may represent a more comprehensive biological understanding, the increased complexity of these models does not appear to add to our understanding of the growth of larger populations. Indeed, the sloppy size model requires the usage of density functions that we have defined arbitrarily, and whose direct observation would be problematic given typical data set sizes. In conclusion, given the easy transition from the simple transition probability model to the matrix algebraic formulation of the problem, we prefer the TP model based on a consideration of the limit of the amount of data readily available, and a general preference for simpler models over more complex models, when both models appear to be adequate for a given task.

Appendix

In this appendix, we review the relationship between the expected intermitotic time of a single cell T and the expected doubling time T_d of a population of cells. We also consider how the doubling time varies when considering the Smith-Martin distribution where the intermitotic time T is generated as the sum of an exponentially distributed variable T_A and a constant T_B. The derivations are from Smith and Martin [41] under their assumptions that the set of cells have a doubling time T_d, and that one can ignore cell loss because the cells are sampled to start a new culture every few days. The derivations are presented here for the sake of completeness.

In the simplest case, T is a constant over all cells, and E[T] = E[T_d] = T; i.e. the doubling time equals the expected intermitotic time. But in general, this equality need not hold. Consider the case where T is exponentially distributed with parameter λ. In this case, $E[T]=\frac{1}{\lambda }$, but $E[T_d]=\frac{\text{ln\hspace{0.28em}}2}{\lambda }$. The doubling time is less than the expected mitosis time because quickly dividing cells decrease the doubling time more than slowly dividing cells increase it. In practice, we let ${\widehat{T}}_d$ be the observed doubling time, and solve for our estimate for $\lambda ,\widehat{\lambda }=\frac{\text{ln\hspace{0.28em}}2}{{\widehat{T}}_d}$.

Now consider the Smith-Martin distribution, where T = T_A + T_B, T_A is random and T_B is a constant. The goal is to show, given that T is exponentially distributed (with parameter λ, that T_A is itself exponentially distributed, and to derive a closed form for its parameter λ_A as a function of λ and T_B. Let A(t) and B(t) denote the sets of cells in state A and B respectively at time t, and let N (t) = |A(t) ∪ B(t)|, the total number of cells at time t.

Let c be a cell in the population at time t. The cell c undergoes mitosis at time t if and only if c leaves state A at time t − T_B. Since the former event is memoryless event whose passage time can be described by an exponentially distributed variable T, the passage time of the latter event can also be described by an exponentially distributed variable. It follows that T_A is also exponentially distributed, and we can define its parameter λ_A using the equation:

$$\begin{array}{l}\lambda \Delta t=P[c\mathrm{\hspace{0.17em} }\text{divides in interval\hspace{0.28em}}(t,t+\Delta t)]\\ =P[c\mathrm{\hspace{0.17em} }\text{leaves state A in interval\hspace{0.28em}}(t-T_B,t-T_B+\Delta t)]\\ =P[c\in A(t-T_B)]{\lambda }_A\Delta t.\end{array}$$

Let N_A(t) and N_B(t) denote the number of cells in the population in state A or state B, respectively, at time t, such that N(t) = N_A(t) + N_B(t). Let t₀ be an arbitrary real number, and let t₁ = t₀ + T_B. The number of new cells created in an interval of length T_B is precisely equal to the number of cells in state B at the beginning of the interval. Thus

$$N(t_1)-N(t_0)=N_B(t_0).$$

Also, presuming exponential growth of the population, the behavior of N(t) can be described by the equation

$$N(t)=N(0)\text{exp}(\lambda t).$$ (A.1)

Thus

$$N(t_0)\text{exp}(\lambda T_B)-N(t_0)=N_B(t_0).$$ (A.2)

Adding N_A(t₀) to (A.2) yields

$$N(t_0)=[N(t_0)\text{exp}(\lambda T_B)-N(t_0)]+N_A(t_0),$$

which leads to (after dividing by N(t₀))

$$\frac{N_A(t_0)}{N(t_0)}=2-\text{exp}(\lambda T_B),$$

so N_A/N is invariant as a function of t.

Therefore, one introduces a “rate constant” λ_A such that the expected number of cells undergoing mitosis at time t + T_B is

$$\lambda N(t+T_B)={\lambda }_A{N}_A(t).$$ (A.3)

The equation relates the rate of mitosis to the rate at which cells leave state A. Since the time to mitosis is exponential, the set of cells in state B is decaying exponentially with parameter λ, and hence the set of cells in state A at time t will also decay exponentially with parameter λ_A, We can use Equation (A.1) to transform the left-hand side of (A.3):

$$\lambda N(t+T_B)=\lambda N(t)\text{exp}(\lambda T_B),$$

and thus

$${\lambda }_A=\frac{\lambda \mathrm{\hspace{0.17em} }\text{exp\hspace{0.28em}}(\lambda T_B)N(t)}{N_A(t)}=\frac{\lambda \mathrm{\hspace{0.17em} }\text{exp}(\lambda T_B)}{2-\text{exp}(\lambda T_B)}.$$