Abstract
Two issues regarding the robustness of the original transmission disequilibrium test (TDT) developed by Spielman et al are: (i) missing parental genotype data and (ii) the presence of undetected genotype errors. While extensions of the TDT that are robust to items (i) and (ii) have been developed, there is to date no single TDT statistic that is robust to both for general pedigrees. We present here a likelihood method, the TDTae, which is robust to these issues in general pedigrees. The TDTae assumes a more general disease model than the traditional TDT, which assumes a multiplicative inheritance model for genotypic relative risk. Our model is based on Weinberg’s work. To assess robustness, we perform simulations. Also, we apply our method to two data sets from actual diseases: psoriasis and sitosterolemia. Maximization under alternative and null hypotheses is performed using Powell’s method. Results of our simulations indicate that our method maintains correct type I error rates at the 1, 5, and 10% levels of significance. Furthermore, a Kolmorogov–Smirnoff Goodness of Fit test suggests that the data are drawn from a central χ2 with 2 df, the correct asymptotic null distribution. The psoriasis results suggest two loci as being significantly linked to the disease, even in the presence of genotyping errors and missing data, and the sitosterolemia results show a P-value of 1.5 × 10−9 for the marker locus nearest to the sitosterolemia disease genes. We have developed software to perform TDTae calculations, which may be accessed from our ftp site.
Keywords: Keywords: misclassification, genetics, statistics
Introduction
In the field of statistical genetics, methods such as linkage disequilibrium (LD) analysis have long been used to fine-map trait genes once linkage analysis has narrowed the gene to a small genomic interval (eg, 1–5 cM).1,2 By LD analysis, we mean any method of analysis that compares differences in allele, haplotype, or multilocus genotype frequency distributions among a case population and a control population. A commonly used LD method is a case control study (a population-based strategy), which uses allele, genotype, haplotype, or multilocus haplotype data from a group of unrelated cases and from controls, individuals who are matched with cases on factors such as ethnicity, gender, and age.1,3 One limitation of such methods is that they are not robust to unbalanced matching of cases and controls.1 As an alternative, methods that use family-based controls have been proposed as a replacement for population-based methods.4– 8 Such methods are robust to population stratification (unbalanced matching). Building on the work of Falk and Rubinstein,4 Ott,9 and Julier et al,10 Spielman et al6 developed the McNemar test as a test for linkage and named it the transmission/disequilibrium test (TDT). The sampling unit for this test is a trio of a father, mother, and an affected child genotyped at a di-allelic marker locus that is hypothesized to be close to a trait locus, and for which at least one of the parents is heterozygous at the marker locus. An important feature about this statistic is that it is valid (ie, does not increase type I error), as a test of linkage, for multiplex families11 (although the TDT is not valid as a test of association in the presence of linkage for multiplex families). As a result, the original TDT is one of the most widely studied statistical genetics tests of the last decade (the original 1993 paper has over 1500 citations in the ISI Web of Science as of this writing.)
Two potential limitations of the TDT statistic regard its robustness. Curtis and Sham12 showed that computation of the TDT statistic on trios in which one parent is missing marker genotype data increases the type I error rate of the statistic. Also, Gordon et al,13 using simulated data, demonstrated that random genotyping errors that result in Mendelian consistent genotype data for trios also cause an increase in type I error when these data are analyzed with the TDT. Mitchell et al14 proved analytically that undetected genotyping error can cause apparent transmission distortion at markers with alleles of unequal frequency, that this distortion is in the direction of over-transmission for common alleles, and thus undetected genotyping errors may contribute to an inflated false-positive rate among reported TDT-derived associations.
A number of authors have developed extensions of the TDT that address the first robustness issue and that are valid in the presence of missing parental genotype data.15–17 In particular, Weinberg’s reformulation of the TDT in a likelihood framework17 made it possible to address both robustness issues. Regarding the genotype errors robustness issue, Gordon et al13 developed an extension of the TDT, called the TDTae (subscript ‘ae’ means ‘allowing for errors’), which is a valid test for linkage with genotype data from trios in the presence of random genotyping error. To our knowledge, however, no one has developed a TDT that addresses both of these robustness issues jointly for general pedigrees. The purpose of this work, therefore, is the presentation of a new TDT, which we also call the TDTae, that is a valid test for linkage in the presence of LD for pedigrees that have any number of untyped parents and that have random genotyping errors. We note that our ‘new’ TDTae reduces to the original TDTae13 when we assume (Materials and methods – Appendix) that R2 = R12, and the genotype error model considered assumes errors in alleles as opposed to genotypes.13,18
One of the key features of the TDTae is that it assumes a particular error model structure. In their 2001 work, Gordon et al presented an error model assuming that errors are introduced randomly and independently into alleles at a di-allelic locus. This error model was also considered for studies with cases and controls.18 Since that time, a number of new error models, based on differing assumptions about the nature of genotyping errors, have been introduced into the literature.19,20 We comment that our TDTae is capable of using any of these error models. In this work, for reasons that will be described in the next section (Materials and methods – Error models), we consider only three error models: those introduced by Douglas et al,19 Sobel et al,20 and Mote and Anderson.21
It should be noted that recently other TDT tests that allow for random genotyping errors have been published.22,23 The work by Bernardinelli et al uses a Bayesian framework. One advantage of this TDT, which in its present formulation is valid only for trios, is that the Bayesian formulation facilitates addressing the issue of a large number of parameters in the likelihood via Markov chain Monte Carlo (MCMC) methods22 (also see Summary and discussion). The TDT developed by Morris and Kaplan has the advantage of being extendable to multi-locus haplotypes.23
Materials and methods
We begin this section by commenting that all notations used from this point forward are defined in the appendix.
Error models
In this subsection on error models, we describe some general assumptions we make regarding errors. We then list the error models we consider for this work. Finally, we describe some features about the individual error models. To begin, a key assumption that we make throughout this work is that genotyping errors occur randomly and independently in any set of genotype data under consideration. In what follows, we consider three possible error models which we name after their respective authors: (1) Douglas Skol Boehnke (DSB);19 (2) Sobel Papp Lange (SPL);20 and (3) Mote Anderson (MA).21 Each error model can be completely described by its error model parameters. For each error model, we list the parameters below (Appendix – Error model parameters). In supplemental Tables 1–3 (see http://linkage.rockefeller.edu/derek/TDTAE2-error-tables.htm), we document how the penetrance functions (see below; Appendix – Likelihood equation terms) are defined in terms of the specific error model parameters.
Table 1.
Conditional probabilities for trios with genotypes ga, gf(a), gm(a)
|
Parental recoded genotype pair (gf(a), gf(a))
|
||||||
|---|---|---|---|---|---|---|
| Affected child recoded genotype ga | 2, 2 | 2, 1 | 2, 0 | 1, 1 | 1, 0 | 0, 0 |
| 2 | 1 | 0 | 0 | 0 | ||
| 1 | 0 | 1 | 0 | |||
| 0 | 0 | 0 | 0 | 1 | ||
In this table, we compute the conditional probabilities Pr(gk|gf(gk),gm(gk), R1, R2), where gk is the affected child’s recoded genotype (2, 1, or 0) and (gf(gk),gm(gk)) are the parental recoded genotype pair (either (2,2), (2,1), (2,0), (1,1), (1,0), or (0,0)). As we are not assuming imprinting, the pair (gf(gk),gm(gk)) is equivalent to (gm(gk),gf(gk)). Also, the values R1 and R2 refer to the genotypic relative risks f1/f0 and f2/f0, respectively, where f0 = Pr(affected|++ at disease locus), f1 = Pr(affected|+d at disease locus), and f2 = Pr(affected|dd at disease locus)(see Appendix – Penetrances).
Table 3.
Maximum likelihood estimates of TDTae parameters for two SNP markers that show significant evidence for linkage in psoriasis study30
| MLE | R1 | R2 | p11 | p12 | v1 | v2 | v3 | LogLike | LRT | P-value |
|---|---|---|---|---|---|---|---|---|---|---|
| Locus SNP #5 | ||||||||||
| Allele #1 (680 occurrences) | ||||||||||
| H1: | 1.00 | 1.85 | 0.256 | 0.485 | 0.000 | 0.000 | 0.020 | 664.469 | 10.822 | 0.00447 |
| H0: | 1.00 | 1.00 | 0.240 | 0.489 | 0.000 | 0.000 | 0.025 | 669.880 | ||
| Locus SNP #15 | ||||||||||
| Allele #1 (400 occurrences) | ||||||||||
| H1: | 0.47 | 0.81 | 0.129 | 0.409 | 0.033 | 0.000 | 0.016 | 513.988 | 10.914 | 0.00427 |
| H0: | 1.00 | 1.00 | 0.122 | 0.432 | 0.000 | 0.000 | 0.025 | 519.445 | ||
Here, we provide the maximum likelihood estimates of the parameters: the genotypic relative risks R1 and R2, the population genotype frequencies p11 and p12, and the SPL error model parameters v1, v2, and v3 for SNPs #5 and #15 from the psoriasis data set. All parameters are defined elsewhere (Appendix – Error model parameters). Also, we report the maximum log-likelihood of the data under the null (H0) and alternative (H1) hypotheses. The TDTae statistic (LRT) is twice the difference of these log-likelihoods. The P-value computed assumes that the LRT value is drawn from a central χ2 distribution with 2 df. Also, we indicate that the ‘1’ allele was observed 680 times for SNP locus #5, and 400 times for SNP locus #15.
Here, we present a list of some of the features of the different models. Through the remainder of this work, we assume that all marker loci have two alleles, labeled 1 and 2. The DSB model introduces errors into genotypes, and is the only model for which it is not possible for a homozygous 11 genotype to be incorrectly recoded as a homozygous 22 genotype, or vice versa. It is described by two parameters. The SPL model is, for di-allelic loci, described by three parameters. It is the most general error model possible for di-allelic loci, under the constraint that the errors for each genotype are allele-independent.20
The MA model, which is the most general error model possible in the sense that it can describe all other error models, is described by six parameters. The SPL and MA error models allow for the possibility that one homozygote is incorrectly coded as another homozygote. Finally, the models are nested in the following sense: The SPL model reduces to the DSB model by setting v2 = 0; the MA model reduces to the SPL model by setting e31 = e13, e21 = e23, e12 = e32 (see below; Appendix – Error models). This nesting property is useful in our likelihood framework. It allows us to perform a generalized likelihood ratio test24 to determine which error model best fits the data when genotyping errors leading to Mendelian inconsistencies are observed.
Terminology
Consistent
This term is used in reference to a set of genotypes for a given pedigree structure. It means that there are no observed Mendelian inconsistencies in the pedigree for the given set of genotypes.
Valid
This term refers to a property of a test statistic. If a test is valid under some condition, it means that the test statistic maintains the correct type I error rate when that condition is true.
Likelihood function for consistent pedigrees
Assuming that we know the affection status of each individual in a pedigree , we can classify each individual in the pedigree into one of the following mutually disjoint categories:
The individual is a founder.
The individual is an affected child.
The individual is an unaffected child who is a parent.
The individual is an unaffected child who is not a parent.
Without loss of generality, we can reorder the pedigree so that the first i1 individuals are in category (1) (ie, founders), the next i2 individuals are in category 2, and so on. Note that
For our likelihood calculations, we do not consider people in category (4). For a further discussion about individuals in this category, see the Summary and discussion section. Consider now a consistent set of genotypes for the pedigree . Using the notation listed in the appendix and discarding the genotypes of those individuals in category (4), we can write the set as
where the first i1 individuals are founders, the next i2 individuals are affected children, and the remaining i3 individuals are unaffected children who are also parents. Note that the number of elements in this set is n−i4. The likelihood of these data, , is given by the formula:
| (1) |
We compute the conditional probabilities Pr(gk|gf(gk),gm(gk), R1, R2) for all possible consistent trios as a function of the genotypic relative risks R1 and R2 in Table 1.
Our likelihood equation (1) bears a resemblance to the pedigree likelihood equation of Elston and Stewart25 and therefore some further comments on the relation of the two methods are warranted. While both of these likelihood methods are applied to phenotype and genotype data for general pedigrees, there is a major difference between the two. The Elston–Stewart method computes likelihoods as a function of the recombination fraction between a disease and marker locus, whereas our method computes likelihoods as a function of genotypic relative risks. While the Elston–Stewart algorithm is designed to test for linkage whether or not there is any association, our method tests for linkage only in the presence of association.
Note that, in our likelihood equation (1), we assume that founder mating type frequencies are the product of the genotype frequencies for each of the founder parents (terms GF(gaj, p11, p12)). While this assumption may be violated when there is moderate to severe population stratification (the condition for which the original TDT was developed), we make this assumption to reduce the computational complexity of the problem. Please see the Summary and discussion section for more details on this issue.
Likelihood function for inconsistent pedigrees
Having provided the likelihood function for consistent pedigrees (Equation (1)), we now consider the case where the set of observed genotypes is inconsistent. To compute the likelihood of this data set requires that we assume a particular error model . Using the definition of conditional probability and the law of total probabilities, we obtain the likelihood as
| (2) |
where is the set of all sets of consistent genotypes for the pedigree structure is the probability of observing the set of genotypes conditional on the true set of consistent genotypes being and the error model being , and is the likelihood for the set (Equation (1)).
We now provide a more explicit formulation of the conditional probability in Equation (2). Recall from the introduction where we commented that a key assumption of our error models is that errors occur randomly and independently in a set of genotypes. It follows from this assumption that we can write the conditional probability as:
| (3) |
In Equation (3), the penetrance set to 1 for those individuals ai who are missing genotypes for the di-allelic marker locus being tested.
There are several nice features about the likelihood expressed in formulas (1)–(3). First, we note that the likelihood can be computed on a set of inconsistent genotypes from an arbitrary pedigree, not just trios or nuclear families. Second, with the weighting specified in Equation (3) for untyped individuals, we see that the likelihood will be accurate regardless of the number of untyped parents in the pedigree (untyped affected children who are not parents are not used in our calculations). This property is not true for the original TDT when the genotype data are consistent.12 The validity of this likelihood and of the consequent likelihood ratio statistic in the presence of untyped parents extends work previously done by other authors who modified the original TDT to a TDT that is valid in the presence of missing parental data.15–17
Test statistic
Given Equations (1–3), we are now ready to present our test statistic, the generalized TDTae. As mentioned in the appendix (Likelihood ratio test), under the null hypothesis H0, we assume that the genotypic relative risks are both 1; that is, R1 = R2 = 1.0. The generalized TDTae is a likelihood ratio test, and for a given set of observed genotypes (consistent or inconsistent), it is defined as:
| (4) |
It is important to note that, when applying this likelihood ratio test to genotype data for a di-allelic locus, we compute the corresponding statistic treating the 1 allele as the wild-type allele, and the 2 allele as the disease allele.
Maximization
When applying our test statistic, we perform a two-stage maximization procedure. We first compute the log-likelihood under the null and alternative hypotheses using a lattice of points from a multi-dimensional rectangle. We ‘cut’ the cube into a pre-specified number of intervals, and compute the log-likelihoods for the end points of each of the intervals. For example, if we consider the SPL error model, and specify four cuts, then the parameters p11, p12, and v1–v3, all of which have values in the interval [0,1], will be tested at 4 + 1 = 5 values: 0.0, 0.25, 0.5, 0.75, and 1.0. For the relative risk parameters R1 and R2, we initially consider the interval [0, 20]. Thus, in the first stage of our maximization, the log-likelihood is computed for (c + 1)4 + e values under the alternative hypothesis, and for (c + 1)2 + e values under the null, where c is the number of cuts specified, and e is the number of error model parameters for a given error model. The parameter e = 2, 3, and 6 for the DSB, SPL, and MA error models, respectively.
Once the log-likelihoods are computed in the first stage, the parameter values that provide the top five log-likelihoods under each hypothesis are then used as starting values for the Powell maximization procedure.26–28 We use the Powell procedure as implemented in the ‘Numerical Recipes in C’ text.29 The largest log-likelihood from each set of five runs is then chosen as the maximum log-likelihood for each hypothesis.
Null simulations
We simulated 1000 null replicates for each of six different scenarios:
[Two settings for percentage of individuals genotyped (100% or 80%)] × [Three error models (DSB, SPL, or MA)]
In each simulation, 200 fixed pedigree structures with a total of 873 individuals were used. The pedigree structures come from an ongoing psoriasis disease study.30 Each pedigree had at least one affected offspring from a total of 443 affected individuals in all 200 pedigrees. The median number of individuals in a pedigree was four, with the largest pedigree having 13 individuals, and the smallest having three (trio). The SIMULATE program31 was used to simulate the null data, and a computer program was written to both randomly insert errors into individuals’ genotypes and randomly remove individuals’ genotypes from the analysis. The minor marker allele frequency was 0.25. For the error simulations, the following parameter settings were used:
DSB: γ = 0.01, η = 0.04.
SPL: v1 = 0.02, v2 = 0.01, v3 = 0.05.
MA: eij = 0.01(1≤i, j≤3, i≠j).
In addition, we perform the Kolmogorov–Smirnov (KS) goodness of fit test32–34 (as implemented in S-PLUS 6.1) to determine whether the empirical distribution of TDTae statistics for each simulation fits well to a central χ2 distribution with two degrees of freedom, the appropriate null distribution for the TDTae according to likelihood ratio theory.24 A large value for the KS test, or equivalently, a small P-value (less than 0.05) indicates that we reject the null hypothesis that the data come from such a central χ2 distribution.
We used five cuts for the initial search when considering the DSB and SPL simulations, and two cuts when considering the MA simulations. We chose two cutpoints for the MA simulations because each additional cutpoint resulted in a large computational cost.
Real data applications
Psoriasis
We applied our TDTae method to a study of psoriasis. In all, 75 single nucleotide polymorphisms (SNPs) and 32 polymorphic microsatellites from chromosome 17q25 at an average resolution of 80 kb were genotyped in 242 multiply-affected psoriasis families. Significant linkage was found for multiple SNPs in the 17q25 region on Chromosome 1730. We present here TDTae analyses for 16 of the SNP markers. We chose the SPL error model when applying our test statistic for the reason that we consider it to be a reasonable compromise between a general error model (MA) and one with a small number of parameters (DSB), which is more computationally tractable. Also, we used five cuts for the initial search.
Sitosterolemia
We also applied our TDTae method to a study of sitosterolemia, a rare recessive disorder.35 In all, 28 polymorphic microsatellites from chromosome 2p21 at an average resolution of 1 cM were genotyped in 30 nuclear and extended pedigrees. Results of those analyses were published previously,2 and subsequently two genes, ABCG5 and ABCG8, were cloned.36,37 TDT methods were applied because evidence for linkage disequilibrium was detected with several of the loci.2 The P-values reported for the TDTae method are corrected for multiple testing. Also, we note that no observed genotyping errors were found in our analyzed data set. We considered the SPL model, and used five cut points for the initial search.
For a multi-allelic locus, the TDTae statistic is computed by downcoding all alleles to two alleles; the allele of interest vs all other alleles. For a marker with i alleles, each of which appears at least 30 times, i tests are performed. We choose the maximum likelihood ratio test statistic among all alleles, and multiply the corresponding uncorrected P-value by the number of alleles tested. The product of this number and the uncorrected P-value is the corrected P-value. This multiple testing procedure has also been applied to other well-known transmission disequilibrium tests.6,38,39
Results
Null simulations
We present the results of our null simulations in Table 2. These results indicate that, for our simulated data sets, the TDTae maintains correct type I error (with the exception of the MA model at the 10% level of significance when 80% of the individuals are genotyped, which is slightly conservative) and that the empirical distribution is well described by a central χ2 distribution with two degrees of freedom, as indicated by the KS goodness of fit test results (all P-values are >0.05). Again, the only exception to the KS test findings is for the MA model when 80% of the individuals are genotyped. For that simulation, the P-value from the KS goodness of fit test is 0.037. We hypothesize that this lack of goodness of fit stems from the fact that only two cuts were used for MA maximization (Materials and methods–Null simulations) and that therefore the maximum may not have been found in each replicate. Having said that, we do note that the distribution was ‘well-behaved’ in the tails, in the sense that the TDTae test statistic rejected the null hypothesis in the appropriate proportions for the 5 and 1% levels of significance. Also, given the behavior of the statistic for all other simulations, we hypothesize that if we increased the number of cutpoints, the TDTae test statistic would have the appropriate central χ2 distribution for this simulation as well.
Table 2.
Empirical significance levels and 95% confidence intervals for TDTae null simulations (2500 replicates in each simulation)
| Error model | Percent inds genotyped | 10% Significance levela | 5% Significance levela | 1% Significance levela | KS test (P-value) |
|---|---|---|---|---|---|
| DSB | 100 | 0.108 (0.096, 0.121) | 0.050 (0.042, 0.060) | 0.010 (0.006, 0.015) | 0.015 (0.621) |
| 80 | 0.102 (0.090, 0.114) | 0.047 (0.039, 0.056) | 0.009 (0.006, 0.013) | 0.020 (0.275) | |
| SPL | 100 | 0.104 (0.092, 0.116) | 0.047 (0.039, 0.056) | 0.007 (0.004, 0.011) | 0.024 (0.113) |
| 80 | 0.094 (0.082, 0.106) | 0.048 (0.040, 0.058) | 0.009 (0.006, 0.013) | 0.018 (0.395) | |
| MA | 100 | 0.098 (0.087, 0.111) | 0.050 (0.042, 0.059) | 0.012 (0.008, 0.018) | 0.020 (0.297) |
| 80 | 0.086 (0.074, 0.097) | 0.044 (0.037, 0.053) | 0.008 (0.005, 0.012) | 0.029 (0.037) |
95% Exact confidence intervals in parentheses determined using binomial distribution as implemented in program BINOM.1
In this table, the column labeled ‘Error Model’ indicates the specific error model considered (DSB = Douglas–Skol–Boehnke error model (supplemental Table 1); SPL = Sobel–Papp–Lange error model (supplemental Table 2); MA = Mote–Anderson error model (supplemental Table 3)). All supplemental tables may be viewed online at: http://linkage.rockefeller.edu/derek/TDTAE2-error-tables.htm. The column labeled ‘Percent Inds Genotyped’ indicates the probability that each individual was genotyped for each replicate of that simulation (100 = all individuals genotyped; 80 = each individual had 20% probability of missing genotype). The columns labeled ‘x% Significance Level’ report the proportion of replicates for each simulation in which the P-value was less than the value x/100. For these columns, the values reported in parentheses are the lower and upper end points of the 95% confidence intervals, as computed using the method implemented in the BINOM program. The ‘KS Test’ column reports the score of the Kolmogorov–Smirnoff goodness of fit test for the set of 2500 TDTae test statistic values from a given simulation; the null hypothesis is that the TDTae values are drawn from a central χ2 distribution with 2 df. The goodness of fit test is computed using the method implemented in S-PLUS 6.1 (see Electronic Database Information). In this column, values reported in parentheses are the P-values associated with the KS test score.
Psoriasis data set
In Figure 1, we present P-values (−log transformed) for 16 of the SNP markers. This figure indicates that two of the markers (SNPs #5 and #15) displayed significant evidence for linkage at the 5% level with the TDTae after correction for multiple testing via the false discovery rate (FDR) method.40,41 The threshold for 5% significance [−log(P) = 2.34] is indicated in Figure 1 by a horizontal dotted line.
Figure 1.
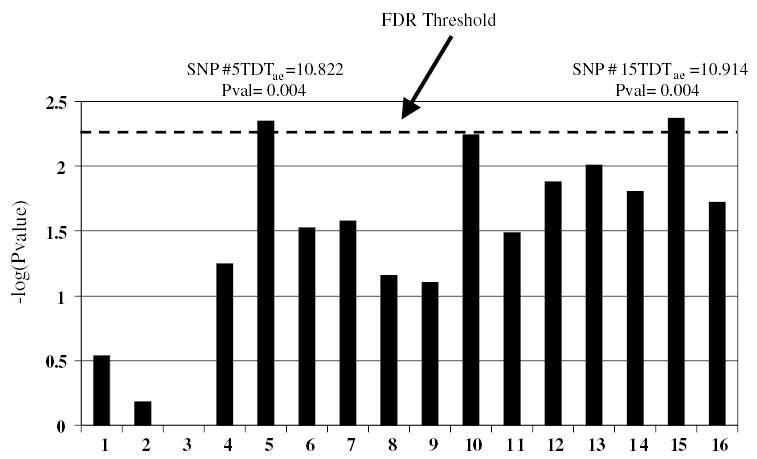
Plot of −log(P-value) for TDTae statistic applied to 16 SNP markers genotyped in Psoriasis study.30 In this figure, the dotted horizontal line (x = 2.34) is the threshold for significance at the 5% level of the value −log(P-value), after correcting for multiple testing using the FDR method.40,41
We also present the maximum likelihood estimates (MLEs) of each of the parameters in the TDTae using the SPL error model for SNP markers #5 and #15 (Figure 1) in Table 3. It is important to note that there were observed genotyping errors for each of these markers. In fact, for marker #15 (the marker with the largest TDTae statistic value), under the alternative hypothesis, the SPL error model MLEs were v1 = 0.033, and v3 = 0.016.
Sitosterolemia data set
In Figure 2, we present corrected P-values (−log transformed) for the 28 microsatellite markers using both our TDTae method (solid lines) and the original TDT method6 (dotted lines). We observe that, in almost all instances, our method provides more significant results than the original TDT method. We note that the most significant P-value for TDTae, 1.57 × 10−9, occurs for marker D2S2298, which is approximately 20 000 base pairs from the genes ABCG5 and ABCG836. Furthermore, the marker D2S414, with the second most significant P-value for TDTae, 1.00 × 10−6, is approximately a half million base pairs from D2S2298. These two markers are the only two that remain significant at the 0.0001 level after correction for multiple testing with the FDR method.40,41
Figure 2.
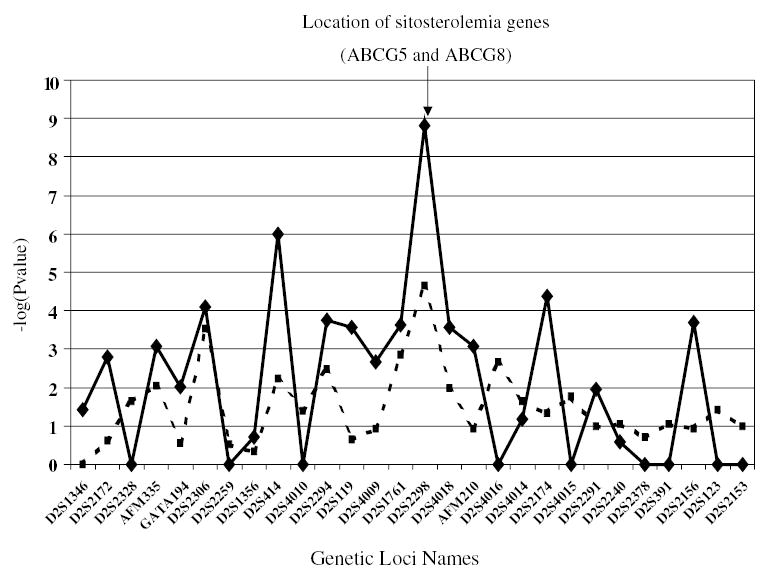
Plot of −log(P-value) for TDTae statistic (solid line) and original TDT (dotted line) applied to 28 microsatellite markers genotyped in Sitosterolemia study. In this figure, we compute P-values for the TDTae applied to microsatellite markers using the following formula: the TDTae statistic is computed by downcoding all alleles at a locus to two alleles; the allele of interest vs all other alleles. For a marker with i alleles, each of which appears at least 30 times, i tests are performed. We choose the maximum likelihood ratio test statistic among all alleles, and multiply the corresponding uncorrected P-value by the number of alleles tested. The product of this number and the uncorrected P-value is the corrected P-value, and this is value that we report (−log transformed).
We comment that our TDTae method is more powerful than the classic TDT method for these data, even though no genotyping errors were observed. The reason for the increase in power is due to the fact that the genotypic relative risks do not satisfy the assumption R2 = R12, based on the MLEs. For example, the MLEs for marker D2S2298 are R1 = 0.03003 and R2 = 0.077182, clearly not satisfying the multiplicative model condition assumed in the original TDT model. Having said that, we comment additionally that even without genotyping error, our method still provides correct type I error rates when there is missing parental data. In the sitosterolemia data set, 16% of all parents were missing all genotype data.
Summary and discussion
Since the development of the first TDT statistic, there has been much methodological research focusing on this test. Two key robustness issues are missing parental genotype information and genotyping errors. While there have been methods developed to address both issues separately, there has been no such method that addresses these issues jointly for general pedigrees. Our work seeks to fill that research void. We have developed the statistic using a likelihood framework, allowing for a more general disease model through the use of the relative risk framework of Weinberg.17 Also, our simulation results suggest that our test statistic maintains proper type I error rate in the presence of genotyping error and missing parental data. Finally, our real data analyses suggest that our test statistic may be powerful for both complex traits (eg, psoriasis) and Mendelian traits (eg, sitosterolemia).
We note that we assumed that the mating type frequencies of founders are given by the product of the individual genotype frequencies, unlike Weinberg.17 We make this simplification to reduce the number of parameters that we must maximize in finding the maximum log-likelihood of the data. While it may be more powerful to use the six mating types, we comment that our simplification reduces the number of parameters to be estimated by three. However, our assumption does make our statistic potentially non-robust to population stratification, the original condition for which the TDT and other statistics were developed.4,6 We plan to extend our method to handle the more general mating-type frequencies proposed in Weinberg’s work.17 However, we conjecture that, to get appropriate maximum likelihood estimates under the null and alternative hypotheses in a reasonable amount of time, we need approximate likelihood solutions like those implemented with MCMC methods (eg, see Sobel et al20). We also make this point in the next paragraph regarding larger numbers of individuals in a general pedigree. We note that the authors Bernardinelli et al22 have already implemented MCMC methods in their version of the TDT allowing for errors.
While we have laid the preliminary groundwork here for our generalized TDTae statistic, we note that this statistic requires further development. The likelihood ratio test is based on large sample theory, and may not be valid for small samples or situations where there is a significant amount of missing data. Also, our method’s computation increases as the number of individuals in a pedigree increases. Thus, at present, our test statistic may only be useful for nuclear families and some smaller extended pedigrees. We plan to further develop this test statistic so that it will be valid for small samples and also that it is computationally feasible for general pedigrees. This may require the use of approximate likelihood approaches.42–44 This work is in progress.
Another important point to mention is that we do not consider unaffected siblings of affected siblings who are not parents in our likelihood formulation (Materials and methods – Individuals in category (4)). We note that, when there are no genotyping errors, such individuals can provide linkage information, particularly when parents are not typed.45 However, it is an interesting and open research question as to whether such individuals provide sufficient additional information when genotyping errors are present to balance the increase in computational cost that results from their inclusion.
Finally, we note that we have developed software to perform analyses using our TDTae method. The software may be downloaded from our website (ftp://linkage.rockefeller.edu/software/tdtae2/). The software will take LINKAGE-format31 files.
Acknowledgments
We gratefully acknowledge grants K01-HG00055 and R01-MH59492 from the National Institutes of Health. Also, we thank Dr Shailesh Patel for thoughtfully providing data from his sitosterolemia study. The psoriasis study is funded in part by NIH grant AR049049. Last but not least, we thank three anonymous reviewers whose comments greatly improved earlier versions of the manuscript. The sitosterolemia study is funded in part by grant NIH NHLBI HL 060613
Appendix A
The following notation will be used through the entire Materials and methods and Results section of this work. We place it here to improve ‘flow’ of the text.
Marker alleles
All alleles will be coded numerically. Unless otherwise stated, it is assumed that all markers are di-allelic, with allele codings ‘1’ and ‘2’.
Genotype parameters
p11 = population frequency of 11 genotype
p12 = population frequency of 12 genotype
p22 = population frequency of 22 genotype = 1−p11–p12
(For a discussion about this choice of parameters vs Weinberg et al’s ‘Mating Type’ parameters, see Discussion.)
Error model parameters
DSB model
γ = Pr(homozygous genotype incorrectly coded as the heterozygous genotype).
η = Pr(heterozygous genotype incorrectly coded as homozygous genotype).
SPL model
v1 = Pr(true homozygote incorrectly coded as heterozygote)
v2 = Pr(one homozygote incorrectly coded as another homozygote)
v3 = Pr(true heterozygote incorrectly coded as a homozygote)
MA model
e21 = Pr(12 genotype observed|11 true)
e31 = Pr(22 genotype observed|11 true)
e12 = Pr(11 genotype observed|12 true)
e32 = Pr(22 genotype observed|12 true)
e13 = Pr(11 genotype observed|22 true)
e23 = Pr(12 genotype observed|22 true)
When discussing an arbitrary error model, we will use the vector notation to indicate the set of error model parameters. For example, when the error model is DSB, and when the error model is SPL. The symbol may also be used to represent a given error model, since (as mentioned above) an error model is completely determined by its parameters. We shall use this equivalence from this point forward.
Penetrances
f0 = Pr(affected| + + at disease locus)
f1 = Pr(affected| + d at disease locus)
f2 = Pr(affected|dd at disease locus)
where ‘+’ refers to a wild-type or low-risk allele at a disease locus, and ‘d’.
Genotypic relative risks
Likelihood Equation Terms
= Pr (observed genotype = i | true genotype = j) for error model (also known as the penetrance function)
(the genotype frequency function for the genotype i).
Pedigree identification
Let a represent an ID for an individual in a pedigree (usually a positive integer). Then,
f(a) = ID of father of that individual
m(a) = ID of mother of that individual
ga = genotype of individual a for given di-allelic locus
Note: For a founder individual with ID s, f(s) = m(s) = 0
= (a1,…,an) = Pedigree of n individuals, in which f(ai) and m(ai) are assumed to be known for each individual ai
Note: Each ai is a unique positive integer representing the ID for ith individual.
= (ga1,…,gan) = Set of consistent genotypes for pedigree
= (g′a1,…,g′an) = Set of observed (possibly inconsistent) genotypes for pedigree
Likelihood ratio statistic
For a parameter ξ in the likelihood equation (3):
= Maximum likelihood estimate of the parameter ξ under H1, where the parameters R1 and R2 are maximized jointly with the other parameters
= Maximum likelihood estimate of the parameter ξ under H0, where the parameters R1 and R2 are fixed at 1.0, while all other parameters are maximized jointly
= Maximum likelihood estimate of the error model parameters for the error model under H1; for example, for the DSB error model
= Maximum likelihood estimate of the error model parameters for the error model under H0; for example, for the DSB error model.
Footnotes
Electronic Database Information
Accession numbers and URLs for data in this article are as follows:
SIMULATE, ftp://linkage.rockefeller.edu/software/simulate
SPLUS 6.1, www.insightful.com
References
- 1.Ott J: Analysis of Human Genetic Linkage Baltimore: The Johns Hopkins University Press; 1999.
- 2.Lee MH, et al. Fine mapping of a gene responsible for regulating dietary cholesterol absorption; founder effects underlie cases of phytosterolaemia in multiple communities. Eur J Hum Genet. 2001;9:375–384. doi: 10.1038/sj.ejhg.5200628. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Breslow NE, Day NE: Statistical Methods in Cancer Research Lyon: International Agency for Research on Cancer; 1980, p 350.
- 4.Falk CT, Rubinstein P. Haplotype relative risks: an easy reliable way to construct a proper control sample for risk calculations. Ann Hum Genet. 1987;51:227–233. doi: 10.1111/j.1469-1809.1987.tb00875.x. [DOI] [PubMed] [Google Scholar]
- 5.Terwilliger JD, Ott J. A haplotype-based ‘haplotype relative risk’ approach to detecting allelic associations. Hum Hered. 1992;42:337–346. doi: 10.1159/000154096. [DOI] [PubMed] [Google Scholar]
- 6.Spielman RS, McGinnis RE, Ewens WJ. Transmission test for linkage disequilibrium: the insulin gene region and insulin-dependent diabetes mellitus (IDDM) Am J Hum Genet. 1993;52:506–516. [PMC free article] [PubMed] [Google Scholar]
- 7.Laird NM, Horvath S, Xu X. Implementing a unified approach to family-based tests of association. Genet Epidemiol. 2000;19 (Suppl 1):S36–S42. doi: 10.1002/1098-2272(2000)19:1+<::AID-GEPI6>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- 8.Martin ER, Kaplan NL, Weir BS. Tests for linkage and association in nuclear families. Am J Hum Genet. 1997;61:439–448. doi: 10.1086/514860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ott J. Statistical properties of the haplotype relative risk. Genet Epidemiol. 1989;6:127–130. doi: 10.1002/gepi.1370060124. [DOI] [PubMed] [Google Scholar]
- 10.Julier C, Hyer RN, Davies J, et al. Insulin-IGF2 region on chromosome 11p encodes a gene implicated in HLA-DR4-dependent diabetes susceptibility. Nature. 1991;354:155–159. doi: 10.1038/354155a0. [DOI] [PubMed] [Google Scholar]
- 11.Spielman RS, Ewens WJ. The TDT and other family-based tests for linkage disequilibrium and association. Am J Hum Genet. 1996;59:983–989. [PMC free article] [PubMed] [Google Scholar]
- 12.Curtis D, Sham PC. A note on the application of the transmission disequilibrium test when a parent is missing. Am J Hum Genet. 1995;56:811–812. [PMC free article] [PubMed] [Google Scholar]
- 13.Gordon D, Heath SC, Liu X, Ott J. A transmission/disequilibrium test that allows for genotyping errors in the analysis of single-nucleotide polymorphism data. Am J Hum Genet. 2001;69:371–380. doi: 10.1086/321981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mitchell AA, Cutler DJ, Chakravarti A. Undetected genotyping errors cause apparent overtransmission of common alleles in the transmission/disequilibrium test. Am J Hum Genet. 2003;72:598–610. doi: 10.1086/368203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Sun F, Flanders WD, Yang Q, Khoury MJ. Transmission disequilibrium test (TDT) when only one parent is available: the 1-TDT. Am J Epidemiol. 1999;150:97–104. doi: 10.1093/oxfordjournals.aje.a009923. [DOI] [PubMed] [Google Scholar]
- 16.Lee WC. Transmission/disequilibrium test when neither parent is available in some families: a non-iterative approach. J Cancer Epidemiol Prev. 2002;7:97–103. doi: 10.1080/147666502321082755. [DOI] [PubMed] [Google Scholar]
- 17.Weinberg CR. Allowing for missing parents in genetic studies of case–parent triads. Am J Hum Genet. 1999;64:1186–1193. doi: 10.1086/302337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gordon D, Ott J. Assessment and management of single nucleotide polymorphism genotype errors in genetic association analysis. Pac Symp Biocomput. 2001:18–29. doi: 10.1142/9789814447362_0003. [DOI] [PubMed] [Google Scholar]
- 19.Douglas JA, Skol AD, Boehnke M. Probability of detection of genotyping errors and mutations as inheritance inconsistencies in nuclear-family data. Am J Hum Genet. 2002;70:487–495. doi: 10.1086/338919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sobel E, Papp JC, Lange K. Detection and integration of genotyping errors in statistical genetics. Am J Hum Genet. 2002;70:496–508. doi: 10.1086/338920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mote VL, Anderson RL. An investigation of the effect of misclassification on the properties of chisquare-tests in the analysis of categorical data. Biometrika. 1965;52:95–109. [PubMed] [Google Scholar]
- 22.Bernardinelli L, Berzuini C, Seaman S, Holmans P. Bayesian trio models for association in the presence of genotyping errors. Genet Epidemiol. 2004;26:70–80. doi: 10.1002/gepi.10291. [DOI] [PubMed] [Google Scholar]
- 23.Morris RW, Kaplan NL. Testing for association with a case–parents design in the presence of genotyping errors. Genet Epidemiol. 2004;26:142–154. doi: 10.1002/gepi.10297. [DOI] [PubMed] [Google Scholar]
- 24.Kendall M, Stuart A, Ord JK: The Advanced Theory of Statistics New York: Oxford University Press; 1994.
- 25.Elston RC, Stewart J. A general model for the genetic analysis of pedigree data. Hum Hered. 1971;21:523–542. doi: 10.1159/000152448. [DOI] [PubMed] [Google Scholar]
- 26.Acton FS: Numerical Methods That Work Washington, DC: Mathematical Association of America; 1970.
- 27.Jacobs DAH: The State of the Art in Numerical Analysis London: Academic Press; 1977.
- 28.Brent RP: Algorithms for Minimization without Derivatives Englewood Cliffs, NJ: Prentice-Hall; 1973, (Chapter 7).
- 29.Press WH, Teukolsky SA, Vetterling WT, Flannery BP: Numerical Recipes in C. The Art of Scientific Computing Cambridge: Cambridge University Press; 2002.
- 30.Helms C, Cao L, Krueger JG, et al. A putative RUNX1 binding site variant between SLC9A3R1 and NAT9 is associated with susceptibility to psoriasis. Nat Genet. 2003;35:349–356. doi: 10.1038/ng1268. [DOI] [PubMed] [Google Scholar]
- 31.Terwilliger JD, Ott J: Handbook of Human Genetic Linkage Baltimore: Johns Hopkins; 1994.
- 32.Smirnoff N. On the estimation of the discrepancy between empirical curves of distribution for two independent samples. Bull Univ Moscou, Ser Int (Math) 1939;2:3–14. [Google Scholar]
- 33.Kolmogoroff A. Confidence limits for an unknown distribution function. Ann Math Stat. 1941;12:461–463. [Google Scholar]
- 34.Conover WJ: Practical Nonparametric Statistics NewYork: John Wiley and Sons; 1980.
- 35.Salen G, Patel S, Batta AK. Sitosterolemia. Cardiovasc Drug Rev. 2002;20:255–270. doi: 10.1111/j.1527-3466.2002.tb00096.x. [DOI] [PubMed] [Google Scholar]
- 36.Lu K, Lee MH, Hazard S, et al. Two genes that map to the STSL locus cause sitosterolemia: genomic structure and spectrum of mutations involving sterolin-1 and sterolin-2, encoded by ABCG5 and ABCG8, respectively. Am J Hum Genet. 2001;69:278–290. doi: 10.1086/321294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lee MH, Lu K, Hazard S, et al. Identification of a gene, ABCG5, important in the regulation of dietary cholesterol absorption. Nat Genet. 2001;27:79–83. doi: 10.1038/83799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Abecasis GR, Cookson WO, Cardon LR. Pedigree tests of transmission disequilibrium. Eur J Hum Genet. 2000;8:545–551. doi: 10.1038/sj.ejhg.5200494. [DOI] [PubMed] [Google Scholar]
- 39.Abecasis GR, Cardon LR, Cookson WO. A general test of association for quantitative traits in nuclear families. Am J Hum Genet. 2000;66:279–292. doi: 10.1086/302698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Benjamini Y, Drai D, Elmer G, Kafkafi N, Golani I. Controlling the false discovery rate in behavior genetics research. Behav Brain Res. 2001;125:279–284. doi: 10.1016/s0166-4328(01)00297-2. [DOI] [PubMed] [Google Scholar]
- 41.Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J Roy Statist Soc B. 1995;57:289–300. [Google Scholar]
- 42.Heath SC. Markov chain Monte Carlo segregation and linkage analysis for oligogenic models. Am J Hum Genet. 1997;61:748–760. doi: 10.1086/515506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Sobel E, Lange K. Descent graphs in pedigree analysis: applications to haplotyping, location scores, and marker-sharing statistics. Am J Hum Genet. 1996;58:1323–1337. [PMC free article] [PubMed] [Google Scholar]
- 44.Weeks DE, Sobel E, O’Connell JR, Lange K. Computer programs for multilocus haplotyping of general pedigrees. Am J Hum Genet. 1995;56:1506–1507. [PMC free article] [PubMed] [Google Scholar]
- 45.Spielman RS, Ewens WJ. A sibship test for linkage in the presence of association: the sib transmission/disequilibrium test. Am J Hum Genet. 1998;62:450–458. doi: 10.1086/301714. [DOI] [PMC free article] [PubMed] [Google Scholar]


