Direct observation of base-pair stepping by RNA polymerase

Abstract

During transcription, RNA polymerase (RNAP) moves processively along a DNA template, creating a complementary RNA. Here we present the development of an ultra-stable optical trapping system with ångström-level resolution, which we used to monitor transcriptional elongation by single molecules of Escherichia coli RNAP. Records showed discrete steps averaging 3.7 ± 0.6 Å, a distance equivalent to the mean rise per base found in B-DNA. By combining our results with quantitative gel analysis, we conclude that RNAP advances along DNA by a single base pair per nucleotide addition to the nascent RNA. We also determined the force–velocity relationship for transcription at both saturating and subsaturating nucleotide concentrations; fits to these data returned a characteristic distance parameter equivalent to one base pair. Global fits were inconsistent with a model for movement incorporating a power stroke tightly coupled to pyrophosphate release, but consistent with a brownian ratchet model incorporating a secondary NTP binding site.

Processive molecular motors tend to move in discrete steps¹. Recent advances in single-molecule techniques have made it possible to observe such steps directly at length scales of a few nanometres or greater. The ability to detect individual catalytic turnovers, as monitored through motor displacement, while simultaneously controlling the force, substrate concentration, temperature or other parameters, provides a means to probe the mechanisms responsible for motility. Single-molecule measurements of stepping have supplied fresh insight into the mechanisms responsible for motion in motor proteins such as myosin, kinesin, dynein and the F₁-ATPase^2–9. A number of processive nucleic acid-based enzymes, such as lambda exonuclease^10,11, RecBCD helicase^12–14 and RNAP^15–19, have also been studied successfully by single-molecule methods, but the comparatively small size of their steps has been experimentally inaccessible up to this point. Movements through a single base pair along double-stranded DNA correspond to a displacement of just ~3.4 Å (ref. ²⁰), which is more than 20-fold smaller than the 8-nm kinesin step⁴ and sevenfold smaller than the 2–3-nm resolution limit attained in most previous work^2,3,14,19,21.

During transcription, E. coli RNAP translocates along DNA while following its helical pitch²², adding ribonucleoside triphosphates (NTPs) successively to the growing RNA. The basic reaction cycle consists of binding the appropriate NTP, incorporation of the associated nucleoside monophosphate into the RNA, and release of pyrophosphate. In addition to following the main reaction pathway, RNAP can reversibly enter any of several off-pathway paused states. For example, RNAP may backtrack by several bases along DNA, displacing the RNA 3′ end from the catalytic centre and temporarily inactivating the enzyme^23–25. Single-molecule studies have shown that backtracking pauses are enhanced under hindering loads and can be triggered by misincorporation of non-complementary NTPs¹⁹. In a separate class of pauses, hairpin structures formed in the nascent RNA can induce pausing via a distinct mechanism²⁶. A third class of pauses occurs commonly and is independent of backtracking¹⁸ or hairpin formation. Regardless of the cause, paused states complicate the interpretation of biochemical studies of RNAP elongation because these kinetic measurements convolve on- and off- pathway events into overall rates. Single-molecule techniques avoid ensemble averaging and permit, in principle, observations that may distinguish between elongation and off-pathway states. The resolution of individual enzymatic turnovers would be especially helpful in unravelling the behaviour of complex reaction cycles for enzymes such as RNAP.

The mechanism that leads to translocation during transcriptional elongation continues to be debated^27–32, and at least two classes of models have been proposed. The first class postulates that a power stroke tightly coupled to pyrophosphate release drives motion²⁹. In the second class, reversible diffusion of the enzyme along the DNA template between its pre- and post-translocated states is directionally rectified through the binding of the incoming NTP, in a brownian ratchet mechanism^30–32. By detecting individual translocation events during transcription and characterizing the force and nucleotide sensitivity of the corresponding motions, one can distinguish between the different classes of mechanism.

Construction of an ultra-stable optical trap

Because the distance spanned by a base pair is so small, it was necessary to construct a stable optical trapping system capable of ångström-level resolution. Sources of noise that hamper optical measurements include drift of the microscope stage (or other nominally stationary components), pointing fluctuations leading to relative motions of the laser beams used for trapping and position detection, and brownian motions of the trapped bead itself. To minimize the noise associated with stage motions, we used a dual-trap ‘dumbbell’ arrangement, described previously¹⁹. In this experimental geometry (Fig. 1a), all components of the assay are optically levitated above the coverglass surface and thereby decoupled from stage drift. A stalled transcription complex¹⁸ containing a biotin tag on the carboxy terminus of the β′-subunit was specifically attached via an avidin linkage to the surface of a 600-nm diameter polystyrene bead. Depending on the desired direction of applied load, either the transcriptionally upstream or downstream end of the DNA was then bound via a digoxigenin antibody linkage to a 700-nm diameter bead, forming a bead–DNA–RNAP–bead dumbbell. Dumbbells were suspended ~1 μm above the microscope coverglass by two independently steered traps, T_weak and T_strong.

Figure 1. Experimental set-up, passive force clamp and sensitivity of the RNAP dumbbell assay.

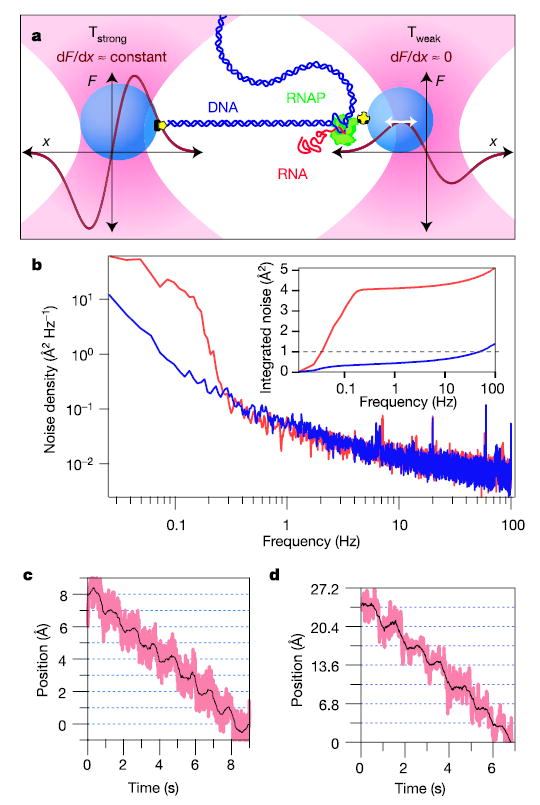
a, Cartoon of the dumbbell geometry with schematic force versus position curves (dark red) shown for both trap beams (not drawn to scale). A single, transcriptionally active molecule of RNAP (green) is attached to a bead (blue) held in trap T_weak (pink, right) and tethered via the upstream DNA (dark blue) to a larger bead held in trap T_strong (pink, left). The right bead is maintained at a position near the peak of the force-extension curve of T_weak, where trap stiffness vanishes (white arrow), creating a force clamp (trap stiffness k = dF/dx). During elongation, the DNA tether lengthens and the beads move apart. Owing to the force clamp arrangement, only the right bead moves: displacement is measured for this bead. b, Power spectrum acquired for a stiffly trapped bead with external optics under air (red) or helium (blue). Inset: integrated noise spectra for air (red) and helium (blue) showing a tenfold reduction in power. c, Steps resolved for a stiffly trapped bead moved in 1-Å increments at 1 Hz. Data were median filtered with a 5-ms (pink) and 500-ms (black) window. d, Steps resolved for a bead–DNA–bead dumbbell held at 27 pN of tension, produced by moving T_strong in 3.4-Å increments at 1 Hz and measuring the corresponding displacements in T_weak.

To isolate the detection and trapping beams from the effects of random air currents, which introduce density fluctuations that perturb the positional stability of laser beams, we enclosed all optical elements external to the microscope in a sealed box filled with helium gas at atmospheric pressure. Because the refractive index of helium is closer to unity than that of air (n_He = 1.000036 compared with n_air = 1.000293), density fluctuations introduce smaller deflections. Using helium, we realized a tenfold reduction in the noise spectral density at 0.1 Hz for a stiffly trapped, 700-nm diameter bead (k = 1.9 pN nm⁻¹), and the integrated system noise power remained below ~1 Å over the bandwidth of interest (Fig. 1b). To illustrate the resolution achieved, we moved a trapped bead in increments of 1 Å at 1-s intervals by displacing T_strong with an acousto-optic deflector (AOD)³³. Steps were clearly resolved, with signal-to-noise ratio of ~1 over a 100-Hz bandwidth (Fig. 1c).

Finally, we implemented a recently developed method to maintain constant force on trapped beads using an all-optical arrangement, without the need for computer feedback³⁴. Such a passive force clamp eliminates artefacts associated with feedback loops and provides exceedingly high bandwidth. To create this clamp, the bead in T_weak was maintained in a ~50-nm region near the maximum of the force-extension curve, where the force is independent of bead position. Force clamps eliminate the need for elastic corrections due to either the compliance of T_strong or the stretching of the DNA along with its associated linkages, so that all molecular displacements are registered in the motion of the bead in T_weak. To demonstrate the resolution achieved in our set-up, a dumbbell consisting of beads connected by a DNA tether (but no RNAP enzyme) was stepped in increments of 3.4 Å at 1 Hz (Fig. 1d).

RNA polymerase takes single-base-pair steps

To resolve individual translocation events, we required that RNAP transcribe slowly enough to time-average to the ångström level over positional uncertainties caused by brownian motions, but quickly enough so that long-term drift did not obscure motion. Because RNAP has different average rates of addition for the four species of nucleotide³⁵, we determined by gel analysis the concentration ratios at which each species becomes equally rate limiting for elongation on our template. Unless otherwise noted, our experiments were conducted at [NTP]_eq = 10 μM GTP, 10 μM UTP, 5 μM ATP and 2.5 μM CTP, concentrations that produce a mean elongation rate of ~1 base pair (bp) s⁻¹ under our conditions (see Supplementary Fig. S1).

In single-molecule records of transcription by RNAP selected for their low noise and drift, we observed clear, stepwise advancements. Figure 2a shows six representative traces obtained under 18 pN of assisting load. Although dwells at some expected positions (Fig. 2a, dotted lines) were missed or skipped, steps were uniform in size, corresponding to nearly integral multiples of a common spacing. To estimate this fundamental spacing, we performed a periodogram analysis³⁶. The position histograms for 37 segments derived from transcription records for 28 individual RNAP molecules were computed and the autocorrelation function calculated for each of these³⁷. These autocorrelations were combined into a global average that displays a series of peaks near multiples of the mean spacing (Fig. 2b), with the first and strongest peak at 3.4 ± 0.8 Å. The power spectral density of this function measures the corresponding spatial frequencies and displays a prominent peak at the inverse of 3.7 ± 0.6 Å (Fig. 2c). This distance is consistent with the crystallographic spacing between neighbouring base pairs in B-DNA³⁸ (3.4 ± 0.5 Å). Although the foregoing analysis was performed on selected traces, a fully automated procedure was also conducted on a continuous, ~300-bp record of elongation, and returned a similar spacing of 3.7 ± 1.5 Å (Supplementary Fig. S2).

Figure 2. RNAP moves in discrete steps.

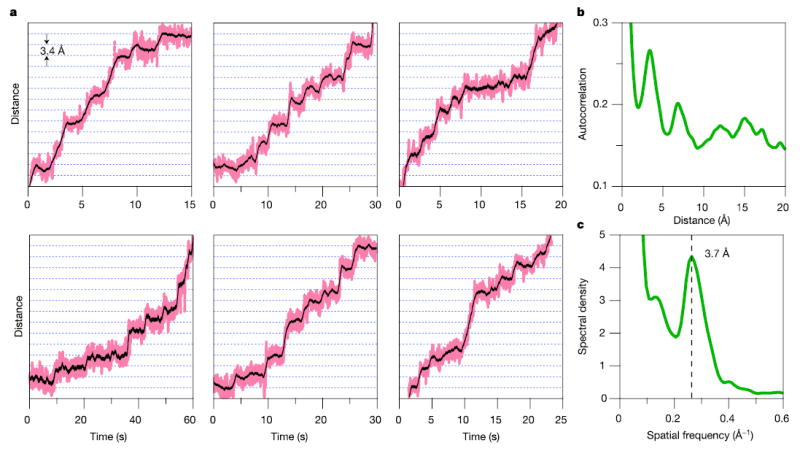
a, Representative records for single molecules of RNAP transcribing at [NTP]_eq under 18 pN of assisting load, median-filtered at 50 ms (pink) and 750 ms (black). Horizontal lines (dotted) are spaced at 3.4-Å intervals. b, The average autocorrelation function derived from position histograms (N = 37) exhibits periodicity at multiples of the step size. c, The power spectrum of b shows a peak at the dominant spatial frequency, corresponding to the inverse of the fundamental step size, 3.7 ± 0.6 Å.

In our records, RNAP does not dwell at every base-pair position along the template. Were certain bases skipped altogether, or merely missed due to finite time resolution? Because RNAP is linked to the bead via the C terminus of its β′-subunit, skipped steps might be explained, in principle, by relative motions of this point of attachment with respect to the catalytic core of the enzyme, allowing the active site to undergo one or more rounds of nucleotide addition before translocation of the attachment point in a single jump, constituting a form of ‘inchworming’ movement. Alternatively, if the upstream DNA exists in a ‘scrunched’ state within the enzyme after templating the production of RNA, as proposed to occur during initiation and during certain regulatory pauses^39–42, then the periodic release of variable amounts of scrunched DNA might also lead to discontinuous enzyme advancement. However, a more parsimonious explanation of our stepping data is that RNAP exhibits heterogeneity in individual nucleotide addition rates during transcription, causing some dwells to occur on timescales too fast to be resolved in our recordings, but maintaining tight coupling between the transcript length and position along the template.

We tested the latter explanation by performing quantitative gel assays at [NTP]_eq, to measure transcript lengths produced by RNAP over a portion of the same DNA template used in our single-molecule studies. Analysis of these gels indicated a variability of more than an order of magnitude in local rates of NTP addition. Expected dwell-time distributions derived from gel analysis are well fitted to the actual distribution of dwell-times measured independently in single molecule records (Supplementary Fig. S3). The close correspondence between variability in next-nucleotide addition rates (measured biochemically) and variability in next-base translocation rates (observed in single molecules) is therefore fully consistent with tight coupling between our attachment point to RNAP on the template and the length of the resulting RNA transcript. Moreover, the observation that RNAP can frequently be seen to step by single base increments (multiple examples of which are found in Fig. 2a) is incompatible with an obligate scrunching mechanism, or with any alternative mechanism where the catalytic core moves with respect to our point of enzyme attachment.

Force dependence of the nucleotide addition cycle

The application of load selectively modulates rates within the biochemical cycle involving motion. A simple Boltzmann relation describes the resulting force–velocity relationship for many mechanoenzymes^3,43,44:

$$\nu (F)=\frac{{\nu }_{\text{max}}}{1+\text{exp}\left[-\frac{(F-F_{1/2})\delta }{k_{\text{B}}T}\right]}$$ (1)

where v_max is the velocity at large assisting load, F_½ is the force at which velocity reaches half its maximal value, k_B is Boltzmann’s constant, T is the temperature, and δ is a parameter that represents the effective distance over which force acts. The physical interpretation of δ depends on the underlying model⁴³. In power stroke models, δ typically represents the distance from the pre-translocated position to the transition state. In such a model for RNAP inspired by ref. 29, this transition state is located between the PP_i-bound and PP_i-released states, where PP_i is pyrophosphate (Fig. 3a), and δ corresponds to some fraction of a single-base-pair separation. In brownian ratchet models, δ typically represents the characteristic distance associated with fluctuations between pre- and post-translocated states. For RNAP, this distance generally corresponds to one base pair. We considered two instances of a brownian ratchet: a model inspired by ref. 32, where translocation precedes NTP binding (Fig. 3b), and a model where translocation can either precede or follow NTP binding (Fig. 3c). Because the enzyme active site is occluded by the 3′ end of RNA in the pre-translocated state, the latter model requires an incoming NTP to occupy a secondary binding site before being loaded into the active site. Such a secondary binding site might represent, for example, the ‘E site’ observed in crystal structures of polymerase II^45,46, or the templated binding sites proposed in biochemical studies^27,28,47. These binding sites are structurally distinct, but the binding of an NTP to either type of site may be modelled by the simplified kinetic pathway shown in Fig. 3c (see also Supplementary Information).

Figure 3. Alternative kinetic models for RNAP translocation.

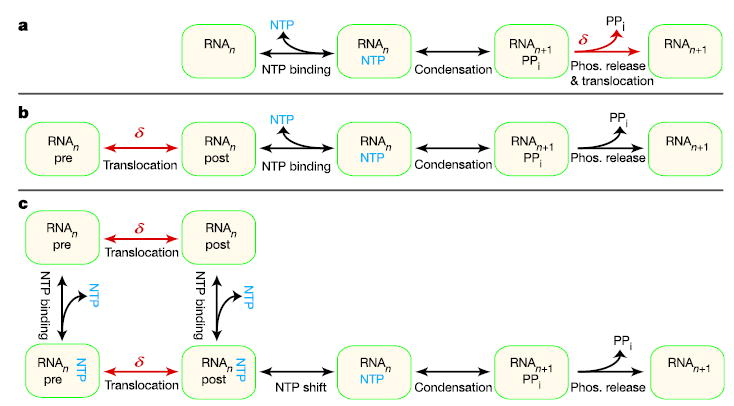
a, A power stroke model where translocation (δ, red) is driven by irreversible PP_i release. b, A brownian ratchet model where reversible oscillation between pre- and post-translocated enzyme states can occur before NTP binding (blue). c, A brownian ratchet model where translocation and NTP binding can occur in either order. This model postulates the existence of a secondary NTP site to accommodate the possibility of nucleotide binding when the enzyme is in its pre-translocated state.

To distinguish between the models of Fig. 3 on the basis of force–velocity behaviour, it was critical to remove load-dependent, off-pathway events from records. In particular, we observed occasional pauses associated with both backtracking¹⁹ and backstepping (Fig. 4). These off-pathway events decrease overall elongation rates by differing amounts depending on load, obscuring the on-pathway load dependence. With the improved resolution obtained, it was possible to identify and remove all rearward motions greater than 1 nm from traces. The run velocity for each molecule was computed by dividing the total distance of advance by the total elapsed time minus any time spent in backtracked states. We note that off-pathway pauses that are insensitive to load (and therefore have no associated motion) do not affect the force dependence of nucleotide addition, because they occur with a fixed probability per unit time.

Figure 4. RNAP backstepping and backtracking resolved at high resolution.

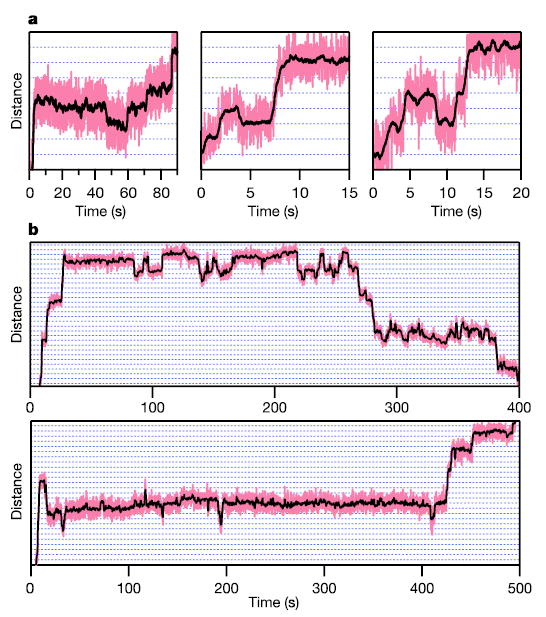
a, Backstepping observed under assisting loads of 18 pN at [NTP]_eq. Molecules were occasionally found to move backward by one base pair (left and middle panels) or by two base pairs (right panel) before resuming elongation. b, Backtracking (>3 bp) under a hindering load of 9 pN. Molecules dwelled at specific preferred locations on the template before irreversibly backtracking (top) or recovering (bottom). Horizontal gridlines (dotted) are spaced at 3.4-Å intervals. (See Supplementary Information for a discussion.)

Elongation velocities were measured over a wide range of assisting and hindering loads (−18 to 28 pN) at four NTP concentrations (1, 10, 100 and 250 × [NTP]_eq), with an average of 32 molecules per data point (Fig. 5a). With backtracking included, the velocity interpolated to zero load at [NTP]_eq was in excellent agreement with an independent estimate obtained through gel-based measurements. Once backtracking pauses were removed, each force–velocity curve was fit individually to equation (1). These unconstrained fits returned a characteristic distance parameter δ = 3.4 ± 0.5 Å (Supplementary Fig. S4).

Figure 5. Force–velocity and Michaelis–Menten relationships along with model fits.

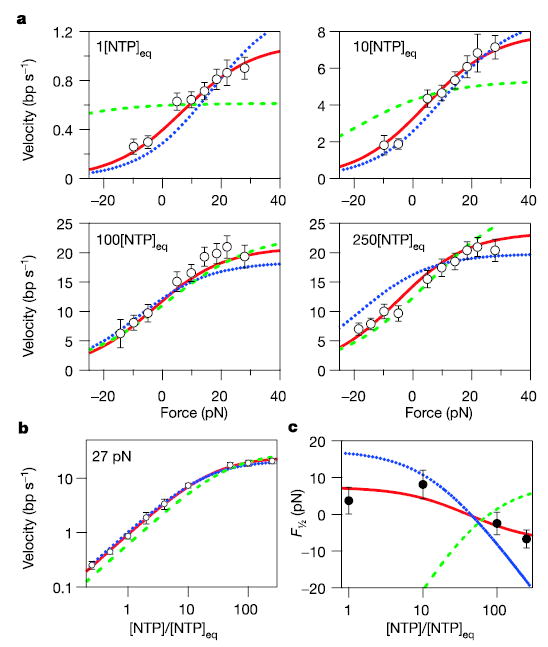
a, b, Measured force–velocity relationships for RNAP at [NTP]_eq, 10[NTP]_eq, 100[NTP]_eq and 250[NTP]_eq, with off-pathway events removed (see text) (a), and single-molecule velocity as a function of [NTP] measured at 27 pN assisting load (open circles) with associated errors (see Methods) (b). Negative forces correspond to hindering loads; positive forces to assisting loads. Global fits to the power stroke model of Fig. 3a (green dashed line), the brownian ratchet model of Fig. 3b (blue dotted line) and the brownian ratchet model of Fig. 3c (solid red line) are shown. c, The F_½ value as a function of [NTP] derived from free fits of the data in a to equation (1) (Supplementary Fig. S4), shown together with predictions from the three models (coloured lines) (Supplementary Fig. S5).

We generated global fits of all three models to our entire data set of velocities (N = 40; Fig. 5a, b). Note that more force is required to hinder elongation with increasing [NTP] (that is, F_½ decreases; Fig. 5c), a trend opposite to that predicted for a power stroke model coupled to PP_i release. The global fit to the power stroke model generated a poor fit (χ_v² = 6.03; v = 35; p(χ_v²) = 5.3 × 10⁻²⁷; five parameters; v is the number of degrees of freedom). These findings, together with a computed distance parameter corresponding to a full base-pair displacement (rather than some fraction of a base pair expected for a power stroke model) and previous results showing that elongation velocity is insensitive to PP_i concentration⁴³, all argue against the mechanism of Fig. 3a.

A global fit of our data to the simple brownian ratchet model of Fig. 3b returned better results (χ_v² = 2.67; v = 37; p(χ_v²) = 1.6 × 10⁻⁷; three parameters), and qualitatively predicted the behaviour of F_½ as a function of [NTP]. An even better fit was obtained for the ratchet model of Fig. 3c, which invokes a secondary NTP binding site. This model predicted all unconstrained F_½ values to within error, and was statistically consistent with the complete data set (χ_v² = 0.64; v = 36; p(χ_v²) = 0.956; four parameters). The fit parameters suggest the presence of a small energetic penalty (~1 kT) associated with nucleotide binding to the secondary site when the molecule is pre-translocated, compared with the post-translocated binding energy (under standard conditions). Saturating NTP concentrations tend to ensure that the secondary binding site remains occupied and thereby bias the enzyme towards the post-translocated state. However, in contrast to the ratchet mechanism of ref. 32, hindering loads can overcome this bias by forcing the NTP-bound form into a pre-translocated state, increasing the force sensitivity at higher NTP levels. This model seems attractive for its simplicity (four free parameters), its ability to fit all available force–velocity data, and the close correspondence to recent structural and biochemical studies supplying evidence for a secondary site^27,28,45,46. Clearly, alternative kinetic schemes may be formulated to fit the data presented here and elsewhere.

The marked improvement in resolution obtained in this optical trapping study has led to direct measurements of base-pair stepping by an individual enzyme and supplied insights into the molecular mechanism of transcription by RNAP. Our data argue directly against any power stroke mechanism that is tightly coupled to PP_i release. Furthermore, although other recent publications have supplied independent biochemical and biophysical evidence in support of various forms of a brownian ratchet mechanism^30,31,48, we propose a specific model incorporating a secondary NTP binding site that is consistent with our data and others^27,45,46. The techniques presented here are broadly applicable. In particular, it may be possible to use our approach to relate the behaviour of a nucleic acid-based enzyme directly to the underlying DNA sequence to which it is bound, facilitating studies of sequence-dependent effects in replication, transcription and translation, and possible use in single-molecule DNA sequencing. The ability to detect motions at the ångström scale in single enzymes opens new avenues for the study of biomolecules.

METHODS

Optical trapping

The overall design of the apparatus has been described^19,34. Salient modifications to our apparatus include the construction of a sealed optics enclosure where helium gas at atmospheric pressure replaces ambient air and the implementation of a passive, all-optical force clamp³⁴. The force clamp was calibrated by measuring the relaxation rate of a 700-nm polystyrene bead (Bangs Labs) after release from a point ~300 nm from the trap centre⁴⁹. In this low-Reynolds-number regime, the velocity is proportional to the force acting on the bead: using this relationship, we found that force remained constant within 5% over a 50-nm-wide clamp region located ~220 nm from the trap centre. During single-molecule transcription experiments, the bead held in T_weak was maintained in this zero-stiffness zone by occasionally moving T_strong by 20 nm whenever the 600-nm bead in T_weak approached the outer limit of the clamp region.

For collection of force–velocity data (only), we used an active, AOD-based force clamp³³, which allowed us to alter rapidly the load on an individual enzyme during a single run, and thereby to cover the entire range of forces. Each RNAP molecule included for analysis was subjected to a cycle of hindering (−5, −10, −14, −18 pN) or assisting (5, 10, 14, 18, 22, 29 pN) loads until it either terminated or stalled. By generating data for each molecule over a range of forces, we minimized variations due to intrinsic velocity heterogeneity¹⁸.

Data analysis

Unless noted, bead displacement data were filtered with a 1-kHz, 4-pole Bessel filter, digitally acquired at 2 kHz, and median-filtered at 50 ms or 750 ms. To determine RNAP step size, we selected 37 segments of transcription through 51-Å-wide windows from 28 molecules at 18 pN or 27 pN of assisting load, then generated position histograms for each of these traces using a bin size of 0.1 Å. Histograms were autocorrelated, normalized by the number of data points, and averaged to form a global autocorrelation function. The power spectrum derived from this autocorrelation function was smoothed with a 5-point binomial filter.

To generate the graphs of Fig. 5, raw data were smoothed with an 800-ms boxcar filter and decimated to 2.5 Hz. Transcriptional pauses associated with ≥1 nm backward motion were removed by an automated algorithm implemented in Igor (Wavemetrics). Errors in velocity were computed as follows. First, the contribution to velocity of the positional uncertainty was estimated from the levels of statistical fluctuation occurring in regions where the enzyme had stalled. Next, the stochastic variation of RNAP motion was estimated using a randomness parameter⁵⁰ of 10 (randomness was estimated by single-molecule analysis; data not shown). Finally, a heterogeneity in the population velocity equivalent to 50% of the mean was assumed¹⁸. These three sources of error were assumed to be independent, combined in quadrature, and used to compile a weighted average of the velocity data and associated uncertainty in the mean, displayed as error bars in Fig. 5a, b.