Mechanistic Analysis of the Mitotic Kinesin Eg5

Abstract

Eg5 is a slow, plus-end-directed microtubule-based motor of the BimC kinesin family that is essential for bipolar spindle formation during eukaryotic cell division. We have analyzed two human Eg5/KSP motors, Eg5-367 and Eg5-437, and both are monomeric based on results from sedimentation velocity and sedimentation equilibrium centrifugation as well as analytical gel filtration. The steady-state parameters were: for Eg5-367: k_cat = 5.5 s⁻¹, K_1/2,Mt = 0.7 μm, and K_m,ATP = 25 μm; and for Eg5-437: k_cat = 2.9 s⁻¹, K_1/2,Mt = 4.5 μm, and K_m,ATP = 19 μm. 2′(3′)-O-(N-Methylanthraniloyl)-ATP (mantATP) binding was rapid at 2–3 μm⁻¹s⁻¹, followed immediately by ATP hydrolysis at 15 s⁻¹. ATP-dependent Mt·Eg5 dissociation was relatively slow and rate-limiting at 8 s⁻¹ with mantADP release at 40 s⁻¹. Surprisingly, Eg5-367 binds microtubules more effectively (11 μm⁻¹s⁻¹) than Eg5-437 (0.7 −m⁻¹s⁻¹), consistent with the steady-state K_1/2,Mt and the mantADP release K_1/2,Mt. These results indicate that the ATPase pathway for monomeric Eg5 is more similar to conventional kinesin than the spindle motors Ncd and Kar3, where ADP product release is rate-limiting for steady-state turnover.

Eukaryotic cell division requires proper assembly and maintenance of the bipolar spindle, an intricate protein complex composed of a dynamic array of microtubules and microtubule-based motor proteins (reviewed in Refs. ^1–7). Bipolar spindle formation requires a specific balance between counteracting forces generated by cytoplasmic dynein and several subfamilies of kinesin-related proteins to organize and position opposite spindle poles (8–15). The BimC kinesins (16–25) contribute to the plus-end-directed force necessary to separate microtubule asters, thus aiding in the establishment and maintenance of the bipolar spindle.

Electron microscopy studies of a BimC family member (DmKLP61F) suggest that these kinesins exhibit a unique homotetrameric structure with two N-terminal motor domains positioned at each end of a coiled-coil stalk, thus facilitating the ability to interact with and slide adjacent microtubules (25–27). Homo sapiens Eg5/KSP, the human homologue of Xenopus Eg5, is a slow, plus-end-directed BimC kinesin that has been shown to localize along interpolar spindle microtubules and at the spindle poles (24, 28, 29). This spindle association is regulated by the cell cycle-dependent phosphorylation of a single threonine within a highly conserved region of the Eg5 tail domain by p34^cdc2 protein kinase (23, 24, 29). Monastrol, a small, cell-permeable molecule, can reversibly inhibit the function of Eg5 to arrest cells in mitosis, providing a useful model for anti-mitotic drug design (30–35).

There are remarkable structural similarities in the catalytic core domain of Eg5, Kar3, Ncd, and conventional kinesin (35–41), yet these proteins exhibit different characteristics in vitro and different cellular functions in vivo (13, 42–46). Each of these kinesins has been shown to function through a characteristic cyclic interaction with the microtubule (Scheme 1) whereby the nucleotide state at the active site modulates the affinity of the motor for the microtubule. The kinetic mechanisms of conventional kinesin, Ncd, and Kar3 have been extensively studied (28, 47–73). The aim of this study was to establish the kinetic basis of force generation of Eg5 in direct comparison to conventional kinesin and other well characterized spindle motors, Kar3 and Ncd.

We have utilized kinetic and thermodynamic approaches to define the mechanochemistry of two truncated human Eg5 motors, Eg5-367 and Eg5-437. Eg5-367, containing the N-terminal 367 amino acids, represents a single Eg5 catalytic domain (33, 35, 36). Surprisingly, we found that Eg5-437, designed to yield a dimeric motor, is monomeric based on results from sedimentation velocity and sedimentation equilibrium analytical ultracentrifugation as well as analytical gel filtration. The kinetics and equilibrium binding characteristics for Eg5 presented here reveal a unique ATPase mechanism more similar to KinN kinesins, such as conventional kinesin, compared with the well studied KinC spindle motors, Kar3 and Ncd.

EXPERIMENTAL PROCEDURES

Experimental Conditions

Experiments were performed at 25 °C in ATPase buffer (20 mm Hepes, pH 7.2, with KOH, 5 mm magnesium acetate, 0.1 mm EDTA, 0.1 mm EGTA, 50 mm potassium acetate, 1 mm dithiothreitol, 5% sucrose). All concentrations reported for experiments are final after mixing.

Expression and Purification of Eg5

We have expressed two human Eg5 constructs as described previously (33). Eg5-367 contains the N-terminal 367 amino acids, Met¹–Gln³⁶⁷ followed by a His₆ tag (molecular mass = 41.7 kDa without MgADP and 42.1 kDa with MgADP), and Eg5-437 contains the N-terminal 437 amino acids, Met¹–Thr⁴³⁷, followed by a His₆ tag (molecular mass = 49.8 kDa without MgADP and 50.2 kDa with MgADP). Both recombinant Eg5 motors were expressed in the Escherichia coli cell line BL21-CodonPlus(DE3)-RIL (Stratagene, La Jolla, CA) and purified using column chromatography. Briefly, cells were diluted after induction to 1 g/6 ml in lysis buffer (10 mm sodium phosphate buffer, pH 7.2, 20 mm NaCl, 2 mm MgCl₂, 1 mM EGTA, 1 mM dithiothreitol, 2 mm phenylmethylsulfonyl fluoride). The soluble cell lysate was loaded onto a 100-ml S-Sepharose (Sigma-Aldrich Co.) column to select for the Eg5 motor domain. Eg5 was eluted from the S-Sepharose column using a linear NaCl gradient (20–600 mm NaCl). Fractions enriched in Eg5 were pooled and dialyzed against nickel-nitrilotriacetic acid buffer (10 mm sodium phosphate buffer, pH 7.2, 20 mm NaCl, 2 mm MgCl₂, 0.1 mM EGTA, 1 mM dithiothreitol, 0.02 mM ATP). The dialysate was loaded onto a 5-ml nickel-nitrilotriacetic acid-agarose (Qiagen, Valencia, CA) column, and Eg5 was eluted using a linear imidazole gradient (0–200 mm imidazole). Fractions enriched in Eg5 were pooled and dialyzed against ATPase buffer plus 200 mm NaCl to remove the imidazole. The dialysate was concentrated by ultrafiltration (Millipore Centriprep 30, Bedford, MA) and further dialyzed against ATPase buffer with 5% sucrose. We determined the Eg5 protein concentration by the Bio-Rad Protein Assay (Bio-Rad Laboratories, Inc.) with IgG as the protein standard. This purification method yielded 40–150 mg of Eg5 protein per 30 g of E. coli cells at >99% purity.

Scheme 1.

Microtubules for Kinetic Experiments

Microtubules were prepared from bovine brain tubulin, and on the day of each experiment an aliquot of tubulin was thawed, cycled, and stabilized with 20 μm Taxol (paclitaxel, Sigma-Aldrich Co.).

Analytical Ultracentrifugation

Sedimentation velocity experiments were conducted at 42,000 rpm, and a sedimentation equilibrium experiment was carried out at 17,000 rpm in a Beckman Optima XLA analytical ultracentrifuge (Beckman Coulter Inc., Fullerton, CA) equipped with absorbance optics and an An60Ti rotor. Velocity and equilibrium data were collected at a wavelength of 235 nm. The conditions for sedimentation velocity experiments included ATPase buffer with and without 50 μm AMP-PNP¹ (a non-hydrolyzable ATP analog) at 25 °C (Fig. 1A). Velocity data were analyzed by DCDT+ (version 1.15) (74) as described previously (75) and, where appropriate, SVEDBERG (version 6.39) (76) to verify the results. The reported weight average sedimentation coefficient values (s_20,w) obtained from DCDT+ were corrected for the solution density and viscosity (75) and were calculated by a weighted integration over the entire range of sedimentation coefficients covered by the g(s) distribution. Equilibrium data were analyzed by NONLIN (version 1.035) as described previously (75).

Fig. 1. Analytical ultracentrifugation and gel filtration.

A, the sedimentation velocity data at 2, 4, and 8 μm Eg5-437 were analyzed for sedimentation coefficient distribution g(s) in the absence of adenine nucleotide and in the presence of 50 μm AMP-PNP (as indicated). The vertical line represents the average Eg5-437 s_20,w, corresponding to the three different protein concentrations in both conditions. For Eg5-437, s_20,w is 3.49 ± 0.08 S. B, analytical gel filtration was performed at 10 μm motor sites with detection by continuous monitoring of intrinsic protein fluorescence. The gel filtration profiles for Drosophila kinesin heavy chain (K401), Eg5-437, and Eg5-367 are shown. The scale at the bottom indicates the elution time. The void volume elutes at 15.6 min (arrowhead) and the included volume at 52.1 min. Inset, semilog plot of the K_av values for four marker proteins (•, ovalbumin; ▴, aldolase; ▪, catalase; ♦, ferritin) versus their known Stokes radii (R_s).

Gel Filtration and Stokes Radii Calculations

Purified proteins were resolved by using a Superose-6 HR 10/30 gel filtration column (Amersham Biosciences) equilibrated in ATPase buffer at 25 °C using the System Gold high-pressure liquid chromatography system (Beckman Coulter Inc.) (Fig. 1B). The elution volumes (V_e) of proteins were determined by intrinsic protein fluorescence detection (Jasco FP-2020, Victoria, British Columbia). The Stokes radii (R_s) of Eg5-367, Eg5-437, and Drosophila kinesin heavy chain (K401) were calculated as described previously (77). Briefly, the partition coefficients (K_av) were calculated for four standard proteins of known Stokes radii (R_s): ovalbumin, 3.05 nm; aldolase, 4.81 nm; catalase, 5.22 nm; and ferritin, 6.10 nm. The apparent Stokes radius of each motor was determined from interpolation of a semilog plot of the markers K_av versus the known R_s of the markers (see Table I).

Table I.

Physical properties of Eg5 motors

Protein	Polypeptide molecular massa	Rsb	s20,wc	Calculated molecular massd	Association state
	Da			Da
Eg5-367	42,119	2.86	NDe	ND	Monomer
Eg5-437	50,217	3.37	3.49	48,229	Monomer
K401	45,531	4.79	5.06	91,902	Dimer

^a The monomer polypeptide with MgADP bound was determined from the amino acid sequence and nucleotide molecular mass (Da).

^b R_s is the Stokes radius (nm) determined by analytical gel filtration.

^c s_20,w is the sedimentation coefficient determined from sedimentation velocity experiments.

^d The molecular mass (Da) was calculated as described (86).

^e ND, not determined.

Phosphocreatine Kinase Coupled Assay

The concentration of active Eg5 sites was determined by performing phosphocreatine kinase coupled assays as previously described (78). Briefly, Eg5 (5 μm final concentration) was incubated with trace amounts of [α-³²P]ATP for 90 min to convert all radiolabeled ATP to ADP (data not shown). In some experiments, additional non-radiolabeled ADP was then added to yield a final concentration of 5–15 μm [α-³²P]ADP. The Eg5·[α-³²P]ADP complex was combined with a creatine kinase/phosphocreatine-based ATP regeneration system to convert unbound [α-³²P]ADP to [α-³²P]ATP. However, ADP tightly bound at the Eg5 active site was inaccessible to the creatine kinase and therefore protected from enzymatic conversion to ATP. This assay measures the Eg5 concentration based on ADP tightly bound at the Eg5 active site. The protected [α-³²P]ADP was quantified as a function of time by incubating the Eg5·[α-³²P]ADP complex with the regeneration system with or without 2.5 mm unlabeled MgATP (Fig 2A). Each data set was fit to the following single exponential function,

Fig. 2. Active site determination and steady-state ATPase kinetics.

A, the Eg5·[α-³²P]ADP complex (final concentration: 5 μm Eg5-437) was incubated with 0.3 mg/ml creatine kinase, 4 mm phosphocreatine in the presence (▴) or absence (▵) of a 2.5 mm unlabeled MgATP chase. Both data sets were fit to Equation 1, providing an active site concentration at 4.72 ± 0.09 μm (+ATP) and 4.77 ± 0.04 μm (−ATP). In the presence of the unlabeled chase, the k_off,ADP was determined to be 0.003 ± 0.0001 s⁻¹. B, the Mt·Eg5 complex was preformed with varying concentration of Taxol-stabilized microtubules, and the reaction was initiated by mixing with MgATP. Final concentrations: Mt·Eg5 complex (0.5 μm Eg5, 0–40 μm tubulin, 20 μm Taxol), 1 mm [α-³²P]MgATP. The data were fit to Equation 2. For Eg5-367 (•),k_cat = 5.42 ± 0.08 s⁻¹ and K_1/2,Mt = 0.46 ± 0.06 μm. For Eg5-437 (▴), k_cat = 3.05 ± 0.08 s⁻¹ and K_1/2,Mt = 7.31 3 0.68 μm. C, ATP concentration dependence. Final concentrations: Mt·Eg5 complex (1 μm Eg5, 40 μm tubulin, 20 μm Taxol), 0–300 μm [α-³²P]MgATP. The data were fit to the Michaelis-Menten equation. For Eg5-367, k_cat = 4.88 ± 0.08 s⁻¹ and K_m,ATP = 26.5 ± 2.0 μm. For Eg5-437, k_cat = 2.84 ± 0.02 s⁻¹ and K_m,ATP = 9.3 ± 0.5 μm.

$$[\text{ADP}]=A\mathrm{\hspace{0.17em} }\text{exp}(-k_{\text{off}}t)+C$$ (Eq. 1)

where the active site concentration is the sum of the amplitude (A) and the constant term (C) to extrapolate to zero time (t). In the experiment with excess unlabeled MgATP, k_off is the first-order rate constant for ADP release in the absence of microtubules.

Steady-State ATPase Kinetics

Eg5 steady-state ATPase activity was determined by following [α-³²P]ATP hydrolysis to form [α-³²P]ADP·P_i as previously described (78). In Fig. 2B, the rate of ATP turnover was plotted as a function of microtubule concentration, and the data were fit to the following quadratic equation,

$$\begin{array}{l}\text{Rate}=0.5\times k_{\text{cat}}\times \{({\text{E}}_0+K_{1/2,\text{Mt}}+{\text{Mt}}_0)\\ -{[{({\text{E}}_0+K_{1/2,\text{Mt}}+{\text{Mt}}_0)}^2-(4{\text{E}}_0{\text{Mt}}_0)]}^{1/2}\}\end{array}$$ (Eq. 2)

where the Rate is the amount of hydrolysis product formed per second per active site, k_cat is the maximum rate constant of product formation at saturating substrate, E₀ is the Eg5 site concentration, K_1/2,Mt is the tubulin concentration as microtubules needed to provide one-half the maximal velocity, and Mt₀ is the microtubule concentration.

Mt·Eg5 Cosedimentation Assays

Eg5 at 2 μm was incubated with varying microtubule concentrations (0–6 μm tubulin) in the absence (Fig. 3A) or presence (Fig. 3C) of increasing MgADP concentrations for 30 min, followed by centrifugation in a Beckman Airfuge (Beckman Coulter Inc.) at 30 p.s.i. (100,000 × g) for 30 min as described previously (67). The microtubule pellet was resuspended in ATPase buffer to equal the volume of the supernatant. Gel samples for the pellet and supernatant were prepared in 5× Laemmli sample buffer, and the proteins were resolved by SDS-PAGE, followed by staining with Coomassie Brilliant Blue R-250. The gels were analyzed with a Scan Maker X6EL scanner (Microtek, Carson, CA), and the proteins were quantified using National Institutes of Health Image (version 1.62) to determine the fraction of Eg5 in the supernatant and pellet at each microtubule concentration. The fraction of Eg5 that partitioned to the pellet was plotted as a function of microtubule concentration (Fig. 3A), and the data were fit to the following quadratic equation,

Fig. 3. Microtubule and ADP equilibrium binding experiments.

A, Eg5 at 2 μm was incubated with varying concentrations of microtubules (0–6 μm tubulin, 20 μm Taxol) in the absence of added nucleotide. The fraction of Eg5 in the microtubule pellet was plotted as a function of the total microtubule concentration, and the data were fit to Equation 3. For Eg5-367 (•), the K_d,Mt = 0.20 ± 0.03 μm with maximum fractional binding at 1.07 ± 0.02. The inset shows the data for Eg5-437 (▴): K_d,Mt = 0.20 ± 0.05 μm with maximum fractional binding at 1.09 ± 0.05. B, a preformed Mt·Eg5 complex was incubated with varying concentrations of [α-³²P]MgADP. Final concentrations: 5 μm Eg5, 6 μm tubulin, 30 μm Taxol, 5–90 μm [α-³²P]MgADP. The concentration of [α-³²P]ADP that partitioned with the Mt·Eg5 complex was plotted as a function of total MgADP concentration (•, Eg5-367; ▴, Eg5-437). The data were fit to Equation 4, which yielded for Eg5-367 the K_d,ADP = 117 ± 86 μm with maximal ADP binding at 3.9 ± 1.9 μm. For Eg5-437 (inset), the K_d,ADP = 202 ± 64 μm with maximal ADP binding at 5.4 ± 1.4 μm. C, Eg5-367 at 2 μm was incubated with 4 μm microtubules plus varying MgADP concentrations (0–2 mm). The fraction of Eg5 bound was plotted as a function of MgADP concentration yielding 100% bound at all MgADP concentrations. Inset, Coomassie Blue-stained SDS gel following sedimentation of Mt·Eg5 complexes in the presence of increasing MgADP concentrations. The supernatant (S) and pellet (P) for each reaction were loaded consecutively with the concentration of MgADP indicated above each supernatant/pellet pair. Lanes 1 and 2 represent a control reaction with 2 μm Eg5-367 plus 2 mm MgADP (no microtubules).

$$\text{Mt}\cdot \text{E}/{\text{E}}_0=0.5\times \{({\text{E}}_0+K_d+{\text{Mt}}_0)-{[{({\text{E}}_0+K_d+{\text{Mt}}_0)}^2-(4{\text{E}}_0{\text{Mt}}_0)]}^{1/2}\}$$ (Eq. 3)

where Mt·E/E₀ is the fraction of Eg5 partitioning with the microtubule pellet, E₀ is total Eg5 concentration, K_d is the dissociation constant, and Mt₀ is the microtubule concentration. For Fig. 3C, the fraction of Eg5 that partitioned to the pellet was plotted as a function of MgADP concentration.

Mt·Eg5·[α-³²P]ADP Cosedimentation Assays

Eg5 at 5 μm was incubated with microtubules (6 and 8 μm tubulin for Eg5-367 and Eg5-437, respectively) and with varying concentrations of radiolabeled MgADP (2.5–100 μm) for 30 min as described previously (72). The reaction mixture was centrifuged, the supernatant was removed, the unwashed pellet was resuspended in 4 n NaOH, and the volume of the pellet was adjusted with buffer to equal the volume of the supernatant. Control reactions were performed at each microtubule concentration in the absence of Eg5 to determine the amount of radiolabeled nucleotide that was non-specifically trapped in the microtubule pellet. The concentration of [α-³²P]ADP for each Mt·Eg5 reaction was corrected for [α-³²P]ADP that partitioned with microtubules in the absence of motor. Fig. 3B shows the data fit to the following quadratic equation,

$$\begin{array}{l}\text{Mt}\cdot \text{E}\cdot \text{ADP}=0.5\times \{(E_0+K_d+\text{ADP})\\ -{[{({\text{E}}_0+K_d+\text{ADP})}^2-(4{\text{E}}_0\text{ADP})]}^{1/2}\}\end{array}$$ (Eq. 4)

where Mt·E·ADP is the concentration of ADP bound to the Mt·Eg5 complex, E₀ is total Eg5, ADP is the total nucleotide present, and K_d is the dissociation constant for ADP.

Acid-quench Experiment

The pre-steady-state kinetics of MgATP hydrolysis for Eg5 in the presence of microtubules was defined in this assay. A preformed Mt·Eg5 complex was rapidly mixed with varying concentrations of radiolabeled MgATP plus 100 mm KCl in a quench-flow instrument (Kintek Corp., Austin, TX). We added the additional salt in the ATP syringe to lower steady-state turnover without affecting the pre-steady-state burst of product formation (Fig. 5A). The reaction was incubated (from 10 ms to 1 s) and quenched with formic acid, and radiolabeled product formation was quantified after separating [α-³²P]ADP plus P_i from unreacted [α-³²P]ATP by thin layer chromatography (78). The concentration of [α-³²P]ADP was plotted as a function of time (Fig. 5B), and the data were fit to the following burst equation,

Fig. 5. Acid-quench kinetics of ATP hydrolysis.

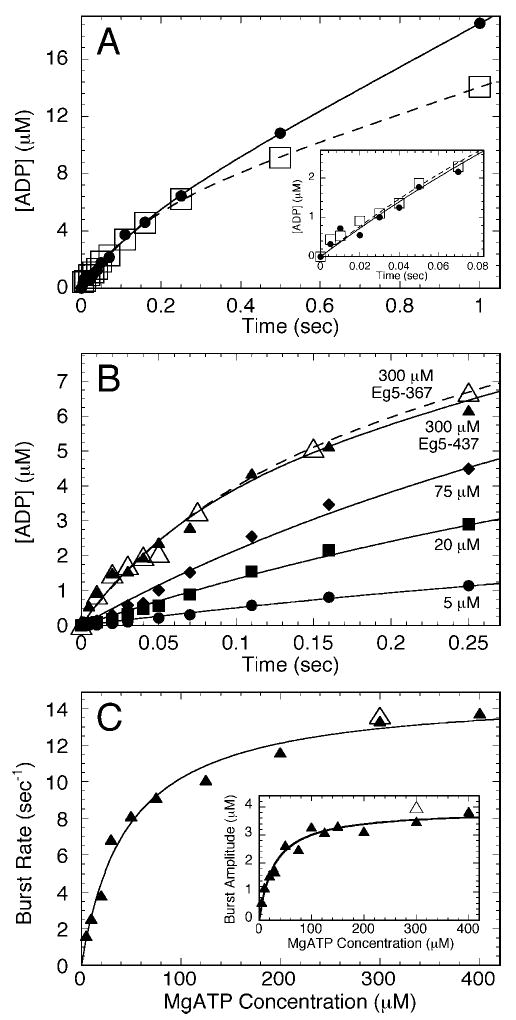
A, time course of radiolabeled product formation after rapidly mixing a preformed Mt·Eg5 complex with [α-³²P]MgATP. Additional salt was added to the MgATP syringe to lower steady-state ATP turnover (•, absence KCl; □, presence KCl). Final concentrations: 4 μm Eg5-437, 6 μm tubulin, 20 μm Taxol, 200 μm [α-³²P]MgATP, ± 100 mm KCl, and the data were fit to Equation 5. The inset shows the first 80 ms. B, time course of ADP·P_i formation by Mt·Eg5-437 complex at increasing MgATP concentrations. Only the first 250 ms is shown to visualize the initial burst phase. The 300 μm MgATP transient for Eg5-367 is indicated (▵). C, the observed rate of the exponential burst phase was plotted as a function of MgATP concentration. The fit of the data to a hyperbola defined the maximum rate constant of ATP hydrolysis for Eg5-437, k₊₂ = 14.9 ± 0.5 s⁻¹ and the K_d,ATP = 46 ± 6 μm. Inset, the amplitude of the burst phase was plotted as a function of MgATP concentration. The data were fit to a hyperbola yielding a maximum burst amplitude at 3.9 ± 0.2 μm, and the K_d,ATP = 30 ± 5 μm. The Eg5-367 burst rate and burst amplitude data at 300 μm MgATP (▵) were indicated on the graphs but were not included in the fits of the data.

$$\text{Product}=(A\times [1-exp(-k_{\text{b}}t)])+k_{\text{ss}}t$$ (Eq. 5)

where A is the amplitude of the initial rapid exponential phase, which corresponds to the formation of [α-³²P]ADP·P_i at the Eg5 active site during the first turnover, k_b is the rate constant of the exponential burst phase, t is time in seconds, and k_ss is the rate constant of the linear phase (μm ADP·s⁻¹) corresponding to steady-state turnover. The exponential rate of the pre-steady-state burst (k_b) and burst amplitude (A) (Fig. 5C) were plotted as a function of MgATP concentration, and each data set was fit to a hyperbola.

Pulse-chase Experiment

This experiment measures the time course of the formation of a kinetically stable Mt·Eg5·ATP intermediate prior to ATP hydrolysis (48). In these experiments, the time course of ATP turnover (from 10 ms to 1 s) was measured by chasing the Mt·Eg5·[α-³²P]ATP intermediate with ~5 mm MgATP (15 mm MgATP in the quench syringe) for 4 s (8–10 half-lives) in the quench-flow instrument. The reaction mixture was terminated with formic acid, and the radio-labeled product was quantified. The data in Fig. 6 (A and C) were fit to Equation 3, and each data set in Fig. 6B was fit to a hyperbola.

Fig. 6. Pulse-chase kinetics of ATP binding.

The preformed Mt·Eg5-437 complex was reacted with [α-³²P]MgATP plus KCl for 0–500 ms followed by the MgATP chase as described under “Experimental Procedures.” Final concentrations: 4 μm Eg5-437, 6 μm tubulin, 20 μm Taxol, 0–400 μm [α-³²P]MgATP, 100 mm KCl, followed by 5 mm unlabeled MgATP chase. A, representative transients fit to Equation 5. B, the rate of the exponential burst phase was plotted as a function of MgATP concentration. The data were fit to a hyperbola to determine the rate of the conformational change after formation of the Mt·Eg5·ATP collision complex. The ATP-dependent isomerization, k₊₁′ = 20.8 ± 1.1 s⁻¹ with K_d,ATP = 45 ± 8 μm. Inset, the amplitude of each burst phase was plotted as a function of MgATP concentration. The data were fit to a hyperbola yielding the maximum burst amplitude at 4.1 ± 0.5 μm, and the K_d,ATP = 22 ± 5 μm. C, comparison of the ATP hydrolysis kinetics by acid-quench (• and ▪) and ATP binding kinetics by pulse-chase (○ and □) at 25 μm (• and ○) and 200 μm (▪ and □) [α-³²P]MgATP. Data were collected for these experiments on the same day using the same enzyme and substrate solutions.

Stopped-flow Experiments

The pre-steady-state kinetics of mant-ATP binding, Eg5 detachment from microtubules, Eg5 association with microtubules, and mantADP release were measured using the SF-2003 Kintek stopped-flow instrument (Kintek Corp.). The instrument was set to show the first 1.4–2 ms of mixing. The mantATP and mantADP experiments were performed with a racemic mixture of mantAXP isomers (2′-mant-3′-dAXP and 3′-mant-2′-dAXP), and excitation wavelength was set at 360 nm (mercury arc lamp) with emitted light measured through a 400-nm cutoff filter (mant λ_em = 450 nm). The mantATP binding data were fit to the following equation,

$$k_{\text{obs}}=\{(k_{\text{max}}\times [\text{mantATP}])/(K_{1/2,\text{mantATP}}+[\text{mantATP}])\}+k_{off}$$ (Eq. 6)

where k_obs is the rate constant obtained from the exponential phase of the fluorescence change, k_max is the maximum rate of mantATP binding, K_1/2,mantATP is the concentration of mantATP required to provide half the maximal rate, and k_off is the observed rate of mantATP dissociation obtained from the y-intercept. The mantATP binding data at low mantATP concentrations (Fig. 4, inset) were fit to a linear function,

Fig. 4. Kinetics of mantATP binding to the Mt·Eg5 complex.

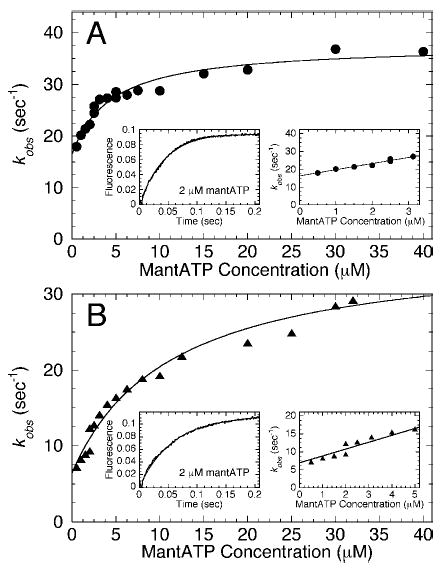
The preformed Mt·Eg5 complex was rapidly mixed in the stopped-flow instrument with varying concentrations of mantATP. Final concentrations: 0.5 μm Eg5 for 0.5–2 μm mantATP and 2 μm Eg5 for 2–40 μm mantATP, 10 μm tubulin, 20 μm Taxol. A, Eg5-367 (•): a representative transient at 2 μm mantATP was fit to a single exponential function and is shown in the left inset. The observed rate of the exponential fluorescence enhancement increased as a function of mantATP concentration. The fit of the data to Equation 6 defined the maximum rate of mantATP binding, k_max = 37.7 ± 1.4 s⁻¹ and K_1/2,mantATP = 4.4 ± 1.1 μm. The right inset shows that, at low concentrations of mantATP (0–3 μm), the rate data were linear. The fit to Equation 7 yielded the second-order rate constant for mantATP binding at 3.43 ± 0.28 μm⁻¹s⁻¹; k_off = 16.3 ± 0.6 s⁻¹. B, kinetics of mantATP binding to the Mt·Eg5-437 complex (▴). The left inset shows a representative transient at 2 μm mantATP fit to a single exponential, and the right inset shows the data at low mantATP concentrations. Conditions and treatment of the data as described in A: k_max = 36.2 ± 2.6 s⁻¹, K_1/2,mantATP = 11.3 ± 2.6 μm, k₊₁ = 1.91 ± 0.22 μm⁻¹s⁻¹, and k_off at 6.9 ± 0.7 s⁻¹.

$$k_{\text{obs}}=(k_{+1}\times [\text{mantATP}])\times k_{\text{off}}$$ (Eq. 7)

where k_obs is the rate constant of the fluorescence enhancement, k₊₁ is the second-order rate constant for mantATP binding, and k_off obtained from the y-intercept is the observed rate of mantATP dissociation from the Mt·Eg5·mantATP ternary complex.

The Mt·Eg5 dissociation kinetics (Fig. 7) and microtubule association kinetics (Fig. 8) were determined by monitoring the change in solution turbidity at 340 nm. The rate constants of Eg5 dissociation from the microtubule were plotted as a function of MgATP concentration, and the data were fit to a hyperbola. The exponential rate constants of Eg5 association with microtubules were plotted as a function of microtubule concentration and fit to the following equation,

Fig. 7. ATP-promoted dissociation of Mt·Eg5 complex.

A pre-formed Mt·Eg5 complex was rapidly mixed in the stopped flow instrument with varying concentrations of MgATP plus KCl. Final concentrations: 5 μm Eg5, 4.9 μm tubulin, 20 μm Taxol, 0–1 mm MgATP, 100 mm KCl. A, the rate of the exponential phase of Mt·Eg5-367 dissociation was plotted as a function of MgATP concentration (•). The data were fit to a hyperbola with the maximum rate of dissociation at 7.8 ± 0.2 s⁻¹ and K_1/2,ATP = 1.9 ± 0.2 μm. Inset, representative stopped-flow transients. B, the rate of the exponential phase of Mt·Eg5-437 dissociation was plotted as a function of MgATP concentration (▴). The hyperbolic fit yielded a maximum rate of dissociation at 8.7 ± 0.3 s⁻¹ with K_1/2,ATP = 15.1 ± 2.5 μm. Inset, representative transients.

Fig. 8. Kinetics of Eg5·ADP association with microtubules.

The Eg5 motor was rapidly mixed in the stopped-flow instrument with increasing concentrations of Taxol-stabilized microtubules. Final concentrations: 1.25 μm Eg5 for 1.25–2.25 μm tubulin and 2.5 μm Eg5 for 2.5–8 μm tubulin, 20 μm Taxol. The rate constant obtained from the exponential phase of each transient (inset) was plotted as a function of microtubule concentration, and the data were fit to Equation 8. For Eg5-367 (•), the second-order rate constant for microtubule association, k₊₅ = 11.0 ± 0.2 μm⁻¹s⁻¹ with k₋₅ = 2.76 ± 1.12 s⁻¹. For Eg5-437 (▴), k₊₅ = 0.66 ± 0.03 μm⁻¹s⁻¹ and k₋₅ = 2.73 ± 0.11 s⁻¹.

$$k_{\text{obs}}=(k_{+5}\times [\text{tubulin}])k_{-5}$$ (Eq. 8)

where k_obs is the rate constant of the exponential phase, k₊₅ is the second-order rate constant for microtubule association, and k₋₅ corresponds to the observed rate constant for motor dissociation from Mt·Eg5 complex as determined from the y-intercept.

Release of mantADP from the Eg5 active site in the presence of microtubules was measured by incubating Eg5 with mantADP at a ratio of 1:2 (Eg5:mantADP) and rapidly mixing the complex with varying concentrations of microtubules plus 1 mm MgATP to chase the Mt·Eg5·mantADP intermediate (Fig. 9). The rate constants for the initial fast exponential phase were plotted as a function of microtubule concentration, and the data were fit to a hyperbola.

Fig. 9. Microtubule-activated mantADP release.

The Eg5·mantADP complex was rapidly mixed in the stopped-flow instrument with varying concentrations of microtubules plus MgATP. Final concentrations: 1 μm Eg5-2 μm mantADP for 1.9–4 μm tubulin and 2 μm Eg5-4 μm mantADP for 2–40 μm tubulin, 20 μm Taxol, and 1 mm MgATP. A, representative transients are shown for different microtubule concentrations, and each was fit to a single exponential function. B, the rate of the exponential phase of each transient was plotted as a function of microtubule concentration, and the data were fit to a hyperbola. For Eg5-367 (•), the maximum rate of mantADP release, k₊₆ = 43.3 ± 0.2 s⁻¹ with K_1/2,Mt = 2.48 ± 0.05 μm tubulin. For Eg5-437 (▴), k₊₆ = 34.2 ± 1.6 s⁻¹ and K_1/2,Mt = 15.2 ± 1.6 μm tubulin.

RESULTS

Oligomeric State of Purified Eg5 Motors

We utilized analytical ultracentrifugation and gel filtration techniques to establish the oligomeric state of our purified Eg5 motors at the conditions used for the kinetic and equilibrium experiments presented here. We performed sedimentation velocity experiments with Eg5-437 in ATPase buffer without added nucleotide (Eg5·ADP) and with the non-hydrolyzable ATP analog, AMP-PNP, to mimic ATP conditions. The g(s) curves for both conditions superimpose, indicating that there is no difference in oligomeric state for Eg5-437 in these adenine nucleotide states (Fig. 1A). DCDT+ analysis of both sedimentation velocity experiments provided an average sedimentation coefficient (s_20,w) at 3.5 S. SVEDBERG analysis of these data also gave an average S value of 3.5 S and an average molecular weight of 44.6 kDa. These results are consistent with the predicted molecular weight of a monomeric Eg5-437·ADP complex (50.2 kDa) (Table I).

Further confirmation that Eg5-437 is monomeric under our experimental conditions was obtained from the results of sedimentation equilibrium centrifugation and gel filtration. The equilibrium experiment was performed using Eg5 at 2, 3, and 4 μm in the ATPase buffer with 50 μm AMP-PNP (data not shown). A global single species fit of these data by NONLIN gave a Z average molecular mass value of 49.3 ± 1.8 kDa, consistent with the expected molecular mass of the Eg5 monomer with MgADP bound (50.2 kDa). In addition, we used analytical gel filtration (Fig. 1B) to compare Eg5-437 with the well established dimeric kinesin, Drosophila kinesin heavy chain, K401 (75), and the Eg5 monomer, Eg5-367 (33, 35, 36). From this experiment, the Stokes radii were calculated: K401, 4.79 nm; Eg5-437, 3.37 nm; and Eg5-367, 2.86 nm (Table I). Taken together, these results indicate that Eg5-437 is monomeric in solution at the buffer conditions reported here. Previous studies with Xenopus Eg5-437GST and untagged Eg5-437 suggested both were dimeric (28); however, studies with His₆-tagged human Eg5-401 indicated that there was an equilibrium of association states between monomers and dimers (34). This evidence suggests that our His₆ tag may be disrupting the formation of a stable coiled-coil in the Eg5-437 motor.

Eg5 Active Site Determination

Kinesin superfamily members share the ability to tightly bind ADP to the active site in the absence of microtubules (70, 79, 80). We exploited this tight affinity for ADP to determine the Eg5 active site concentration for each protein preparation (Fig. 2A). Each data set in Fig. 2A was fit to a single exponential function (Equation 1). The amplitude data provided the active site concentration at 4.75 μm ADP of 5 μm Eg5 sites, and the early time points at 3 and 5 s showed 4.8–4.9 μm ADP. These results demonstrated that >96% of the motor population was active upon purification based on these criteria. In the MgATP chase experiment, the rate constant for ADP release (k_off,ADP) in the absence of microtubules (Eg5-367: 0.02 s⁻¹; Eg5-437: 0.003 s⁻¹) was determined and was comparable to the steady-state k_cat in the absence of microtubules (Eg5-367: 0.018 s⁻¹; Eg5-437: 0.002 s⁻¹). These results indicate that the rate-limiting step for Eg5 is ADP product release in the absence of microtubules, and the significant difference observed between the Eg5 motors suggests that the Eg5-367 nucleotide pocket exists in a more open conformation than Eg5-437, which has a more extended α-helical C terminus.

Eg5 Steady-state ATPase Kinetics

In the presence of microtubules, the steady-state rate of ATP turnover was dramatically increased for both Eg5 motors, which is a characteristic of kinesin-related proteins (70, 79–82). Fig. 2 (B and C) shows steady-state kinetics as a function of microtubule concentration at 1 mm MgATP and as a function of MgATP concentration at 40 μm tubulin, respectively. Eg5-367 (k_cat = 5.5 s⁻¹) appears to be able to turn over ATP ~2-fold faster than Eg5-437 (k_cat = 2.9 s⁻¹) as well as to bind microtubules more tightly under cycling conditions (Eg5-367 K_1/2,Mt = 0.7 μm versus Eg5-437 K_1/2,Mt = 4.5 μm). Both Eg5 constructs show similar values for half-saturation with ATP (Eg5-367: K_m,ATP = 25 μm and Eg5-437: K_m,ATP = 19 μm). These steady-state kinetics are comparable to those determined in previous studies when ionic strength and other experimental conditions are considered (28, 34, 35).

Eg5 Binding to Microtubules

To determine the affinity of Eg5 for microtubules in the absence of added nucleotide, microtubule-cosedimentation assays were performed (Fig. 3A). Eg5 was incubated with increasing concentrations of microtubules, followed by centrifugation and analysis by SDS-PAGE. Eg5 partitioned with the microtubules as a function of microtubule concentration with 100% maximal binding at 2 μm tubulin. The stoichiometry for both Eg5 proteins indicates that one motor domain binds per αβ-tubulin heterodimer. The fit of the data provides K_d,Mt values at 0.2 μm tubulin for each Eg5 motor, which represents the upper limit for the K_d,Mt at the motor concentration used in this assay. Our determined K_d,Mt value in the absence of added nucleotide (0.2 μm tubulin) was ~10-fold lower than the K_d,Mt determined previously by Lock-hart and Cross (2.2 μm tubulin) (28). This difference may be the result of differing buffer conditions as well as the oligomeric state of the motors.

ADP Equilibrium Binding to Mt·Eg5 Complex

To determine the affinity of the Mt·Eg5 complex for ADP, cosedimentation assays were performed (Fig. 3B). A preformed Mt·Eg5 complex was incubated with increasing concentrations of [α-³²P]MgADP, followed by centrifugation. Any radiolabeled MgADP still bound at the active site should partition to the pellet with the Mt·Eg5 complexes. The reaction mixtures at each MgADP concentration were analyzed by SDS-PAGE to verify that 100% of Eg5 partitioned with the microtubule pellet (Fig. 3C). Note that we did not saturate the 5 μm Eg5 sites at 90 μm [α-³²P]MgADP, and the fit of the data provided the apparent ADP dissociation constant for Eg5-367, K_d,ADP = 117 ± 86 μm with maximal ADP binding at 3.9 ± 1.9 μm. For Eg5-437, K_d,ADP = 202 ± 64 μm, and the maximal ADP binding was 5.4 ± 1.4 μm. Because of the weak affinity for ADP and the loss of sensitivity at higher ADP concentrations, the upper region of the curve is not well defined; therefore, the error on these constants is high. However, the results indicate that microtubules rapidly stimulate ADP release from the active site of Eg5 and that most ADP remains in solution as seen previously for conventional kinesin and in contrast to Kar3 (Table II) (72, 83). Fig. 3C also provides insight into the behavior of the Mt·Eg5 complex at increasing MgADP concentrations. Note that at 2 mm MgADP, conditions where one would expect to see motor release from the microtubule, the monomeric Eg5 continues to partition with the microtubule pellet. One interpretation of these data is that the monomer in the absence of the partner motor domain(s) has lost cooperative interactions that facilitate motor domain release as observed previously for kinesin, Ncd, and Kar3 (54, 70, 72). However, the experiments to test this hypothesis have not yet been completed.

Table II.

Eg5 comparison to kinesin, Kar3, and Ncd monomers

Constants		Eg5-367	Eg5-437	Kinesin K341a	Kar3 motor domainb	Ncd MC6c
mantATP binding	k+1	3.4 ± 0.3 μm−1s −1	1.9 ± 0.2 μm−1s−1	20 ± 5 μm−1s−1	1.2 ± 0.02 μm−1s−1	1.1 ± 0.1 μm−1s−1
	koff	16.3 ± 0.6 s−1	6.9 ± 0.7 s−1	113 ± 60 s−1		6.9 ± 7.3 s−1
	k+1′	37.7 ± 1.4 s−1	36.2 ± 2.6 s−1	565 ± 50 s−1
	K1/2,mantATP	4.4 ± 1.1 μm	11.3 ± 2.6 μm	23 ± 10 μm
ATP binding by pulse-chase	k+1′	NDd	20.8 ± 1.1 s−1	ND	498 ± 76 s−1	ND
	Kd,ATP		45 ± 8 μm		82.8 ± 33.1 μm
ATP hydrolysis by acid-quench	k+2	13.6 ± 0.8 s−1e	14.9 ± 0.5 s−1	>300 s−1	16.2 ± 1.9 s−1	11.0 ± 2.3 s−1
	Kd,ATP		46 ± 6 μm		319 ± 92 μm
ATP-promoted dissociationf	k+3	7.8 ± 0.2 s−1	8.7 ± 0.3 s−1	22.5 ± 1.4 s−1	6.7 ± 0.1 s−1	14.0 ± 0.9 s−1
	K1/2,ATP	1.9 ± 0.2 μm	15.1 ± 2.5 μm	72 ± 20 μm	5.7 ± 0.3 μm	19.6 ± 4.5 μm
Microtubule association	k+5	11.0 ± 0.2 μm−1s −1	0.66 ± 0.03 μm−1s−1	10.8 ± 1.4 μm−1 s−1	0.5 μm−1s−1	0.8 ± 0.1 μm−1s−1
	k−5	2.8 ± 1.1 s−1	2.7 ± 0.1 s−1		3 s−1	3.6 ± 0.6 s−1
mantADP releaseg	k+6	43.3 ± 0.2 s−1	34.2 ± 1.6 s−1	303 ± 22 s−1	0.4 ± 0.01 s−1	3.9 ± 0.4 s−1
	K1/2,Mt	2.5 ± 0.1 μm	15.2 ± 1.6 μm	15 ± 3 μm	3.9 ± 0.3 μm	28.0 ± 5.7 μm
Steady-state ATPase	kcat	5.5 ± 0.3 s−1	2.9 ± 0.1 s−1	81 ± 2 s−1	0.49 ± 0.02 s−1	1.9 ± 0.1 s−1
	Km,ATP	25.1 ± 0.7 μm	19.4 ± 1.9 μm	91 ± 10 μm	12.2 ± 2.8 μm	27.8 ± 10.9 μm
	K1/2,Mt	0.71 ± 0.15 μm	4.5 ± 0.6 μm	3.2 ± 0.1 μm	6.0 ± 0.7 μm	9.6 ± 3.9 μm
Mt equilibrium binding	Kd,Mt	0.21 ± 0.06 μm	0.21 ± 0.05 μm	0.22 ± 0.06 μm	0.68 ± 0.13 μm	0.20 ± 0.06 μm
ADP equilibrium binding	Kd,ADP	117 ± 86 μm	202 ± 64 μm	99 ± 20 μm	1.7 ± 0.6 μm	ND

^a Monomeric D. melanogaster kinesin heavy chain, K341 (54, 81, 83, 87).

^b Monomeric Saccharomyces cerevisiae Kar3 motor domain (72).

^c Monomeric D. melanogaster Ncd, MC6 (70).

^d ND, not determined.

^e Burst rate based on single ATP concentration (300 μm MgATP).

^f Turbidity (49, 54).

^g mantADP competed with excess unlabeled MgATP.

MantATP Binding to Mt·Eg5 Complex

MantATP binding experiments were performed to determine the kinetics of nucleotide binding to the Mt·Eg5 complex. Using the stopped-flow instrument to rapidly mix a preformed Mt·Eg5 complex with increasing mantATP concentrations, we measured the exponential increase in fluorescence, which was interpreted as mantATP binding to the more hydrophobic environment of the Eg5 active site (Fig. 4A and B, insets). The observed exponential rate of mantATP binding increased as a function of the mantATP concentration for each Eg5 motor. The maximum rate of mantATP binding (k_max) was 37 s⁻¹, thus indicating a rate-limiting conformational change prior to ATP hydrolysis for both motors. The fit of the initial linear phase yields a second-order rate constant for mantATP binding (k₊₁) at 3 μm⁻¹s⁻¹ for Eg5-367 and 2 μm⁻¹s⁻¹ for Eg5-437 (Fig. 4, inset). The observed rate of mantATP dissociation from the Mt·Eg5 complex (k_off) was 16 s⁻¹ for Eg5-367 and 7 s⁻¹ for Eg5-437 (Table II). We have not interpreted these data to indicate weak binding of ATP because of the mant group on the nucleotide. Instead, we have evaluated the affinity of ATP based on the rapid quench experiments presented below. The mantATP binding kinetics do indicate that nucleotide binding is a fast step in the Mt·Eg5 ATPase cycle.

ATP Hydrolysis Kinetics by Acid-quench

To determine the time dependence of ATP hydrolysis by Eg5, a Mt·Eg5 complex was rapidly mixed in a chemical quench-flow instrument with increasing concentrations of [α-³²P]MgATP (Fig. 5). There was a rapid initial burst of ATP hydrolysis related to the formation of [α-³²P]ADP·P_i at the active site during the first turnover, followed by a slower linear phase of product formation, which corresponded to steady-state turnover. To better define the burst phase, additional salt was added with the MgATP syringe to reduce the linear phase. The results in Fig. 5A show that the initial exponential phase was not affected by the additional salt (100 mm KCl final concentration after mixing), yet steady-state turnover was markedly slower. For Eg5-437, the maximum rate of ATP hydrolysis (k₊₂) was 15 s⁻¹ and the K_d,ATP was 50 μm (Fig. 5C). For Eg5-367, the burst phase was not well separated from the linear steady-state phase at low ATP concentrations even with the additional salt, therefore only a single transient at 300 μm MgATP is shown (Fig. 5B). The rate of ATP hydrolysis was comparable to Eg5-437 at 300 μm MgATP: k₊₂ = 14 s⁻¹ (Fig. 5C). The maximum amplitude of the burst phase (Fig. 5C, inset) was 3.9 μm ADP·P_i per 4.0 μm Eg5 sites suggesting ~97% of the motor population was able to bind and hydrolyze ATP during the first turnover. The burst amplitude data were consistent with our ADP equilibrium binding results for Eg5-437 (Figs. 2A and 3B), where ~3% of the motor sites had ADP bound, thus this population of Mt·Eg5·ADP complexes could not contribute to the first turnover event in this pre-steady-state experiment.

MgATP Binding Kinetics by Pulse-chase

Pulse-chase experiments for the Mt·Eg5 complex were performed as a function of [α-³²P]MgATP concentration to gain insight into the equilibrium constant for ATP binding to the Mt·Eg5 complex and the lifetime of the Mt·Eg5*·ATP intermediate (Scheme 1). Fig. 6 shows that the rate of the exponential burst phase increases with increasing MgATP concentration, and the maximum rate of MgATP binding (k₊₁′) was 21 s⁻¹ and K_d,ATP was 45 μm. The observation that the burst rate in the pulse-chase experiments saturates at increasing concentrations of substrate indicates a rate-limiting conformational change that occurs prior to ATP hydrolysis, consistent with our results from mantATP binding experiments. The K_d,ATP at 45 μm was similar to the K_d,ATP at 46 μm obtained from the acid quench experiments, and the maximum burst amplitude at 4 μm ADP·P_i per 4 μm Eg5 sites was consistent with our acid-quench data. These results indicate that ATP binding is at least a two-step process, yet the Mt·Eg5*·ATP state is not long lived but proceeds directly to ATP hydrolysis.

ATP-promoted Dissociation of Mt·Eg5 Complexes

The pre-formed Mt·Eg5 complex was rapidly mixed in the stopped-flow instrument with increasing concentrations of MgATP plus 100 mm KCl (Fig. 7). In this experimental design, the motor binds and hydrolyzes ATP followed by motor detachment, but the additional salt weakens the interaction of the motor with the microtubule upon microtubule rebinding; therefore, the kinetics of ATP-promoted dissociation can be measured. The insets of Fig. 7 show representative stopped-flow transients corresponding to different MgATP concentrations. The transients show an initial lag due to the time required for ATP binding and ATP hydrolysis prior to dissociation. The dissociation kinetics show an ATP concentration dependence with the maximum rate of Mt·Eg5 dissociation (k₊₃) at ~8 s⁻¹ for both motors. However, the K_1/2,ATP values were 1.9 μm for Eg5-367 and 15 μm for Eg5-437. These results suggest that dissociation is a relatively slow step in the pathway and may be coupled to phosphate release as observed for kinesin (54, 65, 82, 84).

Eg5 Association with Microtubules

We assumed that Eg5·ADP was the intermediate that binds to microtubules, because Eg5 is purified with ADP tightly bound (36). We measured the rate of formation of the Mt·Eg5 complex using the stopped-flow instrument to monitor changes in turbidity as the motor binds to the microtubule (Fig. 8). The observed rate increased linearly with microtubule concentration, and the data revealed a significant difference in the second-order rate constant for microtubule association (k₊₅) for the two motors: Eg5-367, k₊₅ = 11 μm⁻¹s⁻¹ versus Eg5-437, k₊₅ = 0.7 μm⁻¹s⁻¹. The apparent association constant based on steady-state ATPase (k_cat/K_1/2,Mt) predicted the lower limit at 8 μm⁻¹s⁻¹ and 0.6 μm⁻¹s⁻¹ for Eg5-367 and Eg5-437, respectively. These results demonstrate that Eg5-367 binds much more effectively than Eg5-437, although at this time we do not know the structural and/or mechanistic reasons for this difference.

MantADP Release from the Mt·Eg5·mantADP Complex

Eg5 was incubated with mantADP to exchange ADP at the active site with mantADP. MantADP release from the Eg5·mantADP complex in the absence of microtubules was 0.06 s⁻¹ for Eg5-367 and 0.008 s⁻¹ for Eg5-437 (Fig. 9B). These rates are consistent with the rates of [α-³²P]ADP release observed in the steady-state ATPase assays in the absence of microtubules (Fig. 2 and Table II). MantADP release from the Eg5 motor domain was activated by rapidly mixing in the stopped-flow instrument with microtubules plus 1 mm MgATP. The MgATP competes with and effectively prevents rebinding of mantADP to the active site once it is released. Fig. 9 shows the time dependence of the exponential decrease in fluorescence as a function of microtubule concentration, and the maximum rates of mantADP release for Eg5-367 were 43 s⁻¹ and 34 s⁻¹ for Eg5-437 (Fig. 9B and Table II). The microtubule concentration required to produce half the maximal rate of mantADP release (K_1/2,Mt) was 2.5 μm for Eg5-367 and 15 μm for Eg5-437. This difference in half-maximal stimulation was consistent with the K_1/2,Mt observed in the steady-state ATPase assays, indicating that Eg5-367 exhibits a tighter affinity for microtubules during ATP turnover.

DISCUSSION

This study has provided a minimal ATPase mechanism of the human mitotic kinesin, Eg5. Overall, the ATPase mechanism is unique among kinesin superfamily members, but is more similar to KinN kinesins, such as conventional kinesin, compared with the KinC spindle motors, Kar3 and Ncd. Using various kinetic and thermodynamic approaches, we have defined the mechanochemical cycle of two truncated Eg5 motors, Eg5-367 and Eg5-437. Each motor shares many similarities in its mechanochemical cycle; however, there are several significant differences observed.

Each Eg5 motor shares a similar affinity for microtubules under equilibrium conditions. In addition, both Eg5 motors have similar kinetics for ATP binding, ATP hydrolysis, ATP-promoted microtubule detachment, and ADP product release, although differences have been identified in steady-state kinetics and microtubule association kinetics. In the absence of microtubules, a difference in the rate of ATP turnover (k_off,ADP) was observed, suggesting a more open nucleotide pocket of Eg5-367 compared with Eg5-437. Also in the presence of microtubules, a dramatic difference was discovered between the steady-state k_cat of Eg5-367 compared with Eg5-437. Even though ATP hydrolysis and ATP-promoted dissociation are relatively slow steps measured in the study, the k_cat of Eg5-367 (~6 s⁻¹) was around 2-fold faster than Eg5-437 (~3 s⁻¹). This decreased k_cat could be a result of Eg5-437 dimerizing on the microtubule, although we were unable to observe cooperativity between the two heads of the suspected Eg5-437 dimer by performing mantADP release experiments designed to look for head-head communication (data not shown). Currently, we do not have additional evidence to support Eg5-437 being dimeric on the microtubule. On the other hand, the difference in microtubule association kinetics could account in part for the difference in the measured k_cat. Finally, the rate of phosphate release has not yet been measured and could provide a better understanding of the steady-state k_cat.

Another major kinetic difference between our two Eg5 motors was observed in microtubule association (k₊₅ = 11 μm⁻¹s⁻¹ for Eg5-367 versus 0.7 μm⁻¹s⁻¹ for Eg5-437). The steady-state K_1/2,Mt (Fig. 2) as well as the mantADP release K_1/2,Mt (Fig. 9) support this kinetic difference. Furthermore, the association kinetics (Fig. 8) show that Eg5-437 exhibits slow microtubule association rather than more rapid dissociation (k₋₅) upon collision (Table II). One possible interpretation is that the extended C-terminal α-helical sequence of Eg5-437 may result in interference at the microtubule-binding region either through interaction with the catalytic core or the microtubule lattice. The crystal structure of Eg5 identified a unique neck linker docking conformation perpendicular to the long edge of the motor domain when MgADP is bound (36). This perpendicular docking may position the α-helical segment that extends beyond the neck linker in Eg5-437 near the microtubule-binding interface, thus affecting the efficacy of microtubule association.

Eg5 shares structural similarities in the motor domain with Kar3, Ncd, and conventional kinesin (35–40), yet these proteins display differences in the coupling of the ATPase cycle to force generation (Table II). Eg5 exhibits an ATPase mechanism that is more similar to conventional kinesin than the spindle motors, Kar3 and Ncd. Eg5 is similar to conventional kinesin based on its fast ADP product release, slow detachment from the microtubule, and fast microtubule association (Eg5-367). However, Eg5 also displays distinct differences. For Eg5, ATP binding was a two-step process, but there was no evidence of a rapid ATP off rate as observed with kinesin that would result in partitioning of the Mt·Eg5·ATP intermediate. The Eg5 burst amplitude and K_d,ATP were similar for both the acid-quench and the pulse-chase experiments, thus supporting this interpretation. We looked carefully for evidence of processivity especially because of the slow microtubule dissociation and rapid microtubule association kinetics. However, the rapid quench experiments (Figs. 5 and 6) revealed that the burst amplitude during the first ATP turnover was comparable to the enzyme concentration used in the experiment. For a processive motor such as conventional kinesin, one would expect a super-stoichiometric burst amplitude for this experimental design. However, for a homotetrameric kinesin such as Eg5, it may be very difficult to distinguish kinetics suggestive of processivity from kinetics indicative of a high duty ratio motor. In addition, the communication within the homotetramer has not yet been defined. For example, we do not know if the motor pair on one microtubule acts as a single unit with coordination through the anti-parallel stalk to the Eg5 dimer on the other microtubule, or whether there is head-head communication within the single dimer on one microtubule.

We propose the minimal model shown in Fig. 10, where motor binding to the microtubule results in rapid ADP release. ATP binding initiates a series of structural transitions that result in movement of the Switch II cluster for neck linker docking (35, 36), resulting in the Mt·E*·ATP intermediate (Species 2) that proceeds directly to ATP hydrolysis. ATP hydrolysis results in a weak binding state (Species 3); however, we do not yet know the identity of this intermediate. Phosphate release may occur on the microtubule (k₊₄′, Scheme 1) followed by detachment as the E·ADP intermediate as shown for kinesin (59, 65), or detachment may occur as the E·ADP·P_i intermediate (k₊₃, Scheme 1) as observed for Ncd (67, 71). We have presented the neck linker in Species 2 as being docked and parallel to the longest motor edge, based on the KIF1A·AMP-PCP and the Eg5·ADP·monastrol structures (35, 85). We show the no nucleotide state (Species 1 and 5) with an undocked conformation and the detached ADP state (Species 4) with an ordered neck-linker conformation perpendicular to the long edge of the motor based on the Turner et al. structure (36). However, we need additional information about the neck linker conformations during the ATPase cycle to understand its similarities to kinesin and its role in the mechanochemical cycle. The rapid microtubule association kinetics (k₊₅) suggest that the Eg5 motor domain would immediately rebind once detached, thereby assuring that one motor domain of the dimer (or homotetramer) was always bound to the microtubule at any one time. This model acts as the conceptual framework for our future experiments.

Fig. 10. Model for microtubule-Eg5 interaction.

This presentation of Mt·Eg5 ATPase cycle incorporates the specific kinetic steps in Scheme 1 with proposed states on the microtubule. See “Discussion.” Red, Eg5·ATP; blue, Eg5·ADP; red- and white-striped, Mt·Eg5 intermediate after ATP hydrolysis.