Abstract
This paper provides an overview of forward dynamic neuromusculoskeletal modeling. The aim of such models is to estimate or predict muscle forces, joint moments, and/or joint kinematics from neural signals. This is a four-step process. In the first step, muscle activation dynamics govern the transformation from the neural signal to a measure of muscle activation—a time varying parameter between 0 and 1. In the second step, muscle contraction dynamics characterize how muscle activations are transformed into muscle forces. The third step requires a model of the musculoskeletal geometry to transform muscle forces to joint moments. Finally, the equations of motion allow joint moments to be transformed into joint movements. Each step involves complex nonlinear relationships. The focus of this paper is on the details involved in the first two steps, since these are the most challenging to the biomechanician. The global process is then explained through applications to the study of predicting isometric elbow moments and dynamic knee kinetics.
Keywords: Hill model, EMG, tendon, musculotendon complex, pennation angle
The eight-syllable term neuromusculoskeletal in the title of this article simply means that we will be modeling the movements produced by the muscular and skeletal systems as controlled by the nervous system. Neuromusculoskeletal modeling is important for studying functional electrical stimulation of paralyzed muscles, for designing prototypes of myoelectrically controlled limbs, and for general study of how the nervous system controls limb movements in both unimpaired people and those with pathologies such as spasticity induced by stroke or cerebral palsy.
There are two fundamentally different approaches to studying the biomechanics of human movement: forward dynamics and inverse dynamics. Either approach can be used to determine joint kinetics (e.g., estimate joint moments during movements) and it is important that the differences between them are understood.
EMG-Based Forward Dynamics
Flowchart
In a forward dynamics approach to the study of human movement, the input is the neural command (Figure 1). This specifies the magnitude of muscle activation. The neural command can be taken from electromyograms (EMGs), as will be done in this paper, or it can be estimated by optimization or neural network models.
Figure 1.
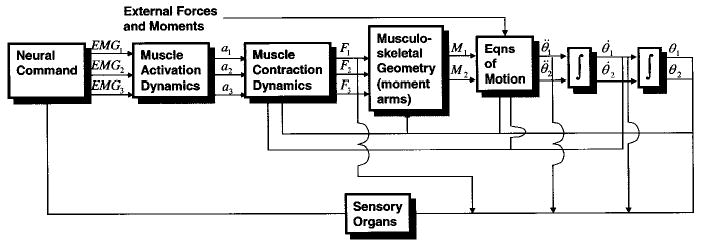
Forward dynamics approach to studying human movement. This flowchart depicts the neural command and forces for three muscles and the moments and joint angles for a two-joint system. As seen here, the three main steps require models of muscle activation dynamics, muscle contraction dynamics, and musculoskeletal geometry.
The magnitudes of the EMG signals will change as the neural command calls for increased or decreased muscular effort. Nevertheless, it is difficult to compare the absolute magnitude of an EMG signal from one muscle to that of another because the magnitudes of the signals can vary depending on many factors such as the gain of the amplifiers, the types of electrodes used, the placements of the electrodes relative to the muscles’ motor points, the amount of tissue between the electrodes and the muscles, etc. Thus, in order to use the EMG signals in a neuromusculoskeletal model, we must first transform them into a parameter we shall call muscle activation, ai (where i represents each muscle in the model). This process is called muscle activation dynamics and the output, ai, will be mathematically represented as a time varying value with a magnitude between 0 and 1.
Muscle contraction dynamics govern the transformation of muscle activation, ai, to muscle force, Fi. Once the muscle begins to develop force, the tendon (in series with the muscle) begins to carry load as well and transfers force from the muscle to the bone. This force is best called the musculotendon force. Depending on the kinetics of the joint, the relative length changes in the tendon and the muscle may be very different. For example, this is certainly the case for a “static contraction.” (This commonly used term is an oxymoron, as something cannot contract, i.e., shorten, and be static at the same time.)
The joint moment is the sum of the musculotendon forces multiplied by their respective moment arms. The force in each musculotendonous unit contributes toward the total moment about the joint. The musculoskeletal geometry determines the moment arms of the muscles. (Since muscle force is dependent on muscle length, i.e., the classic muscle “length-tension curve,” there is feedback between joint angle and musculotendon dynamics in the flowchart.) It is important to note that the moment arms of muscles are not constant values, but change as a function of joint angles. In addition, one needs to keep in mind the multiple degrees of freedom of each joint, as a muscle may have multiple actions at a joint, depending on its geometry. For example, the biceps brachii act as elbow flexors and as supinators of the forearm, the rectus femoris acts as an extensor of the knee and as a flexor at the hip, etc. Finally, it is important to note that the joint moment, Mj (where j corresponds to each joint), is determined from the sum of the contributions for each muscle. To the extent that not all muscles are included in the process, the joint moment will be underestimated. The output of this transformation is a moment for each joint (or, more precisely, each degree of freedom).
Using joint moments, multijoint dynamics can be used to compute the accelerations, velocities, and angles for each joint of interest. On the feedback side, the neural command is influenced by muscle length via muscle spindles, and tendon force via Golgi tendon organs. Many other sensory organs play a role in providing feedback, but these two are generally the most influential.
Problems With the Forward Dynamics Approach.
EMG-driven models of varying complexity have been used to estimate moments about the knee (Lloyd & Besier, 2003; Lloyd & Buchanan, 1996; 2001; Onley & Winter, 1985), the lower back (McGill & Norman, 1986; Thelen et al., 1994), the wrist (Buchanan et al., 1993), and the elbow (Manal et al., 2002). Nevertheless, there are several difficulties associated with the use of the forward dynamics approach.
First, it requires estimates of muscle activation. The high variability in EMG signals has made this difficult, especially during dynamic conditions. Second, the transformation from muscle activation to muscle force is difficult, as it is not completely understood. Most models of this (e.g., Zajac, 1989) are based on phenomenological models derived from A.V. Hill’s classic work (Hill, 1938) or the more complex biophysical model of Huxley (Huxley, 1958; Huxley & Simmons, 1971), such as Zahalak’s models (Zahalak, 1986, 2000).
One way around the problem of determining force from EMG is to use optimization methods to predict muscle forces directly, thus bypassing these first two limitations. However, the choice of a proper cost function is a matter of great debate. Scientists doing research in neural control of human movement find it surprising that biomechanical engineers replace their entire line of study—and indeed the entire central nervous system—with a simple, unverified equation. Nevertheless, some cost functions provide reasonable fits of the data when addressing specific questions. Although optimization methods are more commonly used for inverse dynamic models, performance-based cost functions such as selecting muscles that will maximize jumping height or minimize metabolic energy have been used in forward dynamic models (e.g., Anderson & Pandy, 2001; Pandy & Zajac, 1991).
Another difficulty with forward dynamics is that of determining muscle-tendon moment arms and lines of action. These are difficult to measure in cadavers and even harder to determine with accuracy in a living person. Finally, estimations of joint moments are prone to error because it is difficult to obtain accurate estimates of force from every muscle. To make matters worse, when using forward dynamics, small errors in joint torques can lead to large errors in joint position.
Contrast With Inverse Dynamics Methods
Inverse dynamics approaches the problem from the opposite end. Here we begin by measuring position and the external forces acting on the body (Figure 2). In gait analysis for example, the position of markers attached to the participants’ limbs can be recorded using a camera-based video system and the external forces recorded using a force platform.
Figure 2.
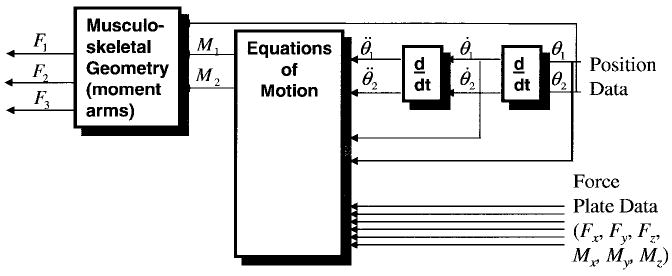
Inverse dynamics approach to studying human movement. This flowchart depicts the angular position for two joints, and the forces for three muscles. Note that the data processing flows from right to left.
The tracking targets on adjacent limb segments are used to calculate relative position and orientation of the segments, and from these the joint angles are calculated. These data are differentiated to obtain velocities and accelerations. The accelerations and the information about other forces exerted on the body (e.g., the recordings from a force plate) can be input to the equations of motion to compute the corresponding joint reaction forces and moments.
If the musculoskeletal geometry is included, muscle forces can then, in theory, be estimated from the joint moments, and from these it may be possible to estimate ligament and joint compressive forces. However, partitioning these forces is not a simple matter.
Problems With the Inverse Dynamics Approach.
As with forward dynamics, inverse dynamics has important limitations. First, in order to estimate joint moments correctly, one must know the inertia and mass of each body segment (this is embedded in the equations of motion). These parameters are difficult to measure and must be estimated. Typically these are estimated using values from cadavers and scaled using simplistic scaling rules, the accuracies of which are rarely verified.
Second, the displacement data must be differentiated to determine segment angular and linear velocities and accelerations. This operation is ill conditioned, which in practice means the estimation of these variables is sensitive to measurement noise that is amplified in the differentiation process.
Third, the resultant joint reaction forces and moments are net values. This is important to keep in mind if inverse dynamics are used to predict muscle forces. For example, if a person activates his hamstrings generating a 30-Nm flexion moment and at the same time activates the quadriceps generating a 25-Nm extension moment, the inverse dynamics method (if it is perfectly accurate) will yield a net knee flexion moment of 5 Nm. Since the actual contribution of the knee flexor muscles was six times greater, this approach is grossly inaccurate and inappropriate for estimating the role of the knee flexors during this task. This problem cannot be overstated because co-contraction of muscles is very common; yet this approach is widely use to estimate muscular contributions.
Fourth, another limitation of the inverse dynamics approach occurs when one tries to estimate muscle forces. Since there are multiple muscles spanning each joint, the transformation from joint moment to muscle forces yields many possible solutions and cannot be readily determined. Traditionally, muscle contributions to the joint moments have been estimated using some form of optimization model (e.g., Crowninshield & Brand, 1981; Kaufman et al., 1991; Seireg & Arvikar, 1973). Alternatively, muscles can be lumped together by groups (e.g., flexors and extensors) to form “muscle equivalents” (Bouisset, 1973). In these models the external flexion or extension moments are balanced with the lumped extensor and flexor muscle groups acting only in extension or flexion (Morrison, 1970; Schipplein & Andriacchi, 1991). Either of these methods can be difficult to justify because they both make an a priori assumption about how the muscles act: either together as fixed synergists or following a cost function. Both assumptions have been shown not to hold up well during complex tasks (Buchanan & Shreeve, 1996; Buchanan et al., 1986; Herzog & Leonard, 1991).
Finally, if one wishes to examine muscle activations, there is no current model available that will do this inverse transformation from muscle forces, if muscle forces could be estimated in the first place. Thus, inverse dynamics is not a good method to use if one wishes to include neural activation in the model. However, this is rarely the goal of an inverse dynamics analysis. It is, on the other hand, the goal of this paper, so the remainder of the paper will be devoted to the different forms of the forward dynamics approach, with one exception wherein a hybrid approach will be considered that uses inverse dynamics to calibrate and verify the forward dynamics solution.
In the remainder of this paper, we will discuss the steps required for the transformations depicted by the boxes in Figure 1: muscle activation dynamics, muscle contraction dynamics, musculoskeletal geometry, and the computation of joint moments and angles. We will then discuss how to adjust (or tune) the model for specific participants and present examples of its use for the elbow and knee joints.
Muscle Activation Dynamics
The transformation from EMG to muscle activation is not trivial. In this section we will examine the many steps necessary to perform this transformation, but one should keep in mind that most researchers use a subset of the approaches that will be described. The basic steps can be seen in Figure 3. Although some type of mathematical transformation must be performed, it is often combined with the next stage in the process—muscle contraction dynamics.
Figure 3.
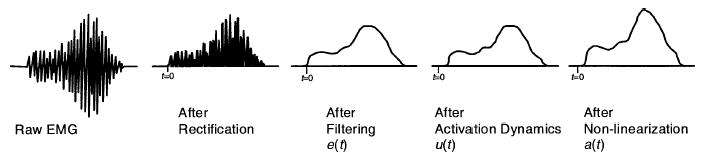
Muscle activation dynamics: Transformation from EMG to muscle activation.
EMG Processing
The purpose of EMG signal processing is to determine each muscle’s activation profile. A raw EMG signal is a voltage that is both positive and negative, whereas muscle activation is expressed as a number between 0 and 1, which is smoothed or filtered to account for the way EMG is related to force.
The first task is to process the raw EMG signal into a form that, after further manipulation, can be used to estimate muscle activation. To accomplish this, the first step is to remove any DC offsets or low frequency noise. With low quality amplifiers or movement of the electrodes, it is possible to see the value of the mean signal of the raw EMG change over time. This is not good because it is an artifact, not part of the signal emanating from the muscle. It can be corrected by high-pass filtering the EMG signal to eliminate low-frequency noise (allowing the high-frequency components to pass through, thus the term high-pass filter). This must be done before rectifying and the cutoff frequency should be in the range of 5–30 Hz, depending on the type of filter and electrodes used. This filter can be implemented in software and, if this is the case, one should use a filter that has zero-phase delay properties (e.g., forward and reverse pass 4th order Butterworth filter), so filtering does not shift the EMG signal in time. Once this is done, it is safe to rectify the signal where the absolute values of each point are taken, resulting in a rectified EMG signal.
The simplest way to transform rectified EMG to muscle activation is to normalize the EMG signal, which is done by dividing it by the peak rectified EMG value obtained during a maximum voluntary contraction (MVC), and then applying a low-pass filter to the resultant signal. Normalizing can be tricky because true maximum EMG values can be difficult to obtain. Questions are often asked about obtaining an MVC: Should it be done differently for each muscle to ensure that a maximal value is reached, or should it just be recorded when maximal joint torque is reached? Should it be recorded under dynamic conditions? Should each muscle be at the peak of its length-tension curve when maximal values are recorded? These are valid questions and are subject to some debate.
We suggest that maximal values be recorded for each muscle separately during muscle testing procedures (e.g., Kendall et al., 1993). If this is done, it isn’t important whether the joint moment is at a peak when the recordings are made because joint moment is a function of all of the muscles’ activities. Ensuring that a muscle is at the peak of its length-tension curve will help ensure that the muscle produces maximal force during the contraction, but this is not important when recording maximum EMG. The bottom line is that if the normalized EMG signal ever goes over 1.0, it is clear that the maximum values were not properly obtained. Well motivated participants can reach true maximal values if care is taken (Woods & Bigland-Ritchie, 1983).
The rectified EMG signals should then be low-pass filtered because the muscle naturally acts as a filter and we want this to be characterized in the EMG-force transformation. That is, although the electrical signal that passes through the muscle has frequency components over 100 Hz, the force that the muscle generates is of much lower frequencies (e.g., muscle force profiles are smoother than raw EMG profiles). This is typical of all mechanical motors. In muscles there are many mechanisms that cause this filtering; for example, calcium dynamics, finite amount of time for transmission of muscle action potentials along the muscle, and muscle and tendon viscoelasticity. Thus, in order for the EMG signal to be correlated with the muscle force, it is important to filter out the high-frequency components. The cutoff frequency will vary with the sharpness of the filter used, but something in the range of 3 to 10 Hz is typical.
Activation Dynamics
Is normalized, rectified, filtered EMG appropriate to use for values of muscle activation? For some muscles during static conditions it may be reasonable, but in general a more detailed model of muscle activation dynamics is warranted in order to characterize the time varying features of the EMG signal.
Differential Equation.
EMG is a measure of the electrical activity that is spreading across the muscle, causing it to activate. This results in the production of muscle force. However, it takes time for the force to be generated—it does not happen instantaneously. Thus there exists a time delay for the muscle activation, which can be expressed as a time constant, τact. This process is called “muscle activation dynamics” (Zajac, 1989), and it can be modeled by a first-order linear differential equation. We will refer to normalized, rectified, filtered EMG as e(t). Note that e(t) is different for each muscle, but for now we shall consider it for a single muscle for the sake of simplicity. The process of transforming EMG, e(t), to neural activation1 u(t), is called activation dynamics. Zajac modeled activation dynamics using the following differential equation:
| (1) |
where β is a constant such that 0 < β < 1. An examination of the term in the brackets2 shows that when the muscle is fully activated, i.e., e(t) = 1, the time constant is τact. However, when the muscle is fully deactivated, i.e., e(t) = 0, the time constant is τact/β. This means that for isometric cases, i.e., when e(t) is a constant, we see that the force rises faster during excitation than it falls during relaxation, which is a well documented property (Gottlieb & Agarwal, 1971; Hill, 1949).
As can be seen, Equation 1 is a differential equation. That is, u(t) is function of the derivative of u(t), i.e., . This means that for discrete input signal, e(t), Equation 1 is best solved using numerical integration, such as a Runge-Kutta algorithm.
Although this first-order differential equation does a fine job of characterizing activation dynamics, we have found that for discretized data a second-order relationship works more efficiently.
Discretized Recursive Filter.
When a muscle fiber is activated by a single action potential, the muscle generates a twitch response. This response can be well represented by a critically damped linear second-order differential system (Milner-Brown et al., 1973). This type of response has been the basis for the different equations to determine the neural activation, u(t), from the EMG input, e(t).
| (2) |
where M, B, and K are the constants that define the dynamics of the second-order system.
Equation 2 is the continuous form of a second-order differential equation; however, when continuous data are collected in the laboratory, the data are sampled at discrete time intervals, resulting in a discrete EMG time series. Therefore it would be appropriate to create a discrete version of the second-order differential equation to process the sampled EMG data. It can be easily shown using backward differences (Rabiner & Gold, 1975) that Equation 2 can be approximated by a discrete equation from which we can obtain u(t), where
| (3) |
where d is the electromechanical delay and α, β1, and β2 are the coefficients that define the second-order dynamics. These parameters (d, α, β1, and β2) map the EMG values, e(t), to the neural activation values, u(t). Selection of the values for β1 and β2 is critical in forming a stable equation, for which the following must hold true:
| (4) |
| (5) |
| (6) |
| (7) |
It should also be realized that Equation 3 can be seen as a recursive filter where the current value for u(t) depends on the last two values of u(t). That is, the neural activation depends not just on the current level of neural activation but also on its recent history. This filter should have unit gain so that neural activation does not exceed 1, and to ensure this, the following condition must be met:
| (8) |
Thus, if γ1 and γ2 are known, β1 and β2 can be found from Equations 4 and 5 and α can be found from Equation 8. This way only three parameters need to be determined to describe this transformation (d, γ1 and γ2).
A time (or electromechanical) delay, d, is included in this equation, which accounts for the delay between the neural signal and the start of the resulting twitch force. Electromechanical delay has been reported to range from 10 msec to about 100 msec (Corcos et al., 1992) and has two components: (a) “a transport problem” depending on factors such as calcium transport time across the muscle membrane, and muscle fiber conduction velocities, and (b) dynamics of force production which depends on chemical dynamics of the muscle depolarization and muscle contraction dynamics (Corcos et al., 1992).
The constraints shown in Equations 4–8 stem from the requirement that the recursive filter or second-order system be stable. An unstable filter will cause the output values of u(t) to oscillate at the natural frequency of the filter or even cause values of u(t) to go to infinity. The constraints are determined from the z transform of the transfer function of the impulse response for Equation 3, which is given by
| (9) |
The roots of the polynomial in the denominator are z = −γ1 and z = −γ2, and the absolute value of these need to be less than 1 to create a stable filter (Rabiner & Gold, 1975).
Previous work on cats has demonstrated why many researchers have experienced difficulties predicting muscle force from rectified and low-pass filtered EMG (Guimarães et al., 1995; Herzog et al., 1998). The main reasons were the inability (a) to attain the best time delay between EMG onset and force onset, and (b) to characterize the observation that the EMG signal was shorter in duration than the resulting force. It can be shown that both of these issues are easily accommodated by the discrete second-order system presented above.
Activation is Nonlinearly Related to EMG
Many researchers assume that u(t) is a reasonable approximation of muscle activation, a(t). But is this the case? Again, this depends on the type of muscle being studied. This is because it has been shown that isometric EMG is not necessarily linearly related to muscle force (e.g., Heckathorne & Childress, 1981; Woods & Bigland-Ritchie, 1983; Zuniga & Simons, 1969). In studies on single motor units, one stimulation pulse will create a twitch response and multiple stimulation pulses will cause multiple twitch responses. If the time between stimulation pulses decreases (i.e., stimulation frequency increases), the twitches will start to merge into each other (i.e., fuse) and the average force produced by the motor unit will steadily increase. However, as stimulation frequency pulse is progressively increased, the twitches will get closer to tetanus, at which point no further force can be produced by the muscle even if stimulation frequency increases. This means there is a nonlinear relationship between stimulation frequency and force for single motor units. This nonlinearity can be offset by other factors such as the recruitment of small motor units at low force levels and larger ones at higher levels (i.e., the size principle).
This nonlinearity is not characterized by the u(t) term. For example, Woods and Bigland-Ritchie showed that while some muscles have linear isometric EMG-force relationships, the relationship for other muscles is nonlinear, especially at lower forces (up to about 30%). They modeled the relationship as a power function,
| (10) |
where the bars indicated variables normalized to maximum and a and b were coefficients whose values were determined experimentally. This relationship was used for the beginning of the curve (the first 30–40%) and a linear function was used for the remainder. Although this mathematical form fit their data rather well, it has two disadvantages. First, it is not a smooth function at the junction between the two curves; that is, the slopes do not match. For mathematical models, functions that are continuous in the first derivative may have advantages. Second, it uses two parameters (a and b) where only one parameter is necessary.
These disadvantages can be corrected by expressing activation as a function of normalized, rectified, processed EMG, u(t), using a logarithmic function instead of a power function (Manal & Buchanan, 2003) for low values and a linear function for high values:
| (11) |
where u(t) is the neural activation (from Equation 3) and a(t) is the muscle activation. The coefficients c, d, m, and b in Equation 12 can be solved for simultaneously and reduced to a single parameter, A, as shown in Figure 4. The transition point (i.e., the ~30% value) is not a constant for u(t), but varies as seen in the figure. The parameter A is used to characterize the curvature and is related to the amount of nonlinearity found in the EMG-to-activation relationship. It varies from 0.0 to approximately 0.12.
Figure 4.
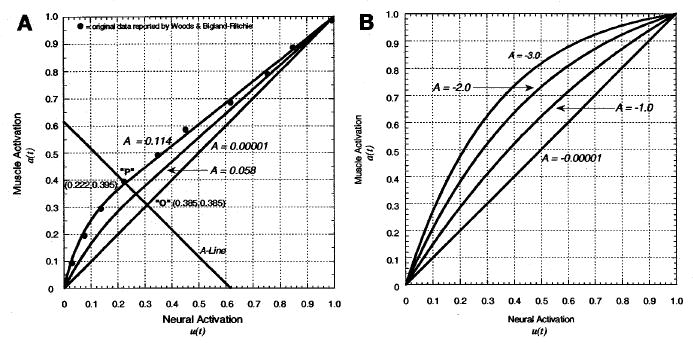
Nonlinearization neural to muscle activation relationship: e(t) → a(t). (A) Dots represent data from Woods and Bigland-Ritchie (1983) for the biceps brachii for the isometric EMG-force relationship (demonstrating that other muscles showed a linear relationship), and the curves represent Equation 11. In this scheme, a perfectly linear relationship would fall on line A= 0. As values for A increase, a nonlinear region is added for lower force levels (left side of the A-line), while linear relationships continue for higher values (right side of the A-line). Point P marks where these two curves join. (B) Equation 12 is used to accomplish the same goals. Here the different shape factors, A, produce different curvature of the relationship. We limit A to be from −3<A<0, where 0 is a straight line.
We have also used an alternative formulation (Lloyd & Besier, 2003; Lloyd & Buchanan, 1996; Manal et al., 2002) that is simpler and yields adequate solutions:
| (12) |
where A is the nonlinear shape factor. Note that this A is different from the A just discussed. Here the nonlinear shape factor, A, is allowed to vary between −3 and 0, with A = −3 being highly exponential and A = 0 being a linear relationship.
Note that for both Equations 11 and 12 a single parameter, A, is used to represent the nonlinearity. The actual value for A is determined in the calibration or tuning process (see section on Model Tuning and Validation).
Muscle Contraction Dynamics
Once muscle activations have been obtained, the next step is to determine muscle forces. This requires a model of muscle contraction dynamics. Physiological models describing this relationship are problematic. For example, Huxley-type models that estimate the forces in cross-bridges are very complex (Huxley, 1958; Huxley & Simmons, 1971; Zahalak, 1986, 2000) and the muscle dynamics are governed by multiple differential equations, which need to be numerically integrated. This makes these models computationally time-consuming to use for modeling forces in multiple muscles. For this reason, many researchers who do large-scale (i.e., with many muscles) neuromuscular modeling use Hill-type models. These models are phenomenological in nature, i.e., the external behavior of the system is characterized rather than the underlying physiology. Nevertheless, they are powerful tools that give reasonable results for most applications. One significant advantage of Hill-type muscle models is that, in most cases, the dynamics are governed by one differential equation per muscle, making modeling using a system of muscles computationally viable.
Hill-Type Models
The general arrangement for a muscle-tendon model has a muscle fiber in series with an elastic or viscoelastic tendon (Figure 5A). The muscle fiber also has a contractile component in parallel with an elastic component (Figure 5B).
Figure 5.
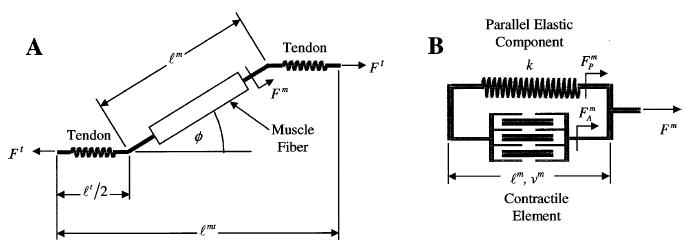
(A) Schematic of muscle-tendon unit showing muscle fiber in series with the tendon. Note the pennation angle, φ, of the muscle fiber relative to the tendon and that the total tendon length, ℓt, is twice that of the tendon on either end of the muscle fiber, ℓt/2. (B) Schematic of muscle fiber with the contractile element and parallel elastic component. The nonlinear tendon stiffness is given by k. The force produced by the contractile element, Fm, is a function of ℓm and νm, while the tendon force, Ft, is a function of ℓt. The total muscle fiber force, Fm, is the sum of FAm and Fpm.
The Hill-type muscle model is used to estimate the force that can be generated by the contractile element of the muscle fiber, with the general form of the function given by
| (13) |
where Fm(t) = time varying muscle fiber force, from now on represented as Fm in text; f(ν) = normalized velocity dependent fiber force; f(ℓ) = normalized length dependent fiber force; a(t) = time varying muscle activation; and Fom = maximum isometric muscle fiber force.
The determination of the activation time series has been described above. In the following we will describe the muscle fiber’s force dependency on muscle length and velocity, and subsequently describe how to calculate the force generated by the muscle-tendon unit.
Muscle Force Changes With Length.
To understand muscle contraction dynamics, we must begin by describing the relationship between muscle force and length. Muscles can be thought of as having an active part which generates force when activated, like a motor, and a passive part that applies a resistive force when stretched beyond a resting length, like a rubber band.
The active part of muscle is due to the contractile elements. These yield a peak force when the sarcomeres are at an optimal length, i.e., when there is optimal overlap of the actin and myosin myofilaments. When the muscle is at a length above that optimal length, it cannot generate as much force because there is less actin-myosin overlap which reduces the force-generating potential of the muscle. Likewise, if it is below that length, its maximal potential force will drop off as well. Human muscles reach their peak force values when the sarcomeres are at a length of 2.8 μm (Walker & Schrott, 1974). When the sarcomeres within a muscle fiber are at this length, we say that the fiber is at optimal fiber length, ℓom.
Mathematically, it is often more helpful to consider the force-length relationship in dimensionless units, as shown in Figure 6. Muscles can be assumed to produce zero force when shorter than 50% and longer than 150% of their optimal length, as shown here. Although this curve has been modeled as a second-order polynomial (Woittiez et al., 1984), it is actually a bit more complex than that and is perhaps best modeled using the force-length relationship described by Gordon et al. (1966). We use a curve created by a cubic spline interpolation of the points defined on the Gordon et al. curve (Figure 6). This curve is normalized for force and length where the normalized length-dependent muscle force, , and normalized muscle length , are given by
Figure 6.
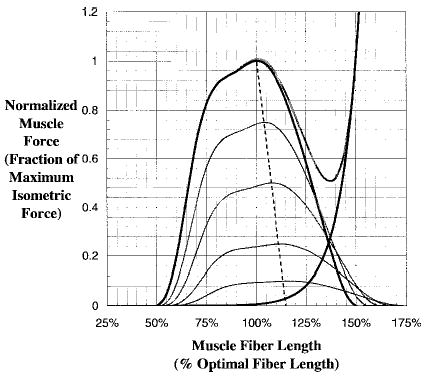
Normalized force-length relationship for muscle. Thick dark lines indicate maximum activation, whereas the light thin lines are lower levels of activation. Note that the optimal fiber length is longer as the activation decreases. In the figure, λ = 0.15, which means the optimal fiber length is 15% longer at zero activation.
| (14) |
| (15) |
where FAm is the muscle force represented by the active part of the force-length curve. Note that a(t) is accounted for since the level of muscle activation determines the maximum isometric force produced by the muscle.
The muscle force-length is also coupled to the level of activation. Huijing (1996) has shown that optimal fiber lengths increase as activation decreases (Figure 6), which has also been reported by Guimarães et al. (1994). This coupling between activation and optimal fiber length is incorporated into our muscle model using the following relationship developed by Lloyd and Besier (2003):
| (16) |
The percentage change in optimal fibre length, ℓ, defines how much the optimal fiber length shifts to longer lengths, ℓom(t), at time t and activation a(t). For example if ℓ = 15%, then the optimal fiber length would be 1.15 at zero activation level.
The passive force in the muscle is due to the elasticity of the tissue that is in parallel with the contractile element (Figure 5B). Passive forces are very small when the muscle fibers are shorter than their optimal fiber lengths, ℓom, and rise greatly thereafter. We use an exponential relationship that is described by Schutte (1992). This passive muscle force function is given by
| (17) |
where is normalized passive muscle force and is normalized muscle length. The actual passive muscle force is a function of maximum isometric force (Zajac, 1989), given by
| (18) |
The total normalized isometric muscle force is the sum of the active and passive components, which can be scaled to different muscles to provide total isometric muscle force, Fm, (see Figure 5B) by
| (19) |
Note that Fm here only accounts for the force-length relationship of muscle, whereas it also should depend on muscle fiber velocity which will be described next.
Muscle Force Changes With Velocity.
Although most people use the Hill equation to describe muscle fiber force, fewer people recall that Hill first formulated it to examine the heat associated with muscle contractions (Hill, 1938). He found experimentally that when a muscle was shortened a distance x, it gave off a “shortening heat” (H) such that
| (20) |
where a is a thermal constant related to the cross-sectional area of the muscle. Hill also speculated that a/Fom was a constant (~0.25), where Fom is the maximum muscle force generated when the muscle fibers are at optimal length, ℓom.
Hill next looked at the total energy of the system, which is the sum of the energy associated with the shortening heat and that due to work (force × distance). Thus,
| (21) |
From this equation we can see by differentiation that the rate of energy liberation is
| (22) |
Finally, Hill proposed that this rate of energy liberated must be proportional to the change in force. Since muscle forces started at maximal values, Fom, this can be written as
| (23) |
where the constant b defines absolute rate of energy liberated. This is the Hill equation. It can be rewritten as
| (24) |
where νm is the muscle fiber contraction velocity, which in this equation is muscle shortening velocity only (i.e., concentric contractions).
Hill-type models take into account the force-length and force-velocity relationships. Combining these two relationships can be difficult, since the force-velocity relationship was derived at optimal fiber length and the force-length relationship allows for nonoptimal length. However, Equation 24 must be modified to be used at different lengths if it is to be useful. There are two ways in which the force-length and force-velocity relationships could be most readily combined for shortening muscle. The first is as follows:
| (25) |
In this first method we replace optimal muscle force by the muscle force at other lengths, Fm(ℓ), according to the force-length curve. Is this a valid way to account for the force-length relationship? Epstein and Herzog (1998) point out that if this were true, at maximal velocity, νom (recall that Hill showed that muscle force is zero at maximal velocity), Equation 25 could be rewritten as
| (26) |
Since a and b are constants, this implies that maximal muscle fiber velocity depends on a muscle’s length. However, Edman (1979) showed that νom is constant for most of a muscle’s operating range. For this reason, Epstein and Herzog state that the preferred combined equation is
| (27) |
where fA(ℓ) is the normalized force-length relationship.
The previous development is for shortening muscle only, and lengthening muscle must be accounted for differently. The general function to describe this is given by
| (28) |
where a′ and b′ are the eccentric values for a and b, and is the multiplier of Fom to set the limit for the maximum eccentric muscle force. The value of has been shown to range between 1.1 to 1.8 (Epstein & Herzog, 1998); however, we use a value of 1.8 as suggested by Zajac (1989). The a′ and b′ are eccentric coefficients. Mathematically, it is best to normalize muscle velocity values, expressing them in dimensionless units as f(ν).
Modeling the Tendon.
Since the tendon is in series with the muscle, whatever force passes through the muscle must also pass through the tendon, and vice versa. For this reason, the force in whole muscle cannot be considered without examining how that force affects the tendon.
Tendons are passive elements that act like rubber bands. Below the tendon slack length, ℓst, the tendon does not carry any load. However, above the tendon slack length it generates force proportional to the distance it is stretched. Zajac (1989) observed from the literature that the strain in tendon is 3.3% when the muscle generates maximum isometric force, Fom, and that tendons fail at strains of 10% when forces are 3.5 Fom (Figure 7). Tendon strain can be defined as
Figure 7.
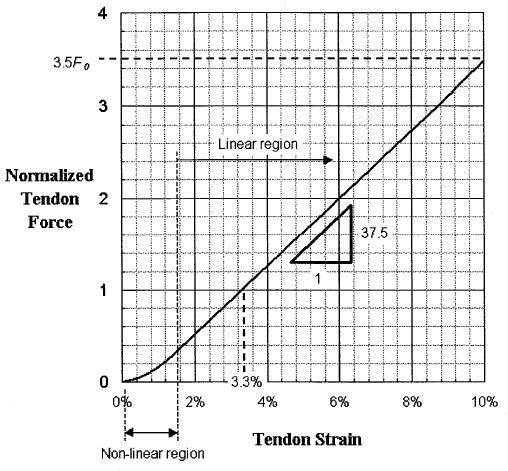
Normalized force-length relationship for tendon (adapted from Zajac, 1989).
| (29) |
Of course, the force varies with the strain only when the tendon length is greater than the tendon slack length; otherwise the tendon force is zero.
Most people model tendon as a simple straight line with a positive slope for values above the tendon slack length. However, tendon is made up of collagen that has a wave-like crimp when unloaded. When tensile force is first applied to unloaded collagen, the crimp flattens out as the fibers take up load. In this mode the tendon has low stiffness with a nonlinear force-strain relationship. However, when the crimp flattens, the tendon exhibits greater stiffness and a linear force-strain relationship with an elastic modulus of 1.2 GPa. Again, to normalize the curve to enable scaling to different muscles, the elastic modulus is divided by the tendon stress at maximum isometric muscle force, suggested by Zajac (1989) to be 32 MPa, which gives a normalized elastic modulus of 37.5. Subsequently the normalized tendon force, , is given by (shown in Figure 7).
| (30) |
Since the tendon becomes thicker and stronger as muscle strength increases, it has been proposed (Zajac, 1989) that the final tendon force can be calculated by multiplying by the maximum isometric muscle force, that is,
| (31) |
Pennation Angle.
The pennation angle is the angle between the tendon and the muscle fibers (Figure 5A). Although for many muscles the pennation angle is negligible, for others it can be substantial. For a muscle with a pennation angle greater than zero, the muscle force will be generated at an angle to the tendon (Figure 5A). Since the tendon is in series with the muscle fibers, the force in the tendon, Ft, is given by
| (32) |
For muscles with a small pennation angle, the pennation angle will have little effect on the force in the musculotendonous unit. However, for muscles with large pennation angles (e.g., those greater than 20° as are found in the triceps surae), the pennation angle can have a significant effect on the force.
Is the pennation angle constant? Unfortunately for those of us who model such things, the answer is no. Kawakami et al. (1998) used ultrasound to show that the medial gastrocnemius muscle can change its pennation angle from 22° to 67°, depending on joint angles and amount of muscle activation. Although there have been a few simple models reported that describe pennation angle changes with muscle activation, very little has been done to verify these with in-vivo imaging studies (such as ultrasound). Nevertheless, from studies of animal muscles, some clever researchers have created quite elaborate models (e.g., Woittiez et al., 1984) and some simpler models (Scott & Winter, 1991) that can be used to predict pennation angle in the contracting muscle. We prefer simpler models, as they are quicker to compute and have been shown to track pennation angle well (Scott & Winter, 1991). These models assume that muscle has constant thickness and volume as it contracts (Scott & Winter, 1991). A typical equation to calculate pennation angle, φ(t), at time t is
| (33) |
where ℓm(t) is the muscle fiber length at time t, and φo is the pennation angle at muscle optimal fiber length, ℓom.
Physiological Parameters That Can Be Adjusted
All of the equations developed above are normalized functions to describe the dynamic force-generating ability of the muscle-tendon unit. To scale these equations to model different muscles, we must include physiological parameters that characterize the individual muscle properties. These are maximum muscle force, Fom, optimal muscle fiber length, ℓom, tendon slack length, ℓst, and the pennation angle at optimal muscle fiber length, φo.
The optimal fiber length, tendon slack length, and pennation angle are measured from cadavers for which Yamaguchi et al. (1990) have summarized the results of many studies for a large number of muscles in the human body. Of these three parameters, tendon slack length is the most difficult to measure, but it can be approximated using a numerical method (Manal & Buchanan, 2004). However, maximum muscle force is determined a bit differently.
The term Fom corresponds to the peak force that a muscle can produce at its optimal muscle length and is related to a muscle’s cross-sectional area. Simply put, muscles with more sarcomeres in parallel can generate more force. The best parameter to describe the amount of sarcomeres in parallel is a muscle’s physiological cross-sectional area or PCSA. The PCSA is defined as a muscle’s volume divided by its optimal fiber length. Typically, the volume of a muscle is calculated from its weight multiplied by the density of muscle tissue: 1.06 g/cm3 (Mendez & Keys, 1960).
Muscle is generally assumed to have a constant value for maximum stress (recall that stress is force divided by area). Thus, by knowing the PCSA and multiplying by maximum muscle stress, we can estimate maximum muscle force. This is a problem, however, as values reported for maximal muscle stress have varied considerably (from 35 to 137 N/cm2). Buchanan (1995) pointed out that when values for PCSA are taken from the literature and maximal elbow moments are recorded for individuals, the corresponding maximal stress computed for flexors is substantially different from that for extensors. This may simply be due to measuring PCSA data from cadavers and applying it to younger people, as flexors and extensors may atrophy at different rates with disuse—a common state for bedridden elderly (the most common precondition of cadaver specimens). But whatever the cause, this is a potential problem for doing accurate muscle modeling. That is, applying a single value for maximal muscle stress to cadaver-based PCSA values to obtain maximal muscle force may yield models that are too strong or weak in flexion or extension. However, appropriate scaling can be better obtained by accurate measurement of maximal joint moments for each muscle. This can then be distributed to the various muscles according to the relative PCSA values.
Another parameter that can be considered is maximum muscle fiber contraction velocity, νom. It is different for fast- and slow-twitch muscle fibers. A usual way to represent maximum contraction velocity is to express it as the number of optimal fiber lengths per second, i.e., normalized maximum contraction velocity, . Typical values for this are less than or equal to 8 ℓom/s for slow-twitch muscle fibers and approximately 14 ℓom/s for fast-twitch muscle fibers (Epstein & Herzog, 1998). Zajac (1989) suggested that for modeling mixed fibers, which most muscles are, is a good approximation. This is the value we currently use for all muscles in our models. That is, we treat νom as a constant. However, νom could be varied depending on the relative fiber mixes in muscles. The fiber mixture percentages listed by Yamaguchi et al. (1990) would be a good starting point, but it is well known that people do have different fast-twitch to slow-twitch fiber ratios.
Putting It All Together
When the physiological parameters are combined with the Hill-type model, we see that muscle-tendon force (for we see in Figure 5A that it is really tendon force that causes the joint moment, but we shall call this the musculotendon force, Fmt) is a function of many things. This can be written as shown:
| (34) |
That is, the musculotendon force is a function of the muscle-tendon’s activation, a, length, ℓmt, and velocity, νmt. All of these variables change as a function of time and are the inputs to muscle-tendon model. (In fact, ℓmt and νmt also change as a function of joint angle, θ, but we will discuss that later.) Equation 34 shows that muscle force is also dependent on musculoskeletal parameters that are generally assumed not to change: maximal isometric muscle force (Fom), optimal fiber length (ℓom), tendon slack length (ℓst), and pennation angle at optimal fiber length (φo). This function (Equation 34) is complex and highly nonlinear. It involves not just the force-length and force-velocity relationships (e.g., Equation 13), but also the force in the muscle must be solved to equal the force in the tendon (Equation 32). Equation 34 can written in another form which permits us to see how muscle-tendon force is actually calculated, i.e.,
| (35) |
The total force developed by the muscle fiber is represented by the term in the brackets above, as schematically shown in Figure 5B. Although this may not look it, this is actually a nonlinear first-order differential equation.
Since the muscle-tendon force functions are nonlinear differential equations and the model inputs are discrete signals, the equations must be numerically integrated (for which we use a Runge-Kutta-Fehlberg algorithm). Following is a brief description of the process. Starting with a value for ℓm, fiber pennation angle is calculated using Equation 33. Subsequently, the tendon length is computed from ℓt = ℓmt − ℓm cos(φ), since muscle-tendon length, ℓmt, is one of the known inputs to the muscle-tendon model (this will be discussed in detail in the next section). Once tendon length is established, tendon force can be determined using Equations 29, 30, and 31. From this point we calculate normalized velocity-dependent muscle fiber force, f(ν), by rearranging terms in Equation 35 to get
| (36) |
Note that fA(ℓ) and fP(ℓ) can be calculated since we know ℓm. Also note that a(t) is an input. Once f(ν) is calculated, we can solve for fiber velocity, νm, from Equations 27 or 28 (depending on whether this is an eccenric or concentric contraction). Once we know νm, we numerically integrate foward to get the next ℓm in time. Since the value for ℓm has now changed, the whole loop starts all over again. This continues iteratively until we have calculated the muscle-tendon forces to the end of input time series of a(t) and ℓmt(t). This is carried out for each muscle in the musculoskeletal model so all muscle-tendon forces are estimated.
Musculoskeletal Geometry
Important variables in the above approach are the length and velocity of the whole muscle (i.e., the musculotendonous unit). They play an important role because of the force-length and force-velocity relationships. But how does one compute the length of a muscle, let alone its velocity? And once the force is calculated, it is important to compute the corresponding contribution to joint moment. This requires knowledge of the muscle’s moment arm, which can be shown to be a function of the muscle’s length.
To compute both the length and the moment arm for a musculotendonous unit, a musculoskeletal model is required. These models must account for the way musculotendon lengths and moment arms change as a function of joint angles. The better musculoskeletal models include information about the geometry of the bones and the complex relationships associated with joint kinematics (e.g., Delp & Loan, 1995; Delp et al., 1990). For example, most joints do not act as simple hinges. They allow for translation and rotations that can be rather complex. Thus the joint centers are not fixed. The implication is that the moment arms (i.e., distance from the joint center to the muscle’s line of action) will change as well. In addition, the musculoskeletal models must account for the fact that muscles do not follow straight lines. The muscle paths are far more complex, and defining anatomically appropriate models involves the use of sophisticated computer graphics. And even when a musculoskeletal model is constructed, it is rather difficult to verify, requiring many hours of anatomical research if one wishes to make sure the musculotendon geometry is anatomically accurate. Finally, muscle moment arms and musculo-tendon muscle lengths can be very difficult to scale from one individual to another (Murray et al., 2002).
Musculotendon Lengths and Moment Arms
When we use musculoskeletal models to examine the length of a muscle, we generally consider the length of the muscle and tendon together. This is because geometrically the muscle and tendon act together as one musculotendonous unit. This musculotendonous unit can be treated as a straight line, a collection of line segments, or a curve. As mentioned before, describing a musculotendonous unit as a straight line connecting its origin to its insertion is an oversimplification and can be problematic. This is because nearly every muscle will bend or wrap around other structures at some joint configuration. For example, most extensor muscles wrap around bones (consider the triceps brachii wrapping around the distal humerus). Likewise, most flexors are constrained at some joint angles by superficial tissues (e.g., retinaculum). Since these constraints will change with particular joint configurations, models of the musculoskeletal geometry tend to be very complex.
The moment arm of a musculotendonous unit, r(θ), can be found readily from its length, ℓmt(θ), and joint angle, θ, using the tendon displacement method described by An et al. (1984):
| (37) |
This equation can be easily derived from the principle of virtual work. Note that the moment arm changes as a function of the joint angle. For biarticular muscles (muscles that cross two joints), the moment arm is a function of two joint angles, which is why, unless one wishes to have a model that is valid at only one joint configuration, obtaining moment arm values from a textbook is ill-advised.
Computing Joint Moments and Angles
Once all the muscle forces are computed and their corresponding moment arms are estimated, their contributions to the joint moment can be found by multiplication. If this is done for all the muscles at a particular joint, the corresponding joint moment, Mj, can be estimated:
| (38) |
Here the muscle force is from Equation 35 and the moment arm is from Equation 37. Note that the subscript i has been introduced, which corresponds to the particular muscle, for these must be summed over all m muscles. This moment is the contribution that the muscles make to the total joint moment.
Once the muscular contribution to the joint moment is computed, the contributions from other sources can be added appropriately. There may be moments due to external loads or gravitational forces or intersegmental dynamics. All of these must be summed to compute the total joint moment.
The joint moments, in turn, will cause movement to take place (unless it is physically prevented). The movement will be represented by the resultant joint angles and must be computed using methods from basic dynamics (i.e., Lagrangean or Eulerian dynamics). These equations depend on the number of joints and the number of degrees of freedom at each joint, and they can become very complex as one moves beyond simple single-joint models. Note that to solve these equations, inertial parameters must be estimated for each of the moving body segments.
Model Tuning and Validation: Some Examples
Let us consider an example of a neuromusculoskeletal model by examining the human elbow during a flexion-extension task. We will collect EMGs from the seven primary muscles involved in flexion and extension: the biceps brachii short head, biceps brachii long head, brachialis, brachioradialis, and the three heads of the triceps (i.e., long, medial, and lateral). To calibrate the model, we shall record forces from a load cell located at the distal forearm a known distance from the elbow joint center. A cast will be placed on the participant’s distal forearm and will be bolted to the load cell to ensure that accurate measurements are made. The load cell can measure three forces and three torques, and from these we can determine the elbow moments. Forces and torques from the load cell and EMGs for each muscle are collected synchronously at 1,000 Hz.
EMGs are recorded using either intramuscular electrode pairs or bipolar surface electrodes placed approximately 2 cm apart. EMGs are processed according to methods reported by Buchanan et al. (1993) and are summarized here. EMGs are preamplified electronically (in hardware) before data acquisition by amplifying (gain of 60dB) each channel and band-pass filtering (30 Hz–10 KHz) the signal to remove both low and high frequency noise. A second amplification for each channel is undertaken to maximize the magnitude of the EMG activity within the ±10 volt operating range of the analog to digital data acquisition card. The data acquisition begins with the participants generating maximal muscle activations. These will be used later to normalize the EMG data. During the actual data collection, participants are instructed to simply produce time-varying flexion and extension moments at the elbow.
Using the Models
The digitized EMG signals are full-wave rectified and linear enveloped using a 4th order low-pass Butterworth digital filter with a cutoff frequency of 4 Hz. All EMGs were divided by the peak volitional EMG for the corresponding muscle (which was processed the same way), resulting in processed EMG values, e(t), in the range between 0 and 1 for each muscle (Figure 3).
The e(t) values for each muscle can then be converted to u(t) via Equation 3, and the u(t) can then be converted to a(t) using Equation 11 (or Equation 12). Note that coefficients are required for these transformations which are not known: γ1, γ2, d, and A. Initial guesses can be made for these (γ1 = 0.5, γ2 = 0.5, d = 40 ms, and A = 0.1) and they will be refined later.
The muscle contraction dynamics step requires that we use Equation 35 to estimate the force in each muscle. As previously described, this is not a trivial procedure because the force in each tendon must be equilibrated with the force in each muscle so that they balance. Note that this also requires input from the next step—the musculoskeletal geometry model—because we need values for the musculotendon length as well as for some of the other parameters. We will use the musculoskeletal model described by Murray et al. (1995) to define the musculo-tendon lengths and moment arms as a function of joint angle. The output of this step is elbow flexion-extension moment and there is no need to proceed with the multijoint dynamic part of the model since this task was done with the arm in a fixed position, locked to a load cell. Although it is a simplification to consider that the muscle velocity is zero, we will do so for this example.
Before we return to the procedure for refining the coefficients, let us recall that the output of the entire process, based on the EMG input values, is joint moment. However, we know the actual corresponding joint moments because we measured them with a load cell. Thus, by comparing the computed values for joint moment with the experimentally determined values, we should be able to see how well our model fits the data.
Adjusting Parameters
We can now return to the coefficients. We guessed at initial values for the coefficients, without expecting the model output to agree with the measured moment particularly well. We can now look at the output of the model—how well it predicted joint moment—and use this to refine the coefficients, thereby tuning the model to the participant. This can be done mathematically using a nonlinear optimization. If desired, some of the parameters of the musculoskeletal model can be adjusted as well. For example, values for tendon slack length can be estimated and used for initial guesses, but these can be allowed to vary over the biologically reported range (e.g., + or – 1 standard deviation) in order to fit them for our participant. In this way the model can be tuned for each person. This tuning can be described mathematically as follows:
| (39) |
The squared difference between the model-predicted joint moment and the measured moment is summed over n samples. For a 5-s trial collected at 1,000 Hz, the squared differences are summed over 5,000 samples. As much as possible, coefficients and parameters should be constrained to operate within physiological limits. For example, the time delay term, di, should be constrained to be between 10 and 100 ms. Typical values are 40 ms. The nonlinear shape factor A should be constrained such that 0 < A ≤ 0.12, which yields linear (A near zero) to nonlinear (A = 0.12) force-EMG curves that fall within physiological ranges. In addition, Equations 4–8 are established so that muscle activations are constrained to be less than or equal to 1.
The objective function in Equation 39 can be minimized by adjusting the coefficients for each muscle. This process is performed off-line and convergence is generally obtained within a few minutes. To accelerate the process, we currently resample the data at 100 Hz before the optimization begins. A schematic of the optimization process is illustrated in Figure 8. Randomly choosing the coefficients or using values optimized for a different participant will generally result in poor agreement between the model-predicted moment and the measured moment from the load cell. In contrast, excellent agreement is possible when the model has been tuned or calibrated (see Figure 9).
Figure 8.
Flowchart of the modeling procedure. EMG is processed to obtain muscle activation while the position data is used to obtain musculoskeletal lengths, velocities, and moment arms. Together these are put into a Hill-type model to estimate musculotendon forces, and these in turn are multiplied by their moment arms and summed to obtain joint moment. This estimated moment is compared with the measured moment. In the optimization process, parameters in the model are adjusted to minimize the difference between measured and predicted joint moments. Once the parameters are tuned, the optimization part of the model is removed and it can now be used to predict joint moments for novel tasks.
Figure 9.
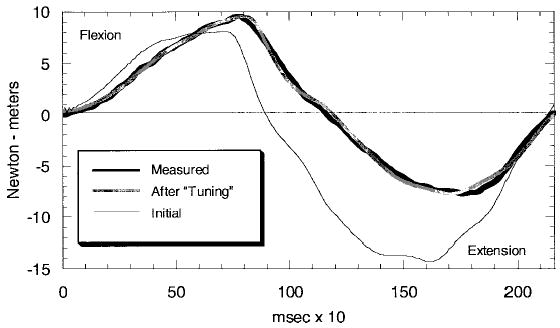
Output of the model described in the section on Model Tuning and Validation. Values for elbow moment recorded experimentally are compared with those estimated by the model before model parameter adjustment and after optimization or tuning.
Too Many Parameters Is Not Good.
The more parameters that are allowed to vary, and the more those parameters are allowed to vary, the better the fit will be between the estimated joint moment and the measured joint moment. However, that does not mean it is best to vary as many parameters as possible.
Models having many parameters generally have little predictive ability. For example, Zheng et al. (1998) created a model that estimates muscle forces from EMGs, and it yields predicted joint moments that are very close to those determined using inverse dynamics. But their model requires that the parameters be determined or reevaluated at each instant in time. That is, the model is accurately adjusted to fit the data at each time step. But with many time steps, and perhaps hundreds or thousands of parameters to adjust during the course of a single movement, it is highly likely that accurate predictions could be made. The problem with this approach is that the model is “overfit.” This means the model cannot be used in any predictive way. If parameters must be recalculated or adjusted for each trial, the model cannot be used to predict novel data. While this may not have been a problem for Zheng et al.’s application, it means that such models will have very limited predictive power.
A predictive model is one that can be calibrated with some data and appropriate parameters can be adjusted within reasonable amounts. Those parameters that correspond to physically established measurements should not be allowed to be adjusted beyond physiological norms. Then, once the parameters are adjusted, the model can be used with novel data (from tasks unlike those for which it was trained) without further adjustment of the parameters. In this way the robustness of the model’s ability to predict the correct answers can be ascertained.
Ideally, models should be as simple as is reasonable. The fewer parameters that are adjusted, the more faith can be put in the biomechanics undergirding the model and the less people will suspect it to be a mathematical exercise in curve fitting (Heine et al., 2003). The researcher should feel a tension between having a better fit and having too many model parameters, because each adjusted parameter makes the model less convincing and diminishes its power.
Dynamic Cases: Using a Hybrid Approach
The above procedure can and has been used also for studies of limb dynamics. Once the joint moments are determined, it is relatively straightforward (although certainly nontrivial) to calculate the resultant movement using multijoint dynamics. With greater numbers of segments in the model, there is much increased complexity of the model and solving the dynamical equations can be computationally quite intensive.
Another approach can be a hybrid scheme that combines forward and inverse dynamics methods (see Figure 10 for schematic of the process). We have used this approach (Lloyd & Besier, 2003) to examine the loads experienced by the muscles and ligaments in the knee during running and cutting maneuvers. In this study, EMGs were collected from 10 muscles and muscle forces and resulting joint moments were estimated. Data to derive the muscle forces were recorded in a gait laboratory wherein the joint angles were determined using video cameras to track the position of markers attached to the body, and the ground reaction forces applied to participants’ feet were measured from force plates. Using a kinematic model to determine joint movements and ground reaction force data, the knee joint flexion-extension moments were estimated using inverse dynamics. The corresponding knee joint flexion-extension moments were also estimated using the forward solution, using EMGs and the ankle, knee, and hip joint kinematics as inputs.
Figure 10.
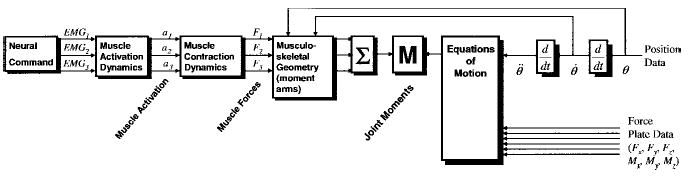
Hybrid Forward-Inverse dynamics approach to studying human movement and determining muscle forces for people performing tasks in movement laboratory. This simplified schematic depicts the angular position for one joint, and the forces for three muscles. Note that both the forward and inverse dynamics approaches provide estimates for joint moments, which can be used for validation of modeling.
Calibration of this EMG-driven model entailed the comparison of the joint flexion-extension moments from the forward solution with those from the inverse dynamics solution. The squared differences between these two solutions (i.e., Equation 38) were used to adjust the model parameters, as described above. Three gait trials and two trials recorded from an isokinetic dynamometer were used to calibrate the model. There were 18 parameters adjusted in the model to over 500 data points from the 5 calibration trials, so it could not be argued that it was just an exercise in curve fitting. The 18 parameters were categorized into muscle-tendon parameters and EMG-to-activation parameters. The muscle-tendon parameters included tendon slack lengths for each muscle in the musculoskeletal model and maximum flexor and extensor muscle stress. The EMG-to-activation parameters were γ1, γ2, and A, the same values were used for all muscles.
The advantage of the hybrid scheme is that the joint moments from the forward and inverse solutions can be used to cross-validate the forward modeling method, of course within the error associated with inverse dynamic methods. The calibrated forward model (EMG-driven) produced exceptionally good predictions of the inverse solution of the knee flexion-extension moments from over 200 other trials (Figure 11); average R2 = 0.91 ± 0.04. In addition, keeping muscle-tendon parameters constant and only permitting the EMG-to-activation parameters to be adjusted, the model was able to predict trials 2 weeks apart with no loss in predictive ability. Once the model was calibrated and shown to be able to predict joint moments very well, we had increased confidence in the estimates of muscle forces and joint moments. We were then able to use the calibrated model to estimate loads experienced by the ligaments in the knee during the tasks performed by the participants. This method is being used to determine the joint contact forces in walking, running, and cutting maneuvers. (Note that these forces are different from the ground reaction forces determined from inverse dynamics.)
Figure 11.
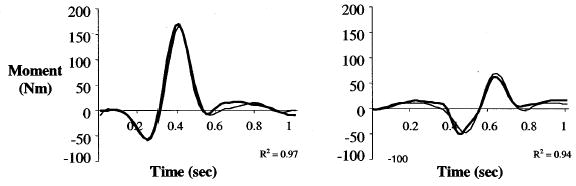
Typical results for predictions of knee joint moments from the calibrated Hybrid Forward-Inverse Dynamics approach: Crossover cut (left) and straight run (right). Thick line represents the EMG-driven model results; thin line represents the inverse dynamics results. (Adapted from Lloyd & Besier, 2003)
Summary
In this paper we have shown how to estimate joint moments from EMG signals using a forward dynamics approach. This approach uses a Hill-type model that accounts for force-length and force-velocity relationships. The model results are verified by comparing the predicted joint moments with the measured moments. These models have tremendous importance in estimating muscle forces during various tasks—something that is difficult to achieve with other models. For example, optimization-based models may be able to predict forces, but they do not account for differences in an individual’s neuromuscular control system, which may be impaired.
The accuracy of these models is greatly influenced by the accuracy of the anatomical data, which must include a full model of the musculoskeletal geometry. This approach is, by necessity, rigorous. Many previous models of muscle force or joint moment from EMGs have been shown to be grossly inaccurate. Only by basing a model on a solid biomechanical and anatomical foundation can reasonable results be achieved.
Acknowledgments
This work is supported, in part, by US NIH grants R01-AR46386, R01-HD38582, and P20-RR16458, as well as from the Australian NHMRC (991134 and 254565), West Australian MHRIF, and AFL Research and Development Board.
The authors wish to dedicate this paper to the memory of Dr. Catriona Lloyd who died on the 8th of March, 2004, one week before her 40th birthday. Catriona was beloved wife, mother, friend, and scientist whose warmth and love will be greatly missed by all who had the great pleasure of knowing her.
Footnotes
Zajac referred to this as muscle activation. We use the term neural activation because we consider muscle activation to be the transformation from e(t) to u(t) to a(t) whereas Zajac called the step from e(t) to u(t) muscle activation. That is, we describe muscle activation as requiring an additional step, and hence have introduced the term neural activation to describe the intermediate stage.
For this type of first-order differential equation, the term in brackets is equal to the inverse of the time constant of the equation. That is, the solution to the equation df(t)/dt + (l/τ) f(t) = 0 is f(t) = Ae−t/τ. The time constant of the equation, τ, determines the rate of exponential decay.
References
- An KN, Takahashi K, Harrigan TP, Chao EY. Determination of muscle orientations and moment arms. Journal of Biomechical Engineering. 1984;106:280–282. doi: 10.1115/1.3138494. [DOI] [PubMed] [Google Scholar]
- Anderson FC, Pandy MG. Dynamic optimization of human walking. Journal of Biomechical Engineering. 2001;123:381–390. doi: 10.1115/1.1392310. [DOI] [PubMed] [Google Scholar]
- Bouisset, S. (1973). EMG and muscle force in normal motor activities Basel: Karger.
- Buchanan TS. Evidence that maximum muscle stress is not a constant: Differences in specific tension in elbow flexors and extensors. Medical Engineering and Physics. 1995;17:529–536. doi: 10.1016/1350-4533(95)00005-8. [DOI] [PubMed] [Google Scholar]
- Buchanan TS, Almdale DPJ, Lewis JL, Rymer, WZ Characteristics of synergic relations during isometric contractions of human elbow muscles. Journal of Neurophysiology. 1986;5:1225–1241. doi: 10.1152/jn.1986.56.5.1225. [DOI] [PubMed] [Google Scholar]
- Buchanan TS, Moniz MJ, Dewald JPA, Rymer WZ. Estimation of muscle forces about the wrist joint during isometric tasks using an EMG coefficient method. Journal of Biomechanics. 1993;4:547–560. doi: 10.1016/0021-9290(93)90016-8. [DOI] [PubMed] [Google Scholar]
- Buchanan TS, Shreeve DA. An evaluation of optimization techniques for the prediction of muscle activation patterns during isometric tasks. Journal of Biomechical Engineering. 1996;118:565–574. doi: 10.1115/1.2796044. [DOI] [PubMed] [Google Scholar]
- Corcos DM, Gottlieb GL, Latash ML, Almeida GL, Agarwal GC. Electromechanical delay: An experimental artifact. Journal of Electromyography and Kinesiology. 1992;2:59–68. doi: 10.1016/1050-6411(92)90017-D. [DOI] [PubMed] [Google Scholar]
- Crowninshield RD, Brand RA. A physiologically based criterion of muscle force rediction in locomotion. Journal of Biomechanics. 1981;14:793–801. doi: 10.1016/0021-9290(81)90035-x. [DOI] [PubMed] [Google Scholar]
- Delp SL, Loan JP. A graphics-based software system to develop and analyze models of musculoskeletal structures. Computers in Biology and Medicine. 1995;25:21–34. doi: 10.1016/0010-4825(95)98882-e. [DOI] [PubMed] [Google Scholar]
- Delp SL, Loan JP, Hoy MG, Zajac FE, Topp EL, Rosen JM. An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Transactions on Biomedical Engineering. 1990;37:757–767. doi: 10.1109/10.102791. [DOI] [PubMed] [Google Scholar]
- Edman KA. The velocity of unloaded shortening and its relation to sarcomere length and isometric force in vertebrate muscle fibres. Journal of Physiology. 1979;291:143–159. doi: 10.1113/jphysiol.1979.sp012804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Epstein, M., & Herzog, W. (1998). Theoretical models of skeletal muscle New York: Wiley.
- Gordon AM, Huxley AF, Julian FJ. The variation in isometric tension with sarcomere length in vertebrate muscle fibres. Journal of Physiology. 1966;185:170–192. doi: 10.1113/jphysiol.1966.sp007909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottlieb GL, Agarwal GC. Dynamic relationship between isometric muscle tension and the electromyogram in man. Journal of Applied Physiology. 1971;30:345–351. doi: 10.1152/jappl.1971.30.3.345. [DOI] [PubMed] [Google Scholar]
- Guimaraes AC, Herzog W, Hulliger M, Zhang YT, Day S. Effects of muscle length on the EMG-force relationship of the cat soleus muscle studied using non-periodic stimulation of ventral root filaments. Journal of Experimental Biology. 1994;193:49–64. doi: 10.1242/jeb.193.1.49. [DOI] [PubMed] [Google Scholar]
- Heckathorne CW, Childress DS. Relationship of the surface electromyogram to the force, length, velocity, and contraction rate of the cineplastic arm. American Journal of Physical Medicine. 1981;60:1–19. [PubMed] [Google Scholar]
- Heine R, Manal K, Buchanan TS. Using Hill-type muscle models and EMG data in a forward dynamic analysis of joint moment: Evaluation of critical parameters. Journal of Mechanics in Medicine and Biology. 2003;3:169–186. [Google Scholar]
- Herzog W, Leonard TR. Validation of optimization models that estimate the forces exerted by synergistic muscles. Journal of Biomechanics. 1991;24(Suppl):31–39. doi: 10.1016/0021-9290(91)90375-w. [DOI] [PubMed] [Google Scholar]
- Herzog W, Sokolosky J, Zhang YT, Guimaraes AC. EMG-force relation in dynamically contracting cat plantaris muscle. Journal of Electromyography and Kinesiology. 1998;8:147–155. doi: 10.1016/s1050-6411(97)00015-1. [DOI] [PubMed] [Google Scholar]
- Hill AV. The heat of shortening and the dynamic constants of muscle. Proceedings of the Royal Society of London Series B. 1938;126:136–195. doi: 10.1098/rspb.1949.0019. [DOI] [PubMed] [Google Scholar]
- Hill AV. The abrupt transition from rest to activity in muscle. Proceedings of the Royal Society of London Series B. 1949;136:399. doi: 10.1098/rspb.1949.0033. [DOI] [PubMed] [Google Scholar]
- Huxley AF. Muscle structure and theories of contraction. Progress in Biophysical Chemistry. 1958;7:255–318. [PubMed] [Google Scholar]
- Huxley AF, Simmons RM. Proposed mechanism of force generation in striated muscle. Nature. 1971;233:533–538. doi: 10.1038/233533a0. [DOI] [PubMed] [Google Scholar]
- Kaufman KR, An KN, Litchy WJ, Chao EY. Physiological prediction of muscle forces—I. Theoretical formulation. Neuroscience. 1991;40:781–792. doi: 10.1016/0306-4522(91)90012-d. [DOI] [PubMed] [Google Scholar]
- Kawakami Y, Ichinose Y, Fukunaga T. Architectural and functional features of human triceps surae muscles during contraction. Journal of Applied Physiology. 1998;85:398–404. doi: 10.1152/jappl.1998.85.2.398. [DOI] [PubMed] [Google Scholar]
- Kendall, F.P., McCreary, E.K., & Provance, P.G. (1993). Muscles testing and function Philadelphia: Williams & Wilkins.
- Lloyd DG, Besier TF. An EMG-driven musculoskeletal model for estimation of the human knee joint moments across varied tasks. Journal of Biomechanics. 2003;36:765–776. doi: 10.1016/s0021-9290(03)00010-1. [DOI] [PubMed] [Google Scholar]
- Lloyd DG, Buchanan TS. A model of load sharing between muscles and soft tissues at the human knee during static tasks. Journal of Biomechanical Engineering. 1996;118:367–376. doi: 10.1115/1.2796019. [DOI] [PubMed] [Google Scholar]
- Manal K, Buchanan TS. Modeling the non-linear relationship between EMG and muscle activation. Journal of Biomechanics. 2003;36:1197–1202. doi: 10.1016/s0021-9290(03)00152-0. [DOI] [PubMed] [Google Scholar]
- Manal K, Buchanan TS. Subject-specific estimates of tendon slack length: A numerical method. Journal of Applied Biomechanics. 2004;20:195–203. [Google Scholar]
- Manal K, Gonzalez RV, Lloyd DG, Buchanan TS. A real-time EMG driven virtual arm. Computers in Biology and Medicine. 2002;32:25–36. doi: 10.1016/s0010-4825(01)00024-5. [DOI] [PubMed] [Google Scholar]
- McGill SM, Norman RW. Partitioning of the L4/L5 dynamic moment into disc, ligamentous and muscular components during lifting. Spine. 1986;11:666–678. doi: 10.1097/00007632-198609000-00004. [DOI] [PubMed] [Google Scholar]
- Mendez J, Keys A. Density and composition of mammalian muscle. Metabolism, Clinical and Experimental. 1960;9:184–188. [Google Scholar]
- Milner-Brown HS, Stein RB, Yemm R. Changes in firing rate of human motor units during linearly changing voluntary contractions. Journal of Physiology (London) 1973;228:371–390. doi: 10.1113/jphysiol.1973.sp010193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrison JB. The mechanics of the knee joint in relation to normal walking. Journal of Biomechanics. 1970;3:51–61. doi: 10.1016/0021-9290(70)90050-3. [DOI] [PubMed] [Google Scholar]
- Murray WM, Buchanan TS, Delp SL. Scaling of peak moment arms of elbow muscles with upper extremity bone dimensions. Journal of Biomechanics. 2002;35:18–22. doi: 10.1016/s0021-9290(01)00173-7. [DOI] [PubMed] [Google Scholar]
- Murray WM, Delp SL, Buchanan TS. Variation of muscle moment arms with elbow and forearm position. Journal of Biomechanics. 1995;28:513–525. doi: 10.1016/0021-9290(94)00114-j. [DOI] [PubMed] [Google Scholar]
- Onley SJ, Winter DA. Predictions of knee and ankle moments of force in walking from EMG and kinematic data. Journal of Biomechanics. 1985;18:9–20. doi: 10.1016/0021-9290(85)90041-7. [DOI] [PubMed] [Google Scholar]
- Pandy MG, Zajac FE. Optimal muscular coordination strategies for jumping. Journal of Biomechanics. 1991;24:1–10. doi: 10.1016/0021-9290(91)90321-d. [DOI] [PubMed] [Google Scholar]
- Rabiner, L.R., & Gold, B. (1975). Theory and application of digital signal processing Englewood Cliffs, NJ: Prentice Hall.
- Schipplein OD, Andriacchi TP. Interaction between active and passive knee stabilizers during level walking. Journal of Orthopaedic Research. 1991;9:113–119. doi: 10.1002/jor.1100090114. [DOI] [PubMed] [Google Scholar]
- Schutte, L.M. (1992). Using musculoskeletal models to explore strategies for improving performance in electrical stimulation-induced leg cycle ergometry PhD Thesis, Stanford University.
- Scott SH, Winter DA. A comparison of three muscle pennation assumptions and their effect on isometric and isotonic force. Journal of Biomechanics. 1991;24:163–167. doi: 10.1016/0021-9290(91)90361-p. [DOI] [PubMed] [Google Scholar]
- Seireg A, Arvikar RJ. A mathematical model for evaluation of forces in lower extremeties of the musculoskeletal system. Journal of Biomechanics. 1973;6:313–326. doi: 10.1016/0021-9290(73)90053-5. [DOI] [PubMed] [Google Scholar]
- Thelen DG, Schultz AB, Fassois SD, Ashton-Miller JA. Identification of dynamic myoelectric signal-to-force models during isometric lumber muscle contractions. Journal of Biomecanics. 1994;27:907–919. doi: 10.1016/0021-9290(94)90263-1. [DOI] [PubMed] [Google Scholar]
- Walker SM, Schrodt GR. I segment lengths and thin filament periods in skeletal muscle fibers of the Rhesus monkey and the human. The Anatomical Record. 1974;178:63–81. doi: 10.1002/ar.1091780107. [DOI] [PubMed] [Google Scholar]
- Woittiez RD, Huijing PA, Boom HB, Rozendal RH. A three-dimensional muscle model: A quantified relation between form and function of skeletal muscles. Journal of Morphology. 1984;182:95–113. doi: 10.1002/jmor.1051820107. [DOI] [PubMed] [Google Scholar]
- Woods JJ, Bigland-Ritchie B. Linear and non-linear surface EMG/force relationships in human muscles. An anatomical/functional argument for the existence of both. American Journal of Physical Medicine. 1983;62:287–299. [PubMed] [Google Scholar]
- Yamaguchi, G.T., Sawa, A.G.U., Moran, D.W., Fessler, M.J., & Winters, J.M. (1990). A survey of human musculotendon actuator parameters. In J.M. Winters & S.L-Y. Woo (Eds.), Multiple muscle systems: Biomechanics and movement organization (pp. 717–773). New York: Springer-Verlag.
- Zahalak GI. A comparison of the mechanical behavior of the cat soleus muscle with a distribution-moment model. Journal of Biomechanical Engineering. 1986;108:131–140. doi: 10.1115/1.3138592. [DOI] [PubMed] [Google Scholar]
- Zahalak GI. The two-state cross-bridge model of muscle is an asymptotic limit of multi-state models. Journal of Theoretical Biology. 2000;204:67–82. doi: 10.1006/jtbi.2000.1084. [DOI] [PubMed] [Google Scholar]
- Zajac FE. Muscle and tendon: Properties, models, scaling, and application to biomechanics and motor control. Critical Reviews in Biomedical Engineering. 1989;17:359–411. [PubMed] [Google Scholar]
- Zheng N, Fleisig GS, Escamilla RF, Barrentine SW. An analytical model of the knee for estimation of internal forces during exercise. Journal of Biomechanics. 1998;31:963–967. doi: 10.1016/s0021-9290(98)00056-6. [DOI] [PubMed] [Google Scholar]
- Zuniga EN, Simons DG. Nonlinear relationship between electromyographam potential and muscle tension in normal subjects. Archives of Physical Medicine and Rehabilitation. 1969;50:613–620. [PubMed] [Google Scholar]


