Abstract
Molecular activation by blackbody photons, first postulated in 1919 by Perrin, plays a dominant role in the unimolecular dissociation of large ions trapped at low pressure in a Fourier-transform mass spectrometer. Under readily achievable experimental conditions, molecular ions of the protein ubiquitin equilibrate with the blackbody radiation field inside the vacuum chamber. The internal energy of a population of these ions is given by a Boltzmann distribution. From the temperature dependence of unimolecular dissociation rate constants measured in the zero-pressure limit, Arrhenius activation parameters equal to those in the high-pressure limit are obtained.
Introduction
In 1919, Perrin1 proposed that unimolecular reactions could be activated by molecular absorption of blackbody photons generated by the surroundings. This mechanism was quickly discounted by both Langmuir2 and Lewis3 and has even been described as “untenable” in modern chemical kinetics textbooks.4 The subsequently accepted Lindemann–Hinshelwood mechanism,5,6 in which molecules are excited and de-excited by non-reactive collisions, has been tremendously successful in explaining the observed unimolecular reaction kinetics over a wide range of pressure. Extrapolation of thermal reaction rates to zero pressure in this mechanism results in a rate constant of zero. However, recent experimental evidence clearly demonstrates that this is not the case.7–16 McMahon7 showed that dissociation rates of weakly bound cluster ions stored in a Fourier-transform mass spectrometer were independent of pressure below ~10−8 Torr. Subsequent results with deuterated ions8,15 were consistent with the expected shifts in the absorption spectrum under a Planck distribution. These results provide firm evidence for blackbody photon activation at these low pressures. Dunbar9 has modeled these processes for small ions and has shown that the absorption of blackbody photons is the rate limiting step in the observed dissociation process. Here, we demonstrate that under readily achievable experimental conditions, activation of ubiquitin ions (8.6 kDa) by blackbody photons is significantly faster than the dissociation processes. Under these conditions, where dissociation is the rate limiting step, ions equilibrate with the blackbody radiation field inside the vacuum chamber, and the internal energy distribution of a population of ions is given by a Boltzmann distribution. From the temperature dependence of the unimolecular rate constants for dissociation, Arrhenius activation parameters equal to those in the high-pressure limit are obtained even in the complete absence of collisions! This method provides a route to measuring accurate dissociation energetics and dynamics for large ions, information that is difficult to obtain by other methods.
Experimental Section
Instrumentation.
Experimental measurements were done using an external electrospray ionization source Fourier-transform mass spectrometer with a 2.7 T magnet. Details of this instrument17 and of the blackbody dissociation experiment are given elsewhere.13,14 Temperatures were measured using two calibrated copper–constantan thermocouples mounted on either side of the cell. These temperatures were corrected to that measured by a thermocouple previously (and temporarily) mounted in the center of the cell. This correction is less than 1 °C. Following a temperature change (typically ~10 °C), the vacuum chamber was allowed to equilibrate for a minimum of 3 h. The thermocouples reached their steady-state temperature in roughly half this time. Bovine ubiquitin was obtained from Sigma Chemical Company (St. Louis, MO) and was used without further purification. Ions were formed from a 60/40 methanol–water solution; ~1% acetic acid was added to enhance production of the 11+ charge state.
Dissociation rate constants are obtained from the slope of ln {[Mn+]/([Mn+] + ∑[Dm+])} vs reaction time, where Mn+ and Dm+ refer to the parent and daughter ions, respectively, with n and m protons attached. These rate constants are for the dissociation of the precursor ion itself. For example, [M + 5H]5+ ions of ubiquitin, i.e., the 5+ charge state, fragment by consecutive loss of water molecules. By summing the abundance of all fragment ions, the rate constant for loss of water from the molecular ion is obtained. For the 11+ ion, where competitive fragmentation is observed, a single rate constant for dissociation of the precursor ion to form all fragment ions is obtained.
Modeling.
Minimum energy structures of (ala-gly)n were found using molecular mechanics with the CVFF force field (Discover v. 2.9.5 in Insight II, Biosym Technologies, San Diego, CA). These structures were used as starting geometries in MOPAC 6.0 and subsequently minimized at the AM1 semiemperical level. Vibrational frequencies and transition dipole moments were obtained from these minimized structures.
Results and Discussion
The blackbody infrared radiative dissociation (BIRD) kinetics for the 11+ and 5+ charge states of ubiquitin formed by electrospray ionization were measured at cell pressures below 4 × 10−8 Torr. Increasing the cell pressure from 2 × 10−8 to 2 × 10−7 Torr with butane had no effect on the measured dissociation rate constant for the 5+ ion, indicating that collisions do not influence the dissociation kinetics in this experiment, consistent with earlier blackbody dissociation results for large ions.13 Figure 1 shows BIRD spectra from the kinetic data at intermediate times and temperatures for both these ions. Ubiquitin is a protein consisting of 76 amino acid residues. The 11+ ion dissociates predominantly by cleavage of the amide backbone on the C-terminal side of residue 52. This produces two fragment ions of complementary mass and charge, denoted as y244+/b527+ complementary ion pairs, where y and b refer to the C- and N-terminus fragments, respectively.18 Cleavage after residue 18 also occurs to produce y588+/(b18 − H2O)3+ in smaller abundance. No loss of water from the molecular ion itself is observed. In contrast, the 5+ ion dissociates exclusively by loss of water and/or ammonia at these temperatures; we are unable to unambiguously assign this loss. Backbone cleavage does not occur for this ion. Facile loss of water from molecular ions of both protonated peptides19 and multiply protonated protein ions20 has been reported previously. Molecular ions with water molecules attached are not observed and do not interfere with these experiments. From the temperature dependence of the dissociation rate constants (Figure 2), Arrhenius activation parameters for these processes are obtained. The 11+ and 5+ ions have activation energies (Ea) of 1.6 and 1.2 eV and pre-exponential factors (A) of 1017 and 1012 s−1, respectively.
Figure 1.
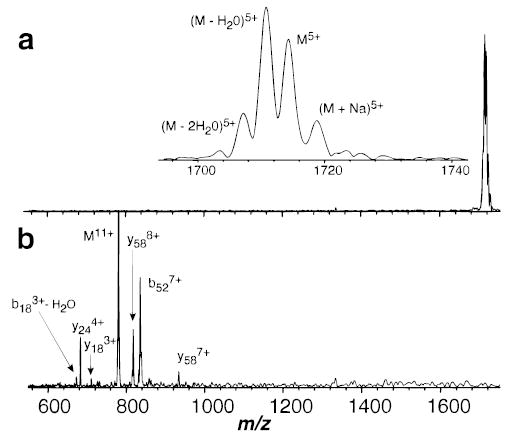
Blackbody infrared radiative dissociation spectra of ubiquitin (a) 5+ with 60 s reaction delay at 417 K and (b) 11+ with 75 s reaction delay at 423 K, measured in the Berkeley external electrospray ion source Fourier-transform mass spectrometer.
Figure 2.
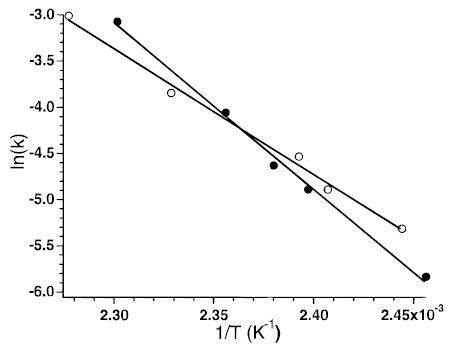
Arrhenius plot for dissociation of ubiquitin 5+ (○) (Ea = 1.2 eV; A = 1012 s−1) and 11+ (•) (Ea = 1.6 eV; A = 1017 s−1).
In order to extract useful information from these parameters, the internal energy distribution of these ions must be known. By analogy to the Lindemann–Hinshelwood mechanism, we show that these ions are in the equivalent of the “high-pressure limit”, i.e., their internal energy is characterized by a Boltzmann distribution. In the high-pressure limit of the Lindemann–Hinshelwood mechanism (Figure 3), the rate of molecular deactivation is rapid compared to the reaction kinetics. That is, k−1,c[M] >> kd in reaction 1 (k1,rad, k−1,rad = 0);
Figure 3.
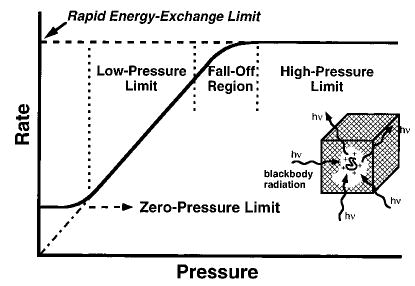
Modified Lindemann–Hinshelwood plot showing effects of pressure on unimolecular dissociation rates of small molecules (solid line). Classically, the rate constant in the low-pressure limit extrapolates linearly to zero in a collisionless environment. Recent experiments show that at low pressure (<10−8 T), the unimolecular rate constant is nonzero and independent of pressure, and that molecular activation occurs by absorption of blackbody radiation. The rapid energy-exchange (REX) limit for larger molecules is indicated by the dashed line.
| (1) |
| (2) |
where subscripts “uni”, “c”, “rad”, and “d” denote the observed thermal rate constant, energy dependent state-to-state collisional and radiative energy transfer rate constants, and energy dependent dissociation rate constants, respectively. Under these conditions, the concentration of the activated complex is in a steady-state that is pressure independent, and the thermal reaction kinetics are given by kdk1,c/k−1,c where the energy dependent ratio k1,c/k−1,c results in a Boltzmann distribution provided kd is much smaller than k−1,c, i.e., kuni is determined entirely by the dissociation kinetics of a Boltzmann distribution of ions. Equation 2 shows that as the pressure of M is reduced, k−1,c[M] can become as small as kd giving rise to the “fall-off” region. At these pressures and lower, extracting information about the dissociation process requires detailed knowledge of the collisional process which is difficult at best to model, particularly for large ions. At the “zero-pressure” limit ([M] = 0), molecular activation occurs by blackbody photons generated by the surroundings, and the observed reaction rates are again pressure independent. For small weakly bound molecules in the zero-pressure limit, k−1,rad << kd, and the observed reaction kinetics reflect only the rate of photon absorption (k1,rad). No information about the dynamics of the dissociation process is obtained. Threshold activation energies can be extracted from the experimentally measured value of the Arrhenius activation energy (Ea) by adding on a large correction factor to take into account the difference in energy between populations of reactant and transition state ions as well as other minor corrections.9
For polymers such as peptides and DNA, the number of oscillators, and hence the number of blackbody photons exchanged with the chamber walls, will increase approximately linearly with size. In contrast, dissociation rates decrease with increasing ion size for a fixed internal energy, or for ions in thermal equilibrium, the dissociation rate is independent of molecular size for a given dissociation process. Thus, for larger ions, k1,rad, k−1,rad >> kd and the measured reaction rates are given by kdk1,rad/k−1,rad where the ratio k1,rad/k−1,rad results in a Boltzmann distribution and kuni is again given by the dissociation kinetics of a Boltzmann distribution of ions. To obtain a more thorough understanding of the effects of ion size on the relativerates of k1,rad, k−1,rad, and kd, we use the generic peptide (ala-gly)n as a model. Vibrational frequencies and the associated transition dipoles (μ) were calculated at the AM1 semiempirical level for n = 4 and 5. Larger ions were scaled linearly by appending the difference in the set of vibrational modes for these ions to those of (ala-gly)5 to take into account the low-frequency cooperative modes for larger systems without having to calculate these explicitly. Rate constants for the absorption and emission of blackbody radiation were calculated using a weakly-coupled harmonic oscillator model given by eq 3 for absorption and by eq 4 for spontaneous and stimulated emission:
| (3) |
| (4) |
where ρ(hν) is the radiation density at ν given by the Planck distribution formula. is the microcanonical transition probability of the nth quantum of the mth frequency mode and includes both the occupation probability and the enhanced transition probability of excited harmonic oscillators,21 and Ai,j and Bi,j are the Einstein coefficients for spontaneous and stimulated processes, respectively, given in eqs 5 and 6:
| (5) |
| (6) |
Microcanonical unimolecular dissociation rate constants were calculated using RRKM theory.22 The C–N stretch of the backbone of the first ala-gly subunit was used as the reaction coordinate;23 transition state frequencies were varied to provide Arrhenius pre-exponential values of 1012 and 1017 s−1 to model the measured values for the 5+ and 11+ ions, respectively. Assuming that all the processes are statistical, the time evolution of a population of these ions can be modeled within the discrete value master equation formalism.9,24,25 From the temperature dependence of these calculated rate constants, Arrhenius activation parameters are obtained.
For (ala-gly)8 (1.0 kDa), we calculate an overall dissociation rate of 0.0006 and 0.011 s−1 at 400 and 430 K, respectively, for a dissociation process with a high-pressure limit value of A∞ = 1017.2 s−1 and a threshold dissociation energy, of Eo = 1.52 eV. This corresponds to Arrhenius activation parameters of Ea = 1.44 eV and A = 1015.0 s−1. In the high-pressure limit, Ea > Eo, indicating that these ions are not in thermal equilibrium with the chamber walls. The difference in internal energy of a population of these ions vs a thermal Boltzmann distribution is shown in Figure 4a. The population of ions at higher energy is depleted relative to a Boltzmann distribution due to the increasing relative rate of kd to k1,rad, k−1,rad with ion internal energy. This shifts the distribution to lower energy resulting in Arrhenius activation parameters that are smaller than their high-pressure-limit values (1.61 eV and 1017.2 s−1). Thus, the measured Arrhenius values would underestimate the values obtained under the high-pressure-limit assumptions.
Figure 4.
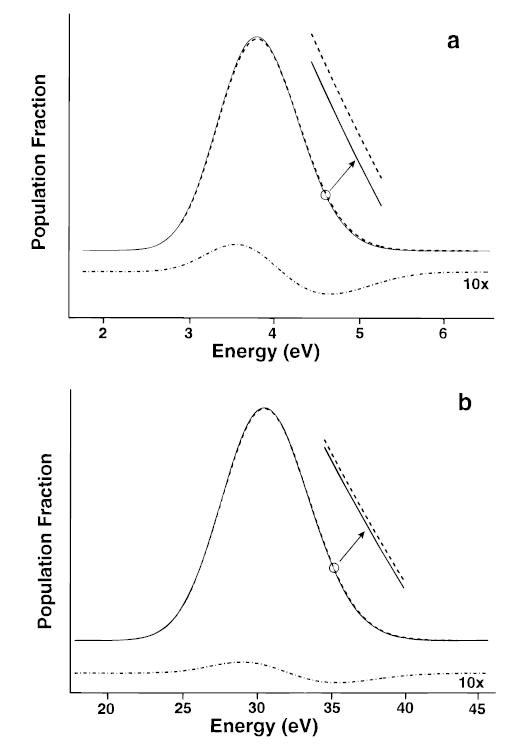
Internal energy distribution of ions at 430 K in thermal equilibrium (Boltzmann distribution, dashed line) and dissociating population distributions calculated from the master equation model (solid line) for (a) (ala-gly)8 (1.0 kDa) and (b) (ala-gly)64 (8.4 kDa). Residual plot (×10, dash-dot line) shows the difference between the distributions calculated for a Boltzmann and from the master equation model.
For (ala-gly)16 (2.1 kDa) under these same conditions, the population of ions at higher internal energies is still depleted, but less than for n = 8. The Arrhenius activation parameters of 1.54 eV and 1016.2 s−1 are close to those in the high-pressure limit, but are still outside the experimental error possible in our experiments. Multiplying the transition dipoles by a factor of 2 increases k1,rad, k−1,rad by a factor of 4 and should effectively simulate (ala-gly)64 (8.4 kDa). For the process described above, the overall dissociation rate constants at 400 and 430 K are 0.0007 and 0.018 s−1, respectively, and correspond to Arrhenius activation parameter of Ea = 1.60 eV and A = 1016.9 s−1. The difference in internal energy vs a Boltzmann distribution is shown in Figure 4b. The depletion of the population at higher energy is significantly less than that of (ala-gly)8, and the Arrhenius activation parameters are equal to those calculated using a fixed Boltzmann energy distribution within the errors of our experiment. Thus, this process falls under the high-pressure-limit assumptions and the measured Arrhenius values reflect the true values. We call this the “rapid energy-exchange (REX) limit” which includes energy transfer either via black-body photons or thermal collisions (Figure 3). A similar result is obtained using Eo = 1.2 eV and A = 1012 s−1, simulating dissociation of the 5+ ion of ubiquitin.
The values of k1,rad, k−1,rad we calculate for (ala-gly)64 (8.4 kDa) should dramatically underestimate those of ubiquitin (8.6 kDa) due to strong absorbers, such as hydroxyl groups, that are present in the side chains of residues in ubiquitin but not in (ala-gly)64. In addition, recent results for proton-bound N,N-dimethylacetamide and glycine homodimers suggest that the absorption rates calculated using AM1 values may be too low.26 Both these factors indicate that for the two dissociation processes calculated above, ubiquitin ions should also be in the REX limit at temperatures less than ~430 K, i.e., the internal energy of the ions will be given by a Boltzmann distribution. It is interesting to note that at 400 K, an (ala-gly)64 ion with the most probable energy exchanges ~8 eV/s with its surroundings. This corresponds to 70 photons/s using the most probable photon energy, or the equivalent of exchanging the entire internal energy of the ion every 3 s. In contrast, the dissociation rate constant is 0.0007 s−1 at this temperature. At 10−8 Torr, the collision frequency for the 11+ ion with butane is ~2 s−1.27 The total average energy of butane at 400 K is 0.27 eV. Thus, if every collision resulted in complete energy transfer, i.e., leaving butane at 0 K, the maximum energy transfer rate via collision is only ~0.6 eV/s. Obviously, the actual collisional energy transfer is only a small fraction of this value. Thus, collisions play an insignificant role compared to blackbody photon exchange in ion thermalization at this temperature and pressure, consistent with the observed pressure independent dissociation kinetics.
The measured value for the frequency factor of 1017 s−1 for the 11+ ion provides further evidence that these ions are in thermal equilibrium with the vacuum chamber walls. For small molecules, a value of 1015–1017 s−1 is typical for highly entropically favored processes such as direct bond cleavages.24,28 If k1,rad, k−1,rad is similar to kd, then the measured kinetics would be slower than if the ions were fully equilibrated, resulting in a smaller measured value of A than its high-pressure limit value. The measured A-factor is comparable to the highest that have been previously observed for small molecules suggesting that conditions satisfying the REX limit have been established. However, an even higher A-factor than has been measured for small molecules cannot entirely be ruled out due to the potential for complex dissociation pathways in large ions that may be even more entropically favored. Although not conclusive, this high A value supports our conclusion that the ion population is in thermal equilibrium with the chamber walls and that dissociation does not deplete the concentration of the activated complex measurably. This satisfies the requirements of the high-pressure or REX limit. Thus, information about both the energy and mechanisms for the dissociation of large ions can be deduced directly from these measured Arrhenius parameters.
The high value for A for the formation of the y244+/b527+ complementary ions observed here is inconsistent with the generally accepted mechanism for formation of y and b ions,29 in which a hydrogen rearranges from some other part of the molecule to the amide nitrogen. Rearrangement reactions typically have lower A values (vide infra). This cleavage occurs adjacent to an aspartic acid residue. Similar facile cleavage after acidic residues has been reported previously for other peptides30,31 and a mechanism in which the hydrogen from the carboxylic acid is transferred to the amide nitrogen prior to dissociation has been proposed.30 The A value of 1017 s−1 measured in our experiments indicates that this backbone site is protonated in both the reactant and transition state ions and a rearrangement to form the activated complex does not occur. This suggests that the most stable structure for the reactant ion is one in which a salt-bridge is formed between the carboxylate of aspartic acid (residue 52) and the amide nitrogen of the adjacent glycine residue (Figure 5). This salt-bridge could be further stabilized by a charged basic group such as a protonated side chain of arginine-54, an interaction that has been recently observed in arginine-containing peptides.13,14 This would dramatically increase the basicity of the amide nitrogen, making protonation at this site in both the reactant and transition state ions favorable. The conformation of this highly charged ion is likely to be significantly extended32 which should enhance free rotations in the transition state, resulting in an entropically favorable dissociation at this site.33 It is possible that the reactant ion is a relatively long-lived intermediate with a low activation energy for formation, and dissociation of this intermediate is the rate-limiting step we observe. This intermediate could correspond to the proposed salt-bridge structure, or a proton-bound species in which the hydrogen rearrangement and subsequent bond cleavage has already occurred. We are unable to distinguish these two reaction pathways although recent results for intermediate charge state ions of ubiquitin support the salt-bridge mechanism.34
Figure 5.
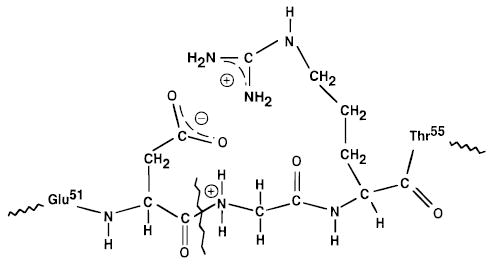
Illustration of the proposed salt-bridge between the carboxylate of aspartic acid-52 and the amide nitrogen of the adjacent glycine residue which would facilitate the direct bond cleavage of ubiquitin 11+ to form the y244+/b527+ complementary ions. This salt-bridge could be further stabilized by close interaction with an additional protonated residue such as the side chain of arginine-54.
The measured dissociation rates for the 5+ ion are similar to those of the 11+ ion. Rates of photon absorption and emission for these ions should be comparable; small shifts in absorption frequency and intensity should have minor effects under the relatively broad Planck distribution at ~430 K. Thus, these ions must also be equilibrated with the vacuum chamber temperature, a conclusion supported by our calculations. The activation energy of the 11+ ion is higher than that of the 5+ ion, despite its much higher charge state. Thus, lowering of bond dissociation energies due to Coulomb repulsion is not a factor in the dissociation processes observed for these ions. Six-membered-ring rearrangements in small molecules have A values typically around 1012 s−1.28 Thus, the A value of 1012 s−1 measured for the 5+ ion of ubiquitin is consistent with a relatively simple molecular rearrangement to produce the observed loss of water. If this fragmentation process were possible in the 11+ ion, it should be kinetically observable. Its absence indicates that the additional charges on the 11+ ion must shut down this reaction pathway. This is likely due to Coulomb effects on ion conformation; a lower charge state ion would have increased flexibility enhancing local folding interactions which would favor the rearrangement reaction for loss of water.
In conclusion, molecular activation by blackbody photons becomes increasingly important in the unimolecular dissociation of large ions. Both theoretical and experimental evidence indicates that dissociating ubiquitin ions come to thermal equilibrium with the blackbody radiation field generated by the surroundings under readily achievable experimental conditions. From the temperature-dependent kinetics, accurate measurement of the energetics and dynamics of dissociation processes for large ions is made possible. This information, which has not been accessible via other methods, should greatly improve our understanding of dissociation processes that are critical for the direct sequencing of large DNA35 and protein molecules36 and for the investigation of specific non-covalent interactions of biomolecules37 by mass spectrometry.
Acknowledgments
The authors would like to thank Professors J. I. Brauman, P. A. Demirev, R. C. Dunbar, T. B. McMahon, C. B. Moore, D. M. Neumark, R. J. Saykally, and I. W. Smith and Mr. D. S. Tonner for helpful discussions. This research would not have been possible if not for the generous financial support provided by the National Science Foundation (CHE-9258178), National Institutes of Health (1R29GM50336-01A2 and S10RR05651-01 for partial support of our computer graphics facility), and Finnigan MAT through sponsorship of the 1994 American Society for Mass Spectrometry Research Award (E.R.W.).
References
- 1.Perrin J. Ann Phys. 1919;11:1–5. [Google Scholar]
- 2.Langmuir I. J Am Chem Soc. 1920;42:2190–2205. [Google Scholar]
- 3.Lewis GN, Mayer JE. Proc Natl Acad Sci USA. 1927;13:623–625. doi: 10.1073/pnas.13.8.623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Steinfeld, J. I.; Francisco, J. S.; Hase, W. L. Chemical Kinetics and Dynamics; Prentice Hall: New Jersey, 1989.
- 5.Lindemann FA. Trans Faraday Soc. 1922;17:598–604. [Google Scholar]
- 6.Hinshelwood CN. Proc Roy Soc London, A. 1927;113:230–236. [Google Scholar]
- 7.Tholmann D, Tonner DS, McMahon TB. J Phys Chem. 1994;98:2002–2004. [Google Scholar]
- 8.Tonner DS, Tholmann D, McMahon TB. Chem Phys Lett. 1995;233:324–330. [Google Scholar]
- 9.Dunbar RC. J Phys Chem. 1994;98:8705–8712. [Google Scholar]
- 10.Dunbar RC, McMahon TB, Tholmann D, Tonner DS, Salahub DR, Wei D. J Am Chem Soc. 1995;117:12819–12825. [Google Scholar]
- 11.Lin CY, Dunbar RC. J Phys Chem. 1996;100:655–659. [Google Scholar]
- 12.Sena M, Riveros JM. Rapid Commun Mass Spectrom. 1994;8:1031–1034. [Google Scholar]
- 13.Price WD, Schnier PD, Williams ER. Anal Chem. 1996;68:859–866. doi: 10.1021/ac951038a. [DOI] [PubMed] [Google Scholar]
- 14.Schnier PD, Price WD, Jockusch RA, Williams ER. J Am Chem Soc. 1996;118:7178–7189. doi: 10.1021/ja9609157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Schindler T, Berg C, Nieder-Schatterburg G, Bondybey VE. Chem Phys Lett. 1996;250:301–308. [Google Scholar]
- 16.Gross, D. S.; Williams, E. R. Int. J. Mass Spectrom. Ion Processes. In press. [DOI] [PMC free article] [PubMed]
- 17.Gross DS, Williams ER. J Am Chem Soc. 1995;117:883–890. [Google Scholar]
- 18.Roepstorff P, Fohlman J. J Biomed Environ Mass Spectrom. 1984;11:601. doi: 10.1002/bms.1200111109. [DOI] [PubMed] [Google Scholar]
- 19.Ballard KD, Gaskell SJ. J Am Soc Mass Spectrom. 1993;4:477–481. doi: 10.1016/1044-0305(93)80005-J. [DOI] [PubMed] [Google Scholar]
- 20.a Little DP, Speir JP, Senko M, O’Connor PB, McLafferty FW. Anal Chem. 1994;66:2809–2815. doi: 10.1021/ac00090a004. [DOI] [PubMed] [Google Scholar]; b Senko M, Beu SC, McLafferty FW. Anal Chem. 1994;66:415–417. doi: 10.1021/ac00075a016. [DOI] [PubMed] [Google Scholar]
- 21.The occupation probability is calculated by systematically eliminating each vibrational frequency from the density of states giving the number of ways to configure the energy among the remaining oscillators given n quanta of energy in the mth vibrational mode. The enhanced transition probability for absorption from the n to the (n + 1) level is (n + 1) times as likely as the (n = 0) to (n = 1) transition. Similarly the emission probability from the n to the (n − 1) level is enhanced by a factor of n above the (n = 1) to (n = 0) transition.
- 22.The direct count Beyer–Swinehart algorithm was used to determine the sum and density of states.
- 23.Griffin LL, McAdoo DJ. J Am Soc Mass Spectrom. 1993;4:11–15. doi: 10.1016/1044-0305(93)85037-X. [DOI] [PubMed] [Google Scholar]
- 24.Gilbert, R. G.; Smith, S. C. Theory of Unimolecular and Recombination Reactions; Blackwell Scientific Publications: Oxford, 1990.
- 25.A set of coupled linear integro-differential equations describing the kinetics of a population of ions at discrete 100-cm−1 intervals is solved simultaneously to give the overall unimolecular dissociation rate constants.
- 26.Price, W. D.; Schnier, P. D.; Williams, E. R. J. Phys. Chem. Submitted for publication.
- 27.The collisional rate was calculated using a value for the butane polarizability of 8.2 × 10−24 cm3 The single charge cross section was multiplied by 11. The resulting collision rate is approximately the same as that calculated using the collisional cross section measured for this ion by Covey T, Douglas DJ.J Am Soc Mass Spectrom 19934616–623. [Google Scholar]
- 28.Benson, S. W.; O’Neal, H. E. Kinetic Data on Gas Phase Unimolecular Reactions; U.S. National Bureau of Standards: Washington, 1970.
- 29.Biemann K, Martin SH. Mass Spectrom Rev. 1987;6:1–76. [Google Scholar]
- 30.Yu W, Vath JE, Huberty MC, Martin SA. Anal Chem. 1993;65:3015–3023. doi: 10.1021/ac00069a014. [DOI] [PubMed] [Google Scholar]
- 31.Qin J, Chait BT. J Am Chem Soc. 1995;117:5411–5412. [Google Scholar]
- 32.a Schnier PD, Gross DS, Williams ER. J Am Chem Soc. 1995;117:6747–6757. [Google Scholar]; b Clemmer DE, Hudgins RR, Jarrold MF. J Am Chem Soc. 1995;117:10141–10142. [Google Scholar]; c Wood TD, Chorush RA, Wampler FM, Little DP, O’Connor PB, McLafferty FW. Proc Natl Acad Sci USA. 1995;92:2451–2454. doi: 10.1073/pnas.92.7.2451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.The interaction with arginine-54, as shown in Figure 5, may reduce free rotation in the transition state. This would not be the case if this interaction was via a protonated residue on the b ion. Whether this is an issue depends on the shape and position of the barrier for the charge separation process.
- 34.Jockusch, R. A.; Schnier, P. D.; Price, W. D.; Strittmatter, E. F.; Demirev, P. A.; Williams, E. R. Anal. Chem. Submitted for publication. [DOI] [PMC free article] [PubMed]
- 35.a McLuckey SA, VanBerkel GJ, Glish GL. J Am Soc Mass Spectrom. 1992;3:60–70. doi: 10.1016/1044-0305(92)85019-G. [DOI] [PubMed] [Google Scholar]; b Little DP, Chorush RA, Speir JP, Senko MW, Kelleher NL, McLafferty FW. J Am Chem Soc. 1994;116:4893–4897. [Google Scholar]
- 36.a Hunt DF, Yates JR, III, Shabanowitz J, Winston S, Hauer CR. Proc Natl Acad Sci USA. 1986;83:6233–6237. doi: 10.1073/pnas.83.17.6233. [DOI] [PMC free article] [PubMed] [Google Scholar]; b Loo JA, Edmonds CG, Smith RD. Anal Chem. 1993;65:425–438. doi: 10.1021/ac00052a020. [DOI] [PubMed] [Google Scholar]; c Senko MW, Speir JP, McLafferty FW. Anal Chem. 1994;66:2801–2808. doi: 10.1021/ac00090a003. [DOI] [PubMed] [Google Scholar]
- 37.a Ganem B, Li YT, Henion JD. J Am Chem Soc. 1991;113:6294–6296. [Google Scholar]; b Smith DL, Zhang Z. Mass Spectrom Rev. 1994;13:411–428. [Google Scholar]; c Smith RD, Light-Wahl KJ, Winger BE, Loo JA. Org Mass Spectrom. 1992;27:811–821. [Google Scholar]


