SIMULTANEOUS CORRECTION OF GHOST AND GEOMETRIC DISTORTION ARTIFACTS IN EPI USING A MULTI-ECHO REFERENCE SCAN

Abstract

A computationally efficient technique is described for the simultaneous removal of ghosting and geometrical distortion artifacts in echo-planar imaging (EPI) utilizing a multi-echo, gradient-echo reference scan.

Nyquist ghosts occur in EPI reconstructions because odd and even lines of k-space are acquired with opposite polarity, and experimental imperfections such as gradient eddy currents, imperfect pulse sequence timing, B₀ field inhomogeneity, susceptibility, and chemical shift result in the even and odd lines of k-space being offset by different amounts relative to the true center of the acquisition window. Geometrical distortion occurs due to the limited bandwidth of the EPI images in the phase-encode direction. This distortion can be problematic when attempting to overlay an activation map from a functional MRI (fMRI) experiment generated from EPI data on a high-resolution anatomical image.

The method described here corrects for geometrical distortion related to B₀ inhomogeneity, gradient eddy currents, radiofrequency pulse frequency offset, and chemical shift effect. The algorithm for removing ghost artifacts utilizes phase information in two dimensions and is thus more robust than conventional one-dimensional methods. An additional reference scan is required which takes approximately 2 minutes for a matrix size of 64 × 64 and a TR of 2 seconds. Results from a water phantom and a human brain at 3 Tesla demonstrate the effectiveness of the method for removing ghosts and geometric distortion artifacts.

Introduction

Echo-planar imaging (EPI) has become a common acquisition method for high temporal resolution applications such as functional MRI (fMRI) and diffusion-weighted imaging (DWI). EPI suffers from two major sources of artifacts: N/2 or Nyquist ghosts, and geometric distortion. The ghosts degrade image quality and signal-to-noise ratio (SNR), and the geometric distortion makes it difficult to co-register EPI images with conventionally acquired anatomical images. These artifacts become more apparent at higher magnetic field strengths where local variations in magnetic field caused by susceptibility gradients cause severe phase distortions in the NMR signal. For example, in a typical EPI fMRI brain scan, the magnetic field inhomogeneity in the nasal sinuses is on the order of 1 ppm (125 Hz. at 3 Tesla). Since the spins will have de-phased by 4 revolutions over the 32 ms acquisition time, the magnitude of the geometrical distortion in this area will be approximately 4 pixels for a 64 X 64 matrix with a 125 kHz bandwidth. The resulting misregistration of the EPI scans relative to high-resolution anatomical images can lead to misinterpretation of functional activation maps. Furthermore, misregistration of activation maps with anatomical images can be dangerously misleading when fMRI is used for presurgical planning. The ghost artifacts can also lead to inaccurate calculations of the apparent diffusion coefficient (ADC) in DWI experiments.

Methods proposed to correct for the ghost artifact include one-dimensional phase correction using non-phase encoded or phase-encoded reference scans [1, 2], and two-dimensional correction using the phase information from the EPI image [3]. Methods to correct for geometric distortion involve collecting conventional gradient echo, offset spin-echo, or EPI images at different values of TE in order to estimate the B₀ field inhomogeneity [4, 5, 6]. A method using a multi-echo reference scan was recently proposed by Chen and Wyrwicz [7]. However that method is very computationally intensive. In clinical applications of DWI or fMRI, where viewing of the results is desired within a short time frame, the method of Chen and Wyrwicz may not be feasible. In research fMRI applications, it is often desirable to process the data before the subject leaves the scanner to check for motion artifacts and subject compliance and to redo the fMRI scan if necessary. Online processing is particularly useful in pediatric applications, the focus of research in our center, where failure rates due to motion or subject noncompliance are higher than in adults [8].

In this paper we propose a method to simultaneously correct for ghosting artifacts and geometric distortion with use of the multi-echo reference scan. The distorted EPI images are first corrected for ghosting based on the method proposed by Chen and Wyrwicz [9], and then for geometric distortion based on the phase images generated from the reference scan. For a 64 X 64 matrix the multi-echo reference scan can be acquired in 128 seconds with a 2-second repetition time.

The algorithms used to perform the ghost correction and distortion correction were implemented in Interactive Data Language (Research Systems, Inc., Boulder, CO)¹. The parameters needed for these corrections are calculated from the reference scan, and these parameters may then be used to correct all EPI scans subsequently acquired during an imaging session, as long as the subject does not move. Once the necessary parameters are calculated from the multi-echo reference scan, the only added computational costs required to apply the corrections to subsequent scans are an additional Fourier Transform, multiplication, and addition for the ghost correction, and a sinc interpolation for the geometric distortion correction. These corrections therefore add minimal computational time at no cost in SNR.

Theory

The multi-echo reference scan

The multi-echo reference scan is the same as an EPI scan with the phase blips turned off, and the pre-dephase gradient used for phase encoding. If there are N_y lines in the k_y direction, then the sequence will be repeated N_y times, each time using an incremented value for the pre-dephase gradient. By rearranging the data corresponding to each echo, N_y echo images may be reconstructed. Diagrams of the multi-echo reference scan and the EPI sequence are shown in Figure 1. The multi-echo reference scan encodes the de-phasing of the spins due to all off-resonance related factors including B₀ inhomogeneity, readout gradient eddy currents, radiofrequency (RF) pulse frequency offset, and chemical shift effect, except for eddy currents induced by the phase blip gradients.

Figure 1.

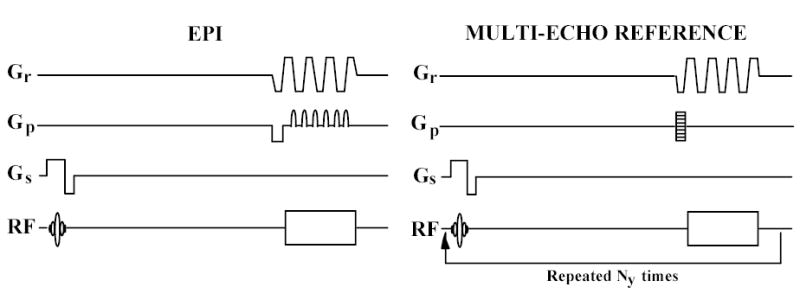
Pulse sequence timing diagrams for a) the blipped EPI sequence and b) the multi-echo reference sequence.

Correction for ghosting

Asymmetry between the odd and even lines in EPI images results in the formation of N/2, or Nyquist ghost artifacts. A common way to correct for this is to acquire an EPI image with the phase-encoding blips turned off. The k_y lines are then Fourier-transformed to obtain the phase information. For a linear correction, a line is fit to the phases; for a non-linear correction, the phase information is used directly. Both methods work well when the only cause of the ghosting is the shifting of the peak of the echoes due to imperfect timing in the pulse sequence. However, in the presence of strong B₀ inhomogeneity and other off-resonance effects, both methods have shortcomings. The linear correction method does not take into account distortions of the echo signal, and thus does not suppress the ghosts as well as the non-linear method [1]. However, serious errors in phase correction at individual pixels along the readout direction may cause streak artifacts at those locations when the non-linear method is used [2]. The multi-echo reference data, however, provides sufficient information to correct for the de-phasing of the spins between the even and odd lines on a pixel-by-pixel basis. Because a complete 2-D phase map is computed from the multi-echo reference scan, it is less vulnerable to errors than the conventional non-linear method.

The multi-echo images are in the undistorted image space, whereas the EPI images have some geometrical distortion. It is possible, however, to construct images in distorted image space from the multi-echo reference data by “simulating” an EPI sequence. With k_y = −N_y/2, −N_y/2+1, −N_y/2+2, …, −2, −1, 0, 1, 2, …, N_y/2−3, N_y/2−2, N_y/2−1, and N_echo = 1, 2, 3, …, N_y−1, the k-space data for the EPI image may be obtained by taking the data for k_y= −N_y/2 from the 1^st echo, the data for k_y= −N_y/2+1 from the 2^nd echo, and so on up to the data for k_y= N_y/2−1 being obtained from the N_yth echo. The k-space data obtained in this manner will be identical to the k-space data for the EPI sequence:

$$S(k_x,k_y)=ME(k_x,k_y,k_y+\frac{N_y}{2}+1)$$ (1)

where ME(k_x,k_y,N_echo) is the (k_x,k_y) data point in the Nth echo image.

Buonocore has shown [3] that ghosts may be eliminated in EPI images by reconstructing images from the even and odd lines of k-space separately, with zero-filling of missing lines, and applying a phase correction φ_CORR(x,y) to either image. The sum of the two images will then be free of ghosts. Chen and Wyrwicz have shown [9] that φ_CORR(x,y) may be estimated by acquiring an additional set of EPI data, but with the readout gradient shifted so that the even lines of k-space are acquired during the odd, rather than the even, echoes. φ_CORR(x,y) is found by reconstructing images from the even echoes only of both datasets, and taking the complex ratio.

Following the method of Chen and Wyrwicz, we compute the odd and even echo image from equation (1) by using only the even k_y lines (the choice of even vs. odd is arbitrary), and shifting the echo number by either zero or one. Additional images may be found by shifting the echo number by different amounts. Thus for varying values of the echo shift N_shift, phase reference images in distorted coordinates may be constructed as follows:

$$S(x,y,N_{shift})=\sum _{k_x}\sum _{k_y=even}ME(k_x,k_y,k_y+\frac{N_y}{2}+1+N_{shift})e^{\frac{-2\pi i{k}_{x}x}{N_x}}{e}^{\frac{-2\pi i{k}_{y}y}{N_y}}$$ (2)

For N_shift ≠ 0, some values of $k_y+\frac{N_y}{2}+1+N_{shift}$ will fall outside the range of values where the multi-echo reference data exists; those lines are set to zero.

The data is separated into N_shift=even and N_shift=odd. On a pixel-by-pixel basis, the phases are fit as a linear function of N_shift. Using the method of Ahn and Cho [10], the slopes may be estimated without the need for phase unwrapping. The linear component is removed, and the intercepts are estimated as the average of the linearly de-trended phases. φ_CORR(x,y) is found from the difference of the intercepts. In practice we have found that using values of N from − 4 to + 4 is sufficient to estimate φ_CORR(x,y) adequately although more phase reference images may be incorporated as needed. φ_CORR(x,y) is then used, as in Buonocore [3], to correct the phase of the image from the odd echoes of the EPI data as follows, such that the resultant image will be free of ghosts:

$$\begin{array}{l}S(x,y)=\sum _{k_x}\sum _{k_y=even}EPI(k_x,k_y)e^{\frac{-2\pi i{k}_{x}x}{N_x}}{e}^{\frac{-2\pi i{k}_{y}y}{N_y}}+\\ e^{i{\phi }_{CORR}(x,y)}\sum _{k_x}\sum _{k_y=odd}EPI(k_x,k_y)e^{\frac{-2\pi i{k}_{x}x}{N_x}}{e}^{\frac{-2\pi i{k}_{y}y}{N_y}}\end{array}$$ (3)

Due to errors in the estimation of the phases at specific locations where the ghost image overlaps with the parent image, this algorithm fails in a few isolated pixels. To correct for this, a goodness-of-fit parameter GF = χ/(DOF+1) is calculated for each pixel where χ is the square root of the chi-squared error statistic given by χ² = ∑(φ_fit − φ_actual)²/N and DOF is the number of degrees of freedom of the fit. φ_CORR(x,y) is interpolated in the pixels that fail to meet the goodness-of-fit criterion GF < 0.1.

Correction for geometric distortion

For an EPI scan, where the bandwidth in the read direction is much larger than in the phase-encode direction, Jezzard has shown [5] that the geometric distortion correction problem reduces to solving for a set of 1D unwarps in the phase-encode direction. Jezzard’s procedure involved finding a B₀ field map from a double gradient-echo image and was only able to correct for the geometric distortion due to B₀ inhomogeneity. Furthermore, a phase-unwrapping procedure was necessary when the phase difference between the two images exceeded π.

The multi-echo reference scan, however, encodes the phase evolution not only from B₀ inhomogeneity, but also from chemical shift and readout gradient eddy currents. There is the additional advantage that no phase-unwrapping is necessary even in areas of high B₀ inhomogeneity. From the Fourier Shift Theorem, the displacement (in pixels) of each pixel in the phase-encode direction is given by the number of revolutions of de-phasing over the acquisition time. A pixel shift map Δ_y(x,y) is calculated, and the undistorted EPI image is computed from sinc interpolation of the distorted magnitude EPI image, as sinc interpolation yields the best result for band-limited data [11].

In order to compute Δ_y(x,y), even and odd echo images are calculated from the multi-echo reference data by performing the 2-D FFT for each echo. These images, not to be confused with those described in equation (2), are in the undistorted image space. Due to the even-odd echo asymmetry the even and odd echo images are processed separately. On a pixel-by-pixel basis, a linear fit is performed to the phases as a function of echo number, without the need for phase unwrapping, using the method of Ahn and Cho referenced earlier [10]. The slopes estimated from the even and odd echo images are averaged, and Δ_y(x,y) readily calculated by multiplying the result by N_echoes/2π. The multi-channel modulation method proposed by Chen and Wyrwicz [7] also avoids the necessity of phase unwrapping. However, this method is much more computationally expensive, and may not be feasible if immediate viewing of the data is desired in clinical applications.

Materials and Methods

The multi-echo reference scan was implemented on a 3 Tesla Bruker Biospec 30/60 MRI scanner. The reconstructions described above and ghost correction using a conventional non-phase encoded reference scan were implemented in IDL. Imaging experiments were then performed on a ball of water and a human brain in order to demonstrate the effectiveness of the corrections for ghosting and geometrical distortion.

Single-shot EPI images were taken of a water phantom and of a human brain. Imaging parameters were: matrix size = 64 X 64, FOV = 25.6 cm X 25.6 cm, slice thickness = 5 mm, TE = 38 ms, TR = 2 s, bandwidth = 125 kHz for the human brain. For the water phantom, bandwidth = 50 kHz was used in order to exaggerate the geometric distortion. In addition, the even and odd echoes were deliberately misaligned in the water phantom in order to exaggerate the ghost artifact.

Results and Discussion

The ghost artifacts in both the water phantom image in Figure 2A and in the human brain image in Figure 3A were corrected via the technique shown above and also via a conventional non-phase encoded reference scan [1]. Both techniques were comparable in correcting for the ghosts on the water phantom as shown in Figures 2B and 2C. However, in the human brain, the conventional technique generated some streak artifacts in the region of frontal sinuses and temporal bones as shown in Figure 3B. These artifacts are not present in the image corrected via the multi-echo reference scan as shown in Figure 3C.

Figure 2.

Demonstration of ghost correction in a water phantom. A: The uncorrected EPI image with the outline of the ROI used for the ghost-to-signal comparison. B: The image corrected using a conventional non-phase-encoded reference scan. C: The image corrected using the multi-echo reference scan. Images B and C are windowed and leveled identically to show the effectiveness of both algorithms.

Figure 3.

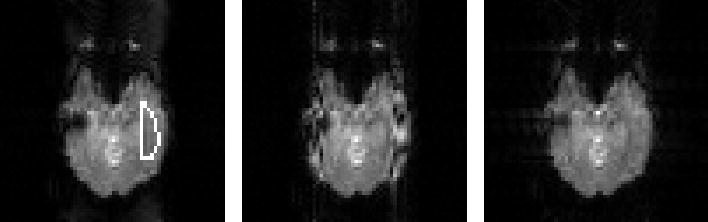
Demonstration of ghost correction in a human brain. A: The uncorrected EPI image with the outline of the ROI used for the ghost-to-signal comparison. B: The image corrected using a non-phase-encoded reference scan. C: The image corrected using the multi-echo reference scan.

To quantitatively evaluate the effectiveness of both algorithms, an ROI was drawn on the most lateral part of the object as indicated in Figures 2A and 3A, where the ghost artifacts are the most intense. A ghost-to-signal ratio (GSR) was calculated by shifting the ROI by N/2 pixels in the y direction, and dividing the average signal intensity in the ghost region by the average signal intensity in the image region. Results are shown in Table 1. For both the ball of water and the human head, the proposed method is shown to be slightly more effective in reducing Nyquist ghost artifacts than the conventional non-phase encoded reference scan. For the human head images, our method reduces the ghost intensity to 29% of the uncorrected value as compared with the conventional method, which reduces the ghost intensity to 42% of the uncorrected value. For the water phantom images, our method reduces the ghost intensity to 2% of the uncorrected value as compared with the conventional method, which reduces the ghost intensity to 3.3% of the uncorrected value.

Table 1.

The ghost-to-signal ratio (in percent) for the human brain and water phantom shown in Figures 2 and 3, for the uncorrected images, and the images corrected with the non-phase-encoded reference scan and the multi-echo reference scan.

	Uncorrected	Non-phase-encoded reference	Multi-echo reference
Water phantom	105	3.5	2.1
Human brain	25.3	10.6	7.4

The geometric distortion correction algorithm was also applied to the images of the water phantom and human brain in Figures 4 and 5. The uncorrected and corrected images for the water phantom are shown in Figures 4B and 4C. The first echo image of the multi-echo reference scan is equivalent to an undistorted conventional gradient echo image and is displayed for comparison in Figure 4A. For the human brain, a superior slice was selected for display where distortion is more apparent. The uncorrected and corrected EPI images of the brain are shown in Figures 5B and 5C. Again, the first echo image of the multi-echo reference scan representing the undistorted gradient echo image is displayed in Figure 5A for comparison. The geometric distortion correction yielded excellent correspondence between the corrected EPI images shown in Figures 4C and 5C and the reference images shown in Figures 4A and 5A.

Figure 4.

Demonstration of geometrical distortion correction in EPI images of a ball of water at 3 T. A: The first echo image of the multi-echo reference scan. B: The uncorrected EPI image. C: The EPI image corrected for geometrical distortion using the multi-echo reference scan.

Figure 5.

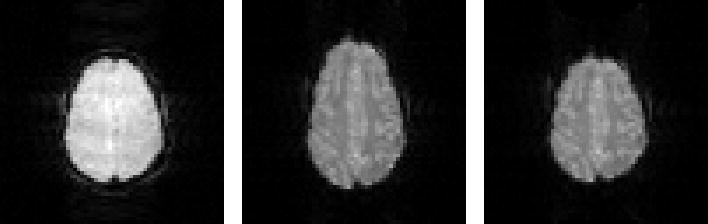
Demonstration of geometrical distortion correction in EPI images of a human brain at 3 T. A: The first echo image of the multi-echo reference scan. B: The uncorrected EPI image. C: The EPI image corrected for geometrical distortion using the multi-echo reference scan.

Conclusion

We have implemented an easy and time-efficient method for correcting for ghosting and geometric distortion simultaneously by using a multi-echo reference scan. The multi-echo reference scan can be obtained in approximately 2 minutes with a 2 second TR if there are 64 lines in the phase-encode direction. This scan can be used to simultaneously correct for both Nyquist ghost artifacts and for geometric distortion. Once the appropriate parameters are calculated from the reference scan, the corrections can be implemented with minimal cost in computational time and no cost in SNR. The correction can then be applied to all EPI data sets subsequently acquired during an imaging session, as long as the subject does not move. As advanced imaging methods are implemented at increasingly higher magnetic field strengths, applying corrections such as described here becomes increasingly important.

EPI images of both a ball of water and a human brain at 3 Tesla were acquired and the method described above effectively corrected for both the ghosting and the geometric distortion in those images. The parameters needed for the corrections were computed in approximately 1 second for each 64X64 slice on a Dell 933 MHz Pentium III workstation running Windows NT. The total time needed to reconstruct each slice, including both the ghost and geometric distortion correction, was approximately 0.012 seconds. For a typical fMRI dataset consisting of 24 slices and 100 time points for a total of 2400 images, the correction parameters may be computed in under 30 seconds, during which time the first fMRI task may be performed by the subject. The entire fMRI dataset may then be reconstructed in approximately 30 seconds, allowing for the images to be viewed before the subject leaves the scanner.