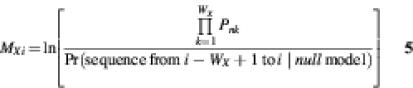Statistical significance of clusters of motifs represented by position specific scoring matrices in nucleotide sequences

Abstract

The human genome encodes the transcriptional control of its genes in clusters of cis-elements that constitute enhancers, silencers and promoter signals. The sequence motifs of individual cis- elements are usually too short and degenerate for confident detection. In most cases, the requirements for organization of cis-elements within these clusters are poorly understood. Therefore, we have developed a general method to detect local concentrations of cis-element motifs, using predetermined matrix representations of the cis-elements, and calculate the statistical significance of these motif clusters. The statistical significance calculation is highly accurate not only for idealized, pseudorandom DNA, but also for real human DNA. We use our method ‘cluster of motifs E-value tool’ (COMET) to make novel predictions concerning the regulation of genes by transcription factors associated with muscle. COMET performs comparably with two alternative state-of-the-art techniques, which are more complex and lack E-value calculations. Our statistical method enables us to clarify the major bottleneck in the hard problem of detecting cis-regulatory regions, which is that many known enhancers do not contain very significant clusters of the motif types that we search for. Thus, discovery of additional signals that belong to these regulatory regions will be the key to future progress.

INTRODUCTION

It is estimated that 1.5% of the human genome encodes proteins via the ‘genetic code’ (1). Equally important are the regulatory signals, within a more extended genetic code, that control the manner in which the proteins are synthesized. These regulatory signals, or cis-elements, are typically protein binding sites that possess characteristic sequence patterns (motifs); however, these patterns are typically too short and degenerate for accurate detection of cis-elements (2). Fortunately, there is much evidence that cis-elements occur in clusters rather than in isolation. Although transcription factor binding sites may be located many tens of kilobases away from the transcription start site, they generally occur within enhancers or silencers extending over a few hundred base pairs that contain multiple cis-elements (3). There is further evidence that mRNA 3′-end processing (4), mRNA localization (5) and alternative splicing (6) are controlled by clusters of signals. Thus, it appears to be a widespread phenomenon for molecular biological processes to be regulated by clusters of signals that are individually weak but collectively strong.

A number of more or less ad hoc algorithms for detecting cis-element clusters have been proposed in the past (7–13). To assess predictions made by such a method, it is extremely valuable to know the statistical significance of each prediction, i.e. the probability of obtaining the result merely by chance. None of the previous methods includes an analytic calculation of statistical significance, with the exception of a technique by Wagner based on Poisson statistics (14). The major limitation of Wagner’s method is that it represents cis-elements using degenerate consensus sequences, rather than the more general position specific scoring matrices (PSSMs) (15). A further undesirable feature of many previous methods is the use of arbitrary threshold parameters, such as a window size within which the cis-elements must occur.

Ockham’s razor is a widely accepted criterion for choosing among alternative methods. With this principle in mind, we have designed a method to detect cis-element clusters that is about as simple and general as can be achieved. Our method finds the optimal motif cluster obtained by summing PSSM scores for the motifs, and subtracting a linear ‘gap penalty’ for the spacer sequences between motifs. In principle there is just one undetermined parameter: the gap penalty. Unlike most previous methods, our technique has a solid statistical foundation, being based on a log likelihood ratio of observing the data given a model of cis-element clusters versus a model of background DNA. The Neyman–Pearson lemma states that log likelihood ratios are the most powerful statistic for distinguishing between hypotheses. Our model of cis-element clusters is for cis-elements to occur with a uniform (Poisson) distribution of some intensity—a reasonable minimal assumption model. The intensity parameter of this distribution corresponds in a one-to-one fashion with the gap penalty. A DNA background model that adequately reflects the properties of natural DNA is more problematic to construct. We try three versions: an independent mononucleotide model estimated from the query sequence, a higher order Markov model estimated from genomic DNA, and a locally varying mononucleotide model estimated from a sliding window within the query sequence.

Our method incorporates an analytic calculation of statistical significance, extending the technique of Claverie and Audic for calculating significance of individual PSSM matches (16). Having identified a motif cluster with some raw score (sum of PSSM scores minus gap scores), we can calculate its E-value, i.e. the number of times we expect to observe a cluster with this score or greater by chance, in a random sequence of specified length and nucleotide composition. Thus, E-values <1 become increasingly significant. We demonstrate that, as expected, the E-values accurately reflect the number of motif clusters we observe in synthetic sequences generated by each of the three background models. In addition, using the sliding window background model, the E-values are astonishingly accurate for natural DNA sequences (after masking the most egregious tandem repeat and low complexity regions). We name our method COMET: cluster of motifs E-value tool.

We use COMET to study two types of regulatory region: promoters regulated by the transcription factor LSF and muscle specific regulatory regions. LSF regulates a diverse set of cellular and viral genes (17–26). One defined biological function of LSF is an essential role in mediating cell cycle progression, via regulation of thymidylate synthase expression (26). There is evidence that the transcription factors Sp1 and Ets-1 may co-regulate genes with LSF (27,28). In this study, we restrict attention to sites of LSF regulation close to transcription start sites, searching for these regulatory regions by detecting clusters of motifs for LSF, Sp1, Ets-1 and the TATA box. For muscle specific regulatory regions, we look for clusters of motifs for the transcription factors Mef-2, Myf, SRF, Tef and Sp1, as previously suggested by others (9).

MATERIALS AND METHODS

COMET’s scoring scheme

We wish to find the segment within a query DNA sequence that has the maximum score according to the following log likelihood ratio formula:

score (segment) = log{[prob(segment | cluster model)]/[prob(segment | null model)]}1

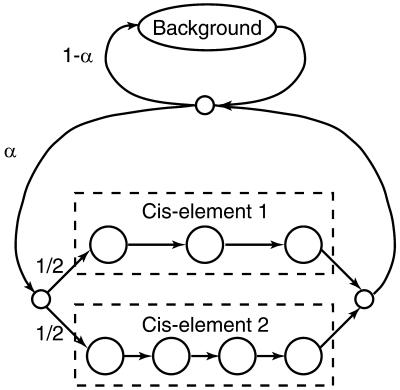
Three different null models were tried: independent nucleotides with frequencies estimated from the entire query sequence; a fifth order Markov model based on hexamer frequencies in human chromosome 20 (29); and independent nucleotides with frequencies estimated separately at each position, from a window of width 2w + 1 bp centered on that position (w = 75 by default). The cluster model assumes that cis-elements occur in a Poisson process of some intensity, embedded in random DNA generated by the null model. The cis-elements are modeled by mononucleotide frequency matrices that are specified by the user. If a mononucleotide null model is used, the cluster model is equivalent to the hidden Markov model shown in Figure 1, with the emission probabilities of the background state equal to those of the null model. α in Figure 1 is related to the expected average distance between motifs in a cluster, a, by α = 1/(a + 1). COMET allows the user to specify a value for a.

Figure 1.

A hidden Markov model of cis-element clusters. The large circles represent states that emit single nucleotides. The small circles represent silent states that do not emit, and the arrows represent allowed transitions between states. The cis-element states emit nucleotides with probabilities obtained from the count matrix for this cis-element. The background state emits nucleotides with background probabilities. Non-palindromic cis- elements are duplicated so that they are represented once on each strand.

In the Markov case, the cluster model combines a mononucleotide model of cis-elements with a higher order model of the spacer sequences between them. Since there has been some controversy over how best to combine two such models (30), we give a careful description of our method. The cluster model generates the DNA segment in two stages, first generating the locations and sequences of the cis-elements, and then emitting the sequences of the spacer regions between them. In the first stage, the model generates a gap length (possibly zero) from a geometric (memoryless) distribution, then randomly selects a cis-element and generates its sequence from the mononucleotide model, generates another gap, and so on. In the second stage, the gaps are filled with spacer sequences. Two distinct probability distributions can be proposed for the generation of the spacer sequences:

Pr(spacer sequences | cluster model) = Pr(spacer sequences | null model)2

Pr(spacer sequences | cluster model) = Pr(segment | null model; cis-element sequences)3

In equation 2, each spacer sequence is generated as if it were not attached to the rest of the segment. Equation 3 uses the probability that the null model generates the whole segment, conditional on the cis-element sequences already being present. Thus, it considers oligonucleotides that straddle cis-element boundaries. It seems reasonable that the null model should apply to these straddling oligonucleotides (conditional on the sequence within the cis-element), and so we use equation 3, which combines the mononucleotide and Markov models in the manner of Liu et al. (31) rather than Thijs et al. (30).

In order to calculate equation 1, the standard Forward algorithm can be applied to a given DNA segment (32), but we wish to determine which segment within a sequence has the maximal score. One pass of the Forward algorithm suffices to obtain the score of every segment with a given starting point. Therefore, to cover every segment it would be necessary to repeat the Forward algorithm starting from every nucleotide in the sequence. The time requirement of this procedure scales quadratically with sequence length. Desiring a faster algorithm with linear scaling, we use the Viterbi algorithm instead of the Forward (32). This has the effect that, rather than calculating the total probability of the DNA segment given all possible arrangements of cis-elements within the segment, we just calculate the probability for the optimal (most probable) arrangement of cis-elements. An additional advantage is that for this Viterbi case, we are able to calculate E-values.

The algorithm to find the highest scoring segment is a one-dimensional analog of the Smith–Waterman algorithm (33) for pair-wise sequence alignment. If S_i is the score of the optimal segment that ends at position i in the sequence, we obtain the recurrence:

where g is the gap penalty: g = –ln(1 – α), W_X is the width of cis-element X, and M_Xi is the log likelihood ratio score for cis-element X, ending at position i in the sequence:

P_nk is the probability of observing nucleotide n at position k of the cis-element, where n refers to the nucleotide at position i – W_X + k in the sequence. The values of P_nk are obtained from a user-supplied count matrix for the cis-element, which specifies how often the nucleotides A, C, G and T are observed at each position in a sample of known cis-elements of this type. One pseudocount was added to all counts in estimating the cis-element and null models (corresponding to use of a uniform Bayesian prior).

Each motif contributes M_Xi – T to the overall score, where T = –ln(α/number of cis-elements in the model). To fulfill an assumption of the E-value calculation, choices for X in equation 4 where M_Xi – T would be negative are ignored. After finding the optimal segment in the sequence, suboptimal segments are found using a one-dimensional analog of the Waterman–Eggert algorithm (34).

E-value calculation

To attach statistical significance to cluster scores, we calculate the number of times a cluster of a given score or greater would be expected to occur under the null model—the E-value. We approximate the occurrence of positive-scoring motifs in a random sequence as a compound Poisson process. In other words, motif locations are Poisson distributed with frequency ν, and each motif has a score drawn independently from some distribution Z. It is necessary to calculate ν and some properties of the distribution Z; we explain how this is done below. The cluster scores S follow an extreme value distribution with the E-value (E) defined as:

where N is the length of the sequence, λ is the unique positive root of:

and the finite length correction is given by:

indicates the expected value of a distribution. If a motif cluster is found as a result of scanning multiple sequences, the E-values calculated for each sequence are summed to give an overall E-value.

This result is related to the well-known BLAST statistics of Karlin and Altschul (35). They consider the optimal segment score in a sequence where each residue type receives a score s_i, and occurs with probability p_i. This optimal segment score also follows an extreme value distribution, where λ is the unique positive solution to:

Their K is given by a more complex formula. Our equation 7 for λ can be obtained as a continuous limit of equation 10. Suppose that a sequence consists of many small fragments of width ε. In each fragment, a motif can occur with probability εν, or a ‘gap’, with score – gε, can occur with probability 1 – εν. Equation 10 then becomes:

In the limit where ε tends to zero, equation 11 reduces to equation 7. The equations for K and F can be derived in a similar manner, but in practice their values are far less important than that of λ, which appears in the exponent of the extreme value distribution. A detailed mathematical treatment of this and related results will be presented elsewhere (J.Spouge, manuscript in preparation).

As indicated above, we now briefly describe three ways to calculate ν and the required expectations involving the distribution Z. The most direct approach is to enumerate all possible DNA sequences of length equal to the longest cis-element, and simply measure the frequency of positive scoring motifs and the distribution of their scores. An alternative method is random generation of a large number of these sequences. Finally, ν and Z can be obtained using a dynamic programming technique introduced by Staden (36). To use this method the PSSM scores must be discretized into bins. Furthermore, ν and Z must be calculated separately for each PSSM and then added. Overall, the E-value calculation makes three assumptions: that positive scoring motifs are rare (∼1% in practice), and that the motifs do not have a significant tendency to overlap themselves or one another.

As described above, the E-value calculation cannot be used with a null model that varies along the sequence, as the sliding window model does. To handle this case, after obtaining clusters and their raw scores, the sequence is broken into fragments of length 2w + 1 bp. E-values are calculated separately for each fragment, using equation 6 without the finite length correction, and taking the nucleotide frequencies to be uniform within each fragment. These E-values are then summed. Two final technicalities are that motifs are not permitted to overlap masked nucleotides, and the sequence length N in equation 6 is conservatively replaced with the number of unmasked bases. (Masking is described later.)

The results reported below were obtained with parameter a, the expected distance between cis-elements in a cluster, set to 35 bp. COMET is robust to changes in a: setting a to 20 or 50 gave essentially the same results. If w (the sliding window parameter) is increased significantly from the default value of 75, the E-values for clusters in genomic DNA become underestimated (i.e. lower than they should be), owing to local fluctuations in nucleotide abundances. We experimented with a scheme to train a and also the transition probabilities leading into each cis-element type (Fig. 1), but did not observe any improvement in performance (data not shown).

Count matrices for cis-elements

LSF binding sites were assumed to cluster with binding sites for Sp1, Ets and the TATA box. We constructed a novel count matrix for the Ets motif (Table 1) from a manual alignment of 39 natural binding sites of several members of the Ets protein family (37). The LSF matrix was described in Frith et al. (11), the TATA box matrix in Bucher (38) and the Sp1 matrix was taken from the TRANSFAC database (39), accession no. M00196. We obtained data for muscle specific motifs from the logistic regression analysis (LRA) study of Wasserman and Fickett (9). These regulatory regions are assumed to consist of Mef-2, Myf, SRF, Tef and Sp1 binding sites. These five motifs were represented using one of two alternative sets of count matrices: ‘muscle derived’ (derived from data including the sequences that the method will be tested on) and ‘non-muscle derived’ (from data entirely independent of the test sequences). The muscle derived matrices more accurately represent these cis-elements, but involve a circular dependence on the sequences to be tested.

Table 1. Count matrix representation of the Ets cis-element motif.

	1	2	3	4	5	6	7	8	9	10	11
A	7	15	2	29	0	0	39	33	10	6	7
C	3	5	17	7	0	0	0	0	2	8	1
G	10	12	18	3	39	39	0	0	26	6	13
T	5	5	1	0	0	0	0	6	1	18	2

Human Promoter Database

Human transcription start sites were located by aligning sequences from three sources against the draft human genome. The sequence sets used are: 274 human promoter sequences from the Eukaryotic Promoter Database (EPD), 2312 full-length 5′ untranslated regions (UTRs) (40) and 2251 cDNAs constructed using the oligo-capping method (41). These sequences were aligned against the April 16, 2001 version of the draft human genome at NCBI (1) using megablast (42). Low complexity regions and human repeats were masked during the word finding stage, but not the extension stage, using the option -F ‘m D;R’. Strict criteria were used to remove sequences with ambiguous alignments. EPD sequences were removed if megablast returned more than one alignment, or if the alignment did not include the transcription start site. For the 5′ UTRs and the oligo-capped cDNAs, sequences were removed if: they aligned with more than one genomic contig; they aligned with both strands of the contig; more than one alignment was returned, and these alignments did not occur in an order consistent with a single transcript with introns spliced out; more than one of the transcript’s alignments overlapped in the genomic sequence; more than 10 bases in the transcript were aligned to multiple positions in the genomic sequence; the first nucleotide in the transcript did not align, allowing for a possible non-aligning partial oligo-cap sequence.

Sequences longer than 100 bases that did not survive this process were shortened to 100 bases and re-aligned, and a few more good alignments were obtained. Similarly, rejected 5′ UTRs <100 bases were lengthened to 100 bases using the GenBank sequences referenced in this dataset, to get a few more good alignments. Finally, the transcription start sites extracted from this process were made non-redundant. If any pair of sites was located on the same strand of the same contig within 2000 bases of one another, one of them was removed (with priority EPD > 5′ UTRs > oligo-capped cDNAs). In the end, 2005 transcription start sites remained.

RESULTS

We developed a C++ program, called COMET, to search for clusters of cis-element motifs in DNA sequences. COMET is available as a web server or for download at http://zlab.bu.edu/∼mfrith/comet. The program takes as input a set of sequences to search and a set of user-specified motifs in the form of count matrices. It then finds optimal scoring motif clusters in the sequences, where a candidate cluster receives positive scores for the motifs that it contains, minus a linear ‘gap penalty’ for the spacer regions between its motifs. In this way, a ‘raw score’ is associated with each predicted motif cluster. Finally, the program calculates an E-value for each predicted cluster, i.e. an estimate of how many times a cluster of this raw score or greater would be expected in random DNA sequences of given lengths and nucleotide compositions.

Accuracy of the E-value calculation

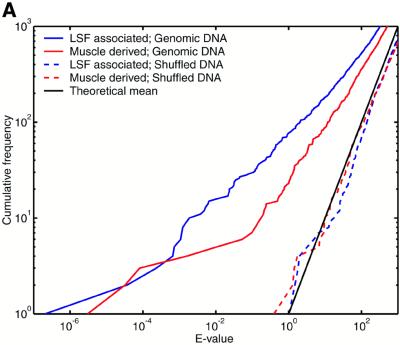
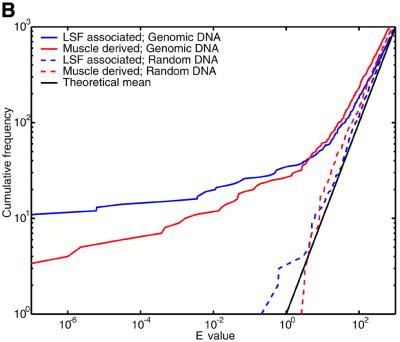
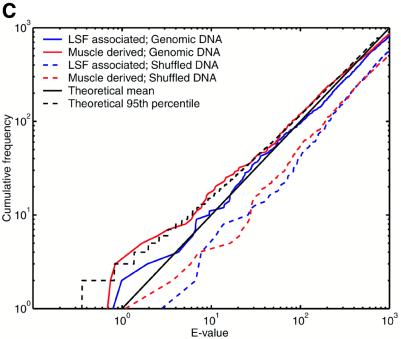
The E-value indicates the number of times we expect to see a motif cluster of a given raw score or greater purely by chance, under a null model. The challenge here is that natural DNA sequences possess statistically unusual properties that are not captured by any straightforward null model. Problematic phenomena include tandem repeats, so-called low complexity sequence and local fluctuations in GC content. So it is necessary to test whether the E-value calculation gives meaningful results for natural sequences. To this end, we analyzed a set of 2005 sequences, each of length 2 kb, extracted from random locations in the draft human genome (NCBI version dated April 16, 2001). We crudely handled tandem repeats and low complexity regions by masking them using the programs Tandem Repeats Finder (43) and dust (R.Tatusov and D.Lipman, manuscript in preparation), thus eliminating ∼5% of the total sequence from consideration. We then used COMET to identify clusters of either LSF associated or muscle derived motifs. Since 4 Mb of sequence only covers ∼0.1% of the genome, we do not expect it to contain a substantial number of regulatory regions of these types. For comparison, we also tested each null model against synthetic sequences: for the two mononucleotide null models these were pseudorandomly shuffled versions of the genomic sequences, and for the Markov null model a random 4 Mb sequence was generated from the model itself. Figure 2 indicates that, using all three null models, the E-value calculations are highly accurate for the synthetic sequences.

Figure 2.

Motif clusters found by COMET in natural and synthetic sequence sets, using three different null models. Either of two motif sets was searched for: muscle derived and LSF associated (see text for details). The y-axis indicates the number of clusters found with E-value lower than the value indicated on the x-axis. (A) Null model = independent nucleotides with frequencies estimated from each query sequence. (B) Null model = fifth order Markov. (C) Null model = independent nucleotides with frequencies estimated from a sliding window. The theoretical lines indicate the mean and 95th percentile for the number of observations at each E-value, according to a Poisson distribution.

The null model of independent nucleotides estimated from each query sequence consistently overestimates the statistical significance for natural sequences (Fig. 2A). This result can be explained by fluctuations in GC content within each sequence. We had higher hopes for the Markov null model, which can incorporate higher abundances of both GC-rich and AT-rich oligonucleotides, as well as accounting for the reduced presence of the CpG dinucleotide and similar phenomena. Figure 2B shows that the E-values for natural sequences become reasonably accurate only after the first 70 or so clusters. We do not expect this number of genuine cis-element clusters to be present. That the predictions with the most significant E-values are indeed false positives is suggested by their occurrence in sequences with unusual GC composition. While the Markov model captures GC content biases in small oligonucleotides, it does not capture extended biases over longer sequence regions. In contrast, E-values calculated for natural sequences with the sliding window null model show remarkable agreement with theoretical expectations (Fig. 2C). A certain degree of random fluctuation from the theoretical mean is inevitable, and the dashed black line indicates the 95th percentile of expected fluctuations (under a Poisson distribution). The numbers of LSF associated motif clusters never exceed the 95th percentile, and the muscle derived clusters do so only marginally. In comparison, one would only trust BLAST E-values to be accurate plus or minus a few orders of magnitude. Using the sliding window null model, we have accurately solved the problem of ascribing statistical significance to motif clusters in natural as well as synthetic DNA sequences, and we use this null model for the remainder of the study. A potential disadvantage of this technique is that it may penalize regions of unusual sequence composition that are caused by the presence of cis-elements, e.g. some CpG islands may be arrays of Sp1 binding sites. If the sequences are not masked, a handful of extremely significant motif clusters appear, but otherwise the results look extremely similar to those in Figure 2C (data not shown).

Motif clusters in known regulatory regions

We obtained the sequences of 27 experimentally supported muscle specific regulatory regions, and nine LSF regulated promoters. The 27 muscle regulatory regions are a non-redundant subset of 43 sequences from the LRA study (9). The LSF-regulated sequences are taken from our earlier study (11), with sequences >2 kb shortened to 2000 bp, centered on the known LSF binding site. To investigate the feasibility of detecting these types of regulatory regions by searching for motif clusters, we examined the E-values of clusters in these sequences. Equation 6 indicates that the E-values are linearly proportional to the sequence length (we do not use the finite length correction). Since these sequences have differing lengths, we rescaled all the E-values to mimic a sequence length of 2 kb, so that the results are more easily comparable. The sequences were not masked for this investigation. The LSF count matrix was constructed, in part, from LSF binding sites in the nine LSF regulatory regions. Therefore, we used a jack-knife procedure to scan these sequences, omitting from the LSF count matrix any sites that came from the sequence being scanned. To scan the muscle regulatory regions, we used both the muscle derived and non-muscle derived matrix sets, following the procedure used in the LRA study (9).

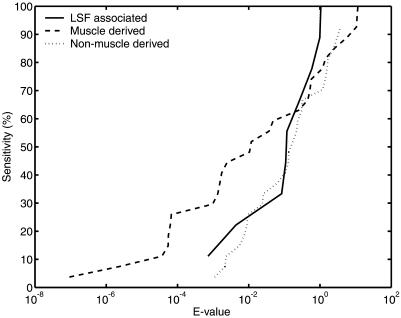
Figure 3 plots the proportion of known regulatory regions containing a motif cluster with E-value below a particular threshold. With muscle derived matrices, approximately half of the sequences contain clusters with E-values <10^–2; a few sequences contain clusters as significant as 10^–7. For all three sets of matrices, 70% or more sequences contain a motif cluster with E-value below the randomly expected value of 1. Approximately 30% of the sequences do not contain significant motif clusters, indicating that discrimination of regulatory regions from background sequence is likely to be a difficult problem, at least based on our current biological knowledge concerning the subtle signals in these regulatory sequences.

Figure 3.

E-values of motif clusters found by COMET in known regulatory regions. COMET was used to find clusters of LSF associated motifs in LSF regulatory regions (solid line), and clusters of muscle derived (dashed line) and non-muscle derived motifs (dotted line) in muscle regulatory regions. The y-axis indicates the proportion of regulatory regions that contain a motif cluster with E-value lower than that indicated on the x-axis.

Motif clusters in human promoters

Although transcription factor binding sites are frequently distant from transcription start sites, they are believed to be enriched in proximal promoter regions. Hence, by restricting predictions of regulatory signals to promoter sequences, it should be possible to decrease the false positive rate dramatically without increasing the false negative rate too much. By considering several sets of experimental data, we have constructed a database of human transcription start sites, which we call the Human Promoter Database (HPD). With 2005 entries the HPD was, to our knowledge, the largest database of human promoters until recently (44). We use COMET to look for LSF and muscle related regulatory signals in sequences obtained from the HPD.

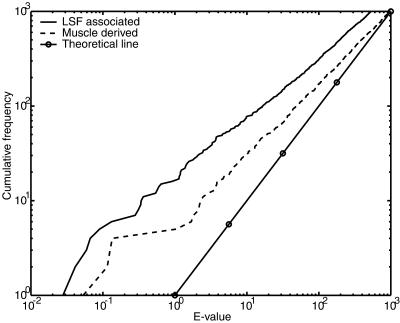
We extracted genomic sequences from –1499 to +500 relative to 2005 transcription start sites in our HPD. These sequences were masked and scanned with COMET to identify clusters of LSF associated or muscle derived motifs. Figure 4 shows that clusters with low E-values occur more often than is expected for random DNA, indicating that COMET is sensitive to the enrichment of cis-elements in promoters. This effect is more pronounced for LSF associated motifs, which is not surprising since this motif set includes the ubiquitous TATA box and Sp1 sites.

Figure 4.

Cumulative frequency plots of motif cluster E-values found by COMET in promoter sequences. COMET was used to find clusters of LSF associated motifs (solid line without circles) or muscle derived motifs (dashed line) in a set of promoter sequences. The y-axis indicates the number of clusters with E-value lower than that indicated on the x-axis. The theoretically expected line is marked with circles.

The promoters with the most significant clusters of LSF associated (considering only those with at least one LSF motif) and muscle related motifs are listed in Table 2. Compared with muscle specific gene regulation, LSF is not very well studied and, therefore, not much information is available for the regulation of predicted genes in Table 2A. For four of the five predicted muscle-related genes in Table 2B, various experimental data support our predictions. (i) The 14-3-3 family of proteins has been shown to be a signal-dependent regulator of muscle cell differentiation. One study indicates that 14-3-3 binds to histone deacetylases HDAC-4 and HDAC-5, and prevents them from binding to and inhibiting myocyte enhancer factor-2 (MEF2) (45). Another study shows that 14-3-3 forms a complex with MEF2 in vivo and specifically enhances MEF2 transactivational activity (46). Here, we predict that 14-3-3 is regulated by MEF2. This is an intriguing and testable hypothesis. (ii) In agreement with our prediction, experiments show that serum response factor (SRF) binds to the promoter region of α-cardiac actin and regulates its expression (47,48). (iii) In agreement with our prediction, recent work shows that MEF2 and SRF regulate carnitine palmitoyltransferase (49). (iv) Adenylate kinase 1 (AK1) catalyzes phosphotransfer reactions, which couple ATP production and utilization. AK1 is essential for the maintenance of cellular energetic economy, enabling cardiac and skeletal muscles to perform at the lowest metabolic cost (50–52). Its expression is muscle specific and developmentally regulated (53,54). Here we predict that AK1 is regulated by MEF2.

Table 2. The five most significant LSF associated motif clusters and the five most significant clusters of muscle derived motifs in the promoter sequence set.

	Gene product	Motifs
A	Platelet glycoprotein IIb	5 LSF, 2 Sp1, 7 Ets
	Cytohesin-2	1 LSF, 6 Sp1
	β-1,6-N-acetylglucosaminyltransferase	2 LSF, 3 Sp1, 2 Ets
	Proteasome inhibitor hPI31 subunit	2 LSF, 2 Sp1, 2 Ets
	α-1-antichymotrypsin	4 LSF, 1 Sp1, 1 Ets
B	p53-associated gene (Mdm2)	3 mef2, 1 myf
	YWHAH gene for tyrosine 3-monooxygenase/tryptophan 5-monooxygenase activation protein (14-3-3)	2 mef2
	α-cardiac actin	3 srf
	Carnitine palmitoyltransferase I, nuclear gene encoding mitochondrial protein	1 mef2, 1 myf
	Cytosolic adenylate kinase (AK1)	1 mef2

To construct this table, the sequences were scanned with COMET using count matrices for LSF, Sp1 and Ets, but not the TATA box. Clusters without an LSF motif are omitted. The gene product descriptions were obtained from GenBank (http://www.ncbi.nlm.nih.gov) (71).

Discrimination of known regulatory regions from large sequence sets

A basic question is: To what extent can COMET discriminate known regulatory regions from background sequence? To investigate this question, we can pick an E-value threshold that achieves a given sensitivity for identifying known regulatory regions, and examine the corresponding prediction rate in background sequences. A higher prediction rate indicates lower specificity. We examine two sets of known regulatory regions: the 27 muscle regulatory regions using the muscle derived matrices, and the nine LSF regulatory regions using the LSF associated matrices. We examine two sets of background sequences: 2005 randomly chosen human genomic sequences and 2005 human promoter sequences. All sequences were masked. It is possible that the background sequences may contain genuine muscle or LSF regulatory regions. However, we do not observe significant clusters for random genomic sequences (Fig. 2C). We predict, with some confidence, a few human promoter sequences to be regulated by muscle derived matrices (Table 2B). Nonetheless, these represent only 0.25% of the 2005 sequences. Thus, for the analysis in this section, it is reasonable to treat the above two sets of sequences as negative controls.

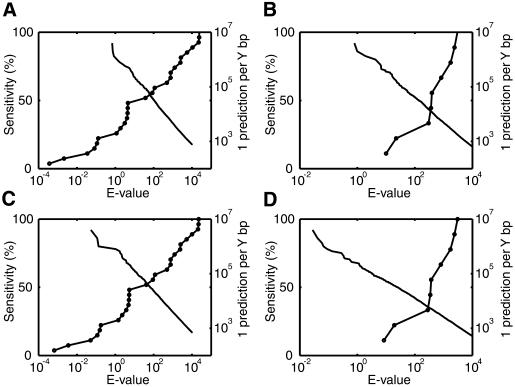
After obtaining raw scores for motif clusters in the known regulatory regions, we calculate their E-values as if these scores had been found in one of the background sequence sets. Thus, the raw scores are similar to those calculated for Figure 3, but the E-values are less significant since we mimic discovering them in a larger sequence set. Figure 5 includes superimposed plots of the proportion of known regulatory regions detected at each E-value threshold, along with the prediction rate in background sequences at the same E-values. These plots can help to judge whether or not COMET is discriminatory enough for a particular application. For example, if we would like to achieve a sensitivity of 60% in known muscle regulatory sequences, we need to use an E-value cutoff of 10², which corresponds to a prediction rate of 1 per 50 kb in random genomic sequences (Fig. 5A), and 1 per 29 kb in human promoter sequences (Fig. 5C). Such a performance may be acceptable for some applications, for example, searching for muscle related regulatory sites in a 100 kb stretch of genomic sequence identified by linkage analysis.

Figure 5.

Plots of trade-off between sensitivity and background prediction rate for finding motif clusters, as the E-value threshold is varied. The line marked with circles indicates the proportion of true regulatory regions identified by COMET at different E-value thresholds. The unmarked line describes the background prediction rate, in terms of the average number of base pairs between predictions, on a control sequence set over the same range of E-values. (A) Sensitivity for muscle regulatory regions versus prediction rate for genomic sequences, using muscle derived motifs. (B) Sensitivity for LSF regulatory regions versus prediction rate for genomic sequences, using LSF associated motifs. (C) Sensitivity for muscle regulatory regions versus prediction rate for promoter sequences, using muscle derived motifs. (D) Sensitivity for LSF regulatory regions versus prediction rate for promoter sequences, using LSF associated motifs.

Comparison of COMET’s performance with Cister and LRA

Since COMET is a new method, we would like to compare its performance with earlier methods. Here, we investigated COMET’s ability to discriminate known regulatory regions from a background sequence set, and compare with two earlier studies using Cister (11) and LRA (9). Table 3 shows, for the three matrix sets, the prediction rate in 2005 randomly chosen human genomic sequences at E-value thresholds that ensure close to 60% sensitivity (percentage of known regulatory regions detected). This table also lists comparable results for Cister (11) and LRA (9). It should be noted that for Cister the sequences were masked using RepeatMasker (A.F.A.Smit and P.Green, http://ftp.genome.washington.edu/RM/RepeatMasker.html), and for LRA an unspecified masking procedure was used. Thus, prediction rates per unmasked base pair should be compared. The results for muscle derived matrices are available for all three methods. COMET and Cister perform comparably. It is unclear if the reported prediction rate for LRA was for unmasked base pairs. If so, LRA performed similarly on this test set. For LSF associated and non-muscle derived motif sets, Cister’s prediction rates are three times lower than those of COMET. One possible advantage of Cister is that it uses the forward–backward algorithm rather than the Viterbi algorithm and, thus, considers all possible arrangements of cis-elements rather than just the optimal arrangement. However, Cister requires more parameters to be set than COMET does, and Cister’s output consists of posterior probability curves which can be harder to interpret than COMET’s predicted sequence segments.

Table 3. Prediction rates for three methods in human genomic sequence, at thresholds that give sensitivities close to 60%.

Method	Motif set	Sensitivity	Prediction rate
			Per total base pairs	Per unmasked base pairs
COMET	LSF associated	5/9	1 per 12 kb	1 per 11 kb
	Muscle derived	16/27	1 per 30 kb	1 per 29 kb
	Non-muscle derived	16/27	1 per 5.7 kb	1 per 5.5 kb
Cister	LSF associated	6/9	1 per 63 kb	1 per 33 kb
	Muscle derived	16/27	1 per 68 kb	1 per 35 kb
	Non-muscle derived	16/27	1 per 32 kb	1 per 17 kb
LRA	Muscle derived	60%	1 per 32 kb
Non-muscle derived		Not reported

Finally, we consider another background sequence set to further compare the performance of COMET, Cister and LRA. We use the same background set as in the LRA study (9), which consists of eukaryotic promoters from the EPD (55). We obtained sequences in the range –249 to +50 for all 1390 entries in release 66_1 of EPD. The known regulatory regions and the background sequence set were analyzed exactly as in the previous section except that, for consistency with the earlier studies, no sequences were masked.

Table 4 lists the percentage of EPD sequences predicted to have a cis-element cluster at an E-value threshold that produces ∼60% sensitivity for the known regulatory regions. Comparable data for the Cister and LRA methods are also given. These results suggest that Cister performs slightly better than the other two methods. COMET is not far behind, while the LRA approach performs significantly worse using non-muscle derived PSSMs.

Table 4. Percentages of EPD sequences with a predicted motif cluster, at thresholds that ensure ∼60% sensitivity, for three methods.

Method	Motif set	Sensitivity	Percentage of EPD sequences with a predicted cluster
COMET	Muscle derived	16/27	4.7
	Non-muscle derived	16/27	7.4
Cister	Muscle derived	16/27	2.9
	Non-muscle derived	16/27	5.2
LRA	Muscle derived	60%	4.0
	Non-muscle derived	60%	13.0

The EPD sequences are of length 200 bp for the LRA method, and 300 bp for the other two methods.

The overall conclusion is that the three methods exhibit similar performance. Therefore, COMET has much to recommend it, as it is the simplest method, with the smallest number of adjustable parameters and it incorporates an analytic calculation of statistical significance. In truth, none of these methods is yet sufficient for accurate detection of transcription regulatory sequences on a large scale. We believe that the main limitation is not algorithmic, but insufficient knowledge of the signals that constitute these types of regulatory region.

DISCUSSION

We have introduced the first method to detect clusters of cis-elements based on matrix representations that incorporates a calculation of statistical significance. Our method is extremely general, in that it makes minimal assumptions about the clusters, has minimal parameters and avoids arbitrary cut-offs. It considers both the strengths of individual motifs and the tightness of their clustering, combining these features into a single score. With careful choice of the null model, the E-values are extremely accurate for human genomic sequences as well as synthetic sequences.

Although COMET performs comparably with two alternative methods (that are more complex and lack E-value calculations), all current methods perform poorly overall in detecting regulatory regions. Our investigations make the fundamental problem very clear: many of the known regulatory regions that we studied simply do not contain very significant clusters of the cis-elements that we searched for. Increasingly sophisticated algorithms will not alleviate this situation, but rather the priority should be improved understanding of the signals contained in these regulatory regions. We can see four possible ways in which our current knowledge may fall short: (i) inadequate representations of the cis-elements that we know about, (ii) ignorance of other cis-elements contained in these types of regulatory region, (iii) ‘diffuse’ signals such as nucleosome binding properties may constitute important parts of these regulatory regions, and (iv) each regulatory region may contain a unique combination of signals so that there are no ‘types’. The first two problems relate to the principal difficulties facing a user of COMET: how to obtain matrix representations of the cis-elements and, especially, how to choose a set of cis-elements to search with.

We do not think our matrix representations of cis-elements are so inaccurate as to fully explain the shortfall in prediction accuracy. Methods to account for correlations between positions, such as maximal dependence decomposition (56) or Markov models, may improve accuracy, but require more training data than is usually available. More significant problems are the limited availability of matrices, and the variable length and half-site organization of some cis- elements. The TRANSFAC database contains over 300 matrices. While this may sound like a small fraction of the 1850 transcription factors preliminarily predicted in the human genome (57), many transcription factors belong to families that share very similar DNA binding preferences. For example, the roughly 20 members of the Sp/KLF family all bind to similar cis-elements, having maximum affinity for either the GC-box or the GT-box (58). Therefore, a few hundred matrices may cover a much larger range of transcription factors, neglecting small variations in DNA binding preference within families. Some matrices in databases like TRANSFAC may be of poor quality (59). In part, the problem is that traditional matrix representations cannot account for the flexible DNA binding properties of some transcription factors. For example, nuclear hormone receptors bind to pairs of half sites that can be arranged as direct or inverted repeats, separated by various distances (60). Such flexibility can be accounted for by generalizing PSSMs into very simple hidden Markov model representations of cis-elements (61,62), or even by constructing a number of alternative PSSMs for one type of cis-element.

We chose the cis-elements for LSF and muscle specific regulatory regions based largely on anecdotal evidence, and there is no reason to think we have saturated the types of cis-element commonly found in these regions. To get a handle on additional elements that may be present, we could screen against all known motifs from TRANSFAC, or apply various algorithms to discover novel motifs common to these sequences (63–65). Phylogenetic footprinting, by indicating evolutionarily conserved regions of the sequences, may help to identify additional cis-elements (66–70). However, our investigations of estrogen response elements indicate that these cis-elements are often not conserved between human and mouse (R.O’Lone, M.C.Frith and U.Hansen, manuscript in preparation).

Analysis of nucleosome binding properties would require new computational tools. If regulatory regions are to some extent piecemeal and contain unique combinations of cis-elements, it may be possible to find them by searching for significant clusters using a universal collection of motifs. However, we believe that evolution is more likely to have duplicated and reused regulatory modules rather than reinventing them from scratch.

Even with current performance, COMET is able to make useful biological predictions. Application of COMET to the 2005 human promoter sequences led to five promising predictions of muscle specific cis-element clusters. Among them, α-cardiac actin and carnitine palmitoyltransferase have been experimentally shown to be regulated by muscle specific transcription factors; 14-3-3 and cytosolic adenylate kinase have clear experimental evidence to be muscle specific. Currently, no study indicates the regulation of Mdm2 by muscle specific transcription factors. Thus, the latter three genes represent predictions by COMET, which can be tested experimentally. So, application of COMET with a stringent E-value threshold, while achieving only a low sensitivity, can generate promising predictions of functional cis-element clusters.