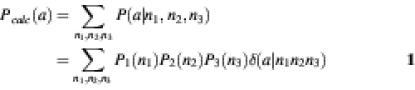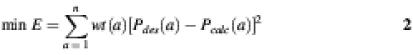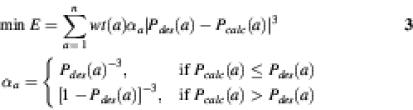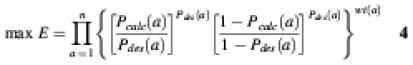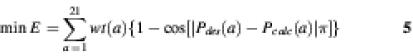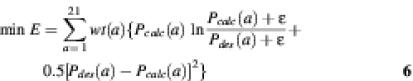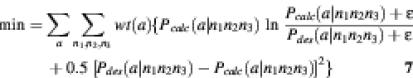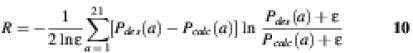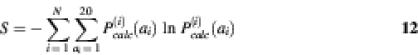Abstract
Protein combinatorial libraries provide new ways to probe the determinants of folding and to discover novel proteins. Such libraries are often constructed by expressing an ensemble of partially random gene sequences. Given the intractably large number of possible sequences, some limitation on diversity must be imposed. A non-uniform distribution of nucleotides can be used to reduce the number of possible sequences and encode peptide sequences having a predetermined set of amino acid probabilities at each residue position, i.e., the amino acid sequence profile. Such profiles can be determined by inspection, multiple sequence alignment or physically-based computational methods. Here we present a computational method that takes as input a desired sequence profile and calculates the individual nucleotide probabilities among partially random genes. The calculated gene library can be readily used in the context of standard DNA synthesis to generate a protein library with essentially the desired profile. The fidelity between the desired profile and the calculated one coded by these partially random genes is quantitatively evaluated using the linear correlation coefficient and a relative entropy, each of which provides a measure of profile agreement at each position of the sequence. On average, this method of identifying such codon frequencies performs as well or better than other methods with regard to fidelity to the original profile. Importantly, the method presented here provides much better yields of complete sequences that do not contain stop codons, a feature that is particularly important when all or large fractions of a gene are subject to combinatorial mutation.
INTRODUCTION
Protein combinatorial libraries provide new ways to probe the determinants of protein folding and to identify novel folding amino acid sequences. A library of protein sequences is constructed by simultaneously randomizing the entire protein or a subset of preselected residues. Such diversity is generated using a variety of synthetic methods or by introducing partially random genes for bacterial expression (1) or ‘display’ using phage (2) or yeast (3). Sequences with desired properties are selected using a particular assay, e.g., small molecule binding or enzymatic activity. If molecular biological methods are used to create the library, then selected sequences can be readily identified by amplifying and sequencing their respective genes. Such sequencing of selected proteins identifies the allowable substitutions at each residue. As observed among naturally occurring protein variants, at some positions only a few amino acids may be permitted, while at other sites, a wide range of amino acids may be tolerated (4). The variability of those sequences folding to a given structure or those possessing a particular function can be broadly investigated using such experiments. Combinatorial experiments have been used both in the de novo design of sequences consistent with α-helical and β-sheet topologies (5) and in biophysical studies of proteins (6,7).
The large number of possible sequences can be a limitation in combinatorial experiments. A 100-residue protein has more than 10130 possible sequences, obviously an impractical number of possibilities. Simultaneously randomizing only 10 amino acid positions leads to a sequence space of 2010 ≈ 1013 different sequences. Depending on the methods used, efficient screening is possible only for about 108–1011 peptides at a time. Thus, methods for reducing the possible diversity must be implemented. In some combinatorial experiments, only limited sites are selected to be simultaneously randomized. The selection of these sites is guided by knowledge of the structural and functional features of the protein (8). Another approach to limiting the size of a library is by reducing the variability at sites being mutated, i.e., less than 20 amino acids are permitted at selected positions (9). For example, the Hecht group has taken advantage of the ‘degeneracy’ in the genetic code to hydrophobically pattern combinatorial protein libraries, where only either hydrophobic or hydrophilic amino acids were permitted at preselected sequence positions (5). In general, such efforts in diversity reduction often involve qualitative considerations of structure and sequence properties.
A quantitative approach of defining a focused subset of sequences can not only reduce the size of a library but also increase its efficiency, e.g., increase the fraction of structured or functional sequences (10,11). Such quantitative approaches should be based upon information about which properties confer desired structural and functional properties. These methods identify which residue positions in a protein should be variable and the degree of variability at each site. In addition to using such information to reduce the number of amino acids at selected sites, a library can be further focused using a non-uniform distribution of the permitted amino acids at each site. For example, among the many sequences that fold to a particular structure, both valine and isoleucine may be observed at a particular site i, but valine may occur with a much higher frequency. It would be very useful to determine the entire set of amino acid frequencies at each residue among sequences having a common structure (the sequence profile). Multiple sequence alignments can yield such profiles from naturally occurring sequences where the sequence diversity often is due to evolution from a common ancestor (12). Such evolutionary profiles, however, are the result of the necessarily limited sampling of sequences over the course of evolution. In addition, the many different biological pressures on determining sequence properties can obscure which residues are conserved due to function from those that are structurally important. Moreover, there may be many sequences that nature has neither used nor tried which fulfill the stability and functional requirements associated with a particular protein structure. Identifying viable sequences is of interest in both understanding the range of sequence diversity allowed for particular protein structures, and for discovering novel proteins.
To address this large range of sequence variability, statistical theories for protein combinatorial libraries are being developed that identify the features of sequences likely to fold to a given backbone structure (10,11). Given a target structure and sequence–structure compatibility scoring function, the methods estimate the probabilities of amino acids at each position in a given structure among sequences subject to arbitrary physical, functional or synthetic constraints. Such information is a natural input to the design of combinatorial experiments.
There are several methods for experimentally creating protein libraries. Libraries may be constructed via conventional peptide synthesis in combination with split-pool methods. However, such peptide synthesis in the traditional stepwise fashion is usually practical for only short sequences (N < 50, where N is the number of residues). Also any selected proteins would be difficult to amplify. Experimentally, combinatorial protein libraries are more often constructed by expressing an ensemble of partially random gene sequences. Positions in the open reading frame are randomized. For each such randomized codon, n1n2n3, nucleotides ni may be added according to predetermined ratios of adenine (A), thymine (T), guanine (G) and cytosine (C). If each nucleotide is present with equal frequency at each codon position, such a library encodes all 20 amino acids, biased according to the degeneracy of the genetic code. Constraining nucleotide identity at one of the codon positions is a frequently used method for limiting the number of amino acids (13). More generally, a non-uniform distribution of nucleotides is necessary to encode peptide sequences that have a non-uniform bias toward specific amino acids. The most direct means of doing this is by using pre-formed trinucleotide phosporamidites, where oligonucleotides can be specified that precisely determine the frequencies of each amino acid at each position (14,15). However, trinucleotide methods are experimentally involved and not yet available commercially. A more economical and straightforward route to design the nucleotide mixture is by independently specifying the frequencies of each nucleotide rather than each codon. The nucleotide frequencies can be chosen such that the protein library translated from the gene library best reproduces the desired amino acid profile.
Several algorithmic methods have been developed to generate such nucleotide mixtures that encode the amino acids with desired probability distributions at predetermined sites. Most often these are cast as an optimization problem. An objective function that quantifies agreement between the desired amino acid frequencies and those coded for by a set of random genes with independent nucleotide frequencies is optimized. LaBean and Kauffman used a spreadsheet and a refining grid search algorithm to exhaustively search the nucleotide composition space (16). A genetic algorithm with local optimization strategies based on the downhill simplex method has also been developed based upon a χ2-type objective function (17). Kretzschmar et al. applied an algorithm based on a Monte-Carlo method to search nucleotide composition using three different scoring functions and applied it to subtilisin mutagenesis (18). Wolf and Kim also applied optimization theory to solve for nucleotide frequencies at codon positions in an attempt to approximate amino acid probabilities (19). Each of these methods were developed primarily to solve the nucleotide problem for a single amino acid residue (or a small number) rather than the gene library for a whole protein sequence. The methods developed by Schwiehorst (17) and Wolf and Kim (19) consider the problem of stop codons and/or rare codon usage in the host organisms. They address these problems by manually optimizing weighting factors in the objective function or by including additional constraints on the amino acid frequencies. However, these are time-consuming trial and error approaches for solving the problem for even a single residue.
Here we present a computational method that takes as input a desired set of amino acid probabilities for an entire protein and calculates the independent nucleotide probabilities at each position among a set of partially random genes. The calculated gene library can be created using DNA synthesis methods and expressed to generate a protein library with a desired profile. The fidelity between the desired probability and those calculated is quantitatively evaluated using the linear correlation coefficient and a relative entropy, each of which provides a measure of profile agreement at each position of the sequence. We demonstrate the capabilities of the method by applying it to three globular proteins. The utility of such methods for specifying libraries of gene sequences that permit large-scale variability is examined.
METHODS
For this study, we take that the amino acid frequencies at selected residue positions (possibly the entire protein) has been predetermined. What remains is to identify the independent nucleotide frequencies at each codon position among partially random genes that code for these sequences.
Let P1(n1),P2(n2),P3(n3) be the probabilities of the four possible nucleotides (ni = A,G,T,C) in the first, second and third position of a codon respectively. If these are treated as independent, the probability that amino acid a will appear as encoded by the codon n1n2n3 is P(a|n1,n2,n3) = P1(n1)<P2(n2)P3(n3)δ(a|n1,n2,n3), where δ(a|n1n2n3) = 1 only if n1n2n3 is a codon for amino acid a and is zero otherwise. If the codons of amino acid a are equally likely (no codon bias), the probability of an amino acid is the sum of codon probabilities corresponding to this amino acid.
Objective functions
Objective functions quantify the difference between an input desired amino acid probability distribution and the amino acid probability distribution expected from the nucleotide probability distribution. To find the nucleotide probabilities that best reproduce desired amino acid frequencies, the objective function is optimized (usually minimized). Below we present several different objective functions that have been suggested previously. In each case, the nucleotide frequencies are varied so as to minimize (or maximize) the scoring function E.
Objective function 1. (18):
The sum is over all possible amino acids at a site, usually n = 20, and wt(a) is a user-specified weighting factor allowing for amino acids of special interest to be favored. This scoring function is based on the χ2 function.
Objective function 2. (18):
Objective function 3. (18):
This function (equation 4) is derived from maximum- likelihood for the polynomial distribution. The value of the objective function is between 0 and 1. The maximum value is only obtained for a perfect match with the desired amino acid probability distributions.
The above three objective functions have been compared, and it was concluded that the objective function equation 4 has an advantage over the first two (18). The calculated amino acid probability distribution does not miss any amino acids in the desired distribution, and there is a balanced representation of amino acids having both low and high probabilities.
Objective function 4. (19):
The shape of function 1 – cos[|Pdes(aa) – Pcalc(aa) | π] is basin-like. The objective function is chosen to allow a moderate difference between the desired and calculated probability.
A new scoring function is presented here. It is composed of two terms, a χ2 function, which quantifies the absolute difference between the desired and calculated amino acid probabilities, and a relative entropy term (20). Such relative entropies are commonly used to quantify the ‘distance’ between two probability distributions and are strong indicators of when information in one distribution is not contained in the other.
Objective function 5:
Here, ε is introduced as an arbitrary small constant (ε = 10–6) so as to avoid numerical instability if Pdes(a) vanishes. This form of the objective function is motivated by maximum entropy methods that are often used in data fitting and image restoration (21). The logarithmic term makes this function sensitive to codons having low desired probabilities, which is particularly important for minimizing the appearance of stop codons.
Objective function for codon bias
Most protein libraries are expressed in particular organisms, where the codons for the same amino acid are not used with equal frequency (22). By way of example, here we focus on the codon bias of the yeast Saccharomyces cerevisiae. Thus, if expressed in yeast, the gene library solved by above objective functions (equation 6) may not match the desired amino acid probability distribution. The frequency of codon usage in yeast may also be implemented in the form of an objective function.
This is easily accomplished for the 64 codons by treating each as a separate term of the objective function. The probability that amino acid a will appear as encoded by the codon n1n2n3 is Pcalc (a|n1,n2,n3) = P1(n1)P2(n2)P3(n3)δ (a|n1,n2,n3). The desired probability of an amino acid a is Pdes(a). The desired probability of that amino acid a will be present as encoded by the codon n1n2n3 is Pdes(a|n1,n2,n3) = ka(n1n2n3)Pdes(a), where ka(n1n2n3) is the frequency with which the codon n1n2n3 is used for amino acid a in yeast. This leads to the following objective function which now includes a sum over each codon.
Bounds on probabilities
Each scoring function is optimized subject to the usual constraints on the nucleotide probabilities: 0 ≤ Pi(ni) ≤ 1 and ΣniPi(ni) = 1. In the objective function, the stop codons are treated as effective ‘amino acids’. Thus the objective function includes the weighted sum of 20 amino acids plus stop codons. It is possible that for the optimum, the calculated probability of a stop codon is high, which would prematurely terminate the protein sequence. To prevent the stop codon, an additional constraint may also be introduced: Pcalc(stop codon) < Pstop where Pstop is a predetermined bound on the probability of a stop codon (19).
RESULTS
Solutions for the objective functions were obtained using the CFSQP optimization routine (23). The weights wt(a) in equations 6 and 7 were set to 1. The results can be sensitive to the initial values, so several different sets of initial values were chosen for each nucleotide probability. Such initial conditions include a uniform distribution Pi(ni) = 0.25, a normalized random distribution of the Pi(ni), and values of the Pi(ni) yielding the codon of the most probable amino acid or linear combinations of the most probable amino acids. The best scoring set of nucleotide probabilities for these different initial conditions were selected.
We apply this computational method using the objective function in equation 6 to the amino acid probabilities of several structures, including the SH3 domain (PDB no. 1CKA), the engrailed homeodomain (PDB no. 2HDD) and cold shock protein A (PDB no. 1MJC). The choice of desired or target probabilities for the amino acids is arbitrary. Here this input amino acid probability distribution was determined using the statistical method for protein libraries (11), where this method takes as input a target structure and an energy function that quantifies sequence–structure compatibility: for each target backbone structure, the method yields the probabilities of each of the amino acids at each residue site.
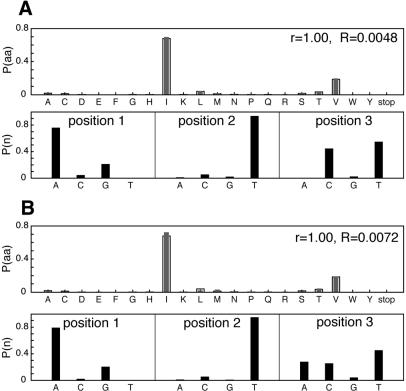
The calculation is illustrated by considering a particular amino acid position in a protein, here site 54 of the SH3 domain. Figure 1 shows the desired frequencies of the amino acids. Using this distribution, the optimization of an appropriate objective function yields the calculated nucleotide probabilities (see Fig. 1). A gene library can then be constructed having the independent frequencies of each of the nucleic acids at each position of the codon site for position 54. The set of amino acid frequencies at site 54 that would result from expressing the gene library is here termed the calculated amino acid distribution (see Fig. 1). A polynucleotide library may then be synthesized having the calculated nucleotide frequencies. For example, at site 54, Ile has a desired probability of (Pdes = 0.679). The calculated probability of observing this amino acid at this position (if all members of the library are correctly expressed and the library is large), is the sum of the probabilities of its codons (ATT, ATC and ATA). From the calculated nucleotide frequencies, we see that
Figure 1.
Probability distributions of amino acids P(aa) and nucleotides P(n) for site 54 of the SH3 domain. (A) Calculated using objective function presented in this work (see equation 6). (B) Calculated using objective function in equation 7 that includes codon bias. For P(aa), desired probability distribution (open bars) and that encoded by calculated gene library (filled bars). r is the linear correlation coefficient, and R is the relative entropy.
which is in good agreement with the desired probability for Ile.
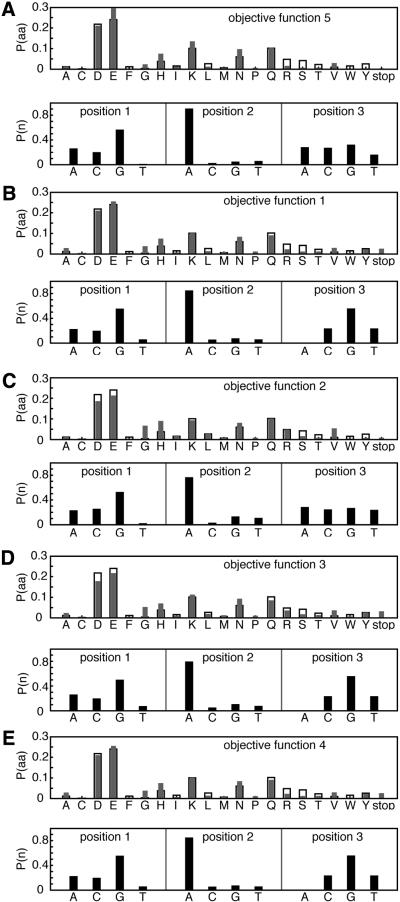
Using each of the objective functions, the nucleotide probabilities may be determined for a given desired amino acid probability distribution. Although the calculated amino acid probabilities are well recovered in Figure 2, we note that the underlying nucleotide distribution is not unique and depends on the objective function used.
Figure 2.
Probability distributions of amino acids P(aa) and nucleotides P(n) for site 14 of the SH3 domain calculated from different objective functions: (A) equation 6 (this work); (B) equation 2; (C) equation 3; (D) equation 4; (E) equation 5. For P(aa), desired probability distribution (open bars) and that encoded by calculated gene library (filled bars). r is linear correlation coefficient, and R is relative entropy.
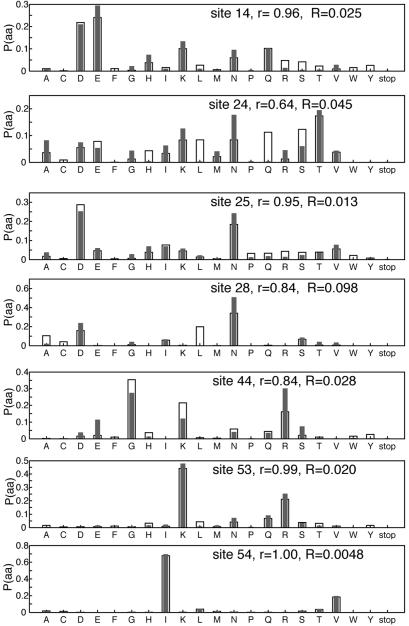
The desired and calculated amino acid probability distributions of selected sites in the SH3 domain are compared in Figure 3. In general the calculated probabilities agree well with desired ones. In most cases exact match between the desired probability distribution and that calculated cannot be achieved due to the partial independence of the nucleotides in each codon. Depending on the objective function used, Pcalc(a) may underrepresent some amino acids and overrepresent others. For example, at site 44, it is difficult to generate high probabilities of both Gly (codon GGN) and Lys (AAA and AAG) without generating high probabilities of Arg (AGA and AGG) and Glu (GAA and GAG). Distributions at residues where both polar and hydrophobic amino acids are probable (e.g. sites 24 and 28) can be difficult to match, again due to ‘codon overlap’. At such sites it may be best to further restrict the distribution to a particular class of amino acid properties.
Figure 3.
Probability distributions of amino acids P(aa) of selected sites of the SH3 domain. Desired probability distribution (open bars) and that encoded by calculated gene library (filled bars). r is linear correlation coefficient, and R is relative entropy.
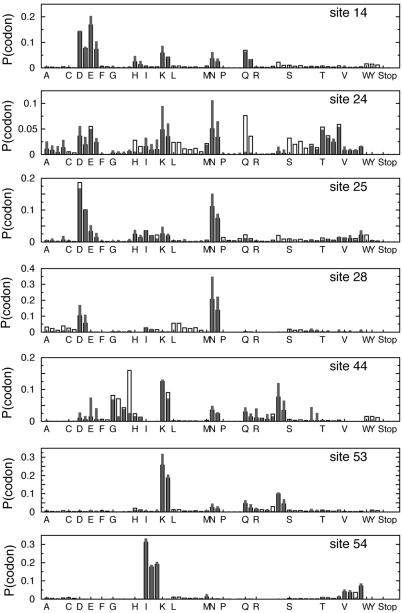
Figure 1 also shows an example of results calculated using an objective function for the codon bias of a particular organism. Here we consider the codon biases of the yeast S.cerevisiae. For example, the codons for Ile, ATT ATC ATA, are not equiprobable and have frequencies of 46, 26 and 28% respectively. The desired amino acid probability of Ile is 0.679. We may address these preferences by constraining the probability of each codon in the objective function (equation 7): Pdes(ATT) = 0.679 × 46% = 0.312, Pdes(ATC) = 0.679 × 26% = 0.177, and Pdes(ATA) = 0.679 × 28% = 0.190. Using equation 7 as the objective function, the method attempts to recover the desired probability of each codon rather than each amino acid. The calculated amino acid probabilities agree well with the desired amino acid probabilities, and can be calculated as done previously. For example, considering Ile again,
in good agreement with the desired frequency of Ile. Across a variety of different positions, the calculated amino acid probability distributions for the protein library expressed with the codon biases of the yeast S.cerevisiae agree well with the desired probability distribution. With the exception of Leu [which is problematic due to the fact that it has the largest variety (six) of codons], the codon usage from the calculated nucleotide library is in agreement with the bias associated with S.cerevisiae (Fig. 4).
Figure 4.
Probabilities of each codon for selected sites of the SH3 domain for the protein as expressed in yeast. The desired frequencies of the codons for each amino acid are determined using the codon usage observed in S.cerevisiae. For each amino acid, the probabilities of each codon are shown, e.g., the probabilities of the four codons for alanine (A). Desired codon probabilities (open bars). Probabilities of codons in calculated gene library (filled bars).
To evaluate the calculated profiles, it is helpful to use a measure of the discrepancy between desired and calculated probabilities. Here two measures were used: the linear correlation coefficient (r) and relative entropy (R) (20). The value of the linear correlation coefficient r varies between 1 and –1. If two profiles are identical, r = 1, while r = 0 if the two profiles are essentially uncorrelated. Here a relative entropy R is chosen that has a symmetric form (H.Kono and J.G.Saven, unpublished data)
where ε = 10–6 sets the lower bound of the probability. R varies in the range of [0, 1]. If the two profiles are identical, R = 0. If there is a significant difference between two profiles, the relative entropy approaches unity. The linear correlation coefficient (r) and relative entropy (R) were calculated for each residue site along the sequence of each target structure. The discrepancies between two profiles appear as peaks in the correlation coefficient r and in the the relative entropy R.
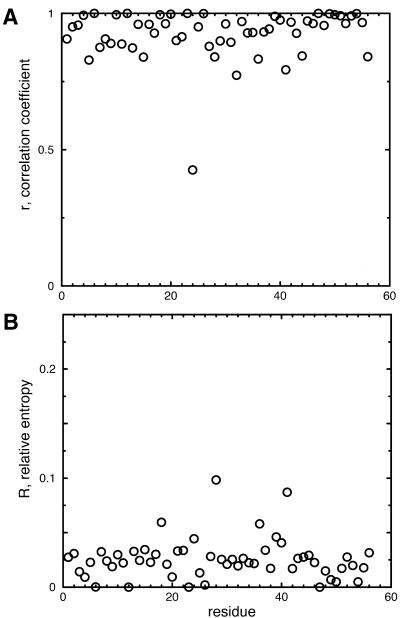
Plots of the linear correlation coefficient (r) and relative entropy (R) using equation 6 (this work) are presented for the SH3 domain (Fig. 5), and results for three different proteins using different objective functions are summarized in Table 1. Good correlation between the desired probability distributions and those calculated is obtained for most of residue sites (1 ≥ r > 0.8 and 0 ≤ R < 0.05). At several sites, none of the objective functions accurately reproduces the input amino acid probabilities, but this is due to the nature of the genetic code and independence of nucleotide probabilities; it is difficult (or not possible) to reproduce the target probabilities at these sites using independent nucleotides. As quantified by the values of r and R, however, the results using equation 6 are as good or better than those obtained using other methods.
Figure 5.
Correlation coefficient r (A) and relative entropy R (B) of each residue in the SH3 domain calculated, where r and R quantify the similarity between a desired amino acid probability distribution at each residue and that encoded by a calculated gene library resulting from the optimization of objective function 5 (equation 6).
Table 1. Linear correlation coefficient (r) and relative entropy (R) for three protein libraries.
| Equation no. | SH3 domain (PDB no. 1CKA) | Engrailed homeodomain (PDB no. 2HDD) | Cold shock protein A (PDB no. 1MJC) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <r> | σr | <R> | σR | <r> | σr | <R> | σR | <r> | σr | <R> | σR | |
| 6 | 0.93 | 0.09 | 0.025 | 0.018 | 0.89 | 0.12 | 0.031 | 0.016 | 0.90 | 0.13 | 0.028 | 0.019 |
| 2 | 0.94 | 0.06 | 0.023 | 0.016 | 0.91 | 0.07 | 0.028 | 0.015 | 0.91 | 0.11 | 0.025 | 0.015 |
| 3 | 0.81 | 0.22 | 0.047 | 0.048 | 0.84 | 0.13 | 0.044 | 0.034 | 0.81 | 0.19 | 0.053 | 0.052 |
| 4 | 0.93 | 0.06 | 0.027 | 0.019 | 0.88 | 0.08 | 0.031 | 0.019 | 0.88 | 0.13 | 0.030 | 0.018 |
| 5 | 0.94 | 0.06 | 0.023 | 0.016 | 0.91 | 0.07 | 0.028 | 0.015 | 0.91 | 0.11 | 0.025 | 0.015 |
Desired protein probabilities (profiles) are obtained from a statistical theory of protein libraries (11). Shown for each protein are the averages of r and R across all N residues of each protein. Also shown are the standard deviations of r and R. Equation 6 denotes this work.
Premature termination of the protein sequence will be caused by stop codons, which can greatly reduce the number of full-length protein sequences. To quantitatively describe the percentage of complete protein sequences among the total number sequences expressed from the calculated gene library, we also calculate the yield y:
where P(i)calc (stop) = P1(T)P2(A)P3(A) + P1(T)P2(A)P3(G) + P1(T)P2(G)P3(A) is the calculated probability of a stop codon at residue site i, and N is the total number of residues of the protein sequence.
The yields of full-length sequences of three protein sequences are shown in Table 2. If the gene sequences are constructed using equimolar amounts of A, T, G and C, the probability of a stop codon per residue site is 3/64 = 0.047. The yield of a protein library expressed using such nucleotide probabilities is low (7%) even for relatively small 50-residue sequences (see Table 2). Great improvements of yield are obtained using each of the objective functions, since the target probabilities of stop codons are usually zero. The probabilities of stop codons in the calculated gene library depend on which objective function is used. The yields obtained using objective function in equation 6 (≥96%) are much greater than the yields obtained using other objective functions (Table 2). While it is possible to use additional constraints to reduce the presence of stop codons with the other objective functions, we find that doing so decreases fidelity to the target amino acid distribution (data not shown).
Table 2. Yields (see equation 11) of the the complete protein libraries as expressed by the calculated gene libraries for each of the three proteins in Table 1.
| Yield | SH3 domain (PDB no. 1CKA) | Engrailed homeodomain (PDB no. 2HDD) | Cold shock protein A (PDB no. 1MJC) |
|---|---|---|---|
| Equal molar of A,T,G,C | 0.068 | 0.071 | 0.036 |
| Equation 6 (this work) | 0.98 | 0.99 | 0.96 |
| Equation 2 | 0.39 | 0.31 | 0.23 |
| Equation 3 | 0.40 | 0.22 | 0.18 |
| Equation 4 | 0.27 | 0.16 | 0.12 |
| Equation 5 | 0.39 | 0.31 | 0.23 |
Numbers of residues in each protein: 56 (1CKA), 55 (2HDD) and 69 (1MJC).
As mentioned in the Introduction, the large number of possible sequences can be a limitation for combinatorial experiments. For example, simultaneously randomizing all amino acid positions in a protein sequence of the SH3 domain leads to a sequence space of 2056, i.e. around 1072 different sequences. Using the statistical theory that identifies the probabilities of amino acids at each position in a given structure (11) together with the computational method presented in this paper, the number of possible sequences can be greatly reduced. To quantitatively describe the size of the protein library, we calculate the sequence entropy S, which is a measure of the effective number of sequences (24):
where P(i)calc(ai) is the probability of amino acid j at site i, and N is the length of the protein sequence. The total sequence entropy for this protein is S = ln2056 = 168. For the calculated SH3 domain amino acid probabilities based upon independent nucleotide frequencies, the sequence entropy diminishes by more than 28 orders of magnitude. This effective number of amino acid sequences can be further reduced by including additional constraints on protein sequence properties (e.g. lower overall energies) so as to further limit the diversity of the library.
CONCLUSION
A computational method is presented to calculate pseudo-independent nucleotide probabilities for each codon position in partially random gene sequences coding for a target protein structure. Such a gene library can encode a protein library having a desired amino acid probability distribution. The yield of complete sequences is larger than that of other methods, even when the entire protein is subject to mutation. The results can be used to direct the partially random synthesis of polynucleotides so as to yield focused combinatorial libraries of proteins and peptides. Such methods, when used in tandem with theoretical methods for library design, provide a targeted means both for the partial design and discovery of novel proteins and for exploring the sequence variability of known proteins.
Acknowledgments
ACKNOWLEDGEMENTS
We thank Professor Eric Boder for the codon biases associated with S.cerevisiae. J.G.S. gratefully acknowledeges support from the University of Pennsylvania, from the Research Corporation in the form of a Research Innovation Award, and from the National Science Foundation (CHE 9816497 and CHE-9984752). J.G.S. is a Cottrell Scholar of Research Corporation and an Arnold and Mabel Beckman Foundation Young Investigator.
REFERENCES
- 1.Kamtekar S., Schiffer,J.M., Xiong,H., Babik,J.M. and Hecht,M. (1993) Protein design by binary patterning of polar and nonpolar amino acids. Science, 262, 1680–1684. [DOI] [PubMed] [Google Scholar]
- 2.Hoess R.H. (2001) Protein design and phage display. Chem. Rev., 101, 3205–3218. [DOI] [PubMed] [Google Scholar]
- 3.Boder E.T. and Wittrup,K.D. (1997) Yeast surface display for screening combinatorial polypeptide libraries. Nat. Biotechnol., 15, 553–557. [DOI] [PubMed] [Google Scholar]
- 4.Reidhaar-Olson J.F. and Sauer,R.T. (1998) Combinatorial cassette mutagenesis as a probe of the informational content of protein sequences. Science, 241, 53–57. [DOI] [PubMed] [Google Scholar]
- 5.Moffet D.A. and Hecht,M.H. (2001) De novo proteins from combinatorial libraries. Chem. Rev., 101, 3191–3203. [DOI] [PubMed] [Google Scholar]
- 6.Gu H.D., Yi,Q.A., Bray,S.T., Riddle,D.S., Shiau,A.K. and Baker,D. (1995) A phage display system for studying the sequence determinants of protein-folding. Protein Sci., 4, 1108–1117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kim D.E., Gu,H.D. and Baker,D. (1998) The sequences of small proteins are not extensively optimized for rapid folding by natural selection. Proc. Natl Acad. Sci. USA, 95, 4982–4986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Arkin A.P. and Youvan,D.C. (1992) An algorithm for protein engineering: simulation of recursive ensemble mutagenesis. Proc. Natl Acad. Sci. USA, 89, 7811–7815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Balint R.F. and Larrick,J.W. (1993) Antibody engineering by parsimonious mutagenesis. Gene, 137, 109–118. [DOI] [PubMed] [Google Scholar]
- 10.Zou J. and Saven,J.G. (2000) Statistical theory of combinatorial libraries of folding proteins: energetic discrimination of a target structure. J. Mol. Biol., 296, 281–294. [DOI] [PubMed] [Google Scholar]
- 11.Kono H. and Saven,J.G. (2001) Statistical theory for protein combinatorial libraries. Packing interactions, backbone flexibility, and the sequence variability of a main-chain structure. J. Mol. Biol., 306, 607–628. [DOI] [PubMed] [Google Scholar]
- 12.Lüthy R., Bowie,J.U. and Eisenberg,D. (1992) Assessment of protein models with 3-dimensional profiles. Nature, 356, 83–85. [DOI] [PubMed] [Google Scholar]
- 13.Ting A.Y., Witte,K., Shah,K., Kraybill,B., Shokat,K.M. and Schultz,P.G. (2001) Phage-display evolution of tyrosine kinases with altered nucleotide specificity. Biopolymers, 60, 220–228. [DOI] [PubMed] [Google Scholar]
- 14.Zehl A., Starke,A., Cech,D., Hartsch,T., Merkl,R. and Fritz,H.J. (1996) Efficient and flexible access to fully protected trinucleotides suitable for DNA synthesis by automated phosphoramidite chemistry. Chem. Commun., 23, 2677–2678. [Google Scholar]
- 15.Gaytan P., Yanez,J., Sanchez,F., Mackie,H. and Soberon,X. (1998) Combination of DMT-mononucleotide and Fmoc-trinucleotide phosphoramidites in oligonucleotide synthesis affords an automatable codon-level mutagenesis method. Chem. Biol., 5, 519–527. [DOI] [PubMed] [Google Scholar]
- 16.LaBean T.H. and Kauffman,S.A. (1993) Design of synthetic gene libraries encoding random sequence proteins with desired ensemble characteristics. Protein Sci., 2, 1249–1254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Tomandl D., Schober,A. and Schwienhorst,A. (1997) Optimizing doped libraries by using genetic algorithms. J. Comput. Aided Mol. Des., 29–38. [DOI] [PubMed] [Google Scholar]
- 18.Jensen L.J., Andersen,K.V., Svendsen,A. and Kretzschmar,T. (1998) Scoring functions for computational algorithms applicable to the design of spiked oligonucleotides. Nucleic Acids Res., 26, 697–702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wolf E. and Kim,P.S. (1999) Combinatorial codons: a computer program to approximate amino acid probabilities with biased nucleotide usage. Protein Sci., 8, 680–688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Durbin R., Eddy,S., Krogh,A. and Mitchison.G. (1998) Biological sequence analysis: Probabilistic models of proteins and nucleic acids. Cambridge University Press, Cambridge, UK.
- 21.Press W.H. Teukolsky,S.A., Vettering,W.T. and Flannery,B.P. (1992) Numerical Recipes in C. The Art of Scientific Computing. Cambridge University Press, Cambridge, UK.
- 22.Kane J.F. (1995) Effects of rare codon clusters on high-level expression of heterologous proteins in Escherichia coli. Curr. Opin. Biotechnol., 6, 494–500. [DOI] [PubMed] [Google Scholar]
- 23.Lawrence C., Zhou,J.L. and Tits,A.L. (1997) User’s guide for CFSQP version 2.5: A C code for solving (large scale) constrained nonlinear (minimax) optimization problems, generating iterates satisfying all inequality constraints. Technical Report TR-94-16r1, University of Maryland, College Park, MD 20742, USA. http://64.238.116.66/aemdesign/FSQPframe.htm
- 24.Sander C. and Schneider,R. (1991) Database of homology-derived protein structures and the structural meaning of sequence alignment. Proteins, 9, 56–68. [DOI] [PubMed] [Google Scholar]