On the dissociation and conformation of gas-phase methonium ions

Abstract

The dissociation pathways of both doubly and singly charged methonium ions, (CH₃)₃N⁺ –(CH₂)_n–⁺N(CH₃)₃·X⁻ (n = 6,10; X = Br, I, and OAc), are measured using blackbody infrared radiative dissociation (BIRD) and SORI–CAD in a Fourier transform mass spectrometer. SORI–CAD of the doubly charged decamethonium ions results primarily in the formation of even electron ions by hydrogen rearrangements. In contrast, homolytic bond cleavage to form two odd electron ions is highly favored in the hexamethonium ion, presumably due to increased Coulomb repulsion in this ion. For BIRD of the singly charged salts, ions are mass selected and dissociated by heating the vacuum chamber to elevated temperatures. Under the low pressure conditions of our experiment, energy is transferred from the chamber walls to the ions by the absorption of blackbody radiation. From the temperature dependence of the unimolecular rate constants for dissociation, Arrhenius activation energies in the zero-pressure limit are obtained. The primary dissociation pathways correspond to counterion substitution reactions which result in loss of N(CH₃)₃ and CH₃X. For hexamethonium and decamethonium with X = Br or I, the branching ratios for these pathways differ dramatically; the ratio of loss of N(CH₃)₃ and CH₃Br is 3.8 and 0.4 for hexamethonium and decamethonium bromide, respectively. The hexamethonium acetate salt has a branching ratio of 0.1. The Arrhenius activation energies for hexamethonium (Br or I) and decamethonium (Br or I) are 0.9 and 1.0 eV, respectively. This value for hexamethonium acetate is 0.6 eV. Molecular dynamics simulations and Monte Carlo conformation searching are used to obtain the lowest energy structures of hexamethonium and decamethonium bromide. These calculations indicate that the methonium ion folds around the counterion to form a cyclic salt-bridge structure in which both quaternary nitrogens interact with the oppositely charged counterion. The significantly different branching ratios observed for these ions is attributed to the large change in orientation of the counterion with respect to the ammonium centers as the number of methylene groups in these ions increases. Similar ion conformational differences appear to explain the fragmentation for the OAc counter ion as well.

1. Introduction

Diquaternary ammonium ions have been used for a variety of biochemical applications, such as herbicides (diquat, paraquat), anti-hypertensive drugs (hexamethonium), and muscle relaxants (decamethonium, succinylcholine, curare alkaloids). Mass spectrometry has been successfully applied to the characterization of such ions using a variety of desorption ionization and spray techniques [1–7]. For example, Hercules et al. [1] used laser desorption to ionize a variety of diquaternary ammonium salts. The most intense peaks were due to singly charged ions formed by deprotonation or demethylation of one of the ammonium centers. A variety of fragments formed by substitution reactions initiated by the counterion were also observed. Aubagnac et al. [2] compared fast atom bombardment (FAB) and electrospray ionization (ESI) spectra of (C₂H₅)(CH₃)₂N⁺ –(CH₂)_n–⁺ N(CH₃)₂(C₂H₅)·X⁻(n = 3, 6; X = Br, I). These techniques produced primarily singly charged ions corresponding to (M²⁺·X⁻)⁺ and fragment ions resulting from a variety of substitution pathways corresponding to counterion attack at carbons adjacent to the quaternary ammonium group, and at the hydrogens two methylene groups away from the nitrogen.

Diquaternary ammonium ions also provide an excellent opportunity to investigate the role of intramolecular interactions between charges [3,4]. Cooks et al. [3] measured secondary ion mass spectra of a variety of diquaternary ammonium ions and found that dications were only observed when the intercharge separation was greater than ~9 Å. The lack of intact dications in species with smaller intercharge separation was attributed to increased Coulomb repulsion resulting in dissociation of these ions. The dissociation of doubly charged methonium ions (n = 2–7, 9, 12) has been studied by Fales and Zhang [4] who found that the predominant fragments correspond to homolytic bond cleavage forming two radical cations, trimethylamine and the complementary (M-59)⁺, as well as a hydrogen rearrangement with the loss of a trimethylammonium ion and (CH₃)₂N = CH₂⁺. The effect of voltage offset of the collision cell on the abundance of these product ions was also investigated.

Eyler et al. [5] recently reported the use of ESI with Fourier transform mass spectrometry (FTMS) [8] to study the dissociation and reactivity of doubly charged pyridinium cations. For these experiments, FTMS has the advantage of long ion storage times and extensive capabilities for tandem MS and MSⁿ. Numerous dissociation methods have been combined with FTMS including collisionally activated dissociation (CAD) [9,10], sustained off-resonance irradiation (SORI) CAD [11,12], multiple excitation collisional activation (MECA) [13], photodissociation with both IR [14,15] and UV [16,17] photons, and surface-induced dissociation (SID) [18,19]. More recently, it has been demonstrated that ions can be made to dissociate in an FTMS cell at pressures below 10⁻⁸ Torr by absorption of blackbody photons generated by the chamber walls [20–24]. From the temperature dependence of the unimolecular rate constants for dissociation, activation energies in the zero-pressure limit can be obtained. McMahon et al. [21] found that weakly bound cluster ions, [(CH₃)₂CO]·Cl⁻, (C₆H₆)·Cl⁻, and (CH₃OCH₃)_n·H₃O⁺ (n = 2, 3), undergo dissociation near room temperature. Price et al. [23] demonstrated that biomolecule ions as large as ubiquitin formed by ESI could be readily dissociated at elevated chamber wall temperatures. Activation energies for dissociation of singly and multiply protonated peptide ions were measured. Lin and Dunbar [24] measured the activation energy for dissociation of Si(C₂H₅)₄⁺ and obtained a dissociation threshold energy using a modified Tolman equation as well as master-equation modeling [25].

We report here the use of blackbody infrared radiative dissociation (BIRD) to study the dissociation pathways of hexamethonium and decamethonium salts. Arrhenius activation energies in the zero-pressure limit are obtained. Significant differences in the lowest energy dissociation pathway for these salts are observed and are attributed to differences in ion conformation as indicated by molecular dynamics simulations and Monte Carlo conformational searching.

2. Experimental

All measurements were carried out on an external electrospray ionization source Fourier transform mass spectrometer which has been described elsewhere [26]. Ions were generated at atmospheric pressure (solution flow rate of 2.0 μl min⁻¹ to a 50 μm I.D. aluminum clad fused silica capillary biased at ~2.5 kV) and desolvated in a stainless steel capillary heated to ~175 °C. The heated capillary, first, and second skimmers were biased to approximately 50, 15, and 3 V, respectively. Ions were accelerated/decelerated electrostatically through a total of five stages of differential pumping into the ion cell, where they were collisionally trapped for 1.0 s using N₂ which was introduced through a piezoelectric pulsed valve (K.J. Lesker, and Co, Livermore, CA) to a pressure of ~2 × 10⁻⁶ Torr. After the ion collection event, a mechanical shutter was closed to prevent additional ions from reaching the cell. The trapping voltage is 4.0 V and is reduced to 1.0 V for detection. An Odyssey Data Station (FT/MS, Madison, WI) is used for data acquisition and analysis. Ions are isolated using SWIFT [27] and are excited prior to detection by a r.f. frequency sweep (120 V peak-to-peak, 3200 Hz μs⁻¹), with 256 K data points collected. The main chamber was pumped by two 1500 1 s⁻¹ cryopumps (Cryotorr 8, CTI Cryogenics, Mansfield, MA). At room temperature, the base pressure was ~1 × 10⁻⁹ Torr. This increased to ~7–10 × 10⁻⁹ Torr when the main chamber was heated to ~218 °C. The chamber is heated via a resistive heating blanket controlled to ± 0.5 °C by a proportional temperature controller (model 4002A, Omega, Stamford, CT). The temperature of the chamber was monitored by a J-type (iron-constantan) thermocouple mounted between the heating blanket and the vacuum chamber. The response of this thermocouple and of a T-type (copper-constantan) thermocouple, mounted inside the vacuum chamber adjacent to the cell, was calibrated to that of a thermocouple temporarily mounted in the center of the cell. The temperatures reported in these experiments are from measurements of the chamber wall temperature that are corrected to the temperature inside the cell. This correction has a negligible effect (<3%) on the reported activation energies.

The doubly charged hexamethonium and decamethonium ions were dissociated with SORI–CAD [11,12], using an excitation frequency 4994 and 3056 Hz higher than the cyclotron frequency of these ions, respectively, applied for 0.5 s. The cell pressure was increased to 1 × 10⁻⁶ Torr with N₂ introduced through a pulsed valve during and for 0.5 s after the excitation. Fragment ions were excited and detected following a further 1 s delay. The maximum energy to which the ions were excited was varied by changing the attenuation of the off-resonance excitation, in steps of 0.5 dB, over the appropriate range to give from zero to complete dissociation of the ¹²C isotope of the parent ion.

Hexamethonium bromide and decamethonium bromide were obtained from Sigma Chemical Co. (St. Louis, MO). Both species were electrosprayed from methanol at a concentration of 5 × 10⁻⁵ M. The corresponding iodide and acetate salts were produced by a 10% dilution (by volume) of the bromide solution with 1 × 10⁻³ M KI (in 10% H₂O/90% methanol) or KOAc (in 20% H₂O/80% methanol), respectively.

Molecular modeling was carried out with macro model (version 4.5, Columbia University, Department of Chemistry). A low energy conformation of the bromide and the acetate salt was obtained by a total of 1.2 ns of dynamics simulations (1.0 fs step size) at 300 K, with the geometry minimized to convergence at 0 K after every 10 ps. A conformation search using the AMBER forcefield was then carried out. The starting geometry for this search was obtained from the minimized (0 K) geometry obtained from the dynamics simulation. All structures within 3 kcal mol⁻¹ of the lowest energy structure found were retained from a sampling of 5000 structures, obtained by randomly changing a torsion angle in the starting geometry and minimizing the resulting structure to convergence. Structures are collected into groups of similar conformations using the MCCLUS algorithm [28]. In addition, the vibrational frequencies of the lowest energy conformations are calculated in order to confirm that the lowest energy structures are at a minimum on the potential energy surface (i.e. that all vibrational frequencies are real), and for calculating the truncated Boltzmann distribution.

3. Results and discussion

3.1. Ion formation

Electrospray ionization of the methonium ion salts, (CH₃)₃N⁺–(CH₂)_n–⁺N(CH₃)₃·X⁻, (n = 6, 10; X = Br, I) produces both the singly charged salt, (M²⁺·X⁻)⁺, and the doubly charged ion, M²⁺. The relative intensities of the singly and doubly charged ions differ dramatically with solution and instrumental conditions, with the ratio of doubly to singly charged ions varying from ~10–0.1. Afew characteristic fragment ions corresponding primarily to loss of N(CH₃)₃ or CH₃X from (M²⁺·X⁻)⁺ are observed in low abundance. The extent of fragmentation relative to the precursor does not change significantly over the range of capillary-skimmer voltages typically used. This indicates that some of these smaller ions exist in solution and are not formed exclusively by collisional activation in the electro-spray source.

The counterion in the methonium salts was replaced in solution by the addition of iodide (I⁻) or acetate (OAc⁻) in the form of a potassium salt. For hexamethonium ion, this resulted in almost complete conversion to the iodide salt and ~30% conversion to the acetate salt, respectively. For the decamethonium ion, nearly complete conversion to the iodide salt was observed, but a negligible quantity of the OAc salt ( < 5%) was formed. The relative affinities of the methonium ions for the counterions reflects the nucleophilicities of these counterions [2].

3.2. Fragmentation pathways

With the chamber temperature at 30 °C, no dissociation of isolated (M²⁺·X⁻)⁺ ions occurs with storage times up to 120 s. This indicates that insufficient energy is imparted to the ions in the electrospray interface or ion injection system to induce dissociation. At chamber temperatures above 150 °C, dissociation begins to occur on this time frame indicating that ions absorb energy from the chamber walls. At pressures below 10⁻⁸ Torr, at which all of these experiments are performed, energy is transferred to the ions through the absorption of blackbody photons produced by the chamber walls [20–25].

Dissociation spectra for hexamethonium bromide at a cell temperature of 229 °C are shown in Fig. 1 for delay times of 10 and 45 s. The fragmentation pathways are given in Scheme 1. The predominant fragment ion (~79%) is formed by Br⁻ attack at the methylene carbon adjacent to the quaternary nitrogen, with subsequent loss of trimethylamine, N(CH₃)₃, to give species II (Scheme 1, reaction a). A lower intensity fragment ion is observed which corresponds to attack of the counterion on the methyl group of the quaternary nitrogen, resulting in loss of CH₃Br, to give species III (reaction b). A second low intensity fragment, corresponding to cyclization of III with subsequent loss of trimethylamine to give species IV, is also observed (reaction c) [4]. From the early times shown in the breakdown curve for this ion (Fig. 2), it is apparent that species IV is formed from III rather than directly from the molecular ion. SORI–CAD of III resulted in exclusive formation of IV, consistent with the scheme shown. The branching ratio of reaction a to b, taking into account reaction c, is 3.8. For the I⁻ salt, the same fragmentation pathways are observed, with a branching ratio of 4.0. For hexamethonium acetate, loss of CH₃OAc via reaction b is the predominant pathway (90%) with loss of trimethylamine (reaction a) a minor process (10%) resulting in a branching ratio of 0.11.

Fig. 1.

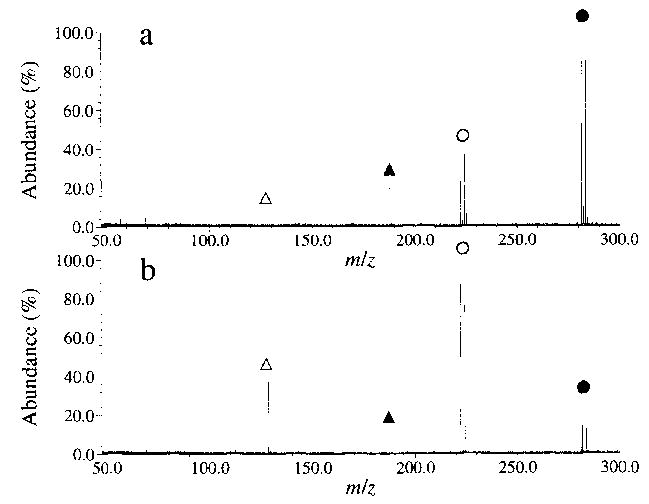
BIRD spectra of hexamethonium bromide (M²⁺·Br⁻)⁺ at a chamber temperature of 229 °C, with delay times of (a) 10 s and (b) 45 s. The isolated (M²⁺·Br⁻)⁺ ion (•) dissociates as shown in Scheme 1, to give species II (○) and species III (▴), which subsequently dissociates to give species IV (▵).

Scheme 1.

Fig. 2.

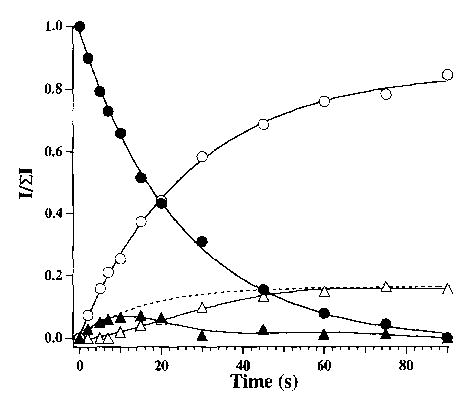
Breakdown curve for the dissociation of hexamethonium bromide (M²⁺·Br⁻)⁺ (•) at 229 °C. The major fragment arises from loss of trimethylamine ((○), Scheme 1, species II). The dashed line is the sum of the intensities of species III (▴) and IV (▵).

Decamethonium bromide dissociates by both pathways a and b (Fig. 3), but the branching ratio is remarkably different from that of hexamethonium bromide. Dissociation by reaction a is the minor process (29%) whereas reaction b accounts for 71% of the product ion signal, giving a branching ratio of 0.4. Again, species III dissociates further to form IV, but in significantly smaller quantities (<5%) (Fig. 4). The same fragmentation is observed for the I⁻ salts, with a branching ratio of 0.3.

Fig. 3.

BIRD spectra of decamethonium bromide (M²⁺·Br⁻)⁺ at a chamber temperature of 229 °C, with delay times of (a) 10 s and (b) 45 s. The isolated (M²⁺·Br⁻)⁺ ion (•) dissociates as shown in Scheme 1, to give species II (○) and species III (▴).

Fig. 4.

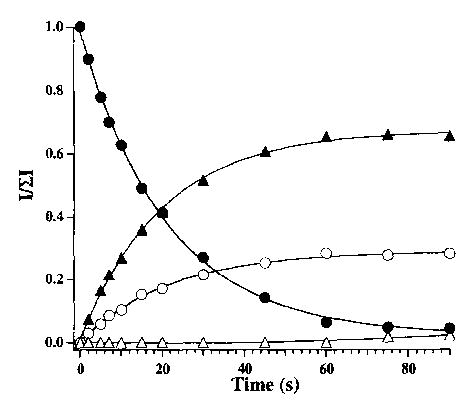
Breakdown curve for the dissociation of decamethonium bromide (M²⁺·Br⁻) ⁺ (•) at 229 °C. The major fragment arises from loss of CH₃Br ((▴), Scheme 1, species III). Minor fragments arising from loss of trimethylamine (○, species II) and subsequent dissociation of species III to species IV (▵) are also seen.

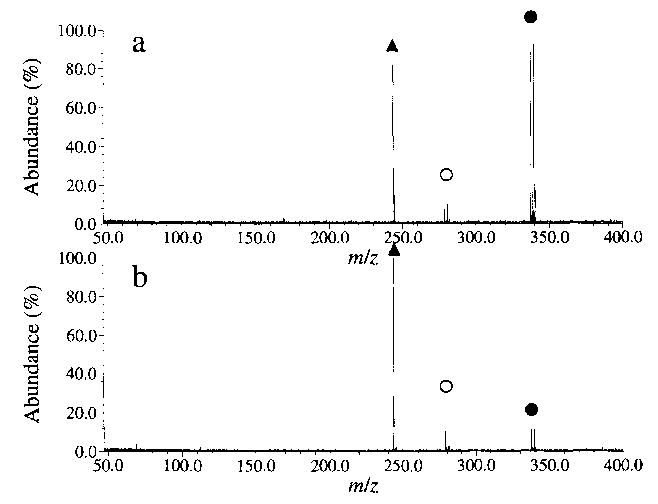
No dissociation of the doubly charged hexamethonium or decamethonium ion (M²⁺) was observed in 120 s at 229 °C, the highest temperature currently obtainable in this experiment. These ions can be readily dissociated using SORI–CAD and show remarkably different behavior (Fig. 5). The decamethonium (Fig. 5(b)) dissociates primarily through formation of two complementary even electron ions, protonated trimethylamine and species VII (45%) (Scheme 2, reaction a). Two other complementary even electron ions, species VIII and IX, are also observed (31%) (Scheme 2, reaction b). A minor dissociation channel, corresponding to homolytic bond cleavage to form the odd electron ion trimethylamine and the complementary (M-59)⁺ is observed (14%) (Scheme 2, reaction c). This fragmentation process was first reported by Fales and Zhang [4]. Ions at m/z 30, 43, 44, and 45, corresponding to CH₄N, C₂H₅N, C₂H₆N, and C₂H₇N, are observed with low intensity as well.

Fig. 5.

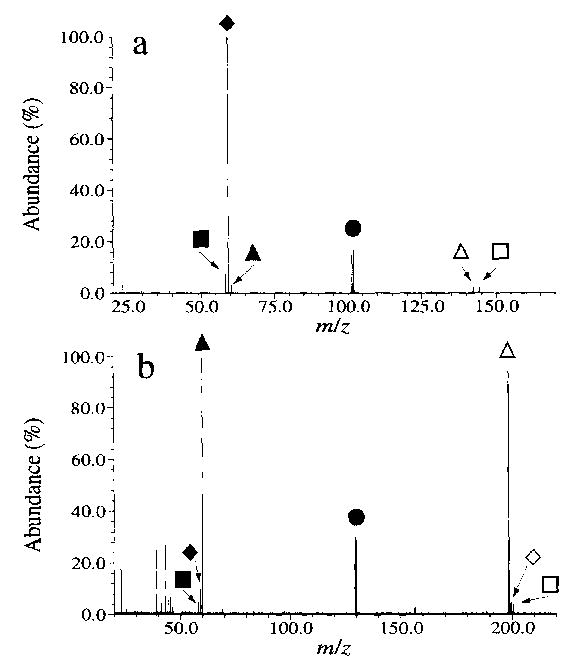
SORI–CAD spectra of dissociation of the all- ¹²C isotope of the doubly charged ions of (a) hexamethonium and (b) decamethonium. The M²⁺ ion (•) dissociates as shown in Scheme 2, to give three pairs of complementary ions, the even electron pairs VI and VII (▴ and ▵) and VIII and IX (▪ and □), as well as the odd electron pair X and XI (♦ and ⋄).

Scheme 2.

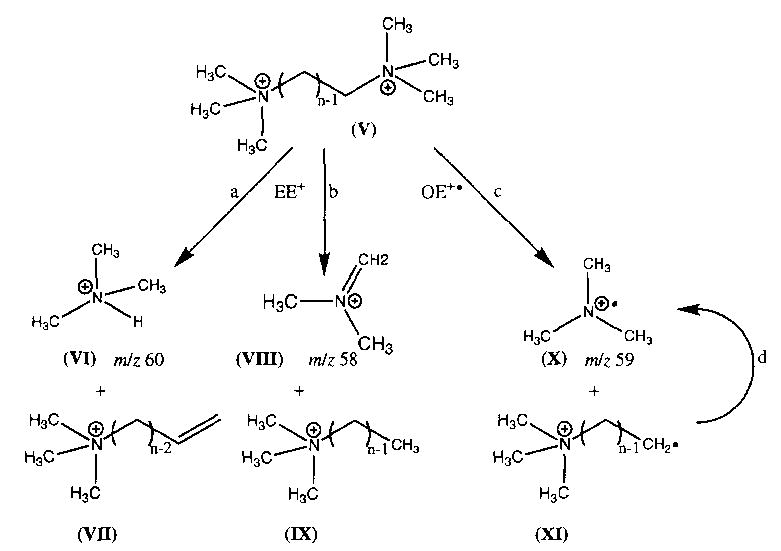
In striking contrast, the primary reaction channel for the hexamethonium is the homolytic cleavage to form species X (89%) (Fig. 5(a)). The complementary (M-59)⁺ is not observed. We attribute this to the subsequent dissociation of this ion to form species X by loss of neutral cyclohexane. Reactions to form the even electron ions via reactions a and b are minor processes (3% and 8%, respectively). Formation of odd electron ions from even electron ions is usually unfavored [29], but this process appears to be enhanced by the closer proximity of the two charges in the hexamethonium than in the decamethonium. This would be expected to lower the barrier for the homolytic bond cleavage.

3.3. Activation energies

Rate constants for the unimolecular dissociation of these ions can be obtained from a plot of ln[M²⁺·X⁻)⁺] as a function of time. Data for hexamethonium and decamethonium bromide are shown in Fig. 6. Similarly, rate constants for each of the hexamethonium and decamethonium ions were obtained and are given in Table 1. From the temperature dependence of these dissociation rate constants, the Arrhenius activation energy (E_a) in the zero-pressure limit can be obtained (Fig. 7, data for hexamethonium and decamethonium bromide ions shown). The activation energies for the dissociation of the hexamethonium and decamethonium are 0.9 and 1.0 eV, respectively; no significant difference was observed for X = Br or I. However, a significant lowering of the activation energy, from 0.9 to 0.6 eV, is observed for the OAc counterion. The fragmentation branching ratio for each precursor does not change over the temperature range studied, indicating that these reaction pathways for a given precursor have indistinguishable activation energies, but slightly different Arrhenius pre-exponential factors. No activation energies for the doubly charged ions could be obtained since these ions did not dissociate at the temperatures achievable in this experiment.

Fig. 6.

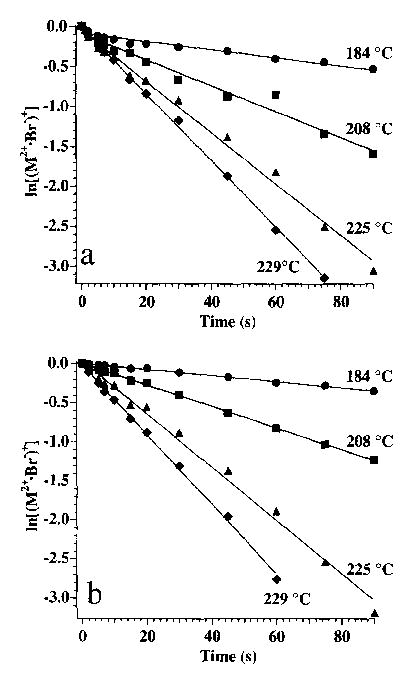
Plots of the ln[(M²⁺·Br⁻)⁺] versus time for (a) hexamethonium bromide and (b) decamethonium bromide at the cell temperatures labeled.

Table 1.

Rate constants for the unimolecular dissociation of singly charged methonium salts at various chamber wall temperatures

Counterion X	Temp. (°C)	Hexamethonium [M2+·X−]+k(T) (s−1)	Decamethonium [M2+·X−]+k(T) (s−1)
Br	229	0.042	0.045
	225	0.032	0.034
	208	0.016	0.014
	184	0.005	0.004
I	221	0.040	0.031
	206	0.019	0.015
	183	0.006	0.005
	159	0.002	0.001
OAc	206	0.11
	183	0.064
	159	0.020

Fig. 7.

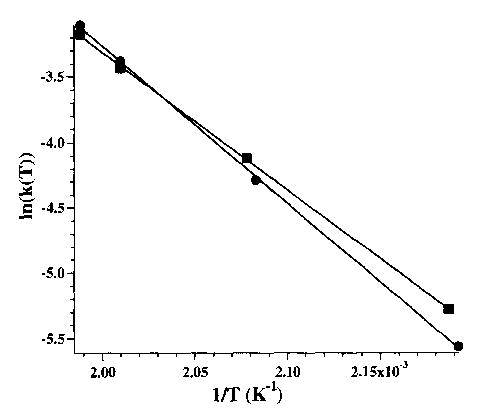
Arrhenius plots of ln(k(T)) versus 1/T for hexamethonium (▪) and decamethonium bromide (•), from which activation energies of 0.9 and 1.0 eV and pre-exponential factors of 10⁷ and 10⁹ s⁻¹, respectively, were obtained.

To relate the activation energies measured in these experiments to the activation energies in the high-pressure limit, a correction for the difference in internal energy distributions between the reactant and the transition state ions must be made. For small ions with low activation energies, the activation parameters in the zero-pressure limit are affected by the rate of ion activation, i.e. the rate of absorption of black-body photons [25]. As demonstrated by Lin and Dunbar [24], the dissociation threshold energy can be reasonably estimated using a truncated Boltzmann model. Applying this method to the dissociation of hexamethonium and decamethonium bromide ions results in precursor threshold dissociation energies of 2.0 and 2.4 eV, respectively¹. However, these ions are larger and have higher activation energies than the ions for which this treatment has been previously applied. For even moderate sized ions, e.g., proton bound dimers of N,N-dimethylacetamide, the assumptions in the truncated Boltzmann treatment begin to break down; namely, the rate of activation becomes competitive with the rate of dissociation [30]. In this situation, the truncated Boltzmann treatment will overestimate the true activation energies for these processes. Thus, accurate assessment of these activation energies requires information about the relative rates of ion activation and dissociation. Within the current uncertainty of this method, the difference in the activation energies for hexamethonium and decamethonium ions is likely to be small. However, the rate of blackbody photon absorption for hexamethonium, X = OAc, should be even higher than that of X = Br or I, due to the presence of the carbonyl group which absorbs strongly in the region of maximum blackbody radiation intensity at ~200 °C (~1 700 cm⁻¹). Thus, the lower measured E_a for this ion must reflect a lower threshold dissociation energy.

3.4. Conformation of methonium ions

The influence of the parent ion conformation on the lowest energy fragmentation pathways of the methonium ions was investigated using molecular modeling. Dynamics simulations and minimizations were done with the hexamethonium and decamethonium bromide (M²⁺·Br⁻)⁺ ions at 300 K for 1.2 ns. Structures were minimized every 10 ps. Simulations at higher temperatures resulted in separation of the bromide counterion. A linear starting geometry of these ions was used. However, both species were found to cyclize within the first 10 ps of dynamics with the Br⁻ shared between the two quaternary ammonium groups at either end of the molecule.

The dynamics simulations indicate the extent of molecular motion at 300 K. However, the lowest energy structures obtained by simulated annealing are minimized geometries at 0 K. Clearly, the ions in this experiment with the chamber at elevated temperatures have significant internal energies, so that dynamical changes in ion structure not indicated by the 0 K structures will occur [31,32]. To obtain an estimate of this motion or ion flexibility, a Monte Carlo conformation search was done. In the Monte Carlo conformation search, a torsion angle in the initial structure is randomly selected and changed. Then, the energy of the resulting structure is minimized to convergence at 0 K. This process is repeated 5 000 times, using the lowest energy structure obtained from the dynamics simulation as the initial geometry. All the resulting minimized structures which have energies within 3 kcal mol⁻¹ of the lowest energy structure found in this search are stored. The search is considered to have converged when the lowest energy conformers are found several times. For hexamethonium and decamethonium bromide, 162 and 639 structures were found, respectively. In order to simplify visualization of this large number of structures, we group them into structurally similar subsets based on the positions of the heavy atoms [28]. For hexamethonium and decamethonium bromide, there are 10 and 79 structural groups, respectively. The members of each group vary from each other predominantly by rotations about the C–N bonds. The lowest energy conformers of each group are super-imposed and shown in Figs 8 and 9, along with a space filling model of the lowest energy conformer of each ion.

Fig. 8.

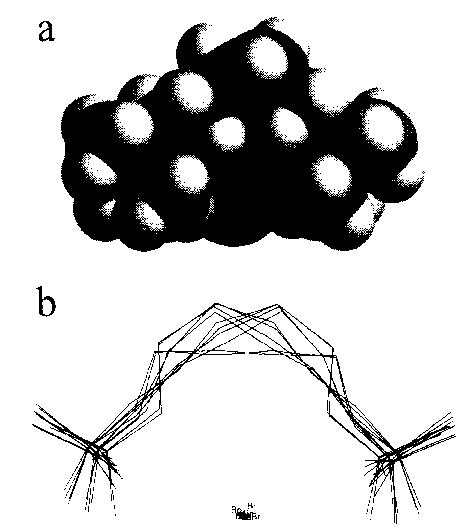
(a) Space filling representation of the lowest energy structure of hexamethonium bromide, showing the bromide ion (labeled) surrounded by the hexamethonium ion, with nitrogen, carbon, and hydrogen indicated in grayscale dark to light, respectively, (b) A stick plot of the lowest energy structures of each of the 10 groups of structures from the Monte Carlo conformational search.

Fig. 9.

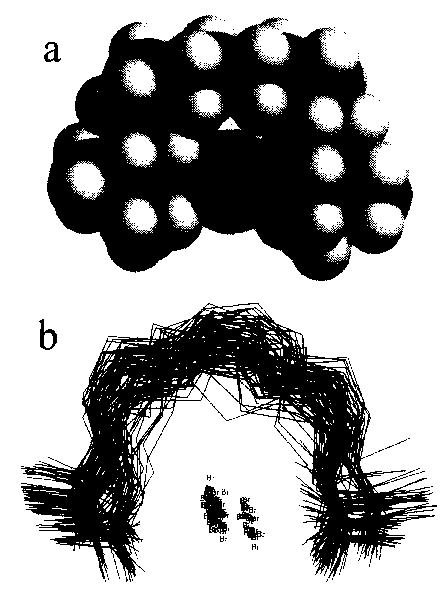
(a) Space filling representation of the lowest energy structure of decamethonium bromide, showing the bromide ion (labeled) surrounded by the decamethonium ion, with nitrogen, carbon, and hydrogen indicated in grayscale dark to light, respectively, (b) A stick plot of the lowest energy structures of each of the 79 groups of structures from the Monte Carlo conformational search.

The structures sampled in the dynamics simulations at 300 K arc all similar to those obtained in the conformation search. The majority of flexibility in these ions at higher temperatures occurs in rotations and torsions of the methylene carbons; no significant change in the interactions between the charged nitrogens and the counterion is observed. The barriers between these structures should be relatively low. Thus, the structures obtained from the conformation search should be representative of the ion structures at the temperatures in these experiments.

These calculations consistently indicate that a linear geometry in which the counterion is associated with one, not both, of the quaternary nitrogens is significantly less stable than the cyclic structure. In order to obtain an estimate of the relative energies of these conformations, the geometry of the doubly charged M²⁺ ion was minimized, resulting in an elongated all-trans structure. The counterion was added and its interaction with the charged quaternary ammonium sites was minimized, keeping the position of all other atoms fixed. The resulting elongated structures are higher in energy than their cyclic counterparts by 45 and 46 kcal mol⁻¹ for the hexamethonium and decamethonium bromide ions, respectively. These values include effects of non-ideal bond lengths of the methylene carbons in the elongated conformers, since these were minimized with charges present on both ends of the molecule. We estimate that this will result in a maximum increase in energy of 37.4 and 23.8 kcal mol⁻¹¹, the approximate Coulomb energy in the M²⁺ hexamethonium and decamethonium ions, respectively [33]. Thus, the cyclic structures are a minimum of ~8 kcal mol⁻¹ more stable than their linear counterparts, and should be the predominant form of these ions under the conditions of this experiment.

Although both the hexamethonium and decamethonium bromide ions fold around the charged counterion, the different number of methylene groups in these ions results in a significantly different orientation of the nitrogen and adjacent carbons with the Br counterion. The average included angle from N–Br–N is 131 ± 4° and 173 ± 5° for hexamethonium and decamethonium bromide, respectively. A nearly linear N–Br–N geometry should optimize the electrostatic interactions and be more favored. This occurs for the decamethonium ion, even though the carbon chain is longer than necessary to achieve this (Fig. 9(a)). The hexamethonium ion is insufficiently long to assume this geometry (Fig. 8(a)).

Substitution reactions occur via “backside attack” by the nucleophile at the reaction center, with a collinear transition state favored [34]. The Br–C–N angles (where C is the adjacent methylene or a methyl carbon) in the lowest energy structures of the hexamethonium and decamethonium ions are approximately equivalent, and are all geometrically unfavorable for substitution reactions. The Br–CH₂–N angle is ~88°. For two of the three methyl groups, this angle is ~83°; the third methyl group is on the opposite side of the nitrogen. Thus, these groups are not favorably oriented for the observed SN₂ reactions, nor can the dramatic differences in branching ratios be explained based on differences in the Br–C–N angles in the lowest energy geometries of these ions.

The difference in branching ratios for these ions is attributable to two factors. The decamethonium is sufficiently long that it can assume a roughly linear Br–CH₃–N geometry while maintaining a favorable N–Br–N orientation. This would favor the loss of CH₃Br which is the major dissociation channel observed for this ion. Although a linear geometry is possible, it should be noted that the most favored transition state geometry may in fact not be linear due to the presence of the extra charge. A similar conformation is not possible for the hexamethonium ion due to its shorter chain length. However, the distance between the Br and the methylene carbon is ~0.2 Å shorter than that between the Br and the nearest methyl carbon in the hexamethonium ion. This difference is only ~0.1 Å in the decamethonium ion. Because the hexamethonium ion cannot orient favorably for substitution reactions, the closer proximity of the Br to the methylene carbon could enhance reactions at this site, resulting in the observed formation of trimethylamine from this ion.

Similar calculations were carried out on the acetate (M²⁺·OAc⁻)⁺ ions. As with the hexamethonium bromide, the acetate salt cyclizes within the first 10 ps of a 1.2 ns dynamics simulation (300 K), and all structures sampled subsequently are cyclic. Monte Carlo conformation searching resulted in 552 structures within 3 kcal mol⁻¹ of the lowest energy structure. These structures cluster into only three groups (Fig. 10). In each of these groups of structures, the two equivalent oxygens each point toward a quaternary nitrogen. The primary dissociation pathway of this ion results from attack by OAc– on a methyl group, with loss of CH₃OAc. This counterion has two oxygens which share the negative charge. The observed fragmentation could be due to a reorientation of the counterion, with one oxygen remaining between the quaternary nitrogens and the other oxygen dropping below this N–O_a–N forming the nearly linear O_b–CH₃–N orientation favored for loss of CH₃OAc.

Fig. 10.

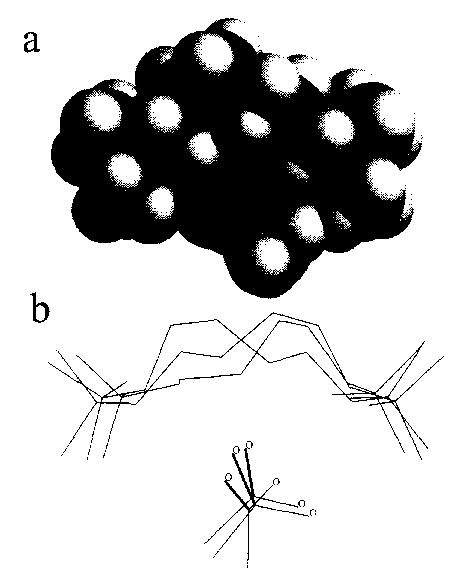
(a) Space filling representation of the lowest energy structure of hexamethonium acetate, showing the acetate ion (labeled) surrounded by the hexamethonium ion, with nitrogen, oxygen, carbon, and hydrogen indicated in grayscale dark to light, respectively, (b) A stick plot of the lowest energy structures of each of the three groups of structures from the Monte Carlo conformational search.

4. Conclusions

Evidence for the effects of ion conformation on the observed fragmentation of methonium ion salts is presented. Calculations indicate that the methonium ions fold around the counterion forming a salt-bridge structure in which both charged nitrogens interact with the oppositely charged counterion. Changing the number of methylene groups between the quaternary ammonium centers from 6 to 10 has a pronounced effect on the geometry of the charge sites relative to the counterion. The dramatic differences in branching ratios observed for the dissociation of these ions is rationalized based on the difference in the orientation of the counterions with respect to the leaving groups. Arrhenius activation energies for these reactions in the zero-pressure limit are measured. The doubly charged ions are thermally more stable than the singly charged salts, and cannot be dissociated by BIRD at temperatures currently obtainable. SORI–CAD of these doubly charged ions shows dramatic differences in the branching ratios for fragmentation. The hexamethonium ion dissociates primarily by homolytic bond cleavage to form two complementary odd electron ions, as opposed to the hydrogen rearrangements primarily observed in the decamethonium ion. This is consistent with the greater Coulomb energy in the hexamethonium ion which lowers the activation barrier for direct bond cleavage. With higher chamber temperatures, it should be possible to measure the activation energies of doubly charged methonium ions as a function of increasing ion size. This would make possible a direct measurement of the effects of Coulomb repulsion on lowering the bond dissociation energy on these ions.