A computerized model for the self—non-self discrimination at the level of the T_h (Th genesis). I. The origin of ‘primer’ effector T_h cells

Abstract

The ability of the immune system to respond by ridding a pathogen without debilitating the host depends upon the ability of the effector T_h (eT_h) to make a discrimination between ‘self’ and ‘nonself’ antigens. This ability is somatically learned and involves The sorting of The somatically generated random repertoire of initial state T_h (iT_h) into two classes of specificity: one, anti-self, the functional expression of which must be inactivated; The other, anti-non-self, the functional expression of which must be activated. We propose a model for The origin of a sufficiency of eT_h anti-non-self and an insufficiency of eT_h anti-self based on two postulates. (i) An antigenindependent pathway to a priming level of eT_h anti-non-self under conditions where iT_h anti-self are effectively deleted by interaction with self. This state is established during a window of fetal development and maintained throughout life because self is persistent. (ii) Associative recognition of antigen (peptide-MHC class II) on an antigen-presenting cell between iT_h and ‘primer’ eT_h that results in The rapid induction of an effective level of helper activity to non-self antigen. A computer simulation is provided that enables evaluation of this model.

Introduction

The vertebrate immune system is a biodestructive ridding mechanism for The elimination of pathogens. The immune system is unique in That The antigen-specific receptors are generated at random by a somatic diversification process. Whether by somatic mutation, gene conversion, gene rearrangement or The combinatorial complementation of subunits, the somatic diversification of a few germline gene segments results in many new specificities, some of which recognize components of The host. When recognition leads to The biodestructive elimination of host components, the results are deleterious. Thus, the immune system requires a regulatory apparatus that is able to uncouple The immediate consequences of The recognition of antigen from The subsequent biodestructive ridding responses. The mechanism that allows The repertoire of randomly generated specificities to be sorted into Those that will not become biodestructive effectors and those that will is generally termed The self—non-self discrimination.

Several mechanisms for The self—non-self discrimination have been proposed over The years, many of which were discussed in a recent publication (1). As a result of this exchange of views we were prompted to develop a simulation tool that would allow an unbiased analysis of The common kinetic processes required by these postulated sorting mechanisms.

This first of two papers aims to illustrate The simulation tool that is computer based and is available via an interactive Internet server (http://www.cig.salk.edu, click on Th genesis). Here we provide The outline of the Theoretical foundation leaving a full description of The mathematics and simulation methods as part of our Internet server link.

All models of The self—non-self discrimination require a mechanism for the sorting of the somatically generated random repertoire that is based on distinguishing the ‘self’ and ‘non-self’ classes of antigen. In the end, this sorting mechanism is the responsibility of the T_h cell that must learn which antigens are self and which are non-self. Upon encountering antigen, the T_h cell must decide if it will proceed down one or another pathway of differentiation. One pathway leads to the inactivation of that cell, the other pathway leads to its activation and the subsequent expression of effector function (eT_h). However, no sorting mechanism can be ‘perfect’ and the sorting mechanism of the self—non-self discrimination has to have a failure rate such that some individuals die, either because they fail to rid a non-self antigen (e.g. a pathogen) or because they in fact rid a self antigen. Evolution then selects on the failure rate such that the probability of a mutation lowering the failure rate is selectable above the combined probabilities of the individual being eliminated by some other pathway (e.g. the failure to run faster than a predator). Our goal when developing this simulation tool was to give quantitative precision to the key steps required by any internally coherent mechanism for the sorting of paratopes. These variables can then be evaluated for experimental reasonableness.

In order to use a random paratopic repertoire to identify nonself antigens in a pool of self antigens, the paratopes have to be sorted according to some property that enables them to distinguish these two classes of antigens. We recall that we are discussing the ‘adaptive’, not the ‘innate’ immune system. The sorting of a somatically generated and selected paratopic repertoire requires a somatic selection mechanism that must be based on the behavior, not some physico-chemical property of antigens as classes.

Conceptual framework

A somatically selected self—non-self discrimination is simply one that acts to sort a large and random repertoire of somatically generated paratopes. The simulation tool that we have developed is designed to investigate the combined effects of the various sources of error in sorting systems that make a self—non-self discrimination. While the simulation tool can be adapted to all of the presently proposed models, we have been encouraged by the reviewers to present this revised version in which we concentrate on our Minimal Model (2). We will deal with ‘other views’ in a second paper (Langman, R. E., Mata, J. J. and Cohn, M., in preparation).

The Minimal Model treats ‘self’ and ‘non-self’ as being indistinguishable except for their behaviors. It is assumed that the behavior which is unique to self antigens is their constant presence, whereas the unique behavior of non-self antigens is their variable presence. In principle, the immune system had two choices, either to remember the antigens that are always present or to remember the antigens that are always absent. While the idea of remembering constantly present or persistent antigens seems intuitively easy and attractive, it turns out that the minimal condition is that the immune system must remember the antigens that have been absent—no memory being needed for persistent antigens. The repository for this memory of unseen or absent antigens is the eT_h cell anti-nonself.

Under the Minimal Model, all T and B cells are ‘born’ with an antigen receptor of a single random specificity. The cells are in a decision or i-state (initial state) of differentiation that is incapable of expressing effector function. The usual way for istate cells to become e-state effectors is for their receptors to first bind antigen and then be informed by eT_h cells whether that particular antigen is non-self. This eT_h cell passes on its information via an antigen-specific link to i-state cells, which then utilize this information and differentiate to the e-state. In the absence of such information (i.e. the absence of eT_h cells with specificity for a persistent self antigen), these i-state cells having bound antigen then proceed to death. Of course, since the informative T_h cells are effectors (eT_h), the next step is to determine where these ‘primer’ eT_h cells come from. This is a non-trivial problem, given that the model at this stage requires eT_h in order to convert iT_h that have bound ligand into new eT_h. The solution to this conundrum depends on the postulate that an antigen-independent pathway exists uniquely for the conversion of iT_h to eT_h. This pathway operates in the extended absence of antigenic encounter, thereby ensuring that only eT_h specific for non-self accumulate as primer. The sorting process is initiated during an embryonic window when the immune system arises in the presence of all self antigens, no non-self antigens and no eT_h. Once initiated, the window closes and the continued presence of self antigens maintains the insufficiency of eT_h anti-self while allowing a priming level of eT_h anti-non-self to arise in the absence of non-self. The immune system is responsive when a priming repertoire of eT_h anti-non-self is established.

These steps can be formulated as a series of rate equations where the rate constants are chosen to be both biologically reasonable and consistent with the requirements of the Minimal Model. Finding solutions to these equations is not difficult and we have programmed one of our web-based servers to find solutions in response to a straightforward set of questions. Indeed we encourage any interested reader to log on to the website (http://www.cig.salk.edu, click on Th genesis) and test it out. The only part of the mathematics and computerese we need to deal with here is how the rate equations are set up.

The Minimal Model in terms of the simulation tool

The T_h cells uses an antigen receptor (TCR), which identifies peptides bound to MHC class II molecules expressed on the surface of the antigen-presenting cells (APC). Under the Minimal Model, interaction between antigen and an iT_h cell results in its being converted into an anticipatory a-state (i.e. antigen delivers Signal[1] that drives the iT_h to become an aT_h). Cells in the a-state await information (i.e. Signal[2]) from the eT_h. If Signal[2] fails to arrive in a given time, then the aT_h cell dies. Only if Signal[2] arrives before that time limit is reached does the aT_h become an eT_h cell. Thus, only iT_h that do not have specificity for self peptides and, therefore, do not encounter antigen can, after a sufficient period of waiting, progress to become eT_h in what we term an antigenindependent step. The result is a series of timed steps that can be converted into rates, which are then used to compute the consequences of choosing various parameters that control these rates.

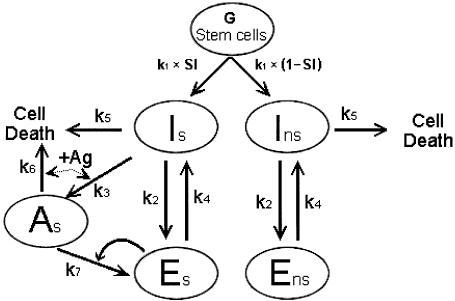
Referring to Fig. 1, the symbols we chose for simplicity in these equations are I for the number of iT_h, A for the number of aT_h and E for the number of eT_h cells. The secondary symbols ‘s’ and ‘ns’ denote the specificities of the various cells with respect to self and non-self respectively. Thus we can write:

1. k₃ as the rate constant for iT_h + Ag → aTh or I_s + Ag → A_s

2. k₂ as the rate constant for iT_h → eT_h or I_s → E_s and I_ns →E_ns

3. k₆ as the rate constant for aT_h + Ag → death or A_s + Ag → death (the antigen in this case is self)

4. k₇ as the rate constant for aT_h, eT_h/Ag > eT_h, where eT_h anti-non-self delivers Signal[2] via associated recognition of antigen (we refer to this as the ‘autocatalytic’ step)

Fig. 1.

The pathway (Th genesis) generating ‘primer’ effector T_h (see text).

Coupled with the turnover rate constant k₅, as well as the rate constant (k₄) for reversion from E to I, these rates of reactions cover the key regulatory events needed to make a self—non-self discrimination.

Since There are no non-self antigens present at the stages of ontogeny that occur under maternal immune protection, there can be no A_ns, although the antigen-independent pathway does allow E_ns to eventually appear. Overall, we assume homeostasis of the number of total cells per milliliter so that the rate of T_h genesis at the level of iT_h is exactly equal to the combined rates of death of all cells from all causes.

These relationships are illustrated in Fig. 1, which also shows the various rate constants that govern each conversion in the state of the cells. Briefly, a pool of precursors (G) generates I cells at k₁G cells per hour. They are split into the anti-self (I_s) and anti-non-self (I_ns) pathways according to the value SI (specificity index), which is simply the proportion of anti-self in the repertoire. Thus k₁G × SI is the number of cells per hour that become I_s and k₁G × (1 - SI) is the number per hour that become I_ns. Then, governed by rate constant k₂, I cells, whether I_s or I_ns, are converted to E_s and E_ns cells respectively as required under the rules of the antigenindependent pathway. In the case of I_s cells, interaction with self antigen drives them to A_s at a rate k₃. Cells in the a-state cannot enter the antigen-independent pathway, only i-state cells can do this. Cells in the a-state require interaction with eT_h (delivery of Signal[2]) to proceed down the pathway to effectors. The E_s and E_ns can revert to the I_s and I_ns states respectively at a rate k₄. I_s and I_ns cells die at a rate k₅ that maintains homeostasis, and A_s cells die at a rate k₆ if they fail to receive Signal[2]. We will deal in a second paper (3) with the ‘autocatalytic’ antigen-driven conversion of aT_h to eT_h by ‘primer’ eT_h shown in Fig. 1 (The k₇ step). Here, we consider the state of the system before encounter with non-self antigen. As a consequence, we will use an approximation to establish the limit conditions for permissible levels of E_s and E_ns.

What Is the SI, why Is it essential and what values can it take?

Given that the paratopic repertoire of T cells Is random with respect to the antigens that are recognized, it follows that in practice some will be anti-self while others are anti-non-self. The goal of the sorting mechanism that we are simulating Is to minimize the number of E_s (because these have the potential to kill the host) and maximize the number of E_ns (because these are required to rid the pathogen). Our simulation is based on real numbers of cells in each compartment and this makes it necessary to determine the actual numbers of anti-self and anti-non-self cells that are present in the population before sorting. Our choices for the values for the rate constants have to be such that we have an effective sorting mechanism. The SI is a definition of the relative numbers of T cells that enter the sorting pathway as anti-self and anti-nonself. SI is defined as the proportion of anti-self in the total repertoire (i.e. anti-self + anti-non-self) and can take values in The range from 1 to near 0 (in principle the smallest value of SI would be 1/repertoire when there is only one anti-self in the total repertoire).

Since we are dealing with the genesis of T_h cells, there has to be a source of iT_h that enter the sorting system after having passed through positive selection as well as a certain amount of negative selection in the thymus. Without having to specify just how much the antigen-specific repertoire has been selected intrathymically we can use SI as a parameter that is independent of the size of the repertoire. The value of SIthat is chosen is a variable that has to be determined by a meld of trial and error plus a measure of common sense. In other words, the value chosen for SI establishes the magnitude of the sorting problem; if, for example, SI = 0.5, then half of the repertoire is anti-self and the magnitude of the sorting problem is large, whereas if SI = 0.0001, then there would be only one anti-self in 10,000 receptors and the sorting problem would be small. The value of SI is a measure of the uniqueness of an antigen in the context of a random paratopic repertoire. Whether the size of the repertoire is such that it divides the antigenic universe into 10⁴ or 10⁸ slices, the value of SIwould be a constant because it measures the relative ratios of the two classes of antigen, self and non-self.

Based on our previous analysis of specificity in T and B cells (4-6), we estimate the value of SI to be 0.01 (i.e. <0.1 and >0.001). However, the simulation tool will accept any value between 0 and 1 chosen by the user.

The principle of a modular T-Protecton is needed

We recall that the B-Protecton arose from our realization that the immune system must have evolved as a modular structure. The ‘B-Protecton’ is defined as the minimum sized sample of B cells from an individual that would have all of the protective properties of the whole (3,4). The Protecton allowed us to resolve the paradox that, as individuals, a mouse with 10⁸ B cells is as well-protected as a human with 10¹² B cells. This means that a human is no different from a pool of B cells made from 10⁴ mice. Our best estimate for the size of the B-Protecton is ∼10⁷ total B cells; meaning that, as an order of magnitude, a mouse has 10 Protectons and a human 10⁵ Protectons.

The concept of a Protecton must also apply to the T cell compartment and we use the symbols T_t and T_b to denote the total number of cells in one T- or B-Protecton respectively. In the case of B cells, their secreted antibodies function concentration dependent and it is relatively straightforward to calculate the structure of the B-Protecton. While T cells must also show a density- or concentration-dependent behavior, the relationship between concentration and function is less well characterized.

While we have at present no way to independently calculate the value of T_t, it seems on a priori grounds that this should not be very different from T_b. It is reasonable, however, to estimate the upper limit to the size of a Protecton at ∼10⁷ cells on the grounds that this is the total number of lymphocytes in the smallest animals with functional immune systems (e.g. the pygmy shrew and humming bird). The tadpole does have an immune system with ∼10⁶ total cells, but it is not clear that this is > 10% effective in protecting the tadpole during its rather short period of developmental existence. Therefore, as an initial guess we started with T_t = 10⁷, keeping in mind that we could always check the effects of different values of T_t in the simulation tool.

Choosing an initial set of rate constants, k₂, k₃, k₄, k₅ and k₆

Starting with a value for k₅ we appreciated that the half-life of an iT_h must be long enough to have a good chance of its being properly sorted and stably functional. A value of 10 h for the half-life seemed too short when we thought about the time (value of k₅) needed to control the antigen-independent generation of eT_h, so we started with k₅ expressed as t_1/2 = 100 h and found after several simulations an optimized value of k₅ expressed as t_1/2 = 128 h. with the slowest rate constant k₅ set at around t_1/2 = 100-150 h we then looked at the fastest rate constant, i.e. k₃, which is the rate of conversion of iT_h to aT_h in the presence of antigen and found that a half-life of 1 h seemed to be of the right order. The remaining rate constants were arrived at by running a range of values for each in the simulator, and selecting for those that optimized the criteria of having few eT_h anti-self (i.e. E_s) and sufficient eT_h anti-non-self (i.e. E_ns).

We arrived at the following rate constants, expressed for convenience in terms of half-lives in hours: k₂ = 40, k₃ = 1, k₄ = 12, k₅ = 128 and k₆ = 5. We recall that k = 0.693/t_1/2.

Homeostasis is a required assumption

T cells are produced throughout the life of the individual. Thus, there must be a homeostatic control of the number of T cells per gram or per milliliter of animal. From this it follows that the input number of T cells must equal the output. The rate constant k₁ deals with the input of I cells and k₅ deals with the predominant output pathway of I cells with a minor output via k₆. Under conditions of homeostasis we need to assign values to either k₅ and k₆, or k₁—not both. The small additional effect of k₆ makes it easier to assign k₅ and k₆, which then sets the value of k₁. Figure 1 also illustrates that if k₅ is set to zero, then the only pathway for I cells to leave is via k₃ and then k₆. If the half-life of I cell turnover is set at 128 h (i.e. k₅ = 5.42 × 10^-3), then the corresponding thymic output computes to be 10⁶ iT_h per day per T-Protecton or 10⁷ iT_h per day per mouse. We use the notation G to symbolize the concentration of precursor iT_h cells so that k₁G gives the number of iT_h per hour, after positive selection, that enters the pool of cells that follows the various pathways indicated in Fig. 1. These inputs and outputs are independent of the actual number of cells in the total measurable pool of I, A and E cells which is set to a total T_t.

What exactly is being simulated?

At this point we have a system of equations and a starting set of values for the variables. However, the results consist of steady-state numbers of all the various cell types and in most cases these are not the kinds of numbers that can be presently measured experimentally. What we would really like to know is whether these numbers are compatible with a protective immune response to non-self antigen without anti-self debilitating the host. While it is evident that at least one E_ns per T-Protecton is required, it is not obvious how many I_ns would be needed to ensure the initiation of a protective response, and the best that can be said about the E_s and I_s populations is that they have to be acceptably small, and certainly less than the E_ns and I_ns populations.

The data in Table 1 are taken directly from the raw numbers obtained from the Internet interface (www.cig.salk.edu, click on Th genesis) and are based on a set of values for the rate constants that we regard as near optimal.

Table 1.

Assigning values to the parameters of Th genesis: the reference Protecton

	Is	Es	As	Ins	Ens	Thymic output
						(k1G per hour)
Cells per T-Protecton (Tt)	603	181	3015	7689386	2306816	42113
Cells per epitope per Tt (Ct)	0.60	0.18	3.0	77.7	23.3

The values of the rate constants were: k₂ = 0.017325 (40 h), k₃ = 0.693 (1 h), k₄ = 0.05775 (12 h), k₅ = 0.005422 (128 h) and k₆ = 0.1386 (5 h), where the times in parenThesis are the half-lives, and k = 0.693/t_1/2; SI = 0.01, T_t = 10⁷,R_t = 10₅ (R_t is the size of the repertoire, see later).The numbers of self and non-self epitopes are calculated As follows: total self epitopes = SI × R_t = 10³, total non-self epitopes = (1 - SI)× R_t = 9.9 × 10⁴. the half-life of the T-Protecton turnover when the rate of input of T cells (k₁ × G) is 42113 computes to be 164 h or 6.8 days (42113 × 10^-7 = 1 - e^-k; k= 0.00422, t_1/2 = 164 h).

The values in Table 1 are artificially significant but they are given in order to show the exact numbers as they appear in the simulator on the Internet server. The calculated values for the actual number of E_s per self epitope per T-Protecton and E_ns per non-self epitope per T-Protecton show a 130-fold difference between the two. While this seems intuitively satisfying, we found ourselves in need of a new parameter that gives a more realistic dimension to the system.

A new parameter, the Priming Inductive Event (PIE)

We calculate the probability of a PIE. PIE is the probability that an E_s and A_s cell will associatively recognize antigen (peptide) in a priming inductive event, the consequence of which is that the A_s becomes an E_s. This initial A—E interaction is an essential component of associative recognition of antigen which requires that only A and E cells specific for the same antigen be allowed to productively interact. For the purposes of this simulation we assume that one antigen produces one peptide which is bound to MHC class II molecules on the surface of the APC. Thus, PIE will depend on the number of APC available to mediate effective presentation of peptide from a given antigen.

The number of PIE per T-Protecton is a function of the number of APC that present a given epitope per T-Protecton. PIE values are calculated as follows. If X is set to equal E cells per epitope per APC and Y is set to equal A cells per epitope per APC, then the probability of an A-E interaction per APC is (1 - e ^-X)(1 - e ^-Y). This is the probability for each APC and, when multiplied by the number of APC per T-Protecton, becomes the value of PIE. When computed for A_s and E_s we obtain PIE_s for anti-self cells and similarly PIE_ns for the antinon-self cells.

The calculation of PIE_ns needs a comment. As we are interested here in the status of the immune system prior to the appearance of non-self antigens, there are no A_ns present. However, to approximate the priming readiness of the system, we used the values for I_ns to make the calculation of PIE_ns. This approximation is reasonable as the conversion of I → A in the presence of antigen is rapid. The second paper (3) will formalize this ‘autocatalytic’ step.

If the number of APC presenting a given self epitope is much below the copy number (C_t) of either A_s or E_s, then all APC will be occupird with one or more A_s or E_s, or both. Under these conditions our calculation treats the APC as producing a single PIE. While this assumption may not be valid, there must be some limit to the maximum number of PIE per APC and at present there is no clear indication of what the limit might be. We will assume it to be one.

There is a trade-off to consider at low and high numbers of APC per epitope per T-Protecton. At low numbers of APC the time it takes for the rare E and A cells to find each other becomes limiting. At high numbers of APC the probability of an A and an E cell finding the peptides from one antigen on a given APC becomes limiting.

In conclusion, we should emphasize that There may be other ways of formulating a PIE, but the one element that seems unavoidable under all models is the critical role of the APC. The Minimal Model only considers APC that present antigen at a functional threshold level as would be expected for self antigens. The limiting factor in this case is the eT_h having to find a corresponding iT_h on the same APC.

Establishing limits to immunity in terms of PIE_s and PIE_ns

The minimal, least stringent boundary conditions would be <1 PIE_s and >1 PIE_ns. However, we would imagine that such a singular dividing line is unrealistic, in part because the risk of inducing immunity toward a self antigen would be unacceptably high. The most stringent yet reasonable value of the autoimmune boundary in terms of PIE_s is <0.01, which means that there would be less than one priming inductive event in 100 T-Protectons per self epitope. The most stringent yet reasonable value of the immune boundary in terms of PIE_ns is >10, which means that There would be >10 priming inductive events per Protecton. We will use these stringent boundary conditions in evaluating the parameters, i.e. PIE_s <0.01 and PIE_ns >10.

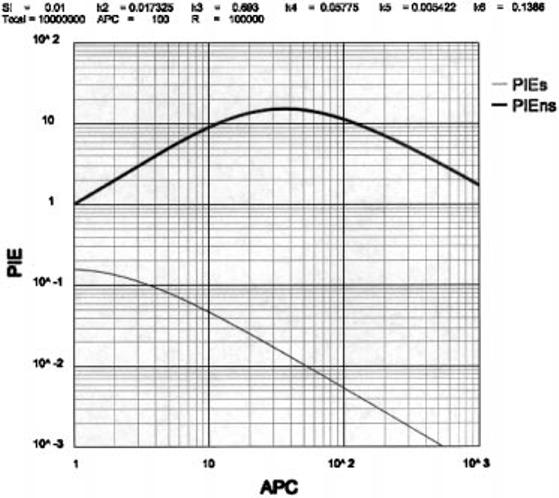
The data in Fig. 2 shows the effect of varying the number of APC per T-Protecton on the values of PIE_s and PIE_ns using our optimal values for the rate constants. In order to meet the PIE_s < 0.01 autoimmune boundary, the number of APC presenting a given self peptide must exceed 50 per T-Protecton. In order to meet the PIE_ns > 10 immune boundary, the number of APC presenting a given non-self peptide must be 15 < APC < 120 per T-Protecton. The result then is that the window of function in this case is rather narrow (50 < APC < 120), but it must be remembered that we have set boundary conditions that are quite stringent. By inspection the two curves suggest that there is unlikely to be a window of joint compliance with stringent boundary conditions over a >2-to4-fold difference in APC numbers separating the upper and lower bounds. We will return to this point later.

Fig. 2.

The relationship between PIE_s or PIE_ns and the numbers of APC presenting a given peptide per T-Protecton.

Estimating limits to the variables under stringent PIE_s and PIE_ns boundary conditions

Based on what we considered to be the optimal set of values in the simulation, we next searched for the upper and lower limits of each parameter. The results are summarized under individual headings.

Limits to the value of SI

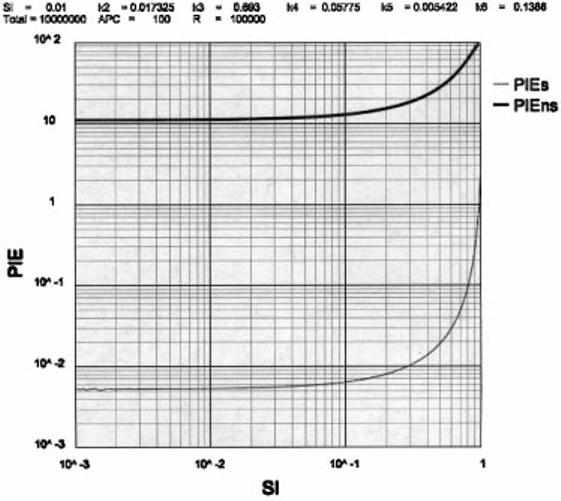
Figure 3 shows a plot of the effect of various values of SI on the number of PIE_s and PIE_ns. Even if we consider stringent values for the autoimmune and immune boundaries (i.e. <0.01 PIE_s and >10 PIE_ns), there is little effect on these boundaries at values of SI < 0.1. Several effects combine to make values of SI > 0.1 unreasonable. When SI >> 0.1 the input of cells (k₁G) increases to result in a half-life of the Protecton (T_t) that decreases sharply from 6.8 days at SI = 0.01 to 6.2 days at SI = 0.1, to 2.9 days at SI = 0.6. At SI > 0.3 the PIE_s boundary of 0.01 is breached. The increase in PIE_ns as SI increases >0.1 is due to the increase in copy number (C_t) of the anti-non-self repertoire. We consider values of SI > 0.1 beyond biological expectation.

Fig. 3.

The relationship between PIE_s or PIE_ns and SI.

Values of SI < 0.001 reduce the numbers of anti-self cells per epitope per Protecton to such low levels (I_s = 0.6, A_s = 3.0, E_s = 0.2) that it becomes unselectable (5). To illustrate this point, E_s = 0.2 means that there would be two effector T_h anti-‘a-given-self peptide’ per mouse (equivalent to 10 T-Protectons).

Limits to the size of the TCR repertoire

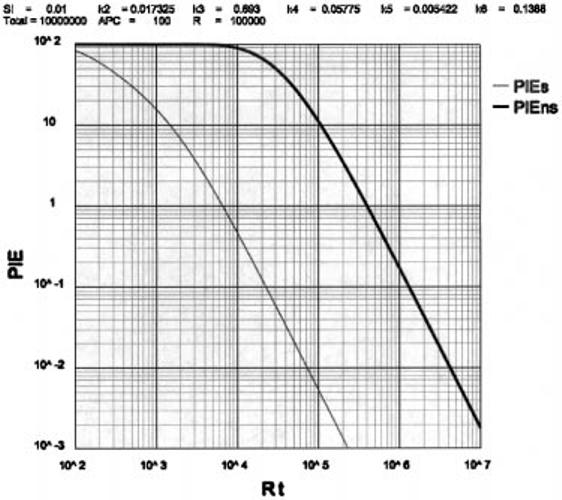
The size of the TCR repertoire, R_t, can be roughly estimated from the amount of information available to TCR recognition in the peptide that binds to MHC. If There are ∼5 amino acid residues that are available to TCR recognition after fixing the anchor residues and if at each position any of 20 amino acids could be inserted, then the maximum number of possible peptides is 20⁵ or ∼3 × 10⁶. Since only about half of the amino acid replacements change recognition in a functional way, a reasonable range would place R_t at > 10⁴ and < 10⁶. In Fig. 4 we plot the PIE_s and PIE_ns for various values of R_t. Using 100 APC per T-Protecton as the standard condition we find that as R_t falls <7 × 10⁴, the upper limit of 0.01 PIE_s is reached, and when R_t rises > 1.3 × 10⁵ the boundary of 10 PIE_ns is breached because the number of cells per epitope is too low to permit sufficient induction on 100 APC and decreasing the number of APC runs into the breaching of the PIE_s < 0.01 autoimmune boundary. Thus, to find such a narrow range for the optimal value of R_t was unexpected when viewed from the uncritical perspective of more-is-always-better.

Fig. 4.

The relationship between PIE_s or PIE_ns and R_t.

Effects due to the size of the T-Protecton

Although homeostasis keeps the number of T cells constant, the actual number of T cells in the T-Protecton (T_t) is largely determined by the size of the repertoire R_t. Setting R_t = 10⁵ and the total number of APC per T_t = 100, the results in Fig. 5 show the effect of varying T_t on the boundary conditions, PIE_s < 0.01 and PIE_ns > 10. There is a surprisingly sharp upper limit of T_t = 1.3 × 10⁷ when the PIE_s boundary exceeds 0.01 and a lower limit of T_t = 9 × 10⁶ when the immune boundary PIE_ns drops <10.

Fig. 5.

The relationship between PIE_s or PIE_ns and the size of the protection (T_t)

Choice of the rate constants

The rate constants show a general pattern of broad limits even under the very restrictive conditions of PIE_s < 0.01 and PIE_ns > 10. This surprisingly broad spectrum of rate constants suggests that evolution did not need a finely tuned set of reactions to establish a functional self—non-self discrimination mechanism. However, the more exacting test of the Minimal Model using the simulator is to use ranges of random numbers and select for systems of parameters that satisfy the PIE boundary conditions.

Using random values of the variables to search for unexpected solutions

The intuitive hunt-and-peck method of searching is usually good enough to identify optimal values for the variables within the bounds of a moderately transparent set of assumptions. However, this does not guarantee that other solutions may not also exist and should be examined in the light of the assumptions that would need to be made. We therefore set up a set of searches based on the use of random values for most of the variables while searching for the largest acceptable repertoire. The rationale for searching for solutions that give the largest possible repertoire that remains functional was that this seemed to be the most likely evolutionary selection pressure and this would reveal those parameters that most severely limit the size of the repertoire.

The results were somewhat surprising in the sense that the values of the rate constants were not a major factor in limiting the size of the repertoire. While this kind of result is often put forward as evidence of the ‘robustness’ of a model, we have interpreted this as simply showing the validity of the principle of the Minimal Model because it provides a mechanism that is largely independent of the size of the repertoire.

One obvious limiting factor in the size of the repertoire is the total number of cells T_t in the T cell Protecton and the copy number (C_t) of T_h cells specific for a given non-self antigen. It is self evident that a value of T_t = 10⁷ and a C_t = 10 would limit The functional repertoire to < 10⁶.

Summarizing the relationship between parameters and boundaries

The limits to the parameters of the T_h-Protecton determined under various boundary conditions are shown in Table 2. Under stringent conditions they are surprisingly narrow and, unsurprisingly, relaxing the boundary conditions broadens the limits, which nonetheless remain quite restricted.

Table 2.

The limits to the parameters of the Th genesis pathway

Parameter	Autoimmune boundary (PIEs)			Immune boundary (PIEns)
	<0.01	<0.1	<1	>10	>1
APC per antigen	>50	>4	>1b	<120	<2000
Specificity index (SI)	<0.1a	<0.1a	<0.1a	<0.1a	<0.1a
Size of Protecton (Tt)	<1.3 × 107	<4.5 × 107	<1.5 × 108	>9 × 106	>1.5 × 106
Size of repertoire (Rt)	>7 × 104	>2 × 104	>6 × 103	<1.3 × 105	<4 × 105

^aSI > 0.1 results in biologically meaningless effects discussed in text. Under stringent conditions PIE_s < 0.01 and SI < 0.1, best estimate SI = 0.01.

^bThe maximum PIE_s is only 0.15 when There is 1 APC per antigen.

The ‘autoimmune boundary’ is the value of PIE_s above which the individual would be debilitated.

The ‘immune boundary’ is the value of PIE_ns below which the response to a pathogen would be ineffective.

It might be added that as a result of the detailed search using random variables as described above, there is an added factor based on the number of APC and the choice of PIE_ns boundary that determines the maximum size of the T cell anti-peptide repertoire (R_t). as the stringency of PIE_ns is decreased, the permissible size of the repertoire increases provided there is a corresponding decrease in the number of APC that can present antigen.

Discussion

The cells of the ‘adaptive’ immune system are born as initial state or i-cells without effector activity. They undergo a self—non-self discrimination, a decision mechanism that sorts the somatically generated paratopic repertoire expressed by i-cells into anti-self, which is purged leaving an anti-non-self repertoire to protect the animal. This decision mechanism is dependent on the sufficiency or insufficiency of eT_h specific for a given antigen. As T_h are born as iT_h, and their ability to make a self—non-self discrimination is dependent on an insufficiency of eT_h anti-self and a sufficiency of eT_h antinon-self, the question arises, what is the origin of these two eT_h states of sufficiency?

Unique to our answer is (i) an antigen-independent pathway from iT_h to eT_h and (ii) the induction of iT_h to eT_h requires associative recognition of antigen. This latter means that antigen (defined as the unit of elimination by the ridding effector function) must be processed to peptide and presented on an APC as a (peptide-class II MHC) complex.

An iT_h and an eT_h must recognize the presented peptides from the single antigen (unit of elimination) and the eT_h must deliver Signal[2] to the iT_h, which then goes on to differentiate to an eT_h (the ‘autocatalyic’ step). The iT_h interacting with an APC in the absence of an eT_h delivered Signal[2] dies. In order for this interaction of associative recognition to take place, the peptides derived from the given antigen must be presented in a ‘signaling patch’, which is the only pathway permitting an eT_h to deliver a signal to the iT_h.

The question of the origin of the priming level of eT_h anti-nonself and the insufficiency of eT_h anti-self is dealt with here by analyzing in detail an antigen-independent pathway from iT_h to eT_h that itself undergoes a self—non-self discrimination.

While there is little disagreement that associative recognition of antigen by i-cells and eT_h operates in the case of B cells and cytotoxic T cells, there is lack of acceptance of this assumption for T_h where an iT_h—APC—eT_h interaction is denied.

The acceptance or denial of associative recognition of antigen for the induction of iT_h is what distinguishes the models (Langman, R. E., Mata, J. J. and Cohn, M.; in preparation). As each APC presents peptides of both self and non-self origin, APC cannot sort the T_h repertoire. The sorting must be antigen specific and dependent solely on the recognition elements of the T_h repertoire itself.

It is the associative recognition of antigen on the APC (iT_h—APC—eT_h) that gives the APC a unique role in regulating the magnitude of the response. Too few or too many APC presenting a given antigen become rate limiting. Too few are limiting because iT_h and eT_h sit around awaiting their turn; too many are limiting because iT_h and eT_h find themselves on different APC unable to communicate. No other model predicts an optimum number of APC because it is assumed that iT_h + APC → eT_h. This latter response would be proportional to the number of APC presenting antigen, of course until it saturates.

Despite a strong intuitive belief that the rates of reaction would place sharp limits on the values of the parameters of the Minimal Model of the self—non-self discrimination, we were wrong. The rate constants of the reactions illustrated in Fig. 1 show a wide range of possible values, limited primarily by the PIE_s and PIE_ns boundary conditions that are chosen. Rather than tout the ‘robustness’ of the model, as if this were an a priori desirable feature of any model, we emphasize the evolutionary advantage of allowing an even quite sloppy range of rate constants to control key elements in the selection process. In other words, once there are two pathways for the iT_h to take, one being antigen-driven inactivation (Signal[1]) and the other being antigen-independent activation, the relative rates can differ several fold and yet permit an adequate self—non-self discrimination to be made. Thus, evolution did not have to get all the different parts and set the rate constants of each just right before a somatic self—non-self discrimination could be made. Certainly over time evolution will optimize these reactions and their rates, but these were not necessarily critical to get the process started.

The effect of the ‘autocatalytic’ step (k₇ in Fig. 1) will be analyzed in a second paper (Langman, R. E., Mata, J. J. and Cohn, M.; in preparation) where the response to non-self antigens will be considered, as will also the other views.

Abbreviations

APC

antigen-presenting cell

aT_h

Anticipatory T_h

C_t

cells specific for a given epitope per T_t (i.e. copy number)

eT_h

Effector T_h

iT_h

Initial state ‘antigen-responsive’ T_h

ns

non-self

PIE

priming inductive event

R_t

size of paratopic T cell repertoire

s

self

T_b

total number of cells per B-Protecton

T_t

total number of cells per T-Protecton