Multicellularity and the functional interdependence of motility and molecular transport

Abstract

Benefits, costs, and requirements accompany the transition from motile totipotent unicellular organisms to multicellular organisms having cells specialized into reproductive (germ) and vegetative (sterile soma) functions such as motility. In flagellated colonial organisms such as the volvocalean green algae, organized beating by the somatic cells' flagella yields propulsion important in phototaxis and chemotaxis. It has not been generally appreciated that for the larger colonies flagellar stirring of boundary layers and remote transport are fundamental for maintaining a sufficient rate of metabolite turnover, one not attainable by diffusive transport alone. Here, we describe experiments that quantify the role of advective dynamics in enhancing productivity in germ soma-differentiated colonies. First, experiments with suspended deflagellated colonies of Volvox carteri show that forced advection improves productivity. Second, particle imaging velocimetry of fluid motion around colonies immobilized by micropipette aspiration reveals flow fields with very large characteristic velocities U extending to length scales exceeding the colony radius R. For a typical metabolite diffusion constant D, the associated Peclet number Pe = 2UR/D >> 1, indicative of the dominance of advection over diffusion, with striking augmentation at the cell division stage. Near the colony surface, flows generated by flagella can be chaotic, exhibiting mixing due to stretching and folding. These results imply that hydrodynamic transport external to colonies provides a crucial boundary condition, a source for supplying internal diffusional dynamics.

The efficient exchange of nutrients, metabolites, and wastes is among the most basic factors affecting the fitness of organisms. Understanding the effect of resource delivery and exchange on metabolic rate, as organisms increase in size, is leading to rapid advances across disparate fields of the life sciences, from comparative biology to ecosystem ecology (1-4). Yet, these insights have not been applied to the analysis of the evolutionary transitions which underlie the hierarchy of life (5, 6). Although cooperative endeavors provide substantial benefits, certain key problems must be solved for a group to emerge into a new complex individual. As lower level units (cells) associate to form groups, the constraints of surface to volume ratio, S/V, and of spatial organization limit the type and extent of interactions with the environment, with profound effects on metabolism, growth rate, viability, and fecundity. We refer to this as the “transport limitation” and view it as a general aspect of evolutionary transitions in individuality.

Nutrient consumption increases proportionally with the size of the organism, creating an increased boundary layer of nutrient depletion. In the absence of active mixing of the medium, this decreases the passive diffusion of nutrients. This transport limitation constraint as size increases can be circumvented in several ways. For example, depending on the geometry, increasing in size may not decrease the S/V ratio; e.g., a cylindrical organism can indefinitely increase in volume without decreasing S/V if its radius r remains constant, for then S/V = 2/r (7). Also, some organisms live in environments that favor the active mixing of nutrients through laminar or turbulent flows (e.g., a sessile organism in a flowing current). There are even unicells that are able to reach the sizes of small multicellular organisms by having specific geometries and living in specific favorable environments (8). We focus here on the lineages that we hypothesize were able to evolve large multicellular forms by actively mixing the surrounding fluid with self-generated flagellar-driven flows.

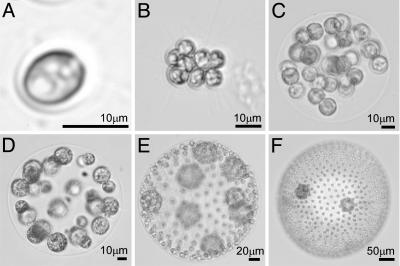
Using as model organisms the volvocalean green algae (class: Chlorophyceae) (9), we study here the biological significance of collective modes of hydrodynamic transport. These aquatic flagellated organisms (Fig. 1) range from unicellular organisms such as Chlamydomonas reinhardtii to colonies made of 4-64 cells with no cell differentiation (e.g., Gonium, Eudorina), to multicellular individuals (e.g., Volvox) composed of 1,000-50,000 differentiated cells (9-11). Specialization into reproductive (germ cells) and vegetative (sterile flagellated cells) functions, termed “germ-soma separation,” characterizes the large members. The number of somatic cells per reproductive cell (S/R ratio) increases with colony size (10). Volvox species with germ-soma separation are not monophyletic. These complex forms have evolved several times independently, from quite different ancestors (11, 12). Supporting this ease of evolutionary transition in Volvocales is the underlying genetic architecture responsible for the separation of germ and soma, which does not involve many genetic steps (9). Note that the number of cells in Volvocales is determined by the number of cleavage divisions that take place during embryonic development. Cell number is not augmented by accretionary cell divisions after juveniles hatch (13).

Fig. 1.

Species of volvocalean green algae spanning a large range in size. Shown are the single-cell C. reinhardtii (A), undifferentiated colonies Gonium pectorale (8 cells) (B) and Eudorina elegans (32 cells) (C), and those with germ-soma differentiation Pleodorina californica (64 cells) (D), V. carteri (≈1,000 cells) (E), and Volvox aureus (≈2,000 cells) (F).

Because the Volvocales are denser than water, they need motility to avoid sinking and to reach light and nutrients (14). Undifferentiated colonies face motility problems even at a small size (e.g., 32-cell colonies, Eudorina; Fig. 1) as a result of the “flagellation constraint” [motility is inhibited during cell division (10)]. Nonetheless, even in the absence of this constraint, larger colonies would sink if they did not increase their flagellar swimming force by investing in somatic cells and the associated extracellular matrix (ECM). This need arises from the enlargement of reproductive cells, which increases the mean density of the colony (15). We argue here that this investment in somatic cells for motility has the additional and important benefit of enhanced molecular transport of nutrients and wastes thanks to the flow created by collective flagellar beating.

Evidence for the importance of flagella- and cilia-driven flows in eukaryotes is provided by the high degree of sequence conservation between flagellar proteins of unicellular organisms such as C. reinhardtii and ciliary proteins of multicellular organisms such as mammals (16, 17). Moreover, it is becoming increasingly clear from a range of recent studies that these flows can play a central role in multicellular systems, broadly interpreted. Examples include morphogenetic symmetry-breaking driven by ciliary flows (18, 19), microfluidic devices that might use bacterial carpets (20), self-concentration of chemotactic bacteria (21, 22), and large-scale coherence in concentrated suspensions (21, 23). Common to all are (i) fluid velocities reaching hundreds of microns per second and (ii) coherent motion with length scales extending over very many cells, exceeding hundreds of microns. Because the diffusion constant D of modest size solutes (a chemical messenger or a metabolite) is at most 10^-6 to 10^-5 cm²/s, advection in flows with the above characteristics can easily dominate diffusion. Let us recall that if a molecular solute of concentration C exhibits transport by diffusion and advection, and u is the local fluid velocity, then

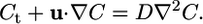[1]

If U is a characteristic fluid velocity varying on a length scale L, then u·▵C ∼ UC/L and D▵²C ∼ DC/L². The ratio of these advective and diffusive terms, or equivalently the ratio of the diffusion time L²/D to the advective time L/U, then defines the Peclet number (24),

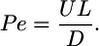[2]

If Pe < 1, diffusion outcompetes transport by advection from the flowing medium, whereas if Pe > 1, advection dominates. When L is the size of a bacterium (≈10^-4 cm) and U is a swimming speed (≈10^-3 cm/s), then Pe ∼ 10^-2 to 10^-1 for small solutes. Advection is therefore negligible (25) and may be ignored in dynamic models of chemotaxis and chemical signaling (26). The situation changes radically when U and L are as large as found in the systems described above, where many closely spaced moving entities (motile bacteria or cilia) collectively generate flows. Then Pe ∼ 10² and advection can not be neglected. Such flows may also exhibit long correlation lengths and times and can be chaotic, as seen even at the single cell level (27), exhibiting stretching and folding that enhance local mixing.

It has been argued that larger differentiated Volvocales with high S/R ratios are efficient in nutrient uptake and storage, especially in eutrophic conditions. This “source-sink” hypothesis (28, 29), in which soma is the source and germ the sink, implies that in large colonies the division of labor prevents the inhibition of nutrient uptake by previously acquired resources (following Michaelis-Menten kinetics). Tests of the source-sink hypothesis have not addressed the effect on nutrient uptake of the mixing driven by the flagella of somatic cells. Here, we specifically investigate the hypothesis that the apparatus that confers motility in large Volvocales also functions to enhance molecular transport, improving the acquisition of molecules important for productivity, and increasing the dispersal of waste products beyond the range of inadvertent diffusive recycling (7, 30). Using a combination of experimental methods, we provide quantitative evidence that collective flagellar beating in a species with germ-soma separation becomes important for enhancing colony growth. Also, we provide measurements of the collective fluid velocities driven by the flagella of the somatic cells at various stages in the life cycle. These results prove not only that the relevant Peclet numbers greatly exceed unity but also show intriguing variations during the life cycle. Taken together, these experimental results highlight a whole range of biologically significant factors in the hydrodynamics of flagellar-driven flows and, more universally, the physical constraints on the evolution of multicellularity.

Volvox carteri, the species used originally to test the source-sink hypothesis (28, 29), was chosen for our experiments because it is large enough to expect advection to have a significant effect on metabolite transport and hence colony growth. It is a colonial green alga formed by ≈1,000-4,000 mortal flagellated somatic cells and ≈8-16 immortal nonflagellated germ cells (9) (gonidia; Figs. 1 and 2). In V. carteri, the reproductive cells do not undergo binary fission; rather, each reproductive cell grows about 2ⁿ-fold in size and then undergoes a rapid, synchronous series of n divisions (within the mother cell wall). This peculiar way of division, termed palintomy, is considered the ancestral developmental program in this group (13). The size a gonidium reaches before cleavage starts positively correlates with the size of the daughter colony it produces. Larger gonidia produce larger daughter colonies with higher number of cells (somatic and reproductive) (31). Thus, gonidia that reach a larger size before cleavage starts have higher fecundity.

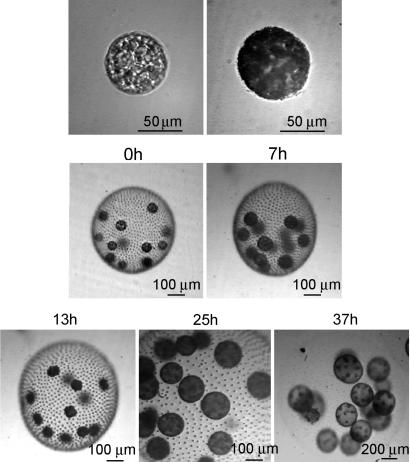
Fig. 2.

The asexual life cycle of V. carteri when synchronized in a 16 h light/8 h dark cycle. 0h (upper), a germ cell from newly hatched colonies; 0h (lower), a newly hatched colony (2 h into the light cycle); 7h (upper), a germ cell reaching the end of its growth phase and ready to start cleavage; 7h (lower), a colony 7 h after having hatched; 13h, 1 h before the end of the light cycle (germ cells are in the middle of their cleavage phase); 25h, 3 h into the next light cycle (in the dark cycle, germ cells finished cleavage and inverted, and now the daughter colonies are fully formed inside the mother colony); 37h, 1 h before the end of the light cycle (daughter colonies have been growing inside the mother colony). Hatching of daughter colonies takes place at the beginning of the next light cycle.

Overview of Approaches and Results

To understand the effect of advection on colony productivity (fecundity), we measured the increase of the gonidium diameter in V. carteri during the growth phase, for a fixed time period before cleavage started. We compared the growth rate of V. carteri germ cells that were liberated by breaking the colonies apart, in deflagellated colonies, and in normal colonies. These gonidia, outside or inside colonies, were placed in either still or artificially mixed medium, with and without the presence of a flagellar regeneration inhibitor. Koufopanou and Bell (29) investigated the effects of isolating germ from soma. Our experiments generalize this work by consideration of the effects of fluid transport. We hypothesize that if advection driven by collective flagellar beating is important for nutrient uptake, then the growth rate of permanently deflagellated colonies placed in still medium ought to decrease. Under the same hypothesis, we expect this negative effect to disappear when those permanently deflagellated colonies are placed in a medium artificially mixed by air bubbling (“sparging”). Our results were in accord with these expectations. This effect is clearly due to modulation of nutrient uptake by advection or its absence. Thus, evidence shows that advection plays a significant role in the fitness of V. carteri colonies, likely by enhancing nutrient uptake.

The second part of our experimental program consists of direct measurements (Fig. 3) of fluid velocities driven by flagellar beating at various stages in V. carteri's life cycle. These data yield the Peclet number and serve as benchmarks for a quantitative theory of nutrient uptake by these organisms. Combined, our results show that the flagellar transport/mixing effect is separate from the mechanisms underlying the source-sink hypothesis. We discuss implications that these effects may have on the emergence of multicellularity, accompanying cell differentiation in this lineage.

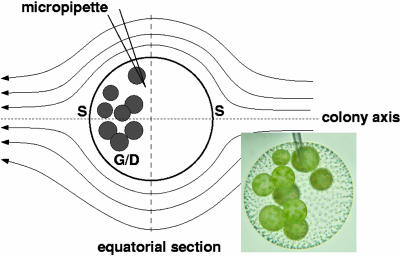
Fig. 3.

Micropipette aspiration of V. carteri for PIV studies. Schematic shows streamlines symmetric about the colony axis, on which are located the two stagnation points (S). Germ cells/daughter colonies (G/D) are located in posterior half of colony. Dashed line indicates equatorial section of PIV flow field used to determine maximum fluid velocity.

Results: Gonidia Growth

Table 1, which is published as supporting information on the PNAS web site, shows all of the parameter estimates with their p values for the whole and reduced model from the additive multiple linear regression analysis. When colonies just hatched the average initial gonidia diameter was 46.81 ± 0.76 μm for the still medium experiments and 52.25 ± 0.92 μm for the sparged medium experiments (n = 60; S, Table 1). The latter experiments were performed 1 week later, continuing the use of the previously synchronized population. Thus, after 1 week, the average initial gonidia sizes from the same population synchronized under the same conditions were slightly larger. The two experiments were started with populations composed of different colony sizes. Small differences were also found between the two replicated experiments within the medium treatments (R2, S and R2, B, Table 1). Nevertheless, there was no significant difference in diameter increase between the gonidia in the still and sparged treatments (i.e., no interaction between the medium treatment and the final diameter; Δd× S, Table 1) and between replicates within the medium treatments (Δd× R2, S and Δd× R2, B, whole model, Table 1). The average gonidium diameter increase in normal flagellated colonies was 12.92 ± 0.90 μm in 7 h (Δd, Table 1; the average final germ cell diameter for the still and sparged experiments was 60.19 ± 0.76 μm and 65.41 ± 0.95 μm, respectively; n = 60).

After correcting for variations between experiments, we found significant differences and interactions between the factors involved in the experiments (medium: still S or bubbling B, deflagellation D, broken colony L, and inhibitor I treatments). There is no evidence that transient deflagellation by itself decreases gonidium diameter growth, likely due to the rapid flagellar regeneration in the absence of the inhibitor (D, Table 1). In contrast, regardless of medium treatment, the gonidia from broken colonies grew on average 3.28 ± 0.61 μm less in diameter than those from normal flagellated colonies (L, Table 1). The gonidia from colonies with the inhibitor treatment grew on average 1.57 ± 0.58 μm less in diameter than those without the inhibitor (I, Table 1). These results were independent of the medium (no interaction between the deflagellation treatment, broken colony treatment, inhibitor, and medium; whole model D× S, L× S, and I× S, Table 1).

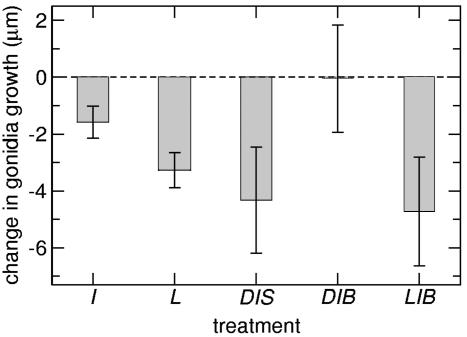
After correcting for the negative effect of the inhibitor, we found an even larger decrease in the average gonidium diameter growth when permanently deflagellated colonies were placed in still medium [-4.31 ± 1.89 μm; S: (D× I), Table 1], i.e., an interaction between the deflagellation and inhibitor treatments. However, the negative effect disappeared when these colonies were placed in bubbling medium [B: (D× I), Table 1]. Thus, permanently deflagellated colonies grew as well as normal flagellated colonies when the medium was artificially mixed! On the other hand, broken colonies behaved the opposite way, for when they were treated with the inhibitor and placed in still medium, there was no additional negative effect [no interaction between broken and inhibitor treatments; S: (L× I), Table 1]. However, there was a significant decrease in germ cell diameter growth when broken colonies with the inhibitor treatment were placed in bubbling medium [-4.73 ± 1.90 μm; B: (L× I), Table 1]. These two negative effects are the largest in the analysis (Fig. 4).

Fig. 4.

Summary of germ cell growth experiments. Data show treatments that significantly affected the growth rate of germ cells compared with those of normal flagellated colonies in standard medium. I, inhibitor treatment; L, broken colonies treatment; DIS, deflagellated colonies with inhibitor in still medium; DIB, deflagellated colonies with inhibitor in bubbling medium; LIS, broken colonies with inhibitor in still medium; LIB, broken colonies with inhibitor in bubbling medium. DIB results illustrate the restoration of normal growth with artificial bubbling.

In summary, we found that inhibiting advection by preventing collective flagellar beating decreases the growth rate of the gonidia within a colony. This negative effect disappears when the medium is artificially mixed, proving that the decrease in growth is due to the decrease in advection.

Because there was no difference in growth rates between colonies in sparged and still media when colonies were not permanently deflagellated, one infers that conditions in the still medium were optimum for the 7 h duration of experiments, and/or that flagellar mixing in the still medium was sufficient for allowing the same nutrient uptake as in the sparged medium. From the negative interaction between broken colonies and the inhibitor, in the bubbling medium, one may infer that bubbling enhanced the absorption of the inhibitor by gonidia unprotected by the ECM. Because the results show that the inhibitor by itself only slightly affected growth (Table 1 and Fig. 3), the ECM is apparently also serving as a protective barrier and transport modulator or “buffer.” The somatic cells in the periphery seem to be the only cells strongly affected by the inhibitor in the intact colony.

Results: Particle Imaging Velocimetry (PIV)

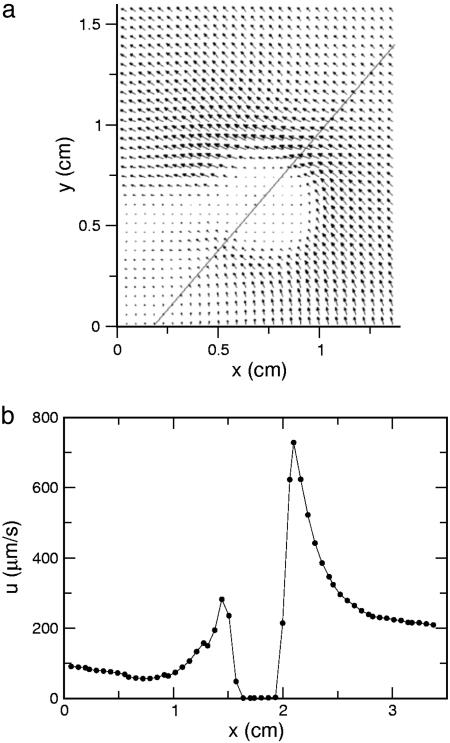
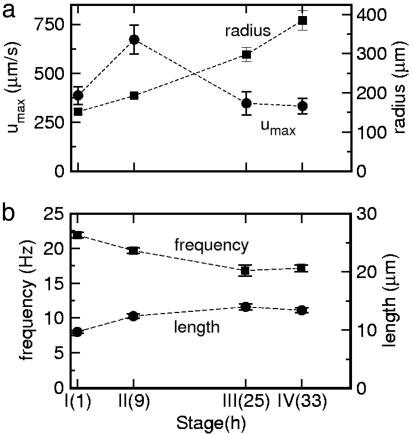
We turn now to direct visualizations of the flow fields around V. carteri. The power of this method for acquiring detailed information about flow fields is demonstrated in Fig. 5, a view along the colony axis. Fluid circulates around the colony equator in a manner directly related to the characteristic rolling motions Volvox displays as it swims. Returning to the flow geometry of Fig. 3, Fig. 6a shows a typical example of a complete flow field, from which it is apparent that the flow extends over many colony diameters, and that the maximum velocity is near the equator. The velocity slice in Fig. 6b reveals a peak of ≈800 μm/s for a colony of radius 200 μm. Collecting together results at the four life cycle stages, Fig. 7a shows that the maximum fluid velocity as a function of time is nonmonotonic, peaking strongly at the division stage. Although the colony diameter increases only ≈30% from the hatch to division stage, the fluid velocity nearly doubles. High-speed imaging of the flagella in both stages showed progressive elongation from 9.7 ± 0.2 μm for recently hatched to 12.4 ± 0.4 μm at the division stage, and on to 13.4 ± 0.4 μm by stage IV. The flagellar beating rates were found to have a slow decline during the whole of the life cycle, from ≈22 Hz when cells have just hatched to ≈17 Hz at the prehatch stage (Fig. 7b). The hydrodynamic mechanism responsible for the marked increase in fluid velocity near stage II is not clear, especially because neither the flagellar length nor beating frequency show a dramatic change there. It is possible that the efficiency of the flagella in producing the streaming motion is a sensitive function of the inter-somatic cell distance.

Fig. 5.

PIV flow field around a sessile V. carteri colony. Taken in a plane perpendicular to the colony axis, this top view shows swirling flows around equator of colony. Bright circles in the superimposed negative image are developing daughter colonies.

Fig. 6.

Results from PIV. (a) Fluid velocity field surrounding an immobilized colony of V. carteri, with equatorial slice indicated. (b) Fluid velocity along equatorial slice.

Fig. 7.

Flow properties and flagella dynamics at four stages of growth. (a) Maximum surface fluid velocities (circles) and colony radii (squares) as a function of time. (b) Flagellar beating frequencies (squares) and lengths (circles) at the same stages as in A. Dashed lines are guides to the eye.

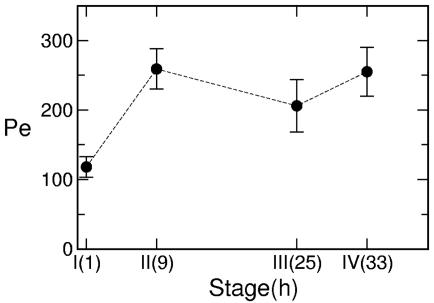
Using the colony diameter as the characteristic length scale, and D = 10^-5 cm²/s as a representative diffusion constant for small solutes, Fig. 8 shows the Peclet number Pe derived from the measured maximum velocities. These exceed unity by two orders of magnitude during the entire life cycle; there is no doubt that advective transport dominates diffusion. Superimposed on the gradual increase in Pe due to colony growth is a spike at the division stage, so the advective transport rate is similarly enhanced.

Fig. 8.

Measure of hydrodynamic transport. Peclet number Pe = 2Ru_max/D calculated from velocity and size data in Fig. 7a with D = 1.0 × 10^-5 cm²/s, a value chosen to give an approximate lower bound on Pe. The dashed line is a guide to the eye.

These flow fields, driven by the surface-mounted flagella, also have remarkable near-field properties. Viewed at higher magnification and with epifluorescence, we find (data not shown) that micrometer-sized tracers trace out a noisy, chaotic flow field with pervasive rotation and localized recycling of the fluid, sometimes followed by ejection of tracers along a fast trajectory. The detailed dynamics in this region requires further study.

Discussion

The germ cell growth experiments show clearly that the source-sink mechanism and flagellar-driven transport are both important for nutrient uptake in V. carteri. Confirming Bell's earlier results, we find that gonidia outside broken colonies suffer a decrease in growth rate, even if the medium is artificially stirred. This is consistent with the postulated role of the ECM in the source-sink model as important in maintaining a high nutrient gradient between the gonidia and the medium. Yet, the growth rate of gonidia within permanently deflagellated colonies was less in unstirred medium, even lower than the growth rate of gonidia from broken colonies. This decrease disappeared when colonies were placed in artificially mixed medium. This is strong evidence that the growth rate of gonidia is limited by the decrease of transport and mixing when colonies are permanently deflagellated, confirming the hypothesis that collective flagellar beating helps colonies of increasing size to ameliorate the metabolic stress created by a transport deficit (7, 30). In the context of the transition from undifferentiated to differentiated Volvocales (15), we see that by investing more in somatic cells for motility, larger colonies also gain the benefit of enhancing nutrient uptake. Of course, how much colonies invest in translocation and nutrient uptake varies with their local environment. Motility may be crucial in large ponds for volvocalean colonies to perform daily migration in the water column to use best resources distributed heterogeneously (32) in space and time (light, nitrogen, phosphorus). In quiescent, small shallow puddles, motility may be less important, but flagellar beating might be crucial for enhancing nutrient uptake by local mixing of fluid.

The PIV studies provide clear evidence that flagellar-driven flows have Peclet numbers as large as several hundred, with significant augmentation at the division stage likely due to the greater metabolite exchange requirements during cell division. Taken together, our results indicate that although the source-sink hypothesis is a factor to consider, it is insufficient to explain the evolution of cell specialization and the transition to higher levels of individuality in this lineage. Motility (10, 15) and flagellar mixing (studied here) must play an important role. With information on colony geometry, flagellar lengths, and beating frequencies, quantitative analysis of the interplay of motility and metabolite uptake at high Peclet numbers is the next logical step.

Methods

All experiments used V. carteri f. nagariensis Eve strain, a subclone derived from the female HK10 strain (kindly provided by D. L. Kirk, Washington University, St. Louis). When synchronized in a light-dark cycle (16 h light, 28°C; 8 h dark, 26°C), it completes one asexual life cycle in 48 h (Fig. 2). Colonies hatch 2 h into the first light period, and gonidia continue to grow until they begin cleavage toward the end of that period. Cleavage, lasting ≈7 h, finishes in the subsequent dark period, followed by inversion to form daughter colonies (still in dark period). By the next light period, daughters are fully formed inside the mother colonies. The daughters grow during the next 24 h and hatch the next day. V. carteri was synchronized in 20-ml test tubes with air bubbling, standard Volvox medium (33), and homogeneous cool white light [≈1,000 footcandles (1 footcandle = 20.76 lx)]. Newly hatched colonies were harvested by slow centrifugation (≈500 × g for 2 min), placed in fresh medium, and randomly separated into thirds: normal, those for deflagellation, and those to be broken. Deflagellation was achieved by lowering the pH from 7.5-8.0 to 4.0 with 1 M HCl solution for 30 s, after which it was quickly returned to normal with 1 M NaOH. A 7-ml Dounce homogenizer was used to free germ cells from the ECM (33).

Immediately after deflagellation and colony disruption, the three subpopulations were randomly placed in wells with still medium or tubes with sparged medium, half with the flagellar regeneration inhibitor and half without it. Total inhibition of flagellar regeneration was achieved with 1 mg/ml colchicine, which binds to tubulin and prevents polymerization of the microtubules (34). Deflagellated colonies without the inhibitor treatment regenerated flagella in 30-90 min. Six-well cell-culture clusters (5 ml) were used for the still medium treatment, and six test tubes (20 ml) with air bubbling were used for the sparged medium treatment. Wells and test tubes were surrounded by diffuse light at ≈1,000 footcandles.

We measured the initial diameter of 30 gonidia of the synchronized population 2 h into the light period (Fig. 2, 0h), and 7 h later the final diameter of 30 germ cells from each treatment before cleavage started (Fig. 2, 7h). Colonies were broken to sample germ cells for initial and final diameter measurements. Two replicates were performed for each medium. Orthogonal diameters d of each germ cell were measured to determine the average cell diameter d, and a multiple linear regression analysis of the form d = d₀ + Σ_i a_iv_i + Σ_ij b_ijv_iv_j was performed by using indicator (dummy) variables v_i = 0,1 to take the nominal factors into account (medium, deflagellation, broken colony, and inhibitor treatments). Reported statistical variations are standard errors. Dummy variables allow analyses of categorical variables by comparison of several regression equations originating from a single multiple regression. jump software (SAS Institute, Cary, NC) was used for the analysis.

In complementary experiments, we measured flagellar-driven flows (35, 36) around V. carteri using PIV. The life cycle was sampled in 2-h windows beginning at each of four stages: I, hour 1 (“growth”); II, hour 9 (“division”); III, hour 25 (“daughter”); IV, hour 33 (“prehatch”). Effects associated with colony translocation were eliminated by holding colonies fixed by micropipette aspiration (Fig. 3). Elsewhere (M. B. Short, C.A.S., S. Ganguly, T. R. Powers, J.O.K., and R.E.G., unpublished work), we show in the context of a detailed model of the flow field generated by the somatic cells' flagella that there are only minor differences in the scales of velocity at the surface of immobilized cells and those that are swimming. Micropipettes with diameters of ≈10 μm were produced with a pipette puller (P-87, Sutter Instruments, Novato, CA). Suction was applied through the gentle withdrawal of a gas-tight syringe attached to the pipette with flexible tubing. The flow past a colony has two stagnation points, and the germ cells lie in the posterior half of the colony near one of them (Fig. 3). To measure the maximum fluid velocity along the colony surface without interference from the micropipette, the aspiration point was chosen midway between the posterior stagnation point and the equator. An equatorial slice yields the peak velocity. Because the microscope depth of field is small relative to the colony diameter, flow fields can be measured at a range of positions through the depth of the colony. Results reported represent those from the midsection.

Flows were imaged with microspheres (Molecular Probes, F8825 carboxylate modified, 1.0 μm, Nile red), viewed by using laser epifluorescence (80 mW, 532 nm), or by dark-field illumination. A typical objective magnification was ×4 on an inverted microscope (Diaphot 200, Nikon). Movies acquired with an analog charge-coupled device camera (SSC-M374, Sony; 480 × 640 pixels) consisted of ≈1,000 images taken at ≈30 frames per s, averaged over ≥200 frames. Commercial PIV software (Dantec Dynamics, Skovlunde, Denmark) was used. Flagellar lengths and beating rates were determined at higher magnification by using a high-speed camera (ES-310T, Kodak).