Torque–speed relationship of the bacterial flagellar motor

Abstract

Many swimming bacteria are propelled by flagellar filaments driven by a rotary motor. Each of these tiny motors can generate an impressive torque. The motor torque vs. speed relationship is considered one of the most important measurable characteristics of the motor and therefore is a major criterion for judging models proposed for the working mechanism. Here we give an explicit explanation for this torque–speed curve. The same physics also can explain certain puzzling properties of other motors.

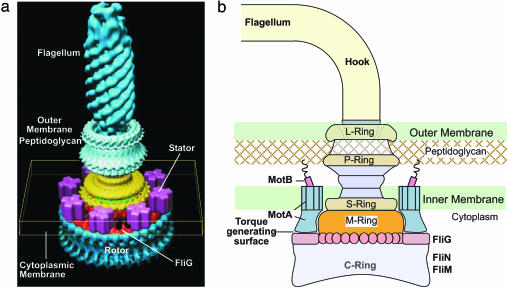
The bacterial flagellar motor (BFM) consists of a rotary motor embedded in the cell envelope connected to an extracellular helical propeller (see Fig. 1) (1–4). The motor is powered by the flow of ions down an electrochemical gradient across the cytoplasmic membrane into the cell. The ions are typically H⁺ (protons) in Escherichia coli and Na⁺ in alkalophiles and marine Vibrio species. For convenience of discussion, we will focus on the proton motor, although most of the discussion applies to the sodium motor as well. The electrochemical gradient, Δ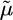 (“proton-motive force” or “sodium-motive force”), consists of a transmembrane voltage and a concentration difference across the membrane, both of which are maintained by various metabolic processes. The proton-motive force is defined as

Fig. 1.

The BFM. (a) The overall structure of the BFM. Figure is courtesy of David DeRosier. (b) A cartoon of the key structural components involved in torque generation.

Here Δψ is the membrane potential, and is the entropic contribution due to the ion concentration difference across the cytoplasmic membrane, k_B is Boltzmann's constant, T is the absolute temperature, and e is the electronic charge. The fundamental question we address here is how the flagellar motor converts 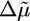into a mechanical torque.

To understand the mechanism of the flagellar motor, we need to understand the mechanochemical cycle of torque generation and how it couples ion flux to motor rotation. The torque–speed relation is the best biophysical probe we have so far to explore the mechanism. It gives a full picture of the power output of the motor under external loads and gives an indication of the energy conversion efficiency. Moreover, the torque–speed curves measured with increasing numbers of stators provide information about individual torque-generating units and their mechanical coupling.

Experimentally, two different methods have been used to measure the torque–speed relationship of the BFM. The first method is electrorotation, in which a cell is tethered to a glass coverslip by a single flagellar filament, external torque, τ_ext, is applied to the cell body with a high-frequency rotating electric field, and the rotation rate of the cell body, ω, is monitored optically (2, 5). A force balance on the motor gives ζω = τ_M + τ_ext, where τ_M is the torque generated by the motor. The frictional drag coefficient is ζ = ζ_M + ζ_L, where ζ_M is the drag coefficient due to internal friction in the motor and ζ_L is the external drag coefficient of the load, in this case, the cell body. The motor torque vs. speed curve is derived from the usual external load torque vs. speed curve as follows. The motor is broken by applying a large external torque to force rotation in the reverse direction. Next, the external torque, τ_ext, is applied to the broken motor, for which the force balance relation is (ζ_M + ζ_ext)ω′ = –τ_ext. Therefore, the motor torque is given by subtracting the broken motor speed from the motor speed: τ_M = (ζ_M + ζ_L)(ω – ω′).

The second method is to tether a polystyrene bead to a flagellar stub with the cell fixed to the surface of a glass coverslip. The rotation speed of the bead is monitored in a weak optical trap while the viscosity of the external medium is rapidly changed by adding Ficoll (6, 7) or while the drag coefficient of the bead is changed by varying the bead size (7). In this case, the motor torque is calculated from τ_M = (ζ_M + ζ_L)ω ≈ ζ_Lω, where the bead drag coefficient ζ_L can be calculated from the Stokes formula, ζ_L = 6π ηR, where R is the bead radius and η the viscosity of the fluid media.

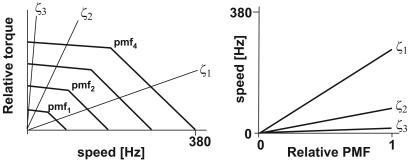
Fig. 2 Left (redrawn from ref. 8) shows idealized plots of the motor torque (normalized to the maximum torque) vs. speed and proton motive force (pmf) (normalized to the maximum pmf). At fixed pmf, the motor–torque curve is swept out by varying the viscous drag on the load, ζ. Fig. 2 Right shows the linear dependence of the speed on pmf. The results of these two approaches are consistent: the torque generated by the motor remains approximately constant up to ≈170 Hz at 23°C and then drops rapidly beyond a “knee” velocity to zero at a velocity of ≈300 Hz. The sodium-driven flagellar motor exhibits a similar motor torque–speed relation (7). The proton-driven motor torque depends strongly on the temperature and on the hydrogen/deuterium isotope ratio in the high-speed region beyond the knee, but not in the low-speed region (9). The motor rotation rates depend linearly on the pmf at both low and high rotation rates (8, 10). The unusual motor torque–speed relation, isotope effect, and pmf dependence are thought to reveal properties underlying working mechanism of the flagellar motor. Here we will show that those observations arise from some very general characteristics of the motor.

Fig. 2.

Idealized motor behavior. (Left) The motor torque–speed curve is nearly constant up to a knee speed, whereupon it decreases nearly linearly. Here, torque is normalized to the maximum torque at stall (ω = 0). The curve is self-similar for increasing pmf. For a given viscous load (characterized by its frictional drag coefficient, ζ_ii = 1, 2, 3), the speed of the motor is determined by the intersection of the “load line” with the motor torque curve. (Right) The motor speed is nearly constant with pmf for different viscous drag loads. The experimental data supporting these idealized curves are given in Fig. 3.

The lack of detailed information about the motor structure and the mechanochemical cycle leaves much room for speculative modeling, and indeed various models have been proposed for the working mechanism of the flagellar motor (see reviews in refs. 2 and 11). However, the three features of the motor torque vs. velocity curve discussed above remain unexplained. Here, we will demonstrate that the mechanochemical behavior of the BFM can be reproduced by any model that incorporates the following physical ingredients.

Assumption A. The rotation of the motor is observed through a soft elastic linkage between the motor and the viscous load.

The soft linkage arises from the elasticity of the “hook” region connecting the rotor and the flagellum and the linkage between MotB and the peptidoglycan (see Fig. 1b) (12). The consequence of this compliant linkage is to allow the motor and the load to move on different characteristic time scales. When coupled to a large viscous load, the soft linkage produces the plateau region of the motor torque–speed curve.

Assumption B. Motor rotation and ion transport are tightly coupled.

First suggested by Meister et al. (13), this assumption is necessary to explain the linear pmf dependence at low speed, and the addition of equal increments of motor torque with each additional stator in resurrection experiments (14, 15).

Assumption C. The power stroke is driven by a conformational transition in the stator that is triggered by the protons hopping onto and off the stator, probably via the MotB residue, D32.

The proton motions are much faster than the mechanical motion of the stator, so the stator conformational movement is the rate-limiting step for the motor. This assumption also was suggested by Gabel and Berg to explain the nearly linear pmf dependence at high speed (8).

Assumption D. The ion channel through the stator is gated by the motion of the rotor.

That is, access of the periplasmic protons to the stator-binding site is triggered by a rotor–stator interaction. Consequently, the ion conductance through the stator varies with the motor speed. This assumption is necessary to explain the concave shape of the torque–speed curve, especially the sharp transition at the knee between the flat and decreasing regions.

Below, we will incorporate these requirements into a simplified model for the BFM and show that it fits the data (see Fig. 3); mathematical details of the model and corresponding structural details of BFM are given in Supporting Text, which is published as supporting information on the PNAS web site. Then, we discuss the correspondence between the model and known BFM structural information. We will see that the physics of the BFM motor torque–speed curve is not sensitive to the details and parameters of the model. Thus, the model should be viewed as a framework for studying the BFM, which can be further elaborated as new experimental inputs become available.

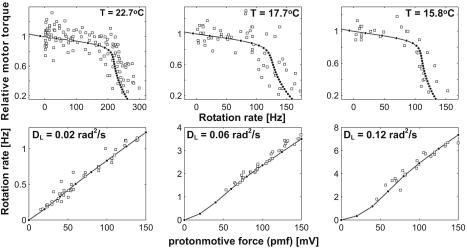
Fig. 3.

Comparison of model calculations and experimental data. (Upper) Experimental torque-speed curves at different temperatures (squares) (data from refs. 6 and 8). The filled dots are calculated from the model. (Lower) The linear dependence of the motor rotation speed with pmf at three different high loads. The experimental data (squares) are taken from Fung and Berg (10). The calculated results are shown as filled dots.

Consider first the situation with only one stator. The motor proteins constitute a system with many degrees of freedom (DoF). Most of the DoF are high-frequency modes compared with rotation, e.g., chemical bond vibrations. The effects of these DoF can be averaged out. However, some DoF have time scales comparable with rotation, for example, the diffusive motion of the stator about its equilibrium position due to elastic linkage between MotB and the peptidoglycan, and the internal conformational changes of the stator discussed below. The dynamics of the motor can be described by a set of multidimensional potentials of mean force as functions of these low-frequency DoF (16).

Current biochemical and structural studies imply that the motor torque is generated by conformational changes in the stator upon ion binding/unbinding to the negatively charged D32 residue on the MotB helices (see Fig. 4; see also Fig. 5, which is published as supporting information on the PNAS web site). This motion is transmitted to the rotor by means of interactions at the rotor–stator interfaces (see refs. 2 and 3 and references therein). The details of these interactions will remain vague until the atomic structure of the stator has been determined; currently the structures of but a few portions of the rotor are available (17–19). We will base our calculations on the rotor–stator interaction model proposed by Blair and coworkers (20, 21); however, we emphasize that our general conclusions depend only on the four assumptions listed above, not on the exact details of the stator model. For example, the mechanical escapement proposed by Schmitt and coworkers (22, 23) will work as well.

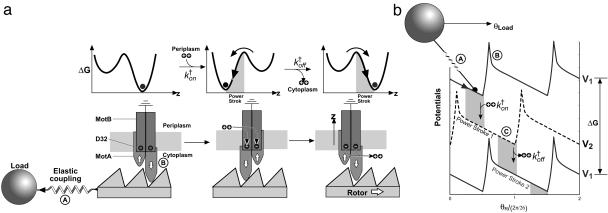
Fig. 4.

The rotor–stator interaction according to the model of Blair et al. (21). The stator assembly MotA₄/MotB₂ is a bistable system: two conformations are separated by an energy barrier. (a) Schematic illustration of one motor cycle. Step 1: at the end of previous cycle, D32 residues on the stator are unprotonated, and the stable conformation is as shown on the left; the cytoplasmic loop of one MotA (the right one in the figure) is down, engaging the rotor. Binding of two protons to the MotB D32 residues neutralizes them, allowing a thermally activated transition to the alternate conformational equilibrium to perform the first power stroke with the other MotA loop engaging the rotor. This process is characterized by the transition rate 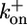, which is a composite of ion hopping on rates and the thermally activated conformational transition rate. Step 2: At the end of the first power stroke, the two binding protons are released to the cytoplasm. This transition triggers another conformational change of the stator so the (right) MotA loop engages to the rotor to perform the second power stroke. This process is characterized by the transition rate 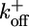, which is a composite of ion-hopping off rates and the thermally activated conformational transition rate. At the end of the cycle, the stator has returned to its conformation at the beginning of the cycle, with the rotor advancing one step to the right. On finishing one cycle, the cytoplasmic loop should traverse a closed cycle with nonzero area, as discussed previously on studying the F₁ motor (24). During the entire two-step cycle, the rotor is almost always engaged, so that the duty ratio is close to 1. The stator loops interact sterically with 26 copies of FliG arrayed circumferentially around the rotor. The asymmetry in the steric interaction determines the direction of rotation [reversals are triggered by reversing this asymmetry in response to CheY binding to the rotor (25); see Supporting Text]. The motion of the rotor is tracked by means of a large load (with drag coefficient ζ_L) attached to the motor via a compliant elastic linkage. This mechanism is only one of the possible schemes consistent with the mathematical model (see Supporting Text). (b) The driving potentials (free energies) of the stator corresponding to a are approximated by identical piecewise linear functions offset by half a wavelength 2π /26. Each transition between the two potentials initiates a power stroke, which, for simplicity, we model as a constant force. The soft elastic coupling between the rotor and the load is indicated by the spring, A. The sharp peaks in the potential labeled B may be due to steric interactions between FliGs and the MotA cytoplasmic loops that prevent thermal fluctuations from taking the system down the backside of the potential. The peaks ensure tight coupling between rotation and proton flux. Each motor cycle transports two ions from periplasm to cytoplasm, which decreases the free energy of the system by 2e × pmf and advances the rotor by 2π /26. The (shaded) transition regions specify the positions where the transitions between the potentials can take place. Labels A–C correspond to Assumptions A–C in the text.

To generate sufficient torque, we assume that one power stroke cycle of the stator is driven by the binding free energy of two protons to the two negatively charged D32 residues on the two MotB helices in the stator (see Movie 1, which is published as supporting information on the PNAS web site). In Blair's model, the cycle is accomplished in two “half” strokes as shown by the cartoon motor in Fig. 4a where two MotA loops alternate in contacting successive FliGs on rotor. Each downward stroke is followed by a recovery stroke, so that the two “pistons” alternate, and the stator is almost always engaged with the rotor; i.e., the duty ratio is 1. The binding energy of the protons to MotB is converted into a “flashing” electric field in the stator that triggers a pair of conformational transitions. The stator can be modeled as an asymmetric bistable system, alternating between two free-energy potential minima as shown in Fig. 4a. The power stroke is generated when the system passes the transition state separating the two potential minima and slides down to the other side. The torque thus generated is transmitted to the rotor when the MotA loops are in contact with the FliGs. The detailed dynamics of the motor can be described by the stochastic motion along the slow DoF driven by the multidimensional potentials of mean force. However, we will focus on the main physics revealed by the motor torque–speed relations without distracting details of the motor function, leaving more detailed descriptions for the future. This mechanism is only one of the possible schemes consistent with the mathematical model (see Supporting Text for discussion).

First, transitions between the two stator conformations require a thermally activated step that triggers the electrostatically driven power stroke. Fig. 4a shows the stator in the left or right potential minimum or, equivalently, the left or right MotA loops down in contact with FliG. Each transition is composed of two consecutive steps: ions hop onto and off the stator generating the flashing electric field that trigger the thermally activated barrier crossing over the transition state of the double well. This process is represented schematically in Fig. 4a Upper by switching between the double-well potentials. We shall assume that these transitions are well characterized by a set of rotor angular position (θ)-dependent composite rate constants k_on and k_off.

Second, we assume that most of the motor dynamics can be described by focusing on a set of one-dimensional “minimum energy paths” in the multidimensional space subtended by the relevant DoF at a given stator conformation [this assumption is related to the so-called reaction path Hamiltonian approximation (26)]. It should be pointed out that the minimum energy path is a reduced DoF, which includes the relative rotation between the rotor and the stator, the MotA loop motion, and the extension of the elastic connection of the stator to its periplasmic anchor (but see Supporting Text and see also Fig. 6, which is published as supporting information on the PNAS web site).

Results

Low-Speed Plateau. Analysis and simulations of the model equations show that, for a motor dragging a large load with a compliant elastic linkage, there exists a time-scale separation between the motor and the load dynamics: t_M << t_L (see Supporting Text). In rotation experiments, viscous loads are attached to the flagellar motor via the hook, which is soft enough to allow the rotor to fluctuate over several step lengths before the load moves appreciably (12). Distending the soft elastic linkage effectively converts the viscous load into a conservative load on the motor. That is, the work done to stretch the linkage can be returned to the motor before it is dissipated by the viscous load (see Fig. 7b, which is published as supporting information on the PNAS web site). The Stokes and thermodynamic efficiencies are defined as the ratios of the power dissipated by a viscous load (Stokes) or the rate of work done against a conservative load (thermodynamic), respectively, to the power consumed by the motor (27). The separation of time scales between the flagellar motor and the load renders the Stokes efficiency nearly equivalent to a thermodynamic efficiency. Thermodynamics dictates that 100% thermodynamic efficiency is approached as the system evolves “infinitesimally” slowly (i.e., reversibly). This requirement is satisfied with a large bead and a soft linkage even at rotation speeds of several hundred Hz, because the bead motion is still much slower than the motor internal dynamics. Furthermore, the soft hook and time-scale separation ensure that the load does not see the details of the free-energy potentials shown in Fig. 3b, but a nearly smooth effective potential. Thus, the measured Stokes efficiency also will be ≈100%, implying that the torque appears nearly constant (27). This region is the operating regime in the plateau of the flagellar motor torque–speed curve, in which the following approximation holds:

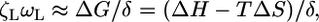[2]

where ω_L is the angular velocity of the load, δ = 2π /26 is the angular step length (i.e., distance between FliGs), and ΔG is the free-energy drop per motor cycle.

Why Does the Motor Torque–Speed Curve Drop Sharply at High Speed?

As the viscous load (e.g., a bead or the cell body) decreases, the tension between the load and the motor relaxes faster, and so the motor works against a smaller elastic load. An elastic load “shears” the potentials toward the left in Fig. 4b, and this shear decreases along with the load. Reduced load shifts the probability density distributions right toward the potential minimum, where the stator contributes zero, or even negative, torque. The average torque between the motor and the load (i.e., the motor torque) is determined by the potential gradients weighted by the probability density; therefore, the apparent motor torque decreases as the load decreases. However, this dependence does not guarantee a concave-down torque–speed curve, because both the motor torque and the rotation speed are affected simultaneously in a complicated way that depends on the potential shape as well as the chemical transition rates. The experimentally observed concave shape of the torque–speed curve in the transition region sets a loose constraint on the relation between the potential shapes and the chemical rates k(θ). The model system presented in this work is only one of the many possible realizations.

In the model we choose k(θ) to be localized around the potential minima of each potential curve (see Fig. 4b and Supporting Text). This localization arises because the ion channels open only at certain relative positions between the rotor and the stator. [Kojima and Blair (21) attribute this localization to charge interactions between the rotor and stator.] The sharp transition in the load–speed curve arises because of a positive feedback mechanism that can be understood as follows (see also Supporting Text and Fig. 6 a and b). At high load, the density function ρ(θ, θ_L) is distributed in the regions with negative potential gradient; thus, the effective chemical transition rate given by Eq. 6 is large. If the torque between the load and the motor decreases, the distribution shifts toward the potential minimum, which further reduces the effective chemical rate. Then, the diffusion of the load has more time to relax the elastic coupling between the load and the motor. This positive feedback mechanism contributes to the observed sharp transition from the regime where the dynamics is limited by the diffusion of the load to a regime where the motor is limited by the thermally excited triggering of the stator power stroke.

Nonlinear pmf Dependence at High Speed. The current model uses thermally excited transitions to describe both ion hopping onto and off the stator, and the corresponding thermally excited triggering of the stator conformational changes (power stroke) as a single step (see Fig. 8, which is published as supporting information on the PNAS web site). Because of this approximation, the model does not reproduce the linear dependence of speed on pmf at low load and high speed (see Fig. 9 a and b, which is published as supporting information on the PNAS web site). Separate treatments are necessary to explain the linear pmf dependence of rotation rate at high speeds (8). In Supporting Text, we use a simple theoretical analysis to show that nearly linear dependence is expected when the stator conformational change is the rate-limiting step (Fig. 9c). However, a definitive explanation awaits knowledge of the stator structure. Various experimental studies suggest the existence of two disconnected half channels open to the cytoplasm and periplasm, respectively (28). Therefore, we suggest that the slow step could be the transition of the MotA₄/MotB₂ complex from a conformation open to the periplasm to a conformation open to the cytoplasm (see Supporting Text).

Torque Speed vs. Stator Number. At high load the motor rotates slowly, and the elastic linkage is fully extended. Under these conditions, the motor is essentially working against a conservative load, and the motor torque is determined by the overall free-energy drop per motor cycle. Provided that the motor is tightly coupled, the motor is then operating close to thermodynamic equilibrium. Thus, the torque generated by several stators will be additive. Indeed, resurrection experiments show that each additional stator adds the same amount of torque, reinforcing the conclusion that ion transport and rotation within the flagellar motor are tightly coupled (15).

At higher rotation rates, the stator dynamics begins to affect the motor torque. While one stator finishes its power stroke, and before it can commence another power stroke, the rotor is being driven forward by other stators so that this stator impedes rotor rotation (the negative slope region in Fig. 4b). Consequently, stators may interfere with one another (as do myosins in a muscle fiber), and the rotation rate at which the motor torque drops zero may decrease as the number of stators increases (see Supporting Text and also Fig. 10, which is published as supporting information on the PNAS web site).

Discussion

In this work, we have demonstrated that the motor speed of the BFM as a function of motor torque and pmf does not depend on the details of the energy-transduction mechanism. We have constructed a mathematical model of the BFM based on the qualitative proposal by Blair and coworkers (21) that incorporates these requirements. Thus, our model is consistent with a large body of experimental observations on the BFM. However, any model that conforms to the listed requirements would do as well as ours.

A central aspect of the mechanochemical measurements summarized in Fig. 3 is that they are performed by observing the motor through the prism of an elastic compliance coupled to a viscous load. Elston et al. (29, 30) have given a detailed mathematical analysis of the role of a soft elastic linkage and time-scale separation on motor performance. The role of elasticity has been discussed by several other researchers in various contexts (31–33). A similar situation holds for other mechanochemical systems. For example, the F₁ motor of the F₁F_o ATPase achieves ≈100% Stokes efficiency when loaded with a long elastic actin filament and exposed to high ATP concentrations. In this situation, the motor dynamics is not rate limiting. However, when the ATP concentration drops, slowing the motor dynamics, the Stokes efficiency drops as well (34, 35). Another example is the motor that drives the gliding motility of the mollicute Mycoplasma mobile. This bacterium can move forward at an amazing speed of several cell-body lengths per second. By attaching to the bacterium a large polyethene bead, Miyata et al. (36) observed that the velocity increased linearly with temperature, exactly what one would expect when the motor is observed through the lens of an elastic compliance (the cell body) attached to a large viscous load.

Another notable feature of our model is the explanation it offers for the sharp transition between the two regimes of the torque–speed curve in terms of positive feedback between the external load and the angle-dependent transition rates between the stator kinetic states. The model makes the experimentally verifiable prediction that increasing stator number will actually decrease motor speed at zero loads.

Methods

The assumptions given above can be cast in form of a mathematical model. The dynamics of a single stator motor pulling a viscous load by means of an elastic linkage can be described by the following Langevin equation:

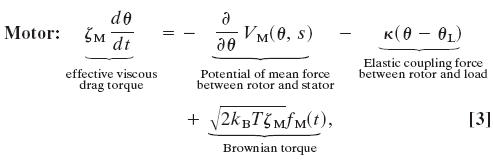
where ζ_M is the effective drag coefficient of the rotor. The viscous load (e.g., the bead in Fig. 4a) is coupled to the rotor via an elastic linkage, which is modeled by a harmonic potential, V_RL = ½κ(θ – θ_L)², where θ_L is the angular position of the load with respect to the rotor (compare Fig. 7a). The last term is the stochastic Brownian force acting on the stator, where f_M(t) is uncorrelated white noise (37, 38). V_M is the potential of mean force along the minimum energy path reexpressed as a function of the rotation angle θ, and s is a binary variable referring to the stator conformational state: right or left piston down. The slope of V_M determines the force profile the stator exerts on the rotor. This potential has not yet been measured, and so for simplicity we choose the two potentials V_M as identical periodic free-energy profiles, each offset by a half-period, as shown in Fig. 4b. The features of the potentials implement the requirements labeled A, B, and C in the cartoon. The high peak at the top of each potential ensures tight coupling between the rotor and stator by preventing a thermal fluctuation from carrying the system to the left and “wasting” a translocated proton. Structurally, this type of interaction is likely due to steric or electrostatic repulsion between an engaged (half) stator and the FliG proteins of the rotor (3). The switching between the two stator chemical states corresponds to switching between the two potential curves shown in Fig. 4b, which can be described by a Kramers jump process between the two stator potential minima.

Simultaneously, the motion of the load is described by the Langevin equation

Here the elastic coupling term appears with sign opposite that in Eq. 3, and ζ_L is the drag coefficient of the load. The last term is the Brownian force on the load. The characteristic time scale for the motion of the load is t_L = ζ_L/κ.

The model Eqs. 3 and 4 can be replaced by the equivalent coupled Markov–Fokker–Planck equations describing the probability density, ρ_j(θ_L, θ, t) of the rotor and load being at position (θ, θ_L) at time t in chemical state j when driven by a single stator (see Fig. 11, which is published as supporting information on the PNAS web site).

Here D_M and D_L are the diffusion constants of the rotor and the bead, respectively, related to the drag coefficients by the Einstein relation, ζ = k_BT/D.

Property D is implemented by the potentials in Fig. 4b by ensuring that chemical transitions between chemical states are localized to a band near the potential minima (shaded in Fig. 4b). Localizing the stator transitions implies that there is a timing mechanism that depends on a rotor–stator interaction so that the power strokes are delivered to the rotor near the optimal angular rotor position (see Fig. 12, which is published as supporting information on the PNAS web site). Blair et al. (3, 21) ascribe this property to a charge–charge pairing between the MotA cytoplasmic loop and the α-helix of FliG. Within this band, the most probable location where transitions take place varies with the rotor speed. This variation is because the effective transition rate is given by weighting the transition rate at each angle, θ, by the probability of being at that position

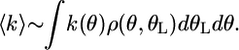[6]

Because of the elastic coupling to the load, the potentials in Fig. 4b will be sheared, skewing the probability density, ρ, and thus the most probable transition locus (see Fig. 6).

To ensure that the transitions obey detailed balance, the rate constants are modeled by

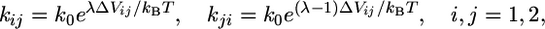[7]

where λ apportions the free-energy difference between forward and reverse rates; in our computations we set λ = 0.5. Note that in diagrams like Fig. 4b, the derivatives of the driving potentials specify the instantaneous torque generated at the rotor–stator interface: τ(θ) =–∂V/∂θ, and the vertical distances between the potentials in the transition region is the thermodynamic contribution from the proton-motive force, 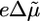(Eq. 1). Thus, the relative vertical distance between a pair of potentials in Fig. 4b gives ΔV_ij(θ), the free-energy change of each transition V_i → V_j in Eq. 7.

For N stators acting in parallel, the total number of chemical states S = 2^N. The stators are placed at an angular distance 2π i/N + Δθ_i round the periphery of the rotor, where Δθ_i is a uniformly distributed random number between [–2π /(26 × 2N), 2π /(26 × 2N)] to minimize the vernier effect (39). [Recent experiments show that, in E. coli, there can be up to 12 stators, and they need not be equally spaced (S. Reid, M. C. Leake, J. H. Chandler, C.-J. Lo, J. P. Armitage, and R.B., unpublished data); however, the stator number and distribution does not greatly influence the ability of our model to fit the data.] Then, for a given stator state configuration (s₁,..., s_N), the composite motor potential is

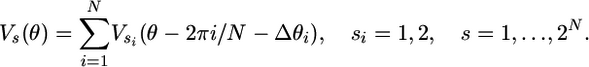[8]

Unless stated otherwise, all of the results shown in this work are computed with N = 8.

Results shown in Fig. 3 are obtained by least-square fitting the experimental data. Numerical calculations show that data fitting is not sensitive to the model parameters (see Table 1, which is published as supporting information on the PNAS web site) as long as the four requirements described above are satisfied. Computational details are given in Supporting Text. Uncertainty of the exact values of the rotor and stator diffusion constants does not affect our ability to fit the motor torque–speed relations, which are mainly determined by the much slower load diffusion constant and effective chemical transition rates.