The Kernel Energy Method: Application to a tRNA

Abstract

The Kernel Energy Method (KEM) may be used to calculate quantum mechanical molecular energy by the use of several model chemistries. Simplification is obtained by mathematically breaking a large molecule into smaller parts, called kernels. The full molecule is reassembled from calculations carried out on the kernels. KEM is as yet untested for RNA, and such a test is the purpose here. The basic kernel for RNA is a nucleotide that in general may differ from those of DNA. RNA is a single strand rather than the double helix of DNA. KEM energy has been calculated for a tRNA, whose crystal structure is known, and which contains 2,565 atoms. The energy is calculated to be E = –108,995.1668 (a.u.), in the Hartree–Fock approximation, using a limited basis. Interaction energies are found to be consistent with the hydrogen-bonding scheme previously found. In this paper, the range of biochemical molecules, susceptible of quantum studies by means of the KEM, have been broadened to include RNA.

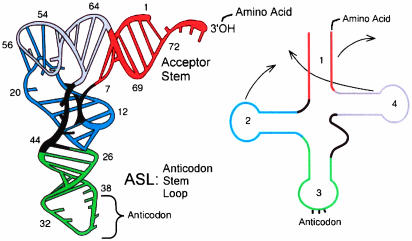
RNA (1) constitutes an important and wide-ranging class of biological molecules. A tRNA molecule is the particular subject of the Kernel Energy Method (KEM) calculation of this paper. tRNAs are composed of a single chain of RNA, 70–90 nt in length, folded into a characteristic L shape. tRNAs are composed of a single chain of RNA, 70–90 nucleotides in length, folded into a characteristic L shape, as in Fig. 1. The two ends of the RNA chain are close to one another at one end of the L-shaped structure, at the top in Fig. 1. An amino acid is attached there. The middle of the RNA chain length forms the anticodon loop, at the bottom of Fig. 1, exposing the three nucleotides that form an anticodon. The other two loops of the trefoil, pictured in Fig. 1 Right, fold in the tertiary arrangement of the tRNA into the corner of the L shape and stabilize the 3D structure of the molecule.

Fig. 1.

tRNA (from ref. 17).

The tRNA molecule is designed to attach to a codon at one end and to deliver an amino acid at the other end. The amino acid methionine is the initiating codon in the protein production process in the ribosome. Such an initiator tRNA is the subject of the energy calculation in this paper.

Given that the RNA molecules described above would be quite interesting to study by use of the techniques of quantum mechanics, the problem they present is their considerable size. That is the problem addressed here, by using the KEM approximation, whose main features are now reviewed.

In the KEM, the results of x-ray crystallography are combined with those of quantum mechanics. The result is a reduction of computational effort and an extraction of quantum information from the crystallography, not otherwise available. Central to the KEM is the concept of the kernel. These are the quantum pieces into which the full molecule is mathematically broken. All quantum calculations are carried out on kernels and double kernels. Because the kernels are chosen to be smaller than a full biological molecule, the calculations are easily accomplished, and the computational time is much reduced. Subsequently, the properties of the full molecule are reconstructed from those of the kernels and double kernels.

Initial studies (2–5) showed that the KEM is capable of achieving good accuracy over a range of different molecules and model chemistries. The background for uniting quantum mechanics with crystallography (6–13) and a review of work related to ours (8) are available in the literature.

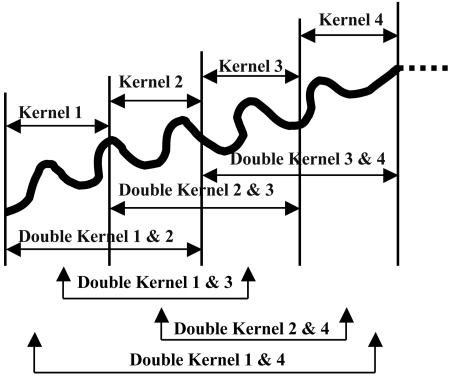
With known atomic coordinates, a molecule is mathematically broken into tractable pieces called kernels. The kernels are chosen such that each atom occurs in only one kernel. Schematically defined kernels and double kernels are shown in Fig. 2, and only these objects are used for all quantum calculations. The total molecular energy is reconstructed therefrom by summation over the contributions of double kernels reduced by those of any single kernels that have been overcounted. Two approximations have been found to be useful. In the simpler case, only the chemically bonded double kernels are considered, and the total energy E in this approximation is

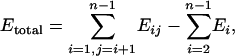[1]

where E_ij is energy of a chemically bonded double kernel of name ij; E_i is energy of a single kernel of name i; i, j are running indices; and n is number of kernels.

Fig. 2.

An abstract sketch of a polymer showing single and double kernels.

In the more accurate case, all double kernels are included, and the total energy is

[2]

where E_ij is energy of a double kernel of name ij; E_i is energy of a single kernel of name i; i, j, m are running indices; and n is number of single kernels.

The KEM is applied to a particular tRNA molecule below.

Energy of a tRNA Calculated by the KEM

The quantum mechanical molecular energy of a particular tRNA of known crystal structure (14) is calculated in this paper with the use of the KEM. The molecule chosen is the yeast initiator tRNA (ytRNA^Met_i), designated in the Protein Data Bank as 1YFG and in the Nucleic Acid Database as ID TRNA12. At the ribosome, protein synthesis requires an initial attachment of a special methionine-accepting tRNA at the P site of the peptide transfer center. Only such an initiator tRNA can donate the first residue in protein synthesis.

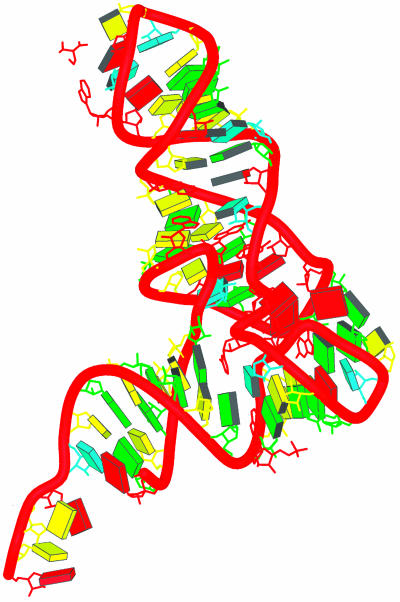
The tRNA 1YFG, pictured in Fig. 3, is such an initiator and the chosen subject of our calculation. The sequence definition of the yeast initiator tRNA is shown in Fig. 4, where the manner of defining the kernels for this molecule may be seen.

Fig. 3.

The crystal structure of tRNA, Protein Data Bank ID code 1YFG and Nucleic Acid Database ID TRNA12, has 75 residues. Each block represents a base of nucleic acid (C, yellow; U, cyan; A, red; and G, green) (adapted from the Nucleic Acid Database) (16).

Fig. 4.

tRNA sequence definition and the molecule divided into 19 single kernels.

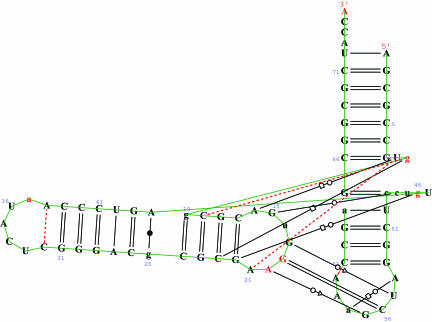
The structure of this molecule has been stabilized by a complicated network of hydrogen bonds, which have been identified through crystallography and are shown in Fig. 5, which was generated by the rnaview program (15).

Fig. 5.

The 1YFG tRNA H-bonding network and the sequence identifications of the types of base pairs (15) (adapted from the Nucleic Acid Database) (16).

tRNA provides a good test case for the application of the KEM to RNA molecular systems. The numerical results obtained in this work use the Hartree–Fock equation and a limited basis. Table 1 lists the results that follow from the application of Eqs. 1 and 2 to the initiator tRNA molecule 1YFG.

Table 1. Energy calculation for 1YFG(tRNA) by HF/STO-3G.

Molecule	No. of atoms	No. of kernels	EKEM* (Eq. 1), a.u.	EKEM† (Eq. 2), a.u.	ΔE = EKEM† — EKEM*, a.u.	ΔE per atom kcal/mol per atom
1YFG (tRNA)	2,565	19	-108995.1741	-108995.1668	-0.0073	-1.79 × 10-3

^*The double kernels included are only those made of single kernel pairs that are either chemically bonded or hydrogen bonded to one another.

^†All double kernels are included.

The molecule consists of 2,565 atoms, which have been broken into 19 kernels (shown in Fig. 4). Thus, the average number of atoms per kernel is ≈135, which is of such a size as to be readily calculable, whereas the original number of atoms, 2,565, is much less convenient to treat as a whole. Table 1 shows that the results of Eqs. 1 and 2 are quite close. They differ by only –0.0073 (a.u.) or –1.79 × 10^–3 [kcal/mol per atom]. This accuracy, achieved by Eq. 1 using Eq. 2, results as a standard, and requires taking into account the presence of hydrogen bonds in the structure of 1YFG. Thus, all of the pair interaction energies between kernels, arising from the hydrogen-bonding network, shown in Fig. 5, are added to the sum from Eq. 1. It may be concluded from Table 1 that the KEM allows for calculation of the Hartree–Fock energy in the case of an RNA molecule as large as the 2,565-atom initiator tRNA. Moreover, the results based on the simpler Eq. 1 approximation give a result very close in energy to that arising from the more complete Eq. 2. This mirrors our previous experience with peptides, a protein, and DNA (2–4). Eq. 1, augmented when necessary to account for hydrogen bonding (as in DNA and RNA), seems to closely approximate the results of Eq. 2. Because of the size (2,565 atoms) of the initiator tRNA, it has not been convenient to calculate the energy of the molecule as a whole, and therefore an absolute standard against which the results of Eqs. 1 and 2 may be judged is not available in this case. However, all our previous tests (2–5) have shown the KEM to be reliable. The use of the KEM approximation has created a calculation procedure for obtaining the quantum state of a molecule when the number of atoms is so great that it cannot be treated in its entirety by standard quantum chemical methods. This is an instance where the KEM has been applied as the lone method of obtaining the quantum energy of a molecule.

We turn now to the matter of the hydrogen-bonding network for the 1YFG initiator tRNA that has been established by crystallography (see Nucleic Acid Database ID TRNA12, in Derivative Data: Hydrogen Bonding Classifications), based upon the experimental distances between putative hydrogen-bonding donor and acceptor atoms. The KEM method should be able to substantiate the validity of such a hydrogen-bonding network based upon the interaction energies that prevail between kernels connected by hydrogen bonds. The interaction energy between a pair of kernels should be negative if that pair is stabilized by the presence of hydrogen bonds. Moreover, the magnitude of the interaction energy would be a measure of the hydrogen-bonding stabilization. The interaction energies between pairs of kernels are data automatically generated in the application of the KEM. Thus, an examination of the interaction energies associated with the kernels related to the hydrogen-bonding network of Fig. 5 is readily available. Table 2 lists all relevant interaction energies arising from kernel pairs that would contain the hydrogen bonds indicated in Fig. 5. The interaction energy, I, between kernels is defined as

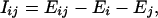[3]

where the symbols on the right-hand side of Eq. 3 retain their prior meaning.

Table 2. Double kernels and interaction energies between kernels corresponding to hydrogen bonding pairs.

Pair number	Pair name	Double kernel pair	Interaction energy (a.u.)
1	A_A1:U72_A	Kernel 1:Kernel 18
2	A_G2:C71_A	Kernel 1:Kernel 18	-0.134709
3	A_C3:G70_A	Kernel 1:Kernel 18
4	A_G4:C69_A	Kernel 1:Kernel 18
5	A_C5:G68_A	Kernel 2:Kernel 17
6	A_C6:G67_A	Kernel 2:Kernel 17	-0.128998
7	A_G7:C66_A	Kernel 2:Kernel 17
8	A_5MC49:G65_A	Kernel 12:Kernel 17	-0.040453
9	A_U50:RIA64_A	Kernel 13:Kernel 16
10	A_C51:G63_A	Kernel 13:Kernel 16	-0.126412
11	A_G52:C62_A	Kernel 13:Kernel 16
12	A_G53:C61_A	Kernel 13:Kernel 15	-0.036467
13	A_U55:G18_A	Kernel 5:Kernel 14
14	A_G57:A20_A	Kernel 5:Kernel 14	-0.041698
15	A_C56:G19_A	Kernel 5:Kernel 14
16	A_A38:C32_A	Kernel 8:Kernel 10
17	A_C39:G31_A	Kernel 8:Kernel 10	-0.027384
18	A_C40:G30_A	Kernel 8:Kernel 10
19	A_C41:G29_A	Kernel 7:Kernel 10	-0.038893
20	A_U42:A28_A	Kernel 7:Kernel 11
21	A_G43:C27_A	Kernel 7:Kernel 11	-0.049226
22	A_A44:M2G26_A	Kernel 7:Kernel 11
23	A_2MG10:C25_A	Kernel 3:Kernel 6
24	A_C11:G24_A	Kernel 3:Kernel 6	-0.112440
25	A_G12:C23_A	Kernel 3:Kernel 6
26	A_C13:G22_A	Kernel 4:Kernel 6	-0.032467
27	A_A14:U8_A	Kernel 2:Kernel 4	-0.027566
28	A_G15:5MC48_A	Kernel 4:Kernel 12	-0.026911

All H-bonding pairs, not involving chemically bonded double kernels, as named in the Nucleic Acid Database for the tRNA of this paper, i.e., NDB ID: TRNA 12. The kernel names are those defined in Fig. 4.

In every instance, the interaction energy is negative, consistent with a stabilizing hydrogen-bonding interaction between the kernels. Thus the energetics available from the KEM provides an independent confirmation of the hydrogen-bonding network obtained experimentally from crystallography.

Discussion and Conclusion

The 1YFG initiator tRNA molecule of this article was treated within the context of the ab initio Hartree–Fock approximation. The basis set used was a limited basis of Gaussian STO-3G type. A limited basis was chosen simply to make the energy calculations as convenient as possible. Previous numerical experience has shown that the KEM can be applied to a wide variety of molecular types with good accuracy. Therefore, it is expected that such accuracy would apply in this instance, in which the energy of the full molecule is not available as an absolute standard of comparison.

The special role played by hydrogen bonding in RNA molecules in general and in the tRNA of 1YFG in particular is discussed here. RNA is not a double helix but rather a single chain, which, on winding back upon itself, is able to form a network of hydrogen bonds among its own bases. The result in the case of the initiator 1YFG is a 3D structure that is stabilized in the characteristic L shape of tRNA molecules. In calculating the energy of such molecules by the KEM, the fundamental physical idea is that the energy of any given kernel is most affected by its own atoms and those of neighboring kernels. A pair of interacting kernels form a double kernel. The most important double kernels are those considered in Eq. 1, namely, those formed of “chemically bonded” single kernels. The phrase “chemically bonded” is meant to signify being bonded together by covalent bonds. However, here, because of its importance in the study of RNA structures, care must be taken to also include in the calculation the effect of Watson–Crick hydrogen bonding between base pairs. This is simply accounted for in the KEM, because the interaction energies between kernels are available as a byproduct of the calculation. The interaction energies between those kernels exhibiting hydrogen bonds are simply summed together with the pure Eq. 1 result to obtain the total energy. It may be mentioned in passing that the hydrogen-bonding interactions were accounted for in this way in the case of DNA molecules as well (4). Good accuracy was obtained from such use of Eq. 1 in the DNA cases that had been examined, where the exact energy for the full molecule was known. For best accuracy, however, all double kernels are calculated and used in Eq. 2. It is encouraging for general utility that Eq. 1 results correspond closely to those of Eq. 2, as indicated in Table 1.

In the KEM, the fragment calculations are carried out on double and single kernels whose ruptured bonds have been mended by the attachment of H atoms. A satisfactory occurrence in the summation of energies is that the total contribution of hydrogen atoms introduced to saturate the broken bonds tends to zero. This happens because the effect on the energy of the hydrogen atoms added to the double kernels effectively cancels that of the hydrogen atoms added to the pure single kernels, which enter with an opposite sign. This cancellation of the mending hydrogen atom energy effects contributes to the accuracy achieved by the KEM.

This paper describes a case wherein the KEM was used to make an ab initio calculation for an RNA molecule, whose size, as measured in number of atoms ≈2,565, would have made it inconvenient to calculate the molecule in its entirety. In future calculations, molecular complexity may present many instances such that the capacity of presently available computers and computer programs is far exceeded. In such cases, the modestly increasing computer time as N (number of atoms) grows, which characterizes the KEM, may be viewed as a valuable circumstance. In the KEM, the molecule is not calculated as a whole. It is only the kernels and double kernels that are calculated, and they are chosen to be very much smaller than the whole molecule. Moreover, because the method constructs a whole from the sum of the parts, it is especially suitable for parallel computation. Insofar as 1YFG initiator tRNA is representative of the RNA class of molecules, the results of this paper show that the KEM makes practical the quantum mechanical study of RNA molecular systems of considerable size.