Intrinsic backbone preferences are fully present in blocked amino acids

Abstract

The preferences of amino acid residues for φ,ψ backbone angles vary strikingly among the amino acids, as shown by the backbone angle φ found from the ³J(H_α,H_N) coupling constant for short peptides in water. New data for the ³J(H_α,H_N) values of blocked amino acids (dipeptides) are given here. Dipeptides exhibit the full range of coupling constants shown by longer peptides such as GGXGG and dipeptides present the simplest system for analyzing backbone preferences. The dipeptide coupling constants are surprisingly close to values computed from the coil library (conformations of residues not in helices and not in sheets). Published coupling constants for GGXGG peptides agree closely with dipeptide values for all nonpolar residues and for some polar residues but not for X = D, N, T, and Y, which are probably affected by polar side chain–backbone interactions in GGXGG peptides. Thus, intrinsic backbone preferences are already determined at the dipeptide level and remain almost unchanged in GGXGG peptides and are strikingly similar in the coil library of conformations from protein structures. The simplest explanation for the backbone preferences is that backbone conformations are strongly affected by electrostatic dipole–dipole interactions in the peptide backbone and by screening of these interactions with water, which depends on nearby side chains. Strong backbone electrostatic interactions occur in dipeptides. This is shown by calculations both of backbone electrostatic energy for different conformers of the alanine dipeptide in the gas phase and by electrostatic solvation free energies of amino acid dipeptides.

The origin of the differences among the intrinsic backbone preferences of the 20 aa is an unsolved puzzle, and these intrinsic preferences (1–6) are an important part of the local structure (7, 8) in unfolded peptide chains that may be used to guide the folding process at early stages of folding. The “intrinsic” conformational preferences are specified by the backbone φ,ψ angles found in short peptides and in the “coil library” (1–6) of Protein Data Bank residue conformations for residues outside repetitive secondary structures (helices, sheets). The existence of different backbone preferences in short peptides in water is demonstrated by values of the backbone angle φ, which can be measured by NMR from the ³J(H_α,H_N) coupling constant (vicinal coupling constant between C_αH and NH protons) by using the Karplus relation (9). These coupling constants are averaged over all backbone conformations that are present. Individual φ-values are obtained for residues in the coil library of the Protein Data Bank, and corresponding values of ³J(H_α,H_N) are found from the Karplus relation and then averaged. In the coil library of Smith et al. (3), average values of ³J(H_α,H_N) range from 5.9 Hz for Gly and 6.1 Hz for Ala to 7.7 Hz for Val. In addition to the different intrinsic backbone preferences, there is a substantial neighboring residue effect: φ angles are shifted toward more negative values if the neighboring residues are aromatic or β-branched (FHITVWY) than if they are not (10, 11). Any attempt to explain the different intrinsic backbone preferences of the amino acids should also give an explanation for the neighboring residue effect. The electrostatic screening model (see below) has been shown to give a plausible explanation for the neighboring residue effect (11).

The purpose of this article is to present data for the ³J(H_α,H_N) coupling constants of the amino acid residues in dipeptides (blocked amino acids) and to consider the meaning of this result for different hypotheses regarding the origin of the different backbone preferences. Disfavored backbone conformations that arise from steric clash between neighboring side chains (12, 13) have been suggested as a main source of local structure in unfolded peptides. More recently steric hindrance to the formation of H-bonds between peptide groups and water molecules has been found to be a major cause of disfavored backbone conformations (14) in Protein Data Bank structures. The disfavored backbone conformations are uncommon in tripeptide segments but become increasingly frequent in tetra and higher peptide segments (14), which suggests that this type of disfavored backbone conformations (over and above those found in the Ramachandran plots for dipeptides) are rare in dipeptides. Pairwise attractive interactions between side chains, which are well known in α-helices (15), have been proposed as a significant source of local structure in unfolded peptides (8). H-bonds between polar side chains and especially backbone –NH groups occur commonly in helix capping (16) and may occur in short peptides. Amino-aromatic, or “pseudo-H-bond,” interaction (17) between a tyrosine ring and the peptide –NH of a nearby glycyl residue was reported for peptides containing the sequence Tyr-Xaa-Gly (18).

The alternative to side chain interactions as an explanation for diverse backbone preferences is electrostatic dipole–dipole interactions in the peptide backbone and side chain-dependent screening of these interactions by water (5, 11, 19–22). We demonstrate that this explanation is plausible for peptides as short as dipeptides by computing values of the backbone electrostatic energy for different conformers of the alanine dipeptide in the gas phase, with the aid of four published ab initio studies (23–26), and also by using delphi (27) to compute the electrostatic solvation free energies (ESF values) in water of the various amino acid dipeptides. The electrostatic screening model (5, 20), which can explain the backbone conformations in highly unstructured peptides, is based on a 1995 proposal by Avbelj and Moult (21) that was developed further by Avbelj (20). The electrostatic screening model proposes that three physical factors are dominant in determining backbone conformations in highly unstructured peptides. The three factors are (i) the local electrostatic energy (E_local) at a given site within the backbone; (ii) the ESF at that site, which depends on the screening interaction of water dipoles with the polar peptide group; and (iii) the torsional potentials V(φ), V(ψ) about the backbone φ and ψ angles.

Results and Discussion

Properties of Dipeptide Coupling Constants. The dipeptide coupling constants ³J(H_α,H_N) (Table 1) have been measured at two pH values (4.9 and 2.9) at 30°C to test for the influence of pH on the coupling constants of ionizable residues. Large changes (≈0.5 Hz) with pH are observed for Asp and Glu; at pH 4.9 both residues should be more than half ionized (28). The intrinsic backbone preferences of these amino acids depend strongly on whether they are neutral or ionized. The coupling constants of these two residues (and probably also of His) can be compared with values for other peptides only if the pH and other solution conditions are identical or if the residues are either fully ionized or not ionized. A small change (0.13 Hz) is observed for His between pH 2.9 and 4.9; His should be almost fully protonated at pH 4.9. The value for His is concentration dependent at pH 4.9 and the reason is not known, but the value at pH 2.9 is concentration-independent and differs only slightly from the 4.9 value. A small change (0.08 Hz) is also observed for Gln; but otherwise, the values at pH 2.9 and 4.9 agree within 0.05 Hz for all amino acids (Pro was not measured), as expected from the estimated accuracy (±0.05 Hz) of the coupling constants.

Table 1. ³J(H_N,H_α) coupling constants (Hertz) in water and coil library data.

Residue	Dipeptide* pH 2.9	Dipeptide* pH 4.9	Coil†	GGXGG‡ GdmCl	fβ-coil§	fβ-uls¶
Gly	5.90	5.85	5.720	N.D.	0.031	0.291
Ala	6.02	6.06	6.075	6.1	0.144	0.271
Val	7.32	7.30	7.547	7.2	0.392	0.534
Ile	7.37	7.33	7.495	7.1	0.359	0.500
Leu	6.84	6.88	6.991	6.8	0.201	0.345
Phe	7.17	7.18	7.351	7.3	0.304	0.506
Met	7.09	7.02	6.974	7.1	0.230	0.401
Trp	6.92	6.91	7.007	7.0	0.257	0.453
Cys	7.30	7.31	7.103	7.3	0.259	0.437
Ser	7.05	7.02	6.615	7.0	0.221	0.421
Thr	7.32	7.35	7.642	7.9	0.296	0.538
Asn	7.50	7.45	7.294	7.7	0.153	0.424
Gln	7.06	7.14	7.050	7.1	0.223	0.430
Tyr	7.12	7.13	7.318	7.8	0.286	0.484
His	7.76	7.89	7.177	7.2	0.248	0.505
Asp	7.51	6.93	6.931	7.8	0.132	0.322
Glu	7.02	6.63	6.495	6.7	0.174	0.351
Lys	6.85	6.83	6.920	7.0	0.229	0.447
Arg	6.91	6.85	6.920	6.9	0.229	0.440

^*The dipeptide coupling constants are independent of peptide concentration, both at pH 2.9 and 4.9, except for the value of His at pH 4.9. The temperature is 30°C. The pH 4.9 values of the dipeptide coupling constants (J-dipep) are discussed in the text.

^†Average coupling constants (J-coil) computed from residue φ-values in the coil library (see Materials and Methods).

^‡These coupling constants (29) (J-GGXGG) were measured for residue X in blocked GGXGG peptides in 6 M GdmCl (pH 5.0) at 20°C.

^§The fraction of residues in the coil library β basin (-180° < φ < -100°; 90° < ψ < 180°) divided by all residues in the φ, ψ map of this amino acid type.

^¶The fraction of residues in the coil library β basin when divided by the number of residues in the upper left strip (-180° < φ < 0°; 90° < ψ < 180°) of the φ, ψ map.

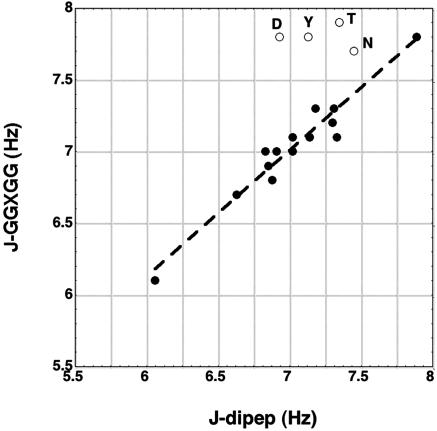
Table 1 compares the pH 4.9 dipeptide coupling constants (J-dipep) with those measured by NMR for blocked GGXGG peptides in 6 M guanidinium chloride (GdmCl) (pH 5.0) at 20°C (29). Fig. 1 shows good agreement between the two sets of coupling constants for all nonpolar amino acids and some polar amino acids. The values agree within ±0.15 Hz, the sum of the expected errors, except for Thr (0.55 Hz), Asn (0.25 Hz), Tyr (0.67Hz), and Asp (0.87 Hz). Besides Tyr, these polar residues occur with high frequency at specific N-terminal position(s) within protein helices (16) and are known to make H-bonds with peptide –NH groups. Thus, the coupling constant differences between dipeptides and GGXGG peptides are probably caused by side chain–backbone interactions in the GGXGG peptides but not in dipeptides. The Tyr ring is known to make a strong amino-aromatic interaction (17) with the peptide –NH of a nearby Gly residue, although 6 M GdmCl is expected to weaken the interaction (18). The coupling constants of another, smaller set of GGXGG peptides were measured in 8 M urea (30).

Fig. 1.

The ³J(H_α,H_N) coupling constant (in Hertz) measured for GGXGG peptides (29) in 6 M GdmCl plotted against pH 4.9 dipeptide values (R = 0.97). See text for why four polar residues (Asn, Asp, Thr, and Tyr; open circles) are outliers.

Table 2 compares the values of ³J(H_α,H_N) for the alanine and valine dipeptides in water with values for two nonpolar solvents, dioxane and CCl₄. The values of ³J(H_α,H_N) for dioxane and water agree well with a 1980 study by Madison and Kopple (31) of the alanine dipeptide; they reported also values of ³J(H_α,H_N) for five other solvents. They studied both the proline and alanine dipeptides and made CD as well as NMR measurements. They concluded that the main backbone conformation of the alanine dipeptide in water resembles that of the proline dipeptide, which is expected to have the polyproline II (P_II) conformation. The single alanine residue of GGAGG has recently been shown to have chiefly the P_II conformation in water (32). In nonpolar solvents, such as dioxane and CCl₄, both the alanine and proline dipeptides are believed to form internal H-bonds (31) whereas the high coupling constants (Table 2) suggest the presence of the β conformation. As shown by their coupling constants, the average backbone conformation of the valine dipeptide differs somewhat from that of the alanine dipeptide in all three solvents, water, dioxane, and CCl₄ (Table 2).

Table 2. ³J(H_N,H_α) coupling constants (Hertz) in two nonaqueous solvents versus water.

Dipeptide	CCl4	1,4-Dioxane	Water
Ala	7.51	8.00	6.06
Val	8.67	9.18	7.30

The value of ³J(H_α,H_N) for the alanine dipeptide in water increases with temperature from 5.70 Hz at 7.0°C to 6.15 Hz at 38.7°C and then increases more slowly as the temperature rises to 67°C (data not shown). This temperature-dependent behavior is similar to that reported for the single alanine of GGAGG (33).

Coil Library Coupling Constants. Because the coil library contains the distribution of φ-values for each amino acid type, it may be used to study how backbone preferences for φ are related to coupling constants. Note that the coil library coupling constants (Table 1) are quite similar to values measured for dipeptides and for GGXGG peptides. Note also that the neighboring residue effect is similar in the coil library and in short peptides in water (10, 11). The explanation for the similarity between backbone conformations in the coil library and in short peptides in water may be that “proteins are constructed from low energy parts” (34), and this maxim applies to backbone φ,ψ angles just as it does to side chain rotamers.

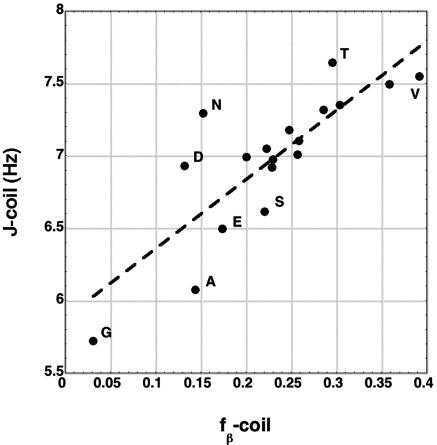
In the coil library, the average coupling constant (J-coil) computed from the φ,ψ map for each amino acid should depend especially on the fraction of residues in the β-basin, f_β-coil, because of the large J-value of β. There are just three basins in the φ,ψ map that are well populated for most amino acids: β (φ = –120°, J = 9.6 ± 0.3 Hz), P_II (φ =–75°, J = 5.8 ± 0.4 Hz), and α_R (φ = –60°, J = 3.8 ± 0.5 Hz). Thus, the J-value of β is considerably larger than those of P_II and α_R. For Gly, Asn, and Asp (and Lys), the α_L basin is also significantly populated with φ =+60°, J = 5.8 ± 0.4 Hz. The J-values and the ± figures refer to the range given by four different parameterizations of the Karplus relation (see Materials and Methods) when rigid conformations with specific values of φ are considered. Similar but somewhat different values for flexible molecules in solution are given by experimental data deposited in the BioMagResBank database (www.bmrb.wisc.edu): β, 8.50 Hz; P_II, 5.24 Hz; α_R, 5.07 Hz (F.A., unpublished). Fig. 2 shows a reasonably good linear correlation (R = 0.82) of J-coil versus f_β-coil (see Table 1), confirming that J-coil does depend significantly on the fraction of residues in the β-basin.

Fig. 2.

The coil library coupling constant is plotted against the fraction of coil library residues in the β-basin (R = 0.82). The major outliers are labeled.

There are reasons to suspect that the α_R basin is not well populated for short peptides in water even though it is well populated in the coil library when reverse turns are included (3). When reverse turns are removed from the coil library (6), the only well populated “core” conformation remaining is P_II (see Fig. 3) (6), and the α_R and β basins are populated only diffusely. When adjacent α_R residues are present in short peptides in water, they can be detected by an (i, i + 1) NH-NH nuclear Overhauser effect, but an NMR study of a seven-residue alanine sequence (4) found no NH-NH (i, i + 1) nuclear Overhauser effect, indicating that the population of adjacent α_R residues is <10%. Electrostatic calculations show that the α_R conformation has an unfavorable backbone electrostatic energy (E_local) (21) provided that helical H-bonds are not formed; screening by water does, however, improve the stability of the α_R conformation (20). These considerations focus attention on whether the upper left strip of the φ,ψ map (uls) (–180° < φ < 0°; 90° < ψ < 180°) that contains just the β and P_II basins is the only well populated region for short peptides in water. NMR and CD study of short alanine sequences (4, 33) in water found that P_II is the only well populated basin for alanine residues at 0°C and that a partial thermal transition from P_II to a β-like conformation occurs with increasing temperature.

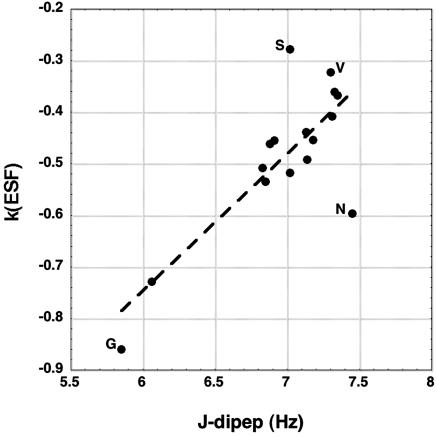
Fig. 3.

k(ESF), taken from the slope of ESF versus E_local for central residues of randomly generated tripeptides (20), is plotted against the dipeptide coupling constants (R = 0.80). The major outliers are labeled. The J-dipep values for Asp, Glu, and His are omitted because ionization is expected to affect J-dipep strongly for these amino acids (see text) whereas the ESF values were computed for the neutral forms.

When the coil library φ-values are taken only from the upper left strip of the φ,ψ map, the plot of J-uls versus f_β-uls gives an improved linear correlation (R = 0.90; data not shown) compared with the plot of J-coil versus f_β-coil (Fig. 2), which is taken from the entire φ,ψ map. This result is useful in showing that, when only residues in the upper left strip are considered, there is a strong dependence of the average J-value on the fraction of residues in the β-basin. Indeed, the dipeptide coupling constants give a reasonably good linear plot of J-dipep versus f_β-uls (R = 0.80; data not shown), suggesting that the pattern of f_β-values is similar for short peptides in water and for the upper left strip of the coil library φ,ψ map. The plot of J-dipep versus f_β-coil is less good (R = 0.66; data not shown).

Relation of Coupling Constants and Coil Library Data to the Electrostatic Screening Model. In the electrostatic screening model (5, 20, 21), the ESF of a peptide group is amino acid specific. The ESF depends on the access of the peptide group to water, and water screens the electrostatic dipole–dipole interactions made by adjacent peptide groups. A small residue like alanine provides better access to water and therefore has a larger negative ESF value than a β-branched residue like valine (20, 21). The ESF varies in an approximately linear manner with E_local (20) (the local backbone electrostatic energy), and the slope of the plot of ESF versus E_local, denoted here by k(ESF), is amino acid-specific and linearly related (20) to the “screening coefficient” of the amino acid residue defined earlier (21). The plot of k(ESF) versus J-dipep (Fig. 3) shows a clear linear correlation (R = 0.80), indicating that the backbone preferences expressed in the J-dipep values are related to those predicted by the electrostatic screening model (5, 20–22). The J-dipep values for Asp, Glu, and His are omitted in Fig. 3 because the J-dipep values were measured for the partly or fully ionized forms whereas the ESF values were calculated for the neutral forms. Table 1 shows a strong dependence of J-dipep on the extent of ionization for Asp and Glu, whose charged groups are near the backbone, and a similar effect is expected for His; the charged groups of Lys and Arg are more remote. Values of k(ESF) are taken from table 2 of ref. 20. for the central residues of a large number of randomly generated tripeptides. Different sets of assumed values of the partial charges on the peptide group were examined (20), and the k(ESF) results shown here (Fig. 3) refer to the PARSE partial charges that are used in delphi (27).

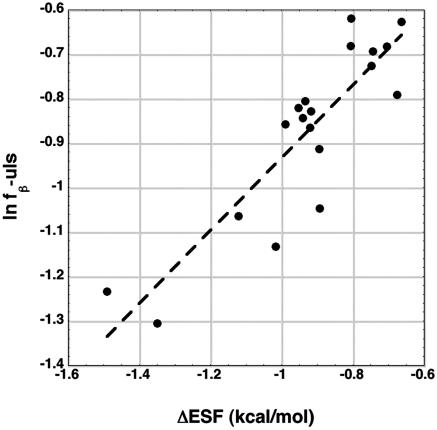
As noted above, the J-dipep values may be determined chiefly by residues in just the upper left strip of the φ,ψ map, and a significant dependence of J-dipep on f_β-uls is observed. Earlier studies of the relation between the electrostatic screening model and the coil library (5, 11) indicated that f_β-uls should depend on ΔESF, the difference between ESF(P_II) and ESF(β), and specifically that ln f_β-uls should show a nearly linear dependence on ΔESF. The data given here for f_β-uls (Table 1) allow this proposal to be tested for the coil library. Fig. 4 shows a good linear plot (R = 0.88) of ln f_β-uls versus ΔESF, using the dipeptide ESF values. This result supports the earlier proposal (5, 20–22) that the electrostatic screening model can predict how an amino acid is distributed between the P_II and β-basins of the coil library.

Fig. 4.

The y axis refers to the fraction of residues in the coil library β basin, which is divided by the number of residues in the upper left strip of the φ,ψ map. The logarithm of this fraction is plotted against the difference in ESF between the P_II and β backbone conformations, ESF(P_II) – ESF(β), for dipeptides (R = 0.88).

Earlier Studies of Backbone Preferences. From the 1960s onward, it was evident that some data for backbone preferences of the amino acids clash with the prevailing random coil model for unfolded proteins. Flory's (35) 1969 definition of a random coil polymer states that a random coil has no strongly preferred backbone conformation and “differences in energy between alternative rotational configurations about a given bond are usually of the order of RT.” Tanford's (36) 1968 summary of his influential work on the properties of denatured proteins was interpreted by a random coil model. Nevertheless, Schellman and Schellman (37) had earlier (1964) pointed out that denatured proteins are not likely to be random coil molecules because of their distinctive optical rotatory dispersion (the forerunner of the modern CD spectrum), which suggests that at most a few backbone conformations are well populated. In 1970, Madison and Schellman (38) reported that both the optical rotatory dispersion and CD spectrum of a proline diamide are closely related to those of P_II, indicating that this dipeptide has a well defined backbone preference and therefore that dipeptides might be good models for the backbone preferences of the amino acid residues in proteins. The Schellman laboratory then explored the possibility that the CD spectra of dipeptides with closed-ring side chains (39) might be used to relate CD spectra to φ,ψ maps. In 1973, Tiffany and Krimm (40) pointed out that the typical CD spectrum of denatured proteins closely resembles that of P_II, and three decades later this subject became a lively research field [see review by Shi, Woody, and Kallenbach (41)].

Modern work on backbone preferences is better known and is reviewed here only briefly. In 1995, Swindells, MacArthur, and Thornton (1) found that the “coil” segments of Protein Data Bank structures give backbone preferences (1) that are related to the Chou–Fasman statistical frequencies of amino acids in α-helices and β-sheets. Serrano (2) then reported that ³J(H_α,H_N) coupling constants measured in peptides give similar values as those computed from the coil library. In this period, the “extended-β” (–120°, 120°) and P_II (–75°, 145°) conformational basins were often not analyzed separately but rather included together within a broad distribution of β conformations (3). Interest in the P_II conformation as a major backbone conformation of short peptides and denatured proteins grew rapidly after 2000 (for review, see ref. 41).

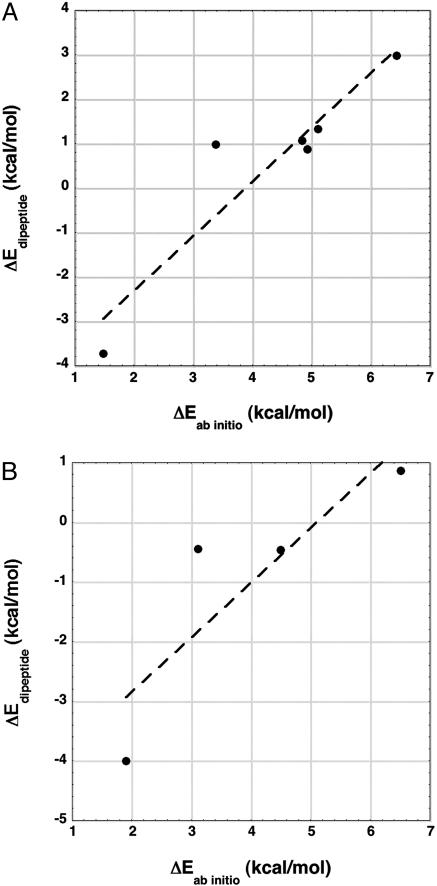
Comparison Between Electrostatic Energy and ab Initio Energy for Conformers of the Alanine Dipeptide. The backbone electrostatic energy of the alanine dipeptide (E_dipeptide) has been computed for various conformers in the gas phase by taking the conformer geometry determined in an ab initio study and using Coulomb's law with atom-centered partial charges (see Materials and Methods). Fig. 5A compares the difference in E_dipeptide between stable gas phase conformers of the alanine dipeptide with the difference in conformational energy (E_{ab initio}) for six conformers (25). The conformer coordinates were not published (25), and the geometries of the conformers were built by using bond angles and distances from discover library (Accelrys, Inc., San Diego). Fig. 5B shows corresponding data for a study (24) in which the conformer coordinates were published but which has only four conformers that can be shown here. The data points for the C7_eq and C7_ax conformers are omitted because they have internal H-bonds and Coulomb's law does not represent these H-bond energies satisfactorily in the calculation of E_dipeptide.

Fig. 5.

The calculated backbone electrostatic energy difference (ΔE_dipeptide, see Materials and Methods) is plotted against the ab initio conformational energy difference (ΔE_{ab initio}) for various gas phase conformers of the alanine dipeptide, taken from ab initio studies in the literature. The geometry of each conformer, which is used in calculating E_dipeptide, is taken from the ab initio study. Similar results are obtained for two other ab initio studies of the alanine dipeptide (data not shown; see text). The data points for the C7_eq and C7_ax conformers are omitted because these conformers have an internal H-bond, whose energy is not well represented by using Coulomb's law. (A) In this study (25), data for six conformers could be shown here. The conformer coordinates were not published, and their geometries were built by using bond angles and distances from discover library. The slope of the line is 1.22 (R = 0.93). (B) In this study (24), data for four conformers could be shown here, and the published conformer coordinates could be used to give the conformer geometry. The slope of the line is 0.92 (R = 0.87).

Surprisingly, the difference in E_dipeptide is proportional to, and approximately as large as, the difference in E_{ab initio}, which includes other energetic contributions such as torsional energy from rotation about the φ and ψ backbone bonds. Similar results, showing a proportionality between E_dipeptide and E_{ab initio}, were obtained from two other ab initio studies (23, 26) of the alanine dipeptide. The slope of the line in Fig. 5A is 1.22, with a correlation coefficient of 0.93, and the slope of the line in Fig. 5B is 0.92, with a correlation coefficient of 0.87. In the other two studies, which have data for four conformers when C7_eq and C7_ax are excluded, the slope ranges from 1.54 (23) to 1.86 (26). All four ab initio studies indicate that E_dipeptide is proportional to E_{ab initio} and the backbone electrostatic energy is large, accounting for a large part of the variation in E_{ab initio} among conformers of the alanine dipeptide. In some cases, the slope is larger than 1 (23, 25, 26), which is unexpected; further work is needed to find the explanation. Note that a dielectric constant of 1 is used in calculating E_dipeptide.

In aqueous solution, the electrostatics are very different from the gas phase because the backbone electrostatic energy is screened by water, like the screening described by the Born equation (42) for an ion in water. Solvation of the alanine dipeptide has been studied ab initio in the presence of four water molecules (43) or with the polarizable continuum model (44) or with a hybrid quantum mechanics/molecular mechanics model (45). The Born equation considers the case when a spherical ion is fully exposed to solvent and water is treated as a continuum solvent. The Born equation gives the fractional extent of screening by water as [1 – (1/D)] = 0.987 at 25°C (D = 78.5). Screening of backbone electrostatic energy in aqueous solution can be evaluated from the screening coefficients computed by Avbelj (20), whose results show that the electrostatic energy of the peptide backbone is screened much less by water than for the ions considered in the Born equation (20).

Conclusions

The intrinsic backbone preferences of the amino acid residues are fully present in blocked amino acids, according to new measurements of ³J(H_α,H_N) for dipeptides, and dipeptides provide the simplest system for analyzing intrinsic backbone preferences. Because pairwise side chain interactions are eliminated and polar side chain–backbone interactions are made improbable as possible explanations for the backbone preferences, the electrostatic screening model becomes the probable explanation. Calculations show that this model is applicable to peptides as short as dipeptides. There are large differences in backbone electrostatic energy between conformers of the alanine dipeptide in the gas phase and the electrostatic dipole–dipole interactions are screened by water in a side chain-dependent manner, giving dipeptide ESF values that differ substantially among the amino acids. The dipeptide coupling constants are correlated with ESF values calculated earlier (20) for randomly generated backbone conformations.

Materials and Methods

Materials and Sample Preparation. Blocked amino acids (e.g., acetyl-Ala-N-methylamide) were purchased from Bachem or Biosyn or otherwise were synthesized from the corresponding methylester by using methylamine at 0°C. NMR samples had 20 mM peptide in 90% H₂O/10% D₂O and either 0.005 M citric acid (pH 2.9) or 0.03 M Na citrate/0.02 M citric acid (pH 4.9). Samples in 1,4-dioxane-d₈ had 20 mM Ala dipeptide or 10 mM Val dipeptide. Samples in CCl₄ had <1 mM peptide because of poor solubility, and external locking was used with a CDCl₃ stem coaxial insert. Concentration dependence was studied between 1 and 20 mM peptide.

NMR Spectroscopy. Coupling constants ³J(H_α,H_N) were measured from 1D-¹H spectra at 30°C in a Varian INOVA 600-MHz spectrometer. The spectral width was 6,000 Hz with 64,000 data points, zero filling to 128,000 data points and 32 scans. Except for glycine dipeptide, coupling constants were measured from H_N resonances, and a band-fitting algorithm was used to calculate the peak frequency of the broad H_N doublet. NMR spectra were processed without filter function to allow selection of the pure Lorenzian lineshape in the fitting procedure (grams program, Thermo Electron, San Jose, CA). Band frequencies, bandwidths, and intensities were allowed to vary simultaneously with no restrictions. The parameters determined in this way were tested by the fitting program based on the maximum entropy algorithm. The coupling constants of the Ala and Val dipeptides were cross-checked by determining them by a second method, based on the well resolved H_α doublets found by decoupling the H_β resonances. The accuracy of the coupling constants is believed to be ±0.05 Hz.

Backbone Electrostatic Energy and ESF. There are several ab initio studies in the literature of conformational energies of stable conformers of the alanine dipeptide in the gas phase. We compare the ab initio energy difference between two conformers with the corresponding difference in backbone electrostatic energy, calculated by Coulomb's law using fixed, atomcentered partial charges and a dielectric constant of 1. To demonstrate generality, we selected four studies with the following levels of theory: MP4/cc-pVTZ(-f) (23), MP2/aug-cc-pVDZ (24), MP2/aug-cc-pVTZ (25), and MP2/6–311++G** (26). The backbone electrostatic energy, which is the total electrostatic energy (E_dipeptide) of the dipeptide, was calculated for various conformations of the alanine dipeptide in the gas phase by using the conformer geometries determined in various ab initio calculations of conformational energy. When the conformer coordinates were not published, the conformer geometries were built by using standard bond angles and distances from discover library. The point atomic charges for the main chain atoms N, H_N, C, and O were equal to –0.28, +0.28, +0.38, and –0.38, respectively, electron charge. Interactions between point charges within a single peptide group were omitted.

The ESF of the two peptide groups in the different amino acid dipeptides was calculated as discussed by Avbelj (5, 20), using the delphi (27) algorithm with water treated as a continuum solvent. The partial charges on the side chains were set = 0 [“PARSE neutral” calculations (20)], and only the ESF values of the peptide groups were calculated.

Coil Library. The coil library used here is described in refs. 5 and 11. Average coupling constants computed from the coil library were found as described in ref. 5.