Theory of the deuterium NMR of sterol–phospholipid membranes

Abstract

A general theoretical model is described for the NMR spectra of mixtures of sterols and deuterium-labeled phospholipids. In the case of homogeneous membranes, the average quadrupole splittings are determined by equilibria between lipids in cholesterol–phospholipid complexes and lipids not in complexes. Chemical exchange of lipids between those in the free state and those in the complex state affects the deuterium resonance line shapes. The lifetime of a phospholipid molecule in an ergosterol–dipalmitoylphosphatidylcholine complex is estimated to be of the order of 10^–5 s on the basis of the observed line broadenings. In the vicinity of a critical point of a cholesterol–phospholipid mixture, fluctuations in the concentration of complexes also can contribute to the deuterium nuclear resonance line broadening. At the critical point, the temperature derivative of the concentration of complexes is discontinuous. There is a corresponding jump in the calculated heat capacity as well as in the temperature derivative of the deuterium NMR first moment.

In a number of studies, it has been proposed that several physical chemical effects of cholesterol (C) on bilayer membranes can be understood in terms of the formation of complexes between C and some classes of phospholipids (1–12). Of particular significance here is the proposal of Phillips and coworkers (5, 6), who suggested that clusters of complexes give bilayers that are heterogeneous along their plane. We have introduced the term “condensed complex” to recognize the well known effect of C in suppressing gauche conformations of the fatty acid chains of phospholipids in the liquid state of bilayers (11, 12). A thermodynamic model was developed to describe this complex formation, using as quantitative guides the phase diagrams that have been determined for C–phospholipid mixtures in monolayers and bilayers (11, 12). In the present work, we show that specific features of the NMR of deuterium-labeled lipids can be accounted for in terms of the kinetic properties of these complexes.

The early deuterium NMR study of Vist and Davis (13) used binary mixtures of C and dipalmitoylphosphatidylcholine (DPPC). The DPPC had perdeuterated fatty acid chains. Their spectra showed an increasing deuterium quadrupole splitting with increasing C concentration, corresponding to the C-mediated ordering of the fatty acid chains of the phospholipid. In addition, the spectra showed enhanced NMR linewidths at intermediate sterol concentrations. A similar and even more pronounced line broadening at intermediate C concentrations was reported recently for DPPC mixtures with ergosterol (E) (14). Both groups of investigators interpreted this line broadening in terms of a phase separation in these membranes, whereby at intermediate sterol concentrations two liquid phases are present. The enhanced linewidth was attributed to a diffusion-limited exchange of phospholipids between domains of the coexisting liquid phases. This interpretation required that these domains be small (20–80 nm). (For additional NMR work with this view, see ref. 15.) In accord with this interpretation, fluorescence microscopy observations have failed to detect phase separation on the micrometer scale (16).

Ternary mixtures of dioleoylphosphatidylcholine (DOPC), C, and DPPC form micrometer-scale immiscible liquid domains easily observed with fluorescence microscopy (16). As described here and in earlier work (12, 17), this immiscibility can be modeled in terms of an intermolecular attractive interaction and a repulsive interaction. The attractive interaction is between C and DPPC, leading to complex formation. The (mean field) repulsive interaction is between the complex and DOPC, leading to immiscibility. The model provides a semiquantitative description of the C, DPPC, DOPC phase diagram and involves no phase separation of C–DPPC, or other binary pairs. In the present work, we show that the chemical kinetics of complex formation and dissociation can account for the deuterium resonance line broadening previously attributed to a phase separation on a submicrometer distance scale (13, 14).

Background Theory and Results

Thermodynamic Model. The general thermodynamic model used here is the same as that used previously to describe C–phospholipid mixtures in monolayers and bilayers, except for the choice of specific parameters (11, 12, 17). We consider a liquid bilayer mixture of C, reactive phospholipid (R), and unreactive phospholipid (U). The condensed complex (CR₂) is formed in a reversible reaction

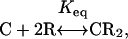[1]

where K_eq is the equilibrium constant. The 1:2 stoichiometry is chosen to fit the experimental data as simply as possible (see below). The regular solution free energy of the equilibrium mixture of C, R, U, and CR₂ is

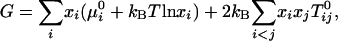[2]

where 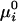is the standard chemical potential of pure component i, x_i is its equilibrium mole fraction, and k_B is Boltzmann's constant. The 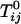are the critical temperatures of the six binary pairs in the four-component mixture. These temperatures are measures of the mean-field repulsions between the various components. In this model, all of the standard chemical potentials are constant and can be set equal to zero except for the chemical potential of the complex, –k_BTlnK_eq. All of the critical temperatures are assumed to be well below 298 K (T_r), except the critical temperature of the binary U–CR₂ pair hereafter denoted simply 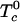. At a given temperature, there are then only two parameters, the equilibrium constant K_eq and the critical temperature 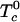. Equilibrium free energies and phase boundaries are calculated as described in ref. 18. The relative order parameter, f, is defined as the fraction of R molecules that are in complexes. For binary mixtures of C and R, f = 2z/((1 – c)(1 + 2z)), where c is the initial mole fraction of C (before reaction) and z is the equilibrium mole fraction of complex.

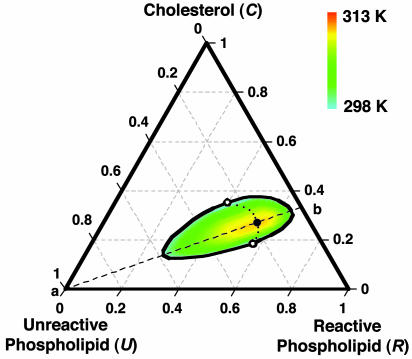
A ternary phase diagram calculated using the model of condensed complex formation is shown in Fig. 1. This diagram models the experimental phase diagram for a ternary mixture of C, DPPC, and DOPC (16). Here DPPC is the reactive phospholipid R, and DOPC is the unreactive phospholipid U. The experimental data used to fix the model parameters are the ternary critical temperature, 313 K, and the closest distance of approach of the miscibility loop phase boundary to the C–R axis. This closest distance of approach is ≈5 mol% U. The parameters used in the modeling are 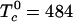and K_eq = 1,270 at 298 K. Given these two parameters, the heat of reaction ΔH = –32.4k_BT_r (–19.2 kcal/mol) is obtained by requiring the model to reproduce the observed ternary critical temperature. Note that ΔH and other energies are given in units of k_BT_r where T_r = 298 K. The critical point composition at the critical temperature of 313 K corresponds to initial concentrations of C and R of 0.27 and 0.54 (large filled circle in Fig. 1). An important feature of the model is that analysis of the ternary phase diagram provides the parameters needed for calculations on the binary mixtures where there are no comparable data.

Fig. 1.

Calculated phase diagram of a ternary liquid mixture containing C, R, and U. C and R form a 1:2 complex (one C, two R). The black outline and the open circles denote the isothermal binodal curve and critical points at 298 K. The large filled circle denotes the ternary critical point at 313 K, and the smaller filled circles denote critical points at intermediate temperatures. The diagram is meant to simulate the experimental phase diagram of C, DPPC, and DOPC, for which the observed critical temperature is 313 K (16). See text for best-fit parameters. The dashed line (a–b) denotes the stoichiometric axis where the initial mole fractions of C and R are in a 1:2 ratio. The ternary critical point lies on this line. The calculated tie-lines (not shown) lie along the same directions as those determined experimentally (25).

NMR Spectra. The deuterium NMR resonance spectra R(ν) for a deuterium-labeled fatty acid chain in a phospholipid molecule were calculated with a generalization of the methods described in ref. 19

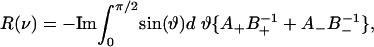[3]

where

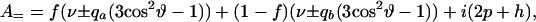and

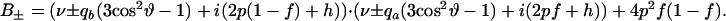The quantities q_a and q_b are deuterium nuclear quadrupole splitting parameters, where subscripts a and b refer to the free and bound (complex) states of the labeled phospholipid molecule. The quantity f gives the fraction of reactive phospholipid molecules in complexes. The kinetic parameter p is given by reaction rate constants

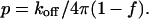[4]

The rate constant k_off gives the rate at which a reactive phospholipid molecule dissociates from the complex. The linewidth parameter h is related to the Bloch equation transverse relaxation time T₂

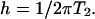[5]

In using Eq. 3, it is assumed that the nuclear spin quantum number and the average molecular orientation (perpendicular to the local plane of the membrane) do not change during the chemical exchange process and that T₂ does not change with membrane orientation in the applied field.

Chemical exchange involves a change of deuterium resonance frequency that ranges from Δν = 2|q_b – q_a| (molecules with ϑ = 0) to 0 (molecules with ϑ = 54°45′). Chemical exchange is fast with respect to all molecules if it is fast with respect to the spectroscopic time scale Δν.

In our analysis of the NMR work (13, 14), the larger quadrupole resonance frequency (2q_b for the complex) is ≈50 kHz, and the smaller resonance frequency (2q_a for the free phospholipid) is ≈25 kHz. In calculating line shapes using Eq. 3, we have used q_b = 1 and q_a = 0.5, so that in the later discussion these numbers are understood to be in units of ≈25 kHz.

Melding of Data. The deuterium NMR data of immediate interest are for E–DPPC mixtures (14), which are similar to earlier results for C–DPPC mixtures (13, 20). The data of ref. 14 are modeled by using the equilibrium constant derived from the analysis of the ternary phase diagram for C–DPPC–DOPC mixtures (16). The thermodynamic and kinetic properties of C–DPPC mixtures are assumed to be similar to those of E–DPPC mixtures. Evidence supporting this assumption in bilayers can be found in refs. 14 and 21.

Note on Order Parameters. Throughout this work, we use the term “f” both as “order parameter,” as well as “fraction of reactive phospholipids in a complex.” Both terminologies are useful. Order parameters are often used to characterize NMR quadrupole splittings and also are used in Landau theory in liquid crystal physics. In the latter connection, our following discussion of critical point fluctuations could be framed in terms of an expansion of the free energy in powers of the order parameter f.

Complex Formation and Molecular Order

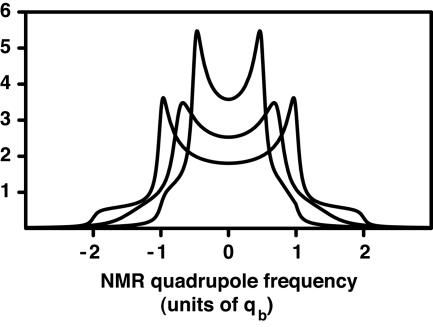
As is widely recognized, the inclusion of C in the liquid state of phosphatidylcholine bilayer membranes leads to increasing molecular order of the fatty acid chains. This ordering is revealed by an increase in the deuterium quadrupole splittings as illustrated by the calculated spectra in Fig. 2. The inner spectrum is for a deuterium-labeled phospholipid in a bilayer containing no C, whereas the middle and outer spectra are for bilayers with increasing C concentrations. As already noted, in previous work on C–DPPC mixtures (13) and on E–DPPC mixtures (14), such spectra have been interpreted in terms of the coexistence of two liquid phases, a phase where the fatty acid chains are relatively disordered, and a C-rich phase where the chains are relatively ordered. It is postulated that the two liquid domains are very small, submicrometer, and that rapid diffusive exchange of phospholipids between the domains leads to exchange narrowed spectra, such as those illustrated in Fig. 2.

Fig. 2.

Calculated deuterium NMR spectra of a hypothetical phospholipid molecule deuterated at a single position on a fatty acid chain. The spectra arise from isotropic distributions of bilayer orientations. Inner, pure phospholipid bilayer (f = 0), quadrupole splitting constant q_b = 0.5. Middle, membrane composed of 50% 1:2 complex and 50% phospholipid (f = 0.5). Outer, membrane composed of only 1:2 complex, quadrupole splitting q_b = 1.0. The spectrum in the middle results from chemical exchange of phospholipids between the bound and free states, given by the rate parameter p = 0.636. For the E–DPPC mixture, this value of p corresponds to a kinetic off-rate constant of 10⁵ s^–1. (For the E–DPPC mixture, q_b is ≈25 kHz). The middle spectrum corresponds to rapid exchange, but a residual broadening is apparent because of the finite exchange rate.

Here, we propose, on the contrary, that in bilayers these sterol-DPPC liquid mixtures form a single thermodynamic phase. The ordering of the fatty acid chains as shown by an increase in the deuterium quadrupole splittings is due to the formation of sterol–DPPC complexes, with high relative order. Phospholipid molecules not in complexes have low relative order. The relative-order parameters are numerically equal to the fraction of reactive phospholipid molecules in complexes, f. We calculate f from the equilibrium constant K_eq for complex formation. This equilibrium constant is determined by the simulation of the ternary phase diagram shown in Fig. 1. We use the 1:2 stoichiometry of one C and two phospholipids, for which K_eq = 1,270 at 298 K. The 1:2 stoichiometry is the simplest one that is consistent with the data and also has been inferred in a number of studies on monolayers (11).

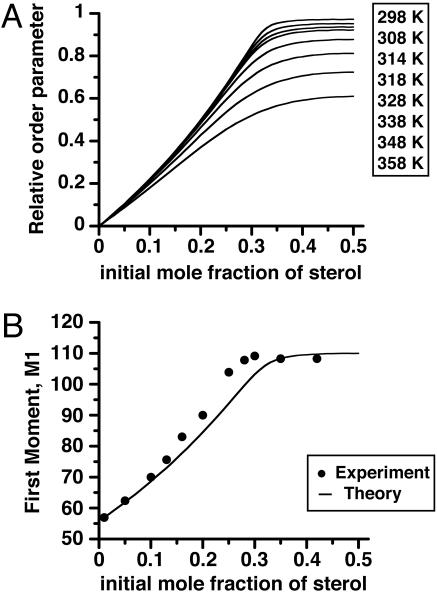
Fig. 3A gives a plot of calculated phospholipid order parameters (f) vs. C concentration for the binary C–DPPC mixture. These plots have a striking similarity to the experimental plots of deuterium NMR first moments vs. sterol concentration in E–DPPC (14) and C–DPPC (20) mixtures. The breaks in the curves (especially at the lower temperatures) were interpreted as representing a liquid–liquid phase boundary (14), whereas we interpret these breaks as representing the completion of the C–phospholipid reaction of complex formation. To illustrate this point, Fig. 3B gives a plot of the first moment M1 of the deuterium NMR as a function of E concentration at 41°C (data points taken from ref. 14). The theoretical curve assumes M1 is a linear function of f using parameters derived from the C–DPPC–DOPC ternary phase diagram (see Fig. 1 for details) and uses the E–DPPC M1 values at 0.00 and 0.35 mol fraction sterol for calibration. The calculations also use the fast exchange limit, where quadrupole splittings are proportional to the order parameter f. Calculated first moments show that this approximation is quite accurate for the kinetic parameter used (see below). The fall-off in order parameters at the higher temperatures in Fig. 3A is due to the thermal dissociation of the complex.

Fig. 3.

Ordering in sterol–phospholipid binary mixtures. (A) The fraction of phospholipid (DPPC) in complex form (order parameter f) in a binary mixture, calculated using the equilibrium constant derived from the phase diagram for the ternary mixture in Fig. 1. (B) First moments for deuterium NMR spectra of sterol–DPPC mixtures. The data points for E–DPPC mixtures are taken from ref. 14. The curve is calculated assuming that the first moment is a linear function of f, using the experimental values of M₁ at 0.0 and 0.35 mol fraction E for calibration (see text). Note that the data points refer to E–DPPC binary mixtures, whereas the curve is calculated for a C–DPPC binary mixture.

Dissociation Kinetics

Hsueh et al. (14) studied the resonance signals for the C15 deuterons of phospholipids using “de-Paked” deuterium NMR spectra. These de-Paked resonance signals are relatively well resolved and separate from the signals of the other deuterons on the perdeuterated fatty acid chains. In contrast, we consider only the outermost signals with the largest splittings. These signals have the disadvantage of overlap with other signals but the advantage of having the largest splittings and therefore the highest sensitivity to motion. Also the de-Paking step is not required to detect the broadenings at intermediate concentrations. The analysis of the experimental NMR spectra in terms of a two-state model is independent of assumptions about the microscopic molecular mechanism. The calculated spectra depend only on the rate constants for exchange and the fractional occupation of two states. Our analysis of the spectra in terms of two-state kinetics is substantially the same as that given earlier (14). The significant difference arises in the interpretation of these NMR parameters in terms of molecular properties.

An important feature noted in the deuterium NMR of sterol–DPPC mixtures is an enhanced line broadening at sterol concentrations intermediate between zero and the higher concentrations. This broadening was interpreted as arising from chemical exchange of deuterated lipids between very small domains (13, 14). Hsueh et al. (14) used an interdomain rate constant of approximately 10⁵ s^–1 in their analysis of the deuterium NMR linewidths. This rate constant corresponds to fast exchange of the C15 deuteron spectra.

In Fig. 2, we show single deuteron spectra calculated using the same rate constant 10⁵ s^–1. In our interpretation, this rate is the off-rate constant for the dissociation of a phospholipid molecule from the complex. The calculated spectra in Fig. 2 for f = 1/2 show broadenings of the same order of magnitude as reported for intermediate C concentrations (14). (The parameters p = 0.636 and f = 1/2 correspond to an off-rate constant of k_off = 10⁵ s^–1.)

As noted above, the analysis of resonance line shapes in terms of a kinetic off-rate constant, and the fraction of the phospholipids in the complex, does not depend on the reaction mechanism, or the stoichiometry. The reaction stoichiometry enters the analysis in relating the composition of the sample to the fraction of phospholipid in the complex. In our simulations, the effects of kinetics on NMR line shapes are easily noticeable in the order parameter range f = 0.1–0.75. We judge the effect of a finite off rate constant on the spectra by calculating difference spectra, R(ν, k_off = 10⁵) – R(ν, k_off = 10⁷). In this parameter range, these differences are large, sometimes comparable with R(ν, k_off = 10⁵) itself. The corresponding C concentration range is 6–27 mol%. In comparison, there is a noticeable experimental line broadening in the de-Paked spectra in the range 13–27.5 mol% (14). [In contrast the first moments of R(ν, k_off = 10⁵) and R(ν, k_off = 10⁷) are the same to within a percent or less, over the entire range of f.]

Critical Fluctuations

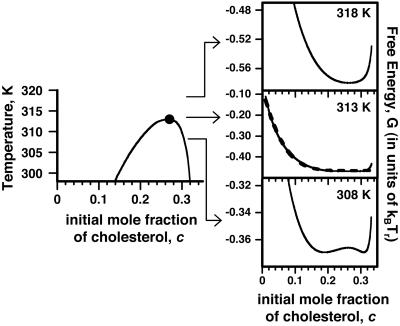
Ternary Mixtures. Deuterium NMR line broadening also might arise from fluctuations in lipid composition related to proximity to a critical point. In principle, this broadening could be dynamic or static (inhomogeneous). Here we estimate inhomogeneous broadening, which can exceed dynamic broadening. One anticipates that static line broadening is of order of magnitude 〈(f – f₀)² 〉^1/2Δν provided the fluctuation is not averaged out by diffusion (f₀ is the order parameter at the critical composition). There is no a priori means to estimate this broadening quantitatively for the binary mixtures in bilayers because there is no information on the binary critical temperatures. The fluorescence data (16) show no evidence of immiscibility for the binary mixtures. [In previous work, our model assumed the critical temperature of the C–DPPC pair to be zero, or at least negligible (12).] However, we can use our model of complex formation to make rough, order-of-magnitude estimates of the effects of critical fluctuations on NMR spectra for the ternary C–DPPC–DOPC mixture near its critical point (large filled circle in Fig. 1 where the initial mol fraction of C, before reaction, is c₀ = 0.27, and the critical temperature is 313 K). These fluctuations are predominantly along a tie line close to the 1:2 stoichiometric axis (dashed line a–b in Fig. 1), thus mimicking a binary mixture. The corresponding pseudo-binary phase diagram is given in Fig. 4 Left.

Fig. 4.

Critical fluctuations in the ternary mixture, C–DPPC–DOPC. (Left) Pseudobinary mixture phase diagram describing liquid–liquid phase separation for compositions along the 1:2 stoichiometric axis (a tie line) where the mole ratio of C to R is maintained at 1:2 (dashed line a–b in Fig. 1). Parameters used are the same as those used to generate the phase diagram for the ternary mixture in Fig. 1. The ternary critical point at 313 K is indicated by the filled circle. (Right) Calculated free energies for compositions along the stoichiometric axis, 5 K above the critical temperature, at the critical temperature, and 5 K below the critical temperature (note different scales). The dashed curve at the critical temperature is the fit to the power series in Eq. 7.

The calculated free energy of this C–DPPC–DOPC mixture as a function of composition along the 1:2 axis is shown by the solid curves in Fig. 4 Right for temperatures near the critical temperature. Note the energy scale in units of k_BT_r. The deuterium NMR spectrum at the ternary critical point is calculated as follows. The resonance spectrum R(ν) in Eq. 3 depends on the order parameter f, R(ν) = R(ν, f). The calculated resonance spectrum 〈R(ν) 〉 is then given by integration

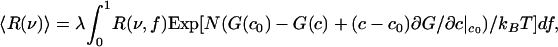[6]

where

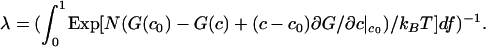Eq. 6 was derived by using the grand canonical ensemble (22, 23) and applies to a binary mixture where fluctuations in the composition are allowed, but the total number of molecules N in a selected group is fixed. The mixture considered is pseudobinary because the probable composition fluctuations are constrained to be along the 1:2 axis, so there is only one composition variable. In the estimate of line shape using Eq. 6 we take N ≥ 2Dρ/π Δν, with the diffusion coefficient D = 5 × 10^–8 cm²/s (15, 24), ρ = 1.66 × 10¹⁴ cm^–2 and Δν = 2.5 × 10⁴ s^–1, and use an approximate linear relationship between order parameter and C concentration: f = 2.73367c + 0.002649 (fit to calculated values of f). The formal integration in Eq. 6 is between f = 0 and f = 1, but because we assume equilibrium is maintained throughout the fluctuation, the maximum value of f used (f = 0.914) is determined by the equilibrium constant together with allowed compositions along the fluctuation path. For calculations, we used N ≈ 166. (The calculations are rather insensitive to the choice of N, and using N = 1,000 leads to similar conclusions.) The principle here is to select a value of N that is large enough that fluctuations cannot be averaged out by translational diffusion and yet small enough that these fluctuations are large and lead to line broadening. (It is also necessary for the fluctuation to last long compared with the lifetime of the complex, so that equilibrium is maintained.) For the calculation, the free energy function is expressed as the sum of quartic and quintic powers of the composition fluctuations

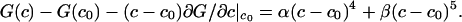[7]

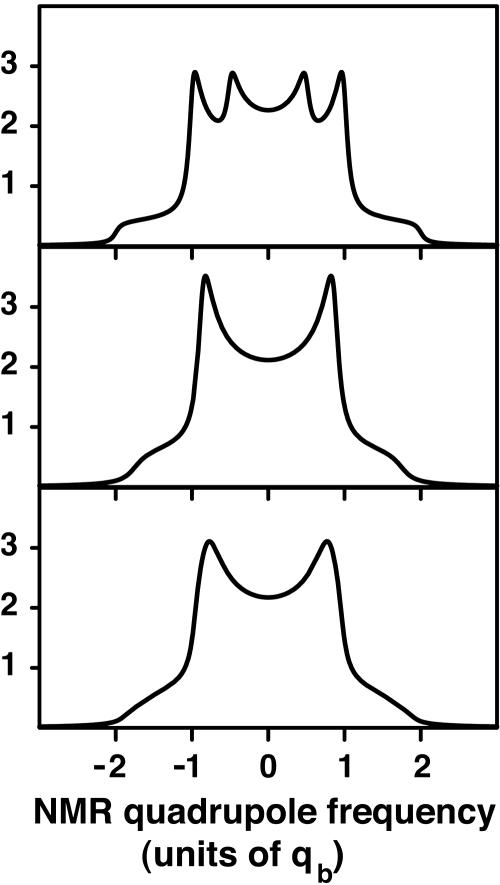
Here α = 51.437k_BT_r, β = 82.153k_BT_r. At the critical point the integral in Eq. 6 was estimated by summing discrete spectra over the allowed range of the order parameter. This estimated critical point spectrum is shown in Fig. 5 Bottom. For comparison, Fig. 5 also gives spectra obtained in the absence of fluctuations (Middle) and in the absence of both fluctuations and chemical exchange (Top). The line broadening due to these fluctuations should be experimentally detectable.

Fig. 5.

Calculated deuterium NMR spectra at the critical point of the ternary C–DPPC–DOPC mixture. (Top) No chemical exchange or composition fluctuations, showing peaks due to complexed and free forms of the phospholipid. (Middle) Calculated spectra with chemical exchange, k_off = 10⁵ s^–1. (Bottom) Calculated spectra including chemical exchange and composition fluctuations at the critical point. At the critical composition the initial mole fraction of C is 0.27, the initial mole fraction of phospholipid is 0.54, and the fraction of phospholipid in complex form (order parameter) is f = 0.74.

At temperatures well above the critical temperature, the fluctuations can be estimated by expanding the free energy G(c) about c₀ and retaining only quadratic terms. This expansion yields the mean square fluctuation amplitude

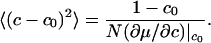[8]

When this equation is used to estimate line broadening, it is found that at 10° above the critical temperature the broadening is comparable with our assumed intrinsic linewidth. Thus, at this temperature the broadening would be barely detectable. However, between this temperature and the critical temperature, the broadening may be observable if the fluctuation lifetimes are long enough. Because the broadening we are discussing is due to a fluctuation in the concentration of complexes at a given temperature, there can be a maximum in this broadening at compositions where the concentration of complexes is intermediate (0 < f < 1).

As the temperature is lowered just below the critical temperature, the amplitude of the fluctuations must become larger, leading to larger line broadening. However, in this range of incipient phase separation, energy terms in the composition gradient are potentially important, making estimates of composition fluctuations even more uncertain. At still lower temperatures, domains of optical size are observed experimentally, and the NMR spectra are superpositions of resolved spectra arising from distinct domains of macroscopic size (25).

The conclusion we reach from the above admittedly very rough calculations is that there may be composition-dependent line broadening due to fluctuations at temperatures within 10° above the critical temperature for the C–DPPC–DOPC ternary mixture, especially near the critical composition. By extrapolation, binary mixtures should also show line broadening under similar conditions. This line broadening would require that the C–DPPC and E–DPPC mixtures have a (possibly unobservable) low temperature miscibility critical point within 10° of the experimental temperature, if this effect were to play a role in the observed broadening (13, 14).

Heat Capacity. The heat capacity of the membrane originating from the thermal dissociation of complexes at the critical point can be calculated from the temperature derivative of the fraction of molecules in complex form (averaged over two phases when necessary).

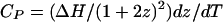[9]

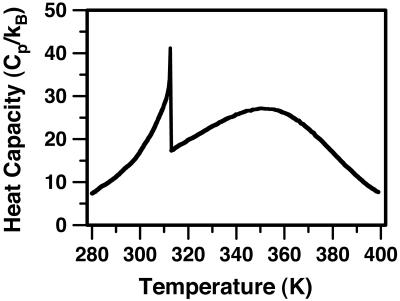
Here z is the equilibrium mol fraction of complex. The heat capacity plot in Fig. 6 uses ΔH = –32.4k_BT_r (–19.2 kcal/mol), the heat of reaction used earlier to calculate the ternary phase diagram in Fig. 1 (A correction to ΔH of the order of 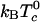has been neglected in Eq. 9.). The jump in heat capacity occurs at the critical temperature and is due to a jump in the temperature dependence of the concentration of complexes. The integral of the jump over background is 0.40 k_BT_r (0.240 kcal/mol). The broad heat absorption at the higher temperatures is due to thermal dissociation of the complexes as discussed in ref. 26. Composition fluctuations could broaden the sharp jump in Fig. 6. A jump in dz/dT also implies a jump in the temperature derivative of the first moment of the deuterium NMR spectra.

Fig. 6.

Calculated heat capacity of the ternary mixture at the critical composition. The heat capacity of the ternary C–DPPC–DOPC mixture was obtained by using Eq. 9 together with ΔH =–19.2 kcal/mol (–32.4 k_BT_r), the heat of reaction used in calculating the phase diagram in Fig. 1. At the critical temperature, there is a jump in the temperature derivative of the concentration of complexes and a corresponding jump in the heat capacity. A jump in the temperature derivative of the first moment of the deuterium NMR is also calculated at the ternary critical point.

Discussion

In the present work we have shown that composition-dependent enhanced NMR line broadening seen in binary mixtures of C–DPPC and E–DPPC may be due to the kinetics of complex formation between these sterols and the DPPC. The rate constant for the dissociation of a DPPC molecule from the 1:2 E–DPPC complex is estimated to be of the order of 10⁵ s^–1, corresponding to a lifetime of 10^–5 s. This source of line broadening is robust in the sense that it holds both below and above a critical temperature and disappears only at the highest temperatures where the complex is dissociated. In general, resonance line broadening due to concentration fluctuations related to proximity to a critical point are superimposed on the line broadening related to the formation and dissociation of complexes. These fluctuations may make a significant contribution to the observed broadening (13, 14).

If we imagine that C–phospholipid complexes diffuse on a square lattice with unit cell area of 60 Ų, and with diffusion coefficient 5 × 10^–8 cm²/s (24), then the time taken for each step is ≈6 × 10^–8 s. Thus, a complex with a 10^–5 s lifetime takes ≈150 steps before dissociating. Note, however, that here dissociation refers to an NMR lifetime, the probability that a bound phospholipid dissociates from the complex. The molecular mechanism might involve exchange of bound and free phospholipid or the disappearance of complex.

As shown in the work of Veatch et al. (25), phase separation into coexisting liquid phases in C–phospholipid ternary mixtures has major effects on deuterium NMR line shapes. At temperatures well below the critical temperatures, distinct NMR spectra are seen for lipids in distinct phases. In this connection it is of interest to note that the model for condensed complexes leads to the prediction of a jump in the temperature derivative of the deuterium NMR first moment, as well as the heat capacity, at the ternary critical point of the C–DPPC–DOPC mixture, as shown in Fig. 6.

Liquid–liquid phase separation in C–phospholipid bilayers was anticipated from spin label studies as early as 1981 and has served as a starting point for speculations concerning cell membranes (27). [See also Lentz et al. (28)] Deuterium NMR evidence for this phase separation in C–DPPC bilayers came from the original study of Vist and Davis (13), and the later closely related work of Hsueh et al. (14) on E–DPPC mixtures. These investigators interpreted composition-dependent line broadening and quadrupole splittings in terms of this putative liquid–liquid phase separation. The NMR investigations (13), spin label studies (29), as well as theoretical work (30) have led to the development of a frequently cited phase diagram for C–DPPC mixtures describing liquid–liquid immiscibility. However, optical fluorescence microscopy has failed to detect the coexisting liquid phases depicted by this C–DPPC diagram. Furthermore, it seems unlikely to us that liquid domains could remain small and invisible to optical microscopy throughout the rather large composition and temperature regions described by the proposed diagram. However, liquid–liquid phase separation is known in many C–phospholipid monolayer binary and ternary mixtures at low pressures, including C–DPPC mixtures (31). Liquid–liquid phase separation is also firmly established experimentally in a number of ternary bilayer mixtures (refs. 25, 32–36; for a recent review, see ref. 37.) Thus, the question of liquid–liquid phase separation in any given mixture is clearly a sensitive function of physical conditions and chemical properties.

We have presented an alternative interpretation of the deuterium NMR of C–DPPC mixtures in bilayers. This alternative interpretation involves condensed complexes but no thermodynamic liquid–liquid phase separation in this specific mixture. That is, we infer that the mean field parameter 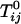in Eq. 2 describing repulsion between C and DPPC or between the complex CR₂ and DPPC is too small to yield immiscibility. (It is possible that there is a hidden liquid–liquid miscibility critical point near or below the solid–liquid transition temperature of DPPC.) Conversely, the corresponding parameter 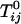for the repulsion between CR₂ and DOPC is large (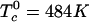) and gives the immiscibility in the ternary C–DPPC–DOPC mixtures modeled in Fig. 1. The model calculations of deuterium NMR line shapes are consistent with the available data and make possible an estimate of the dissociation lifetime of the complex. A caveat to this estimate is the possibility that the observed broadenings also might involve concentration fluctuations related to proximity to an as yet unobserved critical point in binary mixtures of C–DPPC or E–DPPC.

Methods

All calculations were carried out by using mathematica (Wolfram Research, Champaign, IL).