Using Claims Data to Examine Mortality Trends Following Hospitalization for Heart Attack in Medicare

Abstract

Objective

To see if changes in the demographics and illness burden of Medicare patients hospitalized for acute myocardial infarction (AMI) from 1995 through 1999 can explain an observed rise (from 32 percent to 34 percent) in one-year mortality over that period.

Data Sources

Utilization data from the Centers for Medicare and Medicaid Services (CMS) fee-for-service claims (MedPAR, Outpatient, and Carrier Standard Analytic Files); patient demographics and date of death from CMS Denominator and Vital Status files. For over 1.5 million AMI discharges in 1995–1999 we retain diagnoses from one year prior, and during, the case-defining admission.

Study Design

We fit logistic regression models to predict one-year mortality for the 1995 cases and apply them to 1996–1999 files. The CORE model uses age, sex, and original reason for Medicare entitlement to predict mortality. Three other models use the CORE variables plus morbidity indicators from well-known morbidity classification methods (Charlson, DCG, and AHRQ's CCS). Regressions were used as is—without pruning to eliminate clinical or statistical anomalies. Each model references the same diagnoses—those recorded during the pre- and index admission periods. We compare each model's ability to predict mortality and use each to calculate risk-adjusted mortality in 1996–1999.

Principal Findings

The comprehensive morbidity classifications (DCG and CCS) led to more accurate predictions than the Charlson, which dominated the CORE model (validated C-statistics: 0.81, 0.82, 0.74, and 0.66, respectively). Using the CORE model for risk adjustment reduced, but did not eliminate, the mortality increase. In contrast, adjustment using any of the morbidity models produced essentially flat graphs.

Conclusions

Prediction models based on claims-derived demographics and morbidity profiles can be extremely accurate. While one-year post-AMI mortality in Medicare may not be worsening, outcomes appear not to have continued to improve as they had in the prior decade. Rich morbidity information is available in claims data, especially when longitudinally tracked across multiple settings of care, and is important in setting performance targets and evaluating trends.

One-year mortality following hospitalization for heart attack (acute myocardial infarction [AMI]) is an object of surveillance within the National Acute Myocardial Infarction (NAMI) Project, a Centers for Medicare and Medicaid Services (CMS) quality initiative for Medicare's traditional (fee-for-service [FFS]) program (Centers for Medicare and Medicaid Services [n.d.]). Post-AMI mortality for program beneficiaries decreased in the late 1980s and early 1990s, falling to below 32 percent in 1996; by 1999 it had increased to nearly 34 percent. However, the increase is not present in all age cohorts, and is at least partly due to increasing average patient age.

Many factors complicate our ability to interpret AMI mortality trends. For example, improved diagnostic modalities in AMI increase the recorded prevalence of AMI and may cause the case-fatality rate to fall, quite apart from true changes in population risk or health care quality (Pasternak and Braunwald 1994). On the other hand, growing health maintenance organization (HMO) enrollment among the youngest and healthiest Medicare cohort likely makes those continuing to receive FFS medicine—the only ones whose claims records are available for study—an increasingly sicker population. Also, previous years' treatment successes could lead to higher morbidity burdens in today's heart attack patients.

If 1999 heart attack patients are at no greater risk than 1996 patients, then the observed increase in raw mortality rates is cause for alarm. However, if the 1999 patients are sufficiently older and sicker, their observed mortality may even reflect improving care. Mortality predictions that can adjust for shifts in underlying risk are crucial to establishing credible targets for post-AMI mortality.

We hypothesized that morbidity burden increased from 1995 to 1999 and that increasing risk, adequately modeled, would fully explain the mortality increase. Specifically, we examined the explanatory power, and the effect on perceptions of the 1995–1999 mortality trend, of claims-based risk adjustment based on simple demographics and each of three variously sophisticated morbidity profiling methods.

METHODS

Data

The data are from a national AMI surveillance database constructed at Boston University for CMS and described in a detailed report (Ash, Posner et al. 2001). Briefly, we first developed an event-centered, national Medicare claims database relating to all heart attack hospitalizations in each year from 1995 through 1999. Each hospitalization for AMI (including subsequent transfers) is a case-defining “index” event; the unit of analysis is a case. The 365 days prior to the index admission date is the preperiod.

For each case, we retained the diagnoses recorded for the patient in Medicare's MedPAR, Outpatient, and Carrier files during the preperiod and those recorded during the index admission, ignoring possibly misleading diagnoses from claims associated with HCPCS 80000 procedure codes (e.g., laboratory testing). We used CMS's Vital Status files to verify mortality at 365 days postadmission, and extracted age at index admission, sex, and original reason for Medicare entitlement from the Denominator File. Separate data files and analyses were used for events occurring in each year, 1995 through 1999.

Less than 1 percent of cases were excluded for missing, unlinkable, or illogical data (such as death prior to hospital admission). Between 11 and 12 percent of cases in each year were additionally dropped because of incomplete diagnostic information during the preperiod (due either to HMO enrollment or to lack of a complete year of full Medicare benefit entitlement).

For each year we describe cases, giving age, sex, Medicare entitlement, and racial distributions, summary measures of comorbidity, rates of selected medical problems, and one-year mortality. With more than 300,000 cases in each year, standard errors on population percentages are smaller than 1/10 of 1 percent; all differences large enough to be of substantive interest are highly statistically significant.

Morbidity Profiling

We explore four ways to summarize patient risk and predict one-year mortality following admission for AMI. The simplest model (CORE) uses demographic variables only: patient age, sex, and original reason for Medicare entitlement (coded as “aged” versus “disabled or end stage renal disease”). Each other model adds markers for the presence of medical conditions based on ICD-9-CM diagnosis codes. The Charlson model adds indicators only for the few serious medical conditions that contribute to the Charlson Comorbidity Index (Charlson et al. 1987). The other two models add comprehensive lists of indicators for all code-identified medical problems. One uses the Diagnostic Cost Group (DCG) hierarchical condition categories (Ash et al. 2000); the other, Agency for Healthcare Research and Quality (AHRQ) Clinical Classifications Software (CCS, formerly CCHPR) (Elixhauser and McCarthy 1996). We briefly describe each morbidity classification method, and compare the associated models on how well they predict one-year post-AMI mortality and how they affect our perception of the mortality trend.

The most widely used morbidity measure in the research literature was introduced by Charlson and colleagues in 1987; Deyo et al. (1992) adapted it for use with the ICD9-CM diagnosis codes found in administrative data. Each of 17 serious medical conditions—AMI, peripheral vascular disease, stroke, dementia, COPD, rheumatological disease, peptic ulcer disease, liver disease (mild versus more serious), diabetes (with and without complications), hemiplegia, renal disease, neoplasia, metastatic disease, HIV, and CHF—receives an integer weight; their sum is the Charlson Comorbidity Index. We use this index as a descriptive measure of illness burden. In modeling, we use a vector of indicators for the presence or absence of each Charlson comorbidity.

Diagnostic Cost Group (DCG) models, originally developed for Medicare payment models, have since been adapted for broad-based use in risk adjustment. We used DxCG Software, version 5.2 (obtained from http://www.dxcg.com) to calculate a Medicare DCG prospective relative risk score (RRS) to measure morbidity burden and a vector of 118 conditions with “hierarchies” imposed (leading to Hierarchical Condition Categories, or HCCs) for modeling. The RRS averages 1.0 in a representative Medicare population. Hierarchies are important for being able to avoid confounding the effects among clinically related medical problems. For example, only people with nothing more serious than a cough are coded for minor respiratory disease, while those with codes for both a cough and chronic lung disease have only the more serious lung HCC retained.

The Agency for Healthcare Research and Quality (AHRQ) developed its Clinical Classifications Software (CCS, formerly Clinical Classifications for Health Policy Research, or CCHPR) to facilitate summarization of the medical problems coded during hospitalizations as part of its Healthcare Cost and Utilization Project (HCUP). We downloaded code from AHRQ's web site (http://www.ahcpr.gov/data/hcup/comorbid.htm) that implements a classification system with 259 categories. Although CCS was not designed to produce scores, nor to predict any outcome, its availability as a free, readily downloaded, comprehensive classification system for ICD-9-CM codes makes it attractive for use in claims-based morbidity modeling.

Analyses

The CORE covariates, included in all models, are age, sex, and original reason for Medicare entitlement. Age is coded in eight categories (18–64, 65–69, 70–74, 75–79, 80–84, 85–89, 90–94, and 95+). Thus the CORE model has nine parameters—seven indicators for age and one each for sex and Medicare entitlement. The Charlson, DCG, and CCS classifications add 17, 118, and 259 condition indicators, respectively, to these nine. All morbidity vectors are coded using diagnoses from both the 365-day preperiod and the index hospitalization. All models are fit to 1995 data (where one-year mortality was 31.96 percent) using logistic regression to predict mortality. We neither examined the plausibility of individual coefficients nor dropped statistically insignificant or negative coefficients. The fitted models are applied to the remaining years of data, thus producing, for each case in each year, the predicted probability of death for a person with that risk profile and the same relationship between risk and mortality that obtained in 1995. Each model's predictions are averaged in each year to produce an expected death rate based on that year's comorbidity burden and the 1995 risk/mortality relationship. The ratio of observed mortality (O) to the expected (E) for a year is calculated and multiplied by 31.96 percent, the actual death rate in 1995. If, for example, O/E is 1.05, then the risk-adjusted mortality is 1.05 × 31.96 for that model in that year.

For each model we determined the number of parameters actually used in fitting the model to 1995 data, and, for each of the five years, both C-statistics and average death rates within lowest and highest deciles of model-predicted risk. These latter three statistics describe model “fit” in 1995 and validated predictive performance in subsequent years. Because validation measures for 1996 through 1999 varied little, we report results for 1995 and 1999 only.

All analyses used PC SAS Version 8.2 (Cary, NC).

RESULTS

There are over 300,000 cases in each year, with just under half incurred by women (Table 1). From 1995 through 1999, racial distribution changes minimally (a 1.4 decrease in percent of cases of white race), but the age distribution changes a lot. Specifically, mean age increases by 1.1 years, the net result of a small increase (from 6.8 percent to 7.4 percent) in the fraction under age 65 (currently entitled due to either ESRD or disability) and a larger increase in those 85 years or older (from 15.7 percent to 20.3 percent). Both the Charlson Comorbidity Index and the DCG relative risk score reveal an increase of about 10 percent in measured illness from 1995 to 1999. The DCG relative risk scores all exceed 2, revealing populations that are “more than twice as sick as the Medicare average” in terms of next year's expected health care utilization. Codes indicating previous heart attacks are common in the year prior to the index AMI, and their prevalence increases by about 10 percent. Diabetes and congestive heart failure are also frequent (around 40 and 50 percent, respectively) and increasing in prevalence. One-year mortality fell a little from 1995 to 1996 (from 32.0 percent to 31.6 percent), held constant in 1997, but then climbed by a percentage point in each of the next two years.

Table 1.

Characteristics of Medicare AMI Admissions, 1995–1999

Year	1995	1996	1997	1998	1999
Number of Cases	305,468	308,997	306,224	304,882	306,175
Female (%)	48.1	48.4	48.4	49.1	49.6
Race: (%)
White	90.3	89.9	89.5	89.4	88.9
Black	6.7	6.8	7.0	7.1	7.4
Other	3.0	3.3	3.4	3.5	3.6
Mean age	75.5	75.7	75.9	76.2	76.6
Age group: (%)
18–64	6.8	7.0	7.2	7.3	7.4
65–74	38.9	37.6	36.1	34.5	32.6
75–84	38.5	38.8	39.2	39.3	39.6
85+	15.7	16.5	17.5	18.8	20.3
Non-aged orig. entitlement (%)	16.7	16.9	17.1	17.6	17.9
Mean Charlson Index*	3.20	3.26	3.29	3.41	3.49
Mean DCG score*	2.22	2.27	2.33	2.39	2.45
Comorbidities (%)
AMI code (past year) **	31.4	32.2	32.9	33.9	34.6
Diabetes*	38.0	39.3	40.8	42.8	44.7
CHF*	47.8	48.3	48.9	50.1	50.7
One-year mortality (%)	32.0	31.6	31.7	32.7	33.8

^*Comorbidity identification based on all diagnoses detected during inpatient or ambulatory care in the 365-day prehospitalization period plus those identified during the index admission.

^**Comorbidity identification based on the preperiod only. “AMI code” refers to either current (ICD-9-CM code of 410xx) or recent MI (412xx).

Table 2 describes the four models and their performance as predictors of one-year mortality. The Charlson model has many fewer parameters than the DCG model (25 versus 122); the CCS model has over twice as many parameters again (263).

Table 2.

Model Performance Characteristics for Predicting One-Year Mortality Post-AMI

		Models
	Year*	Core	Charlson	DCG	CCSPR
Number of parameters fit**		9	25	122	263
C-Statistics
Fitting	1995	0.65	0.73	0.80	0.81
Validation	1999	0.66	0.74	0.81	0.82
Mean actual mortality % within deciles of model-defined risk
Highest decile	1995	53	64	75	79
Lowest decile	1995	16	8	4	4
Highest decile	1999	57	67	76	80
Lowest decile	1999	17	7	3	3

^*Models are fit to 1995 data and applied to (validated on) 1999 data.

^**Theoretical maximums based on using all classifications in each system are 9, 26, 127, and 266, respectively.

Validation measures of performance (which describe the ability of the model fit on 1995 data to discriminate risk in 1996 through 1999) are as high as the fitting measures (from 1995). It is striking that validation C-statistics for the four models range from 0.66 for the CORE model to 0.74 with the Charlson (a hefty improvement) to over 0.80 with both the DCG and CCS models. As further evidence of the power of the DCG and CCS models, each was used to identify lowest-risk and highest-risk deciles of the 1999 population. For each, their (prospectively identified) lowest-risk group in 1999 has only 3 percent one-year mortality, while 76 percent and 80 percent of their highest risk groups, respectively, die within one year. Figures for 1996 through 1998 (not shown) are similar to those for 1999.

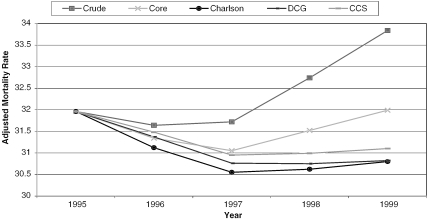
Finally, in Figure 1, we see the results of the various risk-adjusted trend analyses. The top curve, labeled “Crude,” plots the actual mortality experience from 1995 through 1999 (as given in Table 1). It shows sharply increasing mortality from 1997 to 1999. The plotted trend line for the CORE model also increases, but more modestly, from 1997 through 1999. All three remaining models (Charlson, DCG, and CCS) are essentially flat over the same period.

Figure 1.

AMI Morality Trend for Risk-Adjusted Models (1995–1999)

DISCUSSION

This paper derives from a more comprehensive cycle of studies for CMS, including a companion, event-centered database focused on 1998 hospitalizations for congestive heart failure (Ash, Moskowitz et al. 2001). Here, we developed several models to predict mortality in AMI, and found two (based on straight-forward applications of CCS or DCGs) that are particularly powerful. Our findings demonstrate the potential of claims-based risk adjustment used with longitudinal data to support risk-adjusted comparisons of important patient outcomes. It appears that increasing levels of pre-AMI morbidity are adequate to fully explain the rise in observed one-year post-AMI mortality from 1997 to 1999. The CMS has followed its data into 2000, and continues to find increasing mortality. It is not yet known if increasing risk can also explain this finding.

This study has limitations. Most important, we do not know whether improvements in diagnostic coding over time contribute significantly to our finding of more illness in 1999. Here we take some assurance from the fact that the Charlson score (focusing on a few “serious” conditions) and the DCG relative risk score (relying on a comprehensive clinical profile) both observed the same 10 percent monotonic rise in overall morbidity burden between 1995 and 1999; also, that the models built on 1995 data predict no less well in the later years.

“Industrial strength” quality surveillance models based on comprehensive classification systems (such as DCG or CCS) should be pruned to eliminate categories that are either irrelevant to an adult population or not related to mortality; and groomed to ensure clinically credible coefficients. Although we have neither pruned nor groomed, these “raw” models have excellent validated predictive power.

Models for national surveillance should also avoid diagnoses from the index admission that might reflect complications of care. In the current study we merged pre- and index-period diagnoses. Preperiod data could be used to separately identify morbidity issues that were indisputably present at “baseline.”

The current investigation has important strengths. We have introduced a 1995–1999 national AMI database useful for addressing many questions regarding the preadmission health status and postadmission outcomes of Medicare patients hospitalized for AMI. We have used diagnostic information about the medical problems seen for people in all care settings for 365 days prior to their AMI hospitalization (not just inpatient, and not just during the hospitalization) to predict mortality. We have demonstrated the importance of comorbidity measures in prediction and risk adjustment and shown that comprehensive risk adjustment is far more effective than a popular method (Charlson) that relies on a few serious conditions only. We have shown that the recent, disturbing increase in post-AMI mortality in Medicare can be explained by the aging and increasing comorbidity burden of the AMI cohort.

CONCLUSION

This study demonstrates that minimal adaptations of comprehensive comorbidity classification systems applied to appropriately configured administrative datasets can effectively predict subsequent mortality. Both the DCG- and CCS-based models are powerful discriminators. In validation data, there was 3 percent mortality for the 10 percent of the people with lowest model-predicted risk and up to 80 percent mortality for people in the highest decile of predicted risk. The fact that measures of pre-AMI morbidity explain the recent rise in one-year post-AMI mortality, while demographic risk adjusters do not, underscores the need for health-based risk adjustment when monitoring health systems performance.