Abstract
A localization task required participants to indicate which of 4 locations contained a briefly displayed target. Most displays also contained a distractor that was not equally probable in these locations, affecting performance dramatically. Responses were faster when a display had no distractor and almost as fast when the distractor was in its frequent location. Conversely, responses were slower when targets appeared in frequent-distractor locations, even though targets were equally likely in each location. Negative-priming effects were reliably smaller when targets followed distractors in the frequent-distractor location compared to the rare-distractor location, challenging the episodic-retrieval account. Experiment 2 added a 5th location that rarely displayed distractors and never targets, yet responses slowed most when distractors appeared there. The results confirmed that the attentional system is sensitive to first- and higher-order statistical patterns and can make short- and long-term adjustments in preferences based on prior history of inspecting unsuccessful locations.
The limited capacity of the human attentional system, combined with the complexity of the environment, necessitates a mechanism for effective selecting and responding to goal-relevant stimuli while disregarding irrelevant ones. The cost of splitting attention or of being distracted can even be seen in simple experimental tasks such as spatial localization. An example of this type of task (Tipper, Brehaut, & Driver, 1990) required participants to press a key corresponding to the spatial location of a target flashed on a computer display. Performance was slower when two stimuli were flashed and one was a distractor. It is not only extraneous information that interferes with the processing of the current display: Research in attention has also documented that when a stimulus (location or object, depending on the task) that should be ignored (i.e., is the distractor) on the prime display becomes the target on the subsequent probe display, performance suffers compared with trials in which this switch does not occur. This type of interference is commonly referred to as negative priming (Tipper, 1985).
The fact that irrelevant stimuli interfere with performance implicates a selective attention mechanism that directly allocates processing resources to goal-relevant information (e.g., Neill, 1997). Although there is considerable agreement concerning the necessity of a selective attention mechanism, there is less agreement concerning how this selection occurs, that is, how the process of filtering or ignoring the irrelevant is achieved.
Recently, a number of investigators have begun to demonstrate the exquisite sensitivity of the cognitive system to statistical properties of the environment in visual search tasks (e.g., Hoffmann & Kunde, 1999; Maljkovic & Nakayama, 1996) and online adaptation of the attentional system to reflect shifts in environmental parameters (e.g., Chun & Jiang, 1999; Nissen & Bullemer, 1987; Willingham, Nissen, & Bullemer, 1989). Indeed, there is also literature on probability matching phenomena that documents that animals and humans choose a particular option or locality proportional to its probability of being correct; or, at least, they demonstrate a choice distribution among options similar to the probabilities of each being correct (Lovett, 1998; Millward, 1971). It has been shown that participants identify a target more rapidly when other aspects of the display predict the location of the target (Chun & Jiang, 1999; Olson & Chun, 2002).
Given that humans respond more rapidly to visual displays that are familiar and predictable (Biederman, Glass, & Stacy, 1973), it seems reasonable to assume that this facilitation results from learning where to attend within a display. Eye-tracking studies have documented that participants learn where to look in large displays, speeding up performance with practice (e.g., Haider & Frensch, 1999; Lee & Anderson, 2001). Obviously, the ability to learn which regions are most informative is important in situations or scenes that contain multiple stimuli that compete for attention.
The research described in this article attempted to relate recent findings in long-term adaptation of visual attention to issues concerned with divided attention and negative priming. In particular, this article focuses on (a) whether the costs of divided attention are minimized when distractors become predictable and thus less distracting; (b) if they do become less distracting, whether the by-product of diminished interference is a reduction of ostensive suppression, manifested in a reduced negative-priming effect; and (c) whether we can propose a coherent learning mechanism that accounts for both negative priming effects and adaptation to statistical properties of the environment.
Alternative Theoretical Accounts of Negative Priming
Negative priming has spawned a large body of research (for reviews, see Fox, 1995; May, Kane, & Hasher, 1995; Neill & Valdes, 1996; Neill, Valdes, & Terry, 1995). The general phenomenon has been studied in many different experimental paradigms, such as letter naming (Tipper & Cranston, 1985), picture naming (Tipper, 1985), word naming (Tipper & Driver, 1988), and target localization (Tipper et al., 1990). The inhibitory effect of ignoring stimuli or locations has been demonstrated in a wide variety of paradigms. For example, using the Stroop paradigm, Neill (1977) found that participants were slower on trials in which the ink color on the preceding trial matched the color name on the current trial. Tipper (1985) found similar interference in a picture-naming task where the picture to be named matched the name to be ignored on the preceding trial (see also Allport, Tipper, & Chmiel, 1985). Most research into the negative-priming effect has been centered on one of several theories, such as the suppression account of Tipper (Tipper, 1985; see also Banks, Roberts, & Ciranni, 1995; Driver, McLeod, & Dienes, 1992; Houghton & Tipper, 1994; Houghton, Tipper, Weaver, & Shore, 1996) and the episodic-retrieval account of Neill and colleagues (Neill & Valdes, 1992; Neill, Valdes, Terry, & Gorfein, 1992). More recently, there has been evidence to support a view that location-based negative priming is actually an instance of a more general phenomenon known as inhibition of return (IOR; e.g., Christie & Klein, 2001; Milliken, Tipper, Houghton, & Lupiáñez, 2000). This last account is examined in the General Discussion.
The suppression account has been implemented within a neural network (Houghton & Tipper, 1994; Houghton et al., 1996) and has two parts. When a distractor first appears, the activation value of the mental representation of that distractor increases above its resting level. That elevation in activation of the distractor interferes with processing of the target. When the external presentation of the distractor is terminated, the activation level of the representation of this distractor decreases to a suppressed or subbaseline level of activation. If a new display has as its target the object or location that has just been suppressed, and the representation of that distractor has not yet returned to its baseline level of activation, the response will be impaired relative to the detection of a novel target. In other words, according to Houghton and Tipper's model, interference involves the activation of the representation of a distractor, whereas negative priming involves the suppression of that representation (on a subsequent display when the representation is needed).
The episodic-retrieval account of negative priming developed by Neill and Valdes (1992) has a qualitatively different explanation of why negative priming occurs. The episodic-retrieval theory is based on Logan's instance-retrieval theory (Logan, 1988), which involves a race among competing prior instances. The episodic-retrieval account posits that, as a byproduct of an ignored distractor stimulus, a tag or contextual marker is associated with the representation of this distracting information. That “ignore me” tag will compete with another associated tag (i.e., “attend to me”) of the stimulus the next time the system needs to decide whether to process that stimulus further. According to Neill, the ignore tag will be more available due to its recency, making the attend tag less available in comparison with a situation that involves responding to a stimulus lacking this highly available competing tag.
A number of recent articles have provided support for a memory-retrieval account (e.g., DeSchepper & Treisman, 1996; Erickson & Reder, 1998; Lowe, 1998; Reder, Shang, Erickson, & Schyrokyj, 2002) by showing that the downstream costs of ignoring a stimulus can occur at delays unlikely to operate within a suppression mechanism. Alternatively, some results within the negative-priming literature, such as facilitation rather than interference at very short intervals between prime and probe trials, are difficult to explain within the context of a memory-retrieval account (e.g., Tipper & Cranston, 1985; Yee, 1991).
Negative-priming theories and paradigms focus on short-term effects. Although there have been a few studies demonstrating long-term negative priming in tasks involving a wide array of stimulus objects (e.g., Conway, 1999; DeSchepper & Treisman, 1996; Erickson & Reder, 1998; Lowe, 1998; Reder et al., 2002), there have been no studies examining whether learning of statistical patterns over long periods (e.g., many minutes) can influence performance in a target-localization task, or if and how this learning affects negative priming (but see Lambert, Norris, Naikar, & Aitken, 2000). Conceivably, the effects of long-term negative priming could be demonstrated for a target localization task; however, given that object-identification tasks involve many objects whereas target localization tasks involve few locations and only a couple of stimuli, the generality of long-term effects in a target-localization task is not a foregone conclusion.
The experiments described here involve a modification of the target-localization paradigm used by Tipper et al. (1990). Participants were asked to indicate the current location of a target by pressing one of four keys that corresponded to one of four screen positions (and to ignore the position of a distractor if one was also presented). Because previous selective-attention research using this paradigm has focused on the short-term consequences of interference, there has been an emphasis on equating the probability of a distractor in each of the four spatial locations (e.g., Connelly & Hasher, 1993; Park & Kanwisher, 1994). In contrast, we intentionally varied the probability of the distractor by location. In the first experiment, distractors were distributed so that one of the four locations contained 60% of the distractors, another 30%, another 10%, and the final location never contained a distractor (assignment of probability to physical location was randomly determined for each participant). This manipulation enabled us to observe the interaction between the long- and short-term consequences of distractors occurring with different frequency across locations.
We reasoned that, since a distracting stimulus creates a split of attention and thereby increases response time, the impact of a distracting stimulus should be diminished to the extent that it is predictable in a given location. This prediction, or learning, is not expected to be conscious (reportable). There is ample evidence, reviewed later, that learning of base-rate changes in the environment can affect behavior without individuals being able to report these regularities. An analysis of response times to prime displays allowed us to observe whether the interference from a distractor differs as a function of its base probability in a given location. Another question that we addressed is whether response times differed as a function of the location of a target: Targets were equally probable in each location, but the conditional probability of a stimulus being a distractor or a target differed as a function of the location in which it appeared. Finally, of special interest was the question of whether negative priming effects would differ as a function of the location of the distractor in the prime display, and, if so, in what way.
According to the logic of episodic retrieval, greater negative priming should be expected in those locations where distractors dominate. Specifically, the more frequently distractors occur in a location, the stronger the association between the “ignore me” tag and that location. Therefore, it should be especially difficult to respond to a target that appears in the location typically occupied by a distractor.
It is not clear what prediction would be made by the suppression account of Tipper (1985) regarding the current experiments in that the original account stated that negative priming is a short-term process. More recently, Tipper, Weaver, Cameron, Brehaut, and Bastedo (1991) demonstrated that suppression could last several seconds after the selection processes. Regardless, it is fair to say that, according to the proponents of the suppression account, suppression should not last more than a few seconds—otherwise, the existence of this suppression would result in internal representations of the four locations being saturated with suppression.
In this article, we demonstrate the implicit learning of distractor location probability, as manifested by the sharp reduction in interference to distractors in frequent distractor locations. However, contrary to the predictions of the episodic-retrieval account, we also show that locations that more frequently contained distractors produced a reduction in negative priming rather than an enhanced negative-priming effect. We do this by providing a mechanistic account that accommodates the short-term interference results from earlier studies that have supported both the episodic-retrieval and suppression positions and explains long-term learning (i.e., sensitivity to the statistical properties of the display).
Experiment 1
Method
Overview of Procedure and Design
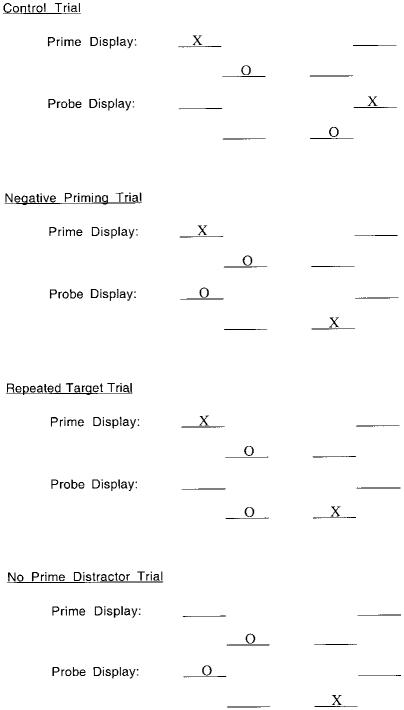
The basic paradigm closely followed the procedure of Tipper et al. (1990). Participants were asked to press a key to indicate the location of a target O while ignoring the location of a distractor X. A trial consisted of a sequence of prime display and probe display.
As mentioned earlier, distractors were not equally likely in each of the four locations: For each participant, each of four experimental conditions was randomly assigned (without replacement) to one of four locations with respect to the frequency that a location would be inhabited by the distractor stimulus. The frequent distractor location contained the distractor (X) on 60% of the prime and probe displays. The medium distractor location displayed the distractor 30% of the time. The rare distractor location displayed the distractor the remaining 10% of the time. The fourth location never contained a distractor. Not all prime displays contained a distractor—approximately 20% of the prime displays did not contain one; however, all probe displays contained a distractor in one of the three possible locations not containing the target. The specific sequence of trial types was randomly determined for each participant.
Procedure, Design, and Materials
Four different types of trials were presented: control, negative prime, repeated target, and no-prime-distractor. Figure 1 illustrates the displays presented for different type of trials. Negative-prime trials refer to those trials in which the probe display contained a target presented in the location that had been occupied by the distractor on the preceding prime display. Unlike in the control trials, negative-prime trials, or no-prime-distractor trials, we did not have a theoretical motivation for having repeated-target trials. We included this type of trial because it is frequently included in experiments of this kind, and we thought it might prove important for theorizing. Repeated-target trials refer to the trials in which the probe target's location matches the location of the target on the preceding prime display. Control trials refer to those trials in which the target's location in the probe display was different from the location inhabited by either the target or the distractor on the preceding prime display. The distractor location for all probe displays was randomly selected from the unoccupied positions, within the constraints of the distribution frequency, in order to make its location unpredictable from the prime display. Note that this means (in contrast to some of the studies in the literature) that a distractor could be repeated from prime to probe displays. Note that because a distractor appeared in one location 60% of the time, it necessarily had to repeat at least 10% of the time. Finally, no-prime-distractor trials refer to the situations in which the prime display contained no distractor. On no-prime-distractor trials, the target appeared in one position for prime and another position for probe displays. Unlike many experiments that use a similar paradigm, in this experiment the locations of the distractor and target were randomly determined for each display and each participant within the constraints of probability and condition type.
Figure 1.
Examples of types of trials consisting of a sequence of two displays: a prime display and a probe display.
Although frequency of distractor in locations varied systematically from never to 60%, targets were presented in each location with equal probability (25%), with one exception: For probe displays on negative prime trials, the three locations that received distractors had a target present 33% of the time. Since negative prime displays only occurred 12.5% of the time, the 25% probability was distorted very little (22% vs. 26%).
Ignoring the practice trials, the absolute number of distractors appearing in each location (for all displays) was 400, 200, 66, and 0 for the frequent, medium, rare, and never locations, respectively. The absolute number of targets was 192 in each location except the never distractor location, which contained 162 targets. Given the inherent complexity of the design constraints, the Appendix provides the exact number of trials of each type, the conditional probabilities of prime—probe pairings, and the mathematics that justifies these probabilities.
Participants indicated the target location on a computer keyboard, using four response keys (D, C, K, M) that mapped spatially onto the four stimulus locations. The keys were covered in blank, yellow stickers. For all trials, the primary dependent measure was the time to correctly identify the target's location. We also recorded accuracy as a function of condition.
The experiment began with 25 control trials to give each participant time to adjust to the unbalanced proportions of distractor locations. The data from these trials were not included in the analysis. The remainder of the experiment consisted of 125 control trials, 96 negative-prime trials, 76 repeated-target trials, and 72 no-prime-distractor trials, occurring in random order and determined separately for each participant. There were 394 trials presented in all.
The four positions in which targets and distractors appeared corresponded to a broad V-shape (see Figure 1). The locations were made salient to the participants by underscoring each position with a white sticker, pasted to the monitor. The widest horizontal distance between two positions (the top of the V) measured 45 mm and subtended approximately 9.46° of visual angle. The smallest horizontal distance measured 17 mm (subtending 3.6°), and the vertical distance measured 12 mm (subtending 2.54°). The stimuli (a white O and a white X) subtended 1.49° vertically and 0.85° horizontally. A small white cross (a + sign), subtending 1.17° horizontally and vertically, was centered in the middle of the display and used as a fixation point. The background for all stimuli other than the stickers affixed to the monitor was black. The room was darkened to facilitate perception.
The display of the stimuli and the timing of the responses were controlled by PsyScope (Cohen, MacWhinney, Flatt, & Provost, 1993) on a computer. For each participant, a unique stimulus sequence was generated randomly in LISP using the statistical constraints specified earlier. The output of this program was the stimulus input file for the PsyScope subprogram.
Participants were tested individually. They were shown the stimulus display and the keyboard and informed that the spatial layout of the marked keys corresponded to the marked positions on the screen. They were instructed to press the key corresponding to the target’s position on the screen for each display. All participants were instructed to position their left hand so that they had different fingers on the C and D keys and their right hand so that they had different fingers on the M and K keys for all trials. Participants were informed that every display would have a target O present in one of four locations underscored by a sticker pasted on the screen. They were instructed to respond to the target as quickly and as accurately as possible. They were also informed that most displays would have an X present in one of the three remaining locations but that the X was to be ignored because it was irrelevant to the task.
Each display began with “Ready?” positioned in the middle of the computer screen. The participant then pressed the space bar to remove the “Ready?” signal and begin the trial. A fixation cross appeared 1,500 ms after the offset of the prompt and remained on the screen for 500 ms. Immediately after the fixation cross disappeared, the prime target and the distractor, if present, appeared on the screen and remained there for 150 ms, after which the screen turned blank until the participant responded. This response was immediately followed by the fixation cross appearing in the center of the screen for 500 ms. Immediately after the fixation cross offset, the probe target and distractor were presented in their locations for 150 ms. Again the screen turned blank awaiting the participant's response. After the participant's response, the trial was complete and the “Ready?” display appeared again to initiate the beginning of a new trial.
Participants
Twenty-four undergraduate students at Carnegie Mellon University participated in this study. Participation helped to fulfill a research-experience requirement of the introductory level psychology courses.
Results
We were primarily interested in response times (RTs) but also analyzed error rates. Because we were interested in performance as a function of location, we could not aggregate trial types over location, thereby leaving few observations per condition. We were not only interested in the effect of the distractor's location but also the effect of the target's location on any given display. Consequently, the data were sorted by both the position of the target and the position of the distractor within a display. This problem of fewer observations per condition than in a balanced location design (that allows greater aggregation) was exacerbated in the rare distractor location.
Because medians of small samples are unreliable indices of the population median (Miller, 1988), and because of the uneven number of observations per cell, we calculated restricted means using a nonrecursive procedure with moving criterion to eliminate the outlying observations, as prescribed by Van Selst and Jolicœur (1994).1The relevant z value was chosen on the basis of sample size from the table of criterion cutoffs provided by Van Selst and Jolicœur. Using the sample's mean and standard deviation, the actual cutoff values were calculated for the sample from the z value. From the observations that fell within the cutoff values, we calculated the restricted mean of the sample. The results of this analysis using restricted means are reported; however, regardless of whether restricted means or medians were used, the latency pattern and inferential statistics tell essentially the same story.
The results are organized in terms of prime displays and probe displays. For a given display, the data were analyzed as a function of both the position of the distractor and the position of the target. Comparisons based on locations refer to the effect of the different frequency of distractors appearing in the various locations. Fisher's PLSD was used for all posttests.
Prime Displays
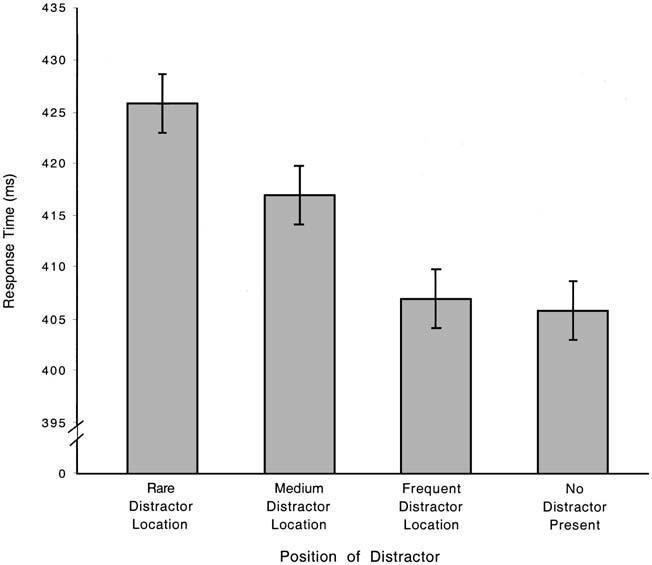
Effects based on location of the distractor. Figure 2 presents the restricted means of participants' correct RTs as a function of where the distractor appeared on a prime display, collapsed over the location of the target. Table 1 presents the corresponding error rates.
Figure 2.
Mean correct response times (with standard error bars) for prime displays, based on position of distractor, in Experiment 1.
Table 1.
Mean Proportion Error Rates on Prime Displays in Experiments 1 and 2 Partitioned as a Function of Target Position and Distractor Position
| Partitioned by |
||
|---|---|---|
| Location | Position of target | Position of distractor |
| Experiment 1 | ||
| Never | .04 | |
| Rare | .04 | .05 |
| Medium | .04 | .05 |
| Frequent | .05 | .05 |
| No distractor | .03 | |
| Experiment 2 | ||
| Outside | .06 | |
| Rare | .04 | .05 |
| Medium | .04 | .04 |
| Frequent | .05 | .03 |
| No distractor | .03 | |
Note. Location refers to the probability of a distractor appearing in that location. No distractor refers to prime displays that did not contain a distractor.
Several single-factor, within-subjects analyses of variance (ANOVAs) were conducted on correct RTs and error rates. Because a location could not contain both a target and a distractor at the same time, the design was not factorial. Separate analyses using location of target and location of distractor as the factor were conducted.
There was a main effect of distractor location on correct RTs, F(3, 69) = 11.41, p < .001, and on errors, F(3, 69) = 2.85, p < .05, such that participants were slower and less accurate to respond on those trials in which the distractor appeared in a location where it was rarely experienced. Consistent with previous research, participants were significantly faster to respond to prime displays containing no distractor than to those than did, t(23) = 3.662, p < .001; however, there was no reliable difference in RTs to the displays containing the distractor in the frequent-distractor location and to the no distractor present displays, t(23) = 0.417, p > .05. Indeed, the RTs were virtually the same for the frequent-distractor condition and the no-distractor condition (see Figure 2).
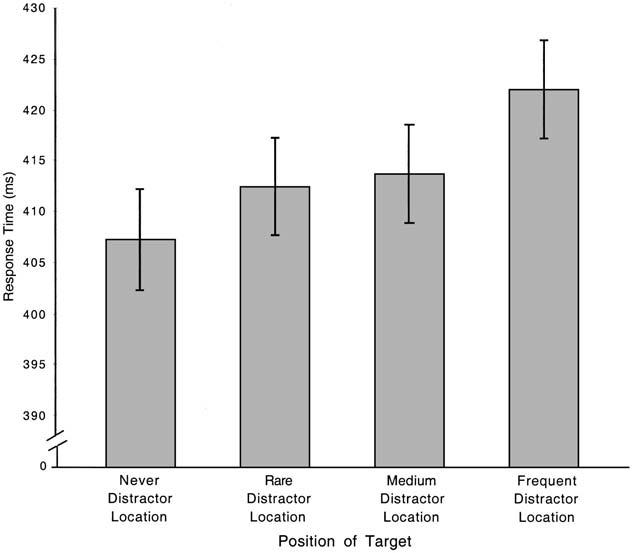
Effects based on the location of the target. Although targets were equally likely in each of the four locations, it was possible for RTs to vary as a function of target location, defined by the likelihood of that location containing a distractor—that is, given that a stimulus was detected in a particular location, the conditional probability that the detected stimulus was a target varied because the probability of its being a distractor varied. Figure 3 presents the means of participants' correct RTs for the same prime display data illustrated in Figure 2 but partitioned as a function of the target's location in the display by collapsing over the position of the distractor in the display (the error rates are included in Table 1).
Figure 3.
Mean correct response times (with standard error bars) for prime displays, based on position of target, in Experiment 1.
A one-way ANOVA on mean correct RTs for prime displays, using target position as the factor, did not produce a reliable main effect of target position, F(3, 69) < 2.0; however, participants were reliably faster to respond to targets that appeared in the location that never contained a distractor than to targets in the location that frequently contained a distractor, t(23) = 2.185, p < .05.
Note that when these data are displayed as a function of the target's location, the direction of the effect is the inverse of when these data are displayed as a function of the distractor location (compare Figures 3 and 2, respectively). Specifically, responses were fastest when the distractor appeared in the frequent-distractor location but slowest when the target appeared in that location. Note that these two analyses are not independent of each other—for a given display, a target cannot occur in the location that is occupied by a distractor, and vice versa. Given this inherent constraint, it is worthwhile to examine whether the effects reported above should be attributed either solely to the location of the target or solely to the location of the distractor.
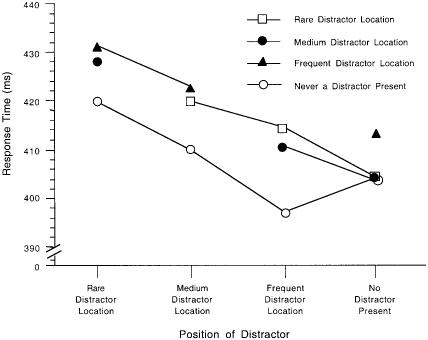
Figure 4 presents the data displayed in Figures 2 and 3, partitioned by both the position of target and distractor. There is a separate function for each position occupied by the target in terms of the frequency of the distractor in that position. Since the target and distractor cannot be in the same location concurrently, there is one point missing for each function.
Figure 4.
Mean correct response times for prime displays in Experiment 1 based on position of distractor, with a separate plot for each position occupied by the target. Levels on the abscissa refer to the location of the distractor for a given display.
Note that the same basic pattern emerges for each level of target position for the effect of distractor location, mirroring the pattern in Figure 2. If one replots Figure 4 to represent location of the target on the abscissa, with a separate function for each level of distractor location, the data will mirror the pattern found in Figure 3. Of course, these data are slightly noisier because some of these conditions have very few data points (e.g., when the distractor is in the rare position).
Although the slower RTs to targets in the frequent-distractor location might be attributable in part to distractors not being in expected locations, the data displayed in Figure 4 suggest that the locations of the target and distractor have separate and roughly additive effects. The data analyses based on location of targets suggest that the adaptation to the statistical properties of the experiment reflects conditional probabilities as well as base rates. Even if one were to ignore the location of a distractor, the conditional probability of a stimulus being a target is not equal in all the locations. For example, if a stimulus appears in the never distractor location, that stimulus must be a target. Conversely, although one quarter of the targets appeared in the frequent-distractor location, the conditional probability of a stimulus that appeared in the frequent-distractor location being a target is less than if it appeared in the rare-distractor location.
Probe Displays
Performance on the probe displays is critical to the questions of whether and how negative-priming effects vary with the base rate (first-order probability) of distractors in the various locations. Before examining these questions, we wanted to establish whether or not the basic negative-priming result was obtained with our modified paradigm. Table 2 presents RTs and error rates for probe displays as a function of target position based on the type of trial: control, negative prime, repeated target, and no distractor present on prime display.
Table 2.
Mean Correct Response Times and Proportion Error Rates for Probe Displays in Experiment 1
| Position of target |
|||||
|---|---|---|---|---|---|
| Type of trial | Never | Rare | Medium | Frequent | Average |
| Control | 400 | 394 | 388 | 406 | 397 |
| (.05) | (.04) | (.04) | (.04) | (.04) | |
| Negative prime | 433 | 423 | 433 | 429 | |
| (.07) | (.04) | (.05) | (.05) | ||
| Negative-prime effect | -38 | -34.5 | -23.5 | -32 | |
| (-.02) | (.00) | (-.02) | (-.02) | ||
| Repeated target | 417 | 404 | 410 | 423 | 414 |
| (.06) | (.03) | (.05) | (.05) | (.05) | |
| No prime distractor | 393 | 407 | 401 | 404 | 403 |
| (.02) | (.04) | (.03) | (.02) | (.03) | |
| Average per location | 403.3 | 409.5 | 405.5 | 416.5 | 410.8 |
| (.04) | (.05) | (.04) | (.04) | (.04) | |
Note. Response times (RTs) are expressed in milliseconds. Error rates appear in parentheses. Position of target is defined by the frequency of distractor appearance in a location. The negative RTs and error rates for the negative-prime effect are calculated by taking the difference between the control and negative-prime trials for the corresponding response measures.
An ANOVA revealed a significant main effect of trial type on RTs, F(3, 69) = 20.28, p < .001. A specific contrast indicated that participants were significantly slower to respond to the negative prime probe displays than control trial probe displays, t(23) = 6.719, p < .001. Other contrasts indicated that the RTs for negative prime probe displays were also significantly slower than for either the repeated-target or the no distractor on probe displays, ts(23) = 3.043, 7.157, ps < .01, .001, respectively. RTs to repeated targets were also significantly slower than to control and no-prime-distractor trials, ts(23) = 2.953, 3.341, p < .01, respectively.
There was a significant main effect on errors for probe display type, F(3, 69) = 3.747, >p < .05, with a contrast showing that participants were more likely to respond incorrectly to negative prime displays than to other trial types, t(23) = 2.363, p < .05. Thus, the typical negative-priming pattern was replicated even though distractors were not equally probable in each location. Of particular interest were the negative-prime effects as a function of location. For each possible location (the never distractor location could not be included), we computed the difference in mean correct RTs between negative-prime and control trials for probe displays. These data are presented in Table 2. Although an ANOVA did not reveal a significant main effect of location on the size of negative-prime effect for RTs (F < 2.0), a specific contrast indicated that the negative priming effect for the frequent location was significantly smaller than for the rare-distractor location, t(23) = 2.123, p < .05.
Discussion
The central question to be addressed in this experiment was whether varying the base rate of distractors by location would have an impact on responses, especially with respect to negative priming, and, if so, in what way. A memory-based explanation such as episodic retrieval would predict faster responding to displays that contain a distractor in the frequent location and also an accentuated negative-priming effect when a target follows a distractor in the frequent-distractor location. The former prediction was supported but not the latter. In fact, the direction of the effect was exactly the opposite of what should have occurred according to the episodic-retrieval account. It is unclear what the suppression account would predict with respect to the present experiment because, as mentioned before, suppression is not posited to last longer than a few seconds.
Inhibition of Return?
The mechanism known as inhibition of return (IOR; Tipper, Driver, & Weaver, 1991) has been offered as explanation for negative priming (e.g., Christie & Klein, 2001; Milliken et al., 2000). IOR postulates that attention is less likely to return to locations that have just been explored. The animal literature reports evidence consistent with this hypothesis; for example, rodents are more likely to travel to novel locations within a maze and are more easily trained on a win—shift strategy (moving to a new location each time) than a win-stay strategy, independent of whether there is reinforcement (in the form of treats) still available in the already visited locations (e.g., Olton & Samuelson, 1976; Olton & Schlosberg, 1978). Whether these animal results generalize to humans is unclear, given that many of the early, seminal studies of negative priming used a biased design (see Christie & Klein, 2001); however, proponents of this theory suggest that when the design does not bias participants to expect targets to repeat in certain locations, negative-priming effects can be explained by an IOR account (Christie & Klein, 2001).
Consistent with the IOR account, there was a reliable effect of slower responding to a target that reappeared in the same location from prime to probe display. This effect may have been smaller than it was in the negative-prime condition because of opposing processes reducing the potency of the IOR effect (e.g., correct responses in the repeated-target condition required an identical keypress for both the probe and prime displays). On the other hand, an IOR account by itself seems incomplete as an explanation for our data since we observed less negative priming in locations that were inhabited more often. The interpretation of this finding is discussed further in the General Discussion.
We propose that, over and above ignoring recently examined locations, the attentional system also learns to which locations attendance is unnecessary. The attentional system rapidly detects the presence and location of a stimulus but must allocate attention to discern its identity. This notion, that where information becomes available relatively automatically but that what information requires attention, has been proposed previously (e.g., Johnston & Pashler, 1990). In order for a location to be negatively primed, the location must have been attended to. Over the course of an experiment, participants learn the odds that a stimulus detected in a particular region of the display will turn out to be a distractor. The attentional mechanism weights recent experiences more heavily than those that have accumulated over time. A study by Snyder and Kingstone (2000) suggested that IOR effect can be present at multiple locations and that its magnitude is largest for the one that was examined most recently. One can speculate that, since the rare-distractor location would be more readily inspected for a target (than the frequent or medium distractor locations), IOR effects would be strongest there because it is the most recently examined location. Although, without modification, IOR cannot explain the effects found here, adding the assumption that IOR only occurs when the stimulus is attended would enable this theory to account for the present results. Exactly how these mechanisms can explain the obtained pattern of data is explained more thoroughly in the General Discussion.
Higher Order Statistical Sensitivity?
Our experiment was carefully designed to ensure that all conditions were equally represented in each location, except for the base rate of distractors appearing in the four locations. In particular, we ensured that the number of negative-priming trials was equal across the three locations that could have negative-priming trials (the one location that never contained distractors could not have any negative-priming trials). These efforts, however, may have had an unintended consequence. From our analyses we know that participants exhibited sensitivity to the conditional probabilities of targets in a location even though the first-order probabilities did not differ (targets were equally likely in each location). This suggests that participants might also exhibit other types of higher-order statistical sensitivities (see Christie & Klein, 2001, for similar ideas).
Specifically, although negative-priming trials were equally likely (i.e., had the same frequency) across the three possible locations, the transition probability that a target would follow a distractor differed dramatically for these three locations. An appropriate analogy might be words of varying frequencies consisting of letter bigrams of different frequencies. Transition probabilities exist among letters that may be independent of the frequency of the words that contain them. Distractors presented in the rare-distractor location on prime displays were much more likely to be followed by a target on the subsequent probe display than were distractors present in the frequent-distractor location. The transition probability that a distractor would be followed in the same location by a target on the probe display was greater than 80% in the rare location. In contrast, the transition probability of a target following a distractor in the frequent location was less than 15%. We do not suppose that participants explicitly calculated these transition probabilities; however, sensitivity to the statistical properties of the environment, as observed in other complex situations (e.g., Chun & Jiang, 1998), may well have influenced performance in this experiment too.
Although the potential for effects due to differential transition probabilities seems likely, our finding of differential negative priming by condition would not be compromised by such an effect. In fact, the differential negative-priming effect was opposite that predicted by the transition probabilities in terms of direction. If participants are sensitive to the different transition probabilities that a target would follow a distractor in a given location, then their responses should be facilitated in the condition where this probability is greatest. In other words, the negative-priming effect should have been smallest in the condition where the target was most likely to follow the distractor, due to expectancy-based facilitation. We found the opposite trend: The negative-priming effect was greatest in the rare-distractor location, where the probability of a target following the distractor was six times that in the frequent-distractor location.
Conceivably, both the processes sensitive to transition probabilities and the tuning of the general attentional procedures (or mechanisms) alluded to earlier had an impact on performance. If both were at play, they worked in opposition, diminishing each other's effects. This interaction suggests that the effect of differential base rates of distractors on the size of negative priming would have been greater had there not also been differential transition probabilities. Experiment 2 was designed to test this conjecture by equating the transition probability of a target following a distractor across locations.
Experiment 2 was also designed to shed light on the degree to which attentional control can be explicitly instructed. Although there is strong evidence that some type of statistical learning of base rates affected performance, what is less clear is whether the observed effects are due to an automatic and implicit learning mechanism. At issue was whether the attentional system can take deliberate, explicit instruction into account such that a location identified as irrelevant can be ignored from the start. When we devised these studies, we were unaware of the considerable literature (e.g., Theeuwes, 1994; Theeuwes & Godijn, 2002; Theeuwes, Kramer, Hahn, & Irwin, 1998; Theeuwes, Kramer, Hahn, Irwin, & Zelinsky, 1999) concerned with this issue and indicating that deliberate efforts to focus attention can still be distracted by irrelevant stimuli.
Experiment 2
A fifth location was added to the possible locations where a stimulus could appear. Participants were advised that, should a stimulus occur there, it always would be a distractor. Moreover, there was no response key corresponding to the fifth position, thereby making it impossible for participants to respond to any distractor displayed there. Distractors occurred in the fifth position on only 4% of the prime displays and never on probe displays. Given that these stimuli appeared on only 2% of the displays, there should have been little opportunity to learn to ignore the irrelevant stimulus if ignoring requires some type of practice. However, if participants could exert some type of conscious or deliberate process to ignore stimuli in that location, there should have been little interference on trials where the distractor occured in that fifth position.
In Experiment 1, there was a monotonic relationship between the likelihood that a location would contain an item at all and the likelihood that it would contain a distractor. If participants were just less likely to attend to a location that more frequently contained stimuli (an IOR account), then the pattern on prime displays and control trials could be explained. This explanation could not account for the differential negative-priming effect, but it might account for the effects on the prime displays. By limiting the type of stimulus to appear in the fifth position to distractors and assigning a very low probability of its appearance, we decoupled the probabilities of a stimulus appearing in a location and that location containing a distractor. If distractors in the fifth (outside) position still cause a slow-down, then an attentional bias for novel locations might be the explanation for the first-order effects we observed on prime displays. That is, rather than learning which locations contain distractors per se, participants may merely be responding to novelty, drawn to locations that have been experienced less often (an IOR account).
Another objective of Experiment 2 was to eliminate potential second-order transition-probability effects, discussed earlier, that may have affected performance. The new design ensured that the location of the target or distractor on the prime display in no way predicted the location of either on the probe display. We predicted that, without these differential transition probabilities, the difference among locations in terms of negative-priming effects would be even greater, still showing the greatest negative-priming effects in the rare-distractor location and the smallest effects in the frequent-distractor location.
Finally, we also included an awareness questionnaire to investigate whether the statistical distributions that affect performance were explicitly or implicitly learned.
Method
Design and Materials
The design and materials for Experiment 2 were identical to the design and materials for Experiment 1 with the following exceptions. In addition to the four standard locations used in Experiment 1, there was a new location placed outside of the broad V shape comprising the four positions used earlier. The only stimuli ever present in this location were distractors in the prime displays. For 4% of the prime displays, the distractor was present in the outside distractor location. As before, white stickers on the screen denoted the four basic locations. The outside location was not denoted with a sticker and had no corresponding response key since participants were told that, should a stimulus appear in that outside position, it would always be a distractor.
For each participant, the location of this outside distractor was randomly assigned to either the left or the right, or on the top or the bottom, of the standard V configuration. When this “outside the V” distractor appeared to the left or right of center, it was shown 29 mm from the fixation cross; for participants assigned to see it at the top or bottom of the display, the distractor appeared 9 mm directly above or below the fixation cross.
The distribution of distractors to the standard four positions differed from that in Experiment 1. In this experiment, each location could contain a distractor. The frequent-distractor location contained a distractor 60% of the time across prime and probe displays. Two intermediate-distractor locations each contained a distractor 17.5% of the time (35% for the two locations combined). The rare-distractor location contained the distractor 5% of the time. These percentages ignore those prime—probe display pairs with the distractor in the outside position.2As in Experiment 1, across prime and probe displays the targets were presented in each of the four standard locations with equal probability, and this was also true for the special, outside-location trials.
The experiment began with 32 practice trials to give participants time to adjust to the unbalanced proportions of distractor locations. The data from these trials are not included in the analysis. The rest of the experiment consisted of 144 control trials, 72 negative-prime trials, 72 repeated-target trials, 96 no-prime-distractor trials, and 16 outside distractor-location trials. These 400 trials appeared in random order for each participant. It is important to note that the pairs of prime and probe displays were arranged in such a way that neither the target's location nor the distractor's location for a given prime display had any predictive validity concerning the location of the target or the distractor for the subsequent probe display. If there was a distractor present in one of the four standard locations on the prime display, there was a 50% chance that the trial would be a control trial, a 25% chance the trial would be a negative-prime trial, and a 25% chance the trial would be a repeated-target trial. For control trials, the target was randomly assigned to one of the other two positions, and the distractor was randomly assigned to any of the nonoccupied locations, with the constraint of maintaining the predetermined frequencies of distractors in each location. For negative-prime and repeated-target trials, the position of the target on the probe display was determined based on the prime display (i.e., the distractor or the target's location, respectively, on the prime display), but the distractor could be in any of the remaining three locations (in accordance with base probabilities).
Given the inherent complexity of the design constraints, we include in the Appendix the exact number of trials of each type, the conditional probabilities of prime—probe pairings, and the mathematics that justifies these probabilities.
Procedure
The procedure for Experiment 2 was almost identical to that of Experiment 1. Concerning the outside position, participants were informed that of target would always appear in one of the four standard locations, and they were not given a key to press that would correspond to the outside distractor location. They were explicitly warned that a distractor might occasionally appear in this outside position but were told that they were to ignore it. After the experiment was finished, approximately half of the participants were administered a questionnaire to determine the extent of their conscious awareness of the distractor base rate in each location.
Participants
Fifty-nine3undergraduate students at Carnegie Mellon University participated in this study to fulfill a research-experience requirement of the introductory level psychology courses. The first 34 participants were tested without completing a questionnaire, while the remaining 25 completed a questionnaire at the end of the study.
Results and Discussion
Given that participants were unaware of whether or not they would be given a questionnaire until after completing the experiment, we treated all 59 participants as one group for purposes of the analyses. For all comparisons, the critical measure was each participant's mean RT for correct responses in each condition. We used the procedure to eliminate outliers described in Experiment 1. Separate within-subject ANOVAs were performed on RT and error rates, partitioned as a function of distractor location and as a function of target location for both prime displays and probe displays. Fisher's PLSD and paired t tests were used for mean comparisons. This time there was a fifth position to consider for prime displays, and all four of the regular locations contained distractors.
Prime Displays
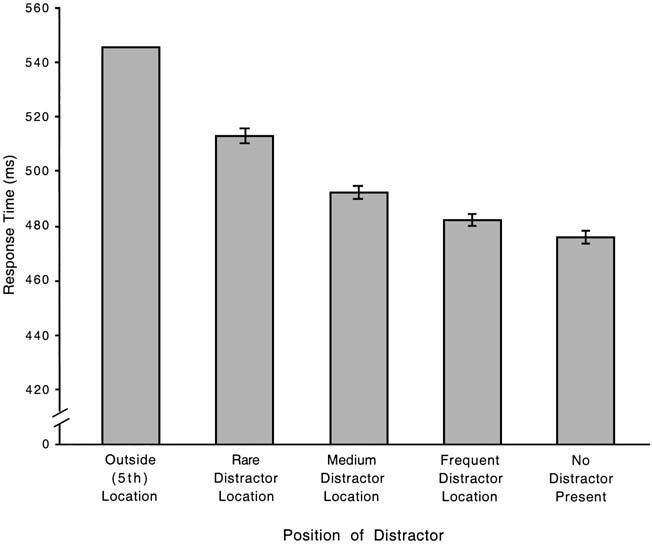
Effects based on distractor location. Figure 5 presents the mean of the participants' correct RTs for prime displays based on the location of the distractor. The standard error bars are based on a pooled estimate of the variance that excludes the outside position because there were too few observations to give a stable estimate. There was a significant main effect of distractor location on correct RTs and on errors, F(4, 232) = 24.01, p < .001, and F(4, 232) = 3.41, p < .02, respectively. The pattern replicated that obtained in Experiment 1; however, this time RTs were reliably faster when there was no distractor at all compared with displays that contained a distractor in the frequent-, medium-, or rare-distractor positions, ts(58) = 2.645, 6.954, and 6.961, and ps < .05, .001, and .001, respectively. Likewise, RTs were reliably faster if the distractor was in the frequent location as compared with the medium or rare location, ts(58) = 5.042 and 6.318, p < .001, respectively. Finally, RTs were also reliably slower if the distractor was in the rare distractor location compared with the medium frequency distractor location, t(58) = 3.984, p < .001.
Figure 5.
Mean correct response times (with standard error bars) for prime displays, based on position of distractor, in Experiment 2. No standard error bar is listed for the outside position due to the small number of observations for that condition.
The effect of distractors in the outside location. Figure 5 also presents the RTs for prime trials in which the distractor occurred in the outside position. Of interest was whether the RT pattern would look more like that of the frequent-distractor location, providing support for a consciously controlled attentional mechanism, or whether the RTs would be comparable to those in the rare distractor location, providing support for an implicitly learned process. Participants were slower to respond when the distractor was in the outside distractor location than they were to either the rare-, medium-, or frequent-distractor locations, ts(58) = 2.633, 4.674, and 5.285, ps < .05, .001, and .001, respectively. These data support the view that faster responding for trials involving distractors in the frequent-distractor location results from participants learning not to attend to stimuli in that location. The fact that the outside position behaved like the rare-distractor location makes less tenable an explanation that the lack of interference in the frequent-distractor location is based on an explicit strategy to ignore that location. Participants were explicitly told that no target would be present in the outside location, and yet distractors in that location still interfered with performance. These data are consistent with the view that there is a bias to attend to novel stimuli or locations.
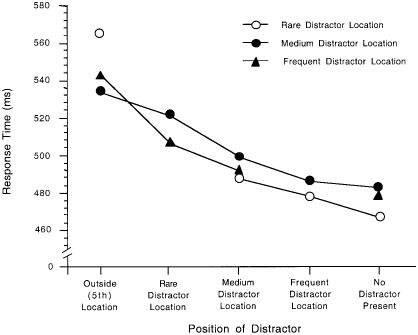
Effects based on the target location. The response latencies to prime displays based on the position of the target showed almost no difference among the locations (499 ms for the rare location and 504 ms for the other two location types), and this pattern was not reliable (F < 1.0). It may be worth noting, however, that this small difference is in the same direction as in Experiment 1 and that this pattern is also evident for the control probe displays (discussed next). Figure 6 plots the latency pattern for prime displays as a joint function of target and distractor position, in the same fashion as Figure 4.
Figure 6.
Mean correct response times for prime displays in Experiment 2 based on position of distractor, with a separate plot for each position occupied by the target.
Probe Displays
Effects based on the type of trial. Table 3 presents the RTs and error rates for probe displays based on the type of trial (i.e., control, negative prime, repeated target, or no-prime-distractor display) and as a function of the position of the target in terms of the frequency of distractor at that location. An ANOVA yielded a significant main effect on RT of trial type, F(3, 171) = 19.35, p < .001. Participants were slower to respond to negative-prime displays than control trials, t(57) = 5.93, p < .001. RTs to probe displays for negative-prime trials were also significantly slower than for displays associated with repeated-target and no-prime-distractor trials, ts(57) = 6.48 and 7.05, ps < .001, for both comparisons. No other contrasts were reliable, and there was no main effect on error rates of trial type for probe displays.
Table 3.
Mean Correct Response Times and Proportion Error Rates for Probe Displays in Experiment 2
| Position of target |
||||
|---|---|---|---|---|
| Type of trial | Rare | Medium | Frequent | Average |
| Control | 474.9 | 503.0 | 492.4 | 490.1 |
| (.04) | (.03) | (.02) | (.03) | |
| Negative prime | 526.5 | 528.0 | 505.2 | 516.7 |
| (.06) | (.03) | (.03) | (.04) | |
| Negative-prime effect | -49.8 | -40.0 | -17.1 | -35.6 |
| (-.01) | (.00) | (-.01) | (-.01) | |
| Repeated target | 473.9 | 490.9 | 489.4 | 484.7 |
| (.04) | (.04) | (.04) | (.04) | |
| No prime distractor | 480.1 | 495.8 | 496.2 | 490.7 |
| (.02) | (.02) | (.03) | (.03) | |
| Average per location | 488.9 | 504.4 | 495.8 | 495.6 |
| (.04) | (.03) | (.03) | (.04) | |
Note. Response times (RTs) are expressed in milliseconds. Error rates appear in parentheses. Position of target is defined by the frequency of distractor appearance in a location. The negative RTs and error rates for the negative-prime effect are calculated by taking the difference between the control and negative-prime trials for the corresponding response measures.
Some of the repeated-target trials were identical displays—that is, the distractor was also repeated from the prime to the probe display. This display repetition was unavoidable due to the constraints of our design; however, based on the arguments of Christie and Klein (2001), we analyzed separately the repeated-target trials that did not contain repeated distractors. In an analysis that compared repeated targets that were nonidentical (distractor in a different location in the probe display than in the prime display) with control trial displays, repeated trials were significantly slower, F(1, 57) = 6.13, p < .05.
Control and repeated trials. For probe displays that were part of control trials, there was a main effect based on the target's position, F(2, 114) = 6.38, p < .01. There was a significant difference in mean RTs for frequent versus rare target positions, t(57) = 2.20, p < .05, such that the participants responded slower when targets occurred in the frequent-distractor location than they did when targets appeared in the rare-distractor location. RTs to medium- and rare-frequency target locations also differed significantly, t(57) = 4.145, p < .001.
For repeated-target trials, there was no effect of target position on RTs; however, a contrast between RTs to the rare- and medium-frequency locations revealed a significant difference, t(57) = 2.28, p < .05, such that participants were slower to respond to a target in the medium-frequency location than they were to a target in the rare-frequency location. There was no reliable target location effect on error rates (F < 1.0).
Negative-prime trials. There was a significant effect of target location for negatively primed probe displays, F(2, 98) = 3.78, p < .05. Participants were significantly slower to respond to a target that was presented in the medium location as compared with the frequent-distractor location, t(57) = 3.94, p < .001. There were few observations for negatively primed probe trials in the rare-distractor location. If a participant erred on all the prime displays in that cell or on all of the probe displays in that cell, the case was missing and could not be used. We suspected that the reason the contrast between the frequent and the rare was not reliable was lack of power resulting from missing participant data caused by too many errors.
The negative-priming effects by target position according to distractor location are shown in Table 3. Some of the analyses were done on fewer cases, the result of some participants making as many errors as there were observations in conditions that contained very few trials. When cases had to be dropped, the degrees of freedom necessarily were reduced.
Targets appearing in each of the three locations produced asignificant negative-priming effect: t(50) = 6.04, p < .001, for the rare location; t(58) = 6.19, p < .001, for the medium location; and t(58) < 2.56, p < .05, for the frequent location. An ANOVA revealed no significant effect of location on negative priming, F(2, 100) < 2.74, p < .05; however, the medium- and rare-distractor positions were both more negatively primed than the frequentdistractor position, t(58) < 2.51 and t(50) < 2.35, respectively, ps < .05, for both comparisons. As noted for Experiment 1, thisa pattern is the opposite of what the episodic-retrieval account predicts (i.e., a greater probability of retrieving an “ignore me” memory trace in the frequent-distractor location).
The nearly 50-ms negative-priming effect in the rare-distractor location condition was even larger than the approximately 40-ms effect found in Experiment 1. Both of these effects are larger than the frequently reported negative-priming effect size, which tends to be closer to 25 ms (e.g., Connelly & Hasher, 1993; Conway, 1999; Hasher, Zacks, Stoltzfus, Kane, & Connelly, 1996; Houghton et al., 1996; Neill, Terry, & Valdes, 1994; Neill et al., 1992; Park & Kanwisher, 1994; Tipper, Weaver, Kirkpatrick, & Lewis, 1991). We discuss possible reasons for this magnitude difference in the General Discussion.
The results from Experiment 2 support the idea that the statistical learning observed in both Experiments 1 and 2 is not under conscious control. If participants could have used a conscious evaluation of the likelihood of a detected stimulus being a distractor, then performance would have been at least as fast when a distractor appeared in the outside position as it was when a distractor appeared in the frequent-distractor location. Instead, despite the fact that participants could not respond to stimuli in that location and were explicitly told that only distractors would appear there, stimuli in that location were just as distracting as ones that appeared in the rare-distractor location.
It is tempting, but unwarranted, to infer that, since explicit knowledge cannot neutralize otherwise distracting stimuli, the learning of the statistical dependencies is implicit. For that reason, we collected questionnaire data to explore whether the learning mechanism was under conscious awareness or operated implicitly.
Conscious awareness data. Approximately half of the participants' awareness of the experimental manipulation was explicitly tested by questionnaire after completing all of the target-location trials. Participants were first asked to speculate on the goals of the study. More than half (56.3%) of these participants had no idea (refused to guess) as to the purpose of the experiment. A little less than a quarter (21.9%) of those surveyed guessed that the experiment was “a reaction time experiment,” and another 18.8% were off topic (e.g., thought it was a hand—eye coordination study). Slightly less than one tenth (9.4%) of the participants came close to the general purpose of the experiment in that they thought that it was testing subconscious perception.
Participants were then asked whether they thought that the distribution of distractors varied for each location. One third (33%) of the participants reported that they thought that the distribution of distractors across the various locations was balanced; another third (36.3%) of the participants reported that they did not pay attention to the distractors and thus had no idea; and the rest (30.7%) of the participants reported that the distribution of the distractors was unbalanced.
After informing those participants who were unaware of the unbalanced distribution of the distractors, all were asked to guess the probability distributions of the distractors at each location. More than half (51%) still reported even or random distribution of the distractors. All other participants guessed a variety of different distributions that were less extreme than our manipulation, such as 30%-30%-20%-20%. Even though participants could not report the probability of how often distractors might appear in a particular location, most of them (90.9%) could report where the outside location was (they had been explicitly told prior to the experiment where to expect it).
Other research (e.g., Lemaire & Reder, 1999; Lovett & Anderson, 1996; Reder, 1987; Reder & Schunn, 1996) also supported the notion of implicit learning of base rates—that is, that the base rates affected performance, but participants were oblivious to the manipulation (see Cary & Reder, 2002, for a review). These data, combined with the recent research of Chun and Jiang (1998, 1999) reinforce the veracity of our awareness data.
General Discussion
The pattern of RTs and errors found in Experiments 1 and 2 underscores the exquisite sensitivity of the human attention system to statistical properties of the environment. Participants were faster (and more accurate) responding to displays in which the distractor appeared in the frequent-distractor location. In fact, responses to displays that contained a distractor in the frequent location were almost as fast as those to displays that contained no distractor at all. The most impressive result was that the size of the negative-priming effect was strongly affected by the frequency with which a distractor appeared in a location. Surprisingly, the more often a distractor appeared in a location, the smaller the size of the negative-priming effect. Some theories without additional assumptions would have predicted that, if there were any effect at all, it would go in the opposite direction.
Our account of this pattern of data draws a distinction between a preattentive-detection phase and a stimulus-identification phase. The former phase enables localization of the stimuli but not their identification. The assumption that stimulus-location detection occurs more rapidly and with less demand for attention than does stimulus identification is consistent with findings in the literature (e.g., Johnston & Pashler, 1990). We assume that the attentional mechanism selects one of the two detected locations to inspect first (i.e., identification of stimuli is not done in parallel). If the first location inspected proves not to contain the target, then the system goes back to inspect the second to ensure that it indeed contains a target.
We further assume that the process of selecting one of two detected stimuli for close inspection is adaptive—that is, the selection process incorporates the prior history of success at selecting stimuli such that if a detected stimulus in a location turns out to be a distractor, that location is less favored the next time a stimulus appears there. (Success experiences also influence selection probabilities, but, for expositional purposes, we focus on failures.) The notion that participants can quickly become sensitive to base rates of distractor locations is consistent with other statistical-sensitivity findings in the literature (e.g., Chun & Jiang, 1999) and with reports of rapid adaptivity (Lemaire & Reder, 1999; Lovett & Anderson, 1996; Nissen & Bullemer, 1987; Reder, 1987; Schunn & Reder, 1998).
The finding that the interference from distractors that appear in the frequent-distractor location is much reduced compared with the rare-distractor location is consistent with the hypothesis that these stimulus locations are less likely to compete for attention, meaning they are less likely to be selected first for identification. The reduction in interference from distractors in frequent-distractor locations follows from the assumptions that the system (a) detects a stimulus in both locations, but chooses to inspect one stimulus first, and (b) selects the one that, based on past experience (in the experiment), is less likely to be a distractor.
With the assumption that stimuli appearing in a frequent-distractor location are less likely to be selected first for identification, one can explain why participants were faster to respond when the distractor appeared in the most frequent location—the other stimulus was more likely to be inspected first. When the location that is selected first for inspection turns out to be the target, RTs are faster because processing terminates with the inspection of only one stimulus. When the selected location reveals a distractor, the attentional system then must inspect the second location to confirm that a target was displayed there.
How does the system adapt and learn which location to prefer? We assume that the success and failure experiences of selecting the correct or incorrect location first are added to the prior history of the attentional system so that the system continually adapts to the shifting base rates. In this way, the system learns to prefer to inspect locations that rarely contain distractors. As a consequence, displays in which the distractor appears in a location that frequently contains the distractor will tend to produce faster RTs since that location will tend not to be the first one selected for inspection. Conversely, displays in which the distractor appears in the rare-distractor location or the target appears in the frequent-distractor location will tend to produce slower RTs because the wrong location will tend to be the first one selected. The latter two scenarios necessitate that two locations be inspected before a correct response can be made.
Does this explanation work? There is both theoretical and empirical evidence to support this reasoning. Theoretically, the explanation was computationally modeled within a cognitive architecture—ACT-R (Anderson & Lebiere, 1998). The model quantitatively reproduced the behavioral patterns exhibited in the experiments (Shang, personal communication, April 27, 2001).4Moreover, the cognitive mechanisms implemented in the model were consistent with the general mechanisms that have been shown to be responsible for other cognitive processes, such as the Stroop effect (Lovett, 2002). Our model assumed four specific procedures (the technical term is productions), one for each location, to inspect the identity of a stimulus in that location. Prior to any inspection production applying, there is a detection phase that detects that one or two locations contain a stimulus. If two locations contain stimuli, then there is competition between the two relevant productions to determine which location will be inspected first. The two competing productions are influenced by their prior history of success—that is, how often the production correctly identified a target versus how often it required that the other production apply to confirm that the target was in the other location.5
Empirically, the notion that procedures will adapt to previous successes and failures has been supported in higher-level domains: for example, deciding whether to search memory or work out the answer (Reder, 1987; Reder & Ritter, 1992), choosing between two problem-solving procedures (Lovett & Anderson, 1996), verifying an arithmetic statement by calculating or using a heuristic (Lemaire & Reder, 1999), or selecting a type of runway in an air traffic controller task (Reder & Schunn, 1999). This account is not completely sufficient, however, in that it would predict that repeated targets would be faster than control targets, and the evidence does not support this. In Experiment 1, there was a significant IOR effect (i.e., repeated targets were slower, not faster). In Experiment 2, the data were more equivocal: Overall, there was a nonsignificant facilitation for repeated targets; however, a special analysis for repeated-target trials that did not repeat the distractor as well (i.e., not identical trials) showed that they were significantly slower than the controls trials, replicating the results of Experiment 1 and previous research (e.g., Christie & Klein, 2001).
Although the current model does not have an inherent bias in its selection of locations to pick the most novel location, such a bias would help explain the outside-position effects as well as any IOR effects. Although the additional assumption of the novelty effect may account for the more subtle aspects of the data, it is interesting to see how many of the more prominent effects can be explained with just these simple assumptions concerning selection among detected stimuli.
Figure 4 illustrates the effects due to the location of the distractor and of the target. These two effects can be thought of as the separate contributions of the relative strengths of each location in the likelihood of a target being present when a stimulus is detected there. Perhaps the reason why both of these locations matter is that there is competition between the location-selection procedures (productions) to determine which location will be selected for a given display. If the success rate of the two locations differs little, then the probability of selecting one or the other will not differ dramatically; however, if one stimulus appears in the rare-distractor location (or in the never-distractor location from Experiment 1) and the other in the frequent-distractor location, the probability of selecting one to try first is strongly skewed toward the rare- (or never-) distractor location.
An Explanation for Negative Priming and Differential Negative Priming
An important aspect of the ACT-R learning mechanism is that it produces power-law learning and forgetting (e.g., Newell & Rosenbloom, 1981; Delaney, Reder, Staszewski, & Ritter, 1998) such that recent feedback has a greater impact in the short term than does the aggregate, long-term feedback (Lovett, 1998). By assuming power-law learning of (successes and) failures of the location-inspection procedures, we can explain negative-priming results in general as well as the specific differential negative-priming results found here. From the assumption that recent experience outweighs long-term experience, it follows that the location that had just been unsuccessfully selected is especially unlikely to be selected on the next display. In other words, we claim that the negative-priming effect in a target-localization task results not from inhibition or suppression but, rather, from the local bias not to select a location that has just failed. By local we mean to indicate that recent experiences receive greater weight than they would if they occurred more remotely in time.
This explanation could account for results from typical negative-priming experiments in which locations do not vary in terms of the probability of a target or distractor appearing in that location in the same way. There is a lowered probability of selecting the location that just held the distractor if and only if attention had been drawn there on the preceding trial (Houghton & Tipper, 1994). If there are two of four locations that contain stimuli on a given display, and the system is not biased to select one first for inspection, then the probability of attending to either one is 50%. This means that, in a typical experiment, the procedure that could be negatively primed is only selected, on average, about half of the time. Thus, negative priming really would only be expected to work half of the time in that situation. Nonetheless, control trials serve as the comparison condition for negative-prime trials and will never have experienced a failure at the target location on the preceding display. Therefore, even if attention is only drawn to the distractor location first on approximately 50% of the prime displays that constitute the first half of a negative-prime trial, there will still be a greater tendency to look in the target's location first on the probe displays for control trials than there will be for negative prime trials.
Why Differential Negative Priming in Our Experiments?
The differential negative-priming effects observed in our experiments can be explained rather simply from the explanations already provided. The prior history of success and failure, based on where distractors have tended to appear, creates a selection bias between two detected stimuli in a display. Overall, the preferred location to inspect first would be the rare-distractor location. In those instances that the rare-distractor location does contain a distractor, the system is likely to inspect that location first and then fail. That recent failure is weighted more heavily (in the short term) and thus there would be a large bias to ignore that location should something appear there again on the next display.
Conversely, when one of the stimuli appears in the frequent-distractor location, attention would not likely be drawn there, meaning that the inspection procedure for that location is unlikely to receive a short-term failure experience. Thus, the frequent-distractor location is less likely to receive a short-term failure experience on a negative-prime trial than is the rare-distractor location. This explains why the frequent-distractor location is less likely to generate a negative-priming effect than the rare-distractor location. The location had to be selected on the preceding display to be punished (inhibited) on the successive display.
Why Do Other Studies Usually Have Smaller Negative-Priming Effects?
The size of the negative-priming effect in the rare-distractor location in our experiments was on the order of 40 ms, which is about twice the size observed in most negative-priming experiments. We have offered an explanation for why we get differential negative priming, depending on the location of the distractor— target pair relative to the frequency of distractors in that location. That account also works to explain the smaller effects in more traditional versions of the paradigm. In the classic paradigm, the overall success—failure rates will be equal across the four locations. This means that, on the prime display of a negative prime trial, the probability of the distractor location being sampled first is 50%, which is less than in the rare-distractor location and more than in the frequent-distractor location in our experiments. Given that a location production will only experience a failure if it is inspected first, our model would predict a weaker negative-priming effect in the traditional paradigm than we found in the rare-distractor location but a stronger one than we found in the frequent-distractor location in our experiments.
Target Localization Versus Object Identification
Does the account we offer for target localization extend to an object-identification task that also shows negative priming? It is not clear that it should. If one conceives of negative priming as a description of a pattern of RTs rather than as an empirical phenomenon, then there is no a priori reason to assume that all tasks that show this RT pattern involve the same set of mechanisms. Nonetheless, consistent with our findings for target localization, in a previous study we have found evidence of both long-term and short-term negative-priming effects in a task that is more similar to an object-identification task than a target-localization task. That task required comparison of two numbers to determine which one is smaller and then judge the font of the smaller one (Reder et al., 2002). In that study, numbers such as 51 might appear periodically in trials, but always as the larger number. RTs became faster on each subsequent trial that involved 51 as the larger number. However, on a still later trial when 51 suddenly became the smaller number, the bias worked against selecting it. In that case, negative priming was as large with many intervening irrelevant trials as the typical negative priming with no delay between ignore and attend trials. (Consult Erickson & Reder, 1998, for a computer-implemented account of this effect.) Our theoretical account for objects involved building “ignore me” and “attend to me” tags on the objects, much like the episodic-retrieval account of Neill (1997). We have implemented that model in SAC (Erickson & Reder, 1998), but it could be implemented in ACT-R as well. In ACT-R, the localization task involves biasing of productions (procedures), which is part of skill memory, whereas the objectidentification task involves biasing attention to different stimuli, not positions.
Reconciling Our Theoretical Interpretation With Other Accounts
The results of our experiments provide consistent evidence that the human attentional system is quite sensitive to probabilities of useful information in various locations and that it adapts rapidly, if implicitly. By using just one mechanism, the human attentional system adapts its inspections of stimuli to reflect both its longerterm and its recent experience (of successful and unsuccessful inspections). Remarkably, although our participants demonstrated strong sensitivity to many statistical properties of the experiment, they were not consciously aware of any manipulation. Participants could not even report with any confidence or accuracy what locations tended to have more or fewer distractors.
We have offered an account for the type of mechanism that can explain the speed-up in RT with predictable distractors. When multiple stimuli are detected in different locations, the attentional system selects which stimulus to ignore based on the likelihood of a location containing a distractor. In addition, our results provide insights into the nature of the negative-prime effect. It is notable that we did not need to posit suppression in order to explain negative priming or differential negative priming. We merely invoked a mechanism that has existed in computer-implemented models of cognition for some time, namely that the learning curve and the forgetting function follow a power law. The power law decay of newly acquired experiences allows the system to keep track of the relative efficiency of locations, adjusting rapidly to changes in base rates.
Although one does not need to invoke a suppression account to explain our results, some aspects of the results are consistent with a suppression account. On the other hand, some of the basic effects, such as faster responding when the distractor is in the frequent-distractor location, do not seem to follow from that sort of account. Episodic retrieval (Neill & Valdes, 1992; Neill et al., 1992), like our account, does not posit suppression in order to explain negative-priming effects; however, episodic retrieval is also challenged by the results reported here in that it should predict more and not less negative priming in the frequent-distractor location.
There is a way to modify the episodic-retrieval view into something very similar to the account proposed here. One must assume that there is a selection phase that occurs after detection of the two stimuli and that an “ignore me” tag is only added to a location when it is selected as the first location to attend. By also positing long- and short-term learning mechanisms for retrieval of these tags such that locations with more tags are less likely to be selected and that tags recently experienced are more available (but availability decays according to a power law), the episodic-retrieval account becomes similar to the mechanism proposed here and, if implemented, also should be able to handle the results.
The IOR account (Christie & Klein, 2001; Milliken et al., 2000) is also partially consistent with our results. Christie and Klein found that negative priming could be explained by IOR when everything else was perfectly balanced. Our design intentionally did not balance the distribution of distractors. Nonetheless, we found evidence to support IOR in Experiment 1 such that repeated targets were also slower than controls (the disadvantage was not as great as a target following a distractor, but it was reliable). It is conceivable that IOR operates whenever attention is drawn to a location. In other words, perhaps in addition to learning where to attend or not attend, there is another process that inhibits returning to a location that was just attended. The IOR effect was smaller in Experiment 2, but when the identical trials were removed, there was a reliable IOR effect. Perhaps the effect was diminished because there were too many complete repetition trials (producing IOR for the distractor) and because of the facilitation of repeated responding (same keystroke).
We suspect that the reason our findings are not as strong with respect to IOR as were Christie and Klein's (2001) is that they used a different paradigm that did not put these processes in such clear-cut opposition. In other words, we believe that both the mechanism we posit (learning which locations are reinforcing) and the mechanism they posited (IOR) operate all the time, sometimes as opposing processes, other times as additive effects. Which mechanism proves to be dominant depends on the nature of the situation (experimental design). Further work may be needed to determine whether our speculation is correct.
Is This Implicit Mechanism Habituation?
The adaptation of the attentional system described here happens implicitly—that is, participants both were unaware that distractors differed in probability at particular locations and were at chance in guessing which locations contained the frequent versus rare distractor. These attentional processes happen so rapidly that it is reasonable for conscious deliberation to not have a place in the behavior. Presumably, other organisms adapt in an analogous fashion. Given that participants demonstrated little interference from distractors that were presented in the frequent-distractor location, this pattern is reminiscent of habituation to the extent that we wonder whether the underlying mechanisms are the same.
Conclusion
Two experiments have shown that there exists an implicit mechanism within the attentional system that learns complex statistical patterns that reflect the probability of co-occurrence of short sequences as well as learning where to prefer to attend and where to prefer not to attend when a stimulus is detected in the environment. We have offered a single learning mechanism that can account for the observed sensitivity to statistical features of the environment and that provides an account of negative priming within the same mechanism. This mechanism does not require the postulation of suppression and illustrates how negative priming can be viewed as merely a component of a general learning mechanism of the statistical regularities in the environment that help the attentional system to focus on relevant information.
Details of Design Constraints
One consequence of the design of Experiment 1 was that the prime display of a trial might have been predictive of the probe display. Table A1 illustrates how often (in Experiment 1) probe targets appeared in the location just previously occupied by prime targets or prime distractors or appeared in previously unoccupied locations. The table also indicates how often probe distractors followed prime targets or prime distractors or appeared in unoccupied locations. Table A2 shows this information for Experiment 2.
Table A1.
Trial Types of Experiment 1 According to Prime Display
| Display | Location in array | Number of trials | |||
|---|---|---|---|---|---|
| Prime trials with distractors | |||||
| Prime | t | - | d | - | |
| Control | - | t | - | d | 8 |
| - | t | d | - | 75 | |
| d | t | - | - | 42 (125) | |
| Negative prime | - | - | t | d | 74 |
| d | - | t | - | 22 (96) | |
| Repeated target | t | - | - | d | 12 |
| t | - | d | - | 64 (76) | |
| Prime trials with distractors | |||||
| Prime | t | - | - | - | |
| No prime distractor | - | t | - | d | 46 |
| d | t | - | - | 26 (72) | |
Note. The presence of a stimulus is represented by the letters t (target) or d (distractor) for each of four possible locations; the absence of a stimulus is indicated by a dash (-).
Table A2.
Trial Types of Experiment 2 According to Prime Display
| Display | Location in array | Number of trials | |||
|---|---|---|---|---|---|
| Prime trials with distractors | |||||
| Prime | t | - | d | - | |
| Control | - | t | - | d | 20 |
| - | t | d | - | 66 | |
| d | t | - | - | 58(144) | |
| Negative prime | - | - | t | d | 50 |
| d | - | t | - | 22(72) | |
| Repeated target | t | - | - | d | 28 |
| t | - | d | - | 44(72) | |
| Prime trials with distractors | |||||
| Prime | t | - | - | - | |
| No prime and outside distractor | - | t | - | d | 72 |
| d | t | - | - | 36(112) | |
| t | - | - | d | 4 | |
Note. The presence of a stimulus is represented by the letters t (target) or d (distractor) for each of four possible locations; the absence of a stimulus is indicated by a dash (-).
Also presented are the conditional probabilities of a probe distractor or probe target appearing in a location, given that a prime distractor or prime target appeared in that location (see Tables A3 and A4 for Experiments 1 and 2, respectively). Given that higher-order expectancy effects seem to have played a role in the participants' performance, it is possible that the predictive power of the prime display could have affected participants' performance on probe trials. We discuss these possibilities here.
Table A3.
Conditional Probabilities of Prime-Probe Pairings in Experiment 1 According to Location X
| Probability of appearing in X |
|||
|---|---|---|---|
| Location X | Probe target | Probe distractor | Probe nothing |
| Prime target | 76/369 = 0.206 | 90/369 = 0.244 | 203/396 = 0.550 |
| Prime target and probe stimulus | 76/166 = 0.458 | 90/166 = 0.542 | |
| Prime distractor | 96/297 = 0.323 | 139/297 = 0.468 | 62/297 = 0.209 |
| Prime distractor and probe stimulus | 96/235 = 0.408 | 139/235 = 0.598 | |
| No prime and probe stimulus | 197/337 = 0.585 | 140/337 = 0.415 | |
Table A4.
Conditional Probabilities of Prime-Probe Pairings in Experiment 2 According to Location X
| Probability of appearing in X |
|||
|---|---|---|---|
| Location X | Probe target | Probe distractor | Probe nothing |
| Prime target | 76/400 = 0.190 | 116/400 = 0.290 | 208/400 = 0.520 |
| Prime target and probe stimulus | 76/192 = 0.392 | 116/192 = 0.404 | |
| Prime distractor | 72/288 = 0.250 | 110/288 = 0.382 | 106/288 = 0.368 |
| Prime distractor and probe stimulus | 72/182 = 0.396 | 110/182 = 0.404 | |
| No prime and probe stimulus | 252/426 = 0.592 | 174/426 = 0.408 | |
There are two things worth noting in these tables and analyses. First, if a given location contained a stimulus (target or distractor) on the prime trial, there was less than a 25% chance of a target appearing in that location on a probe trial. In other words, probe targets were more likely to appear in locations that were previously empty on the prime trials. If a location contained a stimulus on a prime trial and contained a stimulus on the subsequent probe trial, that stimulus was more likely to be a distractor than a target. Potentially, this could have lead to slower RTs for repeated-target and negative-prime trials and faster RTs for control trials.
Second, if a location contained a distractor on the prime trial, there was a 46.8% and a 38.2% chance in Experiments 1 and 2, respectively, of a probe distractor occurring in that location. These percentages may seem high, but it is not the case that the location of a prime distractor is predictive of the location of a probe distractor. Rather, this was an artifact of the manipulation in our experiments. If distractors occur with nonequal frequencies, the probability of a repeated-distractor trial should increase. Happily, the number of repeated-distractor trials was about what one would expect given the unequal frequencies of distractors by location.
In Experiment 1, given the appearance of a prime distractor,
P(repeated-distractor trial)= P(both distractors appear in the frequent location) + P(both distractors appear in the medium location) + P(both distractors appear in the rare location) + P(both distractors appear in the never location) ≅ (0.6)2 + (0.3)2 + (0.1)2 + 02 = 0.46, which is very close to the actual 46.8%.
Likewise, in Experiment 2, given the appearance of a prime distractor, P(repeated-distractor trial) = P(both distractors appear in the frequent location) + P(both distractors appear in the first medium location) + P(both distractors appear in the second medium location) + P(both distractors appear in the rare location) ≅ (0.6)2 + (0.15)2 + (0.15)2 + (0.05)2 = 0.407,
which again is close to the actual 38.2%.
Footnotes
We thank Michael Ayers and Jason Wyse for their help with Experiment 1 and Jason Arndt, Melissa Beck, Rachel Diana, Michael Erikson, Joy Geng, Steve Gotts, Craig Haimson, Marsha Lovett, Margaret Peterson, and Kaia Vilberg for comments on drafts of this article. We thank Steve Gotts for invaluable assistance concerning the relevant literatures and many stimulating discussions.
We were unsure what was the best way to analyze our data, and we put considerable effort into analyzing the data in multiple ways. Fortunately, the different analyses did not change the story in important ways. It is useful to describe these different analyses, to assure the reader both that other analyses produce comparable results and that, from a methodological standpoint, the different analyses mattered little. One method (which we do not report here) involved ignoring the position of the target when analyzing the position of the distractor, and vice versa. With this method, we used the median of the correct RT. The problem with this analysis was that different numbers of displays from different locations (e.g., more displays involving the distractor in the frequent than in the rare position when looking for the effect of target in the medium location) were aggregated, potentially biasing the effects. In the other analyses, we treated each possible combination of target location and distractor location (by trial type) as a separate condition. For this more focused analysis, we calculated median correct RTs as well as the restricted mean correct RTs, which we do report. The pattern of results is similar.
The frequencies of the remaining trials (i.e., those without a distractor in the outside location) were calculated as if those trials did not exist—that is, the remaining frequencies add up to one without the 2% special trials.
We actually tested 63 participants, but four data files were lost from our machines. They were not excluded for any reason other than clerical error.
Shang modeled the data as part of a course project. That model was developed to account for the data that had been analyzed using the means of the correct median RTs. It is unknown how good the quantitative fit would be to the newer analyses, but the qualitative fit should still be excellent.
Although not possible to implement this way within the ACT-R architecture, one could imagine a model that produced these results using a general purpose production that is biased to look at novel stimuli or locations and is punished when inspections are irrelevant (i.e., there is no reward for successes). Within ACT-R, we needed to model the data with rewards and punishments.
References
- Allport DA, Tipper SP, Chmiel NRJ. Perceptual integration and postcategorical filtering. In: Posner ML, Marin OSM, editors. Attention and performance XI. Erlbaum; Hillsdale, NJ: 1985. pp. 107–132. [Google Scholar]
- Anderson JR, Lebiere C. The atomic components of thought. Erlbaum; Mahwah, NJ: 1998. [Google Scholar]
- Banks WP, Roberts D, Ciranni M. Negative priming in auditory attention. Journal of Experimental Psychology: Human Perception and Performance. 1995;21:1354–1361. [Google Scholar]
- Biederman I, Glass AL, Stacy EW. Searching for objects in real-world scenes. Journal of Experimental Psychology. 1973;97:22–27. doi: 10.1037/h0033776. [DOI] [PubMed] [Google Scholar]
- Cary M, Reder LM. Metacognition in strategy selection: Giving consciousness too much credit. In: Izaute M, Chambres P, Marescaux P-J, editors. Metacognition: Process, function, and use. Kluwer Academic; New York: 2002. pp. 63–78. [Google Scholar]
- Christie J, Klein RM. Negative priming for spatial location? Canadian Journal of Experimental Psychology. 2001;55:24–38. doi: 10.1037/h0087350. [DOI] [PubMed] [Google Scholar]
- Chun MM, Jiang Y. Contextual cueing: Implicit learning and memory of visual context guides spatial attention. Cognitive Psychology. 1998;36:28–71. doi: 10.1006/cogp.1998.0681. [DOI] [PubMed] [Google Scholar]
- Chun MM, Jiang Y. Top-down attentional guidance based on implicit learning of visual covariation. Psychological Science. 1999;20:360–365. [Google Scholar]
- Cohen JD, MacWhinney B, Flatt M, Provost J. PsyScope: A new graphic interactive environment for designing psychology experiments. Behavioral Research Methods, Instruments and Computers. 1993;25:257–271. [Google Scholar]
- Connelly SL, Hasher L. Aging and the inhibition of spatial location. Journal of Experimental Psychology: Human Perception and Performance. 1993;19:1238–1250. doi: 10.1037//0096-1523.19.6.1238. [DOI] [PubMed] [Google Scholar]
- Conway ARA. The time-course of negative priming: Little evidence for episodic trace retrieval. Memory & Cognition. 1999;27:575–583. doi: 10.3758/bf03211551. [DOI] [PubMed] [Google Scholar]
- Delaney PF, Reder LM, Staszewski JJ, Ritter FE. The strategy-specific nature of improvement: The power law applies by strategy within task. Psychological Science. 1998;9:1–7. [Google Scholar]
- DeSchepper B, Treisman A. Visual memory for novel shapes: Implicit coding without attention. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1996;22:27–47. doi: 10.1037//0278-7393.22.1.27. [DOI] [PubMed] [Google Scholar]
- Driver J, McLeod P, Dienes Z. Motion coherence and conjunction search: Implications for guided search theory. Perception & Psychophysics. 1992;51:79–85. doi: 10.3758/bf03205076. [DOI] [PubMed] [Google Scholar]
- Erickson MA, Reder LM. The influence of repeated presentations and intervening trials on negative priming. In: Gernsbacher MA, Derry SJ, editors. Proceedings of the Twentieth Annual Conference of the Cognitive Science Society. Erlbaum; Mahwah, NJ: 1998. pp. 327–332. [Google Scholar]
- Fox E. Negative priming from ignored distractors in visual selection: A review. Psychonomic Bulletin & Review. 1995;2:145–173. doi: 10.3758/BF03210958. [DOI] [PubMed] [Google Scholar]
- Haider H, Frensch PA. Eye movement during skill acquisition: More evidence for the information-reduction hypothesis. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1999;25:172–190. [Google Scholar]
- Hasher L, Zacks RT, Stoltzfus ER, Kane MJ, Connelly SL. On the time course of negative priming: Another look. Psychonomic Bulletin & Review. 1996;3:231–237. doi: 10.3758/BF03212424. [DOI] [PubMed] [Google Scholar]
- Hoffmann J, Kunde W. Location-specific target expectancies in visual search. Journal of Experimental Psychology: Human Perception and Performance. 1999;25:1127–1141. [Google Scholar]
- Houghton G, Tipper SP. A model of inhibitory mechanisms in selective attention. In: Dagenbach D, Carr TH, editors. Inhibitory processes in attention, memory, and language. Academic Press; San Diego, CA: 1994. pp. 53–112. [Google Scholar]
- Houghton G, Tipper SP, Weaver B, Shore DI. Inhibition and interference in selective attention: Some tests of a neural network model. Visual Cognition. 1996;3:119–164. [Google Scholar]
- Johnston JC, Pashler H. Close binding of identity and location in visual feature perception. Journal of Experimental Psychology: Human Perception and Performance. 1990;16:843–856. doi: 10.1037//0096-1523.16.4.843. [DOI] [PubMed] [Google Scholar]
- Lambert A, Norris A, Naikar N, Aitken V. Effects of informative peripheral cues on eye movements: Revisiting William James. Visual Cognition. 2000;7:545–569. [Google Scholar]
- Lee FJ, Anderson JR. Does learning a complex task have to be complex? A study in learning decomposition. Cognitive Psychology. 2001;42:267–316. doi: 10.1006/cogp.2000.0747. [DOI] [PubMed] [Google Scholar]
- Lemaire P, Reder L. What affects strategy selection in arithmetic? The example of parity and five effects on product verification. Memory & Cognition. 1999;27:364–382. doi: 10.3758/bf03211420. [DOI] [PubMed] [Google Scholar]
- Logan GD. Toward an instance theory of automatization. Psychological Review. 1988;95:492–527. [Google Scholar]
- Lovett MC. Choice. In: Anderson JR, Lebiere C, editors. The atomic components of thought. Erlbaum; Mahwah, NJ: 1998. pp. 255–296. [Google Scholar]
- Lovett MC. Modeling selective attention: Not just another model of Stroop. Cognitive Systems Research. 2002;3:67–76. [Google Scholar]
- Lovett MC, Anderson JR. History of success and current context in problem solving: Combined influences on operator selection. Cognitive Psychology. 1996;31:168–217. [Google Scholar]
- Lowe D. Long-term positive and negative identity priming: Evidence for episodic retrieval. Memory & Cognition. 1998;26:435–443. doi: 10.3758/bf03201153. [DOI] [PubMed] [Google Scholar]
- Maljkovic V, Nakayama K. Priming of pop-out: II. The role of position. Perception & Psychophysics. 1996;58:977–991. doi: 10.3758/bf03206826. [DOI] [PubMed] [Google Scholar]
- May CP, Kane MJ, Hasher L. Determinants of negative priming. Psychological Bulletin. 1995;118:35–54. doi: 10.1037/0033-2909.118.1.35. [DOI] [PubMed] [Google Scholar]
- Miller J. A warning about median reaction time. Journal of Experimental Psychology: Human Perception and Performance. 1988;14:539–543. doi: 10.1037//0096-1523.14.3.539. [DOI] [PubMed] [Google Scholar]
- Milliken B, Tipper SP, Houghton G, Lupiáñez J. Attending, ignoring, and repetition: On the relation between negative priming and inhibition of return. Perception & Psychophysics. 2000;62:1280–1296. doi: 10.3758/bf03212130. [DOI] [PubMed] [Google Scholar]
- Millward RB. Theoretical and experimental approaches to human learning. In: Kling JW, Lorrin AR, editors. Experimental psychology. Holt, Rinehart & Winston; Oxford, England: 1971. pp. 905–938. [Google Scholar]
- Neill WT. Inhibition and facilitation processes in selective attention. Journal of Experimental Psychology: Human Perception and Performance. 1977;3:444–450. [Google Scholar]
- Neill WT. Episodic retrieval in negative priming and repetition priming. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1997;23:1291–3105. [Google Scholar]
- Neill WT, Terry KM, Valdes LA. Negative priming without probe selection. Psychonomic Bulletin & Review. 1994;1:119–121. doi: 10.3758/BF03200767. [DOI] [PubMed] [Google Scholar]
- Neill WT, Valdes LA. Persistence of negative priming: Steady state or decay? Journal of Experimental Psychology: Learning, Memory, and Cognition. 1992;18:565–576. doi: 10.1037//0278-7393.18.5.993. [DOI] [PubMed] [Google Scholar]
- Neill WT, Valdes LA. Facilitatory and inhibitory aspects of attention. In: Kramer AF, Coles MGH, Logan GD, editors. Converging operations in the study of visual selective attention. American Psychological Association; Washington, DC: 1996. pp. 77–106. [Google Scholar]
- Neill WT, Valdes LA, Terry KM. Selective attention and the inhibitory control of cognition. Interference and inhibition in cognition. In: Dempster FN, Brainerd CJ, editors. Academic Press; San Diego, CA: 1995. pp. 207–261. [Google Scholar]
- Neill WT, Valdes LA, Terry KM, Gorfein DS. Persistence of negative priming: II. Evidence for episodic trace retrieval. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1992;18:993–1000. doi: 10.1037//0278-7393.18.5.993. [DOI] [PubMed] [Google Scholar]
- Newell A, Rosenbloom PS. Mechanisms of skill acquisition and the law of practice. In: Anderson JR, editor. Cognitive skills and their acquisition. Erlbaum; Hillsdale, NJ: 1981. pp. 1–56. [Google Scholar]
- Nissen MJ, Bullemer P. Attentional requirements of learning: Evidence from performance measures. Cognitive Psychology. 1987;19:1–32. [Google Scholar]
- Olson IR, Chun MM. Perceptual constraints on implicit learning of spatial context. Visual Cognition. 2002;9:273–302. [Google Scholar]
- Olton DS, Samuelson RJ. Remembrance of places passed: Spatial memory in rats. Journal of Experimental Psychology: Animal Behavior Processes. 1976;2:97–116. [Google Scholar]
- Olton DS, Schlosberg P. Food-searching strategies in young rats: Win-shift predominates over win-stay. Journal of Comparative and Physiological Psychology. 1978;92:609–618. [Google Scholar]
- Park J, Kanwisher N. Negative priming from spatial locations: Identity mismatching, not distractor inhibition. Journal of Experimental Psychology: Human Perception and Performance. 1994;20:613–623. doi: 10.1037/0096-1523.20.3.613. [DOI] [PubMed] [Google Scholar]
- Reder LM. Strategy selection in question answering. Cognitive Psychology. 1987;19:90–138. [Google Scholar]
- Reder LM, Ritter FE. What determines initial feeling of knowing? Familiarity with question terms, not with the answer. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1992;18:435–451. [Google Scholar]
- Reder LM, Schunn CD. Metacognition does not imply awareness: Strategy choice is governed by implicit learning and memory. In: Reder LM, editor. Implicit memory and metacognition. Erlbaum; Mahwah, NJ: 1996. pp. 45–77. [Google Scholar]
- Reder LM, Schunn CD. Bringing together the psychometric and strategy worlds: Predicting adaptivity in a dynamic task. In: Gopher D, Koriat A, editors. Attention and performance XVII: Cognitive regulation of performance: Interaction of theory and application. MIT Press; Cambridge, MA: 1999. pp. 315–342. [Google Scholar]
- Reder LM, Shang J, Erickson MA, Schyrokyj L. Long- and short-term negative priming. 2002.
- Schunn CD, Reder LM. Strategy adaptivity and individual differences. In: Medin DL, editor. The psychology of learning and motivation: Advances in research and theory. Academic Press; San Diego, CA: 1998. pp. 115–154. [Google Scholar]
- Snyder JJ, Kingstone A. Inhibition of return and visual search: How many separate loci are inhibited? Perception & Psychophysics. 2000;62:452–458. doi: 10.3758/bf03212097. [DOI] [PubMed] [Google Scholar]
- Theeuwes J. Endogenous and exogenous control of visual selection. Perception. 1994;23:429–440. doi: 10.1068/p230429. [DOI] [PubMed] [Google Scholar]
- Theeuwes J, Godijn R. Irrelevant singletons capture attention: Evidence from inhibition of return. Perception & Psychophysics. 2002;64:764–770. doi: 10.3758/bf03194743. [DOI] [PubMed] [Google Scholar]
- Theeuwes J, Kramer AF, Hahn S, Irwin DE. Our eyes do not always go where we want them to go: Capture of the eyes by new objects. Psychological Science. 1998;9:379–385. [Google Scholar]
- Theeuwes J, Kramer AF, Hahn S, Irwin DE, Zelinsky GJ. Influence of attentional capture on oculomotor control. Journal of Experimental Psychology: Human Perception and Performance. 1999;25:1595–1608. doi: 10.1037//0096-1523.25.6.1595. [DOI] [PubMed] [Google Scholar]
- Tipper SP. The negative priming effect: Inhibitory priming by ignored objects. Quarterly Journal of Experimental Psychology: Human Experimental Psychology. 1985;37A:571–590. doi: 10.1080/14640748508400920. [DOI] [PubMed] [Google Scholar]
- Tipper SP, Brehaut JC, Driver J. Selection of moving and static objects for the control of spatially directed action. Journal of Experimental Psychology: Human Perception and Performance. 1990;16:492–504. doi: 10.1037//0096-1523.16.3.492. [DOI] [PubMed] [Google Scholar]
- Tipper SP, Cranston M. Selective attention and priming: Inhibitory and facilitory effects of ignored primes. Quarterly Journal of Experimental Psychology: Human Experimental Psychology. 1985;37A:591–611. doi: 10.1080/14640748508400921. [DOI] [PubMed] [Google Scholar]
- Tipper SP, Driver J. Negative priming between pictures and words in a selective attention task: Evidence for semantic processing of ignored stimuli. Memory & Cognition. 1988;16:64–70. doi: 10.3758/bf03197746. [DOI] [PubMed] [Google Scholar]
- Tipper SP, Driver J, Weaver B. Object-centred inhibition of return of visual attention. Quarterly Journal of Experimental Psychology: Human Experimental Psychology. 1991;43A:289–298. doi: 10.1080/14640749108400971. [DOI] [PubMed] [Google Scholar]
- Tipper SP, Weaver B, Cameron S, Brehaut JC, Bastedo J. Inhibitory mechanisms of attention in identification and localization tasks: Time course and disruption. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1991;17:681–692. doi: 10.1037//0278-7393.17.4.681. [DOI] [PubMed] [Google Scholar]
- Tipper SP, Weaver B, Kirkpatrick J, Lewis S. Inhibitory mechanisms of attention: Locus, stability, and relationship with distractor interference effects. British Journal of Psychology. 1991;82:507–520. doi: 10.1111/j.2044-8295.1991.tb02416.x. [DOI] [PubMed] [Google Scholar]
- Van Selst M, Jolicœur P. A solution to the effect of sample size on outlier elimination. Quarterly Journal of Experimental Psychology: Human Experimental Psychology. 1994;47A:631–650. doi: 10.1037//0096-1523.20.4.905. [DOI] [PubMed] [Google Scholar]
- Willingham DB, Nissen MJ, Bullemer P. On the development of procedural knowledge. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1989;15:1047–1060. doi: 10.1037//0278-7393.15.6.1047. [DOI] [PubMed] [Google Scholar]
- Yee PL. Semantic inhibition of ignored words during a figure classification task. Quarterly Journal of Experimental Psychology: Human Experimental Psychology. 1991;43A:127–153. doi: 10.1080/14640749108401002. [DOI] [PubMed] [Google Scholar]