Identification of transposable elements using multiple alignments of related genomes

Abstract

Accurate genome-wide cataloging of transposable elements (TEs) will facilitate our understanding of mobile DNA evolution, expose the genomic effects of TEs on the host genome, and improve the quality of assembled genomes. Using the availability of several nearly complete Drosophila genomes and developments in whole genome alignment methods, we introduce a large-scale comparative method for identifying repetitive mobile DNA regions. These regions are highly enriched for transposable elements. Our method has two main features distinguishing it from other repeat-finding methods. First, rather than relying on sequence similarity to determine the location of repeats, the genomic artifacts of the transposition mechanism itself are systematically tracked in the context of multiple alignments. Second, we can derive bounds on the age of each repeat instance based on the phylogenetic species tree. We report results obtained using both complete and draft sequences of four closely related Drosophila genomes and validate our results with manually curated TE annotations in the Drosophila melanogaster euchromatin. We show the utility of our findings in exploring both transposable elements and their host genomes: In the study of TEs, we offer predictions for novel families, annotate new insertions of known families, and show data that support the hypothesis that all known TE families in D. melanogaster were recently active; in the study of the host, we show how our findings can be used to determine shifts in the eu-heterochromatin junction in the pericentric chromosome regions.

Repeat elements make up a large fraction of many eukaryotic genomes. Within these regions, the occurrence of Transposable Elements is rampant. The term Transposable Elements (TEs) groups several subclasses of elements that replicate in the genome, either through the reverse transcription of an RNA intermediate (class I elements), or autonomously from DNA to DNA by excision and repair (class II elements). Class I elements are further grouped by the presence (LTR elements) or absence (LINE and SINE elements) of long terminal repeats. Class II elements are largely comprised of elements with terminally inverted repeats (TIR elements). TEs make up large portions of the middle- and high-repetitive segments of genomes and are mostly found in the heterochromatin and centromeric regions (Pardue et al. 1996; Junakovic et al. 1998). Studies show TEs can be deleterious to hosts (Green 1988; Deininger and Batzer 1999) and approximately one-half of Drosophila melanogaster mutations are attributed to TEs (Finnegan 1992). Increasingly, evidence points to other contributions of TEs in the evolution of the host genome and even in shaping chromosome structure (Pardue et al. 1996; Kidwell and Lisch 1997; Labrador and Corces 1997; Pardue and DeBrayshe 1999). They are also the chief cause of gapped regions and poor annotations in up to 10% of currently sequenced genomes. Despite some knowledge about sequence structure in transposons, for example, they typically contain open reading frames in the interior or some characterizing repeat sequences at the ends, their mechanisms for replication are poorly understood, and their classification into families is far from complete. An accurate catalog and phyletic mapping of the instances of TE insertions will help elucidate TE contribution to genetic variability in eukaryote genomes, and refine assemblies of sequenced genomes (Holmes 2002; Bennett et al. 2004).

When studying TEs, it is customary to characterize specific instances (or insertions) by their mechanism of replication and segregate them into TE families—groups of elements that purportedly evolved from the same transposing sequence. However, TE instances are shuffled and scrambled as they evolve, making them difficult to characterize and group. When copies of an invading TE family are not under selective pressure, mutations mangle the sequences of each insertion, resulting in related elements that are of different length, incomplete structure, and beyond recognition by sequence similarity. Furthermore, some autonomously transposing elements have evolved new classes of non-autonomously transposing elements (Vitte and Panaud 2003). In such cases, copies of two different families show sequence similarity in substructures, but differ in their replication method, or in substructure order and content. TEs also show insertion site bias for transposing into adjacent positions in the genome or in a nested fashion (Freund and Meselson 1984; Inouye et al. 1984; Losada et al. 1999). Consequently, many repeat regions are combinations of tandem and nested arrays of complete and partial copies of different TEs that may then transpose together—leading to complex relationships between originating elements and their replicants. These artifacts of TE evolution complicate the definition of element boundaries and cause problems in classifying related elements into subfamilies (Bao and Eddy 2002). Furthermore, these issues make the automation of TE identification an intricate and involved process (Volfovsky et al. 2001; Bao and Eddy 2002; Pevzner et al. 2004).

Current approaches to TE detection identify repeat boundaries by sequence similarity. Such analyses have generally been applied to single genome sequences, with element boundaries defined by finding good matches to a library of canonical TE subfamily sequences (RepeatMasker) (Bedell et al. 2000). Some de novo repeat analysis approaches align genomes to themselves in order to detect repetition and impose element boundaries based on local self-alignment information (Delcher et al. 1999; Kurtz et al. 2000). Once the boundaries are imposed, various methods are used to characterize subfamilies (Agarwal and States 1994; Kurtz et al. 2000; Volfovsky et al. 2001; Bao and Eddy 2002). However, repeat boundaries do not generally correspond to the boundaries of these self-aligned regions. Pevzner et al. (2004) address this issue by proposing repeat boundaries that conform to optimal subrepeats, while Edgar and Myers (2005) annotate repeat boundaries within locally aligned regions using characteristic patterns of particular classes of repeats. All of these approaches depend on the identification of sequence similarity among related elements.

We introduce a novel comparative approach to detect TE insertion sites that is based on the alignment of multiple related genomes. Standard comparative genomic principles dictate that conserved regions in alignments highlight functional elements (Bergman et al. 2002; Boffelli et al. 2003). We find that lack of conservation is equally useful: Inserted sequences that have little or no alignment to other genomes lead to signatures within multiple alignments that can be used to identify TEs. Our approach is to search for disrupted conservation patterns in whole genome alignments, and systematically identify not only the boundaries, but also the age of inserted repeats relative to the other genomes in the comparison.

We report the results of a case study incorporating both complete and draft sequences of four Drosophila genomes: melanogaster, yakuba, pseudoobscura, and virilis. We validate our method by comparing our findings with the manually curated TE annotations in the D. melanogaster euchromatin region. We report novel insertion instances of known TE families as well as novel TE families. We also verify a recent hypothesis by Lerat et al. (2003) that most known TE families in D. melanogaster were recently active. Additionally, we demonstrate how our findings can contribute to the study of the eukaryote host genome by studying shifts in eu-heterochromatin junction in the pericentric chromosome regions of D. melanogaster.

Results

Overview of our approach

We pose our problem as a search for the alignment signature of mobile elements. Given an aligned set of related genomic sequences, S_n, our goal is to identify the set of subsequences, (T₁,..., T_k), which transposed and duplicated along a particular branch in the phylogenetic tree of the given genomes.

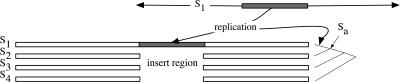
Consider a speciation event causing the recent divergence of two genomes S₁ and S₂ from the cenancestor S_a, as depicted in Figure 1. We expect the sequences of S₁ and S₂ to maintain largely conserved panorthologous regions—regions that are directly derived from a common sequence in the ancestor S_a (contain species divergence) but have not undergone duplication (no paralogy) (Blair et al. 2005). When we align the panortholog regions of S₁ and S₂, we are likely to see some gaps in the alignment due to small insertions or deletions. During the transposition of a repeat element, a relatively long genomic region is exactly duplicated and inserted into a new location in the genome. In the comparison of S₁ and S₂, a transposition event in S₁ will create a long gap in the alignment to S₂ and a match to another region in S₁. When additional related genomes (S₃,..., S_n) are added to the comparison, the likelihood decreases that a random insertion in S₁ will create gapped regions in the comparison with all the other panortholog regions in (S₂,..., S_n) while still exhibiting a match to another region in S₁. The same reasoning extends to more ancient insertion events. An insertion that occurred on the branch leading to S_a from its cenancestor with S₃ will create a gap in both S₃ and S₄ against the mutated remains of the insertion in both S₁ and S₂.

Figure 1.

A replication event with the resulting insertion region and juxtaposed gaps in the multiple sequence alignment of the panortholog subsequences.

Proper delineation of these regions in the context of multiple alignments identifies element boundaries and the time of their insertion within tree branches. Detecting the nonconserved repeat elements within these requires additional filtering to isolate the insertions that are repetitive and appropriately structured.

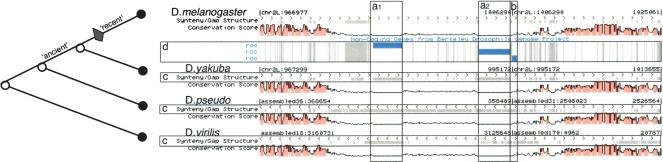
We define the term insertion region (IR) to describe a region in the multiple genome alignment in which a block of conservation between panortholog sequences is interrupted by inserted subsequences in a subset of sequences that came from a particular subtree of the species tree. Figure 2 depicts an example of a TE in the alignment of four Drosophila genomes (melanogaster, pseudoobscura, yakuba, and virilis). The figure shows a K-browser (Chakrabarti and Pachter 2004) image of the alignment and should be interpreted as follows: Each genome is depicted linearly in one panel. The gray blocks indicate gaps in the multiple alignment. The amount of conservation (percent identity) is shown in the pink wiggle plot for each species. The boundaries of an insertion region in D. melanogaster are defined by the intersection of the gaps in each of the three other genomes. In Figure 2, the boundaries of insertion regions a1 and a2 are clearly demarcated by the gap in Drosophila yakuba and are supported by the longer gaps in the two other sequences. Insertion region b is evidently an insertion that occurred before the D. melanogaster–D. yakuba split, indicated by having no gap in D. yakuba. Delineating the 3′ insertion boundary (right-side) of insertion region b is difficult because of assembly and alignment artifacts resulting in choppy gaps in Drosophila virilis. We compare this to the handcurated boundaries in panel d, the noncoding gene track from BDGP (Kaminker et al. 2002).

Figure 2.

An alignment of four Drosophila sequences shown in the K-browser. The species are labeled by D. melanogaster, D. yakuba, D. pseudo (pseudoobscura), D. virilis. Each genome track has a conservation score track (pink) and (c) a gap track (gaps are demarcated in gray). The gaps in three genomes support the correct boundaries of the D. melanogaster insertion regions (a1, a2, and b). The insertion regions match the TE annotations (blue) in the BDGP noncoding gene track (d). The tree on the left-hand side depicts the phylogeny relationships between the species. The diamond shows the branch on which the transposon replications (a1) and (a2) occurred. The “ancient” branch is that on which replication (b) occurred, as indicated by the gaps in D. pseudoobscura and D. virilis but not in D. yakuba.

Once we identify insertion regions, we examine repeat content and structure to filter out microsatellite regions, delineate tandem and nested repeats, and concatenate IRs that oversegmented an insertion element (Methods). Again we exploit the replication mechanism: In the context of the phylogenetic species tree, a subsequence causing an insertion region is restricted to have occurred along a particular branch in the tree as described above (see Fig. 1). Knowledge of the temporal range of the insertion allows us to infer the active time of the repeat structure or structures (if several repeats are in the same insertion region). Related elements that transposed contemporaneously are, in fact, likely to have good local alignment to the element. By locally aligning each insertion region to all other insertion regions restricted to the same branch on the tree, we find the other inserted elements that compete for best local alignment of the region in question. The microsatellite candidates are those that have repeated multiple small sequential hits to self. The tandem insertion candidates are those that repeatedly sequentially align both to self as well as to the same subcomponent in another element. The candidates for nested insertions are those insertion regions with substructures that sequentially align to several components that do not locally align to each other. Lastly, the candidates for concatenation are those within a certain genomic distance that align sequentially to subcomponents in another insertion region.

We define the term repeat insertion region (RIR) to describe an insertion region in which the inserted subsequence also has good local alignment with other insertion regions in that genome, and conforms to our filtering criteria (Methods). The number of remaining repeat insertion regions is dependent on the stringency of this criterion. Each RIR is also associated with a particular branch on the species tree. A full comparative analysis of TE occurrences in a particular genome incorporates the bottom-up identification of the RIRs over branches of the tree.

Below we detail the results of one such full comparative analysis in four Drosophila genomes. We compare our results to the current hand-curated TE annotations in D. melanogaster euchromatin. The comparison allows us to validate our findings (see section “Comparison of Findings With Natural TE Annotations in D. melanogaster Euchromatin”), assess our ability to find correct insertion boundaries (see section “Boundary Detection in IR and RIR Sets”), and determine to what degree our method relies on sequence similarity among the insertion regions for proper detection (see section “Independence From Sequence Similarity”). In addition, we were able to examine the state of the current public TE annotations for Drosophila (see bottom of section “Comparison of Findings With Natural TE Annotations in D. melanogaster Euchromatin”) and offer our discovery of both novel instances of known families and novel families (see “Identification of new Instances of Known Families” and “Proposed New Families in Euchromatin,” respectively).

Case study: Four Drosophila genomes

We tested our method using a whole genome alignment of four Drosophila genomes: melanogaster, yakuba, pseudoobscura, and virilis. We report a comparison of our findings in D. melanogaster euchromatin against the BDGP natural TE annotation set (http://www.fruitfly.org/p_disrupt/TE.html). We note that the D. yakuba and D. virilis sequences are not in finished form in terms of coverage and quality, and anticipate that better results could be attained in the near future as improved assemblies become available.

Using a whole genome alignment of the four genomes, we identified insertion regions (Methods). We followed the filtering method to correct for alignment errors and detect repeat insertion regions. This process results in a set of RIRs. We mapped these regions to branches on the species tree based on the genomes in which the conservation was disrupted. For example, a disruption, or gap, that appeared only in the D. melanogaster genome was associated with the branch labeled by the diamond in Figure 2. We dub these “recent” insertions. Moving up the tree, we identified regions that appeared on the branch separating the D. melanogaster–D. yakuba clade from the rest of the tree (that is, those RIRs appearing in D. melanogaster and D. yakuba, while simultaneously gapping in Drosophila pseudoobscura and D. virilis). We will henceforth dub these insertions “ancient.”

We uncovered 4487 recent IRs, encompassing 4.7% (5.5 Mb) of the D. melanogaster release 4 euchromatin sequence. Additionally, we found 3820 ancient IRs. These encompassed 1.5% (1.7 Mb) of euchromatin sequence. This set collectively contained 6.2% of euchromatin. It represents only insertion regions, prior to any structural assessment or determination of repetition in the genome.

Once we filtered the IRs, we remained with a set of 2008 RIRs, 1710 repeats from the recent branch and 298 from the ancient branch. This set contained 4.6% of the euchromatic sequence. These sequences were not uniformly distributed over the euchromatin portions of the chromosome arms. As noted in Table 1, among the major chromosome arms, composition varies between 3% and 6%. We also note some variation of element density per megabase pair along the major chromosome arms. On chromosome 4, however, we observe a jump to 8% TE composition. This figure is likely to be a gross underestimate since the cytology of chromosome 4 results in middle-repetitive regions that are technically challenging to sequence, assemble, and align (Devine et al. 1997; Hoskins et al. 2002). In general, we estimate that repeat mobile elements make up a larger portion of euchromatin than even the 4.6% represented in our findings, and our estimates will improve with assembly and alignment quality.

Table 1.

Chromosomal distribution of elements for our set of findings, and the BDGP annotations

	% chromosomal composition		TE density (per Mb)
Chr arm	RIRs	BDGP	RIRs	BDGP
X	5.04	3.74	20	12
2L	4.37	3.93	17	14
2R	6.02	4.15	18	15
3L	4.77	3.95	18	12
3R	2.92	2.11	11	10
4	7.90	10.0	53	80
Total	4.56	3.80	17	13

There is notable variation among major chromosome arms and chromosome 4.

Comparison of findings with natural TE annotations in D. melanogaster euchromatin

The set of 1571 annotated natural TEs in the euchromatin region of D. melanogaster release 4 is available at http://www.fruitfly.org/p_disrupt/TE.html. We used this set, henceforth referred to as BDGPTrans, to validate our findings. We evaluated both the unrestricted IR set and the post-concatenation and repeat-filtered RIR set in D. melanogaster.

Since our method is comparative, we could only analyze those portions of the genome that aligned to successfully assembled regions in the other genomes. Of the 1571 full and partial instances of TEs in BDGPTrans, 66 were not incorporated into our alignment, and were therefore impossible to identify using this alignment (see Table 2). The remaining 1505 BDGPTrans TEs comprise the set we were trying to recover in this study. It should be noted that inclusion in the alignment does not necessarily indicate a successful alignment of the region containing the transposable element. For further discussion of these unaligned regions see the section “Sensitivity to Artifacts of Assembly, Alignment, and TE Clustering.”

Table 2.

Summary of presence of BDGP annotations in alignment, and in our RIR findings in D. melanogaster R4

Chr arm	BDGPTrans	Not in alignment	NOT in RIR (false negative)	In RIR (true positive)
X	276	8	52	216
2L	305	16	62	227
2R	312	3	52	257
3L	288	13	65	210
3R	288	5	64	219
4	102	21	33	48

We examined the IR and RIR sets for overlaps with known TEs in BDGPTrans. Within our RIR set, 74.8% (1177) of the 1571 annotations in BDGPTrans were identified. These true positives comprised 1156 of our RIRs (because of some undersegmented tandem or nested repeats in the RIR set). Excluding the 66 annotations not in the alignment, both the IR and RIR sets show 78% sensitivity to the currently annotated TEs in D. melanogaster. The true positive set included instances from all (100%) euchromatin TE families. Only two known D. melanogaster TE families were not represented in our findings, HeT-A and TART-element. Both are known to occur exclusively in heterochromatin. Since our analysis focused on the mostly euchromatin sequences assembled into the chromosome arm scaffolds, we found this to be significant.

Importantly, only five of the recovered annotated TEs appeared on the ancient branch; these are annotated insertions that occurred before the D. melanogaster–D. yakuba split. Analysis of these revealed that they were all partial elements from multicopy families, meaning that another copy from that family was recovered on the recent branch. This implies that at least 74.6% (1172/1571) of the currently annotated TEs in D. melanogaster represent recent insertions (since the yakuba split). Moreover, it implies that all known euchromatin TE families were recently active. This supports a recent prediction by Lerat et al. (2003) in a study of a subset of BDGPTrans that most of the annotated repeat families in the D. melanogaster genome were recently active, and possibly still are.

Boundary detection in IR and RIR sets

The boundaries of an insertion region are defined by the intersection of gaps in the other genomes. As seen in Figure 2, IR b, nonconsecutive gaps could cause oversegmentation in the IR set. The procedure to identify and filter out microsatellite regions, delineate tandem and nested repeats, and concatenate oversegmented IRs results in different boundaries for the RIR set. We assess the reliability of the boundaries detected in the IR and RIR sets as a function of base-pair coverage per instances overlapping the BDGPTrans set. For this purpose, we looked at only the true-positive findings from both sets.

Taking only the findings that overlapped with the BDGP annotated set, we found regions comprising 3.8% (4.5 Mb) of the euchromatin sequence. The current set of BDGP annotations also comprises 3.8% (4.5 Mb) of the euchromatic region. Table 3 summarizes these results, with the chromosome-arm breakdown. We report as false positive the base pairs in these restricted sets of IRs and RIRs that were not part of the actual BDGPTrans annotations. Recall is a measure of sensitivity and reports the percent of true-positive base-pair annotations out of the positive set (the base pairs annotated as TE in BDGPTrans). Precision is the percentage of true positives out of all the base pairs our method annotated as TE component. As expected, the coverage, recall, and precision are much worse on chromosome arm 4 than any of the others because of assembly and alignment artifacts resulting from this arm's cytological characteristics (Devine et al. 1997). In the pre-filtered IR set, we observed a recall rate of 74.2% and precision of 89.1%. In comparison, after identifying and filtering for repeats (which slightly undersegments TEs), the euchromatin coverage of RIRs overlapping BDGP annotations increased by 818 kb to 3.9 Mb, driving sensitivity up to 82.3%, and precision down to 87.9%.

Table 3.

Analyzing base-pair coverage of BDGPTrans annotations in the IR and RIR sets

				IR set					RIR set
Chr arm	Chr length (Mb)	Cumulative length of BDGP TEs (kb)	Cumulative length of RIR set (kb)	TruePos (kb)	FalsNeg (kb)	FalsPos (kb)	Recall (%)	Precision (%)	TruePos (kb)	FalsNeg (kb)	FalsPos (kb)	Recall (%)	Precision (%)
X	22.2	833.0	799.5	546.3	253.2	50.5	68.33	91.54	611.3	188.5	89.2	76.43	87.27
2L	22.4	879.5	818.7	590.1	228.6	38.9	72.08	93.82	660.7	158.0	64.1	80.7	91.15
2R	20.8	861.5	816.8	647.4	169.4	138.4	79.26	82.39	712.2	104.8	202.7	87.17	77.84
3L	23.8	939.5	874.1	664.6	209.5	55.4	76.03	92.31	735.8	138.6	87.2	84.15	89.4
3R	27.9	868.3	820.8	637.1	183.8	14.1	77.61	97.83	696.0	124.9	16.9	84.79	97.62
4	1.3	128.1	86.8	44.3	42.5	86.8	51.03	78.65	54.4	32.4	206.7	62.64	72.45
Total	118.4	4509.9	4216.7	3129.8	1087	384.1	74.22	89.07	3470.4	747.2	668.6	82.28	87.83

We consider “positive findings” to be those regions in the IR and RIR sets that overlapped with BDGPTrans annotations. The positive set columns (4 and 9) show the number of base pairs from the BDGPTrans set that were in our positive findings. Recall is a measure of sensitivity and reports the percent of true positive base pair annotations out of all the base pairs annotated in the “gold truth” BDGPTrans set. Precision is a measure of specificity and reports the percentage of true positive base pairs out of all the base pairs our method annotated as TE component.

Independence from sequence similarity

Ideally, our method would identify repeat mobile elements in the genomes whether or not their sequences were under selection. Given the high divergence rate of repeat noncoding TEs, we must allow for mutations and a high degree of variability. To test how sensitivity (percent of true-positive findings out of the positive set) to the BDGPTrans set varied with sequence similarity (i.e., what happens to sensitivity when filtering the IR set to obtain the RIR set using different similarity thresholds), we extracted the RIRs from the IRs using different settings of e-values for both recent and ancient replications. In all, we used 625 settings with variants of e-value thresholds ranging from 1e3 to 1e-21 for both recent and ancient. The number of RIRs under these different settings varied from 1698 (1616 recent insertions and 82 ancient insertions) in the most stringent setting to 4504 (2346 recent IRs and 2158 ancient IRs) using the most relaxed criteria. Surprisingly, the sensitivity of the RIR sets under these different conditions hardly varied. Throughout the 559 most relaxed criteria, 1177 (74.9%) of the currently annotated TEs were recovered. Under the more stringent criteria, at least 1172 (74.6%) were consistently identified.

This finding implies the following: (1) The BDGPTrans set is limited in its scope, containing mostly really close matches (e-value 1e-21 or better). This was anticipated given the criteria used to confirm findings in BDGPTrans (Kaminker et al. 2002). (2) Given this bias in current annotations, the specificity of our method cannot be determined against currently annotated TEs since elements that are not currently annotated are not necessarily non-TEs. (3) The remaining set of our findings may be searched for new elements of known families, as well as instances of new families.

Identification of new instances of known TE families

We searched for new instances of known TE families within our set of annotations that did not overlap with BDGPTrans. We were relatively stringent in our criteria: In order for an RIR to qualify as a new annotated instance of a particular family, we required that a region have an open reading frame and have hits with an e-value better than 1 (relaxed e-value) to at least 80% of the annotated members of that family.

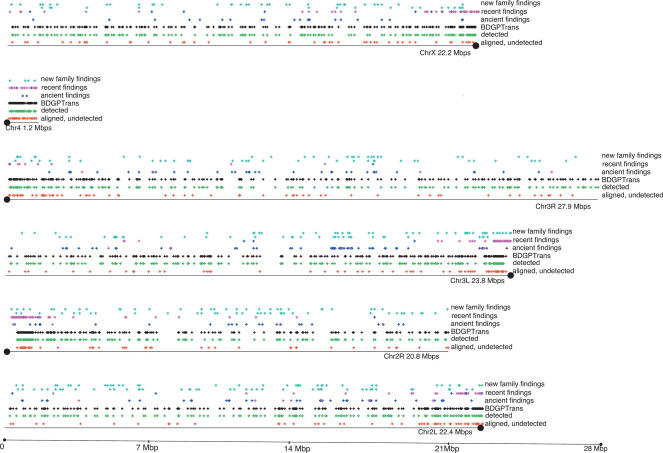
Overall, we found 355 recent elements (shown in the fifth track from the bottom for each chromosome arm of Fig. 3), and 232 ancient ones (shown in the fourth track from the bottom for each chromosome arm of Fig. 3). The distribution of these instances along the chromosome arms is shown in the figure. The instances colored in magenta are ones for which the criterion was tightened even more to require hits to as many other RIRs in the genome as there are family members. Comparing the magenta and blue tracks to the black track, we saw the anticipated increase in density in the proximal chromosome regions. We sought to evaluate this observation using the Wilcoxon rank sum two-sided test (Methods). The null hypothesis we were testing was that the new “recent” annotations were drawn from the same mean spatial distribution with the same mean as the BDGPTrans annotations. Rejecting this hypothesis would imply that there were distinguishing factors about the spatial distribution of our new recent findings versus the BDGPTrans recent findings. On each chromosome arm except arms 2R and 3L, the null hypothesis could not be rejected at the 0.001 level. This means that for the remaining arms, there was no evidence to support a different mean for the spatial distribution of the new annotations and the known ones. We concluded that at least for chromosomes 2L, 3R, 4, and likely for X, our annotations were consistent with the known TE annotations in their distribution along the chromosome arms.

Figure 3.

Distribution of TEs, true positives, false negatives, and new findings along chromosome arms.

Next, we sought to validate our predictions by the contribution of each family type in the annotated set, and our new set of instances. Different classes of elements (as described above) vary in their contribution to the Drosophila euchromatin. In our new annotations, the order and proportion of the contributions were preserved. LTR elements were the most numerous class of TEs (51.8% of our new instances, compared with 43.4% of BDGPTrans elements). LINE-like elements follow (making up 34.2% of our new instances, compared with 10.9% of BDGPTrans elements). These were followed by TIR elements (13.4% of our instances, 23.7% of BDGPTrans instances) and FB elements (1% of our instances, 2% of BDGPTrans elements).

The densities of the different element types are not uniformly distributed among the chromosome arms. For example, it is known that the density of LINE-like elements and TIR elements on chromosome 4 is far greater than on the major chromosome arms and is the major contributing factor to the difference in overall TE density between chromosome 4 and the other chromosome arms (Kaminker et al. 2002). As shown in Table 4, the relative contribution of each family type was conserved between our set and the BDGPTrans annotations.

Table 4.

Contribution of family type to elements on the chromosome arms

	LTR		LINE-like		TIR		FB
Chr	New	BDGP	New	BDGP	New	BDGP	New	BDGP
X	9.7	8.7	7.0	4.6	1.8	3.6	0.2	0.8
2L	8.3	8.4	5.6	6.5	1.8	4.4	0.4	0.3
2R	9.0	8.7	9.0	7.2	2.8	4.0	0.2	0.1
3L	17.4	7.8	8.3	7.0	4.2	3.8	0	0.5
3R	5.8	8.2	1.9	4.7	1.8	3.7	0	0.3
4	1.6	0.7	2.3	1.9	1.1	3.9	0	0.1

For each family type, the first column shows the percentage of new findings of known TE families, and the second column displays the percentage in BDGPTrans.

Lastly, we evaluated our new annotations by looking at the genomic region characteristics of each region. Insertion site preferences for intergenic regions were observed in this set of annotations. 18.7% (110/587) of our annotations were within intergenic transcribed regions of the genome. This is compared with 21.5% of the BDGPTrans set. Only a few of the new annotations, 4.1% (24/587), were found within clusters of previously annotated TEs. These regions have been well explored for TEs, and it is no surprise that our novel findings were not proportionately represented in these regions.

Proposed new families in euchromatin

New families were determined by clustering the RIRs, using their sequence similarity to all other insertion regions. We considered a cluster a “new family” if the intracluster variability fell within a user-defined threshold. This allowed us to use intracluster variability as a metric, as opposed to strictly depending on detecting repeats or open reading frames. The advantage is that the filtering of insertion regions is based on their affinity to a whole host of other IRs, as opposed to the simple application of a sequence similarity threshold. As noted above, applying a similarity threshold limited the findings in the BDGPTrans set to very recent insertions. Using the intraclass variability as a knob to look at many or few members of the original RIR findings, we achieved our goal of identifying families with more ancient insertions, without relying directly on sequence similarity.

We recovered six new families of transposable elements within the Release 4.1 sequences. All six families contained more than five instances. In three of the families, intrafamily variability was below the 2.0 criterion, while in the other three variability was above 2.0. Despite the small sample size (there were 56 new members of new families altogether), the findings adhered fairly well to the distribution of TEs along the chromosome arms, as seen in Table 5. Within these new findings, 75% were insertions associated with the ancient branch, and three families were entirely comprised of ancient insertion regions. The distribution of these findings along the chromosome arms is shown in the cyan tracks 6 (recent) and 7 (ancient) of Figure 3.

Table 5.

Chromosomal distribution of new findings, broken down by relative age in the species tree

Chr	BDGPTrans set (known instances)		“Ancient” TEs of known families		“Ancient” TEs of new families		“Recent” TEs of known families		“Recent” TEs of new families		Subset of new families within threshold <3.0
X	276	17.6%	22	9.5%	19	10.2%	88	24.8%	42	21.0%	6	10.7%
2L	305	19.4%	57	24.6%	50	26.7%	40	11.3%	42	21.0%	15	26.8%
2R	312	19.9%	29	12.5%	39	20.9%	93	26.2%	39	19.5%	8	14.3%
3L	288	18.3%	78	33.6%	39	20.9%	96	27.0%	43	21.5%	12	21.4%
3R	288	18.3%	44	19.0%	40	21.4%	12	3.4%	27	13.5%	14	25.0%
4	102	6.5%	2	0.9%	0	0.0%	26	7.3%	7	3.5%	1	1.8%
Total	1571		232		187		355		200		56

“Ancient” and “recent” designations correspond to the tree in Figure 2. For each set, the number and percent composition is listed.

Detecting shifts in eu-heterochromatin junction

It was evident early on in our analysis that the distribution of recent and ancient findings along the major chromosome arms was not the same (this was confirmed by a Wilcoxon rank sum test). We attribute some of this difference to alignment properties. However, such striking difference must also be indicative of a difference in genomic composition of the chromosome region at the time of insertion. Given the insertion site biases of TEs, we could use our RIR set to note changes in genomic characteristics of the chromosome regions during the time of insertion.

Having noted a clear difference in IR density between the euchromatic and pericentric regions on the chromosome arms, we wished to compare the density of recent to ancient IRs along the arms to indicate any movement of the eu-heterochromatic junction since the D. melanogaster–D. yakuba cenancestor. When such a shift occurs, euchromatic regions gain the compact replicating properties of pericentric heterochromatin, thereby becoming characteristically heterochromatic. Heterochromatization seems to cause distinct variation in the expression of the genes embedded in the shifting euchromatin (Locke et al. 1988). This effect, known as position-effect variegation, is not well understood.

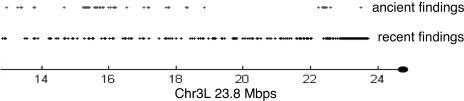
Figure 4 shows the distribution of the recent and the ancient insertions in the proximal regions of chromosome 3L. The most striking variation between recent and ancient was noted on this arm—the null hypothesis that the two distributions were of the same mean was rejected with greatest confidence (at the level of 1e-22). We observed a decided shift: The densely packed insertions in the recent findings were closer to the centromere than in the ancient. A less striking, yet similar effect can be detected in chromosomes X and 4. This leads us to question whether a translocation event occurred on chromosome arm 3L, fueling the heterochromatization of its proximal region. While further study is required for any definitive conclusion, it is evident that identifying the age boundaries on insertions can be used for further exploration of the history of the eukaryote host genome.

Figure 4.

Proximal region of chromosome 3L, contrasting distribution of “recent” and “ancient” findings.

Sensitivity to artifacts of assembly, alignment, and TE clustering

We had already noted that IR identification along the chromosome arm 4 was more dense than in any other chromosome arm. Chromosome 4 is the smallest autosome (∼5 Mb long) and is known to contain two main regions: The centromeric region encompasses roughly 4 Mb of the proximal end, and the remaining 1.2 Mb constitutes the euchromatic region on polytene salivary gland chromosomes. The centromeric region is characterized as heterochromatic. It is known that such pericentric heterochromatin is densely packed with compact, replicating chromatin (Locke et al. 1988). Cytological environments of this kind (highly repetitive) are particularly difficult to sequence (Devine et al. 1997) and assemble (Hoskins et al. 2002). Chromosome 4 therefore provided a good setting in which to assess the sensitivity of our method to poor assembly.

We first examined the cases that were not in the alignment, and therefore could not be detected. We found that the TEs that were not in the alignment were not equally distributed along the chromosome arms. In Table 2, the second column contains the distribution of BDGPTrans along the chromosome arms, while the third column contains the distribution of the unsuccessfully aligned annotations. It was foreseeable that chromosome arm 4 contained a disproportionate number of unaligned known TEs. While the comparative approach does not directly depend on the assembly, this finding does highlight the fact that poor assembly can induce misalignment. With better knowledge of TEs in this region, we could potentially improve assemblies by masking out repetitive portions of trace data and reducing sequence gaps in the assembly as was done in the assembly of heterochromatin in D. melanogaster (Hoskins et al. 2002).

We then looked at those annotations that were in the alignment, but not in our findings. We determined first whether their spatial distribution along each chromosome arm was likely to have been sampled from the same distribution as those our method did identify. Again, we used the Wilcoxon rank sum two-sided test (Methods) to test the “same distribution mean” hypothesis. Rejecting this hypothesis would imply that there were distinguishing factors about the spatial distribution of our true-positive findings versus our false-negative findings.

In each of the major chromosome arms, the “same distribution mean” hypothesis was rejected at the 1e-15 level. In chromosome 4, the null hypothesis was rejected at the 0.006 level. This implied that there was some spatial bias to the findings we did not detect versus those we did, particularly in the major chromosome arms. In Figure 3, each horizontal block represents a chromosome arm, and the circle at the end of each marks the location of the centromere. Each black dot in the black track represents an annotated TE in BDGPTrans (the positive set), each green dot in the green track represents a BDGPTrans annotation that was detected in our RIR findings (true-positive findings), and each red dot in the red track represents a BDGPTrans annotation that was within our alignment but was not detected by our method (false-negative findings). We saw a large concentration of undetected findings along the proximal regions of the chromosome arms. In chromosome 4 we saw a more uniform distribution, owing to the special heterochromatin structure of this arm scaffold. Examining the alignments of the failed cases in the proximal regions of the chromosome arms, we found more gaps and worse overall conservation rates than in the other regions. We concluded that alignment artifacts in the proximal regions of the chromosome arms led to inferior results in these regions, affecting >46% of the findings we failed to detect (we defined the proximal region to be the proximal 3 Mb on each arm).

Lastly, we wanted to see if our method was biased toward finding isolated TEs (those not found within clusters) or TEs that were not in intron regions. We looked at the genomic characterization of the 20-kb region (10 kb up- and downstream) of each of the undetected findings. Annotated TEs are known to have an insertion site bias, typically inserting into or adjacent to another TE, particularly in intron regions (Bartolome et al. 2002). The TEs that were not detected by our method did not show a tendency toward a particular genomic region. While 15% of the undetected findings were within TE clusters (a cluster was defined as five or more TEs within the same 10-kb region), 21% of the TEs in BDGPTrans are clustered. As for TEs within intron regions, 25% of the undetected findings were within introns. By comparison, 22% of the BDGPTrans set are in introns. Given the sample size, these differences are not significant. We concluded that our method was not sensitive to clustering of TEs.

Discussion

Repeat classification is a multifaceted problem that involves many biological tasks, ranging from characterization of mobile elements to analysis of mosaic structure of segmental duplications. Solving all these problems often begins with defining the boundaries of “elementary repeats” (the repeat representation problem), which is the focus of this paper. We present a comparative method for whole genome annotation of repeat mobile elements. Specifically, transposable elements are detected by searching multiple alignments of related genomes for the characteristic signature of TEs in alignment. The signature is a particular disruption in conservation in which a large insertion (with roughly conserved boundaries) appears in the sequences of all the species under one branch of the tree.

In contrast to methods that involve self-alignment of a single genome, our comparative method searches for the molecular artifacts of transposition through disruption in conservation. In particular, this approach has the following three advantages: First, the method relies less on the sequence similarity between different occurrences of TEs than on established methods, and therefore provides a complementary approach to TE identification. As we have shown, it can lead to the identification of more ancient TEs than have been identified hitherto. Second, the comparative approach allows us to place bounds on the date of each insertion event. This information is valuable for refining our understanding of the transposition mechanism (e.g., we can resolve the approximate time of amplification for each TE family), as well as the evolution of the host genome (as per our discussion on the shift of eu-heterochromatin junctions). Finally, the method permits choosing between stringent criteria and low-quality cutoffs on repeat content and structure. This flexibility allows us to mine deep into the mobile past of the genomes at hand. In our case study the method performed with high sensitivity and detected element boundaries accurately.

The comparative annotation of TEs depends on the whole genome alignment used, not directly on the assembly. We did see that specific types of problems in assembly can induce misalignment; however, these are unlikely to lead to the signatures required for TE annotation. If the assembly incorrectly resolved a genomic rearrangement, our method was not affected since whole genome mapping bypassed the error and mapped homologs appropriately. If the assembly did not recover repetitive structures in a particular genome (resulting in assembly gaps), then it could be that the TE sequence would be missing from that genome. This could result in incorrectly dated or, in the worst case, undetected mobile elements (in our case study, this was the scenario for 4% of known TEs). As we rely on the whole genome alignment's ability to infer sequence homology, we are more error-prone as we annotate TEs along higher branches in the tree. Error reduction is likely to be achieved by the addition of well-assembled genomes, and the selection of appropriate evolutionary models behind the alignment. For this reason, poorly characterized genome families are less suitable for this method. However, it should be noted that sequence-similarity-based methods suffer the same fate given their reliance on evolutionary models for establishing local similarity.

Applying our method to complete and partial drafts of four Drosophila genomes, we identified a set of repeat insertion regions that identified 74.8% of the set of known natural TEs, and recovered representatives from 100% of known TE families in D. melanogaster euchromatin. We showed that of the currently known TEs in D. melanogaster, at least 74.6% of insertions occurred since the D. melanogaster–D. yakuba split, and that all known euchromatin repeat families were active since that split. The bias in the set of known TEs can be explained by the sequence-similarity emphasis of current repeat element identification, and the use of single genomes to perform analyses. Our high sensitivity and low false-positive rate are due to the fact that we first searched for the signature of an insertion, and only then applied repeat and content criteria.

Our RIR set contained 4.3% of the euchromatic sequence. We estimate that the actual portion of euchromatin that consists of repeat mobile elements in D. melanogaster is greater than this, since we used stringent criteria to identify our set. As the number and quality of genome sequences increase, we will likely find many new repeat families that were not as recently active as our current set of known TEs.

Methods

Sequence data

Release 4 of the euchromatic sequence of the D. melanogaster genome was made available January 3, 2005 from the Berkeley Drosophila Genome Project's Web site (Celniker et al. 2002; Celniker and Rubin 2003): http://www.fruitfly.org/sequence/release4genomic.shtml. Release 1 of D. pseudoobscura was made available from the FlyBase D. pseudoobscura Web site (Richards et al. 2005): ftp://ftp.hgsc.bcm.tmc.edu/pub/data/Dpseudoobscura/. The scaffolds for the D. yakuba sequence were made available on April 7, 2004. Sequences were obtained from the WUSTL Genome Sequencing Center Web site: ftp://genome.wustl.edu/pub/seqmgr/yakuba/. The D.virilis scaffolds were made available on July 12, 2004, from Agencourt. They can be downloaded from: http://rana.lbl.gov/drosophila/assemblies/. For the purpose of our case study of D. melanogaster euchromatin, we defined “euchromatin” as any sequence that has been assembled into a chromosome arm scaffold, despite the heterochromatic characteristics of the extreme proximal regions of the chromosome arms.

Whole genome homology mapping

To align a fully and partly assembled set of n genomes, it is necessary first to break the sequences down to homologous regions, compute a homology map of these regions, and then globally align each of the components of the map. A homology map consists of a set of homologous regions in which each homology region is a set of n subsequences (beginning, end, chromosome, strand), one for each genome, so that there are no rearrangements within the subsequences. In other words, within a homology region it is possible to align the sequences globally. The homology map consists of labeled regions. Each consists of coordinates for n subsequences.

For the homology map construction, we used the MERCATOR program (C. Dewey and L. Pachter, “MERCATOR: Construction of Homology Maps for Multiple Whole Genomes,” in prep.). The MERCATOR strategy to building homology maps is to use exons that are orthologous in multiple genomes as map “anchors.” All exons are compared against all exons in other genomes, and significant alignments among exons are recorded. All significant alignments are then under consideration as anchors for homology, with the attempt made to throw out those anchors that hinder synteny globally, over the entire multiple alignment.

It is important to note that homology maps can be more general than the definition given above, in particular, the requirement that homology regions span all genomes can be weakened. MERCATOR finds homology regions spanning only a subset of the genomes. However, such regions were not considered in this study.

Multiple alignment of homolog regions

Once we have a homology map (these are the anchors remaining after MERCATOR), we construct a detailed global multiple alignment for each homology region. Global multiple alignments were performed with MAVID (Bray and Pachter 2004). The set of alignments used is available at http://hanuman.math.berkeley.edu/genomes.

Identifying insertion regions

Insertion regions were identified in each multiple-aligned homolog region by searching for interruption in conservation >200 bp long, with gaps of at most 55 bp. We chose the 200-bp threshold based on the lower end of the length distribution of known TEs in BDGPTrans. The gap parameter was chosen in order to allow for small problems in misalignment. Flanking regions were not constrained to align strongly—a minimum 5% conservation was required. Each insertion region was mapped to a branch on the species tree based on the genomes in which the conservation was disrupted. The findings were placed in sets segregated by alignment region and a particular branch on the species tree.

Filtering for repeat insertion regions

While insertion regions have natural boundaries due to the conserved alignments that flank them, a region must show appropriate content and structure and be corrected for over- or under-segmentation of an insertion element. We reason that by definition, an insertion region that is restricted to have occurred along a particular branch in the tree was contemporaneously active approximately at the same time as other insertion regions associated with this branch. Although we cannot infer the exact full sequence of the transposing element at that time, we can assume that the specific insertions of that family from that time period were duplicates. That is, if the elements were under strong selection, we would expect elements of the same family from the same branch to be nearly exactly globally aligned. Clearly, TEs are not under strong selection. Instead, by locally aligning each insertion region to all other insertion regions restricted to the same branch on the tree, we find the other inserted elements that compete for best local alignment of the insertion region.

We performed local alignment of each set of insertion regions using BLAST (Altschul et al. 1990). We varied the significance threshold based on the branch associated with each set of findings. For the recent branch, we used a significance e-value threshold of 1e-10, while for the ancient branch, we used a significance e-value threshold of 0.1. We used such permissive values because these regions are likely to be under no selection. If there was close similarity among them, they will likely have already been detected by previous TE studies (Kaminker et al. 2002). In addition, we searched for open reading frames in each insertion region using our in-house ORF prediction tool (faOrf) (C. Dewey, unpubl.). We used the BLAST hits and ORF predictions to filter for microsatellite regions, delineate tandem and nested repeats, and concatenate oversegmented IRs.

Finding repeats

We sought those insertions that repeated a threshold number of times in the insertion region set, on that branch. Our repeat threshold was 1 (fairly lenient).

Filtering for microsatellite repeat sequences

To address the issue of microsatellite repeats, we filtered for short HSPs (<20 bp) that had short, close, sequential hits to self. Sequential hits were defined as those on the same strand that were some genomic distance away from one another. “Close” defines the genomic distance between hits. In this case, they were constrained to being shorter than the length of the hit itself.

Finding tandem repeats

We wanted to cut insertion regions that contained more than one repeat element. The tandem insertion candidates are those that had large hits (>30 bp) that sequentially aligned both to self and to subcomponents in other elements. To cut the element, we used the boundaries of the self-hits to guide the boundary prediction.

Finding nested repeats

The candidates for nested insertions are those insertion regions with large nonoverlapping hits (>30 bp) that sequentially align to other IRs, where there is no intersection between the set of IRs to which each subcomponent aligned. We used the criterion that no intersection is permitted among the set of IRs to which each subcomponent aligned. We believe this to be overly restrictive, and it is likely that we missed many possibly nested components this way.

Concatenating broken regions

Lastly, given the draft nature of the sequences and the difficulty in aligning repeat regions, many choppy gaps occurred (as observed above in insertion regions a₂ and b in Fig. 2). We concatenated regions within a certain genomic distance (<700 bp) that aligned sequentially to other insertion regions (we didn't constrain the gaps in this instance).

Moving up the species tree, there is an increased likelihood of error due to problems in assembly and misalignment. In the future, we will most likely vary parameters for filtering insertion regions as we process regions from more ancient branches. At present, with the exception of the e-value threshold, all filtering was done with the same parameters.

We note that the filtering process does impose element boundaries based on the local self-alignment information, like the aforementioned current methods. As pointed out, due to TE subfamily evolution, these transitive relationships do not generally apply when classifying TEs or asserting subfamily structure. However, within the restricted temporal range of insertion regions, we can assume that subfamily sequence structure did not drastically change. Likewise, the TE instances of that subfamily resulting from a restricted period of activity may be incomplete (because of mutation since the duplication), but are not likely to be rearranged.

Analytical methods

Alignment of new families

The hits that resulted from local alignment searches using BLAST (Altschul et al. 1990) and BLAT (Kent 2002) provided preliminary alignment of elements within the new families, and new elements of known families. Subsequent multiple alignment was done using CLUSTALW (Thompson et al. 1994).

Calculation of evolutionary distance

Average pairwise distances within the new families were calculated using DNADist, distributed with the Phylip package (Felsenstein 1993). Parameters were set using the Kimura two-parameter substitution model with a 2:1 transition–transversion ratio (Kimura 1980).

Characterizing genomic environment

We reported the content of the flanking 20-kb region of a finding or annotation using the FlyBase D. melanogaster euchromatin annotations of Release 4.1. A finding was reported to be in a TE cluster if the flanking 20-kb sequence region contained more than five annotated TEs. A finding was reported to be in an intron if an annotated intron overlapped with any of the finding's region.

Wilcoxon rank sum test

The Wilcoxon rank sum test (also known as the Mann-Whitney U test) for equal means is a nonparametric test of the hypothesis that two independent samples come from distributions with equal means. The P-value the test returns is the probability of observing by chance the given result if the null hypothesis (means are equal) is true. For example, for a test performed at the 0.05 significance level, a P-value smaller than 5% means that the null hypothesis was rejected. A higher P-value meant that the null hypothesis could not be rejected. The results of our tests are available in the Supplemental material.

Supplemental material

Supplemental material is available at http://baboon.math.berkeley.edu/~caspian/DrosTEs/. The site includes a table showing the coordinates, length, classification, and characterization of genomic environment of the new identified insertion regions of known TE families; a table showing the coordinates, length, and environmental characterization of the new TE families in D. melanogaster euchromatin resulting from our case study; and a table showing the genomic environmental characterization of the BDGP annotated TE instances. Our reported Wilcoxon rank test results are also available. Additionally, the alignments of all the new families and the known TE families with new insertions are available on that site.