Design optimization methods for genomic DNA tiling arrays

Abstract

A recent development in microarray research entails the unbiased coverage, or tiling, of genomic DNA for the large-scale identification of transcribed sequences and regulatory elements. A central issue in designing tiling arrays is that of arriving at a single-copy tile path, as significant sequence cross-hybridization can result from the presence of non-unique probes on the array. Due to the fragmentation of genomic DNA caused by the widespread distribution of repetitive elements, the problem of obtaining adequate sequence coverage increases with the sizes of subsequence tiles that are to be included in the design. This becomes increasingly problematic when considering complex eukaryotic genomes that contain many thousands of interspersed repeats. The general problem of sequence tiling can be framed as finding an optimal partitioning of non-repetitive subsequences over a prescribed range of tile sizes, on a DNA sequence comprising repetitive and non-repetitive regions. Exact solutions to the tiling problem become computationally infeasible when applied to large genomes, but successive optimizations are developed that allow their practical implementation. These include an efficient method for determining the degree of similarity of many oligonucleotide sequences over large genomes, and two algorithms for finding an optimal tile path composed of longer sequence tiles. The first algorithm, a dynamic programming approach, finds an optimal tiling in linear time and space; the second applies a heuristic search to reduce the space complexity to a constant requirement. A Web resource has also been developed, accessible at http://tiling.gersteinlab.org, to generate optimal tile paths from user-provided DNA sequences.

DNA microarrays have become ubiquitous in genomic research as tools for the large-scale analysis of gene expression. The design of DNA microarrays has generally focused on the measurement of mRNA transcript levels from annotated genes, represented either by PCR products comprising entire cDNA sequences (Schena et al. 1995), or by short oligonucleotides complementary to internal regions of spliced messages (Lipshutz et al. 1999). Microarrays of this design allow the simultaneous interrogation of thousands of nucleotide sequences, providing a genome-wide snapshot of transcriptional activity. Since its introduction, microarray technology has advanced to a degree that currently accommodates enough individual array features to represent all the annotated genes in a mammalian genome.

A recent trend in genomics has involved the development of “tiling” arrays: microarrays that represent a complete non-repetitive tile path over a chromosome or locus, irrespective of any genes that may be annotated in that region (Fig. 1, left). This unbiased representation of genomic DNA has enabled the discovery of many novel transcribed sequences (Kapranov et al. 2002; Rinn et al. 2003; Yamada et al. 2003; Bertone et al. 2004; Kampa et al. 2004; Cheng et al. 2005), as well as the global identification of transcription factor binding sites (Ren et al. 2000; Iyer et al. 2001; Horak et al. 2002a,b; Lee et al. 2002; Martone et al. 2003; Cawley et al. 2004; Euskirchen et al. 2004, Odom et al. 2004; Kim et al. 2005).

Figure 1.

(Left) Evolution of genomic tiling arrays. Representing large spans of genomic DNA with bacterial artificial chromosome (BAC) clones facilitates global experimentation using relatively few array features, at the expense of low-tiling resolution. Higher-resolution designs using PCR products or oligonucleotides allow precise mapping of transcripts and regulatory elements, but require labor-intensive or technologically sophisticated approaches to implement. (Upper right) Linear feature tiling with gapped and end-to-end oligonucleotide placement. (Lower right) Overlapping tiles using fractional offset (e.g., one 25-mer probe placed every 5 nt) and single-base offset placement. The latter strategy provides a finer-resolution tiling of the genomic sequence, and can give a more precise indication of where hybridizing sequences are located on the chromosome.

In addition to coding and regulatory sequences, genomes contain repetitive elements that have been introduced and replicated in high copy number over evolutionary time. The frequency and diversity of these repeat sequences increases with the size and complexity of higher eukaryotic chromosomes, accounting for ∼45% of the total nucleotide content of mammalian genomes. In selecting sequences to be represented on a microarray, the exclusion of repetitive elements and other non-unique sequences is a primary goal. The reasons for this are twofold: First, microarray features whose sequences contain repeats present highly redundant hybridization targets; these contribute nonspecific background signals that mask the fluorescence resulting from specific probe hybridization. Second, the inclusion of repeats can significantly increase the number of DNA sequences assigned to array features. This additional sequence content is superfluous, resulting in the suboptimal utilization of the available features on a given array platform.

When representing genomic DNA with short oligonucleotides, near-optimal coverage of the non-repetitive sequence can be achieved in a relatively straightforward manner (Fig. 2B), although a number of important factors should be considered for probe selection. A more problematic situation arises when tile sizes increase, such as when selecting suitable targets for PCR amplification. For this application it is necessary to derive a tile path of larger sequence fragments from the non-repetitive component of the genome (Fig. 2C). Small PCR products can be difficult to resolve in a high-throughput setting, while fragments of several kilobases (kb) in length can limit the precise identification of hybridizing sequences. Balancing these criteria to select appropriate target sequences while avoiding repetitive elements presents a challenging optimization problem. Here we discuss a number of issues central to the problem of partitioning non-repetitive sequences using a range of tile sizes, and present several optimization approaches suitable for both oligonucleotide- and amplicon-based microarray applications.

Figure 2.

The problem of sequence similarity in tiling genomic DNA. (A) The level of similarity of oligonucleotide sequences to the remainder of the genome is represented by descending bars, where longer bars indicate more redundant sequences. If the redundancy exceeds a given threshold, indicated by the dashed line, the sequence is omitted from the tile path (B). Avoiding redundant or repetitive sequences inhibits adequate tiling of the sequence (C). Here, the level of non-repetitive sequence coverage decreases as the minimum tile size increases. At this point it also becomes necessary to use approximations that identify instances of known DNA transposons, retroelements, satellites, and other repetitive sequences, rather than calculating an explicit measure of sequence similarity. (D) In order to recover a higher percentage of non-repetitive DNA, tiling algorithms can be devised that incorporate some redundant sequences (gray) in an optimal fashion, which balances the cost of inclusion against the gain in sequence coverage.

Methods

Tiling discontiguous genome sequences

Genomic tiling arrays are intended to maximally cover a span of non-repetitive DNA with representative sequence fragments, or tiles, whose sizes fall within a prescribed range. The number of repetitive elements included in the tile path should be minimized, while the sequence is partitioned into the fewest number of tiles that can maximally cover the non-repetitive DNA. The sequences included on the array are either PCR-amplified and deposited mechanically onto glass slides via contact printing (Schena et al. 1995), or partitioned further and represented as oligonucleotides that may be printed mechanically or synthesized in situ using photolithographic (Lipshutz et al. 1999; Nuwaysir et al. 2002) or piezoelectric (Hughes et al. 2001) technologies (Table 1). Since the number of available features on a given microarray platform is often dependent on production costs, in practice an optimal tiling solution should arrive at the fewest number of non-repetitive tiles whose lengths approach a pre-determined upper bound.

Table 1.

A comparison of four of the most common DNA microarray formats

	Contact printing	Inkjet synthesis	Affymetrix	NimbleGen
Arraying method	Mechanical deposition	Phosphoramitide synthesis, piezoelectric printing	In situ DNA synthesis (photolithography)	In situ DNA synthesis (maskless photolithography)
DNA size limit	None	∼60 nt	25 nt	∼100 nt
Feature type	PCR products, oligomers	Oligomers	Oligomers	Oligomers
Features/slide	≤40 K	≤40 K	60 K–6.2 M	200–800 K
Array design	Flexible	Flexible	Fixed	Flexible
Fabrication cost	High (DNA preparation)	Moderate	High	Low
Array cost	Low	Moderate	Moderate	Moderate

While contact-printed arrays allow for unlimited customization, the initial production cost can be prohibitive compared with the relatively affordable but fixed-array designs commercially available. Maskless photolithographic arrays represent a trade-off between these platforms, allowing customized design while maintaining very high feature density.

Sequence similarity and single-copy tiling

Genome sequences are not random and therefore contain many redundant subsequences. For the design of tiling arrays it is essential to identify and eliminate non-unique sequences in order to reduce the potential for cross-hybridization of sequences originating from elsewhere in the genome. For shorter sequence tiles, robust methods to address the problem of sequence similarity can be developed, thereby generating a single-copy tile path to be represented on the array (Fig. 2A). To implement this approach we compute the degree of similarity of any given oligonucleotide sequence in a large genome.

This problem can be stated as follows: Given a genomic sequence and an oligomer of length n, find all oligomers in the sequence differing from the input in no more than m places. In theory, we need only create a direct hash table of each sequence to a list of all subsequence occurrences. However, the space required to implement the hash quickly becomes impractical. With 4ⁿ possible oligomer sequences, a hash of size 14 requires 1 gigabyte of storage, in addition to the space needed to store each of the possible index coordinates of the input sequence (another gigabyte for large chromosomes). These requirements impose a practical limitation on the size of hash tables such that n ≤ 14. This is insufficient for most microarray applications, where oligonucleotide sizes are typically ≥25 nucleotides (nt).

To work around these memory constraints and account for sequence mismatches, we adopt a BLAST-like scheme similar to that described in Wang and Seed (2003). A hash table is created based on oligomers of size k < n. When considering a given oligonucleotide sequence, we look up each of the oligonucleotide's n - k substrings of length k, extending each hit to full length as dictated by the substring's position in the oligonucleotide and comparing it with the input sequence. In doing so we can also allow for mismatches, knowing that we will detect all oligonucleotides with no more than two mismatches to the input so long as k ≥ (n - m)/(m + 1). Given a random model of a chromosome of length c, a substring of length k will have an expected c/4^k matches, each of which can be processed in constant time. In such a model our algorithm runs in an expected time of O((n - k)/4^k).

Repeat identification and low-complexity filtering

On a global scale, the implementation of exact methods to address the problem of sequence similarity becomes impractical. Instead, libraries of known repeats are identified in genomic DNA through sequence comparison using local alignment methods (Smith and Waterman 1981; Altschul et al. 1990). This is most easily accomplished through the use of software such as RepeatMasker (http://ftp.genome.washington.edu/RM/RepeatMasker.html), CENSOR (Jurka et al. 1996), Tandem Repeats Finder (Benson 1999), and RECON (Bao and Eddy 2002). Of these, RepeatMasker is widely used and is capable of identifying repeats in a variety of genomes using a database of well characterized families of repetitive elements (Jurka 2000).

In addition to identifying instances of canonical repeat families, it is often desirable to screen genomic DNA for low-complexity sequences: stretches of polypurine/polypyrimidine bases, or regions of extremely high A/T or G/C content. Repeat-Masker is able to filter some low-complexity DNA by default; more extensive filtering is often performed using programs such as DUST (R. Tatusov and D. Lipman, unpubl.) and NSEG (Wooton and Federhen 1993). DUST is included as a component of the NCBI BLAST distribution; NSEG is a member of the SEG family of programs and affords more flexible control over low-complexity filtering by using an information entropy-based model of sequence analysis.

Genomic DNA representation with short sequence tiles

When developing gene-based microarrays with short oligonucleotides, one or more probes are typically selected to represent each gene (Tomiuk and Hofmann 2001; Xu et al. 2002). These are designed to be highly specific to the target gene, to anneal within a suitable affinity range, to occur within annotated exons so that they will hybridize to the mature spliced transcript (Wang and Seed 2003), and are typically positioned proximal to the 3′ end of the gene to increase the likelihood of detecting partially reverse-transcribed messages.

Designing oligonucleotide tiling arrays constitutes a different problem than selecting oligonucleotides for gene-based arrays, primarily because end-to-end or overlapping tile layouts present fewer options with regard to sequence selection. A number of factors should be considered when tiling genomic DNA with oligonucleotides, including tiling resolution, consideration of non-unique subsequences, and hybridization affinity. Subdividing contiguous genomic DNA in a naive, end-to-end fashion offers little opportunity to select optimal probe sequences because the aim is to cover the non-repetitive regions using predetermined spacing constraints. However, several strategies can be used to improve both the annealing specificity and thermodynamic properties of oligonucleotides selected for tiling arrays.

Tiling resolution

An important factor in microarray design entails determining how the remaining non-repetitive DNA should be subdivided and how densely it should be represented by oligonucleotide probes. The serial placement of oligonucleotides along segments of non-repetitive genomic DNA can either be contiguous, covering all of the available sequence, or discontiguous, where gaps of a predetermined size range are allowed between adjacent probes (Fig. 1, upper right). This determination should be made according to the type of experiment for which the microarray is intended, and what kind of biological information the array is capable of measuring given a particular experimental sample.

In the case of ChIP-chip experiments, chromatinimmunoprecipited DNA is hybridized to an intergenic microarray to locate transcription factor binding sites (Horak and Snyder 2002; Wells and Farnham 2002; Buck and Lieb 2004; Hanlon and Leib 2004; Kirmizis and Farnham 2004; Bertone et al. 2005; Rodriguez and Huang 2005). The transcription factor-bound chromatin is sonicated prior to immunoselection in order to shear the DNA into smaller fragments; even so, fragments smaller than ∼500 bp will be largely unaffected by sonication. Since the sample DNA comprises a population of molecules whose sizes will generally exceed 500 bp, it is reasonable to represent the genomic sequence with oligonucleotide probes spaced <500 bp apart. Although closer probe spacing will yield more precise hybridization data, larger gaps are still appropriate for ChIP-chip experiments because this layout will ensure adequate hybridization to the sample DNA.

For the fine-resolution mapping of transcribed sequences, much closer probe spacing is required. Because a large fraction of the coding sequences in many eukaryotes span only tens of nucleotides, most of these would elude detection if the genomic sequence is tiled with significant gaps. Further, if the experiment is intended to measure exon-intron boundaries, it may be desirable to cover the genomic DNA with multiple oligonucleotides such that the starting position of each probe is shifted by several nucleotides in order to overlap the previous oligonucleotide's coordinates (Fig. 1, lower right). Although this strategy increases the tiling resolution, the number of probes required will eventually occupy many more features on the array. It is therefore important to select the desired tiling resolution in a manner that considers the intended microarray platform and optimizes the use of the available array elements.

Oligonucleotide probes that are selected for microarray applications are typically short (25-80 nt) and uniform in length. These assumptions allow the non-repetitive regions to be tiled by adopting a naive approach in which the sequences are subdivided into fixed-size partitions. There will naturally be many cases in which the oligomer length does not divide evenly into the size of a non-repetitive sequence fragment, and the remainder is therefore omitted from the tile path. However, the resulting loss in sequence coverage is inconsequential given the typically short length of the oligonucleotides. In these situations, it is desirable to adjust the placement of oligonucleotides in order to bias the sequence selection toward the optimal criteria, thereby reducing the potential for cross-hybridization to sequences elsewhere in the genome.

Thermodynamic properties of oligonucleotide probes

A third factor concerns the selection of oligonucleotide sequences for tiling arrays based on their predicted hybridization affinities (SantaLucia 1998). When representing individual genes with oligonucleotides, careful consideration is made to select sequences unique to each gene, having thermodynamic characteristics that are optimal for hybridization. For sequences >13 nt, hybridization affinity can be approximated by calculating the melting temperature of the DNA duplex using the standard formula:

where n_[A,C,G,T] indicates the number of instances of each nucleotide present in the DNA sequence. For more precise calculations, we can use a base-stacking approach that takes the exact sequence into account rather than the overall nucleotide composition (Rychlik and Rhoads 1989):

where ΔH is the enthalpy of base stacking interactions, ΔS is the entropy of base stacking, [oligo] indicates the oligonucleotide concentration, and R is the universal gas constant 1.987 Cal/°C × Mol.

Considering these criteria, it is useful to shift the placement of oligonucleotides within each region of non-repetitive DNA in order to reduce the variability of the melting temperatures associated with each probe sequence. In the case of spaced oligo tiling, an individual probe is selected from within each available region such that the calculated Tm is closest to the optimal temperature. For overlapping tiling designs, either the entire set of oligos can be shifted together such that their aggregate Tm is optimized, or the previous approach can be taken and the available regions for oligo placement simply overlap with adjacent regions instead of considering gaps between them.

Optimizing sequence coverage with longer tiles

Representing genomic DNA with tiles of increasing length involves a number of challenges beyond oligonucleotide selection. Sequences of several hundred base pairs are typically amplified by PCR and therefore must conform to certain properties to facilitate high-throughput amplification. Typically, the size distribution of sequences amenable to both PCR amplification and microarray analysis falls between 300 bp and 1.5 kb. Although it is feasible to amplify sequence fragments far exceeding this upper limit, it becomes difficult to determine the locations of hybridizing sequences within larger fragments. Conversely, amplifying thousands of small sequence fragments complicates the production of large-scale projects.

With regard to sequence tiling, a repeat-masked genome sequence can be viewed as containing two categories of nucleotide information: (1) that which comprises the coding, regulatory, and intergenic sequences located in euchromatic regions, together viewed as non-repetitive DNA (nrDNA), and (2) that which belongs to repetitive elements and low-complexity regions (rpDNA). Tiling of repeat-masked sequences can therefore be viewed as a two-class partitioning problem: Given a sequence with some subwords identified as repeat nucleotides and the remaining subwords composed of non-repetitive nucleotides, the sequence is partitioned into non-overlapping tiles of either type such that the total amount of non-repetitive sequence covered is maximized, while the number of repetitive nucleotides included in the resulting tile path is minimized.

The repetitive elements present in most eukaryotic genomes introduce a high degree of fragmentation of the non-repetitive DNA. Avoiding repeats and targeting only the remaining sequence fragments >300 bp in size results in suboptimal coverage of the non-repetitive DNA (Fig. 3). In order to improve the sequence coverage, strategies must be devised to recover some of the non-repetitive fragments that are too small to be efficiently amplified (Berman et al. 2004). This can be accomplished by strategically incorporating short repeat elements that lie between these non-repetitive sequences, effectively joining the adjacent fragments into larger contiguous tiles (Fig. 4). The methods proposed below are designed to obtain optimal tile paths for repeat-masked genomes, maximizing the coverage of non-repetitive DNA while minimizing the number of repetitive elements included in the resulting sequences.

Figure 3.

Representation of repetitive and non-repetitive sequences in genomic DNA. (A) Repetitive (gray) and non-repetitive (blue) segments are oriented vertically; the length of each subsequence is reflected by the height of the corresponding bar. (B) Repeat-masked region of human chromosome 10 showing alternating segments of repetitive and non-repetitive DNA. The high level of sequence fragmentation is clear, as is the wide range of sizes in both repetitive and non-repetitive segments. The horizontal line (red) indicates a segment length of 300 bp; a large number of non-repetitive sequences below this threshold are omitted when using naive tiling methods that simply avoid repeats. (C) Finer-resolution window of chromosome 10 before and after optimal sequence tiling. (Blue bars) Non-repetitive sequence that is covered in each case, (red bars) non-repetitive sequence that is lost. Non-repetitive sequences below the minimum size threshold are omitted when the sequence is tiled in a straightforward manner (left panel). Many of these are recovered after optimal tiling methods are applied (right panel). Note that a small number of repetitive nucleotides (short blue bars extending below the horizontal line) are included in the tile path to increase the overall sequence coverage.

Figure 4.

(A) Graphical representation of repetitive and non-repetitive segments in repeat-masked DNA. (B) In the naive tiling case, many small non-repetitive regions might be lost (yellow). (C) These can be recovered by using partitioning methods that generate an optimal tile path over the sequence.

Algorithms for optimal sequence tiling

Scoring potential tile paths

Given a sequence of nucleotides S_1...n, we would like to find an optimal tile path (possibly not unique) comprising a set of nonoverlapping tiles, potentially separated by excluded regions, that maximizes a scoring function V over all possible tile paths, given by

where w_i is the weight associated with the ith nucleotide, m is the number of tiles, and C is the cost for opening a tile (in this way, fewer longer tiles are favored over the creation of many smaller ones). For a given tile path, each nucleotide in the sequence is either in a tile (which has weights and for non-repetitive and repetitive nucleotides, respectively) or in an excluded region (which has weights and for non-repetitive and repetitive nucleotides, respectively). Thus,

We can also use the scoring function V to evaluate the score of either an individual tile T_i...j or an excluded region X_i...j,

Therefore, the scoring function evaluated over an entire tile path is the sum of all scores for individual tiles and excluded regions,

where {T_a} is a set of all tiles in the tile path and {X_a} is analogously defined. A brute-force algorithm would enumerate all tile paths to find an optimal solution; however, this approach would take exponential time to compute. We impose an additional constraint, that tiles are restricted to lengths between a lower bound l and an upper bound u. Given this constraint, the algorithm we present here solves the problem in linear time.

A dynamic programming solution

Dynamic programming has been successfully applied many times in sequence analysis. Examples include alignment methods (Needleman and Wunsch 1970; Smith and Waterman 1981; Gotoh 1982), gene prediction (Gelfand and Roytberg 1993; Snyder and Stormo 1993), and RNA secondary structure prediction (Zuker and Sankoff 1984). The key idea behind dynamic programming is the reuse of intermediate results. This is usually accomplished by breaking down an exponential search space into subparts, which are evaluated and whose results are tabulated for reuse. The analysis of large search spaces can then be done in polynomial time.

The main iteration of the algorithm can be described as follows: At an intermediate step in the computation we have evaluated the optimal tile paths and their associated scores for all subsequences S_{1.. .1} to S_1...(k-1). In order to find an optimal tile path for the subsequence S_1...k, for each i ∈ [max(1, k - u), max(1, k - l)] we compute the score for the tile path consisting of the optimal tile path from 1...i and the tile T_{(i + 1)...k} using the score of the optimal tile path from 1...i and V[T_{(i + 1)...k}]. Similarly, we also evaluate the score of the tile path consisting of the optimal solution from 1...(k - 1) and the excluded region X_k...k (the kth nucleotide). The optimal tile path for S_1...k is then one of the preceding tile paths having the maximal score. This tile path and its associated score are then stored, and the algorithm proceeds to the next nucleotide in the sequence, k + 1. A schematic of the algorithm appears below.

Given optimal tiles paths for all subsequences S_{1.. .1} to S_{1...(k - 1)} and associated scores

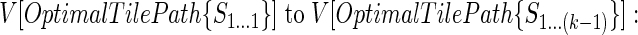STEP 1: For each i ∈ [max(1, k - u), max(1, k - 1)] we construct the following tile path:

and compute its score

We also construct an additional tile path

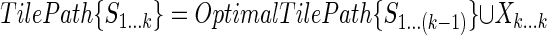and compute its score

STEP 2: From the preceding tile paths computed in Step 1, we select one having the maximal score and store it as OptimalTilePath{S_1...k}, along with its associated score.

STEP 3: Repeat for subsequence S_{1...(k + 1)}.

We used the algebraic dynamic programming (ADP) framework (Giegerich 2000) to recursively construct all possible partitionings and apply the scoring scheme to each solution. Since many partitionings share common subpartitionings, we can tabulate their scores for reuse instead of recomputing them (Fig. 5). Without the tile length constraints, the time and space complexity of this approach would be O(n²), which is inherent in the ADP framework implementation. Given these constraints, the algorithm runs in linear time and space, specifically O((u - l)n).

Figure 5.

Many different partitionings share common subparts. To compute any partitioning with a split at k, the best partitioning for (i, k) and for (k, j) must be known. Since there are many ways to partition the sequence with a split at k, we only need to recursively evaluate a subpartitioning for subword (i, j) and (k, j) once. In all cases where we need the optimal solution for these subwords again, we refer to the pre-computed result instead of considering all further possible partitionings of that subword.

A linear-time, constant-space solution

The dynamic programming algorithm computes an optimal tiling solution over the target sequence. In practice, however, the time and space required to process real genomic DNA sequences preclude the use of this approach for large eukaryotic chromosomes (spanning up to ∼250 Mb). Here we present an alternative method that traverses the sequence in a single pass, placing tiles according to local constraints instead of considering every possible tiling solution. In contrast to the dynamic programming algorithm, the result of this approach partitions the sequence into alternating included regions I_i...j and excluded regions X_i...j. A post-processing step is then required to subdivide the included regions into individual tiles T_i...j satisfying the length constraints.

The scores for included and excluded regions are given by

where the weights corresponding to included regions are the same as those for the tiles in the dynamic programming algorithm 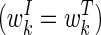. Note that the score for included regions does not account for the tile cost C.

The algorithm partitions the sequence and outputs the region boundaries as processing continues. The sequence is scanned one nucleotide at a time, with the current position denoted by i. During the main iteration we keep track of an earlier position k, up to which an optimal partitioning has been determined. At each step, the algorithm attempts to determine if the window S_{(k + 1)...i} should be classified either as an extension of the last known region R (currently extending up to k), or as the prefix of a new region starting at k + 1. Depending on the type of region R (included or excluded) and the difference D = V[I_{(k + 1)...i}] - V[X_{(k + 1)...i}] between the values of the scoring function for the two potential classifications of the window S_{(k + 1)...i}, the algorithm selects one of three possible options:

1. If R is an included region and D is positive, or if R is an excluded region and D is negative, then R is extended to include the nucleotides up to i (i.e., k:= i);

2. If R is an included region and D < -C, or if R is an excluded region and D > C, then R is terminated at k and a new region of the opposite type is initialized at k + 1 and extended to position i;

3. Otherwise, neither action is taken.

Following this decision, the next nucleotide in the sequence is processed (i.e., i is incremented). The classification of the first and the last regions in the sequence is determined similarly, effectively assuming that the start of the sequence follows an excluded region, and only inspecting the sign of D if R is an included region at the end of the sequence (i.e., when i = n - 1).

Since the number of times each nucleotide is examined is bounded by a constant, the overall time complexity is linear with respect to the size of the input sequence. The algorithm runs in constant space, as we need only keep a running value of D, the values of i and k, and the type of region R. A proof of optimality for this algorithm is presented in the Appendix.

This algorithm imposes no implicit upper bound on the size of nrDNA partitions, although C is effectively a lower bound on tile sizes. Therefore, included regions must be subdivided into smaller tiles whose sizes reflect the desired upper limit for PCR products. In terms of experimental preparation and subsequent microarray data analysis, it is preferable to create roughly equalsized fragments whenever possible. Therefore, the most straightforward tiling of long nrDNA partitions involves 1) taking the ceiling of the length of the partition divided by the maximum tile size, then 2) subdividing the partition into equal-sized fragments of this number.

A further improvement in the time complexity is possible when u ≥ 2l. In this case it can be shown that for k > u, OptimalTilePath{S_1...k} is always one of the following three tile paths:

1. ;

2. ; and

3. , where i + 1 is the starting index of the last tile in the highest-score path of the form .

In other words, the best path is the path ending with a tile of minimal length, or ending with a gap, or the one-nucleotide extension of the last tile in the one step shorter best path ending with a tile. Note that the third choice is valid only when k - i < u, and indeed it can be shown that when u ≥ 2l, this constraint is always satisfied; there is always a path ending with a tile shorter than u, whose score is at least that of the path ending with a tile of maximal size u.

As a consequence of this observation, the algorithm can select the best of the above three choices at each nucleotide, instead of comparing u - l + 2 alternatives. This reduces the time complexity to O(n). In practice, a straightforward implementation of the algorithm finds the optimal tiling of the largest sequenced chromosomes in <15 sec when u = 1500 and u ≥ 2l.

Although the above improvement in time complexity does not hold in general when u < 2l, in practice the algorithm performs better when applying a similar optimization in the general case: Select the best path among the above three choices, unless the third choice is invalid due to the last tile being of length u;in that case, fall back to the previously described algorithm and compute the maximal score among all u - l + 1 paths ending with a tile. Experiments with various genome sequences show that the fallback procedure is invoked very rarely, and this optimization makes a significant difference in the running time.

Results

Tiling statistics for eukaryotic genomes

A summary of tiling genome sequences of various sizes and repeat densities is presented in Table 2. Genomes with relatively few repeats were included from several model organisms, as well as the highly repetitive genomes of more recently sequenced rodents and primates. The sequences were tiled first using a naive approach in which the non-repetitive DNA was subdivided into tiles having lengths equal to the lower size bound (in this case 300 bp). The linear-time tiling method was then applied to the sequences to derive an optimal tile path for each. Table 3 includes a summary of two additional metrics that apply simple tiling schemes to each sequence. Each of the latter methods allows some inclusion of repetitive nucleotides in order to recover a higher percentage of non-repetitive DNA.

Table 2.

Optimal and naive tiling of various sequenced genomes for tile sizes between 300 bp and 1.5 kb

				Optimal sequence tiling
			Naive partitioning				Comparison
Organism	Genome size	Percent repeats	Tile quality	Percent non-repeat bp covered	Percent repeat bp included vs all non-repeat bp	Tile quality	Percent improvement
Pan troglodytes	3,083,993,401	57.74	66.05	89.81	4.23	85.58	19.53
Homo sapiens	3,070,537,687	52.38	66.07	89.60	4.06	85.53	19.47
Rattus norvegicus	2,795,745,218	48.75	66.86	91.43	5.54	85.89	19.03
Mus musculus	2,638,213,512	45.62	66.18	91.09	5.51	85.58	19.41
Caenorhabditis elegans	100,277,879	11.26	84.29	98.54	3.10	95.44	11.16
Drosophila melanogaster	129,323,838	14.23	86.89	99.40	2.62	96.78	9.89
Fugu rubripes	349,519,338	15.06	87.97	99.07	2.13	96.94	8.97
Arabidopsis thaliana	119,186,497	0.16	99.97	100.00	0.00	100.00	0.02

Repetitive elements were identified using RepeatMasker (http://ftp.genome.washington.edu/RM/RepeatMasker.html) and Tandem Repeats Finder (Benson 1999). The genome sequences vary in the degree of repeat density, ranging from mammalian genomes with nearly 50% repeat content to the relatively repeat-free Arabidopsis genome. Obtaining a high degree of non-repetitive sequence coverage for the genomes on the latter end of the spectrum is straightforward. However, as higher eukaryotes are considered it becomes impossible to optimally tile the highly repetitive sequences without further processing.

Table 3.

Comparison of two simple tiling metrics that incorporate repetitive nucleotides to improve non-repetitive sequence coverage

			Case 1: Threshold repeat inclusion (50 bp)			Case 2: Percentage repeat inclusion (25%)
Organism	Genome size	Percent repeats	Percent non-repeat bp covered	Percent repeat bp included vs all non-repeat bp	Tile quality	Percent non-repeat bp covered	Percent repeat bp included vs all non-repeat bp	Tile quality
Pan troglodytes	3,083,993,401	57.74	64.85	4.15	62.04	66.85	17.94	52.24
Homo sapiens	3,070,537,687	52.38	65.01	4.09	62.24	67.11	18.22	52.16
Rattus norvegicus	2,795,745,218	48.75	66.66	4.28	63.68	69.42	19.84	52.24
Mus musculus	2,638,213,512	45.62	77.56	4.30	74.07	80.82	20.15	60.43
Caenorhabditis elegans	100,277,879	11.26	89.71	2.18	96.68	99.84	11.12	87.47
Drosophila melanogaster	129,323,838	14.23	97.63	0.03	99.97	100	2.39	97.55
Fugu rubripes	349,519,338	15.06	95.09	1.86	97.74	100	6.33	93.24
Arabidopsis thaliana	119,186,497	0.16	99.51	1.29	98.22	100	13.29	84.68

In Case 1, repeat sequences ≤50 bp were allowed, and in Case 2 up to 25% of a tile may contain repetitive nucleotides. As in Table 1, tile sizes range from 300 bp to 1.5 kb. Case 1 achieves only marginal improvement in non-repetitive sequence coverage when compared with the same level of repeat nucleotide inclusion in the optimal tiling case. Non-repetitive sequence coverage in mammalian genomes falls sharply in Case 2 despite the inclusion of a high percentage of repetitive DNA. In each case, performance on mammalian genomes is significantly lower than that of the optimal tiling algorithm (Table 2).

In comparing these results, a number of observations become apparent. When the sequences are tiled in a naive fashion, the coverage of non-repetitive DNA decreases dramatically as we progress from the relatively repeat-free Arabidopsis sequence to the larger mammalian genomes. This reflects the higher levels of genomic sequence fragmentation due to increased repeat content, a condition that clearly inhibits the optimal tiling of the sequence.

Applying the optimal tiling algorithm to more complex genomes improves the non-repetitive sequence coverage significantly, while the percentage of included repeats remains very low. The optimal tiling algorithm greatly outperforms the other methods in higher eukaryotes, achieving maximal coverage of non-repetitive DNA with a relatively small increase in repeat nucleotide inclusion. In terms of microarray analysis, it has been empirically shown that the number of repeats included in such an optimal tile path can be effectively blocked through the inclusion of unlabeled low-complexity or repetitive DNA (e.g., Cot-1) in hybridization samples (Rinn et al. 2003).

Discussion

Tiling arrays are becoming an important tool for empirical genome annotation, making available the maximum amount of non-repetitive genomic DNA for microarray interrogation. In designing an optimal tile path for microarray applications, the identification and reduction of similar sequences constitutes a fundamental issue and can significantly reduce artifacts associated with cross-hybridization (Royce et al. 2005). While exact methods can be formulated to address this problem for shorter sequences, such approaches are computationally intractable as sequence tiles become longer. In this case, global approximations based on homology to repetitive elements serve to eliminate redundant sequences on a larger scale.

Numerous options exist for tiling genomic sequences with oligonucleotides, leading to microarray designs of various sequence resolutions and feature densities. Biasing the selection of probes toward uniform thermal properties and eliminating non-unique sequences across the genome can improve the annealing characteristics and hybridization specificity. Although these issues become non-trivial for large genomes, we describe an efficient solution for determining sequence similarity and rejecting non-unique probes that is appropriate for microarray applications.

As sequence tiles increase in size, the sequence fragmentation introduced by repetitive elements reduces the coverage of non-repetitive DNA. For higher eukaryotes, this precludes the use of trivial partitioning strategies where maximal coverage of the non-repetitive sequence is desired. To address this problem, we present space- and time-efficient algorithms for generating optimal tile paths to improve the coverage of non-repetitive sequences while minimizing the number of repetitive nucleotides included. In this manner, a greater number of fragments of sufficient size is recovered for amplification, and a higher percentage of non-repetitive DNA is represented on the array. These approaches enable the construction of tiling arrays that maximize the amount of non-repetitive DNA for the discovery of novel functional elements in eukaryotic genomes.

Appendix A

Proof of optimality for the linear-time, constant-space algorithm

To see why this algorithm produces an optimal partitioning, we proceed by induction on the length of the inspected sequence and assume that the algorithm has been correct prior to the ith element (i.e., the partitioning up to k is optimal, and no decision can be made so far on the window between k + 1 and i). We will show only one case of the proof; the rest is very similar. Without loss of generality, assume that the last known region R, currently extending up to k, is an included region. Consider the case when D < -C, in which the algorithm will terminate R at i and start an excluded region at i + 1. Suppose, however, that there is an optimal partitioning P with score s_P that extends R at least up to position i, contrary to what the algorithm yields. Define a new partitioning N, identical to P except for the window between k + 1 and i, which in N is part of an excluded region, and let us compute its score s_N. There are two possibilities: If in P the included region ends at i and an excluded region starts at i + 1, then N has the same number of partitions as P, but one region boundary has been shifted from i in P to k in N. Hence, s_N is equal to s_P plus the difference in the scores on the window between k + 1 and i; these scores are exactly V[I_{(k + 1)...i}] under the partitioning P and V[X_{(k + 1)...i}] under N, therefore:

since the difference D is negative by our assumption. The second possibility is that the included region starting in P extends after i; this means that in N this region is subdivided into two regions by the excluded region from k + 1 to i, so N contains one more included region than P. Hence,

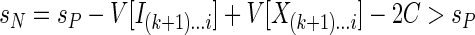again by the assumption that D < -C. Thus, in both cases we have s_N > s_P, which contradicts the assumption of optimality of the partitioning P.

Other partitionings that terminate the included region earlier than i can be shown similarly suboptimal by the following observation. Since by assumption the algorithm postponed the decision until i, the difference D must be between -C and 0 at all intermediate points. For the case when the algorithm postpones the partitioning decision, the proof of correctness is to construct two sequences sharing the same prefix up to i but requiring different optimal partitionings of the window from k + 1to i, which shows that indeed no decision guaranteeing optimality can be made at i. In other words, a partitioning solution not satisfying the tests in the algorithm cannot be optimal.

The correctness of the optimization is a consequence of the following propositions, which we prove under the assumptions that u ≥ 2l and the weights and 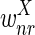are smaller than 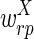and (in particular, without loss of generality we can assume that and 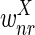are negative, while 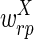and 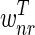are positive).

1. For all k > u it holds that , since the right-hand side is the score of one of the paths from which the path in the left-hand side is chosen as optimal.

2. Hence, for k > u, to find a path of the form with a maximal score among all i ∈ (k - u, k - l], it suffices to consider those paths with i ∈ (k - 2l, k - l].

3. Let j be a value of i ∈ (k - 2l, k - l] that maximizes V[OptimalTilePath{S_1...i}]; in this case it also maximizes . To show that this is true, we first assume the contrary:

   1. Consider the possibility that the maximum of is reached at an index i > j; that is, suppose that for some i ∈ (j, k - l] we have 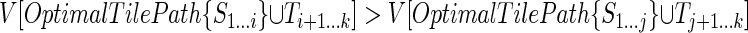. It follows that 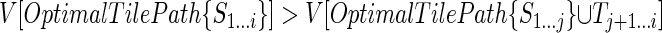. Then OptimalTilePath{S_1...i} cannot end with a tile over S_{j + 1...i}, because in that case its score would, at most, be equal to that of (which itself covers that subsequence with a tile), instead of strictly greater as assumed. Since i - j < l, OptimalTilePath{S_1...i} cannot end with a tile starting between i and j. Hence, it must end with an excluded region; furthermore, the excluded region must start at j + 1, otherwise the score of the optimal tile path ending just before the start of the excluded region would be higher than the score of OptimalTilePath{S_1...j}. Consider then the tile path 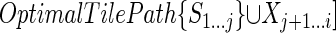; this gives:

      

      which means this tile path has the same score as OptimalTilePath{S_1...i} on the subsequence S_{j + 1...i}, and the highest possible score on S_1...j, by assumption higher than the corresponding score of OptimalTilePath {S_1...i}. Hence, 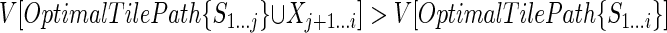, which contradicts the optimality of OptimalTilePath{S_1...i}.
   2. Similar reasoning shows that is higher than the score of any path starting at some i ∈ (k - 2l, j) and ending with a tile extending to k.

Appendix B

Tiling sequences using morphological operations

A number of established methods can be applied to repeat-masked DNA sequences to approximate an optimal tiling solution. By treating a genome sequence as a vector of nucleotide “pixels,” we can use image segmentation techniques such as region growing and other relaxation processes to close small repetitive elements in the genomic sequence, thereby merging the adjacent high-complexity sequences into contiguous tiles. This approach can be expressed using standard binary morphological algebra (Serra 1980; Vernon 1991). We first assign all nrDNA and rpDNA elements from a target genome sequence S to sets A and B, respectively:

Given this conceptual distinction, we can operate on the sequence using binary morphological operations. In order to apply binary operations to repeat-masked genomic DNA, it is necessary to first reduce the mixed nucleotide sequence to a bilevel representation. Thresholding assigns a new binary value b(x) to each nucleotide in the original “greylevel” sequence image, thereby generating a mask of the original sequence. Repeat and high-complexity nucleotides are assigned binary values by the following thresholding operation:

where b(x) is equal to one of two possible assignments [G_nr,G_rp]. This segmentation method discretizes the initial greylevel value g of any nucleotide n according to a predetermined threshold Z, thereby converting nrDNA and rpDNA sequence positions to the binary values prescribed by the parameters G_nr and G_rp, respectively.

The converted bilevel image can now be processed in several ways to yield an expansion of the nrDNA regions into the rpDNA regions. The nrDNA elements in set A can be transformed depending on how they relate to the “background” component of the sequence, comprising the rpDNA elements in B and referred to as the structuring element. The dilation of an input image A by a structuring element B is then described by:

where (A + b) indicates the translation of A by b. Essentially, this implies that in order to dilate set A by the structuring element B, B is first translated by all elements in A. The dual operation to dilation is erosion:

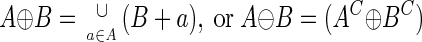where A^c and B^c indicate the complements of A and B, respectively, and (B + a) represents the translation of B by a. The union of these translations constitutes A + B. In cases where the lengths of repetitive elements exceed the degree of dilation, an equal number of erosion operations will restore the repeat, and the adjacent nrDNA regions will remain separate. However, if two dilated nrDNA regions meet, the repeat region will be closed, and erosion will have no effect in that local area. This can be accomplished with a closing operation where we first dilate the nrDNA structuring element, then erode by the same amount. Closing comprises a dilation operation followed by erosion:

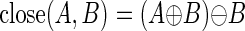In this manner, rpDNA regions whose lengths are less than the number of dilation cycles are closed, and the adjacent nrDNA fragments are effectively merged into larger tiles. Although this approach describes a simple approximation to the tiling problem, it is dependent on the use of a threshold constant for dilation-erosion cycles which corresponds to a fixed maximum number of nucleotides that each repetitive element can span.