Visualizing bacterial tRNA identity determinants and antideterminants using function logos and inverse function logos

Abstract

Sequence logos are stacked bar graphs that generalize the notion of consensus sequence. They employ entropy statistics very effectively to display variation in a structural alignment of sequences of a common function, while emphasizing its over-represented features. Yet sequence logos cannot display features that distinguish functional subclasses within a structurally related superfamily nor do they display under-represented features. We introduce two extensions to address these needs: function logos and inverse logos. Function logos display subfunctions that are over-represented among sequences carrying a specific feature. Inverse logos generalize both sequence logos and function logos by displaying under-represented, rather than over-represented, features or functions in structural alignments. To make inverse logos, a compositional inverse is applied to the feature or function frequency distributions before logo construction, where a compositional inverse is a mathematical transform that makes common features or functions rare and vice versa. We applied these methods to a database of structurally aligned bacterial tDNAs to create highly condensed, birds-eye views of potentially all so-called identity determinants and antideterminants that confer specific amino acid charging or initiator function on tRNAs in bacteria. We recovered both known and a few potentially novel identity elements. Function logos and inverse logos are useful tools for exploratory bioinformatic analysis of structure–function relationships in sequence families and superfamilies.

INTRODUCTION

Which sequence features confer a specific biological function on a class of macromolecules? This question becomes both more acute and more tractable when contrasting classes of molecules with distinct functions yet highly similar structures. In that situation, there may be fewer structural differences to explain the functional differences among classes, but this also means fewer structural differences to detect and test. Highly similar structures also make structural analogy easier to assign. A common complication arises, however, in that structural similarity may derive from common ancestry rather than from functional constraint.

An example of such a problem is transfer RNA (tRNA) identity [reviewed in (1–4)]. A pillar of fidelity in gene expression is the consistency with which specific amino acids are attached to specific tRNAs by enzymes called aminoacyl-tRNA synthetases (aaRSs). In general, there is one population of aaRS in a cell for each of the 20 canonical amino acids. Despite the generally very high structural similarity of all tRNAs, each must interact productively with only one synthetase population to be charged with its cognate amino acid and interact nonproductively with the remaining 19 enzyme populations. The identity of a tRNA refers to this amino acid ‘charging’ specificity. In a simplification, the identity of a tRNA can be thought to depend on a constellation of structural features called ‘identity elements,’ encompassing features that promote recognition and catalytic activity by its cognate aaRS (called ‘determinants’) or discrimination by noncognate synthetases against the same or other features (called ‘antideterminants’) so as to inhibit translationally ambiguous tRNA-binding and aminoacylation.

We (roughly) define a ‘tRNA identity code’ as the set of all identity elements that make tRNAs functionally distinct within a taxonomic lineage. We note five points about identity codes as described in more detail in the aforementioned reviews. First, a complete identity code has never been completely described for any taxonomic lineage. Second, identity codes are not concentrated in one structurally analogous place in tRNAs. There is no ‘identity anticodon’. Although the anticodon and acceptor stem are consistently important for identity, in model organisms identity elements are distributed over the whole tRNA structure and in different places for different amino acid systems. Third, known identity codes vary widely among the three domains of life, and between the cytoplasmic and organellar compartments in eukaryotes. Fourth, antideterminants have proven to be important in tRNA identity codes, and unlike in the primary genetic code, may potentially function only as such, without a corresponding positive function in another system. Fifth, although practically all tRNAs in cells contain a diverse array of base modifications, with a few known exceptions in the anticodon loop among Escherichia coli tRNAs, base modifications have not proven to be important identity elements (2). This last point may be because the base modification reactions themselves are not physiologically and/or evolutionarily reliable enough for synthetase interactions to have evolved to depend on them.

With these points in mind, we proceed to define what we mean by ‘sequence features’ and sets or combinations thereof. A sequence is a vector $\overrightarrow{x}=\langle x_1{x}_2\cdots x_L\rangle$ of dimension L in which each vector element x_l is a member of some alphabet set $\mathcal{X}$, also called the ‘state’ of the sequence at position l, 1 ≤ l ≤ L. A ‘sequence feature’ x_l is a specific state $x_l\in \mathcal{X}$ at a specific position l. For instance, for the purposes of this paper, possible sequence features among (structurally aligned) tRNAs at a given position are members of the aligned RNA alphabet $\mathcal{X}=\{A,C,G,U,-\}$, where the gap state ‘−’ indicates the absence of any nucleotide structure in that tRNA, and l indexes position in a structural alignment. A ‘feature set’ S_l is a subset of all possible states $S_l\subset \mathcal{X}$ at position l. A ‘two-position feature set’ S_k,l is a subset of the Cartesian product of all possible states at two positions k and l, 1 ≤ k,l ≤ L, and a ‘three-position feature set’ S_j,k,l is a subset of the Cartesian product of all possible states at three positions j, k, and l, 1 ≤j, k, l ≤ L.

Indeed, tRNA identity is one example of the general notion of the ‘function’ of a sequence. We represent the universe of functions of a family of biological molecules by the letters $\mathcal{Y}$ when referred to in the abstract. For tRNAs in particular, each possible function, except those of initiator tRNAs specialized to translate start codons, is conveniently associated with a unique letter—the IUPAC one-letter code of the amino acid with which it is charged. To this we add the letter ‘X’ to represent the special initiator function. Thus, for tRNAs, $\mathcal{Y}=\{A,C,D,E,F,G,H,I,K,L,M,N,P,Q,R,S,T,V,W,X,Y\}$ and $\left|\mathcal{Y}\right|=21$.

A pioneering approach to the bioinformatics of tRNA identity was taken by McClain and co-workers for E.coli and Salmonella typhimurium data (5) and subsequently yeast data (6). In this approach, a database of structurally aligned tDNAs was partitioned by their known charging identities into disjoint sets, called ‘isoaccepting classes’. In McClain and co-worker's approach, for each isoaccepting class y of tDNAs, if every member contained features in some feature set S_l, while all tDNAs in all other classes never contained these features, then the features in S_l were said to be identity determinants for class y. Using analogous terms from population genetics, by McClain and co-worker's definition, determinants are features that are ‘private’ to an identity class, but need not be ‘fixed’ within that class. This definition of determinant can be represented by a logical rule in the form ‘a given sequence carries one among a set of states at a given position if and only if the sequence is of class y'. Because of this we call McClain and co-workers approach a ‘logic-based’ approach (actually the theory behind their algorithm was described in a probabilistic framework). We can represent the preceding rule more concisely as S_l ⇔ y. Here and in what follows, implication of or by a set is shorthand for a logical OR among members of the set. McClain and co-workers also examined two- and three-position feature sets to find those that were analogously private to specific identity classes, i.e. they also set out to discover rules such as S_k,l ⇔ y and S_j,k,l ⇔ y.

The logic-based approach yielded many interesting observations that were consistent with experimental data and made new testable predictions. But it is not without certain limitations. First, the logic-based approach is highly sensitive to experimental error and to mutations. In a fully automatic application, experimental errors, including sequencing errors, misspecification of identity or mistakes in the storage and transmission of this information can obscure important signals because it requires only one sequence to cause an intersection of a feature set between two classes. For the same reason, the method is biased toward detecting only strongly selected identity elements. Some sequences in a set could contain mildly deleterious mutations that cause them to overlap with other classes but still be functional within their own class. The logic-based approach would discount the wild-type feature on the basis of the occurrence of only one such mutant.

A third limitation of the logic-based approach as it was implemented, but not in principle, is that it looks for feature sets that are private to only one class. There is no reason a priori why an identity element might not be ‘partial’ in the sense that the presence of a sequence feature restricts the identity of a tRNA to some subset of possible identities. An obvious example of such ‘partial’ determinants is at the classical ‘discriminator’ base position, position 73 (7). Long recognized as an important site contributing to the identity of many classes of tRNAs, it is nonetheless impossible to completely specify among 20 categories with only four states. Using logical implications, we can represent partial identity determinants by the relation S_l ⇔ T, where $T\subset \mathcal{Y}$ is a subset of the possible identities of a tRNA. Such a partial determinant can also be incompletely represented by a simple implication, namely y ⇒ S_l, where y ∈ T.

A fourth aspect of this prior work is not so much a limitation as a tradeoff: when it was done, not much data were available, especially of complete tRNAs for all amino acid classes in the same species. By restricting analysis to a taxonomically limited dataset, the authors recognized that tRNA identity codes evolve and diverge. They could be confident that they were analyzing tRNAs that truly co-exist and function together in the same cell and according to a homogeneous and consistent identity code. Unfortunately this also meant that their sample sizes were small: the identity rules they describe are likely to contain false positives, feature sets that are private to classes by chance alone. Their method does not account for such sampling effects. One way to overcome this problem is to use more data, but when this comes from increasingly diverse species, we become less certain that their identity codes are homogeneous.

We can address all these limitations by taking a fully probabilistic approach to tRNA identity, based on conditional probabilities. For instance, the probabilistic analog to the logical implication S_l ⇒ y is the statement of conditional probability p(y|S_l) = 1. By relaxing the assumption that features S_l must be perfectly correlated with identity classes y and so consider features for which p(y|S_l) < 1, we can consider partial identity elements and also gain a quantifiable robustness to errors and mutations. Using the probabilistic framework of information theory (see Methods), we can also begin to take into account sampling effects.

Sequence logos

We return to the problem we started with: how to find which features confer a specific function to a biological macromolecule. A simplification arises in this problem when considering only one functional class at a time, to which a sequence either belongs or does not belong. For instance, a sequence could be thought of as either binding RNA polymerase with some threshold affinity, or not. In this case, a popular approach is to structurally align sequences that have the function of interest and compare this alignment to a general model of sequences that lack the function, and calculate information statistics based on the Shannon Entropy (8). What is compared are the relative frequencies p_l(x|y) of specific nucleotides or amino acid residues (‘states’) x at specific alignment positions l (i.e. ‘features’) in some structurally aligned functional sequence class y, say at each site in a Pribnow box, to those relative frequencies p(x) in the model, say the nucleotide composition of a genome, where 0 ≤ p(x), p_l(x|y) ≤ 1, ${\sum }_{x\in \mathcal{X}}p\left(x\right)=1$ and ${\sum }_{x\in \mathcal{X}}{p}_l\left(x\right|y)=1$. The information that functional class y confers about the frequencies of states $\mathcal{X}$ at position l is then

$$I_l\left(\mathcal{X}\right|y)=H(\mathcal{X})-e(n\left(y\right))-H_l(\mathcal{X}\left|y\right),$$

where $\mathcal{X}$ is the universe of possible states, $H\left(\mathcal{X}\right)=-{\sum }_{x\in \mathcal{X}}p\left(x\right){log}_2\left(p\right(x\left)\right)$ is the ‘background’ state entropy, $H_l\left(\mathcal{X}\right|y)=-{\sum }_{x\in \mathcal{X}}{p}_l(x\left|y\right){log}_2\left(p_l\right(x\left|y\right))$ is the state entropy at position l among sequences in class y, and e(n(y)) is a correction factor that depends on the size of the sample of sequences of class y. This statistic is commonly visualized as a ‘sequence logo’, (9) a stacked bar graph with position on the x-axis, information on the y-axis, and where each element in every stack is a symbol for each of the states $x\in \mathcal{X}$, with a height h_l(x|y) proportional to the frequency of that state at that position in class y, h_l(x|y) = p_l(x|y)I_l($\mathcal{X}$|y). Additionally, the symbols in a stack are sorted by their height so that the tallest (most frequent) symbols in a stack are at the top.

Gorodkin et al. (10) redefined the heights h_l(x|y) in a way better suited to a highly biased (different from uniform) background distribution. The advantage of their approach is that it corrects for when the background distribution is highly biased, and consequently the most frequent features may not be the most informative. In their redefinition, the height of a feature is proportional to the odds, relative to other possible states at that position, of a feature in the functional class versus the background. More formally, the height of state x at position l is $h_l\left(x\right|y)=(p_l\left(x\right|y)/p(x))/\left({\sum }_{w\in \mathcal{X}}{p}_l\right(w\left|y\right)/p\left(w\right))I_l\left(\mathcal{X}\right|y)$. Stack symbols are sorted by their heights as before.

The sequence logo is a very effective visualization, because the reader's eye is drawn to where the state distribution is most different in the alignment from the background distribution. The stacks of symbols are tallest where there is the most information. The tops of the logos can be read like a consensus sequence, while additional information is shown about the relative frequencies of other states. Not only ‘conservation’—high frequencies of particular states—is important, but also the distribution of a background relative to a model, i.e. biased background state compositions are accounted for. Finally, the sample correction e(n(y)) helps distinguish truly informative state distributions from violations of continuity due to small sample sizes.

Despite the advantages of the sequence logo, it is not ideally suited to the general problem stated above, where multiple classes of structurally related sequences are to be compared, and the unique features that distinguish them are to be found. The reason is that unique features distinguishing individual classes of sequences from each other may be washed out by features that distinguish all classes from the background model. If we looked at a sequence logo for each of the classes individually, a lot of redundant information would be presented, and the more different classes are compared, the harder it is to see what makes each class unique.

Another limitation is that sequence logos are best for showing over-represented features, when under-represented features—features less common than expected—might be of interest. For instance, perhaps in a particular class of transcription-factor binding sites in DNA, a particular position tolerates ‘any base but G’. In the context of tRNA identity, such features may be antideterminants that prevent recognition or catalysis of amino acid addition to tRNAs with specific synthetases.

Here, we introduce two generalizations to sequence logos that address these limitations: function logos and inverse logos. Function logos display features that distinguish a functional subclass within a superfamily of structurally related sequences. Inverse logos display features or functions that are under-represented rather than over-represented. We demonstrate the utility of function logos and inverse function logos by applying them to the visualization of tRNA determinants and antideterminants.

METHODS

Function logos

To define function logos, first note that in a regular sequence logo, which we also call a ‘state feature logo’, information about states for an implicit functional class y of sequences is visualized. In the function logo, we invert the traditional roles of sequence state features and functional classes: the function logo displays information about function for an implicit state x (which at any position implies a feature). In practice, we make a different function logo for each of the possible states that a sequence can have at a particular position. We then calculate the information a given feature carries about the frequencies of various functional classes that sequences can belong to.

More formally, recall that we denote by $\mathcal{Y}$ the universe of all possible functional classes of a sequence. The ‘functional information’ $I_l\left(\mathcal{Y}\right|x)$ that state x confers about the frequencies of sequences of different classes $\mathcal{Y}$ at position l is then

$$I_l\left(\mathcal{Y}\right|x)=H(\mathcal{Y})-e(n_l\left(x\right))-H_l(\mathcal{Y}\left|x\right),$$

where $H_l\left(\mathcal{Y}\right|x)=-{\sum }_{y\in \mathcal{Y}}{p}_l(y\left|x\right){log}_2\left(p_l\right(y\left|x\right))$ is the class entropy among sequences that carry state x at position l, $H\left(\mathcal{Y}\right)=-{\sum }_{y\in \mathcal{Y}}p\left(y\right)$ log₂(p(y)) is the ‘background’ class entropy that depends on the relative proportions of sequences belonging to different classes, 0 ≤ p(y), p_l(y|x) ≤ 1, ${\sum }_{y\in \mathcal{Y}}p\left(y\right)=1,{\sum }_{y\in \mathcal{Y}}{p}_l\left(y\right|x)=1$, and e(n_l(x)) is a correction factor that depends on the size n_l(x) of the sample of sequences that carry state x at position l.

As in a feature logo, the function logo plots functional information as a stacked bar graph with position on the x-axis, and information on the y-axis, in which each element in every stack is a symbol for each of the classes $y\in \mathcal{Y}$. We adopt Gorodkin et al.'s (10) definition for symbol heights for our function logos, so that the height h_l(y|x) of class symbol y at position l is $h_l\left(y\right|x)=(p_l\left(y\right|x)/p(y))/\left({\sum }_{w\in \mathcal{Y}}{p}_l\right(w\left|x\right)/p\left(w\right))I_l\left(\mathcal{Y}\right|x)$. Stack symbols are sorted by their heights as before.

Inverse logos

To visualize the absence or scarcity of features or functions in the logo framework, we introduce the ‘inverse logo’. The inverse logo is a logo, either a state logo or a function logo as defined above, where the relevant frequency distributions have been transformed so as to make small frequencies large and large frequencies small. We compared two different transforms of frequency distributions for the purpose of making inverse logos:

The reciprocal transform,

$$\begin{array}{c}{p}_l^{\prime }\left(y\right|x)=(\left(p_l\right(y\left|x\right)n_l\left(x\right)+q_l\left(x\right){)}^{-1})/\\ {\displaystyle \sum _{y\in \mathcal{Y}}}{\left(p_l\right(y\left|x\right)n_l\left(x\right)+q_l\left(x\right))}^{-1}\end{array}$$

and

$$p\prime \left(y\right)=(\left(p\right(y)n+q{)}^{-1})/{\displaystyle \sum _{y\in \mathcal{Y}}}\left(p\right(y)n+q{)}^{-1},$$

where n_l(x) is the number of sequences carrying state x at position $l,n={\sum }_{x\in \mathcal{X}}{n}_l\left(x\right)$ is the total number of sequences, and q_l(x) (q) is a ‘pseudocount constant’ equal to 0 if ${min}_{y\in \mathcal{Y}}{p}_l\left(y\right|x)>0({min}_{y\in \mathcal{Y}}p\left(y\right)>0)$ and 1 otherwise. The pseudocount method estimates the probability of unobserved states in a sample-size dependent way (11); here, it is necessary to keep our transform mathematically valid even for truly zero conditional state probabilities, i.e. when p_l(y|x) = 0.

The simplex transform, 0

$$\begin{array}{c}{p}_l^{″}\left(y\right|x)=p_l(y\left|x\right)+\left({\displaystyle \underset{y\in \mathcal{Y}}{min}}{p}_l\right(y\left|x\right)-{\displaystyle \underset{y\in \mathcal{Y}}{max}}{p}_l\left(y\right|x\left)\right)/\\ (1/|\mathcal{Y}|-{\displaystyle \underset{y\in \mathcal{Y}}{max}}{p}_l(y\left|x\right))(1/|\mathcal{Y}|-p_l(y\left|x\right)),\end{array}$$

and

$$\begin{array}{c}{p}^{″}\left(y\right)=p\left(y\right)+\left({\displaystyle \underset{y\in \mathcal{Y}}{min}}p\left(y\right)-{\displaystyle \underset{y\in \mathcal{Y}}{max}}p\left(y\right)\right)/\\ \left(1/\left|\mathcal{Y}\right|-{\displaystyle \underset{y\in \mathcal{Y}}{max}}p\left(y\right)\right)(1/|\mathcal{Y}|-p(y\left)\right).\end{array}$$

It is defined so that if $\langle p_l\left(y_1\right|x),p_l(y_2\left|x\right),\dots ,p_l\left(x_{\left|\mathcal{Y}\right|}\right|x)\rangle$ is represented as a point in the $\left(\right|\mathcal{Y}\left|-1\right)$-simplex, then $\langle p_l^{″}\left(y_1\right|x)$, $p_l^{″}\left(y_2\right|x),\dots ,p^{″}(y_{\left|\mathcal{Y}\right|}\left|x\right)\rangle$ is the point along the extension of the line between $\langle p_1\left(y_1\right|x),p_1(y_2\left|x\right),\dots ,p_1\left(y_{\left|\mathcal{Y}\right|}\right|x)\rangle$ and the barycenter, $\langle 1/\left|\mathcal{Y}\right|,1/\left|\mathcal{Y}\right|,\dots ,1/\left|\mathcal{Y}\right|\rangle$, with a shortest distance to the simplex boundary equal to the shortest distance between $\langle p_l\left(y_1\right|x),p_l(y_2\left|x\right),\dots ,p_l\left(y_{\left|\mathcal{Y}\right|}\right|x)\rangle$ and the boundary, such that $arg {max}_i{p}_l^{″}\left(y_i\right|x)=arg {min}_i{p}_l(y_i\left|x\right)$.

tRNA sequence data

In order to attack the problem of visualizing and detecting putative tRNA identity determinants and antideterminants with function logos and inverse function logos, we analyzed a dataset of 655 nonredundant inferred and actual tDNAs from bacteria called the Modified Sprinzl tRNA Database (MSDB) which also forms the basis of a recently introduced automated classifier of tRNA identity called TFAM (12). TFAM relies on what we call ‘profile contrast models’ that are built from the MSDB sequences, that are annotated with good confidence to belong to one of 21 functional classes. That is, in addition to the 20 canonical charging identities, the MSDB contains a separate model for initiator tRNAs. Thus, we have generalized the identity element concept slightly to include initiators as a separate functional class.

In constructing the MSDB, redundant sequences—whatever their possible origin—are removed and certain identity classifications are corrected as detailed in (12). tRNAs in the MSDB come primarily from bacteria related to E.coli and Bacillus subtilis, i.e. γ-proteo-bacteria and low-GC gram-positives, although more distantly related bacteria are also represented. Also described are that the identity annotations for Isoleucine versus Methionine and Alanine versus Valine identity are less reliable than for the other identity classes. Because tRNAs have such highly conserved secondary and tertiary structures, structurally analogous positions within each sequence may be assigned with high confidence, corresponding to a structural alignment that may be indexed in various ways. One such structurally based positional index is curated in the Sprinzl database (13–15) (http://www.staff.uni-bayreuth.de/~btc914/search/index.html), resulting in a widely used coordinate numbering system that can be applied to nearly any tRNA. MSDB uses automatically generated structural alignments of tRNAs made by COVEA (16) from a curated Stochastic Context-Free Grammar model of tRNAs (17). The MSDB alignment is provided in Supplementary Data.

We applied our new definitions of the function logo and inverse function logo to the MSDB. Denoting the possible identity classes by either the one-letter IUPAC amino acid codes (corresponding to their amino acid charging identities) or by the letter ‘X’ (indicating initiator tRNA identity) the class sizes in the MSDB are A = 52, C = 13, D = 21, E = 23, F = 22, G = 45, H = 15, I = 61, K = 22, L = 63, M = 14, N = 21, P = 28, Q = 19, R = 48, S = 53, T = 43, V = 26, W = 18, X = 28 and Y = 20.

As in TFAM, the tRNAs in this dataset were automatically aligned by primary and secondary structural features using COVEA (16) with the prokaryotic tRNA SCFG model called ‘TRNA2-prok.cm’ that comes with tRNAscan-SE (17). The length of this tDNA alignment was 106. After alignment, subalignments were partitioned off by the tRNA functional classes, and converted into profile matrices. Gaps are treated as a fifth state, so the sizes of these matrices are 5 × 106. These profile matrices are also provided in Supplementary Data.

In interpreting our results we assigned as many of the 106 columns as possible a number from the standardized tRNA positional numbering system (13–15). We followed (18) in annotating an anticodon stem of 5 bp instead of 6 in our figures. Positional numbers in the text refer to Sprinzl coordinates.

Variable arm

There are two ‘types’ of tRNAs, types I and II, that are distinguished by the presence or absence of a fifth large stem–loop at the so-called ‘variable arm’ (19). Type II tRNAs carry this large extra stem–loop structure and comprise three functional classes: L, S and Y. Type I tRNAs lack a long variable stem. In the MSDB, we found that two type I tRNAs, K and Q, carried slightly longer variable stems than other type I tRNAs, though not as long as in the type II tRNAs. Because only these five classes have a long variable stem, information computed based on the same background frequencies as for the rest of the sequence will be very high in the variable region, reflecting this structural difference about which we already know. Because instead we wish to analyze features that distinguish among the five classes S, L, K, Q and Y in the variable region, we have selectively renormalized the data in this region based on only these five classes. That is, we assume that only S, L, Q, K and Y frequencies are allowed at variable region stem base pairs e11:e21 to e17:e27 and loop c1 to c5 (in the Sprinzl nomenclature, positions 55–73 in our alignment), and background frequencies for the five classes are adjusted to sum to 1.

Logo generation

The program MAKELOGO from the Delila package (20) accepts as input a ‘symvec’ file containing parameters and option settings. The problems of implementing function logos and inverse function logos from the tDNA profile matrices were reduced to generating appropriate symvec files for input to MAKELOGO. This is performed with a general-purpose logo generation package called LOGOFUN, available for download from http://logofun.lcb.uu.se or from Supplementary Data. Additional tools specific to making tRNA logos are also available in Supplementary Data or http://www.lcb.uu.se/~dave/tRNALOGOFUN.

For both logos, both inside and outside the variable loop, we calculated expected background entropies based on the relative class sizes. For sample sizes up to and including 10 the entropy was computed exactly using a Perl script written for this purpose (provided in Supplementary Data). For larger class sizes, the entropy was approximated. A description of both the exact and approximate calculations can be obtained from (8). We improved the performance of the exact method slightly over the implementation suggested in (8), for generating all possible compositions, by reference to section 7.2.1.3 exercise 3 in (21). For the function logos, we could bound the approximation error at <5% for the results shown here.

MAKELOGO calculates symbol heights from integer frequencies in the symvec file. Therefore, in order to make inverse function logos, we applied the floor function to the transformed frequencies $p_l^{\prime }\left(y\right|x\left)n_l\right(x)$ and p′(y)n, where n_l(x) and n are defined as before, to scale them approximately into integers. Error bars indicate 1 SD, where the standard deviation is computed exactly for a sample size of 10 or less and approximately for larger sample sizes by (k − 1)/n ln 4 where k is the number of classes and n is the sample size. Logos are scaled by their maximum information values which is 4.2175 bits in the function logo and 4.2469 bits in the inverse function logo. Because of renormalization, the maximum information for the variable region is lower. For the function logo 2.1263 bits is the maximum for the variable region and for the inverse function logo the maximum is 2.1722 bits.

RESULTS

We have introduced two generalizations to sequence logos motivated by the problem of visualizing and predicting tRNA determinants and antideterminants. Function logos are designed to display distinguishing features of a functional subclass within a sequence superfamily, and this addresses the problem of visualizing tRNA identity determinants. Inverse logos display sequence features or functions that are under-represented in a set of sequences, and this is suited to visualizing tRNA identity antideterminants.

Function logos and bacterial tRNA determinants

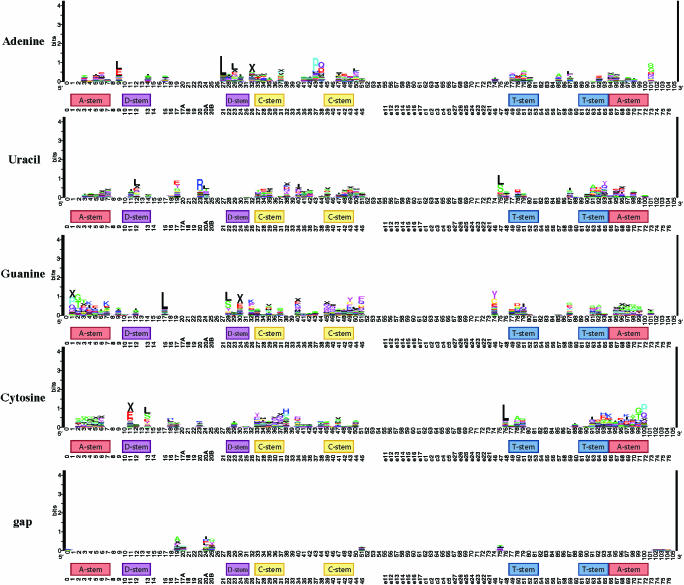
Figure 1 shows five function logos (one for each of the five possible sequence states in aligned DNA sequences including gap) for structurally aligned tDNAs from the Modified Sprinzl Database (MSDB) (12). Presented in this way, the function logos give a highly condensed visualization of very many, if not all, potential bacterial tRNA identity determinants simultaneously.

Figure 1.

Function logos of potential identity determinants among bacterial tDNAs in the structurally aligned Modified Sprinzl Database (12). There is one function logo for each of the five possible states in an RNA alignment; Thymine is represented as Uracil. Letters show tRNA classes associated with the given sequence state at the respective position given by the x-axis. Annotating the x-axis in addition to position in our structural alignment are the locations of the standard stems and the Sprinzl position indexing (13). See text for more detail.

This comprehensive view in Figure 1 shows clearly that most stacks carry more than one letter of appreciable height. So-called ‘mixed stacks’ imply that, from the perspective of primary structural associations, most determinants are ‘partial’, i.e. that they are either shared by more than one identity class, or that the identity associated with them has changed during the divergence of bacterial lineages. The best-known example of a conserved ‘partial’ identity determinant is discriminator position 73. Many of the better-understood determinants in the acceptor stem and anticodon are effectively visualized and show this partial-identity nature.

Many of the putative partial identity elements identified by this method are known to the literature for one of the classes but not the others. Let us turn to examples in the D-stem and loop and its structurally connected bases, since there are fewer proven associations with identity at this location and they are rarer. The unusual importance of D-stem and loop residues for Glu identity (22) is prominently displayed in Figure 1. Many of them individually, however, are shared with other identity classes. For instance, the absence of residue 47 is considered a Glu determinant because it probably helps maintain a U13.G22..A46 base triple likely to be important for structural recognition by GluRS (22). Three of the above four mentioned features, gap47, U13 and A46, are visible in the function logo as associated with tRNA^Glu, but none of them individually is unique to tRNA^Glu. To varying degrees, type II tRNAs with Leu and Ser identities as well as other type I tRNAs with Gly, Gln, Cys and Trp identities can share the absence of residue 47. G22 is not visible at all indicating that, taken alone, it is not particularly associated with any class of tRNA.

There are also cases where Figure 1 points to partial identity elements where both associations have been independently proven in the literature, but their overlapping nature has not been widely publicized. For instance, while G20 was identified as an important Ala determinant in the variable pocket (23), its importance in Val identity was more recently reported (24). Figure 1 shows this feature very strongly associated with both amino acids.

A caution in interpreting function logos: although there is a correction for sample size (which reduces the size of the overall stack if the total number of sequences carrying a feature is small), the logo can show associations that only pertain to some, but not necessarily all, of the sequences in a functional class. So long as the absolute number of sequences carrying a structural idiosyncrasy is large enough and tends to associate with particular classes, it will be visible in the function logo. Thus, as in all methods for data exploration, an investigator using function logos should follow up interesting signals by closely examining the raw data, and—ultimately—by experiments. There are at least two examples of such idiosyncrasies in Figure 1. One example revealed an exceptional subset of tRNAs in the MSDB, known to the literature but which we had previously not been aware of. On the basis of what is known about them, their structural idiosyncrasies probably do not affect their charging identity, but likely completely disrupt their competence for translational elongation. In another example, we have found a subset of tRNAs that have recently diverged in an otherwise highly conserved tRNA structure, which appears in two bacterial lineages and is conserved in one of them. Unlike the first example, the second example appears unknown to the literature and is a candidate for a derived identity determinant.

The first example concerns gap18 and gap19 in the D-loop and G55 in the T-loop, all apparently associated with Gly identity. In fact, only five or six tRNA^Gly or tDNA^Gly (of 45) carry these characters. Five sequences, three tDNAs and two tRNA sequences, carry all three characters, and one tDNA carries only G55. These positions are highly conserved in other tRNAs which normally carry G18 pairing with pseudouridine at position 55 and G19 pairing with C56, all to stabilize the loop–loop interaction responsible for the core fold of tRNAs. The three tDNAs with all three characters come from Staphylococcus aureus which are thought, because of sequence similarities to the two tRNAs in our dataset from S.epidermis (25) and by other evidence, to be involved in peptidoglycan synthesis of the cell wall and not involved in peptide synthesis (26). These authors note the unusual G55 character but not the absence of G18 and G19 plainly visible in Figure 1. An additional tRNA in the MSDB carries G55, from Streptomyces lividans but carries the normal G18 and G19. Similar to this example is the apparent association of gap1 with E and L identity. Two of 23 tDNA^Glu and two of 63 tDNA^Leu are the only four sequences in the whole dataset missing a base in this position in the MSDB. Although gap1 is infrequent even among the E and L classes, they are the only classes in the dataset with this property, and so they are over-represented. Thus, function logos are useful for screening structural idiosyncrasies belonging to particular classes of sequences, but caution must be taken in interpreting them.

The second example again concerns only a small part of the available data but nonetheless shows that function logos can yield interesting predictions of novel candidates for derived identity determinants. This concerns the association of C14 with Trp (Figure 1). Although this association concerns only two tDNA^Trp from Borrelia burgdorfori (27) and Helicobacter pylori (28), their presence is highly interesting as it comes at a nearly universally conserved place in tRNAs, namely the highly conserved U8:A14 base pair that stabilizes the core tRNA structural fold. We confirmed the presence of this highly unusual C14 feature in the respective genome sequences and found it to be additionally conserved in another sequenced H.pylori strain as well as in the related ε-proteobacterial species Campylobacter jejuni. In contrast with A14, U8 is conserved in these unusual tRNAs. This unusual feature was also noticed in a manual comparative screen of genomic tDNAs (29). We suggest that this feature should be examined as a potential Trp identity determinant in these species.

Structural idiosyncrasies also underlie the prominence of features associated with type II tRNAs in the D-loop (or variable pocket), such as A20a with Leu, A20b with Tyr and G20b with Ser identity. The association of A20 with Arg identity is well known (30). An important point is that the function logo method relies on a structural alignment in which structurally analogous components can reliably be assigned. With tRNAs, this begins to break down at the variable region and the so-called variable pocket that includes this part of the D-loop, and is nonetheless likely to be important in tRNA identity.

We found a discrepancy with a reported bacterial identity determinant in Serine. In E.coli, C11:G24 was reported to be an important Serine identity determinant (31) while in Figure 1 we see instead an association of C10:G25, which also associates with Tyr, Cys and Met identities. Indeed, according to Figure 1, the association with Tyr identity is slightly stronger than with Ser identity. A close inspection of the MSDB alignment confirms that C11:G24 is less conserved and less specific to Ser identity than C10:G25. Our result does not contradict that C11:G24 is a Ser identity element in E.coli, but suggests that it is not widely conserved as such.

The importance of base pairs in stems as identity elements points to both an interesting phenomenon and a limitation of the function logo. Unlike in the previous work due to McClain and co-workers, the function logo only represents base variation at the primary structural level. However, base pairs that are known to be associated with certain identity classes in E.coli, such as U1:A72 for Gln (30,32–35) or A1:U72 for Trp (36–39), are clearly visible in Figure 1. An exception is G3:U70 for Ala identity, one of the defining, most highly conserved Ala identity elements (30,40–43). Similar to G20 described above, very few features seem associated with Ala identity that are not also associated with Val identity, or other identities: take for instance A32, U70, C36 in the anticodon, and C60. However, both of these features G3 and U70 taken alone are not strongly associated with Ala identity. Unique features at the secondary structural level that are not strongly associated at the primary sequence level are not adequately seen. This explains the relatively high rate with which TFAM classifies tRNA^Val as tRNA^Ala. That this is an isolated case in the generally high performance of TFAM suggests that the primary structural approach we have taken to the study of identity determinants is quite informative for bacterial tRNAs. Another important point is that if tRNA^Ala and tRNA^Val share so many determinants (Figure 1) and are difficult to distinguish for an automated classifier, then it is likely that few mutations may be necessary to convert a tRNA^Val to an tRNA^Ala. Indeed, a genomic tDNA^Val from H.pylori was reported to contain G3 and T70 (29).

Inverse logos

In order to generate inverse logos we make use of a mathematical transform that manipulates frequency distributions to make frequent components rare and vice versa. We investigated two different transforms of positional frequency distributions for this purpose, the reciprocal transform and the simplex transform defined in the methods. For frequency distributions (otherwise called ‘compositions’) where all possible components are present, the reciprocal transform is identical to the ‘compositional inverse’ defined in the field of the statistical analysis of compositional data (44). We loosely call both the reciprocal and simplex transforms ‘compositional inverses’ in that they both take a composition and transform it into another composition in which rare frequencies are common and common frequencies rare. These transforms also have the following attractive properties: the application of such a transform twice yields the starting composition, and the uniform or unbiased composition, in which every component is equally frequent, is invariant under the application of such a transformation. The reciprocal transform is easy and intuitive to define but relies on pseudocounts to be well defined when compositions are missing a component. Pseudocounts distort such compositions in two ways: first, application of the reciprocal transform twice to a composition does not always give back the composition that was started with, and second, addition of pseudocounts reduces the information content of the composition, an effect that decreases in larger samples but is expected to weaken the signal in sequence or function logos. The simplex inverse solves both of these problems with the reciprocal transform. It always behaves like a true inverse and never reduces the information in the original composition, but it is more complicated to define.

We used constructed examples to investigate the performance of these two different inverses for the general purpose of making inverse logos. We found that even though the pseudocounts introduced by the reciprocal inverse to handle missing data lowers information contents for logos, it generally performs better than the simplex inverse which, while avoiding distortion from introduced pseudocounts, is much more sensitive to small variations among the states observed at high frequencies.

To illustrate the differences between these two transforms, consider an example with sequences that have only three states—$\mathcal{X}=\{A,B,C\}$—that occur in proportions p(A), p(B) and p(C). With three states, positional compositions and their inverses can be illustrated as points in a 2-simplex (a triangle) as shown in Figure 2, which plots the set of compositions listed in Table 1 and their corresponding reciprocal and simplex inverse compositions. The difference between the two inverses is most obvious for compositions that are completely missing state A (compositions 16–20). The reciprocal transform applied to these compositions generates inverse compositions that are all highly enriched in A, thereby losing information about the original relative proportions of B and C. The simplex transform, on the other hand, generates inverses that are more informative about the original ratio of B and C but less clearly indicate the original absence of A. Since it is the absence of A that we wish to capture in inverse logo, this suggested that the reciprocal transform may be better suited to the task.

Figure 2.

A geometric representation of how the simplex and reciprocal transforms map the different compositions of Table 1, which contain three components: A, B and C. In the 2-simplex with p(A) = 1 in the upper corner, p(B) = 1 in the lower left corner and p(C) = 1 in the lower right corner, the original data points are in black at the bottom of the figure and the transformed compositions are shown in color and labeled.

Table 1.

Hypothetical three-component data corresponding to Figure 2

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21
A	22	22	22	22	22	22	22	11	11	11	11	11	11	11	0	0	0	0	0	0	0
B	56	50	44	39	33	28	22	78	67	56	44	33	22	11	100	83	67	50	34	17	0
C	22	28	33	39	44	50	56	11	22	33	44	56	67	78	0	17	34	50	67	83	100

A data matrix describing a constructed dataset of 100 sequences with three possible states, A, B and C. The table shows the observed counts for the three states in each of 21 different sequence positions. The frequency distributions are illustrated in the simplex plot in Figure 2.

We then explored more directly the behavior of these transforms on logos and inverse logos made from hypothetical data with 21 states as in the tRNA identity function data we wished to analyze. The hypothetical frequency distributions for different positions that we analyzed are listed in Table 2, using a uniform background distribution. Figure 3 further illustrates important similarities and differences between the two transforms for making inverse logos. Positions 0–3 illustrate that both inverses correctly yield no signal with compositions containing only one component. Positions 4 and 5 show that when all but one component are present in equal proportions, that this is undetectable in a normal sequence logo but is clearly visualized in inverse logos. However, the reciprocal inverse results in a logo with less information and impact because of the use of pseudocounts. This effect of the pseudocount depends of course on the sample size. In this example the sample size is 420, and for smaller sample sizes the loss of information is even larger.

Table 2.

Hypothetical 21-state data plotted in Figure 3

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
A	420	0	0	0	0	21	0	1	4	20	14	42	400	380	340	300	260	220	180
C	0	420	0	0	21	21	17	16	16	20	16	42	1	2	4	6	8	10	12
D	0	0	420	0	21	21	19	19	24	20	24	42	1	2	4	6	8	10	12
E	0	0	0	420	21	21	15	15	22	20	22	42	1	2	4	6	8	10	12
F	0	0	0	0	21	21	26	26	18	20	18	42	1	2	4	6	8	10	12
G	0	0	0	0	21	21	18	18	26	20	26	42	1	2	4	6	8	10	12
H	0	0	0	0	21	21	21	21	24	20	24	42	1	2	4	6	8	10	12
I	0	0	0	0	21	21	23	23	19	20	17	42	1	2	4	6	8	10	12
K	0	0	0	0	21	21	25	25	17	20	17	42	1	2	4	6	8	10	12
L	0	0	0	0	21	0	16	16	22	20	20	42	1	2	4	6	8	10	12
M	0	0	0	0	21	21	27	27	21	20	21	0	1	2	4	6	8	10	12
N	0	0	0	0	21	21	20	20	25	20	25	0	1	2	4	6	8	10	12
P	0	0	0	0	21	21	21	21	22	20	22	0	1	2	4	6	8	10	12
Q	0	0	0	0	21	21	20	20	23	20	21	0	1	2	4	6	8	10	12
R	0	0	0	0	21	21	23	23	16	20	16	0	1	2	4	6	8	10	12
S	0	0	0	0	21	21	22	22	19	20	19	0	1	2	4	6	8	10	12
T	0	0	0	0	21	21	24	24	23	20	22	0	1	2	4	6	8	10	12
V	0	0	0	0	21	21	23	23	21	20	21	0	1	2	4	6	8	10	12
W	0	0	0	0	21	21	18	18	21	20	20	0	1	2	4	6	8	10	12
X	0	0	0	0	21	21	20	20	20	20	18	0	1	2	4	6	8	10	12
Y	0	0	0	0	21	21	22	22	17	20	17	0	1	2	4	6	8	10	12

A data matrix for a hypothetical dataset of functional class frequencies over 420 sequences of length 18. Logos based on this dataset are plotted in Figure 3.

Figure 3.

A comparison of the performance of the simplex and reciprocal transforms in generating inverse logos (center and right) from the hypothetical data listed in Table 2 and visualized in the original sequence logo shown on the left.

Positions 6 and 7 show very clearly why the reciprocal transform is preferable to the simplex transform despite the loss of information from the latter. The compositions in these positions are very much like those in positions 4, except that the nonzero components have been randomly perturbed by up to about 20%. Positions 6 and 7 carry 0 and 1 counts of component A, respectively. The inverse logo made from the reciprocal transform clearly shows the scarcity or absence of A, while this is completely illegible in the logo made with the simplex transform.

Positions 8 and 10 show that the ability to detect a single rare state drops off rapidly as they become more frequent, becoming in the logos like the unbiased composition in position 9. Position 11 shows that both sequence logos and inverse logos can effectively visualize compositions missing half their components. Positions 12–18 illustrate the effect of a majority component against other equally frequent minority components successively increasing in proportion (similar to the reciprocal inverse in positions 4–5), positions 12–18 clearly yield signals in the normal sequence logo. In position 18, the frequency of A is still 15 times larger than the frequency of any other component, yet the information at position 18 is quite small and the height of A is in fact less than the total height of the other states. Positions 17–18 are comparable with positions 4–7 in the reciprocal inverse logos, giving a sense of scale to the loss of information due to pseudocounts.

The tRNA functional classes in the MSDB are more like positions 6 and 7, than positions 4 and 5, i.e. when a class is strongly under-represented the other classes are observed at slightly varying frequencies. Therefore, despite the mathematical elegance of the simplex inverse, its more faithful representation of the original composition, and the loss of information that occurs in use of the reciprocal inverse, the latter more robustly yields stronger signals in inverse logos on real data.

tRNA antideterminants

Figure 4 shows an inverse function logo computed using the reciprocal transform derived from the modelsets in the MSDB. As with potential determinants visualized in Figure 1, the main result in Figure 4 is that most potential antideterminants visualized by this method are not unique to individual classes. Very little is known about bacterial antideterminants, so it is difficult to evaluate the effectiveness of this method. It is also clear in Figure 4 that any potential antideterminants we have detected with this method have relatively low information compared with potential determinants in Figure 1. Since most antideterminants we have visualized with this method are shared among multiple classes, many of the features we have identified could actually be determinants against the complementary classes of sequences we have identified with Figure 1. Known antideterminants do lie in the same positions as determinants in other systems. One example is the G3:U70 base pair which, aside from its action as an Ala determinant, is an antideterminant against Thr (45). The G3 feature is prominently displayed in Figure 4 as a Thr antideterminant, as well as against other identities. In parallel to the results in Figure 1, U70 is not. Figure 4 also presents a wealth of potentially new candidate antideterminants for further investigation.

Figure 4.

Inverse function logos of potential identity antideterminants among bacterial tDNAs in the structurally aligned Modified Sprinzl Database (12). There is one inverse function logo for each of the five possible states in an RNA alignment; Thymine is represented as Uracil. Letters show tRNA classes under-represented among sequences with the given sequence state at the respective position given by the x-axis. Annotating the x-axis in addition to position in our structural alignment are the locations of the standard stems and the Sprinzl position indexing (13). See text for more detail.

In addition to stack size, error bars are useful indicators of the sample sizes used to compute logo graphs. Supplementary Figures 1 and 2 show versions of Figures 1 and 4, respectively, with error bars indicating one standard deviation as is the common practice with logo graphs. Most of the features we have discussed have information that deviate from 0 by 2 SD.

DISCUSSION

The function logo approach to the tRNA identity problem, as in the previous logic-based approach, was able to predict as potential candidates both known and potentially new identity determinants and antideterminants. The function logos revealed many more interesting features than we discussed, some with quite strong functional associations, for which we could not find mention in the literature. Two examples are U1:A72 with Asn and U17a with both Pro and iMet (the initiator class). But the tRNA identity literature is vast and moves rapidly, however, and although the function logo is useful in synthesizing data for all functional classes of tRNAs, an interpretation of highly condensed data summaries like Figures 1 and 4 is perhaps best left to experts who specialize in individual classes.

The function logo method is an advance over previous bioinformatic efforts applied to tRNA identity because it handles partial identity determinants; it is robust to noise, errors and mutations; and it partly corrects for small size and unevenness in sampling. For instance, although we assume that the identity of each tRNA is known and correct, because the techniques have a fundamentally probabilistic basis, they are somewhat robust to nonsystematic errors or noise, both in the sequencing and the classification of the tDNAs that make up the MSDB.

To address the problem of visualizing antideterminants we introduced an inverse function logo. These could equally be used for inverse feature logos (standard sequence logos). So-called ‘inverse logos’ call most attention to positions where only one state or function is entirely missing and all other states or functions are present according to (a scaling of) their expected frequencies. In a normal logo, such frequency distributions would be hard to recognize and interpret. Thus, the inverse logo visualization is not redundant to the regular logo visualization, although there are exceptional cases where they can show the same results.

There are, however, several issues one must keep in mind when evaluating function logos. We discussed that mixed stacks, where more than one class appears associated with a feature, can imply either partial identity determinants or taxonomic variation in associated classes. That is, taxonomic variation in identity rules can look like partial identity determinants if a small number of functional variants are highly conserved among ancient lineages. This is more likely to appear in more taxonomically complex datasets such as the MSDB, in which low-GC gram-positives and proteobacteria are over-represented. The same possibilities apply when more than one feature appears to imply the same functional class, for instance, U9 and C9, which both seem to contribute to Glu (E) identity (Figure 1). In practice, though, we did not find this type of pattern overwhelmingly reflected in our data.

We emphasize that although error bars and overall stack height are meant to reduce distortions from sampling effects, such distortions are not completely avoided in the function logo. Another caution is that the size of a letter in a function logo should not be seen as proportional to its biochemical importance to identity nor even necessarily its evolutionary conservation, the latter since the mathematical inversion that underlies the definition of the function logo involves a renormalization over all sequences that carry a particular feature, the absolute number of which can be small. The strength of an association as measured by information (the size of a stack) is only an indicator of possible functional importance.

Because of the site-wise parsing of sequence variation in the function logo, what are considered major identity elements may not be as prominent as minor identity elements if the major elements partially overlap with identity elements in other classes and the minor elements are restricted to fewer functional classes. Context-dependent, higher-order dependencies of determinants on other determinants cannot be seen in the function logo. This is one area in which the feature set combinations studied by McClain et al. have an advantage. This comes, however, with the disadvantage that much more data is necessary to discriminate true high-order determinants from false positives.

All bioinformatic approaches are highly sensitive to the details of the alignments used. The function logo in particular will probably work best when a structure or substructure is highly conserved among the different functional classes being analyzed. Otherwise, the biological meaning of analyzing features assuming site-wise independence becomes less clear. This is apparent in the prominent appearance of type II tRNAs Tyr, Leu and Ser, and of the initiator tRNA in Figures 1 and 4, owing to their unique structural differences from other tRNAs. What we see in a function logo of course, are those structural differences that associate with particular classes, and when such structural differences do not contribute to their functional identity, we can be mislead by the function logo approach. It happens though, in the case of type II tRNAs, that their unique structural differences can play some role in their identity, naturally enough.

Which of the two types of ordinary logos, function logos or feature logos, is more convenient depends on the relative sizes of the number of possible states to the number of possible functions, and on the nature of the problem at hand. One motivation for function logos was to visualize the features that distinguish classes. With regular feature logos, finding features that are unique to specific classes involves detecting differences among multiple logos. If more than one state at a given position is over-represented in one functional class, then this information can be detected directly in a standard feature logo but requires comparison of multiple function logos. Obviously, if the number of states is much less than the number of functions, as is the case in the tRNA identity problem, function logos will be more convenient for the purposes of comparing logos.

Function logos, such as sequence logos, include corrections for biases due to uneven and finite sampling, but as currently formulated do not include corrections for phylogenetic dependencies in samples, nor do they detect the evolution of new or altered functions associated with features in taxonomically complex datasets. As such they can clearly be improved not only with respect to the tRNA identity problem but also in the general problem that we stated in the beginning of the paper. Nonetheless, we believe that our results prove that function logos and inverse logos can already be a useful tool for exploratory bioinformatic analysis of structure–function relationships in structurally related sequence families and superfamilies.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR online.