Is Arginine a Zwitterion in the Gas Phase?

It is well-known that amino acids exist as zwitterions in aqueous solution within a range of pH. Whether zwitterions exist in the absence of solvent has been extensively discussed in the literature.^1–6 In the gas phase, experimental evidence that glycine is not a zwitterion has been obtained by millimeter wave spectroscopy¹ and by measurements of substituent effects on gas-phase basicity.² In addition, the potential energy surface of isolated glycine has been thoroughly investigated by ab initio methods.^3,4 At the highest levels of theory, the zwitterion is ~16–20 kcal/mol less stable than the neutral with no barrier for proton transfer between the protonated amino and the deprotonated carboxyl groups.⁴ Calculations indicate that two water molecules complexed with glycine can stabilize the zwitterion; if the two water molecules are hydrogen bonded only to glycine, a barrier to proton transfer occurs although the zwitterion is still higher in energy than the neutral.^4d Results of Rizzo et al.⁵ indicate that electronically excited tryptophan formed in a supersonic jet is a zwitterion. Recently, evidence for salt-bridge interactions in gas-phase peptide ions has been reported.⁷ For example, the most stable form of protonated bradykinin (Arg-Pro-Pro-Gly-Phe-Ser-Pro-Phe-Arg) is one in which both terminal arginine residues are protonated and interact via the deprotonated carboxyl of the C-terminus.^7a Salt-bridge interactions can be significantly stabilized by intramolecular hydrogen bonding to polar groups, such as carbonyl oxygens, which provide the near equivalent of a solvent shell around the charges.⁸ Here, we present experimental evidence that protonated dimers of arginine are bound by a salt-bridge in the gas phase. Further, our calculations indicate that the most stable form of arginine itself is a zwitterion. We believe that this is the first evidence for a stable ground state zwitterion form of an amino acid in the absence of solvent.

The dissociation kinetics of proton-bound dimers of several amino acids were investigated with blackbody infrared radiative dissociation (BIRD) in a 2.7-T Fourier-transform mass spectrometer. These experiments are described elsewhere.⁹ Proton-bound dimers were formed by electrospray ionization and dissociated at cell temperatures ranging from 37 to 149 °C. Unimolecular rate constants are obtained from the slope of ln-{[D⁺]/([D⁺] + [F⁺])} vs time where [D⁺] and [F⁺] refer to the dimer ion abundance and sum of fragment ion abundances, respectively. The resulting Arrhenius plot for dissociation of these dimers is shown in Figure 1. The proton-bound dimer of Gly, (Gly_d), dissociates more slowly than both Ala_d and the methyl ester (ME) of Gly dimer itself (GlyME_d). The increased dissociation rates of the latter two ions are primarily due to their increased molecular size. This results in both an increased rate of blackbody photon absorption and an increased population above the threshold dissociation energy. A small difference in binding energy (<0.05 eV) or relative transition state entropy may also partially contribute to the different dissociation rates. Ala_d and the GlyME_d are isomers. Their similar dissociation kinetics indicate that these ions have comparable binding energies. In contrast, the dissociation kinetics of Arg_d and ArgME_d differ much more dramatically than those of Gly_d and GlyME_d (Figure 1).

Figure 1.

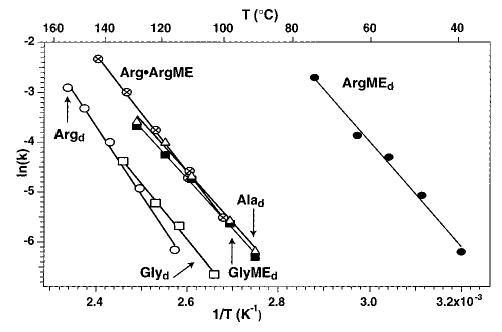
Arrhenius plot for the dissociation of the proton-bound dimer of (○) arginine, (□) glycine, (▪) glycine methyl ester, (▵) alanine, (⊕) arginine·arginine methyl ester, and (•) arginine methyl ester.

Threshold dissociation energies (E_o) can be extracted from these kinetic data by using master equation modeling, the method for which has been described in detail elsewhere.⁹ The results of this modeling are given in Table 1. Assuming a negligible reverse activation barrier for these dissociation processes, E_o can be equated to the binding energy. The dimers of Gly, Ala, and GlyME all have similar binding energies (1.10–1.15 ± 0.05 eV). The similar binding energy for Gly_d and its methyl ester indicates that the hydrogen of the carboxylic acid functional group does not play a role in the binding. This is consistent with the lowest energy ab initio structure in which the protonated N-terminus of one residue interacts with both the N-terminus nitrogen and the carbonyl oxygen of the other.⁹

Table 1.

Measured Arrhenius Activation Parameters of Proton-Bound Amino Acid Dimers and Methyl Esters (ME) Obtained by BIRD

dimer	measured Ea (eV)	measured log A	master eq Eo (eV)
Arg	1.19 ± 0.05	12.8 ± 0.6	1.33 ± 0.08
ArgME·Arg	1.01 ± 0.03	11.2 ± 0.3	1.20 ± 0.05
ArgME	0.91 ± 0.05	12.0 ± 0.8	1.05 ± 0.05
Gly	0.96 ± 0.04	10.0 ± 0.5	1.15 ± 0.05
GlyME	0.86 ± 0.03	9.3 ± 0.4	1.10 ± 0.05
Ala	0.88 ± 0.04	9.5 ± 0.4	1.10 ± 0.05

The binding energy of ArgME_d is slightly lower (1.05 ± 0.05 eV). The side-chain guanidine group is highly basic and is the expected site of protonation. Charge delocalization should occur to a more significant extent on the guanidine group than, for example, on the N-terminus. This delocalization should reduce the ion–dipole interaction, consistent with the decreased binding energy observed. The binding energies for Arg_d and Arg·ArgME are significantly higher (1.33 ± 0.08 and 1.20 ± 0.05 eV, respectively). We believe that the higher binding energies indicate that these dimers are bound by salt-bridges in which both guanidine groups are protonated and the carboxyl group of an Arg is deprotonated, i.e., one of the arginines in the dimer is a zwitterion (Figure 2, part a). The zwitterion form is not possible in ArgME_d. The significantly larger dipole moment of a zwitterion¹⁰ should increase the binding energy of these complexes.

Figure 2.

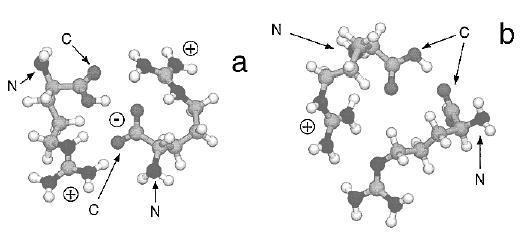
Minimum energy structures calculated at the AM1 semiempirical level of protonated arginine dimers modeled as (a) a salt-bridge in which both guanidine side chains are protonated and the carboxyl group of one is deprotonated, i.e., one arginine is a zwitterion, and (b) a simple proton-bound ion–molecule complex. The C- and N-terminus of each monomer is labeled.

The ~0.15 eV higher binding energy of Arg·ArgME vs ArgME_d is consistent with recent results for protonated complexes of betaine which show an increased binding energy of 0.2 eV when betaine is in its zwitterionic form.¹¹ We attribute the even higher binding energy of Arg_d to extra stabilization of the carboxylic acid group of protonated Arg which solvates the zwitterion (Figure 2a). This is consistent with results from both AM1 and PM3 semiempirical modeling which indicate only one stable structure for Arg_d but several different structures of comparable energy for Arg·ArgME (both modeled as salt-bridges). The existence of several structures for Arg·ArgME but not for Arg_d indicates that the amino and ester groups are less effective in stabilizing the zwitterion.

A zwitterion can be stabilized by a nearby charge, as is the case for the dimer. To determine if arginine by itself is a zwitterion, both the zwitterion and the neutral form were modeled at modest levels of theory.¹² At the BLYP/6-31G* level, the zwitterion is a stationary point and is 1.0 kcal/mol more stable than the neutral with the zero-point correction (0.4 kcal/mol without) (Figure 3). A different neutral conformer observed in the molecular modeling appears to be consistent with an intermediate structure for proton transfer (Figure 3). This conformer is a minimum on the potential energy surface and is 5 kcal/mol less stable than the zwitterion at the BLYP/6-31G* level. At the MP2/6-31G* level, the zwitterion is 0.3 kcal/mol more stable than the neutral form.¹³ We are not currently able to extend the calculations using a higher basis set for this relatively large molecule and have not achieved convergence. However, the excellent agreement between these two different computational methods provides significant support for the comparable stability of the zwitterion and neutral forms.¹³ A key problem with these calculations is the lowest energy neutral geometry may not have been found. However, the similarity in energy of these structures suggests that the zwitterion is likely to be stable in the gas phase.

Figure 3.

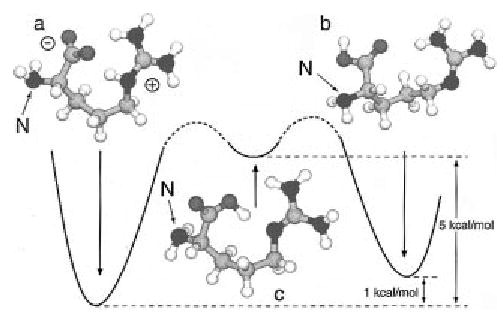
Optimized structures of arginine calculated at the BLYP/6-31G* ab initio level as (a) a zwitterion, (b) the lowest energy neutral conformation found, and (c) a higher energy stable conformer that is consistent with an intermediate to proton transfer from the carboxyl to the guanidine groups. The N-terminus of each structure is labeled.

In conclusion, these experimental results suggest that protonated dimers of arginine are bound by a salt-bridge in the gas phase. This type of interaction appears favored even without intramolecular self-solvation to stabilize the charge separation. For arginine itself, the high basicity of the guanidine side-chain functionality should stabilize the zwitterion vs neutral forms relative to these forms for glycine. Guanidine ((NH₂)₂C=NH) is ~21 kcal/mol more basic than glycine.¹⁴ This difference is larger than the calculated difference in stability between the glycine zwitterion and neutral forms. Thus, from basicity arguments alone, the guanidine side chain should be a competitive site of protonation relative to the carboxylate group making the zwitterion a potentially favored structure for arginine in the gas phase. This conclusion is supported by our ab initio calculations. These results suggest that uncharged arginine is an extremely interesting molecule in the gas phase and that both further measurement, e.g., absorption spectroscopy, and calculations at a higher level of theory are warranted.