The Mechanism of Hydroamination of Allenes, Alkynes, and Alkenes Catalyzed by Cyclopentadienyltitanium – Imido Complexes: A Density Functional Study

Considerable effort has been directed towards the development of procedures for hydroamination across carbon – carbon multiple bonds, and several catalytic systems for allene, alkyne, and alkene hydroamination have been investigated.[1] However, a general catalyst for the hydroamination of nonactivated unsaturated hydrocarbons remains elusive. A catalyst for the selective anti-Markovnikov addition of amines to terminal alkenes would be of particular interest [Eq. (1)].

(1).

Recent kinetic studies have been carried out to elucidate the mechanism of hydroamination catalyzed by cyclopenta-dienyltitanium complexes[2–5] such as the dimethyltitanocene 1 and the imido complex 2a (Scheme 1).[4, 5] Formation of the active monocyclopentadienyltitanium – imido species [CpTi=NR(NHR)] 3a (R = 2,6-Me₂C₆H₃) from both the pyridine adduct 2a and the precatalyst 1 has been established (Scheme 1).[4]

Scheme 1.

Generation of [CpTi=NR(NHR)] 3a from precatalyst [Cp₂TiMe₂] (1) and by equilibration with [CpTi=NR(NHR)py] 2a.[4]

Titanaazacyclobutenes and titanaazacyclobutanes are proposed as intermediates in the catalytic cycle,[2a, 4, 5] in analogy to the [Cp₂Zr(NHR)₂]-catalyzed hydroamination of alkynes[6] or the stoichiometric reaction of allenes with zirconium and titanium pyridine imido derivatives.[7] However, the mechanism of the protonation of the titanacycle by the amine is not well understood. Here we report high-level density functional model calculations on the intermediates involved in this step. The origin of the differences between the activation barriers in allene and alkyne versus the hypothetical alkene hydro-amination catalysis is also explored.

We used the B3LYP functionals,[8] a Hay – Wadt small-core effective-core potential on titanium,[9] and a triple-ζ plus polarization quality basis set[10] for geometry optimization and vibrational frequency analyses.[11] Since total electronic energies are not sufficient for the prediction of barriers for association and dissociation reactions at room or elevated temperature, zero-point vibrational energies and Gibbs free energy corrections have been included for all simplified compounds.

In earlier experimental studies on allene hydroamination, our group observed a first-order dependence on the concentration of catalyst 2a and allene substrate, a zero-order dependence on the 2,6-dimethylaniline concentration, and an inverse first-order rate dependence on the pyridine concentration.[4] The pyridine adduct 2a is stable in the presence of 2,6-dimethylaniline towards formation of species such as [CpTi(NHR)₃] (4a), dinuclear complexes such as 5 a, and free pyridine.[4] Pohlki and Doye observed that the rate of diphenylacetylene hydroamination depends on both the concentration of precatalyst 1 and 4-methylaniline.[5] Their kinetic analysis postulated the existence of preequilibria that inter-convert the active imido species with both titanium amides and dinuclear titanium complexes,[5] and this also explains the low reaction rates of sterically less hindered amines.[3]

We first studied the relative energies of potential catalyst resting states. The preference for pyridine ligation is indeed reproduced by the DFT calculations in the nonsimplified models 2a – 5a (Figure 1).

Figure 1.

Influence (see arrows) of the amide and imide substituents on the computed relative stabilities of CpTi complexes.

Although the computed strength of pyridine coordination to the simplified {CpTi=NH(NH₂)} fragment in 2b is weaker than the driving force for formation of trisamide 4b and dimer 5b, the steric congestion of three 2,6-dimethylanilide ligands at a titanium center inverts the relative stabilities. The computed steric influence of the amine substituents for the stabilities of the titanium species 3 to 5 strongly supports the interpretations of the Doye group.[5]

Next we studied the interaction of these titanium complexes with unsaturated hydrocarbons. The presumed active species 3b weakly coordinates to allene (Figure 2), ethyne (Figure 3), or ethene (Figure 4), and is predicted to undergo a facile [2+2] cycloaddition with each substrate.

Figure 2.

Allene hydroamination pathway: [2+2] cycloaddition, NH₃ coordination, ring inversion via 10, and intramolecular proton transfer.

Figure 3.

Ethyne hydroamination pathway: [2+2] cycloaddition, NH₃ coordination, and proton transfer.

Figure 4.

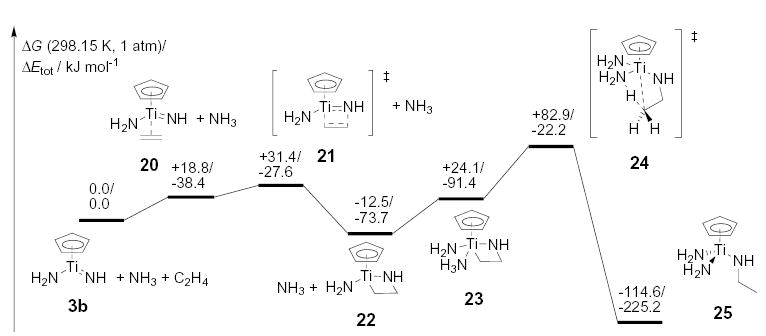
Hypothetical ethene hydroamination pathway: [2+2] cycloaddition, NH₃ coordination, and proton transfer.

Two pathways for the overall hydroamination reaction have been found for each of the hydrocarbon substrates.

1. Coordination of NH₃ and intramolecular proton transfer from the ammine ligand to a carbon atom (Figure 2 to 4).

2. Proton transfer from an amide ligand to a carbon atom without preceding amine coordination (Figure 5).

Figure 5.

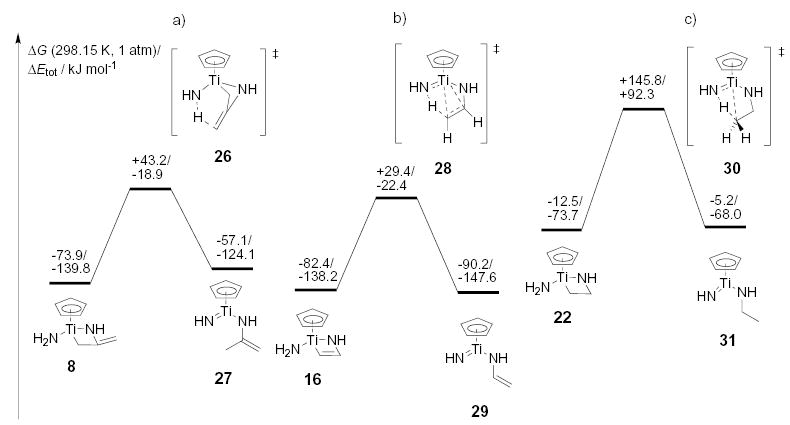
Alternative mechanistic pathways for proton transfer from an amide ligand: hydroamination of (a) allene, (b) ethyne, and (c) ethene.

The coordination of NH₃ in 11, 17, and 23 acidifies the ammine protons compared to those of free ammonia. This is reflected in NBO analyses, which reveal a charge transfer of −0.22 to −0.24 from the ammine ligand to the titanium fragment and a concomitant increase in negative net charge on the C1 carbon atom.[12]

In both the allene and the ethyne pathways, the presence of a vinylamine-type π system facilitates proton transfer. In the allene hydroamination cycle, a proton on the ammine ligand is transferred to the exo-methylene group. In a concerted reaction, the Ti–C3 bond cleaves (2.226 Å in 11, 2.369 Å in 12), the C1–C2 double bond character vanishes (1.358 Å in 11, 1.421 Å in 12), and a C2–C3 double bond is formed (1.475 Å in 11, 1.426 Å in 12; see Figure 2 and 3). In the ethyne pathway, coordination of NH₃ distorts the titanaazacyclobutene (17) (δ(Ti-C1-C2-N1) = 29.5°, see Figure 3). The resulting contribution of a mesomeric structure with a deprotonated dianionic η³-1-azaallyl ligand facilitates the proton transfer. As in the allene hydroamination pathway, the Ti–C bond is cleaved as the proton transfer proceeds (Figure 3).

We next studied the hypothetical ethene hydroamination. The Gibbs free dissociation energy of ethene from titanacycle 22 is computed to be more than 60 kJmol⁻¹ lower than for the corresponding allene or ethyne dissociation reaction. The NH₃ addition to the ethene adduct 22 is slightly disfavored by 10 to 15 kJmol⁻¹ compared to the NH₃ addition to the allene and ethyne analogues 11 and 17 (Figure 4). Furthermore, no π system is present in the titanacycle 23 and thus the σ Ti–C bond has to be directly protonated. As a consequence, the proton transfer is disfavored by an additional 25 to 30 kJmol⁻¹. Altogether, the proton transfer step in alkene hydroamination by CpTi – imido complexes is disfavored by about 100 kJmol⁻¹ compared to the corresponding allene and alkyne proton transfer steps.

Since the ammine complexes and their proton transfer transition states possess the highest coordination number at the respective titanium center in the catalytic cycle, they are especially sensitive to steric congestion. As a consequence, bulky amines and sterically demanding unsaturated substrates might support an electronically disfavored and entropically favored pathway without precoordination of amine, but rather with direct proton transfer from an amide ligand to a carbon atom. The computed energetics for these pathways are shown in Figure 5.

The predicted increase in electronic barriers for the amide protonation transfer compared to the barriers for the respective ammine proton transfer reactions results from the increased distortion of the core structures in the transition states and the lower acidity of the amide protons. Zero point vibration and entropic contributions lower the Gibbs free energy barrier difference between the two pathways to 54 – 63 kJmol⁻¹ by destabilizing the highly ordered ammine proton transfer transition states 12, 18, and 24. This difference could well be overcome by steric congestion induced by bulky substituents of amines and unsaturated hydrocarbon substrates. For comparison, the steric destabilization for complexes with three 2,6-dimethylanilide ligands at a titanium center such as in 4 a and 5a has been computed to be 67 – 78 kJmol⁻¹.

In allene and ethyne hydroamination with the simplified [CpTi=NH(NH₂)] system, where proton transfer takes place after initial amine coordination, the transition state for the cycloaddition is the highest point in the catalytic pathway and thus is rate-determining. However, it remains unclear whether the zero-order dependence on the 2,6-dimethylaniline concentration derived from the kinetic data for allene hydroamination[4] results from a rate-determining [2+2] cycloaddition or a rate-determining proton transfer from an amide ligand. A first-order dependence on the amine concentration can occur if the Gibbs free activation energy for the amine coordination plus proton transfer pathway is higher than the barrier for the initial [2+2] cycloaddition, but lower than the barrier for a competing amide proton transfer. A rate-determining amide ligand exchange with free amine could also result in such a rate law (see Supporting Information for computed ligand exchange pathways).

For alkene hydroamination, our model calculations predict that both the ammine and the amide proton transfer to the Ti–C bond have Gibbs free activation energies that are more than 50 kJmol⁻¹ higher than the cycloaddition step (Figure 4 and 5c). This explains the relative ease of allene and alkyne hydroamination compared to alkene hydroamination. Increasing the rate of this proton transfer step as well as stabilizing the metallaazacyclobutane intermediate compared to the catalyst resting state could be the key to making the alkene process successful. We are using these new insights into the hydroamination mechanism to isolate additional intermediates involved in the catalytic cycle, and to tailor more general hydroamination catalysts.