Abstract
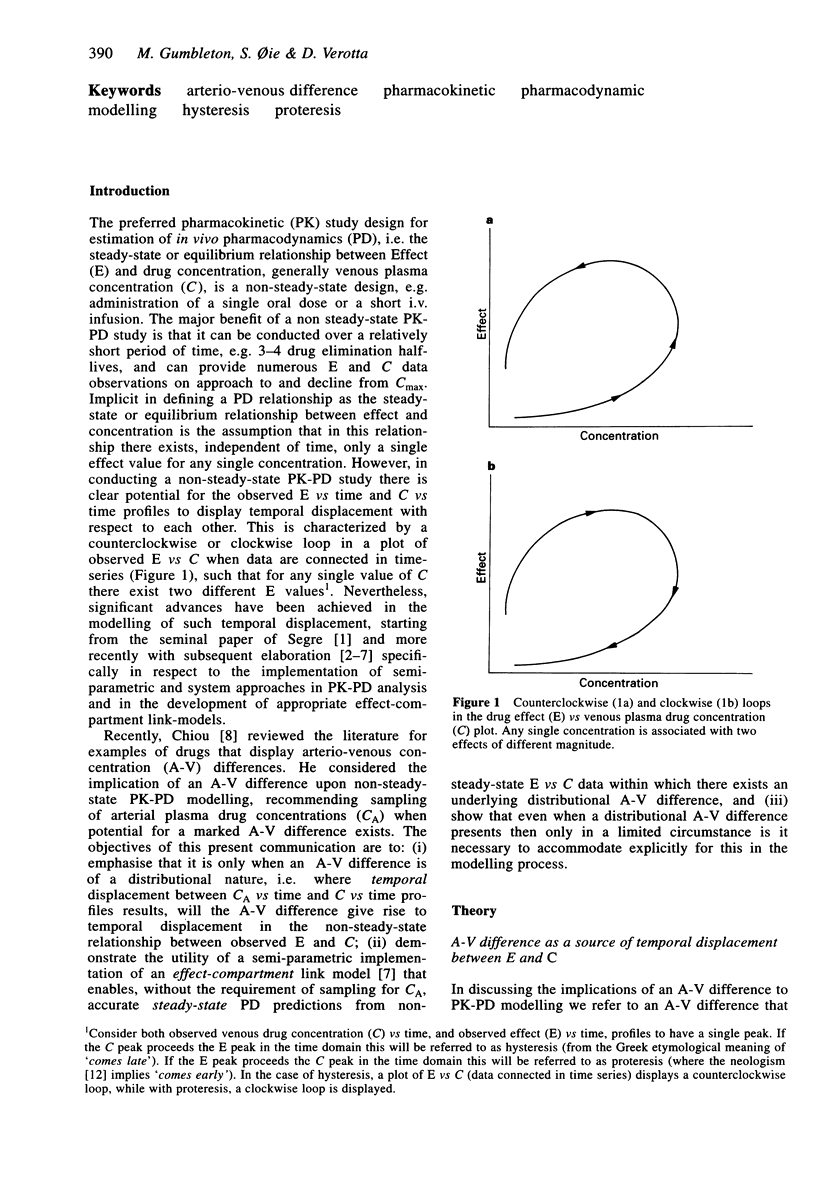
In conducting a non-steady-state pharmacokinetic (PK)-pharmacodynamic (PD) study there is potential for the observed effect (E) vs time, and venous plasma drug concentration (C) vs time, profiles to display temporal displacement with respect to each other. This is most frequently observed when there exists a distributional nonequilibrium across the effect organ giving rise to hysteresis, i.e. observed C preceding E in the time domain, with the resulting potential for a counterclockwise loop to be generated in the observed E vs C plot (when data are connected in time-order). Such temporal displacement does not afford direct prediction of the steady-state E vs C PD relationship. When an arterio-venous (A-V) difference exists across the tissues of the blood sampling compartment (i.e. the arm), and this arises solely from an elimination process then drug concentration in the respective peripheral arterial plasma and venous plasma compartments will be in equilibrium at all times during a non-steady-state PK experiment. If there are no other sources of temporal displacement in the relationship between E and C then the observed E vs C plot will be a direct predictor of the steady-state E vs C PD relationship. In contrast when the A-V difference is of a distributional nature then proteresis, i.e. observed E preceding C in the time domain, will arise with the potential for the generation of a clockwise loop in the observed E vs C relationship. Simulated error-incorporated E vs time, and C vs time, data was analysed by semi-parametric implementation of an effect-compartment link-model that affords accurate steady-state E vs C PD predictions (without the requirement of sampling arterial blood) from data that incorporates the concurrent presence of: (i) distributional nonequilibrium across the effect organ, and (ii) distributional A-V non-equilibrium. Accurate steady-state E vs C PD predictions were achieved irrespective of the comparative magnitudes of the two nonequilibria, i.e. whether the rate of equilibration across the effect organ was faster than, or slower than, the rate of equilibration across the arm (resulting in a clockwise or counterclockwise loop in the observed E vs C plot, respectively), or indeed if one or other of the nonequilibria is essentially absent. When the rate of equilibration across the effect organ is slower than the rate of A-V equilibration (i.e. counterclockwise loop generated in the observed E vs C plot) then the need to model for the underlying A-V nonequilibrium is redundant, i.e. accurate steady-state E vs C PD predictions can be achieved with implementation (strictly incorrectly) of a more simple link parameterised solely to model for distributional nonequilibrium across the effect organ.(ABSTRACT TRUNCATED AT 400 WORDS)
Full text
PDF










Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Campbell D. B. The use of kinetic-dynamic interactions in the evaluation of drugs. Psychopharmacology (Berl) 1990;100(4):433–450. doi: 10.1007/BF02243994. [DOI] [PubMed] [Google Scholar]
- Chiou W. L. The phenomenon and rationale of marked dependence of drug concentration on blood sampling site. Implications in pharmacokinetics, pharmacodynamics, toxicology and therapeutics (Part I). Clin Pharmacokinet. 1989 Sep;17(3):175–199. doi: 10.2165/00003088-198917030-00004. [DOI] [PubMed] [Google Scholar]
- Colburn W. A. Simultaneous pharmacokinetic and pharmacodynamic modeling. J Pharmacokinet Biopharm. 1981 Jun;9(3):367–388. doi: 10.1007/BF01059272. [DOI] [PubMed] [Google Scholar]
- Dayneka N. L., Garg V., Jusko W. J. Comparison of four basic models of indirect pharmacodynamic responses. J Pharmacokinet Biopharm. 1993 Aug;21(4):457–478. doi: 10.1007/BF01061691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuseau E., Sheiner L. B. Simultaneous modeling of pharmacokinetics and pharmacodynamics with a nonparametric pharmacodynamic model. Clin Pharmacol Ther. 1984 Jun;35(6):733–741. doi: 10.1038/clpt.1984.104. [DOI] [PubMed] [Google Scholar]
- Gupta S. K., Hwang S. S., Benet L. Z., Gumbleton M. Interpretation and utilization of effect and concentration data collected in an in vivo pharmacokinetic and in vitro pharmacodynamic study. Pharm Res. 1993 Jun;10(6):889–894. doi: 10.1023/a:1018969429535. [DOI] [PubMed] [Google Scholar]
- Mehvar R. Stereochemical considerations in pharmacodynamic modeling of chiral drugs. J Pharm Sci. 1992 Feb;81(2):199–200. doi: 10.1002/jps.2600810220. [DOI] [PubMed] [Google Scholar]
- Pedraz J. L., Calvo B., Smithers J. A., Thompson G. A. Pharmacokinetic-pharmacodynamic modeling: time-dependent protein binding--an alternative interpretation of clockwise and counterclockwise hysteresis. J Pharm Sci. 1992 Mar;81(3):232–236. doi: 10.1002/jps.2600810309. [DOI] [PubMed] [Google Scholar]
- Segre G. Kinetics of interaction between drugs and biological systems. Farmaco Sci. 1968 Oct;23(10):907–918. [PubMed] [Google Scholar]
- Veng-Pedersen P., Mandema J. W., Danhof M. A system approach to pharmacodynamics. III: An algorithm and computer program, COLAPS, for pharmacodynamic modeling. J Pharm Sci. 1991 May;80(5):488–495. doi: 10.1002/jps.2600800518. [DOI] [PubMed] [Google Scholar]
- Verotta D. Estimation and model selection in constrained deconvolution. Ann Biomed Eng. 1993 Nov-Dec;21(6):605–620. doi: 10.1007/BF02368641. [DOI] [PubMed] [Google Scholar]
- Verotta D., Sheiner L. B. Semiparametric analysis of non-steady-state pharmacodynamic data. J Pharmacokinet Biopharm. 1991 Dec;19(6):691–712. doi: 10.1007/BF01080874. [DOI] [PubMed] [Google Scholar]
- Verotta D., Sheiner L. B. Simultaneous modeling of pharmacokinetics and pharmacodynamics: an improved algorithm. Comput Appl Biosci. 1987 Nov;3(4):345–349. doi: 10.1093/bioinformatics/3.4.345. [DOI] [PubMed] [Google Scholar]
- Verotta D. Two constrained deconvolution methods using spline functions. J Pharmacokinet Biopharm. 1993 Oct;21(5):609–636. doi: 10.1007/BF01059117. [DOI] [PubMed] [Google Scholar]


