Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1961 Jul;1(6):445–466. doi: 10.1016/s0006-3495(61)86902-6

Impulses and Physiological States in Theoretical Models of Nerve Membrane

Richard FitzHugh
PMCID: PMC1366333  PMID: 19431309

Abstract

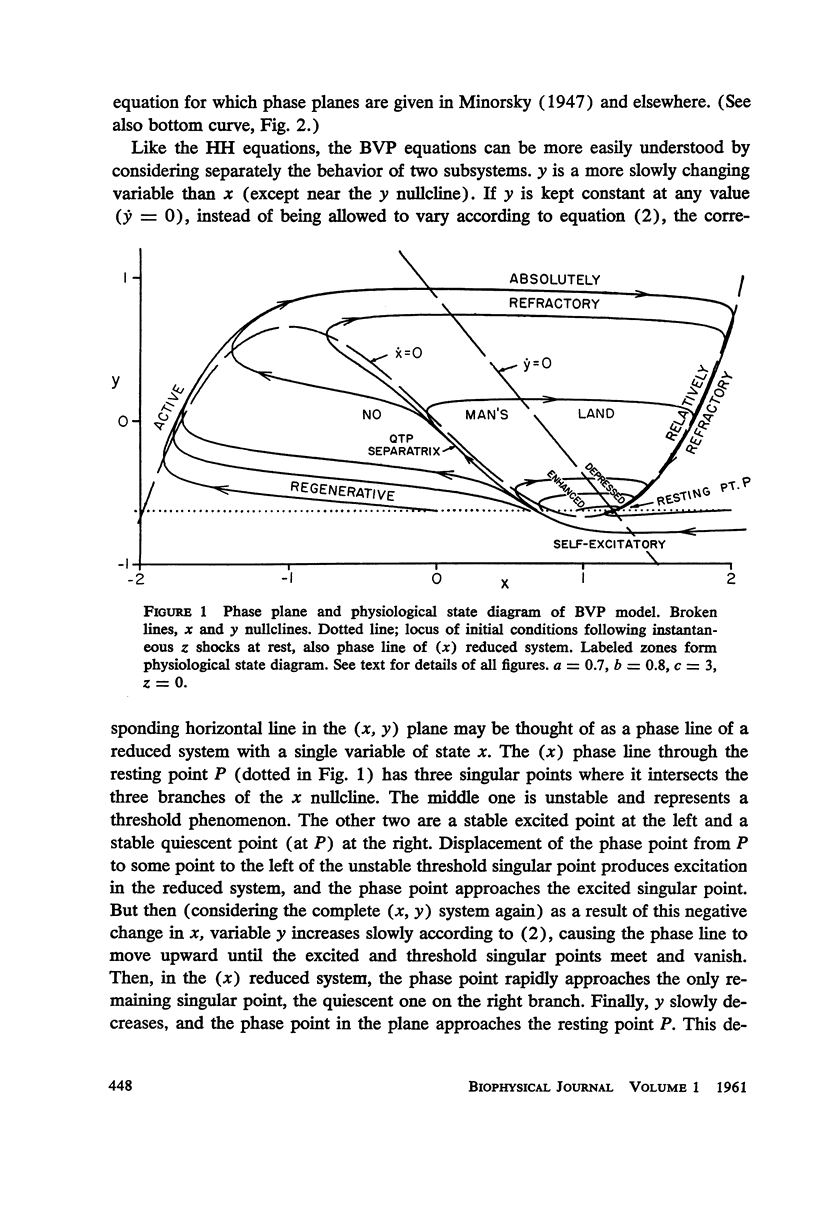
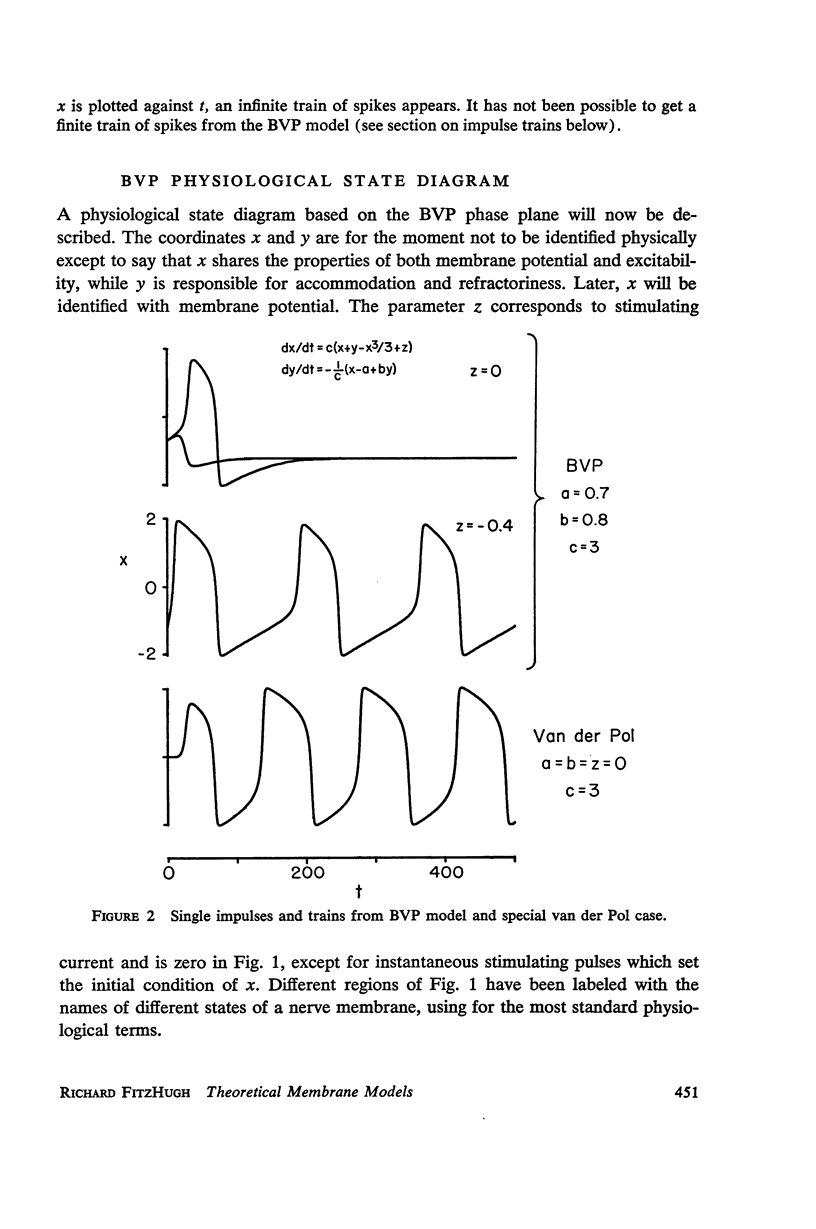
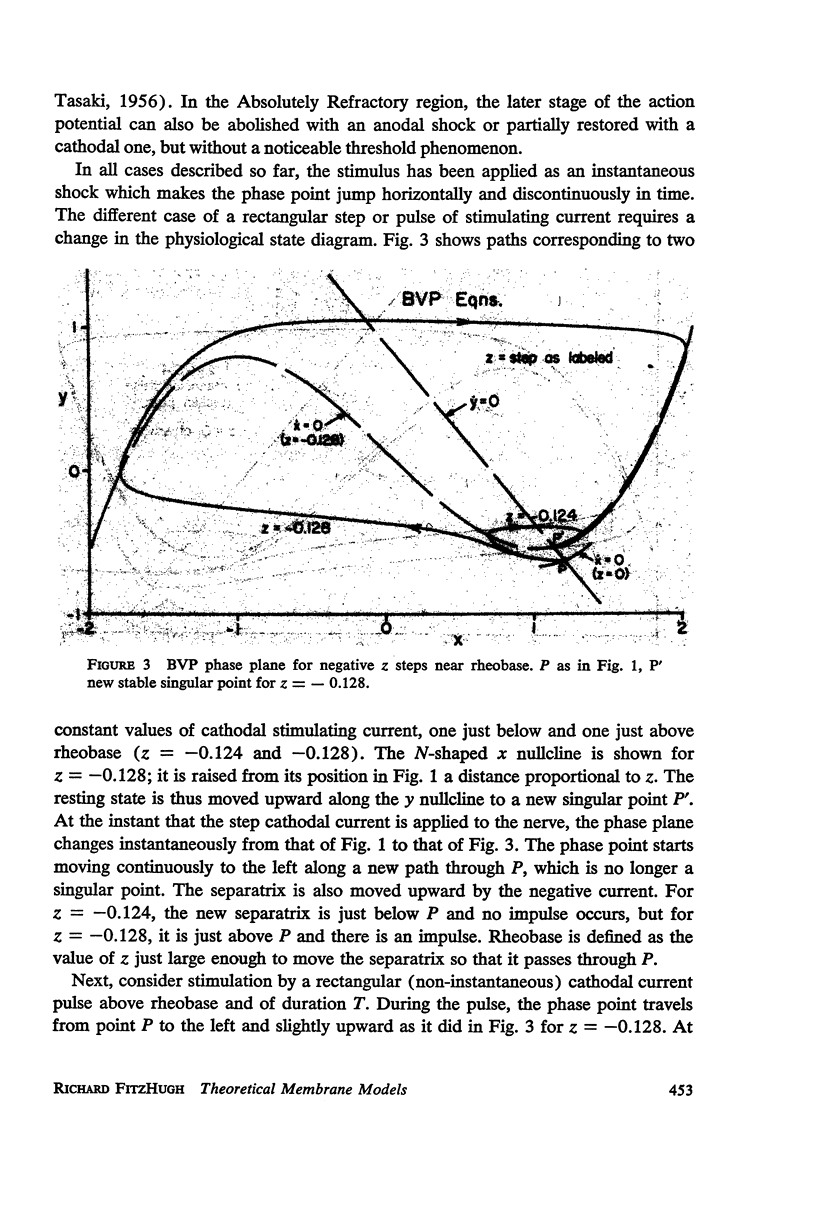
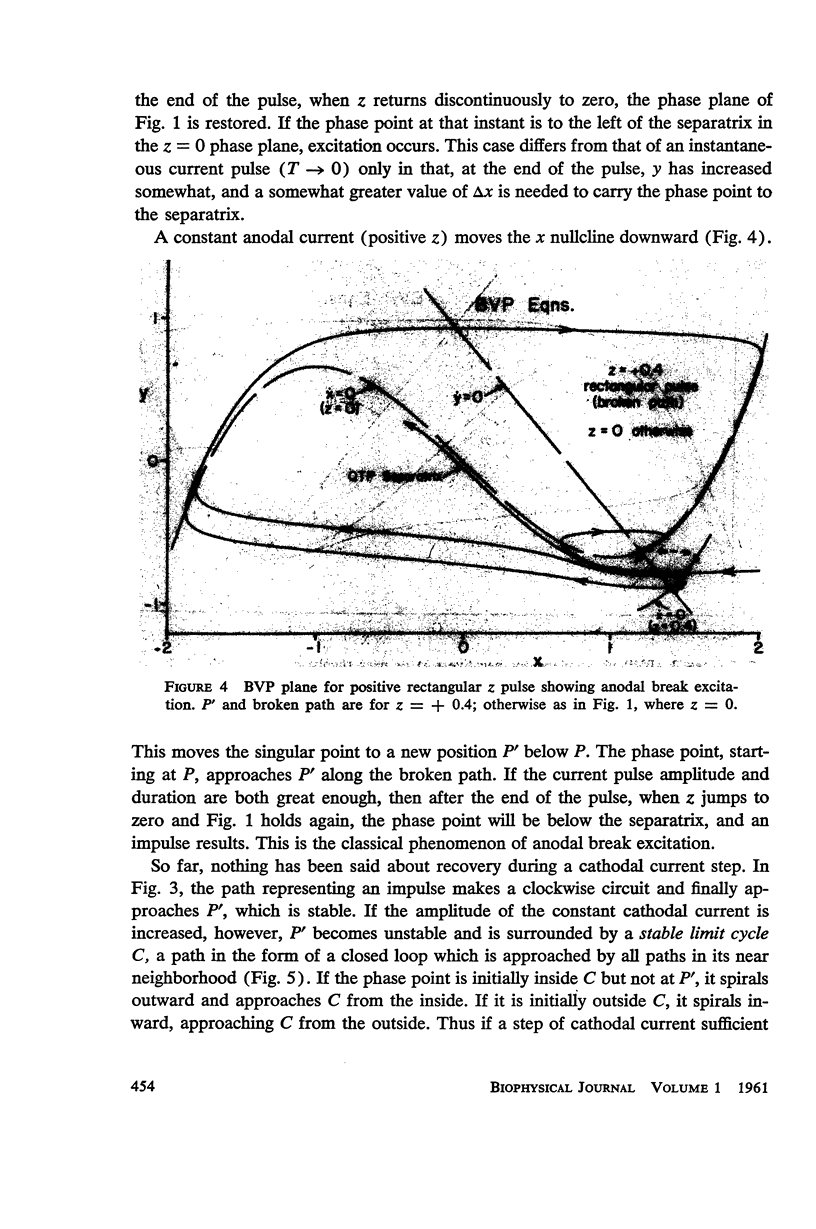
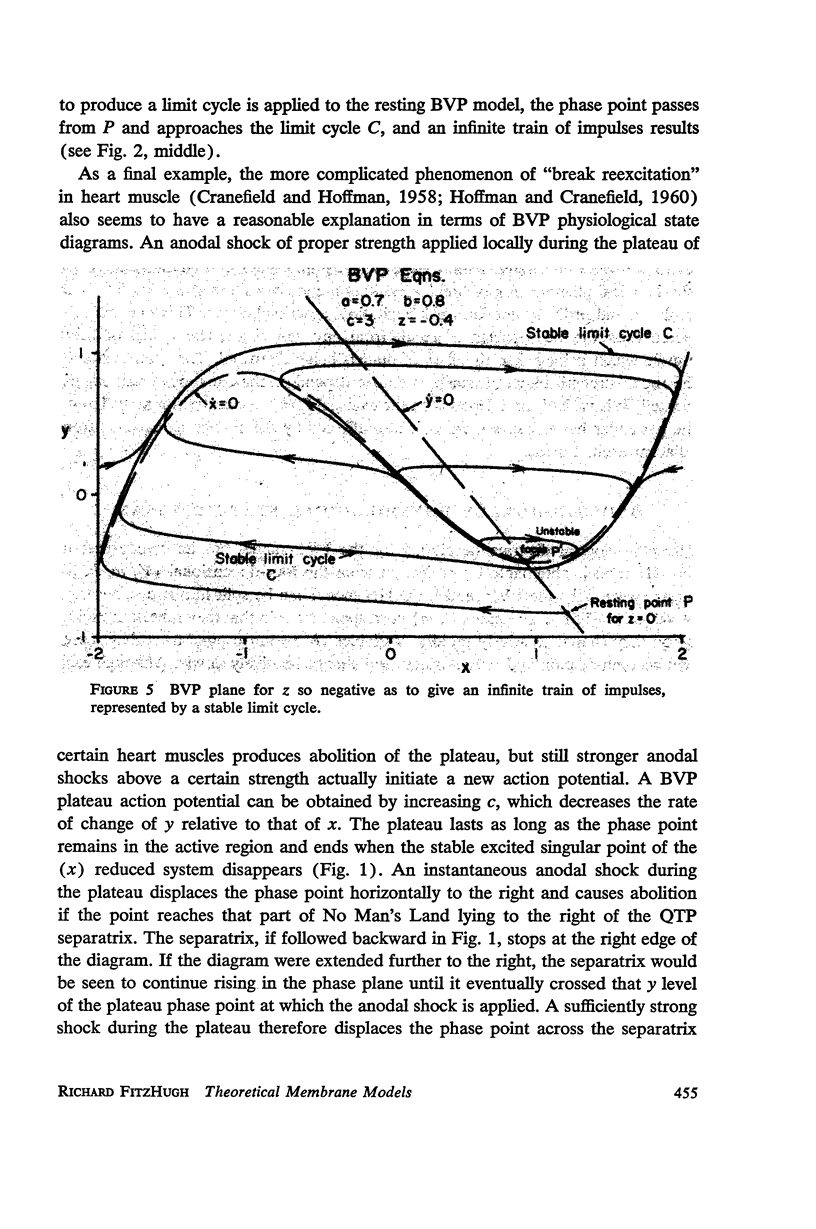
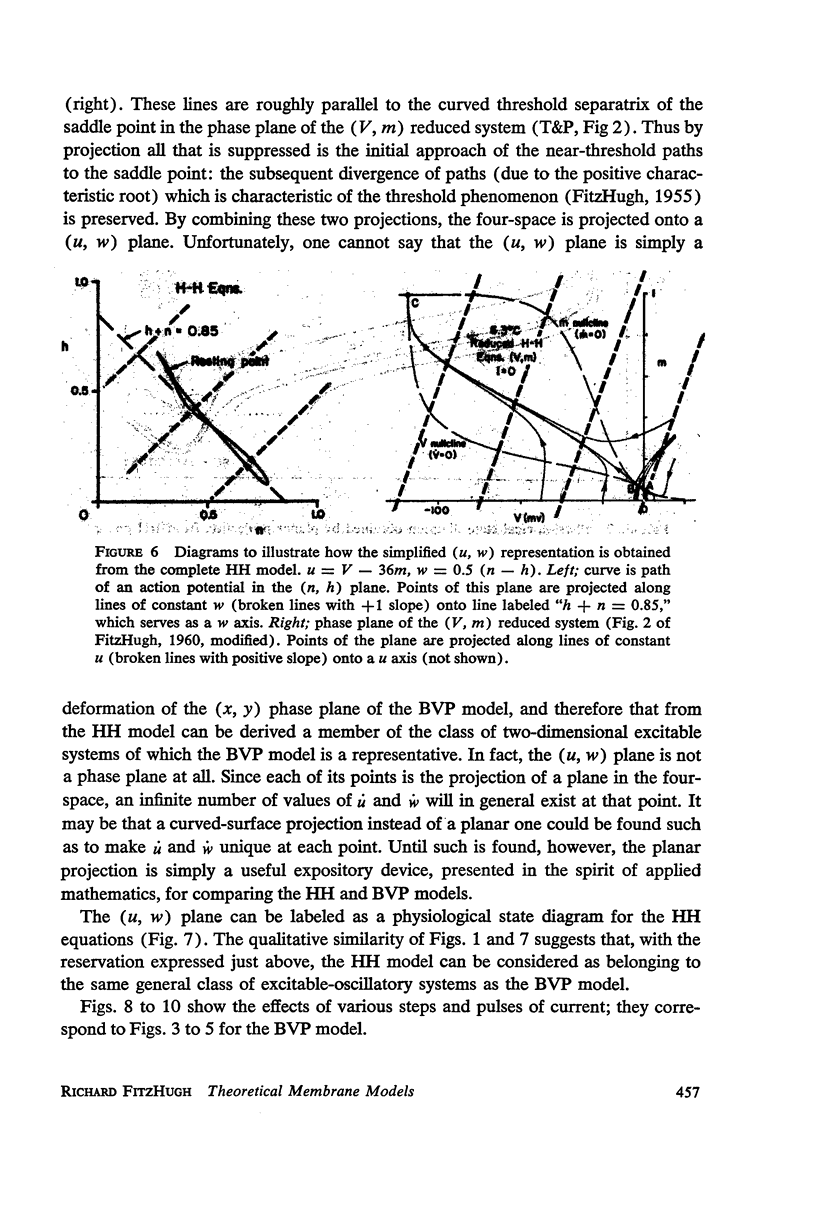
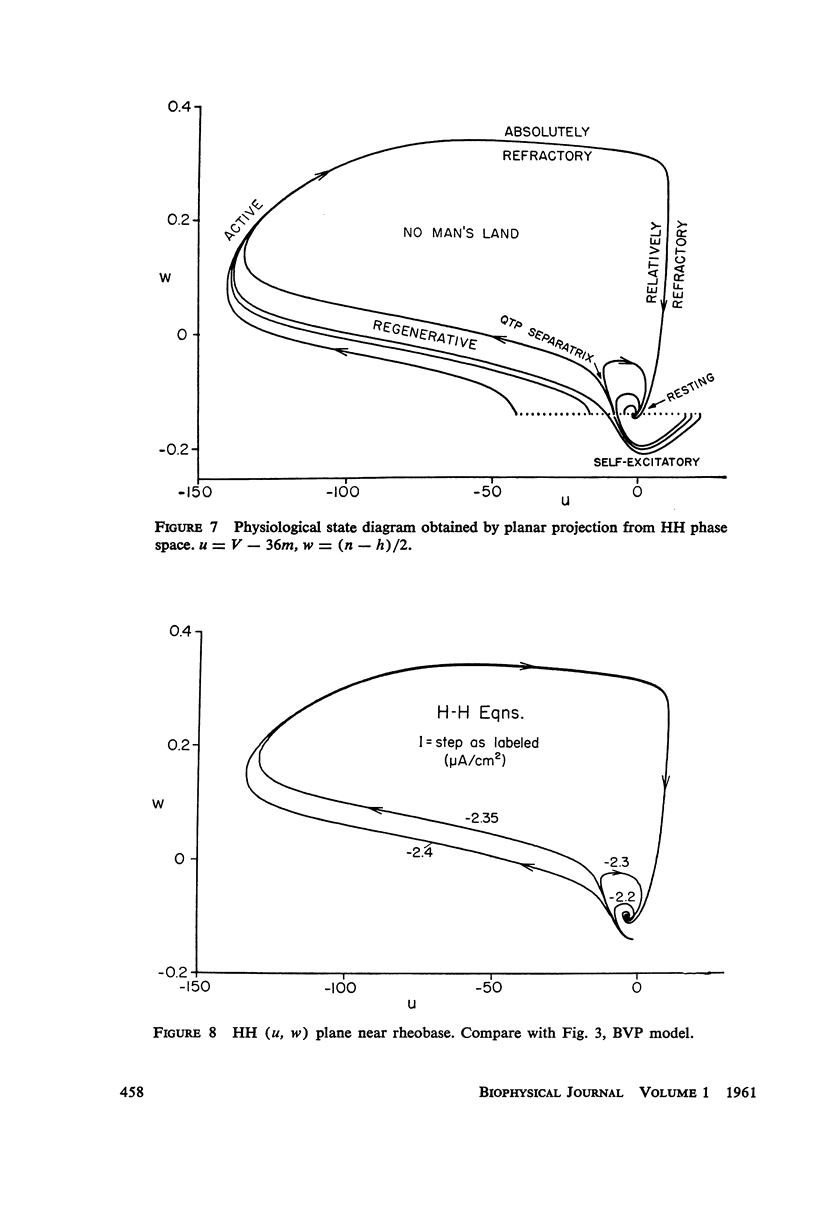
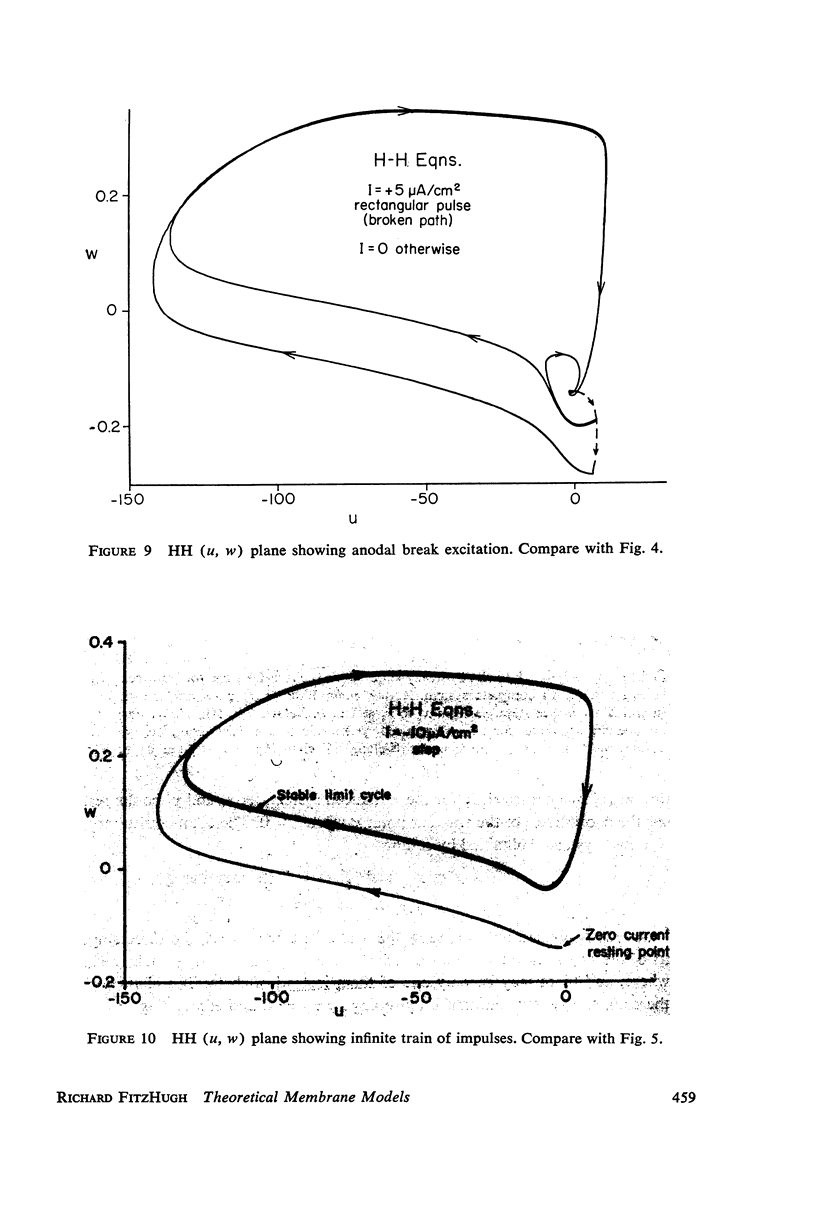
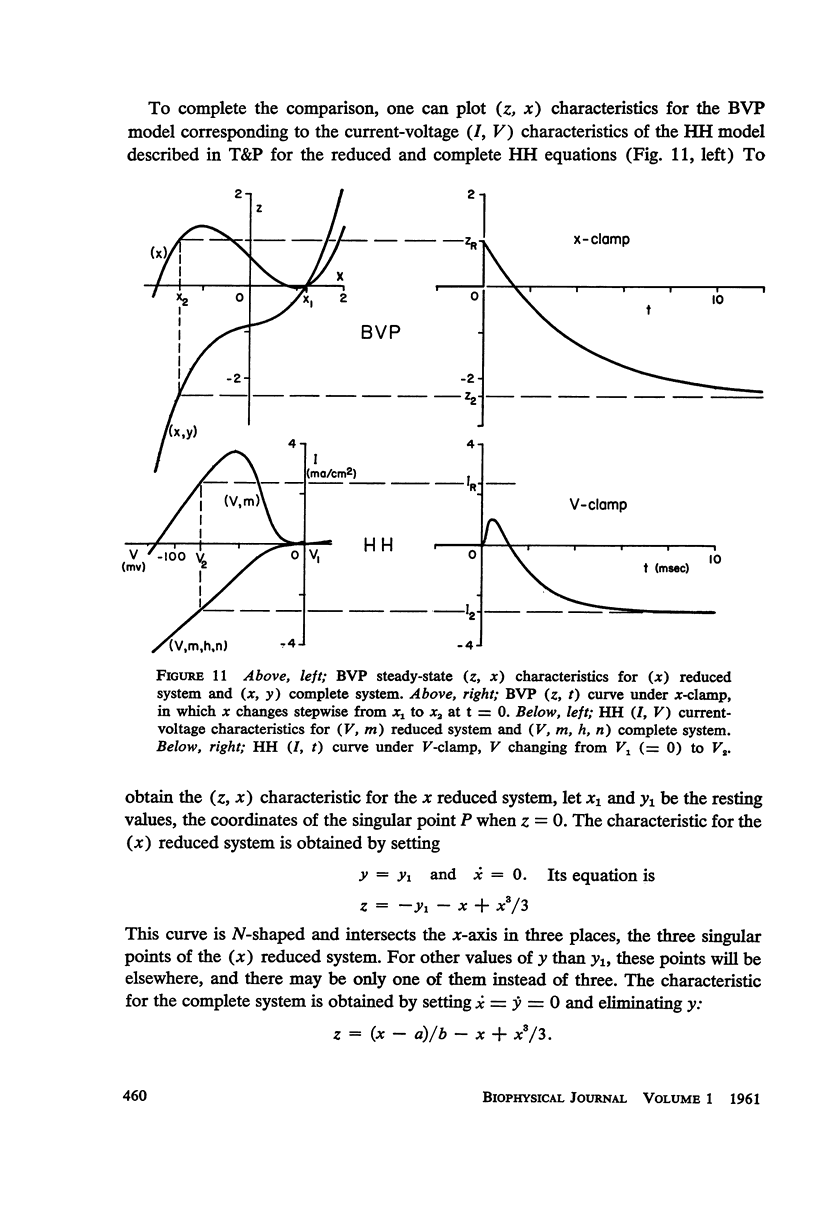
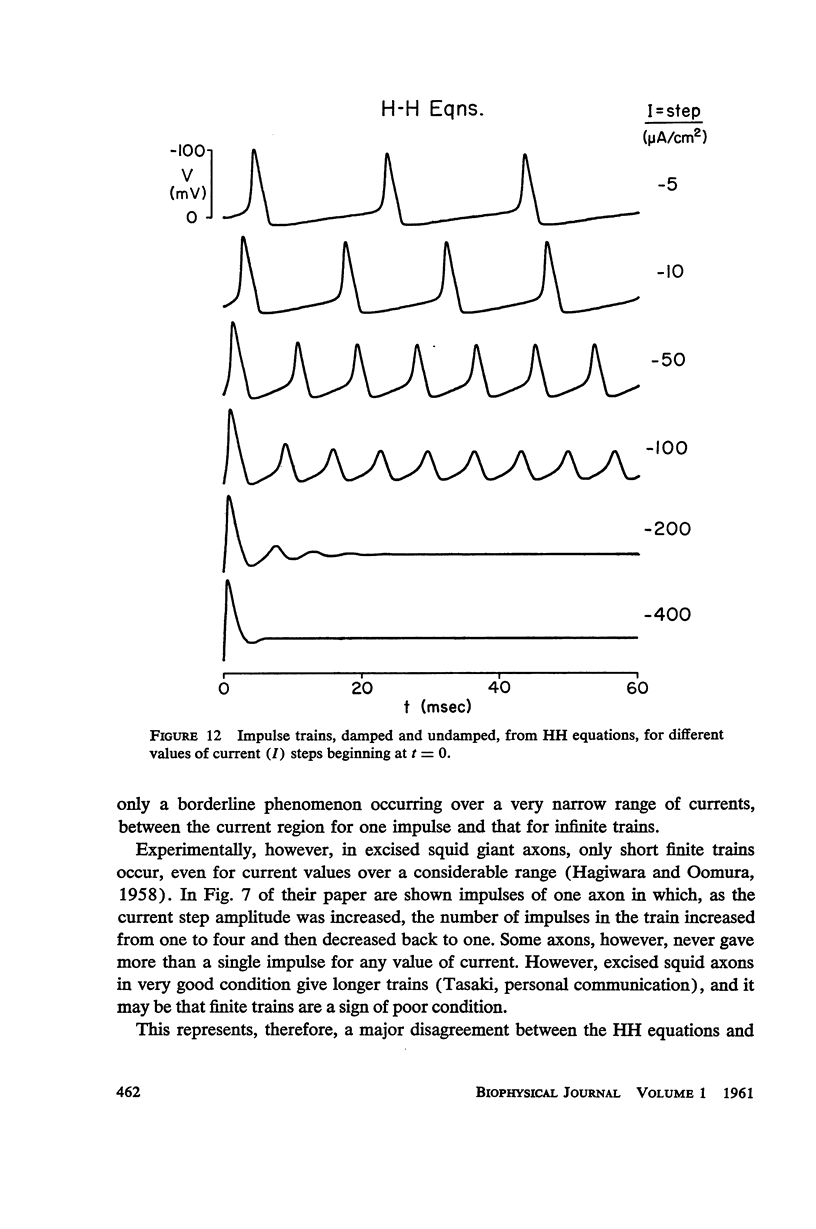
Van der Pol's equation for a relaxation oscillator is generalized by the addition of terms to produce a pair of non-linear differential equations with either a stable singular point or a limit cycle. The resulting “BVP model” has two variables of state, representing excitability and refractoriness, and qualitatively resembles Bonhoeffer's theoretical model for the iron wire model of nerve. This BVP model serves as a simple representative of a class of excitable-oscillatory systems including the Hodgkin-Huxley (HH) model of the squid giant axon. The BVP phase plane can be divided into regions corresponding to the physiological states of nerve fiber (resting, active, refractory, enhanced, depressed, etc.) to form a “physiological state diagram,” with the help of which many physiological phenomena can be summarized. A properly chosen projection from the 4-dimensional HH phase space onto a plane produces a similar diagram which shows the underlying relationship between the two models. Impulse trains occur in the BVP and HH models for a range of constant applied currents which make the singular point representing the resting state unstable.

Full text

PDF
445

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. BISHOP G. H. Natural history of the nerve impulse. Physiol Rev. 1956 Jul;36(3):376–399. doi: 10.1152/physrev.1956.36.3.376. [DOI] [PubMed] [Google Scholar]
  2. BULLOCK T. H. Neuron doctrine and electrophysiology. Science. 1959 Apr 17;129(3355):997–1002. doi: 10.1126/science.129.3355.997. [DOI] [PubMed] [Google Scholar]
  3. CRANEFIELD P. F., HOFFMAN B. F. Propagated repolarization in heart muscle. J Gen Physiol. 1958 Mar 20;41(4):633–649. doi: 10.1085/jgp.41.4.633. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. FITZHUGH R. Thresholds and plateaus in the Hodgkin-Huxley nerve equations. J Gen Physiol. 1960 May;43:867–896. doi: 10.1085/jgp.43.5.867. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. FRANKENHAEUSER B., HODGKIN A. L. The after-effects of impulses in the giant nerve fibres of Loligo. J Physiol. 1956 Feb 28;131(2):341–376. doi: 10.1113/jphysiol.1956.sp005467. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. HAGIWARA S., OOMURA Y. The critical depolarization for the spike in the squid giant axon. Jpn J Physiol. 1958 Sep 15;8(3):234–245. doi: 10.2170/jjphysiol.8.234. [DOI] [PubMed] [Google Scholar]
  7. HODGKIN A. L., HUXLEY A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952 Aug;117(4):500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. KARREMAN G. Some types of relaxation oscillations as models of all-or-none phenomena. Bull Math Biophys. 1949 Dec;11(4):311–318. doi: 10.1007/BF02477983. [DOI] [PubMed] [Google Scholar]
  9. MOORE J. W. Excitation of the squid axon membrane in isosmotic potassium chloride. Nature. 1959 Jan 24;183(4656):265–266. doi: 10.1038/183265b0. [DOI] [PubMed] [Google Scholar]
  10. TASAKI I., BAK A. F. Discrete threshold and repetitive responses in the squid axon under voltage-clamp. Am J Physiol. 1958 May;193(2):301–308. doi: 10.1152/ajplegacy.1958.193.2.301. [DOI] [PubMed] [Google Scholar]
  11. TEORELL T. Application of the voltage clamp to the electrohydraulic nerve analog. Acta Soc Med Ups. 1960;65:231–248. [PubMed] [Google Scholar]
  12. TEORELL T. Electrokinetic membrane processes in relation to properties excitable tissues. II. Some theoretical considerations. J Gen Physiol. 1959 Mar 20;42(4):847–863. doi: 10.1085/jgp.42.4.847. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES