Abstract
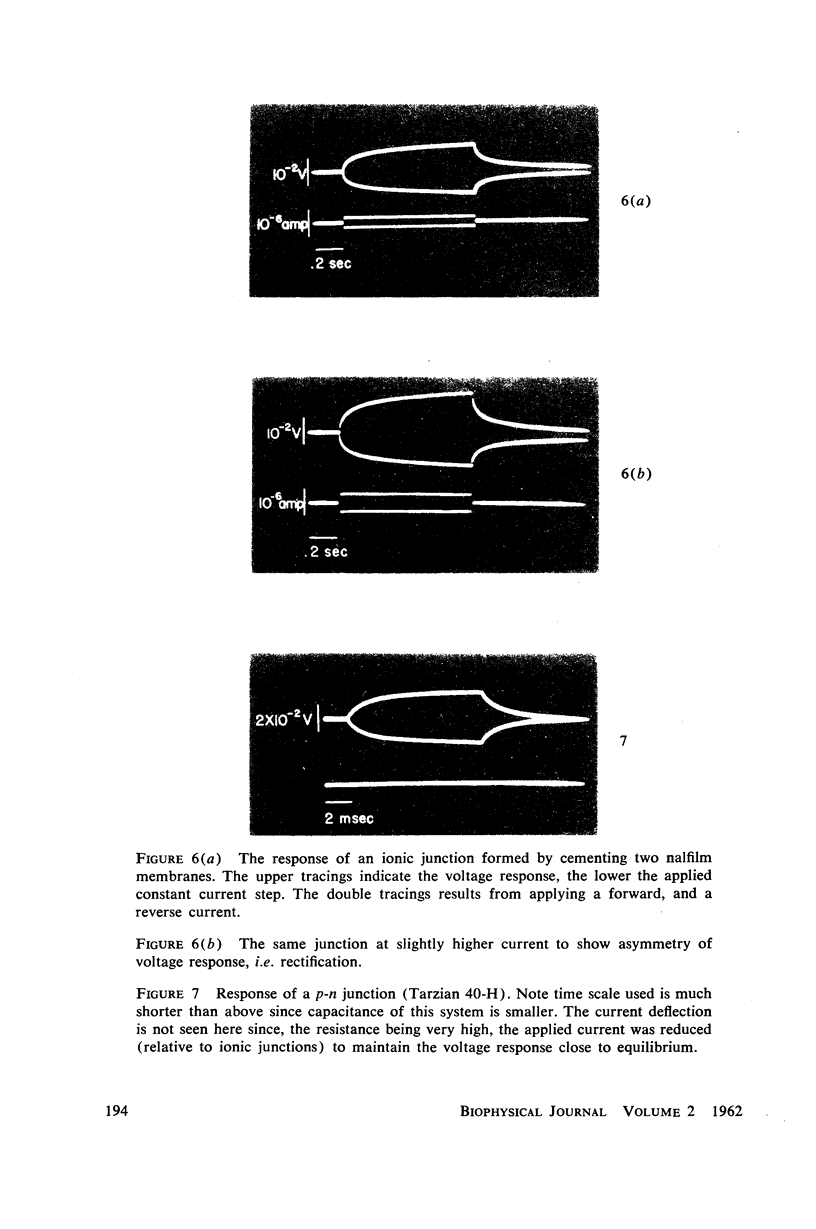
The Poisson-Boltzmann equation, which was derived by Shockley in his treatment of the p-n semiconductor junction at equilibrium, is applied to fixed charge ionic membranes. The fixed charges in ionic membranes play the same role as “doping” ions in semiconductors, the major difference between the two systems being that in the former the mobile particles are ions while in the latter the particles are electrons and phenomenological particles, “holes.” An important consequence of spatial gradients of fixed charge is the presence of space charge regions which give rise to an intrinsic electric field and potential. These quantities are established first for the single “lattice” thus providing a continuous treatment of the Donnan equilibrium invoked by Teorell-Meyer-Sievers in their treatment of fixed charge membranes. It is shown further that when a positive and negative membrane are juxtaposed, the space charge region in the “junction” so formed provides a mechanism for the storage of electrical energy. Thus while the system is basically a “conductor” the presence of transition regions of fixed charge give rise to the additional property of capacitance. Experimental data are presented on ionic and p-n junctions. The implications of this mechanism for the physical basis of capacitance in biological cells are discussed.
Full text
PDF


















Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- MAURO A. Anomalous impedance, a phenomenological property of time-variant resistance. An analytic review. Biophys J. 1961 Mar;1:353–372. doi: 10.1016/s0006-3495(61)86894-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- STOECKENIUS W. An electron microscope study of myelin figures. J Biophys Biochem Cytol. 1959 May 25;5(3):491–500. doi: 10.1083/jcb.5.3.491. [DOI] [PMC free article] [PubMed] [Google Scholar]


