Abstract
In mammals, the circadian pacemaker, which controls daily rhythms, is located in the suprachiasmatic nucleus (SCN). Circadian oscillations are generated in individual SCN neurons by a molecular regulatory network. Cells oscillate with periods ranging from 20 to 28 h, but at the tissue level, SCN neurons display significant synchrony, suggesting a robust intercellular coupling in which neurotransmitters are assumed to play a crucial role. We present a dynamical model for the coupling of a population of circadian oscillators in the SCN. The cellular oscillator, a three-variable model, describes the core negative feedback loop of the circadian clock. The coupling mechanism is incorporated through the global level of neurotransmitter concentration. Global coupling is efficient to synchronize a population of 10,000 cells. Synchronized cells can be entrained by a 24-h light-dark cycle. Simulations of the interaction between two populations representing two regions of the SCN show that the driven population can be phase-leading. Experimentally testable predictions are: 1), phases of individual cells are governed by their intrinsic periods; and 2), efficient synchronization is achieved when the average neurotransmitter concentration would dampen individual oscillators. However, due to the global neurotransmitter oscillation, cells are effectively synchronized.
INTRODUCTION
The suprachiasmatic nucleus (SCN) of the hypothalamus is the center of the circadian pacemaker in mammals (1,2). It receives light information coming from the retina through the retinohypothalamic tract and controls circadian rhythms in other parts of the brain including the cortex and the pineal gland as well as in peripheral tissues such as liver, kidney, and heart, thereby orchestrating the timing in physiology and behavior (1). In natural conditions, the circadian clock is subject to alternance of days and nights and, in response to this cycling environment, phase-locks to the light-dark cycle, enabling the body to follow a 24-h rhythm. The SCN consists of paired nuclei located above the optic chiasm. Each nucleus contains ∼10,000 neurons, characterized by a small size and high density (3). It has been shown that isolated individual neurons are able to produce circadian oscillations, with periods ranging from 20 to 28 hours (4,5).
A remarkable property of circadian rhythms in the SCN is that they are self-sustained in constant condition, i.e., in absence of any external time cue. The core molecular regulatory mechanism underlying these oscillations relies on a negative feedback loop (6). Because free-running periods of isolated neurons are broadly distributed, the self-sustained oscillations indicate that a coupling mechanism is operating between the neurons. The coupling between cells in the SCN is achieved partly by neurotransmitters (3,7). In each SCN, two regions are usually distinguished according to the neuropeptides expressed by the cells in these areas. In the dorsomedial (DM) part, neurons mainly express the arginin-vasopressin polypeptides, whereas in the ventrolateral (VL) part, they produce vasointestinal polypeptide (VIP) and gastrin-releasing peptide (2,8). These three neuropeptides show circadian variation in the level of mRNA in constant condition (9). Their release also undergoes circadian variation (10). In both parts of the SCN, the neurotransmitter gamma-aminobutyric acid (GABA) is also released (3). Although to our knowledge no experimental evidence mentions circadian variation of its concentration, the responsiveness of the SCN to GABA shows daily variation (11).
Several evidences of involvement of neurotransmitters in the intercellular coupling, possibly through regulation of the firing rate, have been put forward (3). Liu and Reppert (11) showed that application of GABA to dissociated SCN cells induces phase-shifts in the firing rhythm of individual neurons and that daily GABA pulses synchronized the rhythm. Furthermore, the firing rate of the SCN neurons is altered by GABAA receptor antagonist (12). Shen and co-workers (13) showed that in transgenic mice overexpressing VPAC2-R, a receptor for VIP, both rhythmicity in constant condition and entrainment by light-dark cycles are affected: these mice exhibit shorter periods in constant darkness and are quickly resynchronized to an 8-h advanced light-dark cycle. Furthermore, VPAC2-R knockout mice are incapable of sustaining normal circadian rhythms of activity behavior and fail to exhibit circadian expression of the core clock genes per1, per2, and cry1 (14). A circadian regulation of VPAC2-R was also shown to be required for a normal cell-to-cell communication (15).
How neurotransmitters interfere with the clock core is not yet fully clear. However, it was shown that treatment of SCN slices with VIP produces phase shifts similar to those induced by light pulses (16,17). Recently, Nielsen and co-workers (18) showed that VIP induces per1 and per2 expression in a phase-dependent manner.
In both regions of the SCN, circadian oscillations are sustained over a couple of days in vitro. Using SCN explants Yamaguchi and co-workers (19) showed that the DM cells are not synchronized when this area is disconnected from the rest of the SCN. This observation suggests that ventrolateral (VL) cells drive the oscillations and that the internal coupling between DM cells is negligible. The average phase of the oscillations in individual neurons is advanced in the DM part with respect to the VL part, indicating that the DM region is the phase-leading part (19). However, only VL cells are light-responsive. In these cells, light interacts with the clock by activating the transcription of per1 and per2 genes.
Treatment with tetrodotoxin (TTX), an inhibitor of Na+ channels, has been shown to alter the overt circadian rhythms as well as the input pathway, but without preventing the individual cells from oscillating (20). Experiments of Yamaguchi (19) suggest that TTX treatment desynchronizes the cells. Upon TTX elimination, cells rapidly synchronize again. Interestingly, the phase of the oscillations after the treatment is the same as before the treatment, indicating that the phase relationship in the coupled system is not established randomly but is intrinsic to the properties of the oscillator network (19).
Here, we present a mathematical model to describe the behavior of a population of coupled SCN neurons. The single cell oscillator is described by a three-variable model similar to the widely used Goodwin model. This model, based on a negative feedback loop, accounts for the core molecular mechanism leading to self-sustained oscillations of clock genes. Based on the above-mentioned results, we assume that the coupling is achieved by neurotransmitters released by each cell and that spatial transmission is fast with respect to the timescale of the oscillations (24 h). Under these conditions, it is a reasonable hypothesis to consider global coupling, achieved through a mean field, defined as the average concentration of the neurotransmitter. The goal of the present article is to show how a simple molecular model can account for the main properties resulting from the coupling of a population of circadian oscillators and provide an experimentally testable mechanism responsible for their synchronization.
We show that a global coupling relying on a mean field is efficient to synchronize a population of 10,000 cells. We then consider a reduced system consisting of two coupled oscillators. Using bifurcation analysis, we determine conditions to achieve synchronization. In particular, we show that the coupling induces a damping in individual clocks, enabling efficient synchronization. This allows the cells to display fast synchronization after transient disruption of the coupling. Next, we simulate the effect of a light-dark (LD) cycle by applying an external forcing and show that coupled oscillators can be entrained by the LD cycle. Finally, we study the interaction between two cell populations, reflecting the two parts of the SCN, and provide an explanation for the counterintuitive observation that the driven region is phase-leading.
MODEL
To simulate circadian oscillations in single mammalian cells, we resort to a three-variable model, based on the Goodwin oscillator (21). In this model, a clock gene mRNA (X) produces a clock protein (Y) which, in turn, activates a transcriptional inhibitor (Z). The latter inhibits the transcription of the clock gene, closing a negative feedback loop. In the original model (21), sustained oscillations could be obtained only by choosing a steep feedback function, with a high Hill coefficient (22). This constraint is due to the linear terms used for the degradation steps. Therefore, we slightly modified this model by using Michaelian kinetics for the degradation steps. In circadian clocks, protein degradation is controlled by phosphorylation, ubiquitination, and proteasomal degradation and thus it is reasonable to assume Michaelian kinetics. Many other models (23,24) rely on Michaelian functions as well.
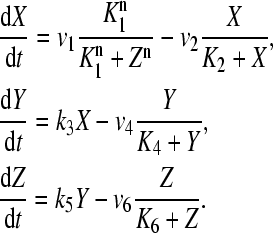 |
In this version, limit cycle oscillations can be obtained for a Hill coefficient of n = 4. The variable X represents mRNA concentration of a clock gene, per or cry; Y is the resulting protein, PER or CRY; and Z is the active protein or the nuclear form of the protein (inhibitor). This model is closely related to those proposed by Ruoff and Rensing (25), Leloup and co-workers (24), or Ruoff and co-workers (26) for the circadian clock in Neurospora.
Two factors influence the dynamics of single cell oscillations: light and intercellular coupling. Both are assumed to act independently from the negative feedback loop and are added as independent terms in the transcription rate of X. Light is incorporated through the time-dependent term L(t). In absence of light, we have L = 0. The global coupling depends on the concentration of the synchronizing factor (the neurotransmitter) in the extracellular medium. Under the fast transmission hypothesis, the extracellular concentration is assumed to equilibrate to the average cellular neurotransmitter concentration. This global variable is referred to as the mean field, denoted by F. The evolution equations for N oscillators (denoted by i = 1,2,…, N) are then written as
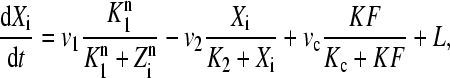 |
(1) |
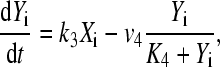 |
(2) |
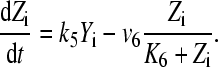 |
(3) |
The parameter K describes the sensitivity of the individual circadian oscillator to the neurotransmitter and is referred to below as the coupling strength. We assume that cells synthesize a neuropeptide denoted by V and that production is induced by the activation of the clock gene (X). A strong candidate regarding the VL cells is the neuropeptide VIP. The evolution equation for the neurotransmitter is assumed as
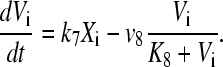 |
(4) |
The precise mechanism for production of the coupling agent is not known. There are delays with respect to clock gene X activity due to transcription, translation, signaling, and diffusion. With the choice of a linear neurotransmitter production by the clock gene, the variable Vi becomes a slightly delayed version of Xi, and the values of parameters in Eq. 4 can be chosen to adjust the delay.
The release of the neurotransmitter is supposed to be fast with respect to the 24-h timescale of the oscillations and becomes homogeneous to establish an average neurotransmitter level, or a mean field F,
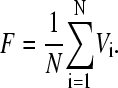 |
(5) |
The average neurotransmitter level F acts on clock gene transcription through a limited number of neuron receptors. This limits the response of neurons to the coupling, as shown for the effect of VIP on the induction of per genes (17). Moreover, there is a maximal activity of fully active promoters. Thus we choose a saturation form of the coupling term in Eq. 1.
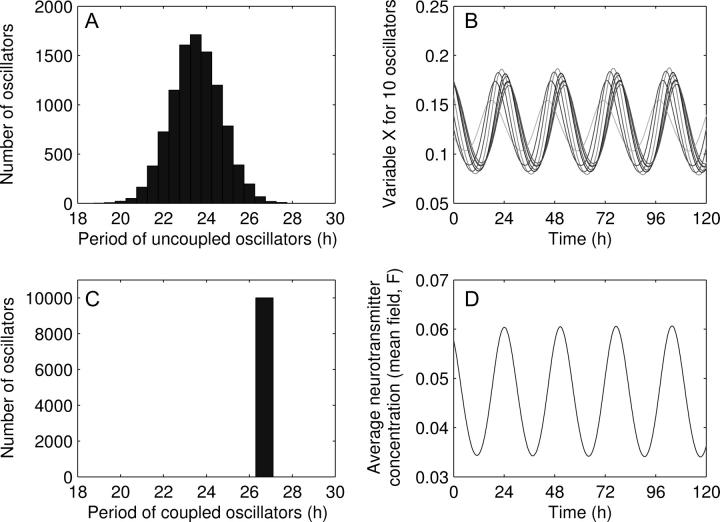
Parameters of the model have been chosen in such a way that the single cell oscillator produces self-sustained oscillations with a circadian period. Their values are given in the caption of Fig. 1.
FIGURE 1.
Synchronization of 10,000 circadian oscillators (R = 0.63). (A) Distribution of the individual periods for K = 0. (B) Oscillations of Xi (in nM) for 10 randomly chosen oscillators. Different individual periods were obtained by rescaling rate constants (production and degradation), namely by dividing v1, v2, k3, v4, k5, v6, k7, and v8 by a scaling factor τi, i = 1,…,N. The values of τi are drawn randomly from a normal distribution of mean 1.0 and standard deviation 0.05. The periods are then distributed according a normal distribution with mean 23.5 h and standard deviation of 5%. (C) Distribution of the periods in the coupled system. (D) Oscillation of the mean field, F. Parameter values are: v1 = 0.7 nM/h; K1 = 1 nM; n = 4; v2 = 0.35 nM/h; K2 = 1 nM; k3 = 0.7/h; v4 = 0.35 nM/h; K4 = 1 nM; k5 = 0.7/h; v6 = 0.35 nM/h; K6 = 1 nM; k7 = 0.35/h; v8 = 1 nM/h; K8 = 1 nM; vc = 0.4 nM/h; Kc = 1 nM; K = 0.5; and L = 0. Concentrations are expressed in nM.
To quantify how good the synchrony is, we calculate an order parameter (27),
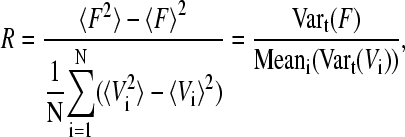 |
(6) |
where 〈…〉 denotes the average over time. This parameter measures the distribution of phases of the oscillators and is ranging between 0 (no synchronization) and 1 (perfect synchronization, with all oscillators in phase).
RESULTS
Synchronizing a population of circadian oscillators
To study the synchronization of a population of cells coupled through a mean field, we consider a system of 10,000 cells with individual periods normally distributed with a mean of 23.5 h, a typical circadian period of mouse, and a standard deviation of 5%. Most periods are then ranging from 20 to 27 hours (Fig. 1 A), as observed experimentally (5). In Fig. 1 B the time evolution of variable X for a sample of 10 oscillators in the coupled system (K = 0.5) is shown. Notice that the coupling leads to a systematic increase of the period (26.5 h, Fig. 1 D). Systematic period changes due to light intensity or serum concentration have been reported (28,29). We could compensate deviations from the 24-h period by changing, e.g., degradation rates. However, because of the lack of in vivo data about compensation, we have avoided this extension of the model. All oscillators are synchronized, leading to a single resulting period, which is identical for all oscillators (Fig. 1 C). Because not all of the oscillators have the same individual period, a perfect synchronization cannot be achieved and phase differences between some oscillators still persist, as observed experimentally (19). We quantified the quality of synchronization by computing the order parameter (Eq. 6). For the case illustrated in Fig. 1, we obtain R = 0.63, which represents a good degree of synchrony.
Individual cells act as damped oscillators
Understanding the dynamics of coupled nonlinear oscillators is not straightforward. Therefore, it is useful to study a reduced system, comprising only two coupled circadian oscillators. We consider here two oscillators having slightly different periods—23.5 and 24.7 h, respectively. For appropriate parameter values, the two oscillators can be synchronized with a relatively small phase-difference (Fig. 2, A and B). The faster one is phase-advanced by 3.1 h with respect to the slower one. Again, we observed that the resulting period, which is ∼30 h, is increased with respect to individual periods.
FIGURE 2.
Coupling between two circadian oscillators. (A) Oscillations of variables X1 and X2, and of the mean field, F, and (B) limit cycle for the system of two coupled oscillators. Individual periods are 24.7 h and 23.5 h, respectively. Concentrations are expressed in nM. (C) Bifurcation diagram as a function of the coupling strength, K. In ordinates is plotted the variable X1 at the steady state (stable, XS or unstable, XU) or at the minimum (Xmin) and maximum (Xmax) of the oscillations. (D) Stability diagram as a function of the coupling strength K, and the ratio r of the periods of the two oscillators. Notation: FP, fixed point; HB, Hopf bifurcation; QP, quasiperiodicity; SA, small amplitude limit cycle; LP, limit point; PD, period doubling bifurcation; and P2, period-2 limit cycle. In C the ratio of the periods has been fixed to r = 0.9. These diagrams have been obtained with XPPAUT (http://www.math.pitt.edu/bard/xpp/xpp.html). Parameter values are the same as in Fig. 1.
To examine the effect of the coupling strength K on the dynamical properties of the two-oscillator model, we plot the bifurcation diagram as a function of this control parameter (Fig. 2 C). When the coupling is small, the oscillators are not well synchronized and display quasiperiodic behavior. For an intermediate coupling strength, the coupling leads to an arrest of the oscillations: both oscillators converge to a steady state. When the coupling strength is larger, after a bifurcation the system tends to a limit cycle corresponding to a synchronized state. For even larger coupling strength, more complex dynamics is seen. The behavior of the two coupled oscillator system also depends on the difference between the individual periods of each oscillator. The closer the individual periods are, the easier is synchronization. With an increase of the coupling strength K, the range of the period ratio r in which synchronization occurs is extended (Fig. 2 D). Outside this range, the system exhibits quasiperiodicity if the coupling strength is small or converges to a stable steady state if the coupling strength is larger. The complex scenario of bifurcations for even two coupled oscillators illustrates that robust synchronization is not trivial, as discussed by Aronson and co-workers (30). Detailed analysis of two coupled oscillators is beyond the scope of this study.
A better understanding of the role of the coupling term on the dynamics of a single cell oscillator can be acquired by examining the effect of a constant mean field on the behavior of a single cell oscillator (Fig. 3). The most striking result is that the constant mean field brings the oscillator out of its oscillatory domain. In the case of synchronized cells (Fig. 1), the mean field F oscillates around an average value of 0.05. Fig. 3 C shows that such a level leads to damped oscillations of individual cells. The period of these damped oscillations, estimated from linear approximation analysis around the steady state of the system, is ∼27 h (Fig. 3 D). However, in the fully coupled system, the mean field is oscillating, and synchronization, instead of damping, is achieved.
FIGURE 3.
Effect of a constant mean field on the dynamics of a single cell circadian oscillator. (A) Bifurcation diagram as a function of the mean field F taken as constant. HB denotes the Hopf bifurcation above which the limit cycle oscillations are abolished (located at F = 4.05 × 10−3). (B) Same as top-left panel with a logarithmic timescale. (C) Time-evolution to the steady state, for F = 0.05. The period of these damped oscillations is ∼27 h. (D) Variation of the period with F in the oscillatory domain (solid curve) and of the damped oscillations around the steady state (dashed curve). In A, B, and D, the two vertical dashed lines indicate the minimum (F = 0.036) and maximum (F = 0.06) values of the mean field F in the coupled state (see Fig. 1 D). These diagrams have been obtained with XPP-AUTO. Parameter values are the same as in Fig. 1.
Our findings demonstrate an efficient way for SCN neurons to synchronize by moving them out of their oscillatory domain. In other terms, due to the average value of the coupling agent, the individual oscillators are damped. Synchronization is achieved by the oscillatory component of the mean field. Thus, the oscillating mean field drives all cells to fast synchronization.
Determination of the optimal coupling strength
We have shown for the case of two coupled circadian oscillators that the choice of the coupling strength K is important to obtain synchrony (Fig. 2, C and D). Considering a population of 1000 circadian oscillators, we studied the effect of K on the synchronization, quantified by the order parameter R (Eq. 6) and on the resulting period (Fig. 4). Better synchronization is achieved when the coupling strength is increased (Fig. 4 A) and this is accompanied by lengthening of the resulting period (Fig. 4 B). For a circadian system, an optimal coupling is reached when the coupling strength K is able to synchronize the oscillators, while keeping the period around a circadian value.
FIGURE 4.
Effect of the coupling strength K (A) on the order parameter R and (B) on the resulting period of the coupled system. This diagram has been obtained for a population of 1000 coupled circadian oscillators. Each dot corresponds to the mean over five runs, i.e., five time-series with different initial individual periods, but generated according the same probability distribution (see Fig. 1). Parameter values are the same as in Fig. 1.
Since coupling (or light) activates transcription in the mammalian circadian clock, systematic changes of the period due to varying neurotransmitter levels or varying light intensity can be expected. Such period changes in our model are shown in Figs. 3 D and 4 B. Without compensation these systematic changes restrict the values of the coupling strength.
Phase relationship conservation after transient desynchronization
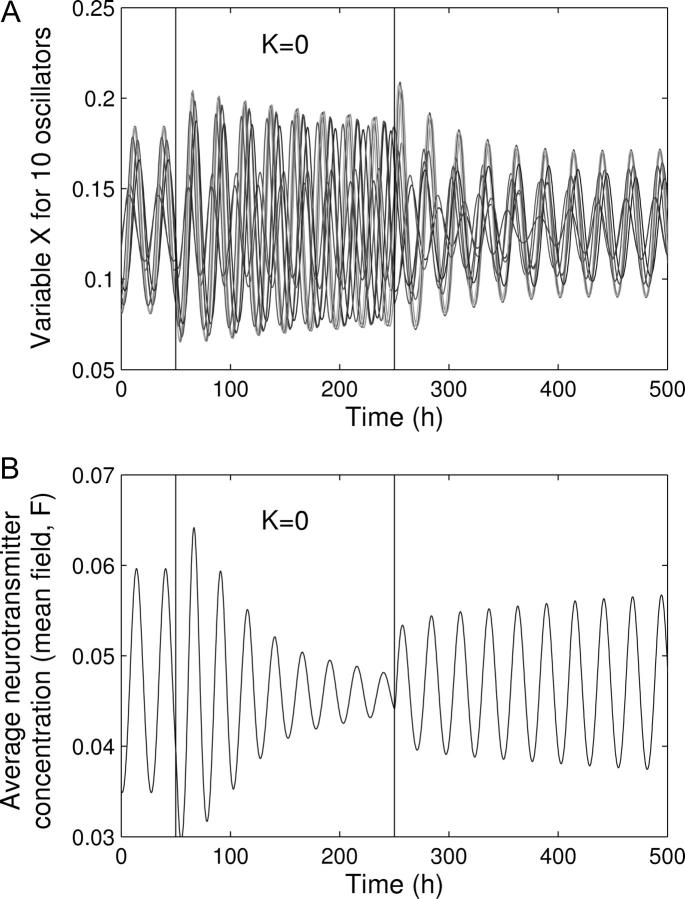
Yamaguchi and co-workers (19) showed that after transient TTX treatment, which disrupts the coupling among the cells by selectively and reversibly blocking the Na+ channels, SCN cells are rapidly resynchronized, displaying the same phase relationship as before the treatment, independently of the duration of the treatment. This implies that the phase relationship between the oscillators is an intrinsic property of the oscillator network and is not established randomly or by the initial condition of the system.
We simulated this experiment by setting K = 0 during 200 h (Fig. 5). During this time, each oscillator evolves toward its own limit cycle and rapidly runs out of phase due to variability in periods. The mean field rapidly dampens out. As soon as K recovers its initial value (K = 0.5), the oscillators are rapidly resynchronized with the same phase relationship, as observed experimentally.
FIGURE 5.
Transient desynchronization of the oscillations. Shown are the oscillations of X for 10 oscillators randomly chosen among a total of 10,000 oscillators. During t = 50 h and t = 250 h (vertical lines), the oscillators are uncoupled (K = 0). During this period of time, each oscillator evolves toward its individual limit cycle characterized by its own period. After this period of time, the oscillators are rapidly resynchronized. Parameter values are the same as in Fig. 1.
There is a strong correlation between the individual period and the phase difference of the oscillators in the coupled system (see curve DD in Fig. 6). The phase difference is computed between neurotransmitter concentration Vi and mean field F by taking time differences of the corresponding maxima. Oscillators with smaller individual periods are advanced with respect to the mean field (positive phase difference) whereas those with larger periods are delayed (negative phase difference). This demonstrates that the phase of a given oscillator in the coupled system is conserved, as observed by Yamaguchi (19). More precisely, the phase difference of an oscillator relative to the mean field is uniquely determined by its individual period.
FIGURE 6.
Relation between the individual period and the phase in the coupled state (maximum of variable V with respect to the maximum of the mean field). A positive value indicates that the phase of the oscillator is advanced with respect to the mean field, whereas a negative value indicates that the phase of the oscillator is delayed. The curve indicated by DD corresponds to the case of constant conditions, illustrated in Fig. 1. The curve indicated by LD corresponds to the case of light-dark conditions, illustrated in Fig. 7.
Such a dependency is qualitatively closely related to the curve observed for the forced damped harmonic oscillator when the phase of the entrained oscillator is plotted against the phase of the periodic force for different forcing periods. If such a dependency were observed experimentally, this would support our prediction that synchronization is achieved when the average neurotransmitter concentration is sufficiently high to force every cell to act like a damped oscillator.
The clock is entrained by a light-dark cycle
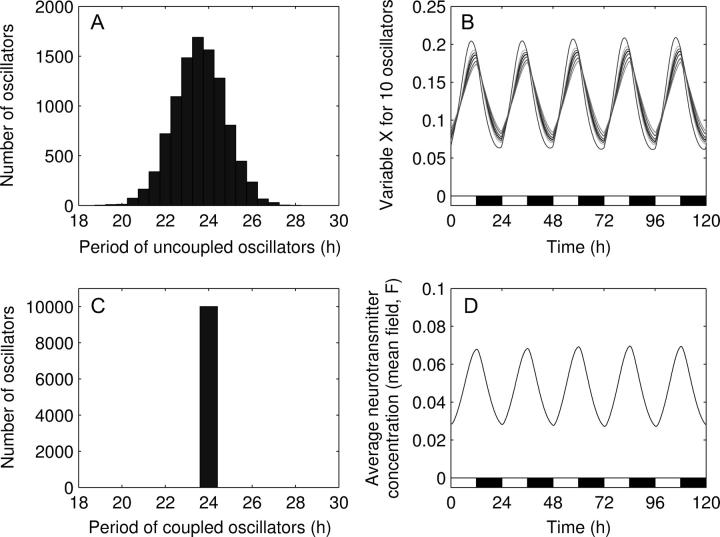
In the natural environment, circadian clocks are subjected to alternance of light and darkness. This external cycle entrains the oscillations precisely to a 24-h period. We simulate the effect of a light-dark cycle by using a square-wave function for the light term, L (see Eq. 1). The term L switches from L = 0 in dark phase to L = 0.01 in light phase. Such a forcing entrains the circadian oscillators to a 24-h period (Fig. 7). Although the system displays a quasiperiodic behavior, the period and the phase of the oscillations are very well conserved. The mean field always reaches its maximum at the end of the light phase. Only the amplitude undergoes very small variations from one cycle to another. This explains why the order parameter is not higher than in the case of constant conditions: R = 0.53.
FIGURE 7.
Entrainment of the 10,000 coupled circadian cell system by a light-dark cycle (R = 0.53). The light-dark cycle is described by a square-wave forcing: L = 0 in dark phases and L = 0.01 in light phases. (A) Distribution of the individual periods. (B) Oscillations of X for 10 randomly chosen oscillators among a total of 10,000 oscillators. (C) Distribution of the periods in the coupled system. (D) Oscillation of the mean field, F. Parameter values are the same as in Fig. 1. Although the system displays a quasiperiodic behavior, the period and the phase of the oscillations are very well conserved. Only the amplitude undergoes very small variations. In B and D, the white and black bars indicate the light and dark phases, respectively.
The periodic forcing also decreases the phase spreading of the oscillators: the phase difference between the oscillators and the mean field is reduced with respect to the case of absence of light-dark forcing (compare curves DD and LD in Fig. 6). In particular, oscillators with a larger period are entrained with a very small phase delay with respect to the mean field, whereas oscillators with a small period display phase advances.
A driven fast-running population is phase-leading
The SCN is conceptually subdivided into two parts, the dorsomedial (DM) and the ventrolateral (VL) part, where different neurotransmitters are released. Results from Yamaguchi (19) raise the possibility that the global oscillatory output from DM part is damped because of a lack of synchrony between the cells when this area is isolated from the VL part, and that the synchrony is achieved through coupling to the VL part. On the other hand, because DM part is phase-advanced with respect to VL, they conclude that the DM part is the driving force.
To account for these specificities we study the interaction between two cell populations (Fig. 8). Each population is composed of 5000 cells. Based on Yamaguchi's results (19), we assume that the coupling is effective only in the first population (VL). Cells in the second population (DM) are not mutually coupled but entrained by the mean field resulting from the first population. Oscillations are self-sustained in both populations, but display a slight phase difference: the DM cells are phase-advanced ∼1 h with respect to the VL cells (Fig. 8 A). A necessary condition for obtaining a phase difference between the two populations is to have the average periods of the two populations slightly differ. In the case illustrated in Fig. 8 A, the mean periods of the two populations are 23.5 and 20 h. This prediction could have been already anticipated from Fig. 6, where it was shown that faster oscillators are phase-advanced with respect to the mean field.
FIGURE 8.
Interaction between two cell populations. Each population counts 5000 cells. Cells from the first population (VL part of the SCN, solid line) are coupled through the mean field they are producing (K = 0.5), whereas cells from the second population (DM part, dashed line) are uncoupled but entrained by the mean field from the first population. Taken individually, cells of both populations undergo limit cycle oscillations, but with a slightly different mean period: the mean periods are 23.5 and 20 h for the VL and the DM population, respectively. (A) Constant conditions. (B) VL cells are entrained by a light-dark cycle, simulated by a square-wave forcing, as in Fig. 7. Parameter values are the same as in Fig. 7. In B, the white and black bars indicate the light and dark phases, respectively.
Only VL cells are responsive to the light pathway. As in Fig. 7, we account for the effect of an LD cycle by applying a periodic forcing, L(t), describing the effect of light (see Eq. 1). Here again the oscillations in the DM part are entrained by the mean field of the VL part and present a small phase-advance with respect to the VL cells (Fig. 8 B).
DISCUSSION
The mechanism of synchronizing a population of circadian oscillators displaying disparate periods is an open and intriguing question. Generally, the dynamics of even a small number of coupled oscillators is extremely complex including toroidal oscillations, deterministic chaos, or coexistence of multiple attractors (31–33). This raises the question of how thousands of circadian oscillators can be synchronized in a robust manner.
Different approaches have been used to couple a population of circadian oscillators, from Winfree's phase oscillators (34,35) to phase-resetting oscillators (36). Closer to our work is the molecular model of Drosophila circadian clock by Ueda and co-workers (37). In this article, the authors studied a model for circadian rhythms in Drosophila. As a single cell oscillator, they used a more detailed model incorporating 10 variables. They then apply a local coupling through each possible variable, and show that for some of them, synchronization occurs. Interestingly, they assessed the effect of fluctuations in parameter values and show that the coupled system is relatively robust to noise. Another theoretical model of coupled circadian oscillators through local coupling has been proposed by Kunz and Achermann (38). Using the van der Pol model, they described possible spatial effects, including wave propagation and pattern formation.
In this article, we present a molecular model that accounts for the main properties resulting from the coupling of a population of circadian oscillators. In the SCN of mammals, among different possible coupling mechanisms, neurotransmitters have been suggested to play a crucial role. By assuming fast diffusion, we use the global neurotransmitter level to couple circadian oscillators.
Global coupling through such a mean field is efficient to synchronize a population of coupled circadian oscillators (Fig. 1), and better synchrony can be obtained by increasing the strength of the coupling. High synchrony is typically accompanied by a period lengthening. Therefore an optimal coupling strength for circadian rhythms is found when it is small enough to keep the period circadian and large enough to achieve synchronization (Fig. 4). A similar change in the period has been observed when we coupled other circadian oscillators through similar mechanisms (not shown), and also by other authors using a different approach for the global coupling (27). This property has been reported in experimental studies. Mice kept in a constant light condition exhibit a lengthening in their period of activity (28,39). In peripheral fibroblast cultures, increasing the serum concentration has been shown to decrease the period of the oscillations (29). Whether there are mechanisms to compensate period changes due to coupling in vivo is still an open question. Compensation is possible if the coupling acts not only on the transcription rate of the clock genes but also on other processes like protein degradation.
Bifurcation analysis of the single cell oscillator revealed that the coupling actually brings individual oscillators into a damped oscillatory domain (Fig. 3). In other words, if the mean field is kept constant, the oscillations dampen out to a steady state. Thus, in the coupled system, individual oscillators would be damped; however, the coupling through the mean field drives them into an oscillatory state. Period estimation from linear analysis of a single oscillator (Fig. 3 D) shows a good agreement with the period of coupled oscillators (Fig. 1 C), indicating that the observed period-lengthening is likely to be due to the intrinsic properties of the core oscillator rather than being a result of the type of coupling considered in this article.
The crucial role of damping to get the fast synchronization is shown as follows:
Increasing the mean value of F leads to a bifurcation from a limit cycle to a steady state.
In the synchronized state, the phase relations are uniquely determined by the period as known from periodically forced damped oscillators.
With a vanishing mean value of F and with a Hill coefficient n = 8, the oscillators are not damped. In these cases, the synchronization was much worse (not shown).
Together, these results suggest that fast synchronization is achieved when the oscillators would be damped.
In summary, we predict that the oscillations are damped by the constant component mean field and, consequently, that they are driven by the oscillatory component of the neurotransmitter concentration. These predictions could be tested experimentally by applying a constant concentration of a candidate coupling factor to isolated SCN cells. For a concentration level corresponding to the average level seen in the coupled system, circadian oscillations should dampen.
The phases of oscillators in the coupled system depend only on their individual periods (Fig. 6). After any transient perturbation, the initial phase is recovered. In particular, oscillators with shorter periods are, in the coupled system, phase-advanced with respect to the mean field, whereas oscillators with longer period are phase-delayed. This prediction can be verified by analyzing time-series of experiments such as those carried out by Yamaguchi (19). Our prediction is that the robust phase relations are governed by the individual periods of the cells (Fig. 6). This explains why cells recover their initial phase relationship after transient disruption of the coupling (Fig. 5). Moreover, resynchronization is fast and efficient because cells are acting like damped oscillators. This is in line with the experimental observation that Per1 and Per2 mutant mice synchronize rapidly to a light-dark cycle (40).
We simulated the effect of a light-dark cycle by square (Fig. 7) and sine (not shown) waves of the light-controlled parameter. In both cases such light-dark cycles entrain the oscillations. Despite the quasiperiodic nature of the behavior illustrated in Fig. 7, the phase and the period of the oscillations are highly precise.
To account for the two regions in the SCN, we studied the interaction between two populations of circadian oscillators (Fig. 8). We showed that a population composed of uncoupled cells can be synchronized by the mean field of the first population. Moreover, the phase-advance observed in the DM part with respect to the VL part can easily be explained if there is a slight difference in the mean periods of individual neurons in each part. To be phase-advanced, DM cells must oscillate with a slightly shorter average period than VL cells. This prediction from the model was confirmed recently (41).
In conclusion, we have introduced a molecular model for the regulatory network underlying the circadian oscillations in the SCN. Our findings proved that a mean field approach can be an effective way to couple a population of circadian oscillators and allows us to clarify the requirement for such an efficient synchronization: the global coupling drives oscillators, which would be damped under a constant forcing. A good synchrony is, however, always accompanied by a slight change of the resulting period. Compensation mechanisms will be the subject of future investigations. Several extensions can be considered. Our approach can be generalized to more detailed models, including ones with interlocked feedback loops, such as those recently published by Leloup and Goldbeter (42), Becker-Weimann and co-workers (43), or by Smolen and co-workers (23). Furthermore, a local coupling approach will be used to study the spatiotemporal cellular organization in the SCN. Further characterization of the SCN dynamics will benefit from the understanding of global coupling, which has already led to some confirmed predictions.
Note added in proof: More recently, Aton et al. (44) showed that the loss of vip in vip-/- mutants disrupted synchrony between rhythmic neurons and that a daily application of VPAC2 agonist restored synchrony
Acknowledgments
D.G. is Chargé de Recherches du Fonds National Belge de la Recherche Scientifique.
This work was supported by the Deutsche Forschungsgemeinschaft (grant SFB 618) and the European Union (Network Biosimulation, contract No. 005137).
References
- 1.Reppert, S. M., and D. R. Weaver. 2002. Coordination of circadian timing in mammals. Nature. 418:935–941. [DOI] [PubMed] [Google Scholar]
- 2.Moore, R. Y., J. C. Speh, and R. K. Leak. 2002. Suprachiasmatic nucleus organization. Cell Tissue Res. 309:89–98. [DOI] [PubMed] [Google Scholar]
- 3.Shirakawa, T., S. Honma, Y. Katsuno, H. Oguchi, and K. I. Honma. 2001. Multiple oscillators in the suprachiasmatic nucleus. Chronobiol. Int. 18:371–387. [DOI] [PubMed] [Google Scholar]
- 4.Welsh, D. K., D. E. Logothetis, M. Meister, and S. M. Reppert. 1995. Individual neurons dissociated from rat suprachiasmatic nucleus express independently phased circadian firing rhythms. Neuron. 14:697–706. [DOI] [PubMed] [Google Scholar]
- 5.Honma, S., W. Nakamura, T. Shirakawa, and K. Honma. 2004. Diversity in the circadian periods of single neurons of the rat suprachiasmatic nucleus depends on nuclear structure and intrinsic period. Neurosci. Lett. 358:173–176. [DOI] [PubMed] [Google Scholar]
- 6.Reppert, S. M., and D. R. Weaver. 2001. Molecular analysis of mammalian circadian rhythms. Annu. Rev. Physiol. 63:647–676. [DOI] [PubMed] [Google Scholar]
- 7.Hastings, M. H., and E. D. Herzog. 2004. Clock genes, oscillators, and cellular networks in the suprachiasmatic nuclei. J. Biol. Rhythms. 19:400–413. [DOI] [PubMed] [Google Scholar]
- 8.Kalamatianos, T., I. Kallo, H. D. Piggins, and C. W. Coen. 2004. Expression of VIP and/or PACAP receptor mRNA in peptide synthesizing cells within the suprachiasmatic nucleus of the rat and in its efferent target sites. J. Comp. Neurol. 475:19–35. [DOI] [PubMed] [Google Scholar]
- 9.Dardente, H., J. S. Menet, E. Challet, B. B. Tournier, P. Pevet, and M. Masson-Pevet. 2004. Daily and circadian expression of neuropeptides in the suprachiasmatic nuclei of nocturnal and diurnal rodents. Brain Res. Mol. Brain Res. 124:143–151. [DOI] [PubMed] [Google Scholar]
- 10.Shinohara, K., T. Funabashi, D. Mitushima, and F. Kimura. 2000. Effects of gap junction blocker on vasopressin and vasoactive intestinal polypeptide rhythms in the rat suprachiasmatic nucleus in vitro. Neurosci. Res. 38:43–47. [DOI] [PubMed] [Google Scholar]
- 11.Liu, C., and S. M. Reppert. 2000. GABA synchronizes clock cells within the suprachiasmatic circadian clock. Neuron. 25:123–128. [DOI] [PubMed] [Google Scholar]
- 12.Shirakawa, T., S. Honma, Y. Katsuno, H. Oguchi, and K. I. Honma. 2000. Synchronization of circadian firing rhythms in cultured rat suprachiasmatic neurons. Eur. J. Neurosci. 12:2833–2838. [DOI] [PubMed] [Google Scholar]
- 13.Shen, S., C. Spratt, W. J. Sheward, I. Kallo, K. West, C. F. Morrison, C. W. Coen, H. M. Marston, and A. J. Harmar. 2000. Overexpression of the human VPAC2 receptor in the suprachiasmatic nucleus alters the circadian phenotype of mice. Proc. Natl. Acad. Sci. USA. 97:11575–11580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Harmar, A. J., H. M. Marston, S. Shen, C. Spratt, K. M. West, W. J. Sheward, C. Morrison, J. R. Dorin, H. Piggins, J. C. Reubi, J. S. Kelly, E. S. Maywood, et al. 2002. The VPAC(2) receptor is essential for circadian function in the mouse suprachiasmatic nuclei. Cell. 109:497–508. [DOI] [PubMed] [Google Scholar]
- 15.Cutler, D. J., M. Haraura, H. E. Reed, S. Shen, W. J. Sheward, C. F. Morrison, H. M. Marston, A. J. Harmar, and H. D. Piggins. 2003. The mouse VPAC2 receptor confers suprachiasmatic nuclei cellular rhythmicity and responsiveness to vasoactive intestinal polypeptide in vitro. Eur. J. Neurosci. 17:197–204. [DOI] [PubMed] [Google Scholar]
- 16.Romijn, H. J., A. A. Sluiter, C. W. Pool, J. Wortel, and R. M. Buijs. 1996. Differences in co-localization between Fos and PHI, GRP, VIP and VP in neurons of the rat suprachiasmatic nucleus after a light stimulus during the phase delay versus the phase advance period of the night. J. Comp. Neurol. 372:1–8. [DOI] [PubMed] [Google Scholar]
- 17.Reed, H. E., A. Meyer-Spasche, D. J. Cutler, C. W. Coen, and H. D. Piggins. 2001. Vasoactive intestinal polypeptide (VIP) phase-shifts the rat suprachiasmatic nucleus clock in vitro. Eur. J. Neurosci. 13:839–843. [DOI] [PubMed] [Google Scholar]
- 18.Nielsen, H. S., J. Hannibal, and J. Fahrenkrug. 2002. Vasoactive intestinal polypeptide induces per1 and per2 gene expression in the rat suprachiasmatic nucleus late at night. Eur. J. Neurosci. 15:570–574. [DOI] [PubMed] [Google Scholar]
- 19.Yamaguchi, S., H. Isejima, T. Matsuo, R. Okura, K. Yagita, M. Kobayashi, and H. Okamura. 2003. Synchronization of cellular clocks in the suprachiasmatic nucleus. Science. 302:1408–1412. [DOI] [PubMed] [Google Scholar]
- 20.Schwartz, W., R. A. Gross, and M. T. Morton. 1987. The suprachiasmatic nuclei contain a tetrodotoxin-resistant circadian pacemaker. Proc. Natl. Acad. Sci. USA. 84:1694–1698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Goodwin, B. C. 1965. Oscillatory behavior in enzymatic control processes. Adv. Enzyme Regul. 3:425–438. [DOI] [PubMed] [Google Scholar]
- 22.Griffith, J. S. 1968. Mathematics of cellular control processes. I. Negative feedback to one gene. J. Theor. Biol. 20:202–208. [DOI] [PubMed] [Google Scholar]
- 23.Smolen, P., P. E. Hardin, B. S. Lo, D. A. Baxter, and J. H. Byrne. 2004. Simulation of Drosophila circadian oscillations, mutations, and light responses by a model with VRI, PDP-1, and CLK. Biophys. J. 86:2786–2802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Leloup, J. C., D. Gonze, and A. Goldbeter. 1999. Limit cycle models for circadian rhythms based on transcriptional regulation in Drosophila and Neurospora. J. Biol. Rhythms. 14:433–448. [DOI] [PubMed] [Google Scholar]
- 25.Ruoff, P., and L. Rensing. 1996. The temperature-compensated Goodwin model simulates many circadian clock properties. J. Theor. Biol. 179:275–285. [Google Scholar]
- 26.Ruoff, P., M. Vinsjevik, C. Monnerjahn, and L. Rensing. 2001. The Goodwin model: simulating the effect of light pulses on the circadian sporulation rhythm of Neurospora crassa. J. Theor. Biol. 209:29–42. [DOI] [PubMed] [Google Scholar]
- 27.Garcia-Ojalvo, J., M. B. Elowitz, and S. H. Strogatz. 2004. Modeling a synthetic multicellular clock: repressilators coupled by quorum sensing. Proc. Natl. Acad. Sci. USA. 101:10955–10960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ohta, H., S. Yamazaki, and D. G. McMahon. 2005. Constant light desynchronizes mammalian clock neurons. Nat. Neurosci. 8:267–269. [DOI] [PubMed] [Google Scholar]
- 29.Nagoshi, E., C. Saini, C. Bauer, T. Laroche, F. Naef, and U. Schibler. 2004. Circadian gene expression in individual fibroblasts; cell-autonomous and self-sustained oscillators pass time to daughter cells. Cell. 119:693–705. [DOI] [PubMed] [Google Scholar]
- 30.Aronson, D. G., G. B. Ermentrout, and N. Kopell. 1990. Amplitude response of coupled oscillators. Physica D. 41:403–449. [Google Scholar]
- 31.Bergé, P., Y. Pomeau, and C. Vidal. 1986. Order within Chaos: Towards a Deterministic Approach to Turbulence. Wiley, New York.
- 32.Grebogi, C., E. Ott, and J. A. Yorke. 1987. Chaos, strange attractors, and fractal basin boundaries in nonlinear dynamics. Science. 238:632–638. [DOI] [PubMed] [Google Scholar]
- 33.Glass, L., and M. C. Mackey. 1988. From Clock to Chaos. Princeton University Press, Princeton, NJ.
- 34.Winfree, A. T. 1967. Biological rhythms and the behavior of populations of coupled oscillators. J. Theor. Biol. 16:15–42. [DOI] [PubMed] [Google Scholar]
- 35.Winfree, A. T. 2002. Oscillating systems. on emerging coherence. Science. 298:2336–2337. [DOI] [PubMed] [Google Scholar]
- 36.Antle, M. C., D. K. Foley, N. C. Foley, and R. Silver. 2003. Gates and oscillators: a network model of the brain clock. J. Biol. Rhythms. 18:339–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Ueda, H. R., K. Hirose, and M. Iino. 2002. Intercellular coupling mechanism for synchronized and noise-resistant circadian oscillators. J. Theor. Biol. 216:501–512. [DOI] [PubMed] [Google Scholar]
- 38.Kunz, H., and P. Achermann. 2003. Simulation of circadian rhythm generation in the suprachiasmatic nucleus with locally coupled self-sustained oscillators. J. Theor. Biol. 224:63–78. [DOI] [PubMed] [Google Scholar]
- 39.Daan, S., and C. S. Pittendrigh. 1976. A functional analysis of circadian pacemakers in nocturnal rodents. III. Heavy water and constant light: homeostasis of frequency? J. Comp. Physiol. [A]. 106:267–290. [Google Scholar]
- 40.Steinlechner, S., B. Jacobmeier, F. Scherbarth, H. Dernbach, F. Kruse, and U. Albrecht. 2002. Robust circadian rhythmicity of Per1 and Per2 mutant mice in constant light, and dynamics of Per1 and Per2 gene expression under long and short photoperiods. J. Biol. Rhythms. 17:202–209. [DOI] [PubMed] [Google Scholar]
- 41.Noguchi, T., K. Watanabe, A. Ogura, and S. Yamaoka. 2004. The clock in the dorsal suprachiasmatic nucleus runs faster than that in the ventral. Eur. J. Neurosci. 20:3199–3199. [DOI] [PubMed] [Google Scholar]
- 42.Leloup, J. C., and A. Goldbeter. 2003. Toward a detailed computational model for the mammalian circadian clock. Proc. Natl. Acad. Sci. USA. 100:7051–7056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Becker-Weimann, S., J. Wolf, H. Herzel, and A. Kramer. 2004. Modeling feedback loops of the mammalian circadian oscillator. Biophys. J. 87:3023–3034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Aton, S. J., C. S. Colwell, A. J. Harmar, J. Waschek, and E. D. Herzog. 2005. Vasoactive intestinal polypeptide mediates circadian rhythmicity and synchrony in mammalian clock neurons. Nat. Neurosci. 8:476–483. [DOI] [PMC free article] [PubMed] [Google Scholar]