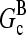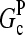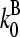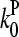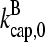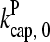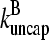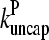The Effect of Branching on the Critical Concentration and Average Filament Length of Actin

Abstract

The dependences of the steady-state critical concentration and average filament length of actin solutions, on the filament branching and capping rates, are calculated using a rate methodology based on the total number of actin filaments. The methodology generalizes calculations of the “treadmilling” actin concentration at which an average filament has net zero growth rate. The predictions of the rate methodology are validated by comparison with stochastic-growth simulations that track the positions of all filament subunits over time. For side branching, the critical concentration drops proportionally to the square root of the branching rate; for end branching the drop is linear. The polymerization response to branching has a maximum as a function of the capping-protein concentration. The average filament length drops with increasing branching, because the critical concentration drops. Even small rates of filament uncapping have a large impact on the average filament length in vitro. The potential significance of these phenomena for cell behavior is evaluated.

INTRODUCTION

The motility of cells, the formation of protrusions such as filopodia and lamellipodia, and the motions of intracellular pathogens, are strongly influenced by extracellular or intracellular factors that stimulate actin polymerization (1,2).

One channel by which actin polymerization can be stimulated is the activation of Arp2/3 complex, a seven-subunit complex of actin-related proteins that can bind to an existing filament and initiate a new branch at the binding site. The newly generated filaments have “barbed” and “pointed” ends, with rapid growth taking place at the barbed ends. The pointed ends are attached to Arp2/3 complex. Arp2/3 complex is constitutively inactive, but can be activated by several intracellular proteins. The activation path can be direct, as in the case of the ActA bacterial surface protein, or proceed via a signaling cascade ending in interactions between Arp2/3 complex and proteins such as those of the Wasp/Scar family (2,3). Filament growth is limited, and an adequate supply of free monomers maintained, by the presence of capping proteins that block the filaments' barbed ends from assembly (4). Capping, however, can be suppressed by the presence of membrane-bound phosphoinositides such as PIP₂, which thus act as polymerization stimulants. Arp2/3 complex also caps pointed ends (5). At present there is no quantitative understanding of the extent of polymerization or changes in filament length caused by Arp2/3-complex-induced branching. Although there have been numerical modeling studies of actin polymerization in vitro in the presence of Arp2/3 complex and capping protein (6,7), there is no straightforward mathematical formula that gives the extent of polymerization or the filament lengths in terms of the relevant protein concentrations, either in vitro or in vivo.

This article takes a first step toward a quantitative understanding of the polymerization response to branching by calculating the critical concentration and average filament length in a simple model of actin polymerizing in vitro. The analysis treats steady-state properties, as might be obtained by allowing a polymerization experiment to run for a long time. Understanding the steady-state properties is a prerequisite for understanding the dynamics, and some of the phenomena thus elucidated will also be present in the dynamic behavior of cells. The model includes polymerization/depolymerization, branching/debranching, and capping/uncapping effects. It is based on a simple rate equation expressing the constancy of the number of filaments in steady state. Within this framework, balancing filament “birth” rates from branching and “death” rates from debranching and depolymerization fixes the critical concentration, which in turn determines the average filament length. The filament length enters the calculation self-consistently because it affects the filament birth and death rates.

Using this model, we develop formulas for the critical concentration and average filament length in terms of the relevant rate parameters. The formulas are backed up by stochastic growth simulations using rate parameters obtained from recent fits to kinetic data. This work has three main goals. First, to obtain a general understanding of branching polymerization that may be transferable to cellular processes, and may be used to make predictions that can be experimentally tested. Second, to establish relationships between the extent of polymerization and filament lengths on one hand, and rate parameters on the other hand, which can be used in combination with in vitro experiments to measure or constrain the rate parameters. Third, to develop key inputs for mathematical modeling of whole-cell behavior based on spatially varying concentrations of actin and related proteins, for example, as applied recently to keratocytes (8); if such modeling studies incorporate the mechanical properties of the actin network, the filament length is also an important input.

The organization of the remainder of the article is as follows. The next section defines the model. Subsequently, we derive the steady-state relation for the filament number, calculate the average filament length in terms of the free-actin concentration, and combine these results to obtain an analytic expression for the critical concentration. We then validate the analytic theory by comparing its predictions with simulation results. Next we discuss the limits of the model used. Finally, we conclude the article with a discussion of the potential significance of the results for actin polymerization in vitro and in vivo.

MODEL

Our model describes the structure of actin in solution with activated Arp2/3 complex and capping protein, having concentrations [Arp2/3] and [CP], respectively. A simplified solution of this model has previously been used to study the dynamics of actin filament cluster sizes (9). The processes included in the model are filament polymerization/depolymerization, capping/uncapping, and branching/debranching. Polymerization is described by a net barbed end polymerization rate 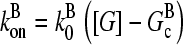and a net pointed-end depolymerization rate 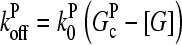(measured in subunits per second), where 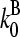and 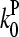are concentration-independent rate parameters, and [G] is the free-monomer concentration. 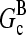is the barbed-end critical concentration, at which the barbed-end on- and off-rates cancel; 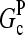is defined similarly for the pointed end. Both 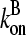and 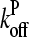are positive, because 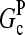is known to be larger than 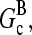and [G] is between 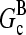and 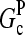in steady state. Capping is described by barbed- and pointed-end capping and uncapping rates 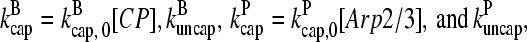where 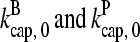are rate parameters. The effects of capping are conveniently summarized by the parameters 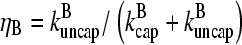and 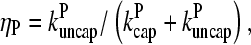which give the equilibrium probabilities for the barbed and pointed ends of a filament, respectively, to be uncapped; the net steady-state growth and depolymerization rates are then 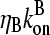and

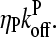
Branching in vitro occurs mainly along filament sides, as shown by several studies (7,10–12). Therefore, our calculations focus mainly on side branching, which is described by a branching rate per filament subunit:

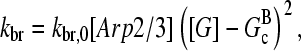(1)

where k_{br, 0} is a rate parameter and the power of two is taken from a recent kinetic analysis (7). Because branching in cells is often restricted to regions very near the plasma membrane, we also include calculations for end branching, in which k_br is the branching rate per filament; it is taken to have the same functional form as the side branching rate. Debranching, either spontaneous or induced by actin-severing proteins such as ADF/cofilin, is described by the average time τ_dis required for a branch to dissociate. Initiation of branching polymerization requires the “de novo” nucleation of at least one seed filament that does not grow from a preexisting filament. However, in steady state such nucleation effects are small in comparison with branching, because their rates are very low. Therefore, we ignore de novo filament nucleation processes. Severing, also ignored, is potentially more important; this is discussed below under “Critique of model”.

Analytic theory of critical concentration and filament lengths

The extent of polymerization in steady state is determined by the critical concentration G_c, which is the maximum concentration of free actin that can remain unpolymerized indefinitely. In the absence of rapid filament nucleation, G_c is nearly equal to the “treadmilling” concentration G_tr at which polymerization of barbed ends is precisely balanced by depolymerization of pointed ends, both in their equilibrium capping states. Balancing these rates at [G] = G_tr, one obtains

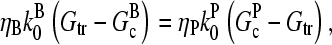(2)

so that

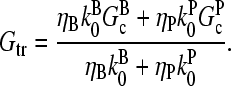(3)

When [G] = G_tr, the change in a filament's length over time is parallel to that of an unbiased random walker moving in one dimension with an absorbing boundary. The random walker is unbiased because forward (increasing length) steps are as likely as backward (decreasing length) steps, and the absorbing boundary corresponds to filaments disappearing when they reach a very short length corresponding to the critical nucleus size. The average displacement for such a walker, before being absorbed, is infinite (13). Therefore, in the absence of severing, the steady-state average filament length will be infinite when [G] = G_tr.

However, in the presence of rapid filament nucleation caused by branching, the time-averaged capping states of the filament ends will differ from the equilibrium values. When a filament is “born”, for example, it is capped at the pointed end and uncapped at the barbed end. If the time for it to reach the equilibrium capping state is a sizeable fraction of the filament lifetime, the critical concentration will differ noticeably from G_tr. We account for this effect by balancing filament creation and destruction rather than polymerization and depolymerization of single filaments. We envisage the following filament “life cycle”: a daughter filament is created as a branch on a mother filament. Its barbed end then becomes capped. Next, the daughter filament dissociates from the Arp2/3 complex on the mother filament. Finally, it depolymerizes.

The steady-state properties implied by this life cycle can be obtained by writing the time rate of change of the total number of filaments N as a sum of creation and destruction terms (9):

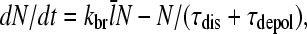(4)

where 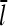is the average number of subunits per filament. The first term on the right-hand side follows from the definition of k_br as a branching rate per filament subunit. The second term states that the destruction of a filament involves first dissociation from the mother filament, which takes time τ_dis, and subsequently depolymerization, which takes time τ_depol. Thus, the steady-state condition for G_c, dN/dt = 0, implies that

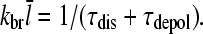(5)

This result uniquely determines G_c. The left-hand side increases with [G], because k_br increases according to Eq. 1, and 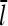will be enhanced by the increasing on-rate. The right-hand side decreases with increasing [G], because the increasing value of 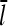and decreasing off-rate cause τ_depol to increase. Therefore, there is only one value of [G] at which the right- and left-hand sides are equal.

One might ask whether or not this analysis gives a constant number of subunits in filaments (the total number of polymerized subunits), as it must for a system in steady state. In fact, both the number of subunits in filaments and the number of filaments are constant. The method underlying the analysis is the calculation of a steady-state filament length distribution, in which both of these quantities are constant. We employ the state-state condition for the number of filaments because it gives the simplest mathematical formulation.

Of the four variables in Eq. 5, the [G]-dependence of k_br is given by Eq. 1, and τ_dis is taken to be independent of [G]. However, the [G]-dependences of 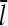and τ_depol are more complex, and are calculated in the next subsection.

Dependence of l̄ and τ_depol on [G]

In the presence of barbed- and pointed-end capping, there are four species of filaments: uncapped, barbed-end capped, pointed-end capped, and capped at both ends. A previous analysis of the filament length distribution of uncapped filaments (14) showed that this distribution decays exponentially as a function of length, and the average filament length is inversely proportional to the difference between the on- and off-rates. Here, we generalize this analysis by calculating 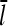with a kinetic model containing transitions between both different filament lengths and different capping states. To keep the subsequent calculation of G_c from becoming too complicated, we treat only the two barbed-end capping states explicitly; the pointed end is taken to be in an average capping state defined by η_P, the probability of its being uncapped.

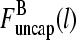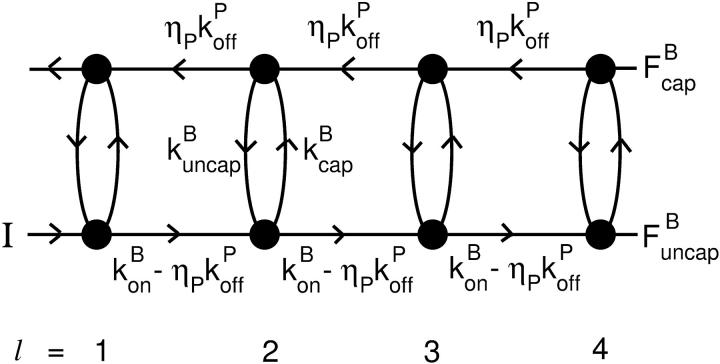
The two filament populations are and 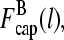which describe the numbers of filaments of length l, uncapped and capped at the barbed end, respectively. The critical nucleus size of actin is several subunits (15,16), and in principle only l-values greater than or equal to this critical size should be included. However, because actin filament lengths are typically 100 subunits or more, the results are not changed substantially if l-values down to 1 are allowed; this simplifies the calculations. At first, we ignore the time τ_dis during which the filament is attached to its mother filament. The rate equations correspond to the flow chart in Fig. 1:

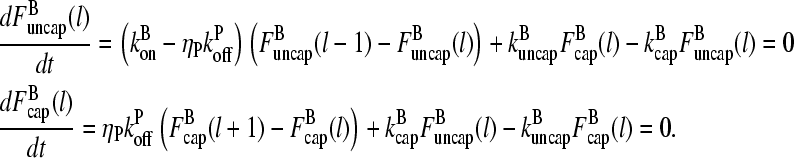(6)

FIGURE 1.

Schematic of rate equation model for two capping-state system (Eq. 6). Uncapped filaments 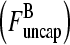enter at the point labeled I and grow at a rate 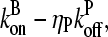until they become capped. Capped filaments 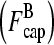shrink at a rate 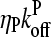or become capped. Capping and uncapping rates are 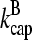and 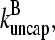respectively.

Here 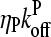is the average off-rate at a filament pointed end, and 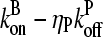is the average net on rate for a filament whose barbed end is uncapped. By treating only barbed-end polymerization and pointed-end depolymerization, these equations ignore fluctuations resulting from cancellation of polymerization with depolymerization at each end. The very high affinities of capping proteins (17) imply that in most cases η_B < η_P, so [G] will not be too close to 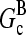; this implies that the barbed-end fluctuations will be small. The pointed-end fluctuations are less important because the filament length is set during the extension phase, when barbed-end growth dominates.

The rate equations are difference equations with constant coefficients. Because there are two first-order equations, there are two linearly independent solutions. The standard approach to solving such equations is to search for solutions of the form

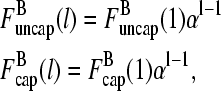(7)

where α is a constant. If two distinct values are obtained for α that lead to solutions of the difference equations, then these are the only solutions (18). Inserting Eq. 7 into Eq. 6, and dividing by α^l−1, gives

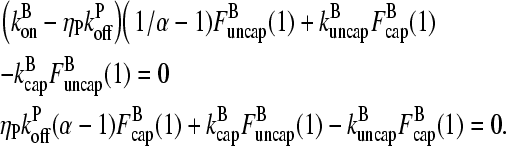(8)

Because the average filament contains many subunits, the filament populations will decay slowly with l, which means that α is close to unity. Therefore, we assume that 1 − α ≡ δ ≪ 1, and thus 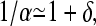so that

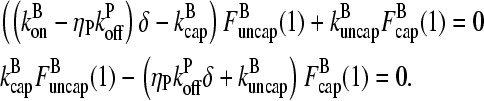(9)

This system of equations will have nonzero solutions for 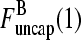and 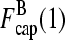only if the determinant of the matrix

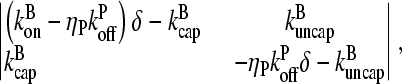(10)

vanishes. The solutions are readily seen to be δ = 0 and

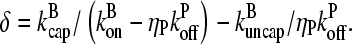(11)

Because they are distinct, we have found all of the solutions of the problem. The δ = 0 solution is unphysical because it leads to an infinite number of filaments.

For the average filament length, we then obtain:

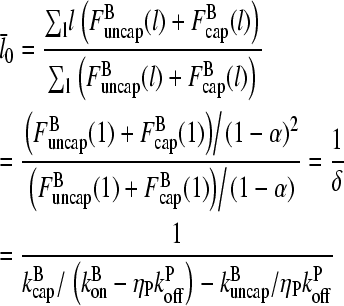(12)

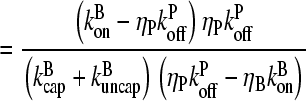(13)

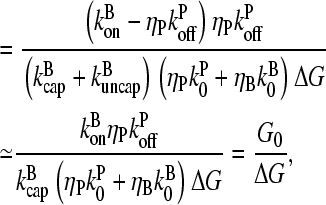(14)

where 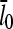is the value of for vanishing τ_dis,

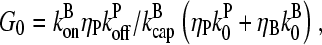(15)

and ΔG = G_tr − [G] is the deviation of [G] from G_tr, which is caused by branching. The approximations made in the last equation, ignoring 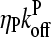relative to 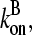and 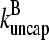relative to 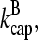are justified because the high affinity of capping proteins ensures that 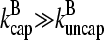; as mentioned above, G_c is not too close to 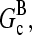which implies that 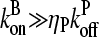. The 1/ΔG dependence of 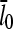is consistent with the previous result (14) that 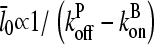for uncapped filaments, because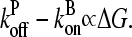

Increasing the branching rate will stimulate polymerization, thereby increasing ΔG and decreasing 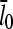. Thus, the effect of branching on 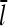is mediated by its effect on ΔG, rather than being direct. Under Discussion, we will show that 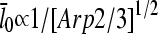for side branching and 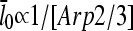for end branching, and evaluate the consequences of these dependences.

The average filament lifetime after debranching, τ_depol, can be obtained from the same rate equations (still taking τ_dis = 0). We envisage a flow I of newly created filaments with free barbed ends entering at the point 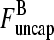(1); defining τ_depol by dN/dt = I − N/τ_depol, we have τ_depol = N/I in the steady state. Balancing the currents coming in and out of the entry point 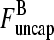(1) (cf. Fig. 1) gives

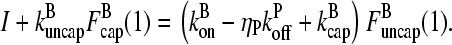(16)

This equation can be solved for 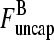(1) by noting that the ratio 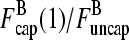(1) is fixed by the eigenvector of the matrix (10) corresponding to the nonzero solution for δ. Straightforward calculation shows that this eigenvector satisfies

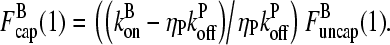(17)

Thus

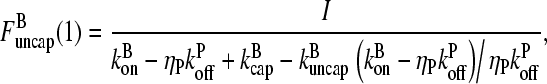(18)

so that

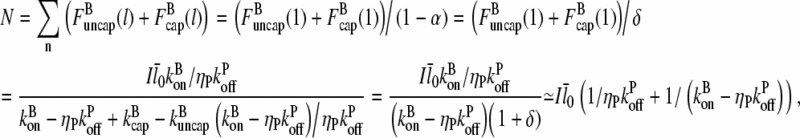(19)

where the last step holds because δ ≪ 1. Then

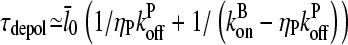(20)

Again using the fact that 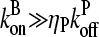in most cases, we have

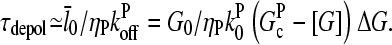(21)

For τ_dis ≠ 0, 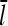increases by an amount 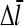equal to the number of subunits that are added to the filament's barbed end before it detaches from the mother filament:

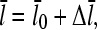(22)

where

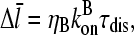(23)

and τ_depol does not change with τ_dis, because it describes the lifetime after dissociation.

Self-consistent calculation of G_c

We now solve Eq. 5 using the [G]-dependences derived above, at first ignoring τ_dis. We express G_c in terms of ΔG: G_c = G_tr − ΔG. Inserting Eqs. 1, 14, 15, and 21 into Eq. 5 yields

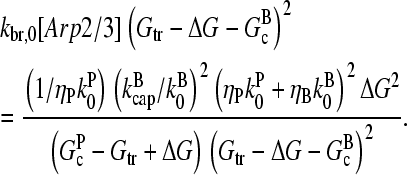(24)

This equation gives rise to a fifth-order polynomial equation for ΔG, which can be solved numerically. However, our main purpose is to obtain an analytic result that can be readily interpreted. For this reason, we develop a simplified expression valid for low branching rates, by ignoring ΔG in comparison with 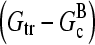and 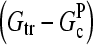in the terms where they appear together. This yields

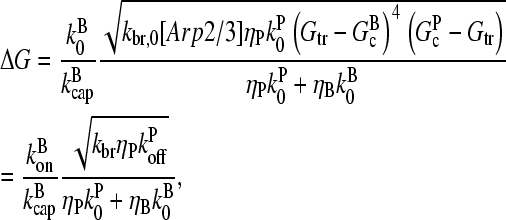(25)

where k_br, 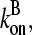and 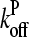are evaluated at [G] = G_tr.

The main feature of this result is that ΔG is proportional to 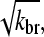and thus to [Arp2/3]^1/2 for small [Arp2/3]. This dependence results from the combination of the 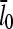factor in the denominator of the left-hand side of Eq. 5, and the proportionality of τ_depol on its right-hand side to 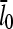. It is thus robust to deviations from the assumed [G]-dependence of k_br. The physical origin of the 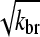dependence is as follows. For the number of filaments to be constant, each filament must on the average generate one daughter filament before being depolymerized. A doubling of ΔG would correspond to halving the filament length, according to Eq. 14; this would in turn halve the filament lifetime according to Eq. 21. Because the number of daughter filaments formed by a given filament is proportional to its length and its lifetime, a fourfold increase in k_br would be required to keep this number constant. The same argument predicts a linear dependence of ΔG on k_br for end branching, because the factor of 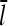on the left-hand side of Eq. 5 would be absent.

We now include the effects of nonzero τ_dis, but assume that τ_dis ≪ τ_depol. In Eq. 5, τ_dis appears directly, and also indirectly through the dependence of 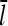(and thus τ_depol) on τ_dis. Including 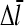(cf. Eq. 22) in Eq. 5, together with Eq. 21, gives

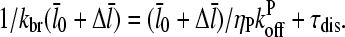(26)

Using Eq. 14 to express 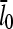in terms of ΔG, letting k_br and 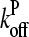take their values for [G] = G_tr, expanding both sides of Eq. 26 to first order in τ_dis (recalling that 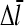is linearly proportional to τ_dis), and multiplying both sides by ΔG, we obtain

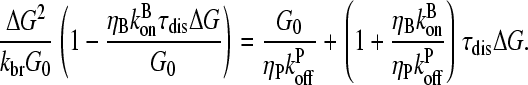(27)

Solving this equation to first order in τ_dis, and using Eq. 15, gives

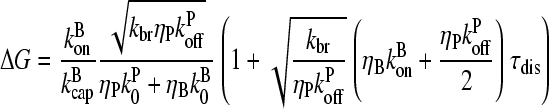(28)

Thus, increasing τ_dis increases ΔG, because a filament's pointed end remains capped until it dissociates, and this lowers G_c.

We now analyze the end-branching case briefly. Using Eq. 21, Eq. 5 with τ_dis = 0 becomes

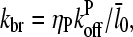(29)

where k_br is the branching rate per filament. Following the same approach as above for small ΔG, Eq. 25 becomes

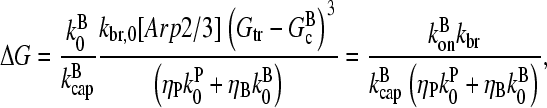(30)

where k_br and 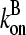are again evaluated at [G] = G_tr. As expected, ΔG varies linearly with k_br instead of as 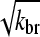; at small [Arp2/3], this gives ΔG ∝ [Arp2/3].

Inclusion of a nonzero τ_dis in a fashion parallel to that for side branching yields

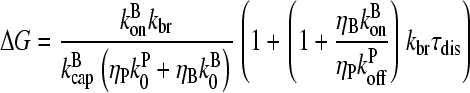(31)

Comparison of analytic theory with stochastic-simulation results for side branching

The stochastic simulations use a methodology used previously to treat actin filament clusters in solution (9). The coordinates of all filament subunits are stored over time. Isolated filaments nucleate slowly in random directions at random points in space, and subsequent growth, depolymerization, capping, uncapping, branching, and debranching events are treated stochastically. New branches appear on randomly chosen filament subunits, at an angle of 70° to the mother filament (although in bulk polymerization the branch geometry does not affect the filament length or critical concentration). Interactions between subunits on distinct filaments, corresponding to steric exclusion, are ignored because of the low volume fraction of actin at typical in vitro concentrations. Polymerization removes free monomers from solution, and depolymerization replaces them. The simulations treat cubic regions of edge length 5 μm, containing up to ∼150,000 actin monomers. The rate parameters are obtained from previous kinetic fits (7), and are given in Table 1.

TABLE 1.

Parameter values

Parameter	Value	Source
	0.07 μM	(7)
	0.69 μM	(7)
	8.7 μM−1s−1	(25)
	1.3 μM−1s−1	(26)
	8.0 μM−1s−1	(7)
	0.80 μM−1s−1	(7)
	4.2 × 10−4 s−1	(7)
	0.0018 s−1	(7)
kbr,0	5.4 × 10−4μM−3s−1	(7)

To evaluate G_c, one could gradually ramp up the total actin concentration (the free-actin concentration at the beginning of the simulations) until polymerization begins. However, this procedure gives a very slow convergence of the concentration to G_c, and also gives noisy 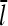results, because of the small number of filaments present. For this reason, we instead treat a system of 2 μM total actin, in which [CP] and [Arp2/3] have values scaled up by a factor of 100, and their corresponding on-rates 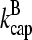and 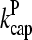are scaled down by a factor of 100. This results in a “linearized” calculation, in which [CP] and [Arp2/3] are effectively constant during the polymerization runs despite most of the actin being polymerized. G_c and 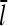are then obtained as time averages over the last half of each run, and the runs are taken long enough that both properties have stabilized at that point. Additional statistical averaging is performed by repeating each run 10 times, with different starting seeds for the random-number generator. This leads to statistical uncertainties of ∼0.002 μM in G_c and 2% in 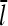. This procedure gives the same G_c and 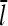results as the ramping-up procedure, but is more computationally convenient.

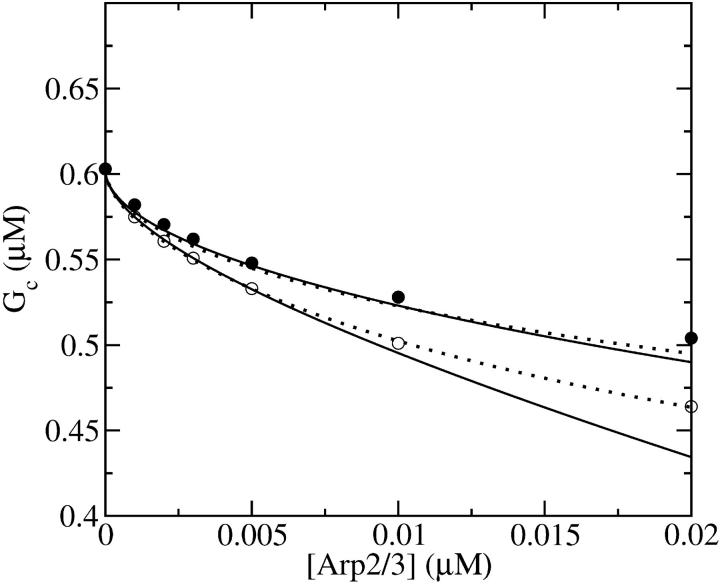
Figs. 2 and 3 show the dependence of G_c on [Arp2/3] for [CP] = 2 nM. Because 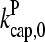is not precisely known, we perform runs for both 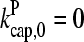and the value from Table 1, which is plausible but not quantitatively accurate. The results for 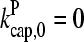(Fig. 2) are shown for both instantaneous debranching (solid circles) and an in vitro debranching rate of 0.0018 s⁻¹ (open circles) derived (7) from fitting microscopy data for debranching (19). For both cases, the agreement between the analytic result of Eq. 28 and the numerical results is excellent. The full numerical solution of Eq. 24 (dotted lines) gives still closer agreement with the simulations. Fig. 3 shows corresponding results using 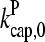from Table 1; the dashed line denotes G_tr. Again, the results for small [Arp2/3] are quite accurate. At larger [Arp2/3], ΔG (the difference between the dashed line and the simulation points) is overestimated by ∼40%, because the decrease in k_br due to decreasing [G] is not included in our approximate solution of Eq. 24.

FIGURE 2.

Effect of increasing Arp2/3 complex concentration [Arp2/3] on critical concentration G_c of actin solution. Capping protein concentration [CP] = 2 nM. Pointed-end capping effects are ignored. (•) Simulation results for τ_dis = 0. (○) Simulation results for τ_dis = 0.177 s⁻¹. (Solid lines) Analytic theory (Eq. 28) for τ_dis = 0 and τ_dis = 0.177 s⁻¹, respectively. (Dotted lines) Numerical solution of Eq. 28 for τ_dis = 0 and τ_dis = 0.177 s⁻¹.

FIGURE 3.

Effect of increasing [Arp2/3] on critical concentration of actin solution with pointed-end capping. [CP] = 2 nM. (•) Simulation results. (Solid line) Analytic theory (Eq. 28) for τ_dis = 0. (Dashed line) Treadmilling concentration G_tr.

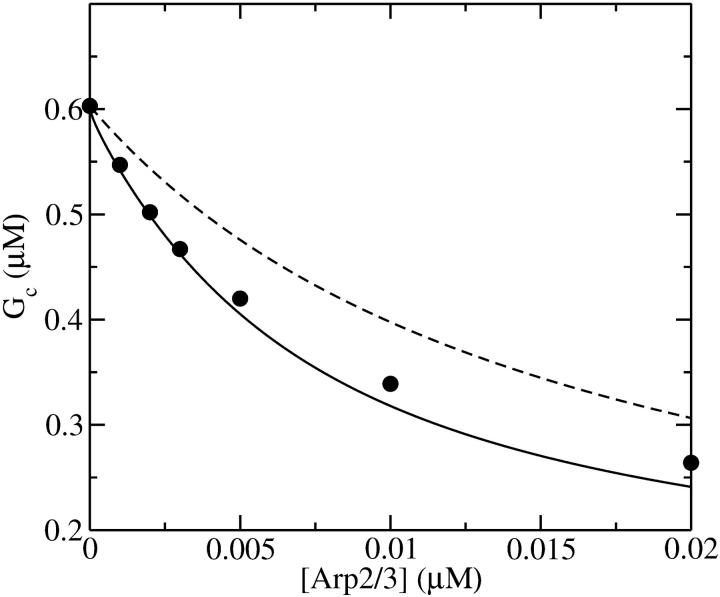
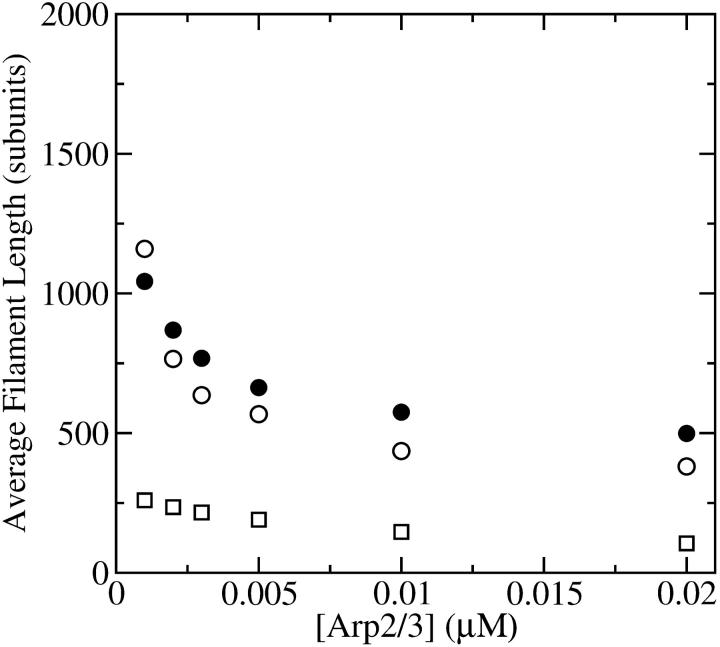
Figs. 4 and 5 compare the analytic theory with simulation results for the dependence of 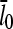on [Arp2/3], again using 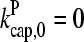as well as the value from Table 1. To correspond as closely as possible to an experiment in which G_c is measured, at each value of [Arp2/3] we use the simulation value of G_c when calculating the on and off rates entering 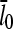. It is seen that the agreement between the theory and simulations is close for both values of 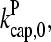with errors of <25%. The squares in Figs. 4 and 5 give the values of 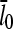that are obtained in the absence of uncapping effects. The significance of the uncapping effects for filament lengths is treated more fully under Discussion.

FIGURE 4.

Effect of increasing [Arp2/3] on average filament length of actin solutions without pointed-end capping. (•) Simulation results. (○) Analytic theory (Eq. 13) using critical concentrations obtained from simulations. (□) Average filament length l_cap (Eq. 37) in absence of uncapping.

FIGURE 5.

Effect of increasing [Arp2/3] on average filament length of actin solutions, with pointed-end capping. (•) Simulation results. (○) Analytic theory (Eq. 13) using critical concentrations obtained from simulations. (□) Average filament length l_cap (Eq. 37) in absence of uncapping.

Critique of model

Here, we discuss the significance of the main approximations made in our model, namely the neglect of filament severing and the possibility that k_{br, 0} decays over time as filaments age.

Severing

Severing is closely analogous to side branching, in that new filaments are generated from an existing filament at a rate proportional to the filaments' length; the rates are thus both defined per filament subunit per second. The spontaneous severing rate is believed to be ∼10⁻⁸ s⁻¹ (20). A rough estimate of the relative importance of severing can be obtained by evaluating the value of [Arp2/3] at which the severing rate equals the value of k_br. If we take a typical value of [G] to be 0.4 μM, roughly halfway between 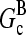and 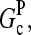straightforward calculations based on Eq. 1 and the rate constant in Table 1 show that [Arp2/3] = 0.17 nM when k_br = 10⁻⁸ s⁻¹. On the scale of Figs. 2–5, this value is essentially at the origin. Therefore, spontaneous severing may safely be ignored. However, several actin-binding proteins, such as ADF/cofilin, are known to accelerate filament severing. Their effects will be significant if the rate of generation of new filaments by severing is comparable to that from branching. In cells, the severing rate is probably less than the branching rate at the cell membrane. If it were not, filaments would sever in the time it takes them to move a branch spacing, and the cortical actin network would contain only one layer of branches; observed cortical actin networks contain many layers. Thus, the effects of severing should not greatly affect our subsequent discussion of branching at membranes.

Nonuniformity of branch distribution

Recent real-time fluorescence-microscopy studies of branching (10,11) have shown that although branches can occur everywhere along a filament, they are more frequent near the barbed end. To account for this, a modification of the side-branching model, in which the capacity of filament subunits to form new side branches diminishes as filaments age, has been proposed (10,11). This suggestion has been supported by an analysis of polymerization data by kinetic simulations (7), which gave an aging time of ∼110 s. We have not found a simple way of including this effect in our analytic theory. However, we have performed a few simulation runs using a parameter set in which k_br,0 decays with filament age, and a correspondingly larger starting value of k_br,0 is used to compensate for the reduced branching of older filaments. The calculated G_c values are within 0.02 μM of those obtained without aging. This suggests that increasing the starting k_br,0 accounts fairly accurately for the effects of aging in vitro. If branching were highly localized near the barbed end, terms treating the interaction of Arp2/3 complex and capping protein would be needed in the model. However, the real-time branching studies do not provide evidence for such a high degree of localization.

In cells, aging at the in vitro rate would not affect branching significantly, because filament subunits branch mainly when they are in close proximity to the cell membrane. At typical intracellular on-rates (21), a subunit will remain in such close proximity for <1 s, much less than the in vitro aging time. However, if aging is greatly accelerated by actin-binding proteins such as ADF/cofilin, the effects could be important.

We also note that the calculation of the filament length at a given value of [G] is not affected by the aging, because the length depends only on the on- and off-rates.

DISCUSSION

The main results of our analysis are Eqs. 14, 28, and 31. Here we use these results to propose experiments to validate the model treated here, to develop hypotheses regarding actin polymerization in cells, and to design in vitro experiments that shed light on the branching process and allow the measurement of key parameters.

Validation of model

Direct validation of the model, for example, by measuring the extent of polymerization as a function of [Arp2/3], is difficult because of the dual functions of Arp2/3 complex in capping pointed ends and generating new branches, and also because of uncertainties in several key rate parameters. However, the dependence of 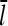on [Arp2/3] and [CP], for large [CP], can be obtained in a form simple enough to be tested by biochemical measurements. Our calculations show that the criterion of large [CP] is fulfilled if [CP] > 2 nM and [CP] > 4[Arp2/3]. Under these conditions, η_B and thus 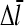(cf. Eq. 23) are small, so we take 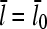. Combining Eqs. 14, 15, and 25, we then obtain

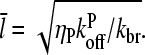(32)

To calculate 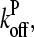we note that according to Eq.3, 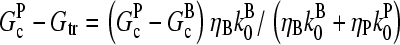; if [CP] is large, 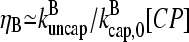and the 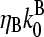term in the denominator can be ignored, so 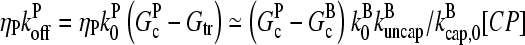. To calculate k_br, we note that for large [CP], G_tr is close to 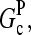and we thus take 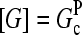in Eq. 1. Inserting these results into Eq. 32, we obtain

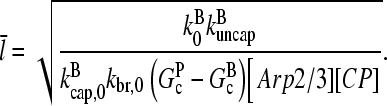(33)

This result has a simple dependence on [Arp2/3] and [CP]. Although the values of the rate parameters entering Eq. 33 are uncertain, the form of this dependence can be compared directly with experiment. For example, if both [Arp2/3] and [CP] are doubled, the measured filament length should decrease by 50%. If either one or the other is doubled, the length should decrease by 30%.

Effect of [CP] on response to Arp2/3 activation

The strength of the response of an actin solution or cell to Arp2/3 complex activation depends on [CP] in a way that can be estimated from the above results. Considering first the effect of pointed-end capping, the response of the cell (assuming that Arp2/3 complex activation enhances pointed-end capping) can be described by the function dG_tr/dη_P. This quantity is positive, because an increase in η_P will lead to depolymerization and thus increased G_tr. Using Eq. 3 shows that

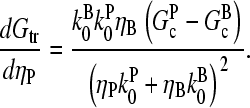(34)

This function has a maximum at 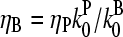; because 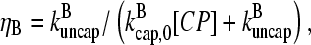this corresponds to an optimal value of [CP]. To understand the origin of this effect, we note that for very large values of [CP], capping pointed ends causes little incremental polymerization because there are few free barbed ends. For very small values of [CP], so much of the actin is already polymerized that capping pointed ends has little further effect.

The response to branching along filament sides in vitro behaves similarly. For small values of [Arp2/3], using the proportionalities 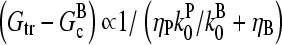and 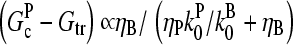in Eq. 28 yields 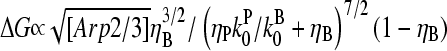; taking η_B ≪ 1 in view of the high [CP] binding affinity gives

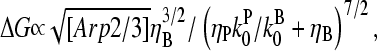(35)

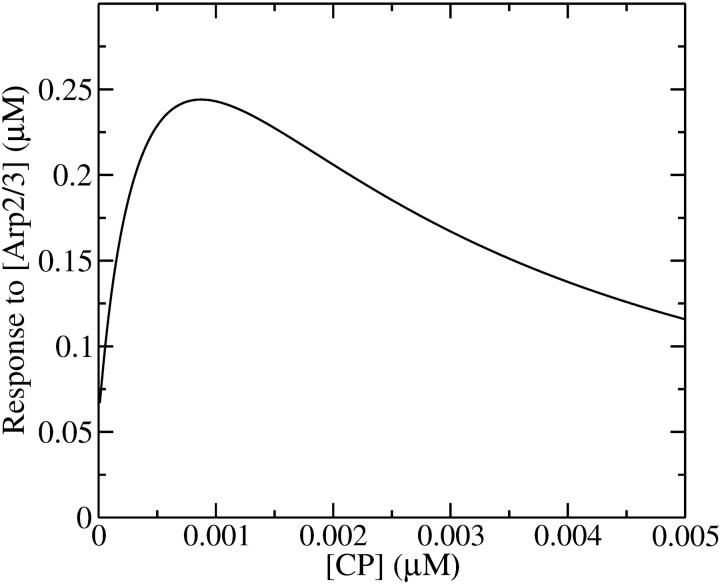
which has a maximum at 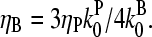This phenomenon is illustrated in Fig. 6, which shows the change in the polymerized-actin concentration (the opposite of the change in G_c) induced in our side-branching model with pointed-end capping by 0.005 μM Arp2/3 complex, as a function of [CP]. The well-defined maximum at [CP] = 0.0008 μM is consistent with the above expectations. Thus, the response of an actin solution to Arp2/3 complex activation is strongest at an optimal value of [CP].

FIGURE 6.

Effect of [CP] on response of G_c to [Arp2/3], defined as G_c([Arp2/3] = 0) − G_c([Arp2/3] = 0.005 μM). Pointed-end capping is included.

This phenomenon should also occur in cells. The stimulation received by a cell is not constant over time. But the characteristic timescale of the polymerization-depolymerization processes is probably not much greater than the filament lifetime τ_dis + τ_depol, which turnover measurements (22) suggest to be ∼20 s. If a stimulus is applied for this length of time or longer, our steady-state analysis may be relevant. New branch formation occurs mainly near filament ends at the cell membrane. Thus, the end branching analysis is appropriate. Eq. 31 yields, in analogy with Eq. 35,

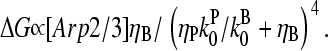(36)

This has a maximum at 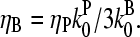When the pointed-end capping effect is added to branching, we expect the optimal value of 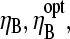to be between the values obtained for branching and pointed-end capping: 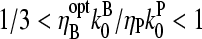; using 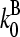and 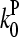from Table 1 gives 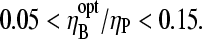To compare this prediction with cellular values of 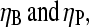we note that the capping and uncapping rate parameters in Table 1 give binding affinities of 2 nM for Arp2/3 complex at pointed ends, and 0.05 nM for CP at barbed ends. If we assume that [CP] is a few times smaller than [Arp2/3] in cells (21), we obtain 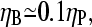consistent with the above range. Thus, it is possible that the values of [CP] in cells are influenced by their need to respond strongly to Arp2/3 complex stimulation.

The existence of an optimal [CP] value for response to branching stimulation may be related to measurements of the motion of Listeria bacteria in pure-protein media (23). These bacteria are partly coated with the ActA protein, which stimulates actin filament branching by activating Arp2/3 complex. The measurements show a velocity maximum as a function of [CP]. Insofar as the motion of the bacterium involves a polymerization response to the branching stimulus provided by activating Arp2/3 complex, the maximum of our calculated polymerization response to Arp2/3 complex activation could be connected with the maximum of the Listeria velocity. Because these experiments used solutions containing ADF/cofilin, we are not able to estimate the optimal value of [CP] for their conditions.

The magnitude of ΔG at cell membranes

The value of k_br to use when applying Eq. 31 to cells is not known. However, the formation of branches roughly every 20 subunits in typical lamellipodial networks (24) suggests that 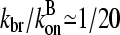. Concentration estimates available for cells (21) suggest that [G] 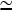100 μM and [CP] 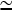1 μM. Using the rate parameters in Table 1, we obtain 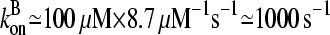and 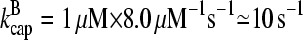. A lower bound for ΔG is obtained if we take η_B = 1. In the absence of τ_dis, Eq. 31 then yields 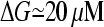; inclusion of the τ_dis term and a more realistic value of η_B would further increase ΔG. The value 20 μM is too large for this theory to accurately predict, but the calculation shows that the effect of branching on G_c is very large. Thus, the branching in the immediate vicinity of the membrane leads to a much lower critical concentration than in the cell interior.

End versus side branching in vitro

The dependence of the filament length on [Arp2/3] provides a direct comparison between the predictions of end and side branching. For side branching, combining Eqs. 14, 22, and 28 shows that for sufficiently small [Arp2/3] (where the τ_dis terms in Eqs. 22 and 28 are small by comparison with the other terms), 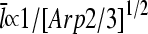. A similar argument shows that 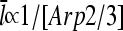for end branching. Measurements of the dependence of 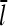on [Arp2/3] could thus provide useful information with regard to the geometry of new branch formation, supplementing existing analysis based on polymerization kinetics and direct observation of branch formation.

Effect of uncapping on filament lengths

In the absence of barbed-end uncapping effects (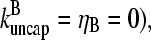 Eq. 13 reduces to

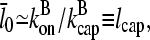(37)

where we ignore the 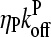term in comparison with 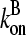. This is the relation resulting from a simple picture in which a filament grows until it is capped, and then depolymerizes. Dividing the numerator and denominator of Eq. 13 by 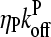gives

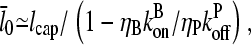(38)

so that the denominator captures the corrections from uncapping effects. Figs. 4 and 5 compare 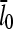with l_cap, and show that even for the rate of only 0.0004 s⁻¹ used here, uncapping can increase 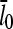under in vitro conditions by a factor of three or more. The increase in 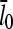results from intermittent uncapping of filaments, which has been observed in fluorescence microscopy studies of filament growth in vitro (5). The effect on filament lengths seen in these experiments was smaller than that predicted here, probably because the timescale of the experiments was too short for steady state to be reached.

We do not have enough information about rate parameters to evaluate the extent of the uncapping corrections in vivo. However, we can estimate the critical value of 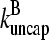required to cause a substantial increase in 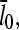which from Eq. 38 (taking η_B ≪ 1) is 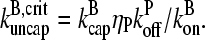The values of η_P and 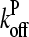in the cellular environment are not known. However, Eq. 21 implies that 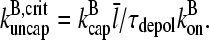Typical filament lengths in branched networks near cell membranes are a few tenths of a micron, which corresponds to 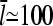; as mentioned above, the filament lifetime is ∼20 s, which implies that τ_depol < 20 s. Thus, using the above values of 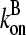and 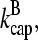we obtain 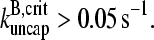This is much faster than the spontaneous uncapping rate of 0.0004 s⁻¹ given above, consistent with the general expectation that spontaneous uncapping is unimportant in cells. However, cell membranes contain uncapping agents, such PIP₂, which might uncap at such high rates.

Evaluation of filament end binding properties from measured filament lengths

Equations 22 and 38 show that the filament length is determined by the on- and off-rate parameters, the “open” fractions η_B and η_P, and τ_dis. For small [Arp2/3], ΔG is small, so that 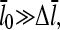and one can take 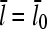. The rate parameters entering Eq. 38 are known. Therefore, measurements of 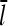could be used to determine the ratio 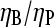in vitro. Rough estimates of η_B exist, and these could be used to determine η_P, and thus give a new way to evaluate the binding affinity of Arp2/3 complex to pointed ends. With the ratio 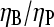established, one can also evaluate G_tr from Eq. 3, which will be useful below.

Evaluation of branching rate parameter from measured ΔG

With G_tr determined as above, ΔG can be obtained from measured values of G_c. If [Arp2/3] is sufficiently small, then η_P in Eq. 28 can be replaced by unity, and the τ_dis term can be ignored. Further, η_B can be obtained from the above-described measurement of 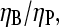so all of the terms entering ΔG are known except for k_br,0. Therefore, this parameter could be evaluated from the measured ΔG.